Flexible Ostinati, Groove, and Formal Process in Craig Taborn’s Avenging Angel*
Antares Boyle
KEYWORDS: Craig Taborn, repetition, ostinato, groove, meter, cycle, jazz
ABSTRACT: Repetition in the music of pianist/composer Craig Taborn engenders diverse temporal experiences at both local and global scales. At the local level, distinctive repetitions that I term flexible ostinati share significant features with the cyclic materials often observed in groove-based musics: they comprise a repetitive, omnipresent stream within the overall texture, provide a rapid isochronous pulse, and imply higher-level metric levels. However, they differ from strict ostinati or the repetitions that Anne Danielsen (2006) terms “basic groove units” in their flexibility at the rhythmic/metric level of temporal experience. This flexibility manifests in two ways: in the material domain, flexible ostinati are often varied significantly across repetitions, while in the interpretive domain, they simultaneously suggest multiple possibilities for pulse, meter, or cyclic beginning/ending. Following Danielsen, who describes groove as emerging from interactions between sounding rhythm and a reference structure, I examine the potential reference structures (meter and cycle) suggested by Taborn’s flexible ostinati. These structures are never fixed, but instead must be constantly negotiated, resulting in engaging grooves that draw the listener into the music’s temporal matrix. I analyze three pieces from Taborn’s 2011 solo album, Avenging Angel, to demonstrate how, across longer stretches of time, diverse forms grow out of these ostinati: “The Broad Day King” layers a surface-level flexible ostinato against slower background cycles that gradually reveal themselves; “Avenging Angel” is structured by the juxtaposition of two contrasting ostinati; and a brief passage in “Neverland” features an elusive groove that dissolves almost as soon as it materializes.
DOI: 10.30535/mto.27.2.6
Copyright © 2021 Society for Music Theory
Introduction
[1.1] Recently, music scholarship has shown a renewed interest in repetition (e.g., Margulis 2014; Butler 2014). One burgeoning area is the analysis of how popular music’s “grooves”—short cyclic materials that repeat continuously throughout a piece or section—create a song’s unique temporal feel and participate in or subvert larger formal processes and structures (Hughes 2003; Danielsen 2006; Butler 2006; Attas 2015; Danielsen 2018). Research on rhythmic feel or “groove” in jazz has traditionally focused more on microrhythmic analysis and/or player interaction than on overt pattern repetition, but cyclic and quasi-cyclic repetition can play as important a role in jazz as it does in other African-American genres such as funk (Logan 1984). The music of contemporary jazz pianist/composer Craig Taborn provides many examples. Below I analyze three pieces from Taborn’s 2011 solo album, Avenging Angel, to show how distinctive repetitions, which I term flexible ostinati, engender diverse groove experiences and underscore larger formal processes.
Definitions and Context
Craig Taborn, Avenging Angel, and Analysis of Improvised Music
[2.1.1] Craig Taborn (b. 1970) is a pianist, composer, and improviser who has performed on more than one hundred albums. Like many artists considered “jazz” musicians by audiences and media, Taborn finds the genre label limiting: he prefers the term “Black improvisational tradition” (Shatz 2017, [6]). Avenging Angel, Taborn’s only solo album, is expansive in range; the excerpts I discuss below represent only a small subset of its stylistic references, techniques, and moods. The album, which was recorded in a single session in 2010 and released in 2011, consists of thirteen improvised tracks. Unlike many improvisations based on an underlying composition, these do not exist in any other studio versions, nor have I found any live recordings that seem to share significant source material with any of the three pieces I discuss in this essay.(1) For this reason, I treat the album’s recorded tracks as autonomous objects of analysis.
[2.1.2] The act of analyzing musical improvisations—and particularly the decision to treat an improvised jazz performance as a musical “work”—has been criticized (Brownell 1994; Monson [1996] 2009). Detractors often cite the distinction between product, the traditional object of musical analysis, and process, the creative and social act by which that product comes to be, and which is foregrounded in improvisational arts.(2) In extreme cases, such perspectives may deny the relevance of structure and organization (properties of musical works that are the traditional concern of analysis) to the aesthetic value of improvised music, despite significant evidence that musicians themselves see these domains as one side of a productive dialectic between constraint and freedom.(3) For instance, in a revealing conversation with collaborator Camille Norment (2020, ¶ 23), Taborn states, “as much as there is this will toward controlling and structuring things in the music-making improvisational act, I try to allow certain elements their own sort of informational life.” Elsewhere, describing a revelation he had upon listening to a recording of a freely improvised concert, Taborn says, “the improvised performances sounded as organized as any of my composed pieces, and they had so much more life” (Shatz 2017, ¶ 29). Both of these comments reveal Taborn’s desire for a balance between structure/organization and the unexpected or spontaneous elements that can give an improvisation “life.”(4) Frustrations with reductive views of improvisation may be behind some artists’ wish to distance themselves from the term. For instance, Taborn remarks (referencing conversations with Vijay Iyer and alluding to the perspective of Wadada Leo Smith), “there is a certain crew of musicians who are done with the term improvisation. . . . Invoking that term brings with it this weight of associations that distance it from other practices, and I don’t think that really functions today” (Norment and Taborn 2020, [28])
[2.1.3] Two substantive concerns with the analysis of music from the Black improvisational tradition should be noted and addressed. First, academic musical analysis has traditionally foregrounded Eurocentric romantic and modernist aesthetic ideals of unity and coherence, and its discourse has often presented analytical readings as authoritative and fixed (Monson [1996] 2009, 134–39). Even as North American music theory is moving away from these outdated models,(5) analysts should remain vigilant in trying to avoid such pitfalls. While my analyses do highlight aspects of unity or coherence I hear in the music, they argue more fundamentally that multiplicity—a refusal of fixity—is essential to its character. For this and other reasons to be elaborated on below, I do not claim them to be authoritative.
[2.1.4] Second, “work-based” analyses tend to privilege the temporal level of the single piece or performance, which in the case of some African diasporic improvised music may be an artificial construction that is less relevant than shorter or longer time spans. As Vijay Iyer writes:
The story that an improvisor tells does not unfold merely in the overall form of a “coherent” solo, nor simply in antiphonal structures, but also in the microscopic musical details, as well as in the inherent structure of the performance itself. The story dwells not just in one solo at a time, but also in a single note, and equally in an entire lifetime of improvisations (Iyer 2004, 295).
Analysts of groove have developed methods that attend effectively to shorter time spans; some of these are described in the next section. The absence of a larger context, however, can be more problematic. Iyer argues that improvisers are more interested in “making improvisations relate to each other” than creating coherence within a particular improvisation. And as several musicologists have noted, analysts who remain laser focused on an individual performance or musician may fail to recognize elements of a broader musical style, not to mention the construction of social and cultural meaning (Wilson 1990; Walser 1993; Floyd 1996; Givan 2014). Any analysis of individual improvisations such as those I provide below, then, should be considered only one piece of a larger puzzle. Our understanding of Taborn’s music will be enhanced by further analytical encounters with his own music, as well as that of his contemporary jazz peers and collaborators (for instance, pianists such as Vijay Iyer and Kris Davis) and influences (such as Sun Ra or Wadada Leo Smith).
[2.1.5] Regardless of their broader context, Taborn’s pieces may be experienced as standalone musical works. One can listen to the album’s tracks individually and return to them again and again for further listening and study; this is indeed how I encountered and grew to know the music addressed in this essay. My analyses are written from the perspective of a devoted record listener, not a performer or live concert attendee, and thus represent only one potential analytical angle. I was, however, able to interview Taborn during the late stages of this project.(6) While our discussion took place too late to shape my analysis, I include some of Taborn’s remarks on his creative process to counterbalance my “outsider” perspective.
[2.1.6] One final point bears emphasis: although I use transcriptions to illustrate points throughout this essay, the object of my analysis is the recording, and I do not intend to claim any notation as definitive. All my transcriptions should be read as analytical acts, each of which conveys only one potential hearing of an infinitely richer sounding music (Stanyek et al. 2014; Rusch, Salley, and Stover 2016).
Theorizing Groove
[2.2.1] The term “groove” has long been used by jazz musicians to describe an essential yet elusive aspect of their performances.(7) In her landmark ethnographic study, Ingrid Monson (Monson [1996] 2009) identifies two meanings for it. The first, a noun, denotes the “rhythmic feel” of a performance or “swing”; (8) what Monson’s interviewee Jerome Harris calls a “rhythm matrix” (67). The second meaning is typically constructed as a verb or a gerund (grooving) and refers to “a rhythmic relation or feeling that exists between two or more parts or individuals”; musicians interviewed by Monson describe it as a “euphoria” (Don Byron) or a “trance” (Michael Carvin). Monson emphasizes that this aspect of groove is “emotional and interpersonal” (68) and is often described with social metaphors (93). Similarly, Paul Berliner defines “striking a groove” as the “negotiation of a shared sense of beat” or as “defining and maintaining a solid rhythmic ground for . . . musical explorations” (1994, 349, 389). Other definitions of groove, intended to encompass African-American music genres beyond jazz, identify more specific rhythmic features. Iyer (2002, 397) defines groove as “a steady, virtually isochronous pulse that is established collectively by an interlocking composite of rhythmic entities and is either intended for or derived from dance.”(9)
[2.2.2] Much of the research on groove in jazz music has been inspired by Charles Keil’s ([1987] 1994) theory of participatory discrepancies (PDs) and has focused on microrhythmic features such as swing ratios and asynchrony between parts or band members (Rose 1989; Ellis 1991; Prögler 1995; Collier and Collier 2002; Benadon 2006; Honing and de Haas 2008). Under this approach, researchers typically work with precise timing data captured with the assistance of software. They then often highlight the interactive and collective strategies emphasized by Monson, Iyer, and Berliner (Doffman 2009a; 2009b).(10)
[2.2.3] Matthew Butterfield notes that “Keil and other PD theorists have tended to discount the effect of syntactical pattern—by which I mean only the specific ostinato pattern that makes up a given rhythmic groove—for the production of engendered feeling in jazz and other groove-based musics” (2006, ¶ 4).(11) Butterfield’s categories of “syntactical” and “sub-syntactical” could also be termed “rhythmic/metric” and “microrhythmic,” invoking Justin London’s proposed threshold of ~100 ms as a rough boundary. For London, this duration is “the shortest interval that we can hear or perform as an element of a rhythmic figure” and thus the lower limit for meter (2012, 27). Butterfield notes that dismissing the relevancy of the syntactical (rhythmic/metric) level for groove counterintuitively implies that the types of rhythmic patterns that distinguish specific genres—which themselves “offer different potentials for expressive movement, and. . . for participatory discrepancies”—are irrelevant. In a recent literature survey on groove, Schmidt Câmara and Danielsen (2018) identify five rhythmic features associated with groove, four of which (regular beat, subdivision of the beat, counter-rhythm, and syncopation) are at the rhythmic/metric level.(12)
[2.2.4] More consistent attention has been given to the rhythmic/metric level in pop music groove scholarship, in which groove is often linked explicitly with cyclic repetition at that level. In an influential and wide-ranging study on the music of Stevie Wonder, Timothy Hughes (2003), in addition to providing microrhythmic data, describes features ranging from local syncopations and “autotelic” grooves to cyclic phrase structures. Hughes clarifies that “a figure is not a groove unless it is designed to be repeated” (2003, 14). For Hughes, such repetitions stimulate an aesthetic experience he terms “flow.” In his book on electronic dance music, Mark Butler offers two definitions of groove that roughly correlate with Hughes’s “groove” and “flow”: “1. a short configuration of bass line and percussion that unfolds in continuously repeating cycles. 2. the way in which the rhythmic essence of a piece of music flows or unfolds” (2006, 326). Butler describes common rhythmic features of repeating loops, such as “diatonic rhythms”—maximally even, nonisochronous patterns—and their role in a metric experience that rewards active listener participation (2006, 98–116). Anne Danielsen (2006), in analyses of funk grooves by James Brown and Parliament, devotes equal time to microrhythmic and rhythmic/metric features. One example of the latter is a technique she terms “counter-rhythm”: a careful balance between syncopation and full cross-rhythm (2006, 70). Robin Attas (2015), in a study of groove in buildup introductions, focuses exclusively on the rhythmic/metric level, identifying features such as “metric polyphony” and “anacrustic cueing.” Danielsen and Attas, like Hughes and Butler, identify both material and experiential components of groove.
[2.2.5] We might understand the role of music analysis as a mediation between the two sides of the groove coin: an attempt, in other words, to describe how repetitive musical material gives rise to particular rhythmic or affective experiences such as Byron’s “euphoria” or Carvin’s “trance.” Much of the literature on groove seeks to further tease out and name these elusive subjective aspects. Of the many associations discussed, I find two particularly relevant to the music I discuss in this essay: (1) the pleasurable urge to embody musical rhythm and/or move to music, and (2) a present-focused temporal experience grounded in the in-time experience of expert performance.(13) In our conversation, Taborn spoke of associating “groove” with repetition that is “static, but moving.”(14) The foundational importance of motion or dance is common to many definitions of groove (e.g., Iyer 2002, 397), while Monson’s description of groove-as-verb—an action in progress—locates this embodied meaning in ongoing temporality. Other aspects of groove, such as the interactions among ensemble members emphasized by Monson, Hughes, and Iyer, are less pertinent to my listener-based analysis of Taborn’s solo piano music.(15)
Example 1. The ostinato in “Bodies We Come Out Of” (Craig Taborn, Light Made Lighter), with two possible higher-level grouping interpretations
(click to enlarge and listen)
[2.2.6] Contemporary jazz often features repetitions at the rhythmic/metric level that resemble the groove materials discussed by pop scholars. For instance, in the track “Bodies We Came Out Of” from Taborn’s 2001 trio album Light Made Lighter (with Gerald Cleaver and Chris Lightcap), the piano ostinato shown in Example 1 cycles continuously for the entire five-minute track. The groove is fleshed out by the drums, which initially clarify the eighth-note subdivisions and 2+3 grouping before becoming more independent, and the bass, which sometimes accompanies the ostinato. The ostinato’s features are essential to the groove’s rhythmic character: it creates a distinctive lilt, bouncing off each shorter/lower tone to land and suspend momentarily on a higher/longer tone. Meanwhile, its pitch patterns lend themselves to multiple higher-level interpretations, as illustrated in the example. Ascending lines in the lower pitches of each pair create two-measure groups, suggesting a sentence-like 2+2+4 phrase structure. Alternatively, hearing the recurring F2–D3 pair in mm. 1, 4, and 7 as a group onset brings out a 3+3+2 pattern that cuts against the duple interpretation (lower set of brackets). This multiplicity of temporal structures calls to mind the experiential effects described by the pop scholars above.
[2.2.7] Inspired by the explicit ostinato-like repetitions in Taborn’s music and their metric effects, my analyses below attend to the rhythmic/metric level, and I understand the grooves to have both material and experiential components. In adopting this outlook, I do not deny the potential relevance of other analytical methods or perspectives on groove. Rather, in that much contemporary jazz features repetitive cycles that resemble pop grooves, I hope that my analysis might help to close the distance between the two fields by bringing analysis of groove across genres into closer dialogue.
Meter and Reference Structures
[2.3] Writers on groove and swing have often linked their rhythmic qualities to a tension between novel events and some kind of reference structure, whether the latter be pulse, meter, a recurring riff or ostinato, or even a musical quotation or topic. Samuel Floyd, evoking Henry Louis Gates’s (1988) concept of “Signifyin(g),”(16) writes, “When sound-events Signify against the time-line, against the flow of its pulse, making the pulse itself lilt freely—swing has been effected” (Floyd [1991] 2002, 57). Central to Floyd’s concept is a kind of give-and-take: rhythmic events do not only push “against” the underlying time-line or pulse, they also fundamentally change it. More recently, Guilherme Schmidt Câmara and Anne Danielsen have written:
Rhythm as experienced always represents an interaction between virtual reference structures and actual sounding rhythmic events. This interaction works in two directions: a groove always generates some form of reference structure, and reference structures are always applied to a groove. It evokes the relationship between meter and rhythm as described by London (2012), who understands meter as all or some aspects of the structure provided by endogenous processes in the perception of rhythm, and rhythm as the exogenous, sounding aspect of this interaction (Schmidt Câmara and Danielsen 2018, 273).
In other words, the playful dialogue between sound events and the time-line described by Floyd may resemble (if not map precisely onto) the relationship between rhythm and meter, so long as meter is understood to be flexible and generated by musical events, rather than rigid and pre-determined. Many theorists consider metric experience key to the groove aesthetic (Pressing 2002; Butler 2006; Butterfield 2006; Butterfield 2010; Attas 2015). In accordance with this, my analyses probe the production and experience of meter, viewing this as a continuous and dynamic process of negotiation. For this purpose, I understand “meter” to be a hierarchy of beat levels to which a listener entrains based on periodic or roughly periodic events, as proposed by theorists such as Maury Yeston (1976), Fred Lerdahl and Ray Jackendoff ([1983] 1996), and Justin London (2012).(17) More recently, theorists such as Danuta Mirka (2009), Nancy Murphy (2015), and Kristina Knowles (2016) have combined aspects of these models with elements from Christopher Hasty’s (1997) processive theory of meter in order to highlight the experience of finding and maintaining meter as an essential and rewarding part of a listener’s rhythmic experience. Meter is one (although not the only) potential “reference structure” in Schmidt Câmara and Danielsen’s sense: it is generated by the sounding rhythms, yet also determines how those rhythms are perceived.(18)
Flexible Ostinati
[2.4.1] The grooves analyzed in the remainder of this essay all feature repetitive materials that I term flexible ostinati. These repetitions are characterized by significant flexibility at the rhythmic/metric level in either or both of the material and experiential domains, or “what is played” (Taborn’s performance) and “what is heard/felt” (a listener’s interpretation).(19) Although a true distinction between these domains is impossible, the loose categories are useful for explanatory purposes. In the material/performance domain, Taborn often varies repetitions significantly and continuously, sometimes to the point where the repetition does not create a distinct unit with clear boundaries. In the experiential/interpretation domain, due to rhythmic complexity or variation, these repetitions often do not articulate a single clear meter. These features distinguish flexible ostinati from basic cyclic repetitions (recall Example 1), in which a “basic groove unit” (Danielsen 2006) with unambiguous meter repeats more-or-less exactly.
[2.4.2] Nevertheless, flexible ostinati groove in a way that rewards attention to the rhythmic/metric level and to both meter and cyclic material as potential reference structures. Three essential features of flexible ostinati establish this groove:
- They comprise a repetitive, omnipresent stream within the overall texture of a passage or piece.
- Their durations imply an unambiguous, isochronous, metronomic fastest pulse layer, known as the “density referent.”(20)
- Features such as repetition and accent act as higher-level grouping mechanisms within the ostinato, suggesting cycle and/or meter, even if varied or irregular.
The first feature renders the ostinato foundational to a passage’s overall aesthetic, allowing for Iyer’s “interlocking of rhythmic entities” to arise between the ostinato and the other parts. The second promotes entrainment, essential for an embodied experience of musical rhythm, and creates an unbroken continuity that is key to groove’s temporal presence.(21) The third feature hints at the kind of cyclic groove unit familiar from instances like Example 1, and also suggests possible metric interpretations. In combination, these characteristics invite listeners to search continuously for meter or something resembling a “basic groove unit” as potential reference structures.
Form in Groove- and Ostinato-Based Music
[2.5] Several scholars have examined the forms generated by repetitive groove-based pop music, often focusing on processes of textural change as elements are added or removed from the repeating cycle (Attas 2015; Butler 2006, 202–55). Danielsen (2018, 46–47) describes the typical “dramaturgy” of groove-based music, with “consecration” and “winding down” phases surrounding a long exposition of the groove itself. Not all repetition-based forms are predicated on processes of intensity change, however. Recent analyses of variable cycles by John Roeder and Michael Tenzer, in music from wide-ranging cultures, demonstrate an array of formal procedures. For instance, Roeder (2019) shows how cyclic duet partners vary their respective repetitions in response to one another, creating formal contrast, broad trajectories, and rhythmic processes that point beyond the repeating cycle. Roeder and Tenzer (2014) analyze how large-scale formal processes emerge in ostinato-based music, including through transformation of the ostinato itself. My analyses demonstrate similar variety in Taborn’s groove-based music, showing how larger forms and processes arise through variation in a flexible ostinato, through the juxtaposition of two contrasting grooves, or through the layering of flexible cycles at different time scales.
[2.6] I inquired of Taborn whether he began the performances on Avenging Angel with a large-scale design or process in mind, and he assured me that in most cases he did not. “It’s really an improvised album in that sense,” he explained, intended to “document engaging in that process.” Most of the performances were based on “kernel information”: small-scale materials or general compositional ideas, such as an intervallic process or pulse concept, which would then be explored in combination. By eschewing preconceived formal designs, he hoped to avoid being “led to the same places all the time.” In this sense, the large-scale processes I describe in my analysis can be viewed as growing organically out of the materials themselves, perhaps in unexpected and spontaneous ways.(22)
“The Broad Day King”
Example 2. “The Broad Day King,” beginning (0:05–0:33)
(click to enlarge and listen)
[3.1] In the album’s opening track, “The Broad Day King,” a deceptively simple ostinato—a single upper-register pitch that repeats in a few basic durations—persists for the entire piece. Example 2 shows a transcription of the beginning with the ostinato on the upper staff. (The transcription adds rehearsal numbers for reference purposes; other notational decisions will be discussed shortly.) Taborn settles into a consistent texture, in which the onsets of sustained chords align with ostinato pitches, at rehearsal 1. The rhythm of the ostinato in this excerpt is typical of the piece: it freely combines durations of eighth, quarter, and dotted quarter notes, with longer durations sounding only infrequently. Without any regular grouping or repeated pattern, the ostinato’s metric implications are ambiguous: it provides a clear density referent (the eighth), two options for a tactus duration (the quarter or dotted quarter), and no higher-level grouping. The airy ostinato seems to float above the music rather than ground it, a sensation supported by its high register. The repetition lacks the defining feature of a typical ostinato: there is no precisely repeated melodic or rhythmic pattern, no identifiable cycle with a beginning and an end.
Example 3. “The Broad Day King,” 0:12–0:33, quarter-note pulse, Orientation 1
(click to enlarge and listen)
Example 4. “The Broad Day King,” 0:12–0:33, quarter-note pulse, Orientation 2
(click to enlarge and listen)
[3.2] It is difficult to transcribe the music in a way that conveys its full range of rhythmic effects. The bar lines and implied tactus values of Example 2 convey one kind of hearing: that of a listener open to flexible tactus lengths and inclined to hear the harmonic arrivals that begin at rehearsal 1 as “downbeats,” as indicated by the solid bar lines that precede them. (The dashed bar lines respond loosely to features such as rhythmic parallelisms and durational accents in the ostinato, but are intended primarily to aid readability and convey a general sense of “measuredness,” not to advocate strongly for a particular interpretation.) The transcription notably does not convey the slight, persistent sense of syncopation that results from an attempt to hear a continuous isochronous pulse in either quarter or dotted-quarter values. My own hearing hovers somewhere in between these two temporal listening strategies. The unpredictability of the ostinato’s onsets registers as something like a gentle syncopation, perhaps felt against a simple quarter-note pulse; however, if asked to identify the phase of that pulse—i.e., to decide which notes are onbeats and which offbeats—I would struggle to settle on an interpretation. To demonstrate, Example 3 and Example 4 renotate the music starting just before rehearsal 1 to suggest two possible phases of a continuous quarter-note pulse. In the figures, bar lines have been removed and all syncopations against the quarter-note pulse are indicated with tied eighth notes. While my hearing aligns more closely with Example 3, in which most of the chordal onsets are interpreted as occurring on beats, I can also entertain the more syncopated orientation of Example 4, in which the ostinato consists primarily of gentle, stylistic offbeats.(23) Although the majority of my transcriptions maintain the notational style of Example 2, which is somewhat easier to read, they should be taken to represent only one aspect of the music’s multifaceted metric implications.
[3.3] The ostinato is flexible in both its material performance (its precise durations) and its interpretation (the period and phase of its beats), creating a loose but ever-present flow. The form of “The Broad Day King” is driven not by the ostinato itself, but by the unfolding of cyclic materials at a much slower time scale. Nearly all of the track’s melodic and harmonic content derives from the simultaneous presentation of two interval cycles, which produces a sequence of dyads (see, e.g., Perle 1977). Two separate interval cycle pairings result in what I refer to as “primary” and “secondary” dyad series. The remainder of my analysis describes these cycles, showing how their varied presentations shape the piece’s form and culminate in a final passage highlighting both the cyclicity of these repetitive materials and the metric playfulness of the ostinato.
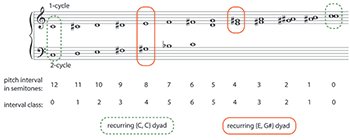
Example 5. Primary dyad series (subject to octave transposition), generated by combining 1-cycle and 2-cycle (“The Broad Day King”)
(click to enlarge)
[3.4] Example 5 shows the primary series of dyads, which is generated by combining an octave of the 1-cycle (chromatic scale) with two octaves of the 2-cycle (whole-tone scale). The dyads provide a rich harmonic palette, cycling systematically through all pitch intervals within an octave (or, when subject to octave displacement, all interval classes). Two pitch-class coincidences repeat within the series, {C, C} and {E,
[3.5] Taborn’s performance is gentle and unhurried, and the primary cycle of dyads is initially presented in such a way as to obscure its ascending melodic lines (Example 6). In this first presentation, the first and last dyads of the series, in which the two voices would meet on the same pitch class, are omitted. The ascent proceeds slowly, interrupted by a long pause in which only the ostinato is heard. Most importantly, melodic attention is directed toward two added pitches, B5 and A5, that repeatedly ring out above the dyads. Of the two triadic centricity candidates, this passage favors E major by frequently adding B (the triad’s fifth) and by omitting the two {C, C} dyads from the series.(24)
Example 6. “The Broad Day King,” section A, first presentation of primary dyad series (0:13–1:05) (click to enlarge and listen) | Example 7. “The Broad Day King,” section A, second and third presentations of primary dyad series (1:05–2:04) (click to enlarge and listen) |
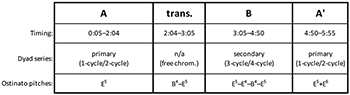
Example 8. “The Broad Day King,” formal diagram
(click to enlarge)
Example 9. Secondary series of dyads generated by combining 3-cycle and 4-cycle (“The Broad Day King,” B section)
(click to enlarge)
[3.6] The second and third presentations of the primary dyad series are more salient than the first. (These correspond to rehearsal marks 2 and 3 in Example 7.) In both cases, Taborn includes the first and last dyads of the series, lingering on {C, C} at the start of the third presentation, while still highlighting E major through added notes and a prominent register change.
[3.7] Example 8 diagrams the piece as an emergent ternary form, providing timings for each large section and listing the dyad series and ostinato pitches used in each.(25) The three presentations of the primary dyad series discussed above constitute the “A” section. Following this, a slow passage (the “transition” of Example 8) introduces the first change to the ostinato and circles gently around some of the prominent harmonies with free chromatic motion. This transition leads to a contrasting B section based on an alternate series of dyads generated by the 3-cycle and 4-cycle (Example 9).
Example 10. “The Broad Day King,” beginning of B section, four presentations of secondary dyad series (3:04–3:34)
(click to enlarge and listen)
[3.8] The structure and presentation of the secondary dyad series heighten tension and create contrast with the preceding section. The 4-cycle heard prominently in the bass voice combines the two major thirds that suggest conflicting centricities, {C, E} and {E,
[3.9] The regular arrivals of strong dyads and ostinato pitches at the opening of this section imply, for the first time, a straightforward simple quadruple meter (see barring in Example 10), in which the ostinato plays a consistent offbeat rhythm. The arrival of the {C, C} dyad every four measures suggests a regular cycle and four-bar hypermeter. Compared to the flexibility that preceded it, this pure-duple groove feels almost restrictive. This sensation, however, is disrupted near the end of the third presentation (twelfth measure of Example 10), when the ostinato resumes its earlier, irregular rhythmic style. Here the regular offbeats are replaced by a free mix of durations, illustrated in simplified form above the staff. Although the fourth presentation of the dyads states a varied repetition of the earlier four-bar rhythm, the missing downbeat now obscures the hypermetric relationship. Without the consistent ostinato offbeats, I find it difficult to maintain feeling
Example 11. “The Broad Day King,” ending of B section, four presentations of secondary dyad series (4:09–4:50)
(click to enlarge and listen)
[3.10] When the secondary dyad series returns (in the seventh notated measure of Example 11), it does so without the strict repetition and meter heard earlier. This time, each presentation attempts the fourth dyad in the series (see brackets in Example 9). In contrast with the lower voice, which usually reaches its expected C4, the upper voice only sounds the A4 of the fourth dyad once before veering off to explore other pitches. For context, Example 11 includes some freer material heard before the dyads return, during which a new upper line is first introduced (first six bars). The pitches of this upper line sound along with the chordal arrivals (the “downbeats” of my transcriptions), but their register and shorter duration align them rhythmically with the ostinato.
Example 12. “The Broad Day King,” A’ section, first three presentations of primary dyad series (4:50–5:26)
(click to enlarge and listen)
[3.11] In the piece’s final A′ section, a slight adjustment to the ostinato adds a new layer of interpretive complexity, while the cycling of dyads achieves a sustained momentum that has previously eluded it. Example 12 shows the first half of this concluding section. Here, the upper line introduced in the previous passage, which reached E6 at the end of Example 11, ceases its wandering and rejoins the ostinato. By rehearsal 10, every second ostinato pitch is consistently doubled at the octave. This introduces a new grouping mechanism to the ostinato—one that is regular in number, but not in duration. If the notes of the ostinato were earlier heard as tactus-level “beats” in an unpredictable but meter-like flow, the high Es now add another hierarchical level to this flexible temporal structure. Meanwhile, the primary dyad series returns, gaining intensity through six successive presentations. (Only the first three are shown in Example 12). As indicated by the close spacing of the rehearsal numbers, the dyads progress relatively quickly, sounding without added pitches or disruptions. With each repetition, the ending and new beginnings are elided into a single {C, C} octave, such that the cyclic nature of the material is finally apparent.
[3.12] One might describe “The Broad Day King” as the album’s “minimalist” piece, a label that seems fitting for music based in ostinato and process. Like many minimalist works, much of the joy of “The Broad Day King” resides in its dynamic metric sensations, which allow constant reinterpretation of its recurring pitch materials. Critically, Taborn avoids strict repetition and predictable process, treating the ostinato and the two series of dyads flexibly. While Taborn’s “kernel” materials (see pargraph 2.6 above) themselves intimate cyclic reference structures, his performance avoids the clear beginnings, endings, and periodicities that would articulate those structures definitively. Only in the final section does the primary dyad series emerge as continuous and regular, exposing the cyclic nature of this improvisational seed while creating a final escalation of energy. The ostinato, on the other hand, never succumbs to straightforward cyclicity. With its shifting rhythms, deceptive simplicity, and delicate articulation, it floats freely above the texture, compelling entrainment to possible pulse streams while refusing to be pinned down by a single metric interpretation.
“Avenging Angel”
[4.0] While “The Broad Day King” embeds its repeating cycles within a relatively conventional ABA' form, flexible ostinati in “Avenging Angel” play a more dynamic role in its formal process. The track is structured around two contrasting ostinati that compete for dominance. I begin my discussion with an account of their individual qualities and the reference structures each suggests, giving special attention to potential metric interpretations of the second ostinato. I then proceed with an overview of the entire track, showing how the two ostinati unfold and interact over the course of Taborn’s performance.
Two Contrasting Ostinati
Example 13. Ostinato 1 as presented at the opening
(click to enlarge and listen)
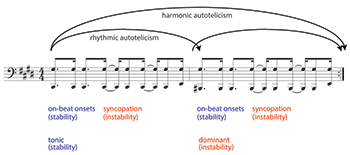
[4.1.1] The piece opens with ominous, low-register material that I call “Ostinato 1.” Ostinato 1 strongly projects a simple quadruple meter (Example 13). Its relatively conventional syncopated rhythm is directed toward downbeat events that function simultaneously as beginning and ending, a feature of many grooves that Timothy Hughes (2003, 15) calls “autotelicism.” This one-bar rhythm is initially repeated at two pitch levels, suggesting an oscillation between tonic and dominant that also generates autotelicism at the two-bar level. Once established, Ostinato 1 begins to slowly transform, suggesting that the piece will have a linear form driven by continuous development rather than a strict cycle. The ostinato is materially flexible (its repetitions vary), but relatively fixed in its metric interpretation. As examples in the next section will demonstrate, the variations on Ostinato 1 that dominate the first few minutes of the piece suggest new harmonies, linear progressions, and formal articulations even as its characteristic rhythmic and textural features are retained.
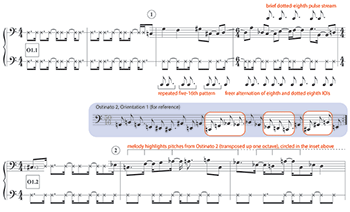
[4.1.2] The second ostinato contrasts with the first in almost every way. Rather than the rumbling chordal repetition of Ostinato 1, Ostinato 2 takes the form of a complex, freewheeling bass line. Its prominent dyadic thirds, fifths, and sixths suggest tertian chords that interlock in a flexible manner—a loose cycle of overlapping harmonies.(26) Once presented in full for the first time, the cycle is almost never varied. While its material identity is fixed, its ambiguous beginning, slippery tonality, and complex metric structure render it highly flexible in interpretation. In the passage that ends the track (4:05–6:49), Ostinato 2 cycles continuously, providing ample opportunities to embody its rhythms and repetitions. This affords contemplation of the ostinato as an external reference structure—one that exists in the mind of the listener, apart from any specific instance, but that is also under constant negotiation due to its flexibility. For a listener, constructing this abstraction and experiencing its multiple metric potentialities is a highly engaging aspect of the passage’s groove. Further, the familiarity gained from repeat listenings to “Avenging Angel” allows one to detect subtle allusions to Ostinato 2 that precede its complete unveiling in the track’s denouement. In the remainder of this section, I discuss interpretation of the ostinato as an abstract entity, returning to analysis of its in-time presentations in the following section.
Audio Example 1. “Avenging Angel,” 5:17–5:40
Example 14. “Avenging Angel,” Ostinato 2 (two alternate orientations)
(click to enlarge and listen)
[4.1.3] Because any single transcription will conceal elements of Ostinato 2’s interpretive malleability, I recommend listening to it before looking at the notated examples. The excerpt in Audio Example 1, drawn from the ending passage mentioned above, fades in mid-cycle and fades out again after approximately three cycles.(27) In moving to assemble a visual representation, one must remain cognizant of notational biases: these include the choice of a starting place (which may not be perceived as such while the ostinato is cycling), enharmonic pitch spellings (which can convey specific harmonic and grouping interpretations), and rhythms (which can imply a particular metric interpretation). Example 14 provides two transcriptions that differ only in their starting place.(28) (Support for hearing each orientation will be discussed below.) Given the ostinato’s range of harmonic potentialities, I have opted for pitch spellings that preserve as many stacked tertian intervals as possible; any grouping or larger tonal implications of these spellings is unintended. Regarding rhythms, Ostinato 2’s two unequal durations are in a two-to-three ratio that is confirmed by the faster notes of Taborn’s melodic lines. In my transcriptions, these isochronous subdivisions are understood to be sixteenth-note pulses, such that the pitches of Ostinato 2 are notated as a string of eighth and dotted eighth notes (for now, without beaming). The gray time signatures provided in this and future examples serve primarily to indicate total duration and should not be taken to carry all the metric connotations that typically accompany time signatures.
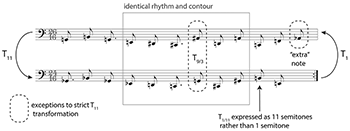
Example 15. Repetition splits Ostinato 2 (shown in Orientation 1) into two halves related by transposition
(click to enlarge and listen)
[4.1.4] As was the case for Ostinato 1, repetition splits Ostinato 2 into two parts; see top and bottom portions of Example 15. In contrast to the tonal relationship between Ostinato 1’s halves, these two are related by semitone transposition. The dashed boxes in the figure highlight two exceptions to the strict transposition and the arrow points to the sole note transposed by 11 semitones rather than 1. This single octave displacement keeps the ostinato’s ambitus within a single octave (C2 to B2) in which all twelve pitch classes are sounded. The rhythms are partially altered across the ostinato’s two halves, although each features a middle zone in which the rhythm and contour are identical (see boxed area in the example.) Despite this significant overlap, the repetition can be difficult to perceive. Slight alterations—the changed durations, the missing/extra note, the octave displacement—significantly mask the melody’s transposed recurrence. This is due not only to the collective impact of all the minor alterations of pitch-class and rhythm, but also to the fact that they occur mostly at the starting and ending edges of each line.(29) As I will argue below, the concealed nature of the repetition allows potential lower-level metric structures to arise which conflict with this apparent upper-level organization.
[4.1.5] Although most conceptions of Ostinato 2 as a fixed abstraction would require it to have a definitive beginning and ending, “Avenging Angel” affords hearing the two halves shown in Example 15 in either order. “Orientation 1” begins with the upper staff material (the “G transposition”), while “Orientation 2” begins with the lower staff material (the “
Example 16. Two interpretations of tactus-level beat groups, shown by beams, within Ostinato 2 (Orientation 2)
(click to enlarge and listen)
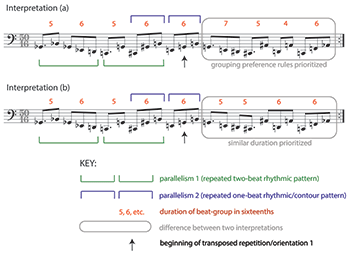
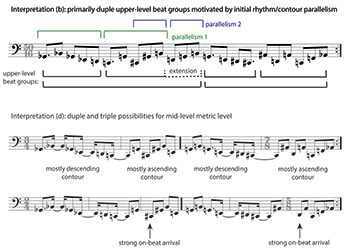
[4.1.6] Metric perception generally begins with the search for a tactus, a primary beat level occurring at a moderate tempo that encourages entrainment.(31) In passages dominated by Ostinato 2, the tactus is not obvious. The ostinato’s eighth and dotted-eighth durations present one option, albeit a relatively fast one. The two durations in a 2:3 proportion resemble those of the asymmetric-yet-maximally-even rhythmic cycles often found in repeating grooves, such as the loops of electronic dance music (Butler 2006, 82–85), but the four dotted eighths are unevenly distributed within the fifty-sixteenth cycle. Because of the tempo and length of the cycle, I find myself grouping the eighth and dotted-eighth notes into slower beats as I listen. I gravitate toward the grouping shown by beams in Example 16, interpretation (a), which points toward Orientation 2. Although I arrived at this hearing intuitively, it follows several logical “preference rules.” All of the dotted-quarter onsets (contextually long durations) and local pitch nadirs initiate beats, the contour never changes within a beat, passing tones do not initiate beats (i.e., are in a metrically weak position), and all ascending perfect fifths—which strongly imply harmonic continuation—occur within the same beat. The last two “rules” reflect an assumption that the ostinato implies tertian harmonies. In addition, the grouping responds to two prominent parallelisms of rhythm and contour at the beginning, shown with green and blue brackets.(32)
[4.1.7] The “preference rules” that guide my interpretation (a) necessarily leave others unfulfilled. Significantly, the beat-groups of interpretation (a) range from four to seven sixteenths in duration, thus violating conventional metric expectations for strict periodicity (Lerdahl and Jackendoff [1983] 1996, 69) or maximal evenness within a non-isochronous beat cycle (London 2012, 128–29).(33) (In practice, the principle of maximal evenness limits the number of distinct beat types to two, “short” and “long.”) Indeed, tapping along to interpretation (a), some of the continuity of pulse I normally experience when I entrain to a tactus becomes attenuated towards the end. This suggests to me an alternate interpretation, shown in part (b) of Example 16. This version makes a slight adjustment to the second half, such that the ostinato is partitioned into a series of beat-groups with only two durations: five sixteenths and six sixteenths. Interpretation (b) preserves the parallelism and other features of (a) in the first half of the ostinato, while violating grouping conventions in the second half(34) in order to prioritize similarity of duration.(35) I find interpretation (b) quite easy to feel, and even a bit more engaging than (a). When I attend primarily to the ostinato itself rather than Taborn’s soloing, I can experience the beat durations as nominally isochronous at a moderate tempo in the range of 68–82 bpm. With more focus, I can hear the two durations as “short” and “long” beats within a non-isochronous cycle, although not one that is maximally even.(36) When I attune to interpretation (b), the accented passing tone, offbeat long note, and lack of parallelism give the second half a pleasantly off-kilter, “syncopated” feel that enhances the sense of arrival on the
Example 17. An interpretation of tactus-level beat-groups, shown by beams, within Ostinato 2 (Orientation 1)
(click to enlarge and listen)
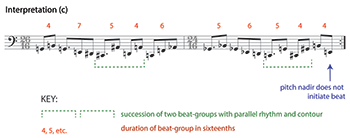
[4.1.8] While interpretations (a) and (b) each provide a compelling entrainable tactus, both are incompatible with the higher-level grouping suggested by the transposed repetition. The arrows in Example 16 show where that repetition begins: in the middle of a tactus beat-group. Thus, a listener committed to (a) or (b) cannot simultaneously experience the two-part division, which requires hearing a strong beginning on this G. Moreover, both (a) and (b) are incompatible with Orientation 1. A commitment to Orientation 1 requires a complete reworking of these mid-level beat-groups, and it is no longer possible to prioritize all of the grouping preference rules previously noted. Interpretation (c) in Example 17 shows what is, to my ears, the best solution, only sacrificing the preference rule for pitch nadirs at the very end. This grouping lacks the low-level rhythmic parallelisms of (a) and (b) highlighted in Example 16 and employs a wider range of beat durations throughout. Indeed, it is impossible to group the events of the ostinato under Orientation 1 such that consecutive groups differ by only a sixteenth, as in interpretation (b). For these reasons, I find interpretation (c) significantly less “catchy” than either (a) or (b). When I listen for the high-level repetition or orient myself to the G beginning, I become considerably more ambivalent about lower-level grouping.
Example 18. Ostinato 2, interpretation (d)
(click to enlarge and listen)
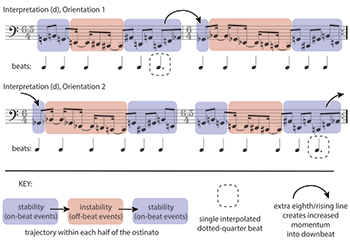
[4.1.9] At least one alternative tactus option remains: a steady quarter-note pulse of around 102 bpm, against which many of the ostinato’s events are syncopated, with a single interpolated dotted-quarter beat. Interpretation (d), shown in both orientations in Example 18, follows a different set of preference rules than (a) through (c). Isochrony is now prioritized, while alignment of beats with event onsets is only a second-level concern. Interpretation (d) has a solid grounding in the style of groove-based music, in which bass line ostinati are often syncopated against a steady pulse. At the same time, other features of most such music that aid a listener’s metric interpretation—including conventional genre signifiers pointing to a specific metric type, regularity in another part, clear harmonic rhythm, or prominent mid-level rhythmic repetitions—are absent here.(37) Perceiving interpretation (d) thus requires some work on the listener’s part, but it offers rewards at higher levels. The interpretation highlights the two-part structure created by the transposed repetition, with each half of the ostinato following a path from stability to instability and back. The single elongated beat at the end of the G transposition creates a slight disruption which, in combination with the rising steady eighth notes, heightens the sense of arrival and resolution of tension at the start of the
Example 19. Mid- and upper-level metric possibilities for tactus interpretations (a) and (d), both shown in Orientation 2
(click to enlarge)
[4.1.10] The flexibility in tactus choice extends to the next highest metric level—that is, to a metric layer that might be notated as the measure or half-measure, and which is often phenomenally prominent in groove-based music. (For instance, consider the measure-length rhythmic repetition present in Ostinato 1 or in the “Bodies We Come Out Of” ostinato shown in Example 1.) For Ostinato 2, I can entertain any of the options shown in Example 19, which depicts two of my possible tactus interpretations, (b) and (d), under Orientation 2 for easy comparison. Interpretation (b), in my hearing, leads to relatively unambiguous higher levels: an essentially duple framework punctuated by the rhythmic surprise of a single beat extension. Naturally, it continues to conflict with the two-part division suggested by the transposed repetition at these higher levels. By contrast, the two halves of interpretation (d), each of which contain six tactus beats, can just as easily be grouped into twos (supported by the strong on-beat arrival on the third of these groups) or threes (supported by the overall contour of the two halves).
[4.1.11] The point of this discussion is not to argue that any of the above metric interpretations is the “correct” one. Rather, it is to demonstrate that Ostinato 2 not only allows a variety of interpretations, but practically demands that a listener experiment with them. Various features of the ostinato compel one to listen metrically. Its strict cyclic repetition encourages an embodied response to its recurring rhythms, the density referent provides a metronomic and omnipresent pulse, and its two durations resemble those of familiar non-isochronous rhythmic and metric cycles. Parallelisms, harmonic implications, and contour all suggest higher-level beat-groups which might serve as a comfortable tactus. At the same time, Ostinato 2 offers no simple solution to the “problem” of finding an entrainable tactus or a hierarchy of beat levels, because any metric interpretation challenges listeners to ignore a contradictory hearing that illuminates some other compelling aspect of the music. Some of these tensions might be understood as a conflict between bottom-up and top-down decision-making. Interpretation (b), for instance, begins with an accessible tactus and builds upon it a multi-tiered metric hierarchy, yet it conceals a fundamental aspect of the ostinato’s pitch organization (the transposed repetition). Interpretation (d), by contrast, prioritizes upper-level structures and sweeping isochrony at the expense of a clearly articulated tactus and unambiguous mid-level groupings.
[4.1.12] Taborn’s own comments about meter suggest that he often thinks in an additive and polyrhythmic way which might resemble some combination of the above interpretations or something entirely different still. In one interview given a few years after Avenging Angel was released, he says, “I deal a lot with multiples; multiple meters that make up even larger groupings. It’s more about doing things modularly. . . . A patterned, grid-like way of playing complicated stuff is too diagrammatic for me” (Whitehead 2013, in response to the prompt “You do like higher metrical games. . . ”) When I asked Taborn how he generally thinks about or feels meter while improvising, his answer was complex. “I tend to organize things in my thinking around larger chunks of rhythm,” he explained, describing midlevel polyrhythmic structures divided into “a big two” (or three) as a kind of “tentpole.” “I’ve internalized pulse rate and rhythmic groove information inside, and then I play with. . . whatever is going on in that piece. Even if it’s something like an eleven-beat thing, I’ll switch the six and five back and forth. . . . It gets very nested and tuplet-y, but it’s really based on the stronger sense of the larger chunks underneath.” When working with polyrhythms, he likes to avoid the kind of rhythmic “problem-solving” in which “the meaning, the multiplicity of the groove, that kind of African feel gets lost and everything gets flattened out—I like to keep the identity of the different layers.” These comments suggest to me that Taborn himself values the kind of temporal multiplicity modeled by my approach, although he may feel it quite differently than I do.
[4.1.13] The particular metric tensions that underlie Ostinato 2 are brought out by the formal and energetic trajectory of the track as a whole. Fragments of the ostinato that appear early in the piece obscure its larger design and promote hearing beat-groups such as those in (a) or (b), which privilege Orientation 2. But in the last section, when the ostinato is finally heard in full, contextual cues and the now-complete transposed repetition support Orientation 1, which conflicts with those earlier interpretations. The incompatibility of these levels rewards a listening strategy that refuses to choose, and instead toggles continuously between interpretations, remaining open to the divergent ways that they color the groove’s events and thus finding novelty and difference in its repetitions.(38)
[4.1.14] The dynamic tension between different grouping criteria and between incompatible lower- and higher-level interpretations resembles the characteristic play between sounding rhythm and external reference structures described by Floyd ([1991] 2002) and Schmidt Câmara and Danielsen (2018). While listening to Ostinato 2, the listener is invited to experiment with different hearings and participate actively and continuously in the creation of meter. Mark Butler describes a similar aesthetic in his work on electronic dance music grooves, writing that metric ambiguity encourages one to “construe the meter actively rather than absorb metric information passively” (2006, 137, emphasis original). Strict repetition, he notes, offers plenty of time for listeners to experiment with different interpretations (127). In the following section, I describe how “Avenging Angel” builds to a conclusion that features extended strict repetition of Ostinato 2, thus culminating in a celebration of its cyclicity and interpretive flexibility.
Formal Process
[4.2.1] Taborn’s six-minute performance of “Avenging Angel” is structured around the steady emergence of and ultimate takeover by Ostinato 2. This dynamic process can be roughly divided into three phases. The first, spanning 0:00–1:30, is based entirely on Ostinato 1. In the second phase, 1:30–4:05, increasingly prominent fragments of Ostinato 2 begin to intrude, blending with and destabilizing Ostinato 1’s groove. In the final phase, 4:05–6:49, Ostinato 2 emerges as dominant, cycling continuously without variation.
Example 20. “Avenging Angel,” first phase (0:00–1:30), based solely in Ostinato 1
(click to enlarge, see the rest, and listen)
[4.2.2] The first phase (Example 20) introduces and expands on the ideas of Ostinato 1. After an eight-bar exposition in which the ostinato’s repeating chords are heard alone, the ostinato begins (at rehearsal A in the transcription) to support simple melodic content and to slowly transform. Initially, only slight rhythmic variations occur. Soon, though, melodic chromaticism destabilizes the opening
[4.2.3] Near rehearsal B, Ostinato 1 abandons the pitch/harmonic repetition that distinguished its first and second measures and is thus transformed into a one-bar structure defined only by rhythm, texture, and the flat contour of its repeated chords. Nevertheless, throughout this opening phase, Ostinato 1’s metric regularity extends to the level of four- and eight-bar phrases. The only notable exceptions to this pure-duple hierarchy are a six-beat transitional phrase extension (going into rehearsal B) and a single six-bar phrase (at B).
Example 21. “Avenging Angel,” start of second phase (1:30–2:15)
(click to enlarge, see the rest, and listen)
[4.2.4] Soon, this regularity is challenged. During the piece’s middle phase, elements of Ostinato 2 begin to intrude, disrupting and distorting Ostinato 1’s groove without ever gaining the upper hand. Example 21 shows an annotated transcription of the passage that begins this phase. A detailed discussion of this representative excerpt will show how the two grooves compete for dominance during this middle phase. Four melodic entrances are numbered ① through ④ above the staff, and prominent occurrences of Ostinato 1’s characteristic rhythm and texture are marked “O1.1”, “O1.2”, etc., for reference. For clarity and simplicity, Example 21 only shows rhythmic notation for most of the left-hand part and for the Ostinato 1 interruptions.
[4.2.5] Following two bars of the default Ostinato 1 rhythm (O1.1), the melodic entrance at ① triggers the first subtle hints of Ostinato 2. First, the accompaniment part begins to play groups of five (2+3) sixteenths. This rhythm anticipates the bass line durations of Ostinato 2—as well as a cycle near the end of phase 3 in which Taborn’s soloing features the same 2+3 pattern—and obscures the
[4.2.6] Over the rest of the passage, allusions to Ostinato 2 become increasingly more overt. The next two melodic entrances at ② and ③ outline a series of Ostinato 2’s pitches, as shown above the staff in the Example.(39) The final melodic entrance at ④ culminates in an exact fragment of Ostinato 2, doubled at the octave for a powerful and memorable impact. Each of these melodic segments, however, is interrupted by a return of Ostinato 1’s original rhythm and texture (O1.3–5) that reorients us to its basic groove. These entrances seem to come in the nick of time, each one pulling us back from a precipitous cliff edge. Finally, after the most prominent intrusion of Ostinato 2 in the final segment, O1.5 introduces a more extended return to Ostinato 1, in a ruminative passage that resembles the longer transition at the end of Example 20.
[4.2.7] Two larger points about the music shown in Example 21 are worth noting. First, its rhythms can always be understood to continue Ostinato 1’s basic quarter-note pulse, even when perception of that pulse is momentarily challenged, and nearly the entire excerpt can be understood in
[4.2.8] Over the next few minutes, uprisings of melodic, rhythmic, and harmonic content reminiscent of Ostinato 2 are continually quashed by returns of Ostinato 1’s basic rhythm and its variations. The conflict plays out in a stunning variety of manners at the local level; here I will only give a sense of the broad sweep. The passage from approximately 2:20 to 2:50 traces a trajectory of intensification resembling that of Example 21 but with increasingly irregular phrase structure. The material that follows (beginning around 2:50) features less blending and more of an alternation between the two grooves, giving Ostinato 2 more autonomy without allowing it to fully blossom. Across all of these passages, tension ratchets up as increasingly longer and more prominent fragments of Ostinato 2 intrude. The middle phase culminates in a kind of sequencing of Ostinato-2-like materials (3:40 to 4:05), ending in a final statement of Ostinato 1 and a brief pause that clears sonic space for the start of the final phase of the piece.
Example 22. “Avenging Angel,” beginning of final phase, first two cycles of Ostinato 2
(click to enlarge and listen)
[4.2.9] Ostinato 2 begins the final phase at 4:05 on the initial G of Orientation 1. Example 22 shows the first two cycles of Taborn’s solo. For listeners conditioned by the ostinato’s structure and by its partial earlier entrances to hear Orientation 2, this new phase seems to start in medias res, almost as if the ostinato had been cycling all along and we have only just tuned in. This impression is reinforced by its soft entrance, which emerges out of the resonance of a crashing chord.
[4.2.10] Ostinato 2 loops continuously without variation for nearly three minutes as Taborn solos over it.(40) Its unchanging repetitions give listeners plenty of time to explore various metric interpretations and experience its differences from Ostinato 1. Ostinato 1 was flexible in its material identity, developing and changing throughout the first and middle phases. Those changes facilitated the creation of larger formal trajectories and phrase structures with clear beginnings and endings. Ostinato 2, in contrast, is entirely fixed in its material identity, creating no hierarchical phrase structures and at times obscuring the sense that it has a beginning at all. Yet it is almost infinitely flexible in its interpretation, rewarding a listener’s continued attention to the sounding music’s interaction with a kaleidoscopic array of potential reference structures.
Example 23. Final phase, last four cycles (6:16–end). The ostinato is shown beamed here according to interpretation (c).
(click to enlarge and listen)
[4.2.11] Although Ostinato 2 itself is unchanging, Taborn’s soloing builds in intensity over it. Factors that contribute to the build include a gradual increase in loudness and rhythmic density, registral expansion and ascent, and eventually, the introduction of chords and rhythmic features such as cross-pulse. While most of the final phase features fluid melodies like those in Example 22, Taborn uses the last few cycles to focus exclusively on the groove’s rhythmic possibilities through repeated articulations (Example 23). In the nineteenth and twentieth cycles, Taborn combines the ostinato with a repeated-note pattern. Although this five-sixteenth recurring rhythm could have fit evenly into the full fifty-sixteenth cycle, Taborn instead introduces a hiccup so that the rhythm aligns differently with the two consecutive cycles. In the twenty-first (penultimate) cycle, the ostinato is paired with chords that alternate inter-onset intervals of five and six sixteenths, finally providing the maximally even division of fifty pulses into nine beats that the ostinato itself declined to offer. The repeated chords in the right hand, which escalate in intensity in the final cycle, recall the earlier repetitions of Ostinato 1. The performance thus ends with a final allusion to the dialectic that has structured its unfolding.
“Neverland”
[5.1] The two pieces analyzed thus far both involve repetition that is long-lasting and obvious, if not always exact. Other improvisations by Taborn, in contrast, feature repetitions that are less pronounced or that occupy much shorter temporal spans. My final example examines a flexible ostinato from “Neverland” that is both elusive and fleeting. Subtle and short-lived repetitions such as this one operate on a subterranean level, initially only pricking at the edge of consciousness, yet compelling one to listen again and again in an attempt to lock into the groove. The analysis to follow examines the hidden cyclic repetitions and rapid dissolution of this “Neverland” ostinato in detail, and also situates it within a broader temporal context to demonstrate its role in a larger form that is not predominantly groove-based.
[5.2] Like “Avenging Angel,” “Neverland” might be heard to proceed through roughly three phases. In this case, the three phases are distinguished by markedly different textures, and each of the latter two involve their own flexible ostinati. The track opens with a bouncy contrapuntal texture in which two voices pass off short motifs.(41) This gives way at about 1:10 to a dreamy passage initially underpinned by a simple triple-time ostinato. This ostinato quickly begins to vary, losing its metric stability and clear basic unit before its recurring fragments fade away entirely.(42) This middle phase is characterized by the slow traversal of a registral arch, a relatively high tessitura, and a texture that primarily combines right-hand melodic material with gentle left-hand accompanimental figurations. Toward the end of the middle phase’s descent, starting around 2:30, Taborn’s left hand begins to pluck out detached low-register pitches that slowly coalesce into a more continuous bass line. As the right hand transitions to playing sustained chords for the first time in the piece (around 2:54), marking the start of the third phase, this new bass line gains energy and begins to convey a more continuous and entrainable pulse.
Audio Example 2. “Neverland,” 2:56–3:34
[5.3] My analysis concentrates on the passage that begins this final phase, in which the bass line is ostinato-like but lacks an obvious basic unit. Certain pitch/rhythmic gestures return, but not in a predictable sequence. Yet the bass line has an undeniable groove—in its motoric pulse, its blend of forward momentum and effortless control, its subtle and ongoing rhythmic interplay with the right hand’s chords—that contradicts any interpretation as a series of disparate fragments. Humming along at the heart of this groove is a loose cyclicity that tugs at a listener’s awareness without being immediately accessible to perception. I encourage the reader to listen to the passage in Audio Example 2 and experience this flexible ostinato before looking at the notation that follows.
Example 24. An elusive and flexible ostinato in “Neverland” (2:56–3:34)
(click to enlarge, see the rest, and listen)
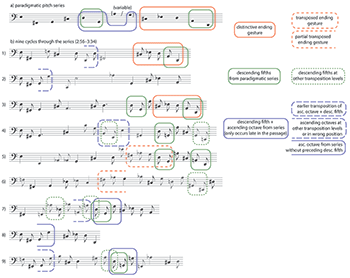
[5.4] In Example 24, part (a) represents the bass line’s loose cyclicity as a paradigmatic pitch series, which is partially referred to in nine consecutive iterations. In part (b), these iterations are aligned vertically in rhythmically proportionate notation. Black noteheads indicate pitches drawn from the series, while other notes are shown in gray. As can be seen from the figure, not all iterations include all pitches, and durations vary (although they exhibit certain global tendencies). I should emphasize that this diagram is an analytical observation, not a claim about authorial intent. I have no reason to believe that Taborn thought of his performance in these terms, and various other representations—differing, for instance, in beginning/ending orientation or in the specific pitches considered paradigmatic—are possible.
Example 25. “Neverland,” first three iterations of the cycle (2:56–3:10), both hands
(click to enlarge and listen)
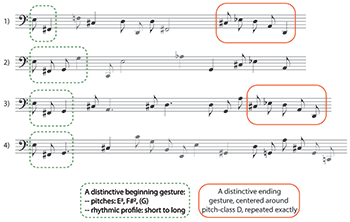
Example 26. Distinctive beginning and ending gestures in the first four iterations (2:56–3:15)
(click to enlarge and listen)
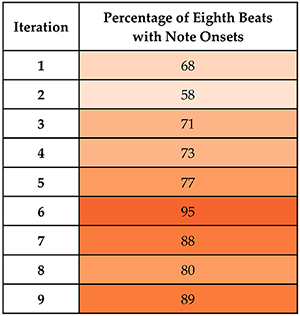
Example 29. Percentage of eighth beats with note onsets in each iteration
(click to enlarge)
[5.5] Although lively and pulse-driven, the passage is flexible in its metric interpretation. Like the ostinato in “Broad Day King” and Ostinato 2 in “Avenging Angel,” the bass line clearly presents a density referent (my notated eighth note), while its larger groupings, including the tactus itself, remain unclear. The quarter pulse presents itself as a likely tactus, but its two possible phases are each plausible at different moments. Neither results in a parallel interpretation of events across iterations. Taborn avoids repetition of patterns that might suggest a familiar metric type such as
[5.6] Repetition is clearest earlier in the cycle, drawing a listener into the groove before the ostinato begins to vary more widely. Each of the first four iterations includes a distinctive beginning gesture, ending gesture, or both (Example 26); whereas iterations after these mostly do not. Iteration 3 includes all twelve pitches of the series. Overall, the number of paradigmatic pitches included in each iteration fluctuates, but trends somewhat lower in later cycles; see Example 27. The first six iterations are also similar in their total durations of nineteen to twenty-one eighth notes. After this, iterations become both shorter and more widely varied, with Iteration 8 lasting only about half the length of earlier cycles (Example 28). The shortening in cycle length in Iterations 6 through 8 mirrors the energy gain happening within each, as the ostinato gradually drops longer durations and moves toward almost steady eighth notes (Example 29).
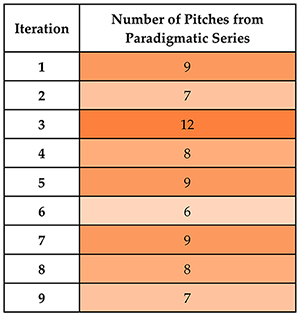
Example 27. Number of pitches from the paradigmatic series included in each iteration (click to enlarge) | Example 28. Duration (in eighth notes) of each iteration, based on the beginning / ending boundaries shown in Example 24) (click to enlarge) |
Example 30. Transposed segments of the paradigmatic pitch series
(click to enlarge and listen)
[5.7] One additional factor complicates precise definition and perception of the cycle: certain segments of it occur in transposition. Example 30 revisits Example 24, adding new annotations to indicate paradigmatic versions of gestures (solid boxes) as well as transpositions (dashed boxes). For instance, the A2–D2 descending fifth that concludes Iterations 1, 3, and 5 also occurs, in approximately the same position, transposed down one and two semitones in Iterations 4 and 6. There is another descending fifth earlier in the paradigmatic pitch series, and other transpositions occur that are less clearly tethered to the series. The five-note ending gesture (red box) from Iterations 1 and 3 occurs up a fourth in Iteration 5, where it does not function as an ending, and a fragment of this version repeats in Iteration 6. Finally, the mid-cycle sequence of pitches D3–G2–G3 that occurs in Iterations 7 and 9 as a variant of the paradigmatic D3–G2–A3 is an exact transposition of an earlier gesture (in Iteration 4) not drawn from the series; ascending octave leaps on their own are also common throughout the ostinato.(43) These details suggest that the series and its iterations as portrayed in the diagram do not tell the entire “varied repetition” story: some of the pitch content and ordering is fuzzy, and smaller gestures (defined by rhythm, contour, and intervallic pattern as well as pitch) also play a role in our perception of repetition and continuity.
[5.8] Fuzzier repetitions and misplaced transpositions make position finding within the cycle difficult. Indeed, although I have thus far referred to portions of the cycle as “beginning,” “middle,” and “ending” for linguistic convenience, an important feature of the ostinato is that subjecting it to variation obscures its boundaries and temporal functions, particularly as it progresses into the later iterations. Thus, while the quantitative data in Examples 27–29 is useful for demonstrating variation and overall trends, the tables’ specificity is misleading in that they presume the existence of nine precisely defined iterations. The problem goes beyond the fact that exact cyclic boundaries are difficult to locate, and even that the tables imply segmented-ness rather than flow. More profoundly, the numbers reflect only one interpretation at the expense of others. They show the flexibility in the ostinato’s material form, but not in our experience of it.
[5.9] The ostinato’s progression is rapid. After a few more literal repetitions that serve to establish it, it peaks in energy (through greater attack density and shorter cycle lengths in the last few iterations) even as its salient features are already disappearing. It begins to dissolve almost before one realizes it is there. After the nine iterations shown in Example 24, the bass line’s tightly spooled energy dissipates as its attacks drift further and further apart. Eventually it is reduced to pointillistic jabs in an otherwise barren sonic landscape. In total, this winding-down process and its eerie conclusion last longer than the cyclic ostinato itself—the entire passage analyzed above takes only thirty-eight seconds of a four-and-a-half minute track. Within the overall composition, it serves as an unusual climax, briefly offering a particular focus and momentum that stand in stark contrast to the heady counterpoint of the piece’s opening and the diaphanous pianism of the middle phase. Yet an easy or stable groove remains tantalizingly out of reach—perhaps like the distant and carefree “Neverland” of the title.
Conclusion
[6.1] My three analyses show the diverse ways that Taborn’s flexible ostinati structure his longer improvisations. In “The Broad Day King,” the groove remains relatively constant across a performance whose form is driven by slower repeating material. Ostinato and background structures share an underlying allegiance to cyclic principles, a connection that is brought to the fore in the final climactic passage. In “Avenging Angel,” contrast, opposition, and blending between two ostinati drive a dynamic back-and-forth, ultimately tracing a large-scale trajectory from one groove state to the other. The flexible ostinato in “Neverland” provides a fleeting moment of rhythmic intensity and focus that is unique within the track as a whole before its groove rapidly dissolves.
[6.2] At the local level, Taborn’s flexible ostinati actively create meter that remains open to multiple interpretations. A density referent provides rhythmic continuity and drive. In combination with cyclic or quasi-cyclic repetition, this omnipresent rapid pulse begs metric interpretation, beginning with the choice of a tactus. Yet even at this most fundamental level of metric experience, the ostinati are flexible, inviting a listener to continuously participate in the creation of their rhythmic structure. This interpretive openness often extends beyond meter to issues of cycle boundaries, pitch centricity, or harmony.
[6.3] By suggesting meter and cycle as potential reference structures yet refusing to fix the identity of those structures, Taborn’s flexible ostinati engender rich temporal experiences that reward sustained aural and somatic engagement. Each immerses a listener in a sensuous present, an ongoing flow characterized by kaleidoscopic metric and interpretive possibilities. The resulting negotiation between listening body and sounding music, the continuous revision of abstract reference structures, the give-and-take as meter shapes rhythm and vice versa—these dynamic interactions lie at the heart of the music’s distinctive groove.
Antares Boyle
Portland State University
School of Music and Theater
Post Office Box 751
Portland, OR 97207-0751
antares@pdx.edu
Works Cited
Abel, Mark. 2014. Groove: An Aesthetic of Measured Time. Brill. https://doi.org/10.1163/9789004242944.
Agawu, Kofi. 2006. “Structural Analysis or Cultural Analysis? Competing Perspectives on the ‘Standard Pattern’ of West African Rhythm.” Journal of the American Musicological Society 59 (1): 1–46. https://doi.org/10.1525/jams.2006.59.1.1.
Attas, Robin. 2015. “Form as Process: The Buildup Introduction in Popular Music.” Music Theory Spectrum 37 (2): 275–96. https://doi.org/10.1093/mts/mtv020.
Benadon, Fernando. 2006. “Slicing the Beat: Jazz Eighth-Notes as Expressive Microrhythm.” Ethnomusicology 50 (1): 73–98. https://www.jstor.org/stable/20174424.
Berliner, Paul. 1994. Thinking in Jazz: The Infinite Art of Improvisation. University of Chicago Press. https://doi.org/10.7208/chicago/9780226044521.001.0001.
Berry, Wallace. 1987. Structural Functions in Music. Dover.
Brownell, John. 1994. “Analytical Models of Jazz Improvisation.” Jazzforschung/Jazz Research 26: 9–29.
Butler, Mark J. 2006. Unlocking the Groove: Rhythm, Meter, and Musical Design in Electronic Dance Music. Indiana University Press.
—————. 2014. Playing with Something That Runs: Technology, Improvisation, and Composition in DJ and Laptop Performance. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195393613.001.0001.
Butterfield, Matthew. 2006. “The Power of Anacrusis: Engendered Feeling in Groove-Based Musics.” Music Theory Online 12 (4). https://doi.org/10.30535/mto.12.4.2.
—————. 2010. “Participatory Discrepancies and the Perception of Beats in Jazz.” Music Perception 27 (3): 157–76. https://doi.org/10.1525/mp.2010.27.3.157.
—————. 2011. “Why Do Jazz Musicians Swing Their Eighth Notes?” Music Theory Spectrum 33 (1): 3–26. https://doi.org/10.1525/mts.2011.33.1.3.
Collier, Geoffrey L., and James Lincoln Collier. 2002. “A Study of Timing in Two Louis Armstrong Solos.” Music Perception: An Interdisciplinary Journal 19 (3): 463–83. https://doi.org/10.1525/mp.2002.19.3.463.
Danielsen, Anne. 2006. Presence and Pleasure: The Funk Grooves of James Brown and Parliament. Wesleyan University Press.
—————. 2010. “Here, There and Everywhere: Three Accounts of Pulse in D’Angelo’s ‘Left and Right.’” In Musical Rhythm in the Age of Digital Reproduction, ed. Anne Danielsen, 19–35. Taylor & Francis. https://doi.org/10.4324/9781315596983-2.
—————. 2018. “Time and Time Again: Repetition and Difference in Repetitive Music.” In Over and Over: Exploring Repetition in Popular Music, ed. Olivier Julien and Christophe Levaux. Bloomsbury. https://doi.org/10.5040/9781501324871.ch-002.
Doffman, Mark. 2009a. “Feeling the Groove: Shared Time and Its Meanings for Three Jazz Trios.” PhD diss., The Open University.
—————. 2009b. “Making It Groove! Entrainment, Participation and Discrepancy in the ‘Conversation’ of a Jazz Trio.” Language & History 52 (1): 130–47. https://doi.org/10.1179/175975309X452012.
Ellis, Mark C. 1991. “An Analysis of ‘Swing’ Subdivision and Asynchronization in Three Jazz Saxophonists.” Perceptual and Motor Skills 73 (3): 707–13. https://doi.org/10.2466/pms.1991.73.3.707.
Floyd, Samuel A. 1996. The Power of Black Music: Interpreting Its History from Africa to the United States. Oxford University Press.
—————. (1991) 2002. “Ring Shout! Literary Studies, Historical Studies, and Black Music Inquiry.” Black Music Research Journal 22 (Supplement: Best of BMRJ): 49–70. https://doi.org/10.2307/1519943.
Gates, Henry Louis. 1988. The Signifying Monkey: A Theory of African-American Literary Criticism. Oxford University Press.
Givan, Benjamin. 2014. “Gunther Schuller and the Challenge of Sonny Rollins: Stylistic Context, Intentionality, and Jazz Analysis.” Journal of the American Musicological Society 67 (1): 167–237. https://doi.org/10.1525/jams.2014.67.1.167.
—————. 2016. “Rethinking Interaction in Jazz Improvisation.” Music Theory Online 22 (3). https://doi.org/10.30535/mto.22.3.7.
Guck, Marion A. 2006. “Analysis as Interpretation: Interaction, Intentionality, Invention.” Music Theory Spectrum 28 (2): 191–209. https://doi.org/10.1525/mts.2006.28.2.191.
Hasty, Christopher F. 1997. Meter as Rhythm. Oxford University Press.
Honing, Henkjan, and W. Bas de Haas. 2008. “Swing Once More: Relating Timing and Tempo in Expert Jazz Drumming.” Music Perception 25 (5): 471–76. https://doi.org/10.1525/mp.2008.25.5.471.
Hood, Mantle. 1971. The Ethnomusicologist. McGraw Hill.
Hughes, Timothy S. 2003. “Groove and Flow: Six Analytical Essays on the Music of Stevie Wonder.” PhD diss., University of Washington.
Iyer, Vijay. 2002. “Embodied Mind, Situated Cognition, and Expressive Microtiming in African-American Music.” Music Perception 19 (3): 387–414. https://doi.org/10.1525/mp.2002.19.3.387.
—————. 2004. “Exploding the Narrative in Jazz Improvisation.” In Uptown Conversation: The New Jazz Studies, ed. Robert G. O’Meally, Brent Hayes Edwards, and Farah Jasmine Griffin, 393–403. Columbia University Press. https://doi.org/10.7312/omea12350-020.
Janata, Petr, Stefan T. Tomic, and Jason M. Haberman. 2012. “Sensorimotor Coupling in Music and the Psychology of the Groove.” Journal of Experimental Psychology: General 141 (1): 54–75. https://doi.org/10.7312/omea12350-020.
Keil, Charles. (1966) 1994. “Motion and Feeling Through Music.” In Music Grooves: Essays and Dialogues, ed. Charles Keil and Steven Feld, 53–76. University of Chicago Press.
—————. (1987) 1994. “Participatory Discrepancies and the Power of Music.” In Music Grooves: Essays and Dialogues, ed. Charles Keil and Steven Feld, 96–108. University of Chicago Press.
Knowles, Kristina Leigh. 2016. “The Boundaries of Meter and the Subjective Experience of Time in Post-Tonal, Unmetered Music.” PhD diss., Northwestern University.
Lerdahl, Fred, and Ray Jackendoff. (1983) 1996. A Generative Theory of Tonal Music. MIT Press. https://doi.org/10.7551/mitpress/12513.001.0001.
Lewis, George E., and Benjamin Piekut. 2016. “Introduction: On Critical Improvisation Studies.” In The Oxford Handbook of Critical Improvisation Studies, ed. George E. Lewis and Benjamin Piekut, vol. 1, 1–35. Oxford University Press.
Logan, Wendell. 1984. “The Ostinato Idea in Black Improvised Music: A Preliminary Investigation.” The Black Perspective in Music 12 (2): 193–215. https://doi.org/10.2307/1215022.
London, Justin. 2012. Hearing in Time: Psychological Aspects of Musical Meter. 2nd ed. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199744374.001.0001.
Madison, Guy, and George Sioros. 2014. “What Musicians Do to Induce the Sensation of Groove in Simple and Complex Melodies, and How Listeners Perceive It.” Frontiers in Psychology 5. https://doi.org/10.3389/fpsyg.2014.00894.
Margulis, Elizabeth Hellmuth. 2014. On Repeat: How Music Plays the Mind. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199990825.001.0001.
Mirka, Danuta. 2009. Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787-1791. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195384925.001.0001.
Monson, Ingrid. (1996) 2009. Saying Something: Jazz Improvisation and Interaction. University of Chicago Press. https://doi.org/10.7208/chicago/9780226534794.001.0001.
Murphy, Nancy Elizabeth. 2015. “‘The Times They Are A-Changin’’: Flexible Meter and Text Expression in 1960s and 70s Singer-Songwriter Music.” PhD diss., University of British Columbia.
Norment, Camille. 2020. “Craig Taborn.” Interview. BOMB, August 3, 2020. https://bombmagazine.org/articles/craig-taborn/.
Perle, George. 1977. “Berg’s Master Array of the Interval Cycles.” Musical Quarterly 63 (1): 1–30. http://www.jstor.org/stable/741747.
Polak, Rainer, Nori Jacoby, Timo Fischinger, Daniel Goldberg, Andre Holzapfel, and Justin London. 2018. “Rhythmic Prototypes Across Cultures: A Comparative Study of Tapping Synchronization.” Music Perception 36 (1): 1–23. https://doi.org/10.1525/mp.2018.36.1.1.
Polak, Rainer, and Justin London. 2014. “Timing and Meter in Mande Drumming from Mali.” Music Theory Online 20 (1). https://doi.org/10.30535/mto.20.1.1.
Pressing, Jeff. 2002. “Black Atlantic Rhythm: Its Computational and Transcultural Foundations.” Music Perception 19 (3): 285–310. https://doi.org/10.1525/mp.2002.19.3.285.
Prögler, J. A. 1995. “Searching for Swing: Participatory Discrepancies in the Jazz Rhythm Section.” Ethnomusicology 39 (1): 21–54. https://doi.org/10.2307/852199.
Roeder, John. 2019. “Timely Negotiations: Formative Interactions in Cyclic Duets.” Analytical Approaches to World Music 7 (1). http://www.aawmjournal.com/articles/2019a/Roeder_AAWM_Vol_7_1.html.
Roeder, John, and Michael Tenzer. 2014. “Large-Scale Formative Processes in Ostinato Music.” Paper presented at Third Annual International Conference on Analytical Approaches to World Music, London, UK, July 1–4, 2014.
Rose, Richard Franklin. 1989. “An Analysis of Timing in Jazz Rhythm Section Performance.” DMA diss., University of Texas at Austin.
Rusch, René, Keith Salley, and Chris Stover. 2016. “Capturing the Ineffable: Three Transcriptions of a Jazz Solo by Sonny Rollins.” Music Theory Online 22 (3). https://doi.org/10.30535/mto.22.3.9.
Sawatzky, Grant. 2017. “An Analytic Framework for Metric Multivalence: Toward a Theory of Phrase Structure in Twentieth-Century Chamber Music.” Paper presented at West Coast Conference of Music Theory and Analysis, University of Victoria, British Columbia, CA, April 21–23, 2017.
Schmidt Câmara, Guilherme, and Anne Danielsen. 2018. “Groove.” In Oxford Handbook of Critical Concepts in Music Theory, ed. Alexander Rehding and Steven Rings. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780190454746.013.17.
Senn, Olivier, Lorenz Kilchenmann, Richard von Georgi, and Claudia Bullerjahn. 2016. “The Effect of Expert Performance Microtiming on Listeners’ Experience of Groove in Swing or Funk Music.” Frontiers in Psychology 7. https://doi.org/10.3389/fpsyg.2016.01487.
Shatz, Adam. 2017. “The Ethereal Genius of Craig Taborn.” The New York Times, June 22, 2017, magazine section. https://www.nytimes.com/2017/06/22/magazine/the-ethereal-genius-of-craig-taborn.html.
Snyder, Bob. 2000. Music and Memory: An Introduction. MIT Press.
Stanyek, Jason. 2014. “Forum on Transcription.” Twentieth-Century Music 11 (01): 101–61. https://doi.org/10.1017/S1478572214000024.
Stover, Christopher D. 2009. “A Theory of Flexible Rhythmic Spaces for Diasporic African Music.” PhD diss., University of Washington.
—————. 2013. “Review of The Philosophy of Improvisation by Gary Peters.” Music Theory Spectrum 35 (2): 261–67. https://doi.org/10.1525/mts.2013.35.2.261.
Temperley, David. 2001. The Cognition of Basic Musical Structures. MIT Press.
Toussaint, Godfried T. 2013. The Geometry of Musical Rhythm: What Makes a “Good” Rhythm Good? CRC Press.
Walser, Robert. 1993. “Out of Notes: Signification, Interpretation, and the Problem of Miles Davis.” The Musical Quarterly 77 (2): 343–65. https://doi.org/10.1093/mq/77.2.343.
Watkins, Holly. 2017. “Toward a Post-Humanist Organicism.” Nineteenth-Century Music Review 14 (1): 93–114. https://doi.org/10.1017/S1479409816000306.
Whitehead, Kevin. 2013. “Interview: Craig Taborn.” EMusic (website), April 22, 2013. https://web.archive.org/web/20130426113347/http://www.emusic.com/music-news/interview/interview-craig-taborn/.
Williams, David Brian. 1975. “Short-Term Retention of Pitch Sequence.” Journal of Research in Music Education 23 (1): 53–66. https://doi.org/10.2307/3345203.
Wilson, Olly. 1990. “The Influence of Jazz on the History and Development of Concert Music [Response].” In New Perspectives on Jazz, ed. David N. Baker, 25–31. Smithsonian Institution Press.
Yeston, Maury. 1976. The Stratification of Musical Rhythm. Yale University Press.
Zagorski-Thomas, Simon. 2007. “The Study of Groove.” Ethnomusicology Forum 16 (2): 327–35. https://doi.org/10.1080/17411910701554013.
Discography
Discography
Taborn, Craig. 2001. Light Made Lighter. Thirsty Ear THI 571112, compact disc.
—————. 2011. Avenging Angel. ECM 2207, compact disc.
Footnotes
* I would like to thank the following individuals: Craig Taborn, for speaking with me about his music; Rory Cowal, for serving as my go-to jazz piano consultant and trusted second pair of ears; and Janet Bourne, Kristi Hardman, Grant Sawatzky, and two anonymous reviewers for their insightful commentary on earlier versions of this article.
Return to text
1. I have listened to all of Taborn’s live solo performances that are available online; however, not many recordings are posted publicly from the years leading up to and immediately following the recording of Avenging Angel. When I asked Taborn if he was exploring similar materials across multiple performances around that time, he gave me a qualified yes, explaining that he was working extensively with certain “algorithmic processes” and “tools,” but that the performances resulting from these generative techniques lacked surface-level resemblances.
Return to text
2. As George Lewis and Benjamin Piekut (2016, 4) note, the product/process binary is a trope of writing about improvisation, where it is often mapped onto a problematic binary between composition and improvisation.
Return to text
3. For a discussion of these issues, see Stover (2013), especially pp. 262–264.
Return to text
4. In my own conversation with Taborn, he expressed similar sentiments on the relationship between structure and spontaneity with regard to metric organization, saying, “If I hear something that’s super rigidly constructed, I like the idea of ‘what would happen if someone just threw some paint at that?’... That creates more interest in that kind of a space. . . . And also, with free spaces, I like introducing elements of structure in there.”
Return to text
5. For instance, the groove literature cited below, as well as recent scholarship on rhythm, meter, and temporality more broadly, collectively suggest substantial disciplinary attention toward a different set of values. Marion Guck’s metatheoretical writings explore the subject position of the analyst and how it is conveyed in analytical writing; see in particular Guck (2006) for an account of analysis as fundamentally relational (that is, existing between a particular individual and some set of musical sounds) and a celebration of the resulting plurality of interpretations.
Return to text
6. The interview took place on February 7, 2021 over video-conferencing software and is referenced throughout this article.
Return to text
7. In establishing the context, definitions, and sources for this project, I refer to two broad categories that are difficult to define, but typically treated as distinct in the analytical/musicological literature: “popular music” and “jazz.” I ask the reader to temporarily forgive this, as one of my larger aims is to further our understanding of the instability and porousness of these categories.
Return to text
8. “Groove” and “swing” are also treated as roughly synonymous by Butterfield (2011) and are tightly associated in Charles Keil’s ([1966] 1994; [1987] 1994) influential articles outlining his theory of participatory discrepancies.
Return to text
9. For helpful recent summaries of groove scholarship, see Butler (2014, 207–211) and Schmidt Câmara and Danielsen (Schmidt Câmara and Danielsen 2018).
Return to text
10. As Benjamin Givan has argued recently, the idea that “dialogical interplay” is central to the jazz aesthetic has become “near-conventional wisdom in the field of jazz studies” (2016, [1]). Givan provides historical and institutional context for the emergence of interaction as a primary research theme, applauding the significant contributions in that area while also calling on scholars to acknowledge “contrasting performance techniques” to avoid “an overly narrow and homogenous conception of the idiom” ([27]).
Return to text
11. This criticism seems more relevant to scholarship on groove in mainstream North American jazz; there has been more attention toward rhythmic patterning in Afro-Cuban and Brazilian music (e.g., Stover 2009).
Return to text
12. A strict separation of these two categories, however, relies on a problematic division between “structure” and “expression” (Butterfield 2006; Schmidt Câmara and Danielsen 2018). Butterfield describes how microrhythmic variations can impact perception of rhythmic/metric elements, for instance by clarifying metric hierarchy (Butterfield 2011) or increasing anacrustic impact (Butterfield 2006; 2011). Anne Danielsen’s (2006; 2010) work also problematizes this boundary.
Return to text
13. Both ideas are captured in the title of Anne Danielsen’s definitive (2006) monograph on the funk grooves of James Brown and Parliament, Presence and Pleasure. Some version of (1) is found in nearly all of the analytical literature on groove, and psychological studies often define “groove” specifically as the (pleasurable) urge to move to music (e.g., with slight variations, Janata, Tomic, and Haberman 2012, 56; Madison and Sioros 2014, 1; Senn et al. 2016, 1). On (2), Danielsen (2006, 192) writes, “There is no distancing from the musical events: one is continuously engaged in the coproduction of gestures; there is a total presence in the groove. Time dissolves. Repetition never becomes repetitive.” Keil’s ([1966] 1994; [1987] 1994) foundational theorization of groove emphasizes musical performance over notation, and the idea that groove involves expert performance is common to the use of the term by jazz musicians, as in the testimonials in Monson ([1996] 2009).
Return to text
14. He also expressed an interest in repetitions that don’t groove, an aesthetic distinction within his music that I do not pursue here.
Return to text
15. These kinds of interactions may still serve as an important reference for a performer. In my conversation with Taborn, he explained that solo performance does not feel all that different from ensemble performance to him, because both are rooted in interaction. “If you just initiate a sound, in any way, in a space, there’s already a million things that are going on acoustically, energetically, psychologically that you can find to respond to. . . With a group there are more people doing that. . . but without it I tend to encounter the thing in the same way.”
Return to text
16. Gates’s concept has been influential on studies of jazz and African-American music. Floyd (1996) presents the most comprehensive application to music, explaining, “In African-American music, musical figures Signify by commenting on other figures, on themselves, on performances of other music, on other performance of the same piece, and on completely new pieces of music.” Although both Gates’s original theory and Floyd’s (1996) application are primarily intertextual and semantic, the concept has also been used to explain the phenomenon of groove in a narrower sense that is intratextual and more abstract (Zagorski-Thomas 2007, 332–33; Danielsen 2018, 41).
Return to text
17. Throughout this article, I used the term “pulse” to refer to any isochronous periodicity, and “beat” to refer more specifically to a pulsation or grouping (not necessarily isochronous) that is interpreted as a level within a metric hierarchy.
Return to text
18. Many theorists of groove have produced compelling analyses using techniques derived from Christopher Hasty’s (1997) theory of meter (Butler 2006; Butterfield 2006; 2011; Attas 2015). These tools are particularly effective for describing the experience of meter from moment to moment and for attributing metric qualia to events. Yet owing to Hasty’s commitment to meter as rhythm and insistency on novelty over cycle, his theory obscures (or, in its orthodox form, denies) the possibility of meter as a reference structure, and for this reason I do not use Hasty’s techniques here. As messy as any negotiation between “meter” and “rhythm” (or, similarly, “cycle” and “iteration”) must be, these productive tensions are at the heart of the experiential aspect of groove that my analyses seek to illuminate.
Return to text
19. The latter could also be termed “perception,” although this word sometimes carries the implication of an exclusive focus on low-level or subconscious cognitive processes that I wish to avoid here. My analyses, which are rooted in my own listening experience, are meant to model interpretation by a listener who is distinct from the performer.
Return to text
20. I follow Danielsen (2006) in using the term “density referent” (Hood 1971) to refer to the fastest pulse level present.
Return to text
21. Pressing (2002, 288), and Abel (2014, 24–31) both describe the metronomic foundation of groove-based music, which distinguishes it from musical traditions (such as European classical music) that feature rubato.
Return to text
22. Here I intend something along the lines of Holly Watkins’s “post-humanist organicism,” in which music is grounded in a “self-organization” that resembles that of living beings by engaging in “spontaneous and adaptive (even intentional) behaviors” (2017, 106). This conception resonates with comments Taborn made to me about his algorithmic processes leading to an “organizational self-similarity” and about the fundamental role of reaction in improvisation, even in solo performance.
Return to text
23. Some support for hearing the ostinato’s onsets as primarily occurring off the beat can be found in the one passage that does suggest a regular meter. That music is shown in Example 10 and discussed below.
Return to text
24. Here, as elsewhere, E major might be heard as V in A minor, another triad highlighted at times. For instance, the introductory material preceding rehearsal 1 suggests A minor.
Return to text
25. My formal analysis focuses on the two contrasting dyad series as structuring elements; other interpretations are also possible.
Return to text
26. Taborn’s soloing above the ostinato seems to follow these rough chordal outlines, but does not provide enough harmonic information to attach definitive chord labels to the transcription. The harmonic and metric ambiguity go hand-in-hand—clear beat groupings might serve to disambiguate the harmony and clear chord identity could define beat beginnings.
Return to text
27. The fade-in point is not entirely arbitrary: in order not to bias hearing toward either of my two orientations, I chose a spot that aligns with neither.
Return to text
28. For the sake of simplicity and consistency, my transcriptions of Ostinato 2 use only notes, not rests, and do not convey articulation/sustain. Taborn usually performs the notated eighth notes as more detached than the dotted eighths.
Return to text
29. This may be the most significant factor in concealing the repetition—psychological research indicates that beginnings and endings may play an outsized role in our recognition of familiar melodies (Williams 1975; Snyder 2000, 225–26).
Return to text
30. The preference for metric readings that align beginnings (or beats) with accents (or event onsets) is culture-specific. For instance, much African music does not do this (Agawu 2006, 23). At the end of this section I explore a metric reading that does not align beats with events.
Return to text
31. Justin London (2012, 31) cites empirical research to support his view that the tactus should fall in the 500–700ms (86–120 bpm) range; however, individual and genre-specific preferences may vary. For instance, my own preference leans toward slower tempi around 60–80 bpm. In jazz, a much faster pulse is frequently treated as a tactus.
Return to text
32. These resemble metric and grouping preference rules that have been articulated by others: for instance, Lerdahl and Jackendoff’s ([1983] 1996, 246–48) MPR 4 (Stress) prefers to align beat onsets with accented events; their MPR 5 (Length) prefers to align beat onsets with long pitch-events; their GPR 3 (Change) positions group boundaries at points of change, such as large leaps; and their GPR 6 and MPR 1 (Parallelism) favors parallel structures in both metric and grouping structures. In an update to Lerdahl and Jackendoff’s rule system, Temperley (2001, 358) adds a rule (his MPR 6) that aligns beat onsets with harmonic changes. While meter and grouping are normally understood as two separate (if interconnected) ways of segmenting musical time, the two processes are difficult to disentangle when listening to Ostinato 2. See Lerdahl and Jackendoff ([1983] 1996, 12–35) on the difference between meter and grouping, and Berry (1987, 317–18) for an alternative view of meter as grouping. In the case of Ostinato 2, the potential collapse of grouping and meter into a single perceptual category is supported by its avoidance of conventional means of articulating meter, as well as by its strict repetition, which aids in making its complex rhythms entrainable. Butler (2006, 129) describes a similar blurring of the boundary between meter and grouping in the case of repeating grooves in electronic dance music.
Return to text
33. Since interpretation (a) violates conventional metric well-formedness rules, the rhythm resulting from its beat-groups might be more profitably compared to familiar ostinato topoi such as time line patterns, which serve as “materially real, widely used, and crucial markers of temporal reference” (Agawu 2006, 3). However, even these patterns rarely feature the number of distinct durations (four) observed here. For instance, in his survey of the rhythmic properties of ostinato topoi, Godfried Toussaint (2013, 27) identifies six “distinguished rhythm timelines” with five onsets and sixteen pulses. Of these six rhythms, two contain only two distinct durations and the remaining four contain three.
Return to text
34. The “violations” are as follows: the C♯2, a dotted eighth and local pitch nadir, and D2, a local pitch nadir, no longer serve as beat onsets; the
Return to text
35. Although we associate isochrony and pulsation with meter, a preference for equality of duration has also been identified in previous formulations of grouping principles. Lerdahl and Jackendoff’s ([1983] 1996, 49) GPR 5 (“Symmetry”) states a preference for subdivision into two groups of equal length (reflecting a binary bias as well as preference for durational similarity). Temperley’s (2001, 69) PSPR 2 (“Phrase Length Rule”) states a preference for phrases of “roughly eight notes.” Although the rule states numerical quantity, not duration, these two variables are closely related in Temperley’s corpus of rhythmically simple folk tunes.
Return to text
36. Widely recognized isochronous meters only use beat ratios of 2:3 or 3:4 at the tactus level (London 2012, 132–35). London hypothesizes several reasons why 5:6 beat ratios are not found among the established meters of the world: at faster tempos, the two durations are difficult to distinguish perceptually, while at slower tempos, one can interpolate an intermediate beat level with durations in a 2:3 proportion. London’s well-formedness constraints (2012, 128–29) also do not allow meters with multiple non-isochronous (NI) levels. More recent collaborative work by London, Rainer Polak, and others (Polak and London 2014; Polak 2018) suggests that these constraints may not be universal; among other things, they identify in some repertoire NI cycles at multiple hierarchical levels and NI cycles at the subtactus level which are not defined by simple integer ratios. Such findings suggest that broad well-formedness constraints may not apply within specific expert contexts.
Return to text
37. Examples of conventional signifiers of meter include the jazz ride cymbal/hi hat pattern, the pop/rock backbeat, and syncopated patterns familiar within a particular style, such as standard clave or time line rhythms. These rhythms repeat at what is typically conceived of as the measure or half-measure level. Syncopated grooves often feature other rhythmic repetitions that are one or two measures long—that is, still typically shorter than Ostinato 2.
Return to text
38. Sawatzky (2017) presents a theoretical model, “metric multivalence,” for understanding situations of metric ambiguity or multiplicity in positive terms (in which meter emerges from co-present grouping structures that mutually inform one another) rather than negative terms (in which these grouping structures are heard to obscure a predefined metric structure).
Return to text
39. Passages like this one also share a general harmonic affinity with the referenced portion of Ostinato 2. Since it is impossible to identify its firm formal boundaries and specific component harmonies with certainty (both here and in the Ostinato 2 passage itself), I focus on the pitch series in my description. That said, it seems likely that harmonic allusions play an important role in the perception of similarity. Specific harmonic progressions may also be guiding Taborn’s improvisation.
Return to text
40. The only exceptions are slight rhythmic variations in the fifth and eighth cycles and single altered pitches in the eighth and twenty-second (final) cycle.
Return to text
41. The attentive listener may note a hint of Ostinato 2 from “Avenging Angel” that creeps in around 0:17–0:25.
Return to text
42. The process by which this ostinato varies and dissolves is somewhat similar to the one described below, but seems to happen more quickly. In the broader sense of the word, its groove—gentle, mysterious, and fluid, with two clear beat levels and a certain pitch/harmonic palette—still underpins the rest of the middle phase.
Return to text
43. This is why I included both versions of the D3–G2–G3/A3 gesture in the paradigmatic series: although neither the A3 nor the G3 occurs in this position as frequently as other notes in the series, the approximate gesture is important and memorable.
Return to text
Copyright Statement
Copyright © 2021 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
10376