Reframing Generated Rhythms and the Metric Matrix as Projections of Higher-Dimensional Lattices in Scott Joplin’s Music*
Joshua W. Hahn
KEYWORDS: meter, rhythm, beat class theory, syncopation, ragtime, poetry, hyperspace, Joplin, Du Bois
ABSTRACT: Generated rhythms and the metric matrix can both be modelled by time-domain equivalents to projections of higher-dimensional lattices. Scott Joplin’s music is a case study for how these structures can illuminate both musical and philosophical aims. Musically, lattice projections show how Joplin creates a sense of multiple beat streams unfolding at once. Philosophically, these structures sonically reinforce a Du Boisian approach to understanding Joplin’s work.
DOI: 10.30535/mto.27.2.10
Copyright © 2021 Society for Music Theory
Introduction
[1] “Dr. Du Bois, I’ve read and reread your Souls of Black Folk,” writes Julius Monroe Trotter, the protagonist of Tyehimba Jess’s 2017 Pulitzer Prize-winning work of poetry, Olio. “And with this small bundle of voices I hope to repay the debt and become, in some small sense, a fellow traveler along your course” (Jess 2016, 11). Jess’s Julius Monroe Trotter is a fictional character inspired by James Monroe Trotter (1842–1892), a Black historian who catalogued Black musical accomplishments.(1) In Jess’s narrative, Trotter writes to W. E. B. Du Bois to persuade him to help publish composer Scott Joplin’s life story. As we imagine reading the work through Du Bois’s eyes, Du Bois’s philosophy ultimately frames the narrative collection for us. In Olio, Trotter’s “bundle of voices” consists of interviews about Joplin, which Jess intersperses with poetry about Black artists of Joplin’s time. Olio is part mathematical poetry, part homage, and part historical fiction about Joplin, ragtime, and Joplin’s Black artistic contemporaries. This article seeks music-theoretical insight within Jess’s fascinating poetry. I frame and motivate this project by tying the theory to Jess’s addressee: Du Bois, an important Black philosophical voice of Joplin’s time, who shared Joplin’s politics of racial uplift.
[2] Du Bois’s ideology of racial uplift, rooted in and informed by his groundbreaking sociological research, depended upon his ability to reject the white supremacy of the dominant culture. Du Bois used hyperspace philosophy to advance his arguments (Zamir 1995). Hyperspace helped him construct a humanized Black subject; in hyperspace, the Black subject can exist outside of and peer into the white world, a strategy that Paget Henry has called potentiated second sight (Henry 2006). Du Bois used hyperspace philosophy to critique white supremacy through concepts such as the fourth dimension of color, second-sight, double-consciousness, and the Veil of Race.
[3] At the turn of the twentieth century, hyperspace philosophy included a wide range of mathematicians, scientists, spiritualists, and philosophers who espoused highly divergent sets of goals and beliefs. Hyperspace philosophers speculated that our world’s three dimensions could be one slice or shell of a larger world of four dimensions. Mathematicians such as Simon Newcomb argued that “space of four dimensions, with its resulting possibility of an infinite number of universes alongside our own, is a perfectly legitimate mathematical hypothesis” (Newcomb 1898, 4). In Charles H. Hinton’s Scientific Romances, referenced in Du Bois’s Harvard notes, Hinton suggests that “in the imaginary physical existence [of four dimensions], much that philosophers have written finds adequate representation.” Hinton sought to “supply us
[4] I advocate for borrowing the techniques and insights of hyperspace philosophy to better understand Joplin’s music. In the first section, I use the geometry of higher-dimensional lattices to model Joplin’s rhythms. The lattice reveals that the generated rhythms described by Jeff Pressing (1983) and the metric matrix described by David Locke (2009) are analogous structures composed of multiple simultaneous beat streams.(2) This insight has important ramifications for rhythm theory more broadly, because previous study of generative rhythms has tended to overlook the existence of multiple simultaneous beat streams. By introducing a second dimension into the model, we can easily highlight multidimensional aspects of the music that were previously difficult to access. The lattice model does not replace previous models, but rather the lattice is one approach among many that are useful for producing analytic insight.
[5] In the second section, I use the model to visualize multiple simultaneous beat streams in specific Joplin excerpts. I also use the lattice to highlight how the beat streams evolve over time in concert with Joplin’s other structural elements. In the third section, I contextualize Joplin’s music within the politics of racial uplift, and I argue that the rhythmic intricacies studied in the second section were critical to Joplin’s own politics.
[6] My application of Locke’s metric matrix, an African musical system, to Joplin, an African American composer, is motivated by Locke’s own interdisciplinary approach and by the presence of African retentions in ragtime. One of Locke’s motivations for using the metric matrix in Yewevu, a West African religious music, is to “strengthen the basis for comparative study of this musical genre,” with the hopes that similar strategies will help scholars in many disciplines, including “African-American and American studies, jazz studies and percussion” (Locke 2010, [1]). Locke’s theory applies to African American music. Locke also uses ideas from African American music to support and develop his metric matrix concept. For instance, he borrows the terminology “rhythm section,” “phrased over the barline,” and “swing timing” from jazz to develop nuances of his theory (2010). The metric matrix is a cross-cultural analytic resource. Furthermore, Samuel A. Floyd Jr. and Marsha J. Reisser (1984, 22) point to “the use of pentatonic scales, large leaps in the melodic lines, the use of short phrases in the construction of melody,
Higher-Dimensional Lattices Model Joplin’s Rhythms
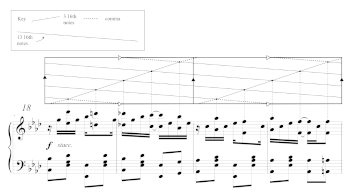
[7] Within Joplin’s music, complex patterns in one dimension of time can be modelled by simpler lattices in higher dimensions. To understand these higher dimensions, we can look to the popular hyperspace philosophy of Joplin’s time. Imagine a second dimension of time perpendicular to our familiar, single temporal dimension. This second dimension manifests itself not as a simultaneous layer, as in multiple simultaneous staves in a printed score, but rather as a linearly independent vector in two-dimensional space. Time events become points located within a two-dimensional coordinate system. Since we typically see our time continuum as one-dimensional, we need to take an imaginative leap to understand objects in this two-dimensional system—a conceptual leap that Du Bois also contemplated.
Example 1. Drawing from Abbott’s Flatland
(click to enlarge)
[8] While studying at Harvard, Du Bois thought deeply about one such scenario. Du Bois studied Edwin A. Abbott’s popular 1884 Flatland: A Romance of Many Dimensions (Zamir 1995, chap. 2). In Flatland, Abbott satirizes Victorian society’s authoritarian views on class and gender using hyperspace philosophy. Abbott describes an encounter with the “King of Lineland” (Example 1). The King “was persuaded that the Straight Line which he called his Kingdom, and in which he passed his existence, constituted the whole of the world
[9] The King of Lineland’s experience of space mirrors a linear concept of time that is the hallmark of traditional European thought. For instance, in classical physics, time is purely chronological and one-dimensional. “In classical physics, we had one clock, one time flow, for all observers
[10] Ragtime has a high degree of temporal multidimensionality. Floyd and Reisser (1984, 45) write, “Some of the musical events that are commonly called syncopations are actually shifts in the metric organization of the melodic material. Heard against the even pulse of the left-hand part, however, when this part is used as a reference, the metric shifts in the melody may be felt as syncopations.” In Floyd and Reisser’s analysis, the meter of the right-hand’s phrase unfolds at a different rate than the left hand, making the music complex and multidimensional. I propose that imagining musical rhythm as a two-dimensional array of events can enable us to visualize these multidimensional aspects of ragtime.
[11] To help visualize extra dimensions of space, the hyperspace philosophy of Joplin’s time involved two techniques: projection and intersection. Through projection, one can try to understand a higher-dimensional object by examining the figure’s shadow cast on a lower-dimensional surface. A second option, intersection, involves examining lower-dimensional slices of the higher-dimensional figure. Tony Robbin argues that ultimately projection proved more vital to modern culture, so this article focuses on that method (Robbin 2006, chap. 11). Projection is philosophically more desirable because it allows us to consider whole figures rather than discrete slices. A shadow of a hyperfigure taken in its entirety contains lines and patterns connected together in a shape that reflects the form of the whole. Taking a slice of a hyperfigure, on the other hand, results in non-linear or idiosyncratic results. Projection is more useful as the basis for a theory, because it is ultimately simpler and more predictable. Rhythms and metric systems that seem asynchronous as distributions of points over one dimension of time can be modelled by simpler two-dimensional figures projected onto a “Lineland” time domain. This new framework is what constitutes the lattice-projection model.
[12] Generated rhythms, a key element of Joplin’s music, can be modelled by projections of two-dimensional lattices. Generated rhythms were originally defined by Pressing (1983). For a rhythm to be generated, every onset in the rhythm must be connected to every other onset in the rhythm by an unbroken chain of onsets that are separated by a constant duration called the generative interval. The chain of onsets, and the durational intervals between the onsets, may wrap from the rhythm’s end back to its beginning any number of times without constituting a break in the chain; when the rhythm is repeated many times in a musical setting, these chains overlap and accumulate into more complex rhythms. Generated rhythms are said to be prime generated when the generative interval’s length in pulses is coprime with the number of total pulses per repeated cycle of music. Prime-generated rhythms have many special properties as discussed below. Marc Wooldridge (1992) determined the frequency of every rhythmic set in Joplin’s syncopated piano music and found that prime-generated rhythms appear more frequently than can be explained by chance alone. He concluded that Joplin preferred prime-generated rhythms.
[13] I have adopted the rhythmic set notation of Erik Demaine et al. (2009), which is based on Godfried Toussaint’s (2005) notation. Within this notation system, the integer n is defined as the total number of available positions within a rhythm, given a smallest durational note value.(4) The integer k is defined as the number of onsets in a rhythm.(5) Using this notation, a generated rhythm with k onsets distributed among n pulses and a generative interval of \(g\) is \(\{ig \mod n: i \in [0, k-1]\}\). This definition uses mathematical set notation and modular arithmetic. The brackets \(\{\}\) denote a set. “\(ig \mod n\)” is the modulo operator, or the remainder after dividing ig by n. The colon “:” is a logical symbol used in set notation equivalent to the short phrase “such that.” The expression \(i \in [0, k-1]\) means that the integer i is allowed to range between the integers 0 and k − 1. Taken together, the notated set indicates that, to generate the rhythm, one takes the integers 0 through \(k-1\), multiplies each one by the generative interval g, and computes their remainders mod n.
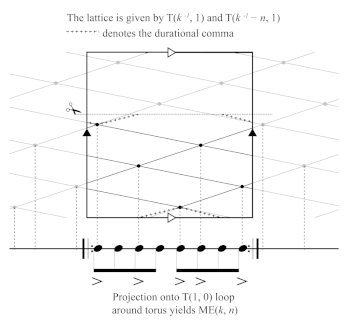
[14] The lattice-projection model enhances the clock-face model of rhythm. The widely used clock-face model arranges all of the possible time points (0 to n − 1) in a circle, spiral or clock face. Examples of authors who have used a clock-face or circular model include Jay Rahn (1987), Toussaint (2003), and Richard Cohn (2016). A defining feature of the clock-face model is that an angular distance between two points on the clock’s face corresponds not to one duration but to two durations simultaneously—one for rotation clockwise and one for rotation counterclockwise. The lattice-projection model unpacks these two simultaneous durations, revealing generated rhythms’ multidimensionality.
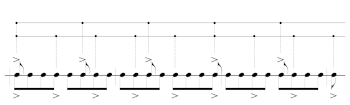
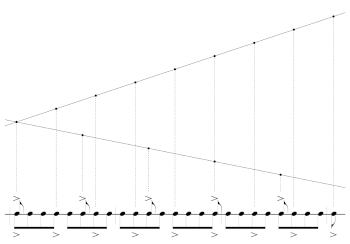
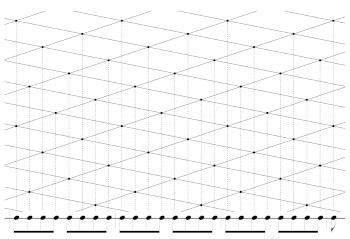
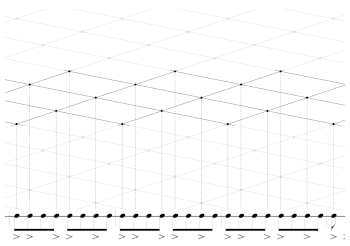
Example 2. 3-generated and 5-generated beat streams shown together
(click to enlarge)
Example 3. The same two beat steams represented by dots along two sloped lines such that the ratio of their slopes is −3:5
(click to enlarge)
Example 4. Copying the sloped lines at the beginning of each bar generates a lattice
(click to enlarge)
Example 5. Select five horizontal rows of dots to yield the generated rhythm with
(click to enlarge)
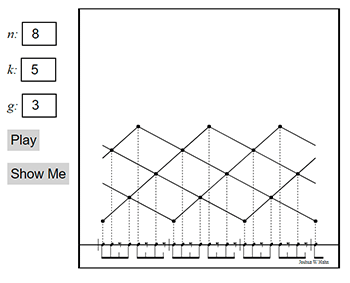
Example 6. Interactive model with construction steps for user-determined values of n, k, and g
(click to interact)
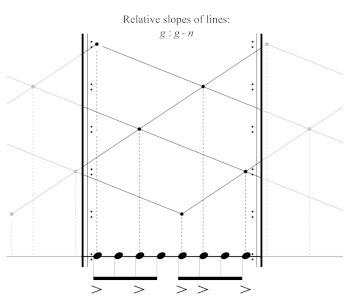
[15] Within generated rhythms, the clock-face model makes no visual distinction between moving clockwise by the distance g and moving counterclockwise by the complementary distance n − g. In reality, both g and n − g are generators with different durational lengths. In their Lemma 3.1, John Clough and Jack Douthett (1991, 144) proved that if g generates the maximally even set M, then n − g must also be a generator of M. The same principle applies to all generated sets, not just those that are maximally even. We can extend Clough and Douthett’s Lemma 3.1 to all generated sets because their proof only relies on the fact that the sets are generated. Using the fact that M is generated, Clough and Douthett write out the { ig mod n : i ∈ [0 , k − 1] } expression of the set M. They show that substituting n − g for g within the set definition yields the inverted set −M. −M, like all generated sets, can be expressed as a rotated version of M. A set’s generators are invariant under rotation. Therefore, since Lemma 3.1 applies to all generated sets, it follows that all generated sets have multiple generators corresponding to both g and n − g.(6) Unlike the clock-face model, the lattice-projection model can visually represent both generators simultaneously.
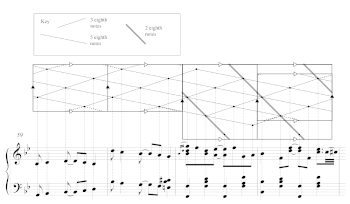
[16] Examples 2–6 illustrate the lattice-projection model for generated rhythms. For this model, we imagine the onsets of a musical phrase to be part of a two-dimensional lattice constructed above the staff. The lattice points project onto the staff’s one dimension of time via vertical dotted lines. To construct the lattice-projection model, start with a stream of straight eighth notes. This example uses n = 8 with bar lines between each successive cycle.(7) Accent every gth eighth note (this example uses g = 3), draw a dot above the accent, and connect the dots with a line. Drop a dotted line from each point to the note it corresponds to. Accent every (n − g)th eighth note, draw a dot above each accented note, connect the dots with a line, and drop vertical dotted lines to the accented notes. After these two steps, we have Example 2. To begin turning this into a two-dimensional lattice, we transform the lines so that the dots remain on their vertical dotted lines, but their slopes have a ratio of g: −(n − g). The lines must intersect at one of the points drawn in the preceding steps. After this transformation, we have Example 3. To complete the lattice, make a copy of the lines and dots at the beginning of every bar (every nth eighth note). This creates the lattice in Example 4. Adjacent points on each ascending line project onto onsets that are g eighth notes apart and adjacent points on a descending line project onto notes that are n − g eighth notes apart. Finally, we create the generated rhythm with k onsets by selecting a vertical section of this lattice that is k lattice points deep (in other words, with exactly k consecutive lattice points on any diagonal line). Example 5 shows this final step. Example 6 is a user interface that accepts arbitrary values for n, k, and g. The interface draws and plays the lattice based on those values. It also guides the user through the steps for drawing the lattice.
[17] The lattice-projection model improves upon the clock-face model by eliminating the visual equivalence between the generative interval g and its inverse, n − g. Instead, g-generated streams move up and to the right as time passes, while (n − g)-generated streams move down and to the right over time. Ascending lines correspond to cycles of onsets separated by a distance g, while descending lines correspond to cycles of onsets separated by a distance of n − g. The model represents both ways of constructing generated rhythms simultaneously.(8)
[18] Lattices can also produce maximally even rhythms, which are important in Joplin’s music. Clough and Douthett (1991) define maximally even sets as sets of points that are spread as evenly as possible within a metric structure. Toussaint (2005) shows that maximally even rhythms are important in many musical traditions.(9) Within Joplin’s music, many of the most common rhythms to appear are maximally even rhythms. In this article, I notate maximally even rhythms using the convention ME(k, n), where k is the number of onsets and n is the total number of isochronous pulses per cycle. The rhythms ME(5, 8) and ME(3, 8) are preferred by Joplin (Wooldridge 1992).(10) Clough and Myerson (1985) prove that maximally even sets with coprime k and n are generated. Clough and Douthett’s Theorem 3.1 shows that when k and n are coprime, maximally even rhythms have two generators given by k−1 and n − k−1, where k−1 is the multiplicative inverse of k mod n.(11) The multiplicative inverse of k mod n is the value k−1 such that kk−1 mod n = 1. Based on this conclusion, it is possible to encompass all maximally even rhythms with coprime n and k within the lattice-projection model by using the method demonstrated in Examples 2–6 and substituting k−1 for g.
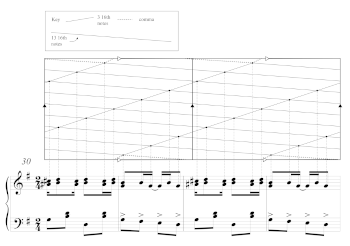
[19] Tyehimba Jess’s Olio inspires several enhancements to the lattice-projection model. Some of Jess’s poetry follows the contours of geometric shapes such as cylinders, tori and Möbius strips rendered according to Jess’s instructions. These geometries further develop the lattice-projection model.
Example 7. Jess’s The Bert Williams/George Walker Paradox in torus form
(click to enlarge)
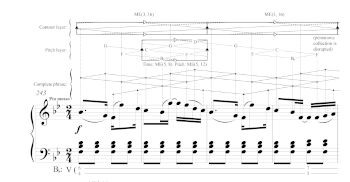
[20] Olio includes two poems on inventive surfaces: The Dunbar-Booker Double Shovel and The Bert Williams/George Walker Paradox. The Dunbar-Booker Double Shovel is voiced from the dual perspectives of the Black poet Paul Laurence Dunbar (1872–1906) and the Black leader Booker T. Washington (1856–1915). Bert Williams (1874–1922) and George Walker (1872–1911) were Black actors, producers, and comedians who collaborated together in plays and minstrel shows. Both poems are printed in two columns on extra-large paper measuring 10 inches wide by 14½ inches tall. Olio provides instructions for folding the poems into several shapes, including a cylinder, a torus, and a Möbius strip. On the flat page, each column contains verse spoken by one of two speakers. When the poem wraps around in a cylinder, torus, or Möbius shape, however, the reader mixes the two poems at will and becomes an active participant by complying with Jess’s directive to “create your own path” (2016, 213). Jess compares this alternating mixture of voices to the sounds of syncopated music, writing that The Dunbar-Booker Double Shovel is “syncopated verse: Dunbar’s dialogue and Booker’s intertwine when combined
Example 8. Cylinder enhancement to the lattice-projection model
(click to enlarge)
[21] Jess’s appendix directs the reader to roll poems into a “cylinder that reads back and forth and up and down, end of line into beginning into end again until there is no beginning
[22] Like the original lattice-projection model, the cylinder model visually separates g and its inverse into linearly independent trajectories, highlighting the rhythm’s multidimensionality. In Example 8, lines that spiral diagonally up the cylinder pass through streams of beats that are faster, while lines that spiral diagonally down the cylinder pass through beat streams that are slower. The multidimensional surface of the cylinder captures both beat streams at the same time.
[23] An improvement upon the cylinder model uses the second of Jess’s manifolds: “When you attach their ends once more, you’ll find their tale told in torus form” (2016, 214). It is possible to use a special property of maximally even rhythms (with coprime k and n) to wrap the cylinder model from top to bottom, as Jess specifies, while preserving quasi-isochronous beat streams in the lattice. That property is the existence of a durational comma, a term codified by Cohn (2016), within every maximally even rhythm with coprime k and n.(13) As I will show, Cohn’s concept of the durational comma is applicable to all maximally even rhythms because of the mathematical properties of the modular multiplicative inverse. The durational comma brings about closure in a maximally even rhythm’s dual generative cycles through an approximation of the generative interval that completes the generative cycle and returns back to the first onset of the cycle. The existence of a durational comma within every maximally even rhythm with coprime k and n is assured by the generative interval k−1. Once the generative cycle reaches the kth onset, the final onset in the cycle, the generative interval has been superimposed a total of k − 1 times. This amounts to a total metric displacement of (k − 1)k−1, which is congruent to 1 − k−1 mod n. Returning to the beginning of the cycle requires moving an additional distance of k−1 − 1, which is a good approximation of k−1. The concept of the durational comma allows k−1 − 1 to stand in for k−1 in order to close the cycle and preserve a quasi-isochronous beat stream. Similarly, the n − k−1 beat stream has a durational comma of (n − k−1) + 1 that preserves quasi-isochrony and returns to the first onset of the generative cycle.
Example 9. Torus enhancement to the lattice-projection model shown with n = 8 and k = 5
(click to enlarge)
[24] Example 9 illustrates this principle. The large square with arrowheads on its sides in Example 9 is an unwrapped representation of a torus. The right side of the large square wraps back to the left side, and the top of the large square wraps back to the bottom of the square. The convention T(p, q), from torus-knot theory, is used to notate torus curves, where p is the number of times the curve wraps from right to left, and q is the number of times the curve wraps from top to bottom. Example 9 shows the lattice formed via the intersections between T(k−1, 1) and T(k−1 − n, 1) (n = 8 and k−1 = 5 in the example). The lattice points are projected onto a ring around the torus given by T(1, 0). The staff below the torus in Example 9 shows how the lattice points project onto onsets over time. If the torus is unaltered and the torus curves are allowed to run their course, the two torus curves intersect n times. The intersections’ projections cycle through n points each separated by an equal distance before returning back to the point they started from. However, after following along either of the torus curves and encountering the first k intersections of the lattice, it is possible to prematurely wrap the generated cycle back to the beginning using a durational comma. In the figure, a thin dotted line with scissors shows where the torus could be cut and reattached to the bottom to complete a quasi-isochronous lattice.(14) A different style of dotted line is superimposed over the original lattice to show how the durational comma fits into the overall lattice structure. ME(5, 8) is shown in Example 9, but the same principle applies to all ME(k, n) where k and n are coprime.
Example 10. Joplin’s Magnetic Rag, mm. 59–62
(click to enlarge)
Example 11. Joplin’s Magnetic Rag, mm. 1–2
(click to enlarge)
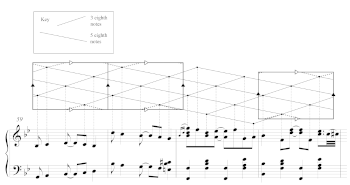
[25] The end of the third strain of Joplin’s Magnetic Rag (1914) illustrates how Joplin integrates these torus structures into his music. In Example 10, two repetitions of ME(5, 8) are followed by a generated rhythm that serves as a smooth transition to a different rotation of ME(5, 8) without interrupting the lattice structure. In Example 10, onsets that are separated by three eighth notes have a diagonally ascending line above them, and those separated by five eighth notes have a diagonally descending line.(15) I draw a box around complete maximally even rhythms to show where a durational comma wraps the beat streams from top to bottom. The ME(5, 8) rhythm in mm. 59–60 expands upon the rhythm heard in the opening introduction of Magnetic Rag
Example 12. Intersection pattern between the 3- and 5-generated cycles and the left hand
(click to enlarge)
Example 13. Joplin’s Magnetic Rag, mm. 59–62, with the left hand’s generated sets represented
(click to enlarge)
[26] The left hand of the pianist also plays a significant role in creating a multidimensional musical setting by providing a separate yet steady tempo at a different rate than the beat streams in the right hand’s rhythms. The most common pattern for the left hand in Joplin’s rags is the rhythm (2222), a 2-generated rhythm, which contrasts with the right hand’s 3- and 5-generated rhythms. The left hand’s steady beat stream intersects with the onsets of the generated rhythms in an oscillating pattern illustrated by Example 12. Example 12 shows a lattice formed by the torus loops T(5, 1) and T(−3, 1). Connecting alternating points together yields T(2, 2), which is a torus link composed of two separate, interlocking loops. One of the loops of T(2, 2) corresponds to onsets in the 3-generated cycle that coincide with the left hand, while the other corresponds to onsets that do not coincide with the left hand. Example 12 illustrates how generated rhythms help to shift flexibly and continuously between an onbeat and an offbeat feel simultaneously. Example 13 shows the bass line switching from following the rhythm of the right hand to a steady quarter-note pulse. After the switch, the quarter-note pulse is represented by thick grey lines superimposed over the lattice of the right hand. The example shows how the left hand's pulse can contribute additional multidimensionality.
Example 14. Bethena, mm. 9–12
(click to enlarge)
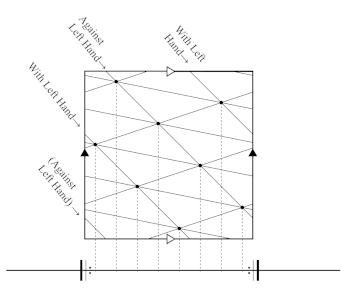
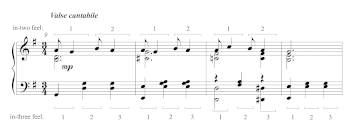
[27] The lattice-projection model creates a spatial framework for David Locke’s concept of the metric matrix (2009). In loose terms, the metric matrix is like a hemiola or cross rhythm, but with more ability to characterize off-beat pulse streams. In a hemiola, you can assume that the duple-meter pulse and the triple-meter pulse will coincide together on the downbeat—but this is often not true in African-diasporic music. To fill this theoretic gap, Locke introduced a system he has called the metric matrix. This system makes it possible to categorize each beat stream by how fast it is unfolding and also by how much temporal displacement it has relative to the downbeat. This concept is useful in Joplin’s triple-meter syncopated music. Locke writes, “multidimensionality is pervasive in music with ternary temporal structure because this type of patterning of time so readily enables three-in-the-span-of-two musical action” (2009, 17). Similarly, in Joplin’s triple-meter syncopated music, the two hands of the pianist outline a two-with-three cross rhythm. Example 14 from Joplin’s Bethena (1905) is an example of the two-with-three cross rhythm in Joplin’s music. The right hand repeats a rhythm consisting of an eighth note followed by a quarter note. Simultaneously, the left hand plays only quarter notes. The rhythm shown in Example 14 occurs throughout Bethena and is especially frequent in the main theme of the composition. This two-with-three structure fits within Locke’s metric matrix framework.
[28] Locke’s choice of musical cubism as a metaphor for the metric matrix resonates with the geometric strategies of this article. Cubist painters were inspired by hyperspace philosophy. The term “fourth dimension” appears in cubist writings, and the figures in cubist paintings resemble hyperfigure projections from mathematical treatises on the subject (Robbin 2006 and Henderson 2013). These cubist geometries are appealing as a metaphor for musical multidimensionality. Cubism also appropriated African art, which presents an unexpected yet complex point of convergence between African culture and the European painters. These painters considered Africans to be “primitives.” Mimicking African masks reflected colonial domination rather than respect (Chave 1994).(16) Nevertheless, cubism’s geometric language makes it a useful metaphor for musical multidimensionality.
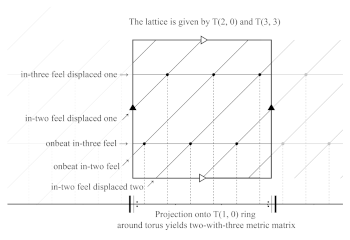
[29] Locke’s metric matrix codifies the musical quality of simultaneous multidimensionality. In ternary structures, the metric matrix contains not only the simultaneous duple and triple pulses that include the downbeat of the meter, but also all the displaced versions of those pulses. In a six-pulse ternary metric structure, the full spectrum of possible beat streams in the metric matrix consists of two displaced versions of the in-three feel and three displaced versions of the in-two feel. Beat streams that include the downbeat are said to be onbeat, while beat streams that do not include the downbeat are said to be displaced. For instance, the beat stream “in-two feel displaced one” has two beats per bar, but the beats arrive one isochronous pulse after the onbeat in-two feel.
[30] Sunzi’s remainder theorem states that for two coprime integers n and m, the value of an integer i mod nm can be determined uniquely by the values of i mod n and i mod m (Yong and Se 2004). Consequently, as long as the numbers of pulses within the beat streams of the metric matrix are coprime, an onset’s position in time is uniquely defined by its matrix-beat-stream membership. This fact suggests that it is possible to construct graphic representations of metric matrices by depicting points in time as points in space, and representing the matrix’s component beat streams as straight lines connecting the points to form a lattice.
Example 15. The metric matrix in torus form
(click to enlarge)
[31] Locke also thought of the matrix graphically: “This temporal matrix is reminiscent of the spatial grid at work in European realistic visual representation, which was based on the logical principles of Euclidean geometry” (2009, 19). In the lattice-projection model, as in Locke’s metaphor, the metric matrix is modelled by a grid. Example 15 represents the two-with-three metric matrix graphically. Each of the matrix’s component beat streams are represented by a loop winding around the torus. T(2, 0) is my notation for two T(1, 0) loops that are equally distributed on the torus. In the model, the two loops of T(2, 0) are the two displaced versions of the in-three feel, and the three loops of the torus link T(3, 3) are the three displaced versions of the in-two feel.(17) The beat streams intersect at six points, and their projections onto the T(1, 0) loop yield their positions in the six-pulse cycle.
[32] Based on these mathematical insights, we can understand the metric matrix within the lattice-projection model enhanced with Jess’s torus. Jess’s metaphors and structures yield powerful insights. In the lattice-projection model, syncopated music doesn’t just elicit a comparison to the paradox of the torus; these rhythms are described by a torus-shaped model.
Analysis of Joplin’s Rags
[33] Lattice projections apply to Joplin’s music. In the following section, I analyze select examples of lattice projections. Wooldridge’s 1992 statistical analysis of generated rhythms in Joplin’s work illuminates how Joplin’s larger body of work can yield to similar strategies as those explored here. Wooldridge studied a sample of 39 piano rags out of the 50 piano pieces that were published in the Collected Piano Works edition (Joplin et al. 1971). He first eliminated all works in triple meter, which left 42 pieces.(18) Then, he eliminated three works with little-to-no syncopation, which left him with 39. Wooldridge’s analysis includes all the music discussed here except for Bethena and the opera Treemonisha.
[34] Wooldridge (1992) focused on identifying generated sets and establishing that they are preferred by Joplin. The outcome of that study included tables of beat-set-class frequencies that Wooldridge used to determine Joplin’s rhythmic preferences. The lattice can further build upon Wooldridge’s algebraic and statistical approach by showing visually how these generated sets interact with one another in specific scenarios, allowing us to see how Joplin’s sequencing of generated sets can fit into Joplin’s overall design goals. In his concluding remarks, Wooldridge anticipated that such a disaggregated analytic approach might be fruitful: “it is possible that rhythmic functions for particular [prime-generated sets], similar to the tonal functions of tonic, subdominant, and dominant, may be found to be operative” (1992, 314). I provide several examples that illustrate how the lattice can interact with Joplin’s more holistic designs. In Magnetic Rag, I use the lattice to reflect on Joplin’s phrase design. In Elite Syncopations, I use the lattice to show how several layers of rhythm interact. In the Treemonisha theme, I use the lattice to comment on the interaction between pitch and rhythm. I also expand upon Wooldridge’s study by including Joplin’s triple-meter rags, which Wooldridge excluded from his analyses.
Example 16. Second strain from Joplin’s Magnetic Rag
(click to enlarge)
[35] The second strain of Joplin’s Magnetic Rag provides an example of how Joplin’s use of generated rhythms and phrase design interact. Written in 1914 and among Joplin’s last compositions, Magnetic Rag is considered to be a particularly faithful representation of Joplin’s intentions for the art of ragtime. Edward A. Berlin, the author of Joplin’s 1996 biography, writes, “Since [Joplin] published [Magnetic Rag] himself, we can assume it reflects his wishes in every respect” (Berlin 1996, 230). In Example 16, a lattice is drawn above the staff such that onsets that are three eighth notes apart are connected with a diagonally ascending line, and onsets that are five eighth notes apart are connected with a diagonally descending line. In measures that form the set ME(5, 8), a box is drawn around the lattice showing where the durational comma wraps the lattice from top to bottom like a torus, creating quasi-isochronous beat streams. Similarly, in mm. 5, 7, and 13 of the strain, one of the 3-generated beat streams wraps from the top of the lattice to the bottom because eight consecutive 3-generated beats makes a complete 3-with-8 cross-rhythm. The wrapping that occurs after eight consecutive onsets is continuous without the use of a durational comma. The second repeat of the phrase is not included because Joplin breaks the rhythmic pattern in the second repeat. This diagram makes it possible to visually trace several simultaneous beat streams through the second strain.
[36] The strain’s phrase design centers around Joplin’s variation of the two-measure unit heard in mm. 22–23 and 30–31 of the strain. Measures 24–25 and 32–33 comprise a V–i harmonic variation of mm. 22–23. In mm. 26–27 and 34–35, Joplin substitutes a new rhythm with seven onsets in mm. 26 and 34, which, along with upward scalar motion, gives a sense of heightened direction and speed. Measures 26 and 34 lead into a third variation of the ME(5, 8) rhythmic pattern in the subdominant. Finally, m. 28 is a downward scalar version of m. 26 that leads into a half cadence. Overall, the 16-bar phrase has a symmetrical or classical-period-like design, with the second half, mm. 30–37, duplicating large parts of mm. 22–29. However, mm. 30–37 lead to even more forward momentum in mm. 36–37, which is composed of two seven-onset generated rhythms and a second half cadence. The second repeat of the phrase is an authentic V–i cadence, which gives a sense of finality to the strain. Joplin manages to make variations on the two-measure rhythmic unit in mm. 22–23 and manipulate the speed and direction of the right-hand melody while maintaining a continuous sequence of interlocking generated sets. As can be seen in the diagram, the six-onset rhythm in mm. 22, 24, 30, and 32 continue all of their component beat streams in the ME(5, 8) rhythms that follow them. This continuity is readily apparent from the lines that connect the onsets in adjacent measures. Measures 26, 28, and 34 create forward momentum by removing the onset on beat 4 and by adding all the remaining onsets. This has the effect of still continuing the beat streams from the ME(5, 8) rhythm in the preceding bar while simultaneously shifting the locations of the onsets and producing a variation with more momentum. This forward momentum helps lead to the cadences that give the strain its symmetric phrase design. The lattice model reveals how Joplin’s inventive use of rhythm interacts with his phrase designs.
[37] It is highly unlikely that the lattice structure pictured in Example 16 could be drawn over a random assortment of rhythmic onsets. Wooldridge (1992, 293) calculated that generated rhythms with g = 3 and n = 8 should occur 23% of the time if rhythms are chosen at random. The second strain of Magnetic Rag is composed of generated rhythms with g = 3 in 15 out of 16 measures, which is approximately four times more frequent than Wooldridge’s calculated random average. A lattice structure such as the one pictured in Example 16 is possible when the phrase consists of generated rhythms, so a continuous lattice structure is very unlikely to be a chance occurrence.
Example 17. Measures 18–21 from Joplin’s Maple Leaf Rag
(click to enlarge)
Example 18. Measures 30–33 from Joplin’s Original Rags
(click to enlarge)
[38] Joplin also used generated rhythms within metric structures with n = 16. Cohn (2016, [5.6]) identified generated rhythms with a 16-pulse cycle in mm. 1–2 and mm. 18–21 of Joplin’s Maple Leaf Rag (1899b). Example 17 shows the maximally even rhythm ME(5, 16), a 3-generated rhythm, in the onsets emphasized by an octave in the right hand, a pattern that repeats continuously throughout mm. 18–28. Similarly, Joplin’s Original Rags (1899a) features the generated rhythm ME(11, 16) prominently in the second strain as shown in Example 18.
[39] As discussed in the preceding section, the lattice is a powerful descriptive model because it visually places equal emphasis both on the g generator and on its partner, the n − g generator. Previous models, such as the clock-face model, emphasized the g generator while overlooking the n − g generator. Within Joplin’s duple-meter rags, g equals 3 in the typical case and n − g = 5. Accordingly, the lattice model is an enhancement over previous descriptive models especially in cases where the 5-generator has musical emphasis. Two such cases are the third strain of Elite Syncopations and the main theme of Treemonisha.
Example 19. The final strain from Elite Syncopations
(click to enlarge)
Example 20. Measures 243–51 from Joplin’s Treemonisha
(click to enlarge)
[40] Elite Syncopations’ fourth strain is a virtuosic, scintillating finale that features a complex rhythm in the right hand, repeating with slight variation over the course of the strain. Joplin provides multiple layers of rhythmic hierarchy in the right hand using octave reinforcement and melodic contour. As in Example 17 from Maple Leaf Rag, the octave-reinforced notes outline 3-generated sets. However, unlike in Maple Leaf Rag, the 3-generation in Example 19 does not continue uninterrupted through each two-measure unit, but rather the rhythm consists of two different ME(3, 8) sets that alternate back and forth. This has the effect of weakening the 3-generated beat streams while the 5-generated beat stream connecting the higher notes in the melody remains continuous and uninterrupted. Moreover, the top notes emphasized by Joplin’s melodic contour conform to the same 5-generated set throughout the majority of the strain. The fourth strain of Elite Syncopations shows how the lattice model can reveal multiple layers of rhythmic activity occurring at different simultaneous tempi, and in particular how the 5-generated beat stream can occupy a position of higher priority than the 3-generated beat stream.
[41] The Treemonisha main theme provides another example of an audible 5-generated rhythm. In the introductory text to the opera, Joplin (1911, 3) writes that “this strain of music is the principal strain in the Opera,” underscoring the theme’s importance. As Example 20 shows, the theme’s melodic contour is guided by an overarching 5-generated rhythm. The 5-generated rhythm starts on the downbeat where the theme begins, includes the higher F in the octave displacement, and includes the highest G of the theme. In m. 246, Joplin creates a variation of the theme where he substitutes the theme’s lowest F for the third of the 5-generated notes. I argue that this note is similarly rhythmically important because it is a low extreme of the melody’s contour, and it occupies the position in the melodic variation that was formerly the highest note in the theme.
[42] Simultaneous with the 5-generated contour are several 3-generated beat streams as shown by the lattice marked “complete phrase.” The onsets of the complete Treemonisha theme do not form a generated rhythm, but the lattice shows the trajectory of several interwoven beat streams. The contour layer’s 5-generated set M(3, 16) has a comma that spans six sixteenth notes. Joplin splits this comma into two three-sixteenth-note units to set up a lilting 3-generated section of the theme beginning on the high F of the theme and extending through the high G of the theme. The 3-generated streams from the comma continue uninterrupted on either side of the comma to generate additional rhythmic onsets. The 5-generated beat stream set up by the contour layer also extends through an additional three onsets encompassing six onsets in total. The Treemonisha theme is an example of the lattice model’s analytic potential. A purely algebraic analysis of the Treemonisha theme would uncover the 5-generated contour set, but because the Treemonisha theme as a whole is not generated, taking a purely algebraic approach would risk missing the intricate interplay of several beat streams that run through this set. A clock-face model would also make these details difficult to discern because, on the clock face, it is difficult to visually parse out the 5-generated streams and the 3-generated beat streams simultaneously. The lattice model shows how each of these beat streams fit together to support the whole.
Example 21. Measures 1–10 from Joplin’s Treemonisha
(click to enlarge)
[43] Joplin’s Treemonisha theme is remarkable in that the pitch and time domains reinforce and complement each other. Although the focus of this article is on the time domain in Joplin’s music, this complementary relationship requires a brief examination of pitch in the Treemonisha theme. In a departure from Joplin’s other syncopated compositions, Joplin abandons the ragtime oom-pah in the bass clef for a sequence of straight eighth notes repeating a 2nd-inversion
[44] The theme’s pentatonic collection, a pitch-domain generated set, mirrors a time-domain generated set in the Treemonisha theme. Generated sets were first described in Pressing’s 1983 article, in which he described a cognitive isomorphism between the rhythm ME(7, 12) (2212221) and the diatonic major scale of European music. Joplin’s Treemonisha theme is remarkable because it contains isomorphic structures running in parallel.(19) In m. 244 and m. 248 in Example 20, the pentatonic collection (
Example 22. Measures 19–22 from Joplin’s Treemonisha
(click to enlarge)
Example 23. Measures 208–10 from Joplin’s Treemonisha
(click to enlarge)
[45] Joplin’s use of the
[46] Beyond these specific examples, lattice projections can be used to interpret Joplin’s larger body of work. As shown in the preceding section, it is possible to use the projection of a lattice to model generated rhythms. Wooldridge (1992, 293) calculated that the generated rhythm with g = 3 occurs in 53% of measures in 39 Joplin compositions studied, which is over twice as likely as Wooldridge’s expectation for randomly chosen rhythms.(21) Generated rhythms’ frequency suggests that lattice projections can uncover insights in other Joplin works.
[47] Likewise, the metric matrix serves an important role in Joplin’s music both rhythmically and as a strategy to differentiate between multiple voices in compound melody. In the main theme of Bethena, the pattern (1212) occurs in the vast majority of measures in the right hand, while the pattern (222) occurs in every measure of the left hand. The pattern (1212) consists of two displaced versions of an in-two feel: an onbeat duple beat stream and a duple beat stream displaced by one eighth note. This two-with-three division between the two hands of the pianist occurs in 12 out of the 16 measures of the main theme. The remaining bars consist of rhythmic pauses between sections of the phrase.
Example 24. Bethena, mm. 13–16
(click to enlarge)
Example 25. Bethena, mm. 77–80
(click to enlarge)
[48] Joplin also used the two beat streams in the right hand to delineate two voices of a compound melody. For instance, in mm. 13–16, shown in Example 24, the displaced in-two beat stream corresponds one-to-one with the top voice. The top voice descends through a melodic line spanning an octave leading to the half cadence in m. 16. Joplin assigns an inner voice to the onbeat in-two beat stream. Similarly, in mm. 78–79, shown in Example 25, multiple voices are delineated by their assignment to different beat streams within the matrix. The two voices’ assignments to different beat streams imply that these matrix partials are separate and distinct musical elements, which supports the metric-matrix framework.
[49] These examples have shown specifically how lattice structures can provide analytic insight in Joplin’s work. Wooldridge’s statistical analysis of generated rhythms suggests that lattice structures can be applied throughout Joplin’s body of work. Although many of these examples are drawn from Joplin’s later works, this is not an indication that his earlier works are less complex. Original Rags and Maple Leaf Rag, as demonstrated in Examples 14 and 15, are rhythmically complex pieces composed early in Joplin’s career.
Scott Joplin, Du Boisian Potentiated Second Sight, and Hyperspace Philosophy
[50] In the opening letter of Olio, Jess’s protagonist Julius Monroe Trotter writes to Du Bois with the hope that his Joplin-related interviews will be published by The Crisis, the magazine of the National Association for the Advancement of Colored People. Since Trotter’s ensuing Joplin dossier is addressed to Du Bois, we imagine Du Bois reading it, and so we see it through his eyes. Furthermore, the poetic form Jess invented, the syncopated sonnet, reveals a Du Boisian perspective. Howard Rambsy II (2008) and Emily Rutter (2015) both explore the relationship between Du Bois’s double-consciousness and Jess’s syncopated verse. Syncopated sonnets combine two voices into one poem in a non-linear format that invites the reader to actively participate in the poetry by choosing a path to read through the lines. The poem “Millie and Christine McKoy” is written in the voices of the conjoined twins Millie and Christine McKoy (1851–1912). The McKoy sisters were singers, dancers, and entertainers who were enslaved at birth but eventually gained their freedom and pursued successful performing careers. In the poem, while one voice says, “We’ve mended two songs into one dark skin,” the other says, “We ride the wake of each other’s rhythm” (Jess 2016, 41). This idea of two simultaneous selves echoes Du Bois’s classic statement of double-consciousness from The Souls of Black Folk, in which he writes that one feels “two warring ideals in one dark body” (Du Bois 1903a, 3). Through the framing letter to Du Bois and the syncopated sonnet form, Olio anticipates the Du Boisian lens of this article.
[51] Kevin Gaines provides an illuminating history of the politics of racial uplift that characterized Joplin and Du Bois’s time. Gaines writes that racial uplift in the early 20th century differed from the ideology of previous generations of Black activists. Earlier activists had focused on fundamental human rights. Racial uplift, however, was a “shift from race to culture, stressing self-help.” This shift “represented a limited, conditional claim to equality” (Gaines 1996, 4). Black leaders’ positions on racial uplift, argues Gaines, were an attempt to forge a positive image for African Americans within a white-supremacist society characterized by Jim Crow laws and open racial discrimination. Du Bois and Booker T. Washington, two of the most important figures championing racial uplift, both believed in education’s power to uplift African Americans. However, they differed in that Du Bois believed in the formation of a “Talented Tenth” to inspire the rest through advanced college degrees (Du Bois 1903b) while Washington advocated for expanding “Industrial Education” or vocational school (Washington 1903). Gaines also emphasizes that there were many different approaches to pursuing racial uplift; some leaders such as Ida B. Wells (1862–1931), Thomas Fortune (1856–1928), and at times Du Bois were able to challenge white supremacy directly in contrast to the more mainstream narratives of self-help for African Americans. Anna Julia Cooper (1858–1964), another important voice of the time, challenged the patriarchal norms of mainstream uplift ideology (Cooper 1892). Racial uplift was championed uniquely by many different voices.
[52] Alongside his political activity, Du Bois produced groundbreaking research in sociology such as The Philadelphia Negro (1899). Du Bois hoped that sociological study would “serve as the scientific basis of further study, and of practical reform” (Du Bois 1899, 4). Crucially, Du Bois was able to identify color prejudice and the color line as the true cause of what others called “the negro problem.” He used this insight to construct an alternative perspective to the narrative of self-help. Du Bois’s attempts to dismantle white supremacy were unprecedented; as Gaines (1996) notes, Black intellectuals were up against a powerful and, at the time, seemingly authoritative pseudoscience of race, which sought to establish white supremacy as a scientific fact. Du Bois suggested that Black poverty persisted not through the fault of Black people themselves, but rather because “a large percentage deserve better ways to display their talent, and better remuneration. The whole class deserves credit for its bold advance in the midst of discouragements” (Du Bois 1899, 316).
[53] This alternative critical frame became more explicit in Du Bois’s later work, developing into what Henry calls potentiated second sight. Henry (2006, 90) defines potentiated second sight as the Black subject’s “very special access and insight into the dehumanizing ‘will to power’ of the European subject.” The definition of second-sight (non-potentiated) arises from Du Bois’s famous explanation of double-consciousness, in which he writes:
The Negro is a sort of seventh son, born with a veil, and gifted with second-sight in this American world,—a world which yields him no true self-consciousness, but only lets him see himself through the revelation of the other world. It is a peculiar sensation, this double-consciousness, this sense of always looking at one’s self through the eyes of others. (Du Bois 1903a, 3)
For Henry, Du Boisian second-sight becomes potentiated when the Black subject uses this unique perceptive power to turn the focus back on the white subject, resulting in a uniquely insightful critique of the white subject. Du Bois’s classic expression of potentiated second sight is in “The Souls of White Folk,” an essay in Darkwater (1920). Du Bois writes, “Of [the souls of white folk] I am singularly clairvoyant
[54] Du Bois’s study of hyperspace philosophy at Harvard facilitated the framing of potentiated second sight. For Henry, Du Bois’s potentiated second sight appeared first in “A Vacation Unique” in the form of the fourth dimension of color (Henry 2006). As discussed in paragraph eight of this article, in Du Bois’s story, being Black means being removed into an alternate frame (the fourth dimension of color) allowing one to see into the white world with greater clarity. Du Bois’s two main sources for hyperspace philosophy were Hinton and Abbott, who appear in Du Bois’s Harvard notes (Zamir 1995). Hyperspace philosophy was popular at the time, appearing in at least fifty widely read articles and short stories in the United States from the late 19th century to the end of the first World War (Henderson 2013).
[55] Hyperspace may have also inspired Du Bois’s invention of “the Black World beyond the Veil,” an idea that would have far-reaching influence on his thinking from that point forward. Shamoon Zamir (1995) argues that the Veil could have been inspired by Du Bois’s study of hyperspace philosophy. In Souls, Du Bois frames the idea of the Veil through a story of his youth in Great Barrington, Massachusetts, when “it dawned upon me with a certain suddenness that I was different from the others; or like, mayhap, in heart and life and longing, but shut out from their world by a vast veil” (Du Bois 1903a, 2). Du Bois stresses that being Black means having the same human impulses of “heart and life and longing” as all people, but that an ever-present, all-encompassing “Veil of Race” ensures that “all their dazzling opportunities, were theirs, not mine.” The Veil recalls the fourth dimension of color because of its invisible vastness. To many subjects in Du Bois’s writings, the Veil is invisible, just as the fourth dimension of color in “A Vacation Unique” is invisible to a white friend before an “operation” makes the friend Black. The Veil also recalls spiritualist speculations about the location of the soul in the fourth dimension, because the soul resides in the same location as the Veil.(22) In Souls, Du Bois writes, “In those sombre forests of his striving his own soul rose before him, and he saw himself,—darkly as through a veil” (Du Bois 1903a, 8). The Veil suggests how the philosophy of hyperspace might have had a broader impact on Du Bois’s thinking beyond “A Vacation Unique.”
[56] To what extent did Joplin share Du Bois’s politics of racial uplift and his potentiated second sight? Treemonisha, with its theme of education as a means of uplift, suggests that Joplin shared Du Bois’s ideology. Potentiated second sight is an alternative frame of reference from which the dominant culture’s Black stereotypes can be dismissed and critiqued. Likewise, Joplin sought an alternative frame within which ragtime’s rhythms could become a positive symbol of Black cultural accomplishment.
[57] Joplin reveals his ideology of racial uplift most clearly in Treemonisha. Treemonisha reflects Du Bois’s politics of uplift through “Joplin’s repeated emphasis on the profound importance of education as a means of self-improvement, one of the opera’s major themes” (Lumsden 2015, 50). As with Du Bois’s Talented Tenth ideology, Joplin believed that a strong Black leader was necessary to uplift African Americans. After Treemonisha’s return, in mm. 33–36 of “We Will Trust You as Our Leader,” the chorus sings, “Lead us, and we will surely rise” (Joplin 1911). The Black community’s collective proclamation reveals the centrality of a Black leader in Joplin’s politics of uplift. However, while Washington and Du Bois’s politics of racial uplift envisioned a domestic role for women, Joplin places a woman in the leadership position. When Treemonisha asks, “who will lead the men?” in mm. 55–56 of “We Will Trust You as Our Leader,” the men reply, “You!” (Joplin 1911). Joplin’s expression of uplift ideology in Treemonisha is similar to Du Bois’s but departs in his selection of a woman to lead (Lumsden 2015).
[58] Joplin’s ragtime piano works reveal his politics of uplift as well. Klaus-Dieter Gross (2000, 395) compared Joplin and Du Bois’s approaches: “Just as Du Bois developed a theoretical frame for analyzing the Black experience from the methods of (European) sociology, Joplin fused ragtime with what he knew of European art music.” According to Edward Berlin, this was especially true of Magnetic Rag: “Revealing Joplin’s aims and attitude, he put the tempo indications in Italian, as is customary in classical music
[59] Jess imagines Joplin’s potentiated second sight in the poem “Berlin v. Joplin: Alexander’s Real Slow Drag,” in which Irving Berlin’s actual published response to allegations of stealing Joplin’s music is printed across from Joplin’s imagined response (2016, 173). In Jess’s “Berlin v. Joplin,” Joplin’s words read between the lines of Berlin’s text, satirizing Irving Berlin’s insistence that “if they could produce the negro and he had another hit like ‘Alexander’ in his system, I would choke it out of him and give him twenty thousand dollars in the bargain” (actual words of Irving Berlin quoted in Edward Berlin 1996, 212). Joplin’s potentiated second sight, as imagined by Jess, reveals the inner workings of Irving Berlin’s desire to profit from Black cultural contributions even as he dehumanizes the Black subject. In the following paragraphs, I investigate the extent to which Joplin may have had the potentiated second sight imagined by Jess.
[60] For Joplin, potentiated second sight functions to dismiss the racialized caricature of ragtime and to criticize racist characterizations of his music. Henry writes that potentiated second sight serves “to see through and implode the imposed stereotype,” and to “provide great insight into the psyche of the creators and perpetrators of this tragic farce” (Henry 2006, 91). Similarly, in School of Ragtime, Joplin writes, “Syncopations are no indication of light or trashy music, and to shy bricks at ‘hateful ragtime’ no longer passes for musical culture” (Joplin 1908, 1). Joplin’s remarks in School of Ragtime “appear to be replies to the criticisms that appeared regularly: that ragtime was just a passing fad; that it was inherently inferior, lacking in any musical merit; and that there was something cheap about music that relied upon syncopations” (Berlin 1996, 178). Berlin provides a detailed account of ragtime’s reception, quoting authors such as Leo Oehmler (1914), Francis Toye (1913), and others, who likened ragtime’s syncopated rhythms to an evil force or sickening epidemic. These attacks on ragtime were often racially charged, such as Toye’s claim that ragtime’s hysteria came from the race of its inventors (1913). Joplin, however, tried to reclaim ragtime as a point of pride when he told the New York Age that “ragtime rhythm is a syncopation original with the colored people” (Walton 1913). In contrast to his critics, Joplin believed that ragtime’s success could uplift African Americans. This dismissal is vital to Joplin’s potentiated second sight.
[61] Even as Joplin sought to join the Black elite, however, ragtime faced criticism from within the Black elite. Ragtime “was seen by many as corrupt music, a form which degraded rather than uplifted blacks” (Gross 2000, 402). In an interview with the New York Age, Joplin acknowledged and fought back against these claims. Joplin told the New York Age that “many African Americans were ashamed that ragtime was a creation of their race.” However, Joplin argued that “it is the unwholesome words and not the ragtime melodies that many people hate” (Walton 1913). A number of popular ragtime songs contained racist “coon song” lyrics. Joplin defended himself against criticism from Black elites by distancing himself from the lyrics associated with ragtime (Berlin 1996).
[62] Joplin and his publisher criticized stereotypes assigned to ragtime explicitly in an elaborate advertisement published in Stark publications and in magazines entitled “A Fierce Tragedy in One Act.” In the advertisement, when a patron enjoying Joplin’s music learns that he is Black, she experiences “Sensations—Perturbation—Trepidation—and Seven Other Kinds of Emotion.” She exclaims, “I’ll never come to this theatre again. I just can’t stand trashy music” (Berlin 1996, 71). Potentiated second sight is the method by which Mrs. Van C’s inner emotions, and the absurdity of her conclusion, become visible.
[63] Joplin constructed an independent frame of reference for evaluating his music’s artistry and humanity. An internal frame of reference is essential for Henry, who writes that potentiated second sight requires “the finding of an independent point of self-evaluation” (Henry 2006, 91). For Joplin, an important internal frame of reference was the deliberate craft of his syncopations. For instance, the purpose of School of Ragtime is to correct the imprecise rendering of the art form. “By giving each note its proper time and by scrupulously observing the ties, you will get the effect. So many are careless in these respects that we will specify each feature,” wrote Joplin (1908, 1). Joplin emphasized his rhythms’ careful harmonization, and the fact that these rhythms must be played slowly to be properly heard. By asking his audience to play skillfully and slowly, he rejected the stereotype, perpetuated by Toye and others, that ragtime is hysterical or nonsensical.
Example 26. The first line from Exercise No. 6 in School of Ragtime
(click to enlarge)
Example 27. The final cadence of Stoptime Rag
(click to enlarge)
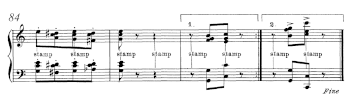
[64] Joplin’s use of multiple staves and dotted lines in School of Ragtime illustrate that Joplin thought it was helpful to think of time spatially. The right hand appears in two versions. The first staff is played normally, and the second staff is “not syncopated” due to added density-referent note values.(23) Joplin explains, “The upper staff is not syncopated, and is not to be played. The perpendicular dotted lines running from the syncopated note below to the two notes above will show exactly its duration” (Joplin 1908, 1). Dotted lines connect analogous time points in the syncopated and not syncopated versions, bridging the divide between the two (Example 26). This striking visual language highlights the spatial relationship between rhythmic onsets on the notated staff. The added density-referent note values show that properly placed rhythmic onsets occupy an equidistant space on the page, and that adhering to this spatial logic will lead to “the proper time divisions to complete the sense intended.” Joplin also used the dotted line in non-pedagogical works. Example 27, depicting the final cadence of Stoptime Rag (1910), shows a typical case of how Joplin used dotted lines to mark foot stomping in the work. Foot stomps and dotted lines also appear in The Ragtime Dance (1902). The foot stomps impart a temporal logic realized as a geometric figure in Joplin’s score. Joplin’s visual language of dotted lines and spatial positioning of onsets support a geometric approach to analyzing his music.
[65] Joplin’s political environment was characterized by the ideology of racial uplift, which sought to raise African Americans’ status in society through self-help and education. At times, Du Bois was able to challenge racism more directly through potentiated second sight, or the reframing of society from the perspective of the Black subject. Joplin was able to identify and challenge racist stereotypes that characterized ragtime, and by extension all African Americans. In a statement of Du Boisian potentiated second sight, Joplin’s School of Ragtime opposes the racial stereotypes assigned to ragtime and teaches readers how to attentively render ragtime’s rhythms.
Conclusion
[66] Rhythms that seem asynchronous in one dimension can be modelled by projections from simpler, higher-dimensional lattices. Similarly, Du Bois used higher dimensions to frame potentiated second sight, a philosophy that serves to humanize the Black subject and critique the white subject.
[67] In a rejection of European worldview, Du Bois writes in “A Vacation Unique” that “ ‘I seriously doubt if there is any truth after all your blatant world-search. Truth is not the object of knowledge nor even consistency. It is the best workable hypothesis’ ” (Zamir 1995 transcribing Du Bois, 225). Hyperspace philosophy, in opposition to traditional European thought, is not concerned with definitively proving the existence of higher dimensions, but rather with considering their existence and expanding humans’ perceptive capacity in the process. Higher dimensions have been used in this article to expand the capacity of a music theory for recognizing the connections between generated rhythms, the metric matrix, and other aspects of the music. This process has required the rejection of traditional, one-dimensional “Western” time. Through lattices in higher dimensions, both Locke’s metric matrix and Pressing’s generated rhythms emerge from a unified, multidimensional concept of time. As the analyses in the second section of this article show, these lattices can reveal new insights about the structure of Joplin’s music.
Joshua W. Hahn
Independent Scholar
Richmond, VA
joshua.w.hahn@gmail.com
Works Cited
Berlin, Edward A. 1996. King of Ragtime: Scott Joplin and His Era. Oxford University Press.
Chave, Anna C. 1994. “New Encounters with Les Demoiselles d’Avignon: Gender, Race, and the Origins of Cubism.” The Art Bulletin 76 (4): 596–611. https://doi.org/10.2307/3046058.
Chireau, Yvonne Patricia. 2006. Black Magic: Religion and the African American Conjuring Tradition. University of California Press. https://doi.org/10.1525/california/9780520209879.001.0001.
Clough, John, and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35 (1): 93–173. https://doi.org/10.2307/843811.
Clough, John, and Gerald Myerson. 1985. “Variety and Multiplicity in Diatonic Systems.” Journal of Music Theory 29 (2): 249–70. https://doi.org/10.2307/843615.
Cohn, Richard. 2016. “A Platonic Model of Funky Rhythms.” Music Theory Online 22 (2). https://doi.org/10.30535/mto.22.2.1.
Cooper, Anna J. 1892. A Voice from the South: By a Black Woman of the South. Aldine Printing House.
Demaine, Erik, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. 2009. “The Distance Geometry of Music.” Computational Geometry: Theory and Applications 42 (5): 492–554. https://doi.org/10.1016/j.comgeo.2008.04.005.
Du Bois, W. E. B. 1899. The Philadelphia Negro: A Social Study. University of Pennsylvania.
—————. 1903a. The Souls of Black Folk. A. C. McClurg and Co.
—————. 1903b. “The Talented Tenth.” In The Negro Problem: A Series of Articles by Representative American Negroes of Today, ed. Booker T. Washington, 31–75. James Pott & Company.
—————. 1920. Darkwater: Voices from Within the Veil. Harcourt, Brace and Company.
Einstein, Albert, and Leopold Infeld. 1938. The Evolution of Physics. Cambridge University Press.
Floyd, Samuel A., Jr. 1991. “Ring Shout! Literary Studies, Historical Studies, and Black Music Inquiry.” Black Music Research Journal 11 (2): 265–87. https://doi.org/10.2307/779269.
Floyd, Samuel A., Jr., and Marsha J. Reisser. 1984. “The Sources and Resources of Classic Ragtime Music.” Black Music Research Journal 4: 22–59. https://doi.org/10.2307/779473.
Foster, Hal. 1985. “The ‘Primitive’ Unconscious of Modern Art.” October 34 (Autumn): 45–70. https://doi.org/10.2307/778488.
Fry, Edward F. 1966. Cubism. McGraw-Hill.
Gaines, Kevin Kelly. 1996. Uplifting the Race: Black Leadership, Politics, and Culture in the Twentieth Century. The University of North Carolina Press. https://doi.org/10.5149/uncp/9780807845431.
Gross, Klaus-Dieter. 2000. “The Politics of Scott Joplin's Treemonisha.” Amerikastudien / American Studies 45 (3): 387–404. https://www.jstor.org/stable/41157951.
Henderson, Linda D. 2013. The Fourth Dimension and Non-Euclidean Geometry in Modern Art. Rev. ed. The MIT Press.
Henry, Paget. 2006. “Africana Phenomenology: Its Philosophical Implications.” Worlds and Knowledges Otherwise 1 (3): 79–112. https://doi.org/10.5840/clrjames20051113.
Hinton, Charles Howard. 1886. Scientific Romances. Swan Sonnenschein & Co.
Jess, Tyehimba. 2016. Olio. Wave Books.
Joplin, Scott. 1899a. Original Rags. Carl Hoffman.
—————. 1899b. “Maple Leaf Rag.” John Stark & Son.
—————. 1902. “The Ragtime Dance.” John Stark & Son.
—————. 1905. “Bethena, A Concert Waltz.” T. Bahnsen Piano Mfg. Co.
—————. 1908. School of Ragtime: 6 Exercises for Piano. Scott Joplin.
—————. 1910. “Stoptime Rag.” Joseph W. Stern & Co.
—————. 1911. Treemonisha. Scott Joplin.
—————. 1914. “Magnetic Rag.” Scott Joplin Music Publishing Co.
Joplin, Scott, Joseph F. Lamb, Arthur Marshall, Scott Hayden, and Louis Chauvin. 1971. Collected Piano Works. Edited by Vera Brodsky Lawrence. New York Public Library.
Locke, David. 2009. “Simultaneous Multidimensionality in African Music: Musical Cubism.” African Music 8 (3): 8–37. https://doi.org/10.21504/amj.v8i3.1826.
—————. 2010. “Yewevu in the Metric Matrix.” Music Theory Online 16 (4). https://doi.org/10.30535/mto.16.4.3.
Lumsden, Rachel. 2015. “Uplift, Gender, and Scott Joplin’s Treemonisha.” Black Music Research Journal 35 (1): 41–69. https://doi.org/10.5406/blacmusiresej.35.1.0041.
Newcomb, Simon. 1898. “The Philosophy of Hyper-Space.” Science 7 (158): 1–7. https://doi.org/10.1126/science.7.158.1.
Oehmler, Leo. 1914. “Ragtime: A Pernicious Evil and Enemy of True Art.” Musical Observer 11 (September): 14–15.
Pressing, Jeff. 1983. “Cognitive Isomorphisms between Pitch and Rhythm in World Musics: West Africa, the Balkans, and Western Tonality.” Studies in Music 17: 38–61.
Rambsy II, Howard. 2008. “Catching Holy Ghosts: The Diverse Manifestations of Black Persona Poetry.” African American Review 42 (3): 549–64. https://www.jstor.org/stable/40301253.
Rahn, Jay. 1987. “Asymmetrical Ostinatos in Sub-Saharan Music: Time, Pitch, and Cycles Reconsidered.” In Theory Only 9 (7): 23–38.
—————. 1996. “Turning the Analysis Around: Africa-Derived Rhythms and Europe-Derived Music Theory.” Black Music Research Journal 16 (1): 71–89. https://doi.org/10.2307/779378.
Robbin, Tony. 2006. Shadows of Reality: The Fourth Dimension in Relativity, Cubism, and Modern Thought. Yale University Press. https://doi.org/10.12987/yale/9780300110395.001.0001.
Roeder, John. 2001. “Pulse Streams and Problems of Grouping and Metrical Dissonance in Bartók’s ‘With Drums and Pipes.’” Music Theory Online 7 (1). https://mtosmt.org/issues/mto.01.7.1/mto.01.7.1.roeder.html.
Rutter, Emily R. 2015. “‘the story usually being ’: Revising the Posthumous Legacy of Huddie Ledbetter in Tyehimba Jess’s leadbelly.” South Atlantic Review 77 (1): 58–78. https://www.jstor.org/stable/43738969.
Schmalfeldt, Janet. 2011. In the Process of Becoming: Analytic and Philosophical Perspectives on Form in Early Nineteenth-Century Music. Oxford University Press.
Schrager, Cynthia D. 1996. “Both Sides of the Veil: Race, Science, and Mysticism in W. E. B. Du Bois.” American Quarterly 48 (4): 551–86. https://doi.org/10.1353/aq.1996.0046.
Toussaint, Godfried. 2003. “Classification and Phylogenetic Analysis of African Ternary Rhythm Timelines.” Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, University of Granada, Spain, July 23–26: 25–36. http://archive.bridgesmathart.org/2003/index.html.
—————. 2005. “The Euclidean Algorithm Generates Traditional Musical Rhythms.” Proceedings of BRIDGES: Mathematical Connections in Art, Music, and Science, Banff, Alberta, Canada, July 31–August 3: 47–56.
—————. 2013. The Geometry of Musical Rhythm: What Makes a “Good” Rhythm Good? CRC Press.
Toye, Francis. 1913. “Ragtime: The New Tarantism.” English Review 52: 375–6.
Trotter, James M. 1968 [1881]. Music and Some Highly Musical People. Charles T. Dillingham. Reprint. Johnson Reprint Corporation.
Wallace, Michele. 2004. Dark Designs and Visual Culture. Duke University Press. https://doi.org/10.1215/9780822386353.
Walton, Lester A. 1913. “Use of Vulgar Words a Detriment to Ragtime.” New York Age, April 3, 1913.
Washington, Booker T. 1903. “Industrial Education for the Negro.” In The Negro Problem: A Series of Articles by Representative American Negroes of Today, ed. Booker T. Washington, 7–29. James Pott & Company.
Wooldridge, Marc C. 1992. “Rhythmic Implications of Diatonic Theory: A Study of Scott Joplin’s Ragtime Works.” PhD diss., SUNY, Buffalo.
Yong, Lam Lay, and Ang Tian Se. 2004. Fleeting Footsteps: Tracing the Conception of Arithmetic and Algebra in Ancient China. Rev. ed. World Scientific. https://doi.org/10.1142/5425.
Zamir, Shamoon. 1995. Dark Voices: W. E. B. Du Bois and American Thought, 1888–1903. University of Chicago Press.
Footnotes
* I would like to thank Ashleigh Gordon, Anthony R. Green, Nora Nunn, and Music Theory Online’s anonymous reviewers for their thoughtful insights, which have contributed significantly to this article. I dedicate this article to the memory of my late grandfather John Kinsey Mealy Jr. (1924–2020), whose lifelong passion for early jazz inspired my interest in Scott Joplin.
Return to text
1. James Monroe Trotter’s Music and Some Highly Musical People ([1881] 1968) appears in Jess’s bibliography to Olio.
Return to text
2. The concept of a beat stream is similar to the concept of a pulse stream proposed by John Roeder (2001).
Return to text
3. Zamir notes that the names of the two characters Du Bois referred to from Abbott’s Flatland were “unclear in the manuscript.” Zamir rendered them as “Mr. Field” and “Mr. Drelic,” but I have substituted “A. Square” and “the King” because those are the only two characters who interacted across the divide between Flatland and Lineland in Abbott’s Flatland.
Return to text
4. The durational value of n has been alternately referred to as the isochronous temporal unit or the density referent (Locke 2009). For instance, in
Return to text
5. k and n are equivalent to John Clough and Gerald Myerson’s d and c, respectively, in their definition of generated sets (1985). The choice of n and k here reflects the fact that this article is focused on the time domain, and d and c stand for the diatonic and chromatic concepts specific to the pitch domain.
Return to text
6. The duple-meter pulse is an unusual case because the generator is equal to its inversion. Some generated sets have more than two generators (the complete set of integers mod 8 can be generated by 1, 3, 5, or 7).
Return to text
7. Graphically, the spacing between each adjacent pair of eighth notes, even those separated by bar lines, must be the same or the lattice will not line up with the eighth notes.
Return to text
8. Jay Rahn (1996, 80) also looks to a higher dimension to unpack generated rhythms’ structure. Rahn writes that diatonic rhythms (which are generated rhythms) “can be understood as twisting or tunneling through time, forming a special, braided structure.” However, the underlying structure of a braid is essentially the same as that of a lattice.
Return to text
9. Toussaint’s list of musical traditions includes European classical music, jazz, Cuban music, middle-eastern music, rock, and African music, among others.
Return to text
10. For convenience, I occasionally notate rhythms as strings of numbers in parentheses, where the numbers specify the number of density referent note values between each successive onset in the rhythm. Rotation of a rhythm is defined as starting the same ordered set of durations from a different onset in the cycle. The density referent note value is the smallest possible note value in the rhythm. For instance, in
Return to text
11. Clough and Douthett (1991) did not name the modular multiplicative inverse specifically, but they instead referred to g1 from their Lemma 3.5. Lemma 3.5 states that when k and n are coprime (substituting k for d and n for c), there is an integer g1 such that kg1 = 1 (mod n). This is the definition of the modular multiplicative inverse.
Return to text
12. This image, taken by Sarah Barker and included courtesy of Wave Books, appears in the appendix to Olio on page 217.
Return to text
13. Cohn (2016) uses the maximally even rhythm ME(5, 16) in the second strain of Joplin’s Maple Leaf Rag as one of his examples of the durational platonic comma. The term “quasi-isochrony” is Cohn’s.
Return to text
14. When ME(k, n) is a hyper-diatonic set, defined by Clough and Douthett (1991) as a set where k is odd and n = 2k - 2, Jess’s Möbius strip surface enhances the model still further. In these cases, Clough and Douthett show that the platonic comma will always be n/2, which means twisting the torus cut along the thin dotted line in Example 9 by 180 degrees before re-closing it, as Jess calls for, has the effect of bringing the kth onset to unison with the first onset, eliminating all discontinuities that would arise from the platonic comma.
Return to text
15. In general, I have chosen to treat the two hands as two distinct rhythmic elements that can be analyzed independently in Joplin. While the left hand typically marks time with a steady stream of beats, the right hand plays complex shifting phrases. The division between these two roles justifies studying the two hands independently.
Return to text
16. Picasso’s Les Demoiselles d’Avignon (1907) is among the first cubist paintings (Chave 1994). Two of the five figures are painted with African masks. Hal Foster (1985) describes “primitivism” in the painting as “an artistic coup founded on military conquest” which “disguises the problem of imperialism in terms of art”; indeed, primitivism is founded on “racial or evolutionary myths.” Complicating matters, Picasso denied that cubism was inspired by African art. However, denials such as these served only to further a Eurocentric narrative that erased the influence of African art and argued that African-like forms emerged independently within European art (Wallace 2004). The connections between primitivism, cubism, and hyperspace were summarized by one critic: “The Primitives
Return to text
17. The torus model for the metric matrix in Example 15 is, by itself, incomplete because the same matrix can be constructed using the intersection of T(3, 0) and T(2, 2). The fact that either of these pairs of torus curves can be used in the model suggests that the two models are individually incomplete, and that perhaps a 3-torus model could encompass both simultaneously.
Return to text
18. Wooldridge chose only duple-meter compositions in his study because “these pieces share a common ‘chromatic’ universe which makes comparison among them more meaningful” (1992, 285).
Return to text
19. “Cognitive isomorphism” is Pressing’s term for describing the similarity between structures in the time domain and structures in the pitch domain that both have generative cycles (Pressing 1983). Similarly, Wooldridge’s Joplin study applies diatonic pitch theory to the time domain (1992).
Return to text
20. Joplin’s gradual unveiling of the Treemonisha theme’s harmonic function is reminiscent of the concept of retrospective reinterpretation discussed by Janet Schmalfeldt (2011), in which the formal function of a passage changes in retrospect based on the material presented later. At first, the Treemonisha theme sounds as if it fulfills a tonic harmonic function. By the end of the overture, in retrospect, the harmonic function of the Treemonisha theme may be interpreted as a part of a cadential
Return to text
21. Wooldridge calculates that Joplin’s preference for generated rhythms is statistically significant with p < .001.
Return to text
22. Du Bois also borrowed from the supernatural beliefs of the African American conjuring tradition (Schrager 1996). An African American supernatural belief held that “being born with a caul, the amniotic veil covering the face of the newly delivered infant, was interpreted as evidence that one was gifted with enhanced insight into the invisible realm. Another well-known belief held that the seventh child of a seventh son or daughter would enjoy an auspicious spiritual lineage” (Chireau 2006, 23). Du Bois’s statement that “the Negro is a sort of seventh son, born with a veil, and gifted with second-sight in this American world” (Du Bois 1903a, 3) borrows the conjure concept to express African Americans’ special powers of insight. Interestingly, conjure plays a central role in both Joplin’s Treemonisha and in Jess’s Olio.
Return to text
23. This also serves as evidence that the density referent is an appropriate concept in Joplin’s music.
Return to text
Copyright Statement
Copyright © 2021 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Andrew Eason, Editorial Assistant
Number of visits:
7299