Onset and Contiguity: Melodic Feature Reduction and Pattern Discovery
Aaron Carter-Ényì and Gilad Rabinovitch
KEYWORDS: schema theory, pitch reduction, pattern discovery, J. S. Bach, J. P. Kirnberger, W. A. Mozart, eighteenth-century music
ABSTRACT: Onset (metric position) and contiguity (pitch adjacency and time proximity) are two melodic features that contribute to the salience of individual notes (core tones) in a monophonic voice or polyphonic texture. Our approach to reductions prioritizes contextual features like onset and contiguity. By awarding points to notes with such features, our process selects core tones from melodic surfaces to produce a reduction. Through this reduction, a new form of musical pattern discovery is possible that has similarities to Gjerdingen’s (2007) galant schemata. Recurring n-grams (scale degree skeletons) are matched in an algorithmic approach that we have tested manually (with a printed score and pen and paper) and implemented computationally (with symbolic data and scripted algorithms in MATLAB). A relatively simple method successfully identifies the location of all statements of the subject in Bach’s Fugue in C Minor (BWV 847) identified by Bruhn (1993) and the location of all instances of the Prinner and Meyer schemata in Mozart’s Sonata in C Major (K. 545/i) identified by Gjerdingen (2007). We also apply the method to an excerpt by Kirnberger analyzed in Rabinovitch (2019). Analysts may use this flexible method for pattern discovery in reduced textures through software freely accessible at https://www.atavizm.org. While our case studies in the present article are from eighteenth-century European music, we believe our approach to reduction and pattern discovery is extensible to a variety of musics.
DOI: 10.30535/mto.27.4.2
Copyright © 2021 Society for Music Theory
1. Introduction
[1.1] Reduction has been a primary focus of Anglo-American music analysis since Schenker’s students immigrated with his ideas to the United States. Few music theorists would deny that identifying the most salient events within a surface texture has value; however, significant theories advanced—including by Schenker, Lerdahl and Jackendoff (1983), and most recently Gjerdingen (2007)—have received criticism for not clarifying their methods. Forte, a champion of analytical formalism, found it curious that “Schenker did not explain in his writings how to carry out a reduction” (1959, 15). Perhaps as a result of Schenker’s avoidance of a formal method starting from the surface, many practitioners of Schenkerian analysis differ in their analyses of the same passages. From a humanistic perspective, this is an advantage: Schenkerian theory allows analysts to represent a wide range of individual interpretations. Empirical and cognitive studies have not deciphered the complex expert intuitions that go into creating a multi-level Schenkerian graph. We suspect that even many musically-trained (or sensitive) listeners may not be able to hear the connection between surface textures and a multi-level Schenkerian reduction, let alone produce one.(1) We are interested in exploring a more formal path to reductions through features that render certain melodic events salient or structural.
[1.2] Lerdahl and Jackendoff’s A Generative Theory of Tonal Music (1983, henceforth: GTTM) is a landmark theoretical study on music’s generative processes. GTTM presents a theory of reduction and a set of criteria called “preference rules,” but the rules are not quantified or implemented. As a result, formalizing GTTM remains a challenge. Hamanaka, Hirata, and Tojo note that “there are few descriptions of the reasoning and working algorithms needed to compute analysis results [in GTTM]” (2006, 254).
[1.3] Readers might be surprised to see Gjerdingen’s name on the above list, given his ideological and technical critiques of Schenkerian theory (e.g., Gjerdingen 2007, 435; Gjerdingen and Bourne 2015, [2.2.1–2.2.6]). Like Gjerdingen (2007, 370), we reject notions of European art-music exceptionalism. We use European Art Music in the present case study, but we view this tradition as one of many world music traditions. On a more technical level, Gjerdingen has strong objections to the recursive, multi-level Schenkerian hierarchy; likewise, we are mainly interested in near-surface skeletons and patterns.(2) Gjerdingen presents and defines his schemata as rich, multi-parametric prototypes rather than formal products of reduction; nevertheless, his schema-finding de facto instantiates pitch reduction or skeleton-finding. Similarly to prior methodologies, Gjerdingen does not formalize principles leading from surface to skeleton; rather, he presents typical exemplars along with a graphic summary for each schema. In contrast to this multi-parametric definition, we focus on the skeletal scale-degree feature of the schemata—especially their soprano skeletons—and aim to find a formal path to a kind of middleground structure, by first generating one or more reductions based on a limited inventory of features. Schemata would thus presumably emerge as common successions within the skeletal layer. Because analysts do not necessarily agree on the correct reduction of a piece and listeners may or may not “hear” reductions, the method we present in this article explores multiple reductions of the same piece in order to discover patterns.
[1.4] Several recent studies (e.g., Finkensiep, Neuwirth, and Rohrmeier 2018; Katsiavalos, Collins, and Battey 2019; Sears and Widmer 2020; Finkensiep et al. 2020) have already proposed and implemented sophisticated algorithms for finding galant schemata; our present proof of concept joins this line of work. Our entry point for finding melodic skeletons is based primarily on onset location and contiguity. Rabinovitch (2018, 2019, 2020) proposes reductive principles implicit in Gjerdingen’s (2007) prototypes and analyses: by prioritizing outer-voice tritones, contiguity, and metrically stressed notes (or consonances displaced by accented dissonances), he manually reconstructs schema-finding as a form of pitch reduction. Hamanaka, Hirata, and Tojo’s (2006) response to GTTM and recent attempts to derive schemata automatically or manually come from proponents of the two theories who note difficulties in articulating and implementing them. Schenkerian theory and GTTM address common-practice tonality at large, while Gjerdingen’s galant schemata apply to a style period (1720–1780). The difficulties in creating a generalized framework for pitch reduction across periods, styles, and musics motivates us to offer a flexible methodology that provides an opportunity for input from multiple analysts. We believe computational analysis can illustrate commonalities among humanity’s musics as well as properties and structures that are particular to some traditions but not others. We have developed tools for algorithmic analysis, which can be freely accessed at www.atavizm.org. Utilizing these MATLAB-based tools and the graphic interface of ATAVizM (Algorithmic Thinking, Analysis and Visualization in Music), others can apply this method to additional monophonic and polyphonic repertoires. The analytical intuitions of multiple users may optimize parameters for the reduction of various styles, articulating implicit aspects of the analytical process. The interaction of multiple analysts with our interface can help optimize parameters for specific genres, such as mid-eighteenth-century galant music, nineteenth-century Romanticism, present-day pop/rock styles, and—of particular interest to us—world music traditions.
[1.5] In this article, we computationally reproduce the analytical pattern-finding or reduction of existing analyses by Bruhn (1993), Gjerdingen (2007), and Rabinovitch (2019). In Section 2, we begin by discussing the theoretical background of reduction procedures. In Section 3, we describe our reduction algorithm. The following three sections (4 through 6) are analytical case studies, in which we reconstruct existing expert analyses to validate our methodological framework for reduction. We algorithmically reconstruct subject-entry–finding by Bruhn (1993) in a Bach fugue from The Well-Tempered Clavier. Afterward, we reconstruct analyses using galant schemata, including Gjerdingen’s (2007) finding of Prinner and Meyer exemplars in Mozart’s piano sonata K. 545/i and part of an analysis by Rabinovitch (2019) of an excerpt by Kirnberger. The algorithm does not specifically look for Prinners or other schemata, nor does it posit them a priori. Rather, it sorts and ranks all n-grams in one or more reduced textures. The ranking of n-grams (in this case scale-degree skeletons) by ATAVizM is based on the tone sequence’s prevalence within a piece (intraopus) or multiple pieces (interopus). In this article we focus on intraopus 4-grams (sequences of four scale degrees in reduced textures) because this aligns with many of Gjerdingen’s schemata. However, ATAVizM may be set to a single size or any range of n (from 2 to 100, though 2 to 6 is generally most productive). Moreover, we intend to focus in the future on interopus patterns, which are likely to reinforce schema-finding in individual pieces. We conclude by offering thoughts on our algorithmic approach’s efficacies and limitations for melodic reduction and pattern-finding and their significance for future work.
2. Background
[2.1] Computational work on pitch reduction spans several decades, with early contributions from Kassler (1975) and Smoliar (1980) and more recent contributions including Kirlin and Utgoff (2008) as well as Marsden (2010). Our theoretical entry point is not categorization into chord tones vs. non-chord tones (e.g., Marsden 2010; Ju et al. 2017); our emphasis on linear melodic features distinguishes our work from other, harmonically-driven studies such as Marsden 2010. However, some reduction criteria are relatively similar. For instance, Marsden’s system considers the metrical strength of events (his criterion 5) and favors reductions with small intervals (his criterion 3).
[2.2] Our work, moreover, is less directly related to generative linguistics than authors like Lerdahl and Jackendoff (1983) or Marsden (2005, 2010). We do, however, incorporate a concept from computational linguistics: skipgrams, or patterns among nonadjacent elements. Studies such as Symons (2017), Finkensiep, Neuwirth, and Rohrmeier (2018), and Sears and Widmer (2020) apply skipgrams to music with a very similar goal: finding n-grams that may ultimately approximate Gjerdingen’s schemata. In addition to considering patterns among nonadjacent melodic events, we emphasize the importance of contiguity. While metric prominence (onset location) is the basis for identifying potential core tones at an initial stage, a second stage of searching for melodic contiguity can ultimately outweigh onset in importance in the final selection of core tones. Our contiguity concept resonates with a wide range of prior sources, including melodic fluency in the Schenkerian tradition (Pastille 1990) and Huron’s studies of conjunct motion in auditory streaming (2001).(3)
[2.3] In our preliminary implementation, we use a finite set of features (onset and contiguity) to create musical reductions. The concept of associative sets from Hanninen (2012) and an algorithm for pattern discovery of recurring patterns (associative sets) based on Carter-Ényì (2016b) help to select between multiple reductions. We aim to find meaningful n-grams aligned with the schemata identified by Gjerdingen, like the Prinner (–––).(4) Our goal is to reveal the n-grams not by telling the algorithm what to search for, but by creating valid reductions of the surface texture through a bottom-up approach of core-tone selection that are independent of n-grams that may ultimately arise. Searching for n-grams in a feature-based reduction, as opposed to sampling at a regular time interval in the surface (surface-level skip-gram), causes schema-like patterns to emerge despite the fact that the algorithm does not know the n-grams or where to find them.
3. Algorithm for Feature Reduction and Pattern Discovery
[3.1] A preliminary set of features, not intended to be exhaustive but productive, marks some notes as more salient and potentially skeletal. As noted, we do not propose to use all features in all analyses: different styles and genres may necessitate additional features. Three of the four calculations can run independently of one another (and in any order); only the fourth feature, contiguity, depends on results from other features. Onset and contiguity seem to be most effective for common-practice music, but other features may be integrated into our methodological framework. In the analytical case studies below, we have assigned points to select melodic elements based on some combination of the following features:
- Onset location (metric placement): notes in a specific metric location receive points, such as notes on beats 1 and 3 in 4/4.(5) While a note being on a “strong beat” is generally viewed as a position of prominence in European classical music, in many other musics syncopation and rhythmic displacement from the beat may be a better indication of a note’s salience or structural importance.
- Pitch contour is the relative height of a note within a local context of several notes (e.g., two notes around it, four notes around it, or six or more). For instance, if a note is higher than the two notes that precede it and the two notes that follow it (a window of five notes including the note itself), it is a local pitch maximum and will be awarded points in the reductive process. It might be helpful in a different piece to identify a local pitch minimum (a note lower than the two notes preceding and the two notes following it). Note that the selection of a window size for binary pairwise comparisons is important (Quinn 1997; Carter-Ényì 2016b). Pitch contour, specifically local maxima and minima, has some bearing on a note’s prominence within the surrounding surface texture. In some contexts, pitch maxima may be heard as melodic accents (Huron and Royal 1996).
- Durational contour is the relative duration of a note within a local context. For instance, if a note is longer than the preceding two notes and the following two notes, it is a local durational maximum and therefore perceptually salient, which may be a criterion for awarding points if one so chooses.
- Contiguity describes notes that are a minor or major 2nd above or below (+/– 1 or 2 semitones) a note that is close in time and has already been awarded points based on other features. Such notes have melodic fluency with potential core tones. This feature requires windowing and comparison to notes before (pre-contiguity) and notes after (post-contiguity, see [3.4]).(6) Contiguity helps to identify skeletal or “structural” lines in music where stepwise motion (melodic fluency) is important. If a melody splits into multiple streams, as in hidden polyphony (compound melody), notes that are contiguous with each other may form a stream that is structurally important (see the first analysis of a Bach fugue in Section 4).
[3.2] The features listed above were selected for transparency of operationalization. The features bear a significant resemblance to Lerdahl and Jackendoff’s (1983) time-span reduction preference rules (TSRPRs). In particular, features 1 and 2 above are related to TSRPRs 1 and 3. Lerdahl and Jackendoff also draw on Gestalt principles and pitch proximity, to which our contiguity feature corresponds. As mentioned above, melodic fluency has been emphasized in the Schenkerian tradition (Pastille 1990), and Huron (2001) has proposed that conjunct motion in voice-leading corresponds to perceptual principles of auditory streaming. Our approach diverges from Lerdahl and Jackendoff and Schenkerian analysis in both theory and implementation since we invoke harmonic and tonal factors only to a limited extent.
[3.3] While onset location appears first in the list above, it does not need to be awarded points before the other features.(7) Only the contiguity feature awards points based on points from other features, so it must be calculated after others. Events lying close in pitch and time to events already marked through a different feature are “infected” with points, joining them in a melodically fluent skeleton. For the reduction implementation in ATAVizM, points for all features are aggregated in a single score matrix and core tones are selected in a single “pass.” While additional passes (including ones that weight the features differently) may be applied recursively to deepen the reduction, that procedure will not be demonstrated here.
[3.4] For contiguity as we have operationalized it, windowing is necessary. The windowing constrains the awarding of points for being within a step of a highly valued note in an adjacent window. Window sizes for selecting notes are flexible; they can be smaller than one beat or arbitrarily large. Generally, we have found an ideal window size to be between one beat and one measure. Windowing may also be used at the later stage of core-tone selection, but that is not always necessary. If contiguity is not applied, there is the possibility of using no window at all for core-tone selection but merely selecting notes that surpass a threshold of points. If a points threshold is applied, the reduction’s rhythm will vary based on the occurrence of some feature or features. After awarding points to notes based on the weighting of the features, the algorithm selects core tones based on one of three methods:
- Beat window: select the highest scoring note within every n-beat(s) window;
- Threshold: select notes with a minimum number of points (or above it);
- Implied harmonic rhythm: if a harmonic rhythm may be implied by another voice (most frequently the bass) or simultaneous movements in a homophonic texture, this feature may substitute for a beat window.
[3.5] There are three sets of resources and assumptions necessary to implement the methodological framework presented here as a functioning algorithm (as available on the web at www.atavizm.org). The algorithm as it stands has the following conditions for data selection and preparation:
- Symbolic data (e.g., engraving files, music XML, or MIDI) is available for a piece of music, and the notation is an accurate representation of the music.
- The symbolic data is segregated by voice (e.g., a MIDI file with channels), and a polyphonic or melody-plus-harmony hearing is reasonable. This framework may also be applied to monophonic repertoires because it is not dependent on harmonic features, making it more generalizable across musical cultures than previous models of pitch reduction.
- The meter is known, either embedded as metadata, input by the user, or estimated by an accurate meter estimation tool.
Methods for meter estimation, such as Brown (1993) and Toiviainen and Eerola (2006), have been implemented in MATLAB as part of the MIDI Toolbox and correctly identify the meter of all of the pieces discussed in this article as duple. In our analytical applications thus far, it has not been necessary to distinguish internally between duple meters (e.g., 4/4 vs. 2/4), but it has been essential to distinguish whether the meter is duple or triple (e.g., 4/4 or 2/4 vs. 3/4 or 3/8).
4. First Analysis: Bach, Fugue in C Minor, BWV 847
[4.1] In this first analysis, we algorithmically reconstruct subject-entry–finding by Bruhn (1993) in Bach’s Fugue in C Minor BWV 847 (The Well-Tempered Clavier, Book I). We also briefly reflect on the relation between the schema-like patterns detected algorithmically with Schenkerian approaches to reducing BWV 847’s fugue subject. Many Schenkerian analysts have addressed BWV 847. Schenker ([1926] 1996) analyzed the piece, and more recently Renwick (1995), Franck (2007), and Marlowe (2014) have published analyses of it.(8) Unlike these abstract, theory-driven analyses, Bruhn’s approach (1993) involves a simpler pattern-finding task—recognizing the recurring subject statements—even if finding and segmenting fugue subjects is already a non-trivial task. It is likely that listeners familiar with fugues can recognize many (if not all) of the subject entries that Bruhn locates, despite the dense texture. In contrast, Schenkerian analyses are both theory-intensive and require highly specialized analytical expertise. The Schenkerian theorists cited here—despite their differences of opinion and methodology—are concerned to a greater or lesser extent with hierarchical issues that our method disregards.
Example 1. Five salient melodic events in the BWV 847 fugue subject
(click to enlarge)
[4.2] The subject includes several note candidates to be considered as melodically salient events. Scale degrees –––– are annotated as skeletal in Example 1. Let us compare features of salience that mark these events for our attention from our present methodological standpoint:
- The initial is on the second eighth note of beat 2, so it is not very salient metrically. However, it is approached by a large leap, which marks it perceptually in terms of pitch contour and opens a different layer of the hidden polyphony. It is also contiguous with the next note, which is metrically strong, affording it retrospective support as a plausible candidate for a skeletal note.
- The “upper neighbor” is stressed by its position at the beginning of beat 3, a relatively strong beat in the notated meter.
- The following is metrically prominent (downbeat).
- is metrically prominent (beginning of beat 3).
- is metrically prominent (downbeat).
These melodic events demonstrate some of the factors contributing to melodic salience. Events 2–5 in the list above are all stressed due to their metric position. All five events are contiguous with one another, creating a stepwise skeletal Gestalt. The salient melodic events (or potential core tones) in this theme illustrate the competition between salience features. They also demonstrate the tension between bottom-up attention to contextual features (e.g., onset on a metrically strong position, contiguity) and theory-driven assumptions (e.g., the possibility of subsuming as an upper neighbor to the head tone in the so-called -line Ursatz schema). The opening scale-degree is less metrically stressed, but the algorithm may still extract it as part of a skeletal reduction on the basis of its contiguity with the following . From a more hierarchical standpoint—be it a Schenkerian hierarchy or an experimental tonal hierarchy (Krumhansl 1990)—the metrically stressed scale-degree (event 2) may be subsumed under the descent of ––. Marlowe (2014, 56–63) juxtaposes graphs by Schenker ([1926] 1996), Franck (2007), and herself for BWV 847. From our surface-oriented (and theoretically divergent) entry point, Marlowe’s comparison sets in relief the tension between the salient and the potential of subsuming it (on some level) under the more tonally stable . We have no intention to deny the usefulness of emergent properties like tonality; our inquiry simply takes a more bottom-up approach. We are hopeful that it would ultimately be possible to reconcile our almost “phonological” approach with broader tonal principles.
Example 2. Feature analysis and points reduction to notes on beat 1 or 3 with scale degrees added
(click to enlarge)
[4.3] Based on the discussion above, it is fair to assume that onset and contiguity would produce a reduction that reveals a recurring pattern in this fugue. Here, we will walk through our reduction algorithm step-by-step. First, we apply only onset reduction. Example 2 contains only a single (“onset”) row of a score matrix, which awards a single point to notes that fall on a strong beat (1 or 3 in 4/4) from Example 1. The reduction (on bottom) includes only those notes.
Example 3. Reduction of BWV 847 fugue subject based on onset and contiguity features
(click to enlarge)
[4.4] Example 3 is produced from a more complex feature-based reduction using both onset and contiguity. As mentioned in [3.3], contiguity must be calculated after other features. This procedural ordering is necessary because contiguity awards points to other notes based on their relationship to notes that already have points. We also mentioned in [3.4] that windowing is part of the process of analyzing contiguity and awarding points. In Example 3, we used a two-beat window that is consistent with the strong beat onset pattern. Thick borders are added between columns of the score matrix representing metric divisions directly before strong beats 1 and 3. In this and subsequent examples, pre-contiguity refers to comparisons of the note listed at the top of the column and preceding notes. Post-contiguity refers to comparisons to following notes. It is impossible to compare the first note to earlier notes, so the first value in this row is not a number (nan). The first time a note is awarded a point for pre-contiguity is on the downbeat of m. 2 (after the second thick border). G4 is contiguous with
[4.5] Onset and contiguity successfully return a reduction that somewhat resembles a middleground reduction. We have already seen that applying only the onset feature analysis (awarding points to notes occurring on beat 1 or 3, as in Example 2) to the subject excerpt and selecting only notes that have points yields a reduction to a scale-degree skeleton (SDS) [–––]. This is a component of Gjerdingen’s Prinner schema, which would also typically contain a –––, ––––, or even ––– as a bass or bass skeleton against it, among other features. Should we consider the a false positive core tone and discard it? We believe that it should not be discarded. The Prinner schema seems to us more attuned to surface salience in the style than a hierarchical approach that subsumes under .
[4.6] Both Schenkerian and Gjerdingen-type reductions rely on tonal contexts, even if they diverge with regard to relevant time scales for such contexts. In contrast, our methodological framework disregards key at the core-tone selection stage. In order to obtain the reduction in Example 3, it is unnecessary to know the key a priori or have a key-finding algorithm. (Of course, the key is not constant in a piece that includes tonal shifts of some kind). The algorithm must first segment and then identify each segment’s key to assess scale degrees accurately in a multi-key work. Instead of basing the reduction on top-down segmentation and key-finding, we endeavor to work in a bottom-up fashion from contextual features through core tones and segments to higher-level determinations, such as the key within a segment parsed through the pattern-finding process.(9) Once segments have been identified, key-finding is necessary to identify scale degrees that may be used to relate n-grams in different keys to each other as scale-degree skeletons (such as –––). First, however, the algorithm looks for interval grams.
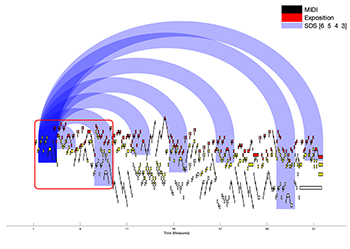
Example 4. Arc Diagram of BWV 847 fugue showing initial exposition (red box) and eight instances of SDS [ ] (corresponding to eight complete subject statements, consistent with Bruhn 1993)
(click to enlarge)
[4.7] Pattern discovery applied to a one-parameter reduction of BWV 847 yields a segmentation that includes all of Bruhn’s eight subject statements.(10) The single feature that produces this analysis is strong-beat onset (notes occurring on beats 1 and 3).(11) Pattern discovery with a two-parameter reduction of onset and contiguity works perfectly well, too, but contiguity is not necessary to replicate Bruhn’s subject-finding. We first sorted all generic interval grams (GIG) in all three voices into groups and then ranked these by their prevalence. Recall that intervals may be measured generically (as in 2nds, 3rds, 4ths) and more specifically (minor 2nds, major 2nds, minor 3rds, major 3rds, perfect 4ths). In the algorithm, the operationalization of generic intervals is that +/–1 is a 2nd (either 1 or 2 semitones). Augmented unisons are not considered distinct from minor 2nds because the algorithm sees the notes as integers (i.e., C4=60), not as letters and octaves. Using a pattern discovery algorithm developed by Carter-Ényì and available as a GUI at www.atavizm.org, the most prevalent pattern discovered is GIG [–1 –1 –1], that is, three descending 2nds.(12) The eight instances returned correspond exactly to Bruhn’s statements. This is illustrated through an arc diagram in Example 4.(13) On some level, three descending steps are a very generic pattern. It is difficult to predict that this would be the basis of the distinctive subject and no other materials in the reduction of this fugue.
[4.8] A generic interval gram (GIG, e.g. [–1 –1 –1]) is not yet a scale-degree skeleton (SDS). To determine that there is a schema-like pattern, we must specify the scale degrees. To draw a scale-degree skeleton from a generic interval gram, we must know the segment’s key. Specification of the SDS serves to narrow the category, eliminating false positives for the Prinner (e.g., SDS [ ]). While GIG [–1 –1 –1] yields only the subject entries and nothing else in this particular piece, we expect that it is too inclusive of a category to avoid false positives for subject entries in fugues at large. Once we have broadly analogous segments (GIGs), we can identify SDSs through various template-matching methods. Because the pieces we are studying have tonicizations and modulations, it is not practical to identify the key(s) until there are potential segments with lengths of a few measures each. The first option for key identification of the segments is to apply a key-finding algorithm to the surface texture of the segment. The MIDI Toolbox includes several implementations of effective key-finding templates based on perceptual research.(14) Of these, Temperley’s algorithm (1999) is the only one that correctly identifies the key for each of the subject statements in BWV 847, clarifying that all of Bruhn’s subject statements correspond with SDS [ ], and no other segments do.(15)
Example 5. Surface of BWV 847, mm. 3–5
(click to enlarge)
Example 6. Reduction of tonal answer against Countersubject 1
(click to enlarge)
[4.9] The second option for converting a GIG into an SDS is to search for tritone resolutions within the GIG segments, for which we need to complete the contrapuntal texture (Example 5). Those familiar with Gjerdingen’s schema theory may note that SDS [ ] is only one feature of the Prinner schema—yet our approach for implementation generally prioritizes melodic skeletons. BWV 847 has two countersubjects. The first countersubject follows the subject closely: it is introduced against the tonal answer in mm. 3–5. Countersubject 1 has a fairly rigid skeleton (GIG [–1 –2 +1]) in five out of six statements.(16) Once we combine the GIG [–1 –1 –1] with the GIG [–1 –2 +1], the scale degrees become apparent ([ ] and [ ]): the tonal center becomes unambiguous through the clarity of the tritone resolution (Example 6).
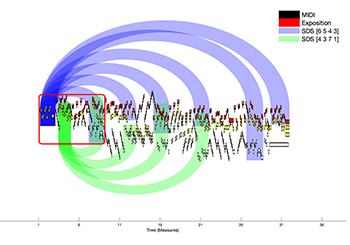
Example 7. Arc diagram of BWV 847, highlighting SDS [ ] and [ ]
(click to enlarge)
[4.10] Where present, the SDS [ ] of Countersubject 1 against the SDS [ ] of the subject completes the outer-voice contrapuntal aspect of the Prinner, though a more typical Prinner bass would be [ ] or [ ]. As the arc diagram in Example 7 illustrates, however, not all of the eight subject statements identified by Bruhn coincide with Gjerdingen’s Prinner. The original presentation of the subject is a single line and therefore only has contrapuntal or harmonic implications rather than a fully fleshed-out instance of a schema.
Example 8. Surface of BWV 847, mm. 26–28
(click to enlarge)
[4.11] The seventh statement of the subject in mm. 26–28 (Example 8) is also accompanied by a countersubject statement from the perspective of melodic contour. Bruhn presumably identifies this location as the sixth statement of countersubject 1 based on contour similarity; however, the intervallic and harmonic content is quite different. The “VI” vertical sonority on the downbeat of m. 27 obscures the SDS [ ]. The resolution is also displaced with B3 [] reiterated on beat 3 of m. 28 before the resolution to C4 []. Although all the notes of [ ] are present in the alto, the onsets do not coincide with the SDS [ ] in the bass. The
Example 9. BWV 847 fugue, mm. 29–31, on three staves
(click to enlarge)
[4.12] All that remains is the eighth and last instance identified by Bruhn (1993), presented in Example 9. From the perspective of the algorithmic process we are advancing, in which GIG groups are discovered and then refined to SDS through template matching, this entry is problematic because of its major-minor modal ambiguity (Picardy 3rd). The specific intervallic sequence of all other subject entries [–m2, –M2, –M2], corresponding to SDS [ ] in minor, is altered to [–m2, –M2, –m2] by the Picardy 3rd, which forces SDS [ ] into a span of a diminished 4th instead of a perfect 4th. Importantly, it still retains the profile of three descending steps. The aforementioned key-finding algorithms accurately identify this passage’s tonic as C, and the key-defining tritone resolution is still apparent.
[4.13] It is possible to identify the passage with a minor-to-major SDS [ ] as having a tonic of C. From our process’s perspective, all subject instances identified by Bruhn may be subsumed under the GIG [–1 –1 –1] and SDS [ ] categories. The original subject presentation is monophonic, with the last two instances (mm. 26–8 and 29–31, Examples 8 and 9) deviating from prior polyphonic instances in terms of their surface expression. However, seven of the eight form complete instances of the Prinner schema. We note that it is also likely that the algorithm could take further steps beyond identifying an SDS toward evaluating whether synchronous events form a complete schema. It seems that the presence of a SDS in a single voice is a strong indicator of an entire schema in the same location. A GIG as generic as [–1 –1 –1] is likely to be too inclusive a category to be considered the same pattern perceptually. As we shall see in the analysis to follow, it is helpful to discard instances in a GIG group that do not conform to a single SDS to ensure that associated patterns share a tonal role.
Example 10. Reduction of K. 545/i, mm. 1–4, based on strong-beat onset alone
(click to enlarge)
5. Second Analysis: Mozart, Sonata in C Major K. 545, first movement
[5.1] The first movement of Mozart’s C Major Piano Sonata, K. 545 is well known for its extensive Prinner content.(18) Gjerdingen (2007) identifies eight instances of the Prinner schema in this movement. It is the very first Prinner stated in the primary theme that poses the challenge to reduction based on metric position alone; this is demonstrated in Example 10.
Example 11. K. 545/i, measures 1–4, right-hand melody
(click to enlarge)
Example 12. MIDI Data interpretation of the trill (K. 545/i, measures 1–4, melody) from KunstDerFuge.com (Hisamori encoding)
(click to enlarge)
[5.2] The opening (Example 11) contains a trill into the ending of the first Prinner in m. 4. It is possible to obtain or generate MIDI or XML data that interprets the trill or not. In this case, the MIDI data that we used (encoded by Hisamori, available on KunstDerFuge.com) realizes the trill as a quintuplet (Example 12).
Example 13. K545/i, mm. 1–4: (top) surface; (middle) feature reduction table; (bottom) reduction based on onset and contiguity
(click to enlarge)
[5.3] Regardless of how the trill is interpreted, is metrically displaced respective to the other Prinner core tones. Because a skipgram based on metric prominence (“on-the-beat-ness”) alone will not reduce to SDS [ ] in mm. 3–4, we must add the contiguity feature.(19) It is difficult here to determine whether the G4 or F4 is more salient. However, following the principle of contiguity, the F4 makes more sense structurally, forming a bridge between G4 and E4. Contiguity “infects” (gives points to) notes that are a step away (1–2 semitones above or below, excluding same note / 0 semitones) from notes already awarded points (in this case 1 for being on the strong beat, see Example 13).(20) Although other parameters are possible, in this case, contiguity only infects notes that occur within the window immediately before or after and not within the same window. For instance, the A5 on the downbeat of m. 3 is a prominent note on many levels. It receives a point for metric prominence. A point for contiguity is then awarded to the G5 on the third beat of the same measure, but not the G5 in the first measure or on the next downbeat because they are more than a (two-beat) window away. It is crucial for the algorithm to avoid awarding a contiguity point to G5 on the downbeat of m. 4 (from the A5 on the downbeat of m. 3) in order for it to select F5 as the core tone for the first two beats of m. 4. F5 receives contiguity points from both the G5 on the third beat of m. 3 and E5 on the third beat of m. 4, accumulating two points total. The G5 on the downbeat of m. 4 only received one point for its onset location, so ultimately it was discarded by the reduction. Note, though, that if it had received any contiguity points for the A5 a full measure before, it would have tied with the F5. Taking the highest-ranked note (based on onset and contiguity) within a two-beat window replicates Gjerdingen’s intuitive reduction into a Prinner, with an SDS [ ] in mm. 3–4 (Example 13).(21)
Example 14. K545/i, mm. 5–8: treble clef surface texture
(click to enlarge)
[5.4] Applying onset and contiguity within a two-beat window reduction yields the Prinner of the primary theme in both the exposition and recapitulation. Other Prinner instances identified by Gjerdingen (2007), however, differ in their harmonic rhythm. All Prinner instances are internally consistent in their harmonic rhythm, so producing reductions at different window sizes (e.g., two beats, four beats, every beat three) solves the problem. This approach resembles solutions like those of Symons (2017) and Finkensiep, Neuwirth, and Rohrmeier (2018). Merely using a window size of four beats instead of two beats accommodates the Prinner instance in mm. 5–8 because [ ] all fall regularly on the downbeat (and beat 3), as seen in Example 14.
Example 15. K545/i, mm. 63–66: (top) surface; (middle) feature reduction table (repeated notes omitted to save space); (bottom) reduction based on onset and contiguity
(click to enlarge)
[5.5] Some of the Prinner instances identified by Gjerdingen are buried within more complex textures, as in the S-based passage in mm. 18–21 and its home-key return in the recapitulation, mm. 63–66. Measures 18–21 and mm. 63–66 contain the most challenging Prinners to identify using our method, the latter in particular. There is a melodic transfer to a higher octave in the second instance in the middle of m. 64; therefore, octave equivalence is needed to consider the passage contiguous. Example 15 (K. 545/i, mm. 63–66) shows the musical surface, a feature reduction table, and a reduction based on onset and contiguity.(22) In this case, adding the contiguity feature does not alter the reduction produced by considering onset (metric prominence) alone. Another kind of skipgram in the reduced texture (not the surface texture) is necessary for locating the Prinner nested within this ––––––– skeleton. While the pattern on downbeats, [–––], is a more logical reduction based on metric salience, a nested [ ], consistent with Gjerdingen’s analysis of the section, is discovered by considering only the notes on beat 3. We believe that a reduction to SDS [ ] is justified by the prevalence of more apparent and unambiguous presentations of the Prinner throughout the piece. In other words, the other appearances of the Prinner may prime listeners to hear [ ] in this context. Despite the comparatively greater metric salience of [–––], which all fall on beat 1, [ ] still has relatively high metric salience because the scale degrees all fall on beat 3, which is also a strong beat in this meter.
[5.6] One might ask, “Why must the recurrence of Prinners elsewhere mean that mm. 18–21 (or mm. 63–66) represent a Prinner?” To assume that the best analysis is the most efficient one is a common trap in music analysis. Surely Mozart and his listeners valued both contrast and cohesion. In a broader analytical framework, such as Hanninen (2012), both associations and disjunctions play a role. Gjerdingen’s schemata, some of which are limited by disjunctions like cadences, are also types of associative sets. Here we focus on the Prinner since—of the schemata identified by Gjerdingen—it most clearly forms an associative set within the piece. We should note, of course, that Gjerdingen is interested in interopus relations across a style, while Hanninen is more concerned with associative sets within a piece, that is, intraopus features.
[5.7] This selection can be implemented algorithmically by using pattern discovery to scan multiple reductions for common patterns. Much like the pattern-discovery algorithm may search multiple voices (as it did in BWV 847), it may also search through multiple reductions for common patterns. In the case of K545/i, the algorithm found [ ] in three different reductions: a two-beat reduction, a four-beat reduction, and a skipgram within the four-beat reduction (i.e., every beat 3).
[5.8] By searching multiple reductions, the pattern discovery also yielded the generic interval gram (GIG) [–1 –1 –1] as the most prevalent pattern, as it did BWV 847.(23) In this case, there are multiple species of GIG in terms of the specific interval composition. The minor SDS [ ] in Bach’s fugue was, in all cases but one, m2–M2–M2, which indicated that they were the same scale-degree skeleton (SDS). Here there are multiple species of GIG. For instance, skipgrams for mm. 63–66 yield two different (GIG) [–1 –1 –1] species spanning a P4: both the symmetrical G–F–E–D (M2–m2–M2) produced by the downbeat, and the asymmetrical A–G–F–E (M2–M2–m2) skeletons outlined by notes on the third beat of each measure. Only one of these corresponds to the Prinner, but which?
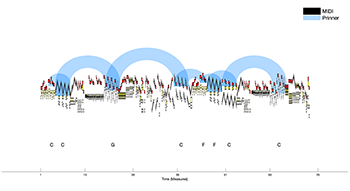
Example 16. Eight instances of the SDS [ ] in K545/i
(click to enlarge)
[5.9] Here we consider the redundancies that result from searching through multiple reductions. A four-beat onset window and a skipgram of a two-beat reduction (i.e., a skipgram of a skipgram) will reproduce results that the algorithm excludes because of redundancy. Once we apply key-finding to potential segments, it is possible to exclude GIG [–1 –1 –1] instances that do not match the predominant scale degree template of SDS [ ]. This process yields eight instances of the soprano SDS [ ], which correspond in number and location to Gjerdingen’s identification of eight Prinners. The algorithm’s output for Prinner locations (with key identifications for each segment) is visualized in Example 16. In this case, we did not apply the algorithm to the homophonic accompaniment to find the contrapuntal skeleton of SDS [ ] or [ ] in the bass. This piece’s texture is highly varied, spanning polyphony, homophony, and textures in between. Applying algorithms designed for multi-voiced textures thus seems ill advised.
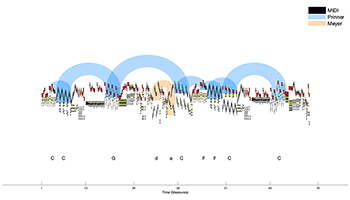
Example 17. Arc diagram of K545/i with instances of the Meyer added in orange
(click to enlarge)
[5.10] Another recurring schema is the Meyer, which occurs twice in the development; see the pale orange arc in Example 17. The Meyer is often deployed on the musical surface of eighteenth-century pieces in a less regular metric guise than the Prinner.(24) Therefore, using a uniform window reduction will not yield all of the scale degrees identified by Gjerdingen.
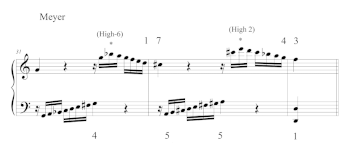
Example 18. Identification of Meyer schema, including the subsidiary melodic features, High- and High-, in K. 545/i, mm. 31–33
(click to enlarge)
Example 19. Reduction of K.545/i, mm. 31–33
(click to enlarge)
[5.11] It is possible to draw out all of the scale degrees of Gjerdingen’s reduction—including the subsidiary High- and High- drops—with some quirky parameters (see Example 18). Such a reduction requires awarding positive points for pitch-contour maxima and negative points for submaxima (second-highest note within a window), which seems too artificial and case-specific. In contrast, a two-beat window with strong-beat and contiguity points (the reduction parameters already presented for the Prinner) yields the same GIG of [–1 +4 –1] for both locations in the development. After identifying the scale degrees through key-finding, ––– emerges as a distinct 4-gram SDS that only yields instances of the Meyer identified by Gjerdingen (see Example 19).
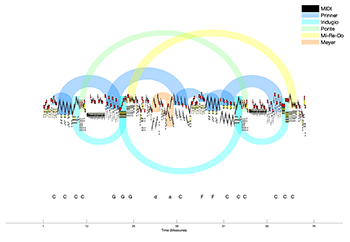
Example 20. K545/i with instances of five schemata
(click to enlarge)
[5.12] We will not address other schemata identified by Gjerdingen, such as the Ponte, Indugio, and Coda (Final Fall), as they are less consistently associated with specific scale-degree skeletons in comparison to schemata like the Prinner and the Meyer. We will note for future research that the segmentation created by this bottom-up approach sets in relief other schemata that Gjerdingen identifies. We observe two high-level instances of the Indugio schema in Example 20. The typical positions within a phrase, section, or composition of schemata like the Indugio, Ponte, Complete Cadence (Mi-Re-Do), or Prinner may ultimately aid in algorithmic schema-finding. However, the question of the syntax governing the successions of galant schemata (e.g., Gjerdingen 2007, 372) lies well beyond this article's scope.
6. Third Analysis: Kirnberger, Sonata for Flute and Continuo in G major(25)
Example 21. Surface of Kirnberger, Sonata for Flute and Continuo in G major, mm. 1–10, with soprano skeletal scale degrees (after Rabinovitch 2019, 35)
(click to enlarge and see the rest)
[6.1] This final analysis is in some ways anticlimactic, because our method, as presented here, does not reveal all Prinner-like structures as it did in BWV 847 and K. 545/i. Its inclusion is necessary, however, for articulating further developmental needs for the implementation. Rabinovitch (2019, 35) contains an analysis of Galant schemata identified in a flute and continuo sonata by Kirnberger; see score in Example 21. Even though Rabinovitch claims that schemata emerge from underlying principles—and derives them in this way—his analysis of Kirnberger was done by hand, leaving room for formalization.(26)
Example 22. One-beat reduction of mm. 2–3 of the Kirnberger revealing a Prinner with consistent harmonic rhythm (one-beat interval)
(click to enlarge)
[6.2] The Prinner accounts for about 40 percent (about four measures) of this ten-measure passage. The first instance starts on beat two of m. 2 (with a partial echo in m. 3), and the second instance on the downbeat of m. 5. It is possible that the same method applied to BWV 847 and K. 545/i could yield the Prinner in mm. 2–3, because this instance of the schema has an even harmonic rhythm of one beat per core tone. Although is displaced, preceding it and following it create contiguity that clarifies that (C5) is the core tone for beat 4 of m. 2 (see Example 22).(27)
Example 23. --- scale degree skeleton for mm. 5–7 of the Kirnberger, after Rabinovitch (2019)
(click to enlarge)
[6.3] The second Prinner, which is located in mm. 5–7 (with a partial, Comma-like echo in m. 8), is in some ways more transparent and in others more obscure than the first. In mm. 5–7, the core tones occur on strong beats without any type of delay. However, unlike the first instance in the piece and all we have analyzed thus far, the Prinner in mm. 5–7 is problematic for our method because the harmonic rhythm is not stable within the schema (see Example 23). Even in Prinners with dissonant notes delaying core tones, as in K 545/i, the underlying harmonic rhythm is often regular. In this case, there is internal variation. The Prinner identified by Rabinovitch in mm. 5–7 begins with a four-beat harmonic rhythm for the time intervals between , , and , but decreases by half to a two-beat harmonic rhythm from to (both occurring in m. 7). Instances of schemata with internal variation in the harmonic rhythm pose a challenge to our method due to its reliance on uniformly-sized windows. With Bach’s and Mozart’s pieces, we “windowed” the surface based on the meter and its subdivisions, making two-beat and four-beat reductions. For Kirnberger’s piece, to discover the Prinner in mm. 5–7, the algorithm would either need to 1 allow patterns that start in one scale of reduction (e.g., a four-beat reduction window) and end in another (e.g., a two-beat reduction window) or 2 rely on information from other voices (introduce some information on harmony, harmonic rhythm, or contrapuntal intervals between voices). Both are plausible algorithmically; however, we have not yet tested the extent to which 1 would lead to a proliferation of false positives. We will do so in future work.
[6.4] Galant schemata are contrapuntal, so it will likely be appropriate to incorporate some vertical considerations, such as consonant and dissonant intervals, into a reduction algorithm. The bass voice (basso continuo) in Kirnberger’s excerpt notably provides information about the harmonic rhythm. In mm. 5–7, the harmonic rhythm fluctuates. In mm. 5 and 6, unlike m. 7, the bass is silent at the onset of beat 3. In the flute, the sweeping gesture and sudden stop on the second eighth note of beat 3 in both mm. 5 and 6 and the rising arpeggio on beat 3 in m. 7 reinforce the bass.(28) The textural variation articulates two changes in harmonic rhythm: a slowing down of harmonic rhythm to a four-beat interval starting in m. 5 and a speeding up of harmonic rhythm from a four-beat interval to a two-beat interval in m. 7. In future work, we will explore which of the two options is more computationally efficient for identifying skeletons with internally varied rhythm. To restate, the two options are (1) pattern discovery that can skip between linear reductions at different window sizes (e.g., start in a four-beat reduction and finish in a two-beat reduction), or (2) reductions that vary in harmonic rhythm based on a consideration of events in additional voices—be they chord changes, interlocking outer voice tritones, or other contrapuntal relations. Option 1 stays true to the single-voice (horizontal) approach presented so far but will significantly increase the number of n-grams that must be considered by the algorithm. That will increase runtime and also create the possibility of many false positives. However, it remains likely that, in the Kirnberger, at least ––– would still be identified because of its prevalence within the excerpt (spanning about 40 percent of it). Option 2 means altering the algorithm so that it is no longer strictly horizontal in its considerations. This approach is less likely to yield false positives, but makes the algorithm even more complex than allowing patterns that skip between reductions (Option 1). Another factor to consider is that Option 1 as a purely linear (and not tonal harmony-based) approach is more extensible than Option 2 to non-Western musics. Whichever way we approach the issue of identifying scale degree skeletons with irregular spacing, the aspects of melodic salience we have presented here—onset and contiguity, in particular—are still productive features for core-tone selection in eighteenth-century European music. We anticipate that other features may be more germane to other eras and regions. While our system is challenged by pattern instances with metric irregularity, we view this as an opportunity for further research.
7. Conclusion
[7.1] Hanninen (2004, 2012) presents a qualitative framework for segmentation based on association and disjunction. Carter-Ényì (2016b) implements an algorithm for identifying recurring contour patterns—or what may be thought of as associative segments—which are then used as a basis for the segmentation of surface-level textures. In this study, we have applied the notion of associativity as a basis for segmentation to reduced textures, focusing on perceptually transparent contextual features of notes as a basis for evaluating their relative importance within a surface texture. After Gjerdingen (2007), we call these important notes core tones. Our theoretical entry point is not categorization into chord tones vs. non-chord tones (e.g., Marsden 2010; Ju et al. 2017), but rather melodic salience. We believe that core tones are perceptually salient primarily through their context within musical structures.
[7.2] Unlike the contour-based algorithm presented in Carter-Ényì (2016b), which considers every note (or the majority of notes) in the surface texture, the method presented here searches for recurring n-grams that form an associative set within reduced textures. Because harmonic rhythm varies within pieces like Mozart’s Sonata K. 545/i, it is necessary to create multiple reductions with different window sizes. Our algorithm searches through multiple reductions for n-grams within a single piece (intraopus). This approach is similar to Hanninen’s concept of associative sets. When a scale–degree skeleton is found to be common, it becomes a basis for choosing between potential reductions (e.g., a two-beat or a four-beat window) within a given time span. This expands upon Hanninen’s theory (2012) and Carter-Ényì’s implementation (2016b): not only do associative sets become the basis for segmentation, they are also a basis for reduction, or more precisely, the process of identifying core tones in a surface texture. Since Gjerdingen proposes schemata as commonplace patterns within a style, one obvious extension of this work is to widen the search through a stylistic corpus, which will likely support the piece-level search for skeletal schemata.
[7.3] Bach’s Fugue in C Minor, BWV 847, may be effectively reduced based on a single feature (strong-beat onset), though the reduction is improved with additional parameters. Mozart’s Sonata K. 545/i varies in texture and harmonic rhythm, which requires more parameters to reproduce aspects of Gjerdingen’s analysis (2007). The excerpt by Kirnberger adds the challenge of an instance of a schema whose harmonic rhythm (and deployment of melodic core tones) accelerates in the middle. Viewed in the context of the musics of the world, the pieces analyzed here by Bach, Mozart, and Kirnberger, are very close to each other, despite differences in style, texture, harmonic rhythm, and some of the techniques used for reduction. This highlights the diversity of surface contexts even within one century and one tradition. The methodological framework that is the basis for the ATAVizM software applies to monophonic repertoires and voices in polyphonic and homophonic textures.
[7.4] Despite our reservations about Lerdahl and Jackendoff’s (1983) formalization, the features we identify correspond to some of their time-span reduction preference rules. The primary difference is that the method presented here does not require segmentation before applying a reduction method. In line with Hanninen (2012) and Carter-Ényì (2016b), segmentation is not a given but is an essential part of the analytical process. Performing this task algorithmically through pattern discovery (finding associations) is suggestive for cognitive studies since segmentation emerges, bottom up, from a limited number of principles.
[7.5] Our aim of reducing surface textures to discover patterns brings this work into close contact with Gjerdingen’s schema theory and, to a lesser extent, Schenkerian middlegrounds. While Gjerdingen is an expert theorist and cognitive scientist, he does not formalize his implicit method for schema-finding. Here we have followed proposals by Rabinovitch (2018, 2019, 2020), who argues that outer-voice tritone preference, preference for metrically stressed events (and removal of accented dissonances), as well as contiguity operate as tacit principles in moving from the surface to the skeleton of core tones. Earlier work by Rabinovitch was done by hand, and some of his work (2019) relies on the metric segmentation implicit in Gjerdingen’s (2007) analyses. Here we operationalize principles of metric regularity, contiguity, and other features of pitch prominence (pitch and durational contour) in a reduction algorithm. This provides a proof of concept for finding schemata—or at least their soprano skeletons—algorithmically without positing them a priori. Instead, they are patterns discovered by taking an inventory of all n-grams and selecting recurring ones. Expanding pattern-finding through onset and contiguity to a corpus of galant music will likely reinforce common skeletal schemata. It remains to be tested at a later stage whether contrapuntal features suggested by Rabinovitch (2019)—especially preference for outer-voice tritones—should be weighted as additional features on the way to reductions, or whether weighting contiguity heavily would be more computationally efficient. Different musics will almost certainly require different combinations of pitch reduction parameters and may reveal new n-grams that do not correspond to Gjerdingen’s galant schemata. In particular, we believe that contiguity may conflict with the angularity of music in tone language cultures of Africa and Asia (Carter-Ényì 2016a; Carter-Ényì and Carter-Ényì 2020).
[7.6] The methodological framework proposed here is highly flexible and applicable to various genres through MATLAB tools and a more intuitive interface available at www.atavizm.org. Since we rely predominantly on contextual melodic features, our method is widely applicable to various musics. Although our present case studies were all taken from eighteenth-century European music, we apply this method to Nigerian story songs elsewhere (Carter-Ényì, Carter-Ényì, and Rabinovitch forthcoming). The methodological framework, moreover, is extensible in principle to many monophonic genres that do not rely on Western tonality. As the discipline of music theory continues to broaden its scope of application to a variety of musics and to explore further intersections with additional methodologies, from the empirical to the critical (Savage and Brown 2013; Ewell 2020), we hope that our approach will enrich the already productive dialogues among music scholars of various orientations. Since our interface is publicly accessible online, other theorists, analysts, and students can experiment with the parameters, contributing to the development of computer-assisted reduction and pattern-finding for a variety of musics and genres.
Aaron Carter-Ényì
Morehouse College
830 Westview Drive SW
Atlanta, GA 30314
Aaron.Carter-Enyi@morehouse.edu
Gilad Rabinovitch
Florida State University
College of Music
PO Box 3061180
Tallahassee, FL 32306
grabinovitch@fsu.edu
Works Cited
Adas, Jane. 1991. Early Eighteenth-Century Sonatas for Woodwinds: Continuo Sonatas for Woodwinds. Garland.
Albrecht, Joshua, and Daniel Shanahan. 2013. “The Use of Large Corpora to Train a New Type of Key-Finding Algorithm.” Music Perception 31 (1): 59–67. https://doi.org/10.1525/mp.2013.31.1.59.
Brown, Judith C. 1993. “Determination of the Meter of Musical Scores by Autocorrelation.” Journal of the Acoustical Society of America 94 (4): 1953–57. https://doi.org/10.1121/1.407518.
Bruhn, Siglind. 1993. J. S. Bach’s Well-Tempered Clavier: In-Depth Analysis and Interpretation. 4 vols. Gorz.
Carter-Ényì, Aaron. 2016a. “Contour Levels: An Abstraction of Pitch based on African Tone Systems.” PhD diss., The Ohio State University.
—————. 2016b. “Contour Recursion and Auto-Segmentation.” Music Theory Online 22 1. https://doi.org/10.30535/mto.22.1.1.
Carter-Ényì, Aaron, and Quintina Carter-Ényì. 2020. “‘Bold and Ragged’: A Cross-Cultural Case for the Aesthetics of Melodic Angularity.” Music & Science 3: 1–15. https://doi.org/10.1177/2059204320949065.
Carter-Ényì, Aaron, Quintina Carter-Ényì, and Gilad Rabinovitch. Forthcoming. “Ńfò: Scale-Degree Skeletons in Nigerian Story Songs.” In New Directions in World Music Analysis. Vol. 2, ed. Somangshu Mukherji, Robert Peck, and Lawrence Shuster. Routledge.
Creel, Sarah C., Elissa L. Newport, and Richard N. Aslin. 2004. “Distant Melodies: Statistical Learning of Nonadjacent Dependencies in Tone Sequences.” Journal of Experimental Psychology: Learning, Memory, and Cognition 30 (5): 1119–30. https://doi.org/10.1037/0278-7393.30.5.1119.
Ewell, Philip. 2020. “Music Theory and the White Racial Frame.” Music Theory Online 26 (2). https://doi.org/10.30535/mto.26.2.4.
Finkensiep, Christoph, Markus Neuwirth, and Martin Rohrmeier. 2018. “Generalized Skipgrams for Pattern Discovery in Polyphonic Streams.” In Proceedings of the 19th International Society for Music Information Retrieval (ISMIR) Conference, Paris, France, 547–53.
Finkensiep, Cristoph, Ken Déguernel, Markus Neuwirth, and Martin Rohrmeier. 2020. “Voice-Leading Schema Recognition Using Rhythm and Pitch Features.” In International Society for Music Information Retrieval (ISMIR) Conference, Montreal, Canada (virtual), hal-02976443f.
Forte, Allen. 1959. “Schenker’s Conception of Musical Structure.” Journal of Music Theory 3 (1): 1–30. https://doi.org/10.2307/842996.
Franck, Peter. 2007. “The Role of Invertible Counterpoint within Schenkerian Theory.” PhD diss., University of Rochester.
Givón, Talmy. 2001. Syntax: An Introduction. 2 vols. John Benjamins Publishing. https://doi.org/10.1075/z.syn1.
Gjerdingen, Robert. 1988. A Classic Turn of Phrase: Music and the Psychology of Convention. University of Pennsylvania Press.
—————. 2007. Music in the Galant Style. Oxford University Press.
Gjerdingen, Robert, and Janet Bourne. 2015. “Schema Theory as a Construction Grammar.” Music Theory Online 21 (2). https://doi.org/10.30535/mto.21.2.3.
Hamanaka, Masatoshi, Keiji Hirata, and Satoshi Tojo. 2006. “Implementing ‘A Generative Theory of Tonal Music.’” Journal of New Music Research 35 (4): 249–77. https://doi.org/10.1080/09298210701563238.
Hanninen, Dora. 2004. “Associative Sets, Categories, and Music Analysis.” Journal of Music Theory, 48 (2): 147–218. https://doi.org/10.1215/00222909-48-2-147.
—————. 2012. A Theory of Music Analysis: On Segmentation and Associative Organization. University Rochester Press.
Hentschel, Johannes, Markus Neuwirth, and Martin Rohrmeier. 2021. “The Annotated Mozart Sonatas: Score, Harmony, and Cadence.” Transactions of the International Society for Music Information Retrieval 4 (1): 67–80. https://doi.org/10.5334/tismir.63.
Huron, David. 2001. “Tone and Voice: A Derivation of the Rules of Voice-Leading from Perceptual Principles.” Music Perception 19 (1): 1–64. https://doi.org/10.1525/mp.2001.19.1.1.
Huron, David, and Richard Parncutt. 1993. “An Improved Model of Tonality Perception Incorporating Pitch Salience and Echoic Memory.” Psychomusicology 12 (2): 154–71. https://doi.org/10.1037/h0094110.
Huron, David, and Matthew Royal. 1996. “What is Melodic Accent? Converging Evidence from Musical Practice.” Music Perception 13 (4): 489–516. https://doi.org/10.2307/40285700.
Ju, Yaolong, Nathaniel Condit-Schultz, Claire Arthur, and Ichiro Fujinaga. 2017. “Non-Chord Tone Identification using Deep Neural Networks.” In Proceedings of the 4th International Workshop on Digital Libraries for Musicology, 13–16. ACM. https://doi.org/10.1145/3144749.3144753.
Kassler, Michael. 1975. “Proving Musical Theorems I: The Middleground of Heinrich Schenker’s Theory of Tonality” (Technical Report no. 103). University of Sydney, School of Physics, Basser Department of Computer Science.
Katsiavalos, Andreas, Tom Collins, and Bret Battey. 2019. “An Initial Computational Model for Musical Schemata Theory.” In Proceedings of the 20th International Society for Music Information Retrieval (ISMIR) Conference, Delft, the Netherlands, 166–72.
Kirlin, Phillip. B., and Paul E. Utgoff. 2008. “A Framework for Automated Schenkerian Analysis.” In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Philadelphia, PA, 363–68.
Krumhansl, Carol L. 1990. Cognitive Foundations of Musical Pitch. Oxford University Press.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Marlowe, Sarah. 2014. “Tonal Answers and Their Role Within Fugal Expositions: Two Revised Paradigms.” Theory and Practice 39: 47–73. https://www.jstor.org/stable/26477726.
Marsden, Alan. 2005. “Generative Structural Representation of Tonal Music.” Journal of New Music Research 34 (3): 409–28. https://doi.org/10.1080/09298210600578295.
—————. 2010. “Schenkerian Analysis by Computer: A Proof of Concept.” Journal of New Music Research 39 (3): 269–89. https://doi.org/10.1080/09298215.2010.503898.
Meyer, Leonard. 1967. Music, the Arts, and Ideas: Patterns and Predictions in Twentieth-Century Culture. University of Chicago Press.
Müllensiefen, Daniel, Bruno Gingras, Jason Musil, and Lauren Stewart. 2014. “The Musicality of Non-Musicians: An Index for Assessing Musical Sophistication in the General Population.” PLoS ONE 9 2: e89642. https://doi.org/10.1371/journal.pone.0089642.
Pastille, William. 1990. “The Development of the Ursatz in Schenker’s Published Works.” In Trends in Schenkerian Research, ed. Allen Cadwallader, 71–85. Schirmer.
Quinn, Ian. 1997. “Fuzzy Extensions to the Theory of Contour.” Music Theory Spectrum 19 (2): 232–63. https://doi.org/10.2307/745755.
Rabinovitch, Gilad. 2018. “Gjerdingen’s Schemata Reexamined.” Journal of Music Theory 62 (1): 41–84. https://doi.org/10.1215/00222909-4450636.
—————. 2019. “Implicit Counterpoint in Gjerdingen’s Schemata.” Music Theory & Analysis 6 (1): 1–49. https://doi.org/10.11116/MTA.6.1.1.
—————. 2020. “Hidden Polyphony, Linear Hierarchy, and Scale-Degree Associations in Galant Schemata.” Indiana Theory Review 36 (1–2): 114–66. https://doi.org/10.2979/inditheorevi.36.1-2.05.
Renwick, William. 1995. Analyzing Fugue: A Schenkerian Approach. Pendragon Press.
Savage, Patrick, and Steven Brown. 2013. “Towards a New Comparative Musicology.” Analytical Approaches to World Music 2 (2). https://www.aawmjournal.com/articles/2013b/Savage_Brown_AAWM_Vol_2_2.pdf.
Schenker, Heinrich. (1926) 1996. “The Organic Nature of Fugue as Demonstrated in the C minor Fugue from Bach’s Well-Tempered Clavier, Book 1.” In The Masterwork in Music: A Yearbook. Vol. 2. Edited by William Drabkin. Translated by Ian Bent et al., 31–54. Cambridge University Press.
Sears, David R. W. , and Gerhard Widmer. 2020. “Beneath (or Beyond) the Surface: Discovering Voice-Leading Patterns with Skip-Grams.” Journal of Mathematics and Music (July): 1–26. https://doi.org/10.1080/17459737.2020.1785568.
Smoliar, Stephen. 1980. “A Computer Aid for Schenkerian Analysis.” Computer Music Journal 4 (2): 41–59. https://doi.org/10.2307/3680082.
Symons, James. 2017. “A Cognitively Inspired Method for the Statistical Analysis of Eighteenth-Century Music, as Applied in Two Corpus Studies.” PhD diss., Northwestern University.
Temperley, David. 1999. “What’s Key for Key? The Krumhansl-Schmuckler Key-Finding Algorithm Reconsidered.” Music Perception 17 (1): 65–100. https://doi.org/10.2307/40285812.
Toiviainen, Petri, and Tuomas Eerola. 2006. “Autocorrelation in Meter Induction: The Role of Accent Structure.” Journal of the Acoustical Society of America 119 (2): 1164–70. https://doi.org/10.1121/1.2146084.
Wattenberg, Martin. 2002. “Arc Diagrams: Visualizing Structure in Strings.” In IEEE Symposium on Information Visualization, 110–16. IEEE.
Footnotes
1. Musically-trained people and/or sensitive listeners might be among those who score highly on a Gold-MSI test (Müllensiefen et al. 2014)
Return to text
2. Gjerdingen and Bourne (2015) suggest a non-uniform musical hierarchy for music, by analogy to Givón’s (2001) discussion of non-recursion among linguistic levels. See also Meyer (1967, 96–7).
Return to text
3. Creel, Newport, and Aslin’s (2004) observations about nonadjacencies in language and music come to mind as well: if speakers of Semitic languages like Arabic can recognize consonant roots like k-t-b as meaningful patterns even when embedded in different patterns of vowels (e.g., kitaab, “book,” kataba, “he wrote,”) it is possible that listeners can group nonadjacent pitches together, especially when they are supported (locally) by contiguity and/or are common schemata of a style. In the linguistic example, consonant sounds are nonadjacent elements (they are separated by vowels) but are adjacent to each other within the category of consonants; in music, nonadjacent pitches in hidden polyphony (compound melody) are adjacent within one layer.
Return to text
4. Similarly, Sears and Widmer (2020) focus on the Mi–Re–Do compound cadence (MRDCC).
Return to text
5. This is similar to Finkensiep, Neuwirth, and Rohrmeier’s (2018) generalized skipgram, which is drawn from computational linguistics. In addition, we considered notes offset by an accented dissonance, but it is hard to connect this to a feature per se. Such events might be identified as salient or structural through other features, especially duration and contiguity, or if all core tones are offset by a regular duration through accented dissonances (Symons 2017).
Return to text
6. We thank a reviewer for pointing out that pre-contiguity (i.e., pitch and time proximity to an important preceding note) may have more to do with salience than post-contiguity (i.e., pitch and time proximity to an important following note). We would like to emphasize, however, that in repeated listening—or in retrospective interpretation of previous melodic notes—post-contiguity may be quite relevant as well.
Return to text
7. Similarly, GTTM’s preference rules are not clearly weighted or ordered, but weightings are desirable for attempts to implement the theory more formally through computations.
Return to text
8. Interestingly, Schenkerian fugal paradigms as proposed by Renwick (1995) and others create a kind of schema theory—an issue that lies well beyond the present scope. In contrast with Schenkerian analysts, our approach is highly surface-driven and prioritizes melodic salience.
Return to text
9. The apparent preference for outer-voice tritone resolutions in galant schemata (Rabinovitch 2018, 2019, 2020) suggests that privileging tritone resolutions as skeletal reveals salient melodic notes as well as a local tonal center, on which the scale-degree identity of the schema depends. What is unclear from the manual reconstruction by Rabinovitch is whether prioritizing tritone resolutions might be obviated by giving a high weight to contiguity, or whether both features should ultimately be weighted in an algorithmic approach to galant-schematic reductions.
Return to text
10. The continuous contour matrix and segmentation method presented by Carter-Ényì (2016a, 2016b) also yields the eight instances. In this case, a pattern that corresponds to the subject and transformations of the subject may be discovered on the surface or in a reduction.
Return to text
11. Note that the reduction based on strong-beats does not include the first in the reduction of the subject in Example 3. While the first of ---- is included in a reduction based on onset and contiguity for the subject, the is not part of the reduction of the tonal answer because scale degree is replaced with [key of v:] in the analogous location. The pattern that ties all statements (including the subject and tonal answer and other transformations) is ---, not ----.
Return to text
12. Although computationally incorrect because they have different semitone values, we maintain the appearance that a descending m2/M2 is –1 in the software to be consistent with the interval naming convention in terms of generic intervals.
Return to text
13. An arc diagram is a type of network diagram ideal for visualizing structure based on recurrent patterns in data strings like music (Wattenberg 2002). Wattenberg’s defunct music-visualization project has inspired ATAVizM.
Return to text
14. Albrecht and Shanahan (2013), Krumhansl (1990), Huron and Parncutt (1993), and Temperley (1999).
Return to text
15. A caveat to this statement, noted by an anonymous reviewer, is that mm. 22–25 present a circle-of-fifths Prinner, that is, a different subcategory of the Prinner.
Return to text
16.
Return to text
17. One might argue that our methodological framework is insensitive to principles of counterpoint and dissonance treatment, yet this gives our method the potential to be generalizable across musics and genres (cf. the discussion of schemata and contrapuntal reduction in Rabinovitch 2019, which accounts for dissonance treatment).
Return to text
18. Marsden (2010), Katsiavalos, Collins, and Battey, (2019), Finkensiep et al. (2020), and Hentschel, Neuwirth, and Rohrmeier (2021) also test their systems on Mozart piano sonatas. Note that the reading in Katsiavalos, Collins, and Battey (2019, 167) of the opening four mm. of K. 545/i as a Meyer schema seems implausible from the perspective of theory and analysis—it is at least inconsistent with the rich and detailed description of the Meyer schema in Gjerdingen (1988, 2007), as well as with Gjerdingen’s (2007) own expert analysis of K. 545/i.
Return to text
19. Adding contiguity does not disrupt the Prinner discovery in Bach’s Fugue in C Minor, BWV 847, but it is more computationally efficient to only use the onset feature for that analysis.
Return to text
20. In Example 13, within the window representing the first half of m. 4, there are multiple Fs, all of which earn 2 points for contiguity.
Return to text
21. Gjerdingen (2007, 365) does not specify core tones for the piece-specific “Opening Gambit” in mm. 1–2. Our approach to reduction ultimately strives to create a consistent stream of skeletal notes, whereas Gjerdingen’s analyses occasionally leave small portions of the piece without skeletal scale-degree annotations.
Return to text
22. We confirmed that adding octave equivalence, wherein the melodic interval of a 9th is equivalent to a 2nd, does not alter the results in the analysis already presented.
Return to text
23. As explained above, –1 is a descending generic 2nd (either m2 or M2), maintaining the naming conventions of intervals.
Return to text
24. The typical metric embedding of the Meyer or –. . . – in the style is discussed in Gjerdingen (1988, see esp. 88–90, figures 5–1 through 5–4): while the core tones of this schema may be deployed at regular time intervals in instances of the schema, often and immediately precede a barline or other metric boundary while and immediately follow it. Therefore, the Meyer’s core tones are often presented in an irregular fashion on the musical surface.
Return to text
25. This sonata is reproduced in Adas (1991, 30).
Return to text
26. We have in fact been able to reconstruct the entire skeleton finding of Rabinovitch algorithmically through a series of steps in ATAVizM, but this required reliance on harmonic/contrapuntal features—we will report about this fuller reconstruction in the future. Of course, different styles and musics would require different combinations of melodic (and at times contrapuntal/harmonic) features in order to be analyzed algorithmically.
Return to text
27. As the lines connecting notes on different staves in the annotations in Example 21 indicate, this also creates an outer-voice tritone, which is given the highest preference in Rabinovitch (2019). It is unclear to us at this stage whether preference for contiguity, preference for outer-voice tritones, or both, are key to schema finding.
Return to text
28. From a slightly different angle, surface melodic groupings (Lerdahl and Jackendoff 1983) support the subdivision into m. 5 and m. 6 as whole-measure units and m. 7 as two half-measure units.
Return to text
Copyright Statement
Copyright © 2021 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
25742