The Logic of Six-Based Minor for Harmonic Analyses of Popular Music
Trevor de Clercq
KEYWORDS: popular music, harmony, tonal ambiguity, tonal fusion, minor tonic, diatonic modes
ABSTRACT: Harmonic analyses of popular music typically take the minor tonic to be Roman numeral “one.” By nature, this “one-based” approach requires a new numbering scheme when songs shift between relative key centers. Recent scholarship has argued, however, that popular music often involves ambiguity between relative tonalities, as exemplified in the “Axis” progression, if not sometimes a tonal fusion of two relative keys. I thus argue for the utility of a “six-based” approach to the minor tonic, where the minor tonic is taken to be scale-degree 6. This six-based approach, common among practitioners of popular music as seen in the Nashville number system, avoids the forced choice of a single tonic, and it thus offers a consistent way to track chord function and behavior across shifts between relative key centers. After considering these shifts in a diatonic context on the levels of both phrase and song form, I posit that popular music involves three possible tonalities, together which form a “triple-tonic complex” akin to Stephenson’s three harmonic palettes: a major system, a parallel-minor system, and a relative-minor system. I conclude by considering how chromatic chords common in a major key, such as II and
DOI: 10.30535/mto.27.4.4
Copyright © 2021 Society for Music Theory
I. Introduction
[1.1] The nature of harmonic organization in contemporary commercially distributed Western Anglophone popular music—sometimes referred to as “rock” but hereafter as “popular music”—has been the subject of much theorization and analytical debate for more than two decades.(1) Approaches include those based on the seven diatonic modes (Moore 1992; Biamonte 2010), three harmonic palettes (Stephenson 2002), and six tonal systems (Everett 2004). Some authors suggest unique schemes for specific artists or sub-styles, such as the music of Radiohead (Osborn 2017), Frank Zappa (Clement 2014), or post-millennial “hipster” rock (Heetderks 2015). Despite the various differences in how these authors cast the harmonic practice(s) of popular music, a feature common to all is that in each, the minor tonic chord is always represented as “i” (i.e., Roman numeral “one”).
Example 1a. Verse material from “Down Under” (Men at Work, 1981), as analyzed by Doll (2011, [4])
(click to enlarge and listen)
Example 1b. Chorus material from “Down Under” (Men at Work, 1981), as analyzed by Doll (2011, [4])
(click to enlarge and listen)
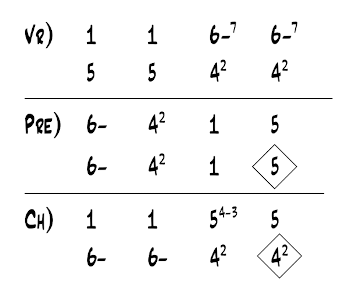
[1.2] As an illustration of this approach, consider Doll’s 2011 analysis of the song “Down Under” by Men at Work (1981). Doll identifies the tonic of the verse as B minor and, as shown in Example 1a, assigns this tonic to Roman numeral i. This assignment determines the Roman numerals for the other chords in the passage, with A major as
[1.3] Many readers may find nothing wrong with Doll’s use of Roman numerals; after all, his approach epitomizes current practice. Yet these Roman numerals imply rather different hearings of the chords in the verse and chorus even though these two sections have almost identical musical content, not only in terms of harmony but melody as well. Admittedly, the switch from B minor on the downbeats of the first and third bars of the verse to D major in the chorus has a significant effect; like Doll, I too hear a shift in tonal emphasis between the two sections. But the Roman numerals exaggerate the effect of this shift. In the chorus, for example, I still hear the B minor chord on the downbeats of the second and fourth bars as the minor tonic from the verse. I also find it difficult to “unhear” the D major of the chorus, which influences my hearing of harmony in the second verse. Even once the song is over, the chorus is such a memorable section that its opening tonic lurks in the back of my inner ear as a reference for any future hearing.
Example 1c. Alternative Roman numeral analysis for the verse material of “Down Under” (Men at Work, 1981) using a six-based approach to the minor tonic
(click to enlarge)
[1.4] A core part of the problem, as I see it, is that the prevailing use of Roman numerals is predicated on the assumption that harmonic function given a minor tonic is best modeled through its relationship with the parallel major tonic. I will refer to this as a “one-based” approach to the minor tonic. In contrast, the harmonic content in “Down Under” involves a play between relative tonics. To better capture this relationship, I propose instead that analysts of popular music favor (at least in some cases) an alternate representation of functional harmony that I call a “six-based” approach to the minor tonic, as shown in Example 1c. In a six-based approach using Roman numerals, the minor tonic is taken to be “vi” rather than a new or different “one” chord.
[1.5] Some readers may be familiar with the debate between do-based and la-based minor solmization systems. According to recent research, roughly three-quarters of music programs use do-based minor for sight-singing coursework, while less than a quarter use la-based minor (Murphy and McConville 2017). Like six-based minor, la-based minor assigns different syllables to the major and minor tonic. But unlike six-based minor, la-based minor is normally dependent on the diatonic mode.(3) The tonic of a melody in Dorian, for example, would be re, the tonic of a melody in Phrygian would be mi, and so on. La-based minor is thus useful for music that expresses pure modal content, such as the folk music used in the Kodály method. In contrast, six-based minor takes the major tonic to be and the minor tonic to be , regardless of other modal inflections in the scalar collection. The minor tonic is thus never or , nor is the major tonic ever or .(4) Admittedly, it is sometimes difficult in popular music to determine whether the tonality of a song is major or minor (or both or neither). This is an important issue, which I will address below (particularly in [4]).
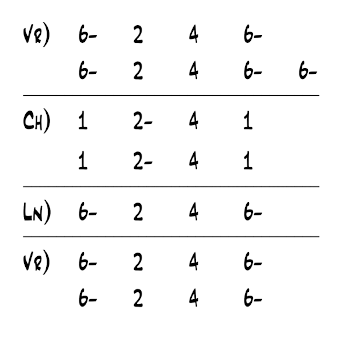
Example 2. Nashville number system chart for verse and chorus material of “Down Under” (Men at Work, 1981)
(click to enlarge)
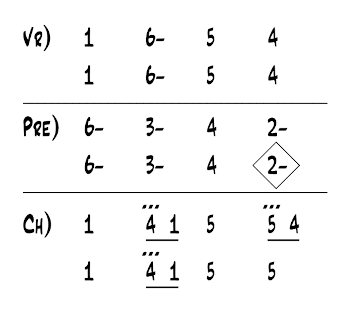
[1.6] Although six-based minor is not commonly found in current music theory scholarship or teaching, it is often used by commercial musicians, particularly those working in the Nashville, Tennessee area. Nashville musicians do not normally use Roman numerals, however; instead, they use an alternative functional chord notation called the Nashville number system, in which six-based minor is standard.(5) As a brief illustration, Example 2 shows the verse and chorus sections for “Down Under” in Nashville numbers. In contrast to Roman numerals, Nashville numbers use Arabic numbers to indicate the scale degree of the chord root, with the quality of the chord indicated through standard jazz/pop shorthand (e.g., a dash after the chord root indicates a minor triad). Other differences between Nashville numbers and Roman numerals exist, including the rhythmic symbols shown in Example 2, but these differences are not directly germane to the issue of one- versus six-based minor and will be explained later as needed.(6) To be clear, there is nothing inherent about the Nashville number system that lends it to six-based minor, and examples of Nashville number charts using one-based minor can be found in multiple sources;(7) nor is there anything inherent about Roman numerals (aside from tradition) that necessitates the use of one-based minor. In what follows, I will use both Roman numerals and Nashville numbers, in part to emphasize that six-based minor is a conceptual approach not tied to any particular scale-degree-based chord notation system.
[1.7] Note also that my use of Roman numerals or Nashville numbers in the following examples is not meant to exclude other analytical methods. Harmonic function categories (e.g., T, S, D) are sometimes useful to highlight general patterns in chord behavior, and I will discuss the interaction of these function categories with six-based minor (especially in [2.6]). Additionally, we could explain chord behavior in popular music through neo-Riemannian transformations (Capuzzo 2004; Forrest 2017) or the idiomatic actions of guitar playing (Easley 2015; Koozin 2011). These analytical frameworks are not mutually exclusive. If, however, an analyst uses a scale-degree-based functional notation system (such as Roman numerals), the choice between one-based and six-based minor is significant, because it influences the types of chord patterns the analyst will observe. More importantly, I posit that six-based minor is generally better suited (although not always) to represent the types of chord behavior found in popular music, especially music from more recent decades. In what follows, I begin by showing how six-based minor intersects with recent scholarship on tonic in popular music—including work on ambiguous, absent, and double tonics—both on a small scale and on the larger scale of song form. I then propose a “triple-tonic complex” for popular music, in which six-based minor and one-based minor combine to create a “super-palette” of common chords. I conclude with a discussion of how six-based minor collapses the landscape of diatonic modes into three modal complexes. Overall, my goal is to show the logic of six-based minor—why it is useful, what issues it resolves, and what insights it can afford us about harmonic syntax in popular music.
II. The False Choice of a Single Tonic
Example 3. Opening verse material from “Don’t Forget Me” (Red Hot Chili Peppers, 2002)
(click to enlarge and listen)
[2.1] An implicit assumption of one-based minor is that, given some passage of music, we can identify some singular tonic pitch.(8) As music theorists have recently acknowledged, however, this is often a difficult task. The conundrum is regularly illustrated with the “Axis” progression (Richards 2017), i.e., C–G–Am–F and its various rotations and transpositions. In particular, the rotation that starts with the minor chord, e.g., Am–F–C–G as heard in the song “Don’t Forget Me” (Red Hot Chili Peppers, 2002) shown in Example 3, lends itself to at least two possible hearings: i–
[2.2] More recently, Nobile has argued that these situations are not really cases of ambiguity—i.e., either/or—but instead involve a “special type of tonality” in which two different tonal centers coexist—i.e., both/and (2020a, 207). In other words, the decision of whether one tonic or another represents the true tonic is a false choice. Adopting a term from Bailey (1985), Nobile refers to this fusion of two keys as a “double-tonic complex.” As Nobile defines it, “key” refers to a single tonal center with one of two possible tonal qualities (e.g., C major or C minor), whereas the double-tonic complex describes the higher-order combination of two keys (e.g., C major and A minor). Nobile’s analyses involve what he calls the “Aeolian-Ionian complex,” in which a major key and its relative minor form a “tonal partnership” (213). One aspect that facilitates this tonal partnership, Nobile observes, is that chords often belong to the same functional category in relative keys. A D-minor chord, for example, typically functions as subdominant (S) in both the key of A minor (as iv) and the key of C major (as ii). Our expectations for chord behavior, therefore, do not hinge on choosing one tonal center (major or its relative minor) over the other. In many cases, we can imagine swapping out one tonic for its relative partner without affecting the logic of the harmonic syntax (Nobile 2020a, 213). For example, we can take the chord progression F–C–Gm–
[2.3] Assuming that Nobile’s notion of the double-tonic complex reflects our hearing (as it does mine), an analytical system that presumes a single tonic becomes awkward. Accordingly, Nobile sometimes avoids Roman numerals in his analyses; at other times, he uses two sets of Roman numerals (as in Example 3 above) or relies on chord function labels (2020a, 219–221). These are all viable methods, although each has its disadvantages when trying to identify harmonic patterns more broadly. Without Roman numerals (or some other scale-degree-based system), it is difficult to identify chord patterns through different transposition levels. While standard function categories like T, S, and D address the issue of transposition and offer great predictive power as compared to Roman numerals, function categories do so at great cost to the precision of that prediction.(9) Dual sets of Roman numerals offer more precise tracking of chords through various transpositions, but they overstate the complexity of the harmonic palette. Example 3, for instance, shows seven or eight different chord types when considering both tonics, even though the passage contains just four diatonic chords. These issues may not matter to someone analyzing a song in isolation. But for those who seek to identify patterns of harmony across many songs and leverage those patterns in their analyses—as Doll, for example, does expertly with his schemas (2017)—these sorts of issues are central.
[2.4] And it is these sorts of issues, among others, that six-based minor resolves. If we allow Roman numeral vi to be the minor tonic, then we require only one analysis for Example 3: vi–IV–I–V. For those used to thinking exclusively in one-based minor, six-based minor may appear equivalent to saying that the song is in the relative major key. But while there may be no superficial difference, there is a considerable conceptual difference. Getting used to the conceptual orientation of six-based minor, especially given an orientation as ingrained as one-based minor, may take practice. Some readers may feel that it is impossible to erase the implication that “I” is a tonic chord and “vi” is not, or that by nature is more central and referential than . Consider, though, that our musical alphabet spans from A to G, and that for a trained musician, there is nothing inherently more central about the note A than any other. In the key of E major, for example, A does not enjoy any special privilege because it is the first letter of the alphabet. The number six, therefore, does not necessarily have to lack special conceptual status because it is not the first number.(10)
Example 4a. Medley of song excerpts using a vi–I–V–IV progression: “All Good Things (Come to an End)” (Nelly Furtado, 2006), “Pocketful of Sunshine” (Natasha Bedingfield, 2007), “Burnin’ Up” (Jonas Brothers, 2008), “Impossible” (Shontelle, 2010), “Counting Stars” (One Republic, 2013), and “Timber“ (Pitbull feat. Kesha, 2013)
Example 4b. Medley of song excerpts using a vi–I–V–ii progression: “What I’ve Done” (Linkin Park, 2007), “Jar of Hearts” (Christina Perri, 2010), “Set Fire to the Rain” (Adele, 2011), “Prayer in C” (Lilly Wood and the Prick, remixed by Robin Schulz, 2014), “Too Good at Goodbyes” (Sam Smith, 2017), and “Trampoline” (SHAED, 2018)
Example 4c. Medley of song excerpts using a ii–vi–I–V progression: “Broken Strings” (James Morrison feat. Nelly Furtado, 2008), “She Wolf (Falling to Pieces)” (David Guetta feat. Sia, 2012), “If I Go” (Ella Eyre, 2014), “Powerful” (Major Lazer feat. Ellie Goulding and Tarrus Riley), “Blinding Lights” (The Weeknd, 2019), “Watermelon Sugar” (Harry Styles, 2019)
[2.5] The effort of developing this new conceptual orientation may not seem worthwhile if the double-tonic complex is not common in popular music. Indeed, Nobile is careful not to overextend his new concept. In most of his examples, the double-tonic complex involves (or requires) a literal union of the major tonic and its relative minor into a four-note sonority on the musical surface, the exception being the Axis progression. Nobile does open the door to other cases that do not include a four-note tonic, writing that progressions containing only the chords Am, C, Dm, F, and G (and transpositions of this set), an emphasis on both Am and C, and a stronger emphasis on Am are especially suited to a double-tonic interpretation (2020a, 215). Nobile does not provide any examples of this situation (aside from the Axis), but songs with progressions that fall under these guidelines are not difficult to find. For instance, consider the six song excerpts in Example 4a, all of which employ the progression vi–I–V–IV. Then consider Example 4b, which includes six excerpts in which a ii chord substitutes (as a subdominant function) for the final IV chord, creating the progression vi–I–V–ii. Finally, consider Example 4c, which provides six excerpts with a rotation of that chord progression, ii–vi–I–V.(11) Some of these excerpts may sound more centered on the major tonic, others on the minor tonic (for whatever reason); but each to my ears conveys a similar double-tonic hearing as the Axis progression.(12) By using six-based minor, as I have done, we can capture the similarity in harmonic content between these songs without having to decide whether each example is in a major key or its relative minor (arguably a false choice), nor must we resort to using two sets of Roman numerals to track just five diatonic triads through transposition. Function categories are a useful additional analytical layer; I notice, for example, that tonic chords (i.e., I and vi) are never placed as the last chord in these four-chord loops. But function labels do not capture some important features, such as that the minor tonic (vi) leads to the major tonic (I) in every excerpt of Examples 4a, 4b, and 4c.
Example 5. Chord progression vi–I–V–iii as found in “Fade to Black” (Metallica, 1984) and “The Unforgiven II” (Metallica, 1997)
[2.6] Nobile’s list of white-note triads typically involved in a double-tonic complex includes all the diatonic triads except Em (iii) and Bo (viio).(13) It may be true that these two chords are not as common in double-tonic complexes as are the other five (Am, C, Dm, F, and G), but that may be simply because these two chords are fairly rare in popular music overall.(14) We might wonder then whether either of these chords could participate in a double-tonic complex. It turns out that the iii chord fits very well into the double-tonic complex, typically acting in a dominant role. The Metallica songs “Fade to Black” (1984) and “The Unforgiven II” (1997), as heard in Example 5, both contain the progression vi–I–V–iii, which bears strong similarity to the progressions in Examples 4a and 4b. Instead of a T–T–D–S pattern, however, the progression in these Metallica songs evinces a T–T–D–D pattern. In terms of harmonic functions, I thus see the diatonic scale as including double tonics (vi and I), double subdominants (ii and IV), and double dominants (iii and V). The status of the remaining diatonic chord, viio, is somewhat more complicated and will be tabled for discussion below (see [4.7]).
Example 6. Verse material from “Treasure” (Bruno Mars, 2012)
(click to enlarge and listen)
[2.7] As another case of iii and V used as double dominants, consider the song “Treasure” by Bruno Mars (2012). The song’s harmonic structure involves a repeating four-bar loop with two different endings, both of which are shown in Example 6. The second system shows the ending prior to a section change, which uses an
III. Large-Scale Aeolian-Ionian Centric Shifts
[3.1] The examples above were mostly brief excerpts, which demonstrated that shifts between a major tonic and its relative minor can create tonal fusion or ambiguity within the span of just a four-bar phrase. Shifts between a major tonic and its relative minor are also common on a larger scale in popular music, especially between different parts of a song. “Down Under,” discussed above, is one example. Like Doll (2011), we might sometimes identify these situations as a modulation between relative tonics; other times, we might classify them as instances of “sectional tonality” or “sectional centricity,” in line with Capuzzo (2009); or we might posit, following Nobile (2020a), a double-tonic complex for the song overall. These are case-by-case decisions, of course, dependent on the strength and nature of this shift between relative tonics.
[3.2] That is to say, a continuum of cases exists in which one or more parts of a song (e.g., verse, prechorus, chorus) will center more strongly on the minor tonic and another part or parts more strongly on the relative major. One-based minor is fairly clumsy in this regard, requiring a strict dividing line somewhere along this continuum where we must decide if and when to change tonics. In contrast, six-based minor allows us to compare songs on this continuum in a more consistent way and avoid the forced (if not false) choice of deciding when and where there exists a true new tonic. I will illustrate this continuum through seven songs, ranging from a song clearly in a major key to one that is much more strongly centered on the minor tonic. The harmonic content of these songs is entirely diatonic, limited to the six major and minor triads derived from a diatonic scale, because it is this diatonicism (in part) that facilitates the ambiguous or double-tonic quality of these examples. I will use Nashville numbers for most of these examples, since they are an efficient tool to summarize harmonic content and form. Melodic aspects are undeniably important too (and influence the decision of tonal centers), but the focus here will mostly be on patterns of harmony through different song sections.
Example 7. Nashville number chart for excerpt (0:36–1:29) of “Photograph” (Ed Sheeran, 2014)
(click to enlarge and listen)
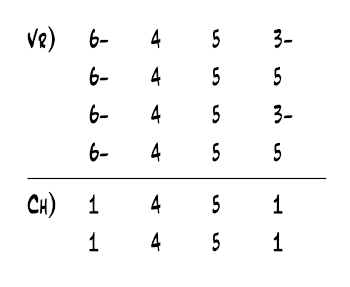
[3.3] The song “Photograph” (Ed Sheeran, 2014), for instance, has a clear major tonic (E) in both the verse (VR) and chorus (CH), as shown in Example 7. (N.B.: Each number in this chart represents a bar of harmonic content, such that each section shown is eight bars long.) Part of what grounds the verse and chorus so strongly in E major is not only the opening major tonic of both sections but also that and are pedaled in the guitar part throughout. This creates a chordal seventh on the
Example 8. Nashville number chart for excerpt (0:12–1:18) of “See You Through My Eyes” (The Head and the Heart, 2019)
(click to enlarge and listen)
[3.4] Even if the prechorus of “Photograph” has only a slight shift in emphasis to the relative minor, it still retains a sense of the relative major (an ephemeral double-tonic complex?), in no small part because of the I and V chords in the prechorus. But if these chords are absent, the tonal center can shift more strongly to the relative minor. The song “See You Through My Eyes” (The Head and the Heart, 2019), as charted in Example 8, illustrates this situation. Like “Photograph,” the verse and chorus are clearly centered on a major tonic, here C major. (N.B.: The underlined Nashville numbers in the chorus belong to the same bar, with the three dots over the first chord indicating that the chord lasts three beats.) We could still posit a large-scale functional circuit, following Nobile (2020b), with the vi chord in the first bar of the prechorus starting the predominant area and the ii chord in the last bar acting as the syntactical dominant (Nobile 2016). But it also seems important to recognize the shift of center to the relative minor, if only fleeting, which creates an important expressive contrast between the prechorus and its surrounding sections. Note, for example, the lyrics in the fifth bar of the prechorus (when the tonicity of the vi chord is especially strong), “Without the dark, there is no light,” as well as other negatively valenced words, including “locked,” “damaged,” “scattered,” “ghost,” and “leaving,” especially as opposed to the positively valenced lyrics of the chorus, e.g., “This could be so easy” and “something so beautiful.” This shift to the relative minor does not warrant abandoning the “one” chord, in that the embers of the major tonic still flicker in this prechorus, yet I want to refer to the first chord in the prechorus as some sort of tonal home. Six-based minor lets me have it both ways.
Example 9. Nashville number chart for excerpt (1:21–2:04) of “Up Against the Wall” (Boys Like Girls, 2006)
(click to enlarge and listen)
Example 10. Nashville number chart for excerpt (0:16–1:03) of “The Damage in Your Heart” (Weezer, 2005)
(click to enlarge and listen)
[3.5] One common songwriting blueprint is a verse more centered on the minor tonic and a chorus more centered on the major tonic, such as in “Down Under” (Example 1), where the positive valence of the relative major helps the chorus feel like the high point of the song (relatively speaking [pun intended]). “Up Against the Wall” (Boys Like Girls, 2006), as charted in Example 9, provides another case of this scenario. It would not be unreasonable to say that this song is in a major key overall, given that the major tonic (E) begins the chorus and also appears in the verse. Yet the opening vi chord of the verse, as in other Axis progressions starting on vi, encourages being heard as the minor tonic. The vocal melody at the beginning of the verse, which descends E–
Example 11. Nashville number chart for excerpt (0:00–0:56) of “Chandelier” (Sia, 2014)
(click to enlarge and listen)
Example 12. Nashville number chart for excerpt (0:07–0:50) of “Innocence” (Avril Lavigne, 2007)
(click to enlarge and listen)
[3.6] In the preceding four examples, each chorus began with the major tonic. The use of six-based minor may thus appear to be predicated on the tonality of the chorus (or some other part of the song). But even if the “major-ness” of the chorus is decreased and the “minor-ness” of the verse is increased, we may still perceive a general (if subtle) shift between relative tonics from section to section. In other words, it may be clear that both the verse and chorus are more strongly centered on the minor tonic, yet the faint glimmer of the major tonic is enough to connect all these examples (and others) along a continuum that six-based minor tracks in a consistent way. For instance, the song “Chandelier” (Sia, 2014), charted in Example 11, has a strong emphasis in both the verse and prechorus on the minor tonic (
Example 13. Vocal melody and chords for excerpt (0:24–1:04) of “Miss Americana & the Heartbreak Prince” (Taylor Swift, 2019)
(click to enlarge, see the rest, and listen)
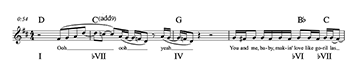
[3.7] As the final step along this continuum from a minor tonal center to its relative major, consider the song “Miss Americana & the Heartbreak Prince” (Taylor Swift, 2019). The entire song includes only three chords—G major, A major, and B minor—with the B-minor chord sounding like a strong minor tonic. Lacking any indication of the relative major in the harmonic domain, we may think that one-based minor would be more appropriate here. Yet consider the structure of the vocal melody, as shown in Example 13 (notated in a half-time feel). The beginning of the verse emphasizes the note B, but by the fourth and fifth bar, the vocal part outlines melodic shapes suggestive of D major (on “Running through rose thorns, I saw the scoreboard”). The melody in the prechorus also emphasizes the note D in its first half as well as through leaps down from A to D ( to ) in its second half. Finally in the chorus, the vocal uses melodic shapes strongly associated with a D-major tonality. The first half of the chorus keeps flirting with cadential tension around and an ambiguously (or blues-ily) tuned (noted by the asterisk), coming to land on in the third bar. This cadential tension is then resolved in the last four bars of the chorus, where the melody outlines D-major triads and D-major cadential motion, especially at the end (on the lyrics “You play stupid games, you win stupid prizes”). We might, therefore, say that the harmonic and melodic content of this song implies (at various times) different relative keys, i.e., some sort of melodic-harmonic “divorce” (Temperley 2007) or “split” (Ferrandino 2017). This emphasis on D major in the vocal, even if subtle, is important enough to make me want to hear D as , which is in conflict with hearing B as tonic if I were to use one-based minor.
IV. The Triple-Tonic Complex
[4.1] Thus far, I have focused on tonal fusion or ambiguity involving two relative keys that share the same diatonic collection. This is not, however, the only type of tonal fusion or ambiguity involving two keys in popular music. The more oft-discussed case is when a single tonic pitch or chord can be easily identified but the mode (major, minor, or otherwise) is unclear.(19) Temperley, for example, advises identifying the key of a song solely by its tonal center (e.g., G or A), without any indication of quality.(20) It is for this reason that Roman numerals in popular music are independent of mode—an F major chord, for example, is
Example 14. Melody and chords from verse material of “Blue on Black” (Kenny Wayne Shepherd Band, 1998)
(click to enlarge, see the rest, and listen)
[4.2] The double-tonic complex between parallel keys (if we call it that) is a common feature of popular music. Its roots can been traced to electric and country blues songs of the 1930s, ‘40s, and ‘50s (Wagner 2003; Everett 2004), such as “Cross Road Blues” (Robert Johnson, 1937) and “Young Fashioned Ways” (Muddy Waters, 1955). The song “Blue on Black” (Kenny Wayne Shepherd Band, 1998) illustrates this situation, as transcribed in Example 14. The tonic pitch here is clearly D, but trying to categorize the song as either D major or D minor is difficult. The acoustic guitar (the primary instrument in the harmonic layer) does not play an audible chordal third on the tonic harmony, and the other two chords in the progression—C major and G/B—do not settle the issue since the former implies D minor whereas the latter implies D major. The vocal melody offers no help either, as it freely floats between D major and D minor. We might be tempted to label cases like this as modal mixture. But the situation here seems categorically different from the modal mixture typically found in classical music, where the quality of the tonic triad is clear and scale degrees are “borrowed” from the parallel mode—with the word “borrow” implying a main key and a peripheral key. Instead, popular music often involves parallel key centers on a more equal footing. Everett (2004), for example, delineates between “common-practice” modal mixture (his tonal systems 1a, 1b, and 3a) and “blues-based” mixture (his tonal system 4). Admittedly, Everett categorizes blues-based mixture (in his Table 1) as “minor-pentatonic-inflected major-mode systems,” which could be read as still implying a more primary key (major) and a more secondary key (minor); indeed, if I were to forced to choose, I would say that “Blue on Black” is in D major rather than D minor.(21) But this is arguably another false choice, similar to that between relative keys discussed above.
Example 15a. Chorus material for “Gorilla” (Bruno Mars, 2012)
(click to enlarge and listen)
Example 15b. Verse material for “Gorilla” (Bruno Mars, 2012)
(click to enlarge and listen)
[4.3] Harmony in popular music can thus be seen to commonly involve three possible keys—the major key, the parallel minor, and the relative minor—which I refer to as the “triple-tonic complex” for popular music. Some songs use only one of these tonalities; others use two; and some songs employ all three. “Synchronicity II” (The Police, 1983), for example, contains sections centered on three distinct tonics:
Example 16a. Stephenson’s three harmonic palettes (2002, 96) contrasted with the triple-tonic complex
(click to enlarge)
Example 16b. A super-palette and anti-palette of harmonies for popular music, based on Stephenson (2002, 96)
(click to enlarge)
[4.4] The idea that popular music involves three different tonalities is not new. Stephenson, for example, suggests three harmonic palettes for rock music—natural minor, chromatic minor, and major—each of which provides a set of common chords used within a given song. Stephenson’s chart of harmonic palettes (2002, 96) is reproduced as the top three staves in Example 16a.(22) His chromatic-minor system, for instance, includes both a major tonic as well as the parallel minor tonic and, aside from the II chord, involves further mixture between parallel major (IV and V) and minor (
[4.5] The logical next question is: When we are faced with a minor tonic, how do we know if we are dealing with a case of parallel minor or relative minor? Specifically, how do we know whether to call a real-world minor tonic “one” or “six,” since both ways are valid? Some cases are fairly straightforward. If a song involves fusion, ambiguity, or shifts between two relative tonalities (as seen in various examples above), use six-based minor. In contrast, if a song has a clear tonic pitch but involves fusion, ambiguity, or shifts between parallel keys—such as found in songs like “Kiss on My List” (Hall & Oates, 1980), “Ghostbusters” (Ray Parker, Jr., 1984), “Janie’s Got a Gun” (Aerosmith, 1989), “Kiss from a Rose” (Seal, 1994), or “A Wolf at the Door” (Radiohead, 2003)—one-based minor seems more appropriate. Given the diversity of harmonic practices in popular music, however, not all cases are so straightforward. This is especially true when a song has no obvious correspondence with either the relative or parallel major key. I will thus propose two basic strategies: a “contextual” six-based minor approach and a “default” six-based minor approach.
[4.6] To begin with, consider that despite the variety of chord types indicated in Stephenson’s harmonic palette for the major system (Example 16a, third staff from the top), the vast majority of chords in popular music given a major tonic are I, IV, and V.(24) This situation is not unlike classical music, where I, IV, and V chords constitute the bulk of harmonic sonorities given a passage in a major key.(25) A central reason why one-based minor works so well for classical music is that scale-degrees 1, 4, and 5 (assuming one-based minor) are also the most frequently occurring chord roots in a minor key.(26) We could adopt a similar strategy for popular music, where we base our decision about one- versus six-based minor on how the most frequent chord roots in a song map to the major key. A song like “Bad Guy” (Billie Eilish, 2019), which is composed entirely of the chord loop Gm–Cm–D with the G-minor chord as tonic, maps better to typical harmonic events in G major (with the chord progression analyzed as i–iv–V) than typical harmonic events in
[4.7] My own preference, however—formed only after years of experimenting with the contextual approach—is for a “default” use of six-based minor. By this strategy, I assume six-based minor unless there are significant factors working against it (such as consistent shifts between parallel tonics mentioned above). A central reason for a default of six-based minor is just simplicity. Most songs are not as circumscribed in their harmonic content as those mentioned in the previous paragraph, and having to consistently weigh two methods can become analytically paralyzing. Moreover, if we allow for each traditional harmonic function to encompass two diatonic scale degrees—6 and 1 as tonic, 2 and 4 as subdominant, and 3 and 5 as dominant (as discussed above in section [2])—then one-based minor does not offer much additional utility over six-based minor in clarifying tonal function. To understand this last point better, consider that a substantial difference between classical music and popular music is the frequency of chords with a root of B, given a white-note collection that centers on C or A. In a classical work in C major, for example, chords with a root of B typically function as dominant sonorities (viio) and thus typically lead to tonic sonorities (e.g., C major). In a classical work in A minor, however, chords with a root of B typically function as subdominant (or predominant) sonorities (iio) and thus typically lead to dominant sonorities (e.g., E major). One-based minor is an essential analytical tool for classical music, since it sorts out the different behavior of this common chord root between relative keys. In popular music, though, chords with a root B given a white-note collection that centers on C or A are extremely rare.(27) One-based minor is thus less essential for popular music, since tonal function is generally consistent between relative keys.
Example 17. Nashville number chart for excerpt (2:02–3:10) of “Umbrella” (Rihanna feat. Jay-Z, 2007)
(click to enlarge and listen)
[4.8] As a result, my own labeling of the Gm–Cm–D loop in “Bad Guy” (Billie Eilish, 2019) is vi–ii–III, with each of these chord roots following their typical functional associations (T–S–D) in the relative major. For those not used to six-based minor, seeing the D-major chord represented as “III” is probably jarring. Would not V of vi be more accurate?(28) Without question, the D-major chord functions as the tonal dominant of G minor. In the charts that follow, however, I will label V of vi chords as III for two reasons: 1) This is how they are represented in the Nashville number system, which does not have a way to indicate secondary chord function (since the “slash” indicates chord inversion); but also 2) Our recognition of the chord’s location in the scale precedes and is not mutually exclusive of our reading of the chord’s function. Six-based minor already takes this last point for granted, in that ii functions as iv of vi and vi functions as i of vi. If we have already accepted the polysemic quality of chord labels, then it should not be problematic to understand III as the dominant of vi. As an illustration, consider the song “Umbrella” (Rihanna feat. Jay-Z, 2007). Richards admits that the choice between reading passages of this song in the major key or the Aeolian mode is “tantalizingly insoluble” (2017, [33]). Indeed, the song’s chorus, post-chorus, and bridge—charted in Example 17—involve shifting weights between two relative keys. The chorus opens with a rotation of the Axis progression that initially emphasizes the major tonic (
Example 18. Nashville number chart for excerpt (1:18–2:24) of “Grenade” (Bruno Mars, 2010)
(click to enlarge and listen)
[4.9] For those adopting a default six-based minor strategy, the appearance of a tonal dominant to the minor tonic is thus not sufficient reason to use one-based minor. As another case study, consider the verse and chorus of “Grenade” (Bruno Mars, 2010), as charted in Example 18. The verse here is undeniably centered on the minor tonic (D minor), and I hear the final two bars as a strong
V. Modal Double-Tonic Complexes
Example 19. Transcription of melody and chords in chorus of “Radioactive” (Imagine Dragons, 2012)
(click to enlarge and listen)
[5.1] The III chord discussed above is a glimpse into how harmonic sonorities outside the diatonic palette of I, ii, iii, IV, V, and vi are represented in six-based minor. In this final section, I will continue the exploration of six-based minor beyond this handful of chords. Consider, for example, the song “Radioactive” (Imagine Dragons, 2012). In terms of harmonic content, the song consists entirely of the repeated four-chord loop Bm–D–A–E (sometimes with the last chord omitted or in first inversion); the melody and chords for the first half of the chorus are transcribed in Example 19. If we were to consider the chord progression Bm–D–A–E in isolation, without listening to the song, we might expect the tonic to be A major (as ii–IV–I–V). But tonic identification is a process that should be done by ear, a process more complex than simply matching chords to key signatures. And thus despite the chord content in “Radioactive” aligning with A major, I do not hear A major as tonic. What is the tonic, then? The B minor chord is a strong contender, given that it begins each phrase; the melody’s octave leap in the first bar additionally reinforces B as a tonal center. We might say, therefore, that this song is in B Dorian.(31) To my ear, though, the D major chord also possesses a sense of tonic, with the last three chords in the loop sounding like I–V–II (or I to V followed by V of V). With this hearing, we might say that the song is in D Lydian. Which chord, then, is the “true” tonic? Must we choose a single tonic here? Note that, given the hearing of a B minor / D major complex, this chord progression is very similar to the double-tonic chord progression in Example 4b, vi–I–V–ii, only with the last chord having a major rather than minor quality. As a result, I see this as another case of double tonic, just not an Aeolian-Ionian complex; instead, I view this as a Dorian-Lydian complex. For the same reasons that six-based minor was better suited to handle the former, it is better suited to handle the latter. (As mentioned above in [1.5], recall that six-based minor, unlike la-based minor, takes the major and minor tonic chords to be I and vi respectively, regardless of other modal inflections in the scale.)
[5.2] The relevance of diatonic modes to the analysis of popular music has been somewhat contentious.(32) My own experience is that it is difficult to find entire songs that stay consistently within any diatonic mode besides Aeolian or Ionian. This search becomes especially challenging if we are looking for songs that employ triadic structures and that go beyond a simple palette of just two, three, or four looped chords. It is much easier to find isolated moments or passages that provide a taste of modality, even if the song overall does not express a pure diatonic mode. Examples of a Dorian-Lydian complex may thus be rare for a song overall, but we can still appreciate instances of this flavor on a smaller scale.
Example 20. Nashville number chart for excerpt (2:20–3:17) of “Rocket Man” (Elton John, 1972)
(click to enlarge and listen)
[5.3] The song “Rocket Man” (Elton John, 1972), for instance, provides an example of a Dorian-Lydian complex confined to a single song section. A chart for the last verse, prechorus, and chorus of the song are shown in Example 20 using six-based minor (in a half-time feel). The harmonic content of the final verse (starting around 2:20) consists of a toggle between Gm7 and C7, which although could be heard as a ii–V alternation in F, I hear (in part because of the melodic structure) as Dorian i–IV motion.(33) Nonetheless, my chart takes G minor to be vi. There are at least two reasons why six-based minor is useful here. For one, the minor tonic in the verse is fleeting. The
Example 21. Nashville number chart for excerpt (0:31–1:20) of “Bulletproof” (La Roux, 2009)
(click to enlarge and listen)
[5.4] Although diatonic modes are defined in terms of a scalar collection, the harmonic instantiations of those modes—as seen in the last two examples—involve characteristic chords, such as II in a major key for Lydian and IV in a minor key for Dorian. As a result, the simple appearance of one of these chords can be sufficient to give the listener a hint of modality, even if evanescent. In this regard, consider the song “Bulletproof” (La Roux, 2009). Like other examples, the chorus of this song is strongly centered on the major tonic (
Example 22. Transcription of melody and harmonic content for chorus of “Amaranth” (Nightwish, 2007)
(click to enlarge and listen)
[5.5] The verse progression in “Bulletproof” (vi–II–IV–vi) also reminds me of the harmonic progression in another song from around the same time, “Forget You” (CeeLo Green, 2010), which consists solely of the chord loop I–II–IV–I.(35) The difference between the two progressions is solely the swapping of the minor tonic for its relative major. What these two songs again underscore is that patterns of chord behavior in popular music can be observed between relative tonics, which six-based minor is well-suited to reveal. What other correspondences might we observe, therefore, between typical harmonies in a major key and its relative minor? After the Ionian palette, one of the most common non-diatonic chords in a major key is
Example 23. Nashville number chart for excerpt (0:50–1:31) of “Save Me” (Fleetwood Mac, 1990)
(click to enlarge and listen)
[5.6] To further illustrate this functional correspondence, consider the song “Save Me” (Fleetwood Mac, 1990), which is charted in Example 23 using six-based minor (with C as ). In his discussion of the natural-minor system, Stephenson mentions this song as an instance of chromaticism introduced into the harmonic palette via a Neapolitan chord (2002, 90). Indeed, if we were to analyze this song using one-based minor (with A as ), the chord at the beginning of the prechorus (
Example 24. Nashville number chart for excerpt (0:32–1:24) of “Love Will Save the Day” (Whitney Houston, 1987)
(click to enlarge and listen)
[5.7] As a final example of a possible Phrygian-Mixolydian complex, consider the song “Love Will Save the Day” (Whitney Houston, 1987). The song begins with a clear tonic, which I will take here to be D minor (even though the exact tuning on the recording is somewhere between D and
VI. Conclusion
[6.1] In summary, I do not claim for any of these examples that one-based minor is inherently wrong, does not model the reader’s hearing, or cannot reveal interesting patterns of harmony. I do claim, however, that many harmonic patterns in popular music can be observed between relative rather than parallel tonalities, and six-based minor by nature is better suited to reveal these patterns than one-based minor. The extent to which chord patterns, given a minor tonic, are more similar to chord patterns in the relative major, the parallel major, neither, or both is an open question. But to address this question, six-based minor is a useful complement to one-based minor.
[6.2] We might wonder why the relative-key relationship is especially prevalent in popular music. One factor may be the typical structure of melodies in this style. In particular, melodies in popular music are primarily pentatonic, not diatonic as is more typical of common-practice era music.(37) There is, however, no true parallel key for pentatonic melodies. There of course exist both a C-major pentatonic collection (C, D, E, G, A) and a C-minor pentatonic collection (C,
[6.3] While still recognizing these shifts between relative tonics, all of the examples above appear non-modulatory when using six-based minor. For those used to thinking in one-based minor, these six-based analyses may appear to misrepresent or underrepresent the changing tonal centers in the song. One might argue, moreover, that the apparent lack of modulation found in Nashville number charts using six-based minor is prescriptive rather than descriptive, in that it is simply a tool to get a session musician to play the right chord at the right time rather than a method to reflect our hearing. I find the distinction between prescriptive and descriptive to be very blurry in this case, though. If session musicians are trained to read chord changes using six-based minor, they will inherently become used to thinking about harmony and harmonic relationships in this way. I see very little meaningful difference, for example, between a musician calling an A-minor tonic chord vi in the heat of a gig versus thinking of the A-minor tonic chord as vi more systematically.
[6.4] More importantly, if six-based minor is a conceptual approach to harmony common among many of the musicians creating popular music, it seems reasonable that it should also be a conceptual approach to harmony common among those analyzing popular music. I realize that many (if not most) music theorists (including myself) have devoted years if not decades to thinking exclusively in one-based minor and training their students to think exclusively in one-based minor. This may be warranted if the only style under consideration is classical music. But if our goal is to include more popular music in the classroom, perhaps in part to help address the lack of diversity in the typical music theory classroom (de Clercq 2020), it will presumably require a more diverse analytical toolbox. Without question, Roman numerals and Nashville numbers are only two components of that expanded toolbox. But if we choose to employ these tools, which have historically shown themselves to be very powerful, let us recognize and appreciate the various ways that they can be wielded.
Trevor de Clercq
Middle Tennessee State University
Department of Recording Industry
1301 East Main Street, MTSU Box 21
Murfreesboro, TN 37132
tdeclercq@mtsu.edu
Works Cited
Bailey, Robert. 1985. “An Analytical Study of the Sketches and Drafts.” In Prelude and Transfiguration from “Tristan and Isolde,” ed. Robert Bailey, 113–46. W.W. Norton.
Biamonte, Nicole. 2010. “Triadic Modal and Pentatonic Patterns in Rock Music.” Music Theory Spectrum 32 (2): 95–110. https://doi.org/10.1525/mts.2010.32.2.95.
—————. 2017. “Pop/Rock Tonalities.” In Tonality Since 1950, ed. Felix Wörner, Ullrich Scheideler, and Philip Rupprecht, 89–101. Franz Steiner.
Budge, Helen. 1943. “A Study of Chord Frequencies Based on the Music of Representative Composers of the Eighteenth and Nineteenth Centuries.” PhD diss., Columbia University.
Capuzzo, Guy. 2004. “Neo-Riemannian Theory and the Analysis of Pop-Rock Music.” Music Theory Spectrum 26 (2): 177–99. https://doi.org/10.1525/mts.2004.26.2.177.
—————. 2009. “Sectional Tonality and Sectional Centricity in Rock Music.” Music Theory Spectrum 31 (1): 157–74. https://doi.org/10.1525/mts.2009.31.1.157.
Clement, Brett. 2013. “Modal Tonicization in Rock: The Special Case of the Lydian Scale.” Gamut 6 (1): 95–142.
—————. 2014. “A New Lydian Theory for Frank Zappa’s Modal Music.” Music Theory Spectrum 36 (1): 146–66. https://doi.org/10.1093/mts/mtu002.
—————. 2020. “Convention and Invention in Harmonic and Melodic Theories for Rock Music.” In The Bloomsbury Handbook of Rock Music Research, ed. Allan Moore and Paul Carr, 107–27. Bloomsbury. https://doi.org/10.5040/9781501330483.ch-008.
Covach, John, and Andrew Flory. 2018. What’s That Sound? An Introduction to Rock and Its History. 5th ed. W.W. Norton.
de Clercq, Trevor. 2015. The Nashville Number System Fake Book. Hal Leonard.
—————. 2016. “Measuring a Measure: Absolute Time as a Factor for Determining Bar Lengths and Meter in Pop/Rock Music.” Music Theory Online 22 (3). https://doi.org/10.30535/mto.22.3.3.
—————. 2019. “The Nashville Number System: A Framework for Teaching Harmony in Popular Music.” Journal of Music Theory Pedagogy 33: 3–28. https://jmtp.appstate.edu/nashville-number-system-framework-teaching-harmony-popular-music.
—————. 2020. “A Music Theory Curriculum for the 99%.” Engaging Students: Essays in Music Pedagogy 7. https://doi.org/10.18061/es.v7i0.7359.
—————. 2021. “How Should Corpus Studies of Harmony in Popular Music Handle the Minor Tonic?” In Proceedings of Future Directions Music Cognition Conference, virtual, March. http://org.osu.edu/mascats/proceedings/.
—————. Forthcoming. “A Corpus Analysis of Harmony in Country Music.” In The Oxford Handbook of Music and Corpus Studies, ed. Daniel Shanahan, Ashley Burgoyne, and Ian Quinn. Oxford University Press.
de Clercq, Trevor, and David Temperley. 2011. “A Corpus Analysis of Rock Harmony.” Popular Music 30 (1): 47–70. https://doi.org/10.1017/S026114301000067X.
Doll, Christopher. 2011. “Rockin’ Out: Expressive Modulation in Verse-Chorus Form.” Music Theory Online 17 (3). https://doi.org/10.30535/mto.17.3.3.
—————. 2017. Hearing Harmony: Toward a Tonal Theory for the Rock Era. University of Michigan Press. https://doi.org/10.3998/mpub.3079295.
Duinker, Ben. 2019. “Plateau Loops and Hybrid Tonics in Recent Pop Music.” Music Theory Online 25 (4). https://doi.org/10.30535/mto.25.4.3.
Easley, David. 2015. “Riff Schemes, Form, and the Genre of Early American Hardcore Punk (1978–83).” Music Theory Online 21 (1). https://doi.org/10.30535/mto.21.1.3.
Everett, Walter. 2004. “Making Sense of Rock’s Tonal Systems.” Music Theory Online 10 (4). https://mtosmt.org/issues/mto.04.10.4/mto.04.10.4.w_everett.html.
Ferrandino, Matthew. 2017. “Multi-Centric Complexes in Rock.” Presentation at the Annual Conference of the Society for Music Theory, Arlington, VA, November 3.
Forrest, David. 2017. “PL Voice Leading and the Uncanny in Pop Music.” Music Theory Online 23 (4). https://doi.org/10.30535/mto.23.4.6.
Heetderks, David. 2015. “Hipster Harmony: The Hybrid Syntax of Seventh Chords in Post-Millennial Rock.” Music Theory Online 21 (2). https://doi.org/10.30535/mto.21.2.5.
Houlahan, Micheál and Philip Tacka. 1992. “Reader’s Response: The Americanization of Solmization - A Response to the Article by Timothy A. Smith ‘A Comparison of Pedagogical Resources in Solmization Systems’.” Journal of Music Theory Pedagogy 6: 137–51. https://jmtp.appstate.edu/reader’s-response-americanization-solmization-response-article-timothy-smith-‘-comparison.
—————. 1994. “Continuing the Dialogue: The Potential of Relative Solmization for the Music Theory Curriculum at the College Level.” Journal of Music Theory Pedagogy 8: 221–25. https://jmtp.appstate.edu/readers’-comments-continuing-dialogue-potential-relative-solmization-music-theory-curriculum-college.
Koozin, Tim. 2011. “Guitar Voicing in Pop-Rock Music: A Performance-Based Analytical Approach.” Music Theory Online 17 (3). https://doi.org/10.30535/mto.17.3.5.
Moore, Allan. 1992. “Patterns of Harmony.” Popular Music 11 (1): 73–106. https://doi.org/10.1017/S0261143000004852.
—————. 1995. “The So-Called ‘Flattened Seventh’ in Rock.” Popular Music 14 (2): 185–201. https://doi.org/10.1017/S0261143000007431.
Murphy, Barbara, and Brendan McConville. 2017. “Music Theory Undergraduate Core Curriculum Survey: A 2017 Update.” Journal of Music Theory Pedagogy 31: 177–227. https://jmtp.appstate.edu/music-theory-undergraduate-core-curriculum-survey-2017-update.
Newton, Neil. 2019. “Chromatic Linear Progressions in Popular Music.” In The Routledge Companion to Popular Music Analysis: Expanding Approaches, ed. Ciro Scotto, Kenneth Smith, and John Brackett, 235–48. Routledge. https://doi.org/10.4324/9781315544700-16.
The Nielsen Company. 2019. “Nielsen Music Year-End Music Report U.S. 2019.” https://static.billboard.com/files/pdfs/NIELSEN_2019_YEARENDreportUS.pdf.
Nobile, Drew. 2016. “Harmonic Function in Rock Music: A Syntactical Approach.” Journal of Music Theory 60 (2): 149–80. https://doi.org/10.1215/00222909-3651838.
—————. 2020a. “Double-Tonic Complexes in Rock Music.” Music Theory Spectrum 42 (2): 207–26. https://doi.org/10.1093/mts/mtaa003.
—————. 2020b. Form as Harmony in Rock Music. Oxford University Press. https://doi.org/10.1093/oso/9780190948351.001.0001.
Osborn, Brad. 2017. “Rock Harmony Reconsidered: Tonal, Modal, and Contrapuntal Voice-Leading Systems in Radiohead.” Music Analysis 36 (1): 59–93. https://doi.org/10.1111/musa.12085.
Richards, Mark. 2017. “Tonal Ambiguity in Popular Music’s Axis Progressions.” Music Theory Online 23 (3). https://doi.org/10.30535/mto.23.3.6.
Riley, Jim. 2010. Song Charting Made Easy: A Play-along Guide to the Nashville Number System. 2nd ed. Hal Leonard.
Schenkius, Patrick. 2011. “Slash Chords: Triads with a 55 ‘Wrong’ Bass Note?” Dutch Journal of Music Theory 16 (1): 47–52.
Smith, Timothy. 1991. “A Comparison of Pedagogical Resources in Solmization Systems.” Journal of Music Theory Pedagogy 5: 1–23. https://jmtp.appstate.edu/comparison-pedagogical-resources-solmization-systems.
—————. 1992. “Liberation of Solmization: Searching for Common Ground.” Journal of Music Theory Pedagogy 6: 153–68. https://jmtp.appstate.edu/author’s-reply-liberation-solmization-searching-common-ground.
—————. 1994. “Ending the Dialogue: Imaginary Solutions are No Solution.” Journal of Music Theory Pedagogy 8: 227–30. https://jmtp.appstate.edu/readers’-comments-ending-dialogue-imaginary-solutions-are-no-solution.
Snodgrass, Jennifer. 2016. Contemporary Musicianship: Analysis and the Artist. Oxford University Press.
Spicer, Mark. 2017. “Fragile, Emergent, and Absent Tonics in Pop and Rock Songs.” Music Theory Online 23 (2). https://doi.org/10.30535/mto.23.2.2.
Stephenson, Ken. 2002. What to Listen for in Rock: A Stylistic Analysis. Yale University Press. https://doi.org/10.12987/yale/9780300092394.001.0001.
Temperley, David. 2001. The Cognition of Basic Musical Structures. MIT Press.
—————. 2007. “The Melodic–Harmonic ‘Divorce’ in Rock.” Popular Music 26 (2): 323–42. https://doi.org/10.1017/S0261143007001249.
—————. 2009. “A Statistical Analysis of Tonal Harmony.” http://davidtemperley.com/kp-stats/.
—————. 2011a. “The Cadential IV in Rock.” Music Theory Online 17 (1). https://doi.org/10.30535/mto.17.1.8.
—————. 2011b. “Scalar Shift in Popular Music.” Music Theory Online 17 (4). https://doi.org/10.30535/mto.17.4.3.
—————. 2018. The Musical Language of Rock. Oxford University Press. https://doi.org/10.1093/oso/9780190653774.001.0001.
Temperley, David, and Trevor de Clercq. 2013. “Statistical Analysis of Harmony and Melody in Rock Music.” Journal of New Music Research 42 (3): 187–204. https://doi.org/10.1080/09298215.2013.788039.
Wagner, Naphtali. 2003. “‘Domestication’ of Blue Notes in the Beatles’ Songs.” Music Theory Spectrum 25 (2): 353–65. https://doi.org/10.1525/mts.2003.25.2.353.
Williams, Chas. 2017. The Nashville Number System Gigbook. Chas Williams.
Wyatt, Keith, and Carl Schroeder. 1998. Harmony and Theory: A Comprehensive Source for All Musicians. Hal Leonard.
Footnotes
1. There is no good, concise term as of yet to refer to the broad array of contemporary commercially distributed musical styles in Western English-language popular music, even though there is general consensus that styles such as pop, rock, R&B, rap, and country comprise a family of related styles. Although the term “rock” has been used to refer to this larger family of styles by numerous authors (e.g., Doll 2017; Covach and Flory 2018; Temperley 2018), I prefer to not use the term “rock” in this way due to the implied placement of rock music (in the narrower meaning) at the center of this musical family and the concomitant marginalization of other styles, such as country and R&B. Instead, I will use the term “popular music,” since these are the styles that for decades now have had the greatest proportion of listenership (in excess of five percent each) in Western English-language countries (e.g., Nielsen 2019). I thus intend for the approach discussed here to cover a wider repertoire than previous studies of harmony that have been restricted to “pop/rock” (e.g., Biamonte 2017) or “rock” in the narrower sense (e.g., Temperley 2011a) but to cover a more limited repertoire than other meanings of “popular music” that include jazz or other styles with a current listenership share of only one or two percent.
Return to text
2. Doll’s labeling of chords given a minor tonic follows the customary procedure in analyses of popular music to relate all Roman numerals to the major scale with the same tonic note, regardless of whether the tonic chord is major or minor (e.g., Wyatt and Schroeder 1998; Biamonte 2010; Snodgrass 2016).
Return to text
3. For more details on la-based minor, particularly as it compares to do-based minor for teaching sight singing in college-level courses, see the back-and-forth exchanges in the Journal of Music Theory Pedagogy between Smith (1991; 1992; 1994), who advocates for a do-based approach to minor, and Houlahan and Tacka (1992; 1994), who advocate for a la-based approach.
Return to text
4. The notion that IV or V might act as a “hybrid tonic” (as in Duinker 2019) is possible, although it still involves a deeper-level major tonic assigned to I.
Return to text
5. Examples of six-based minor in practice can be found in the Nashville number charts for “The Devil Went Down to Georgia” (The Charlie Daniels Band, 1979), “I Shot the Sheriff” (Eric Clapton, 1974), “I Will Survive” (Gloria Gaynor, 1978), “Sultans of Swing” (Dire Straits, 1978), and “Thnks fr the Mmrs” (Fall Out Boy, 2007) in Williams 2017.
Return to text
6. A detailed explanation of the Nashville number system, especially as it compares to the Roman numeral system, can be found in de Clercq 2019.
Return to text
7. For examples of Nashville numbers used with one-based minor, see the charts for “Before” (Jim Riley, 2010) in Riley 2010; “Before He Cheats” (Carrie Underwood, 2005) in de Clercq 2015; and “Spooky” (Classics IV, 1967) in Williams 2017.
Return to text
8. Although Nobile posits no function-as-category associations of Roman numerals, for example, the exception is tonic (2016, 157). He states, for example, that “tonic function is different from the others, in that it is the most closely associated with a specific chord (namely I)” (164).
Return to text
9. To illustrate this balance between predictive power and precision, consider a two-category functional system that includes T (tonic) and N (non-tonic). This system could predict with 100% accuracy that all T chords will move to either a T or N chord, but it offers no information about chord behavior within the T or N categories. Similarly, a one-category functional system using C (for “chord”) would predict with 100% accuracy that all harmonies are indeed chords but lack any specific details on how those chords behave.
Return to text
10. Perhaps because I listened to a lot of heavy metal in high school and college, the number six—three of which in a row make the number of the beast—seems like a natural choice for the minor tonic.
Return to text
11. Some listeners might hear one or two of the examples in Example 4c with different tonal centers than indicated by the Roman numerals. For example, “Blinding Lights” (The Weeknd, 2019) opens with a sustained F-minor chord that at first sounds very much like tonic given the lack of any other aural information. But the melody in these cases is an important factor, with the synthesizer and vocal of “Blinding Lights” composed from the
Return to text
12. I cannot help but point out that one song in Example 4b is entitled “Prayer in C” (Lilly Wood and the Prick, remixed by Robin Schulz, 2014), yet the Wikipedia page for this song (https://en.wikipedia.org/wiki/Prayer_in_C) as of December 23, 2020 was adamant that the song “is actually recorded in the key of A minor.” The Wikipedia page, however, was edited on May 2, 2021 (by user Thumperward, according to the page history) to remove “utter garbage sourced to nothing reliable.”)
Return to text
13. These two chords are in parentheses Nobile’s Example 12b (2020a, 219), although a G/E chord (alternatively read as iii7 or a fusion of iii and V) appears in the prechorus of “Private Eyes” (his Example 3).
Return to text
14. See Chapter 3 (“Harmony”) in Temperley 2018, particularly pages 42–44.
Return to text
15. We might consequently also say the V chord should be a sus4, although the vocal melody and piano part use sufficiently to overwhelm the in the guitar in these cases.
Return to text
16. In Nashville numbers, chord symbols that look like fractions indicate “slash” chords, which are scale-degree equivalents of pop chord symbols that show a chord over a bass note (like Cm/G). The number in the “numerator” indicates the scale degree of the root and the chord quality (with major assumed unless otherwise indicated), while the number in the “denominator” indicates the scale degree of the bass note.
Return to text
17. As some evidence in this regard, the Wikipedia page for “Chandelier” (as of October 7, 2021) says that the song is “in the key of
Return to text
18. See de Clercq 2016 for a methodology for determining bar lengths in popular music based on half-time and normal drum feels.
Return to text
19. See, for instance, the discussion in Chapter 2 (on “Key and Mode”) in Stephenson (2002). For examples of triadic modal patterns in rock, see Biamonte (2010).
Return to text
20. Temperley (2018, 32). Doll (2017, 22) similarly suggests abandoning the notion of “key” in favor of “center” (a single note) and “tonic” (a single chord).
Return to text
21. Temperley (2001, 259) categorizes the tonality of “Blue on Black” as Dorian, i.e., as having a minor tonic triad. Indeed, the amount of minor-mode content in the melody and solo guitar is greater overall than the amount of major-mode content. For a similar example of disagreement about the quality of the tonic triad (and thus key) in a blues-based song, compare my Nashville number chart (2015) for “Fancy” (Reba McEntire, 1990), which posits a key of
Return to text
22. The top three staves in Example 16a reproduce Stephenson’s Example 4.23 but adapt it through a few cosmetic changes, including changing the Roman numerals to the popular style, replacing the applied chords with more general scale degree versions, removing the chord-correspondence lines, and removing the courtesy accidentals for ease of reading.
Return to text
23. Stephenson does mention the Neapolitan chord (
Return to text
24. In a corpus of 200 country songs, of which about 98% include a major tonic chord only, I found that I, IV, and V accounted for over 80% of chord instances (forthcoming). Similarly, I found in a corpus of 200 rock songs that given songs with a major tonic, I, IV, and V accounted for almost 80% of chord instances (2021, Table 4).
Return to text
25. Evidence for this claim can be found in the work of Budge (1943), where around 75% of chords in music from 1700–1830 have roots of scale-degrees 1, 4, 5. This figure drops to about 60% for mid-19th-century music, although the majority share still remains. Additionally, a small corpus study by Temperley (2009) on examples from a leading music theory workbook shows about two-thirds of harmonies based on roots of scale-degrees 1, 4, or 5 given works in a major key.
Return to text
26. See the distribution of chord roots given a minor tonic in Temperley 2009.
Return to text
27. Here again, see Chapter 3 (“Harmony”) in Temperley 2018, particularly pages 42–44. See also de Clercq (forthcoming, Table 2). When chords built on this scale degree do appear, they are usually involved in a circle-of-fifths progression that is cycling between two relative tonics, such as in “I Will Survive” (Gloria Gaynor, 1978) or “My All” (Mariah Carey, 1997).
Return to text
28. I will avoid using the forward slash with Roman numerals to indicate secondary (or applied) chords, writing “V of V” instead of “V/V,” for example. I do so primarily to avoid the potential confusion with the forward slash in pop chord symbols and Nashville numbers, where it indicates a chord over a bass note (e.g., Dm/F or 2m/4).
Return to text
29. Richards hears the second and sixth bars of the post-chorus as a second-inversion I chord (
Return to text
30. The term “double-plagal cadence” is adopted here from Everett (2004, [11]).
Return to text
31. Note that B Dorian is the key given for this song on Wikipedia (as of October 7, 2021). https://en.wikipedia.org/wiki/Radioactive_(Imagine_Dragons_song)
Return to text
32. See Clement 2020 for an overview of analytical methods that use diatonic modes and some of the critiques of those methods. See also Clement (2013, 2014) for the specific case of Lydian tonality in rock.
Return to text
33. F major, for example, is the primary view of Newton (2019, 238). One reason I do not hear the verse to “Rocket Man” as in F is the vocal melody, which uses notes from the
Return to text
34. As such, the move to II in the chorus could be construed as an example of “scalar shift” (Temperley 2011b), which emphasizes that particular moment through tonal reorientation.
Return to text
35. The I–II–IV–I chord loop, as an instance of Doll’s “slouching schema” (2017, 148), can be traced back at least to 1960s pop/rock, such as heard in the Beatles song “Eight Days a Week” (1964).
Return to text
36. My corpus work with Temperley (2011), for example, shows
Return to text
37. In a k-means clustering of melodic data in a corpus of rock music, Temperley and I found that a two-category solution divides songs into one category in which the five degrees of the major pentatonic scale are the most common and a second category in which the degrees from a combination of the major pentatonic and its parallel minor pentatonic scale are the most common (2013, 199).
Return to text
Copyright Statement
Copyright © 2021 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
19121