A Bevy of Biases: How Music Theory’s Methodological Problems Hinder Diversity, Equity, and Inclusion
Justin London
KEYWORDS: Philip Ewell, anti-racism, inductive theories, implicit bias, confirmation bias, overfitting, analytical corpora
ABSTRACT: This article is in response to and in broad support of Philip Ewell’s keynote talk, “Music Theory’s White Racial Frame,” given at the 2019 Annual Meeting of the Society for Music Theory, and essay, “Music Theory and the White Racial Frame” (2020a). In his address and its companion essay, Ewell notes how the repertoire we study and teach, as well as the theories we use to explain it, are manifestations of whiteness. My article will show, first, that the repertory used in the development of theories of harmony and form, as well as (and especially) music theory pedagogy comprises a small, unrepresentative corpus of pieces from the so-called “common practice period” of tonal music, mostly the music of Bach, Haydn, Mozart, and Beethoven, and only a small subset of their output. We (mis)use this repertory due to a combination of implicit biases that stem from our enculturation as practicing musicians, explicit biases that stem from broadly held aesthetic beliefs regarding the status of “great” composers and particular “masterworks,” and confirmation biases that are manifest in our tendency to use only positive testing strategies and/or selective sampling when developing and demonstrating our theories. The theories of harmony and form developed from this small corpus further suffer from overfitting, whereby theoretical models are overdetermined relative to the broader norms of a musical practice, and from our tendency to conceive of our theoretic models in terms of tightly regulated “scripts” rather than looser “plans.” For these reasons, simply expanding our analytic and/or pedagogical canon will do little to displace the underlying aesthetic and cultural values that are bound up with it. We must also address the biases that underlie canon formation and valuation and the methodologies that inherently privilege certain pieces, composers, and repertoires to the detriment of others. It is thus argued that working toward greater equity, diversity, and inclusion in music theory goes hand in hand with addressing some of the problematic methodologies that have long plagued our discipline.
DOI: 10.30535/mto.28.1.4
Copyright © 2022 Society for Music Theory
1. A Wake-Up Call from Phil Ewell
[1.1] At the 2019 Annual Meeting of the Society for Music Theory, Professor Philip Ewell gave a plenary session address on “Music Theory’s White Racial Frame.” His remarks were subsequently published and elaborated in a series of blog posts and his 2020a Music Theory Online article, “Music Theory and the White Racial Frame.” Professor Ewell’s keynote was one of the most powerful talks I have ever witnessed at a music theory meeting. In it, he shared his personal history and experiences as a BIPOC music theorist, offered his observations of the field, and raised the call for the music theory community to commit to antiracism in three broad ways.(1)
[1.2] First, Professor Ewell called for greater diversity in the range of music that we study—and especially the music we study and teach the most—and our approaches to that music, to counter the whiteness of the Western art-music canon (the “WAM canon”), the music theory analytic canon (a subset of the WAM canon), and the music theory teaching canon (a subset of the music theory analytic canon). This is critical because the WAM canon carries with it a host of assumptions and presumptions regarding race, gender, and class that shape how we think and talk about music in ways both large and small. Second, Professor Ewell called for greater inclusivity in terms of “who gets to be a music theorist” with regard to undergraduate and graduate theory programs as well as entry-level employment opportunities. Third, he called for greater equity in terms of the possibilities for advancement and service within the field, especially with respect to leadership roles in our societies and publications.
[1.3] The music theory community was quick to respond to Ewell’s address, at least in terms of the first charge, i.e., making the music theory canon more diverse. We had already been striving for some time to make changes with respect to gender inclusion, as there are now anthologies and readers dedicated to music and music theory by women (Straus 1993; Briscoe 2004; Parsons and Ravenscroft 2016, 2018; see also Hisama 2000). Paula Maust’s website Expanding the Music Theory Canon (2021) is dedicated to teaching examples by BIPOC and women composers, and Ewell himself is at work on a new undergraduate theory textbook (Ewell et al. 2023). The need for inclusion is particularly acute; as Ewell points out in his 2020 MTO article, only 1.67% of the musical examples in the seven most commonly used music theory textbooks in the USA are by non-white composers (Ewell 2020a, [3.1]).
[1.4] While greater diversity in our concert repertoire and classroom is welcome, I do not believe it will ultimately be an effective anti-racist strategy. As the WAM tradition is overwhelmingly white and male, adding a relatively small number of works by women and BIPOC composers runs the risk of tokenism. Ewell notes:
This distinction between “white repertoire” and “white theory” is of vital importance insofar as our white racial frame can only envision one (expanding the repertoire) and not the other (studying nonwestern music theory). This relates to the distinction between “diversity” and “antiracism” that I made above. To “diversify” our repertoire by adding a few POC composers actually reinforces our white frame. (2020a, [3.4])
In other words, if these “diversity examples” are only added as alternative illustrations of harmonic patterns, formal archetypes, and contrapuntal schemas derived from the white, male majority practice, they will do little to change what we listen to, and more importantly, how we think about what we listen to.
[1.5] Music theory is largely an inductive practice, based upon a very small number of privileged examples from which more general principles of harmony, phrase structure, rhythm, and form are derived. Moreover, the use of this set of examples, cherry-picked from a “common practice period” (hereafter “CPP,” roughly 1700–1900), privileges certain parameters such as melody, rhythm, and (especially) harmony over others like timbre and texture. This approach to theory and analysis is highly problematic in and of itself, for it leads to theories of musical structure which are necessarily incomplete, which in turn warps our analytic practice. The problem may be diagnosed as follows:
- Music theory of the common practice era (i.e., theories of harmony, melody, rhythm, and form) proceeds inductively from a small, unrepresentative corpus of examples, mostly the music of Bach, Haydn, Mozart, and Beethoven, and only a small subset of their output.
- We routinely fail to acknowledge the various biases that underlie the construction of this corpus, including implicit biases that come from our active enculturation as practicing musicians, explicit biases that stem from broadly held aesthetic beliefs regarding the status of “great” composers and particular “masterworks”, and confirmation biases that are reinforced by our tendency to use only positive testing strategies and/or selective sampling when developing and demonstrating our theories.
- Compounding the issue noted in the first point, we often position singular pieces as privileged exemplars that serve as the model for a structural type (the “Beethoven Op. 2/1 problem,” as pointed out by BaileyShea 2004).
- Our theorizing from a small set of samples consistently leads to overfitting, whereby theoretical models are overdetermined relative to the broader norms of a musical practice.
- Moreover, these overfitted models are couched in terms of tightly regulated “scripts” rather than looser “plans” for the organization of musical structure, most especially in the context of theories of musical form (Schank and Abelson 1977).
[1.6] This constellation of problems is both socially and theoretically undesirable. Moreover, simply adding a few more examples of rondo form or parallel period phrase structure by non-white, non-male composers will not displace the music-theoretic presumptions and norms stemming from music theory’s white racial frame, but, as noted in the quotation from Ewell above, will reinforce it. Thus, Ewell’s wake-up call for music theory to assess its whiteness, and its role in promoting that whiteness, is not only an opportunity for us to work toward greater equity, diversity, and inclusion, but also to address some problematic methodologies that have long plagued the discipline. Indeed, one cannot do the former without doing the latter.
[1.7] In the following sections of this article, each of the above points will be examined in turn. Part 2 will address the small and questionably representative nature of music theory’s analytic and pedagogical canon; Part 3 will define and document the various biases which have led to the formation and (mis)use of that canon; and Parts 4 and 5 will discuss the central problem of overfitting, the Achilles heel of our analytic practice formed by the combination of strong induction, small samples, and music theory’s reflexive use of exemplars and paradigmatic cases. The article concludes with a consideration of the prospects for progress and the need for our collective self-awareness of the bevy of biases that are widely held and which underlie many of music theory’s common practices.
2. The Myth that Music Theory Studies the Music of the Common Practice
[2.1] Facial recognition technology (FRT) is a form of machine learning/AI that uses massive data sets of images (mainly scraped off social media) to train algorithms for the classification and recognition of individuals and groups. A number of recent studies, importantly, have pointed out the problems in both the development and implementation of FRT. As Bacchini and Lorusso note:
Face recognition technology, as it is produced, implemented and used in Western societies, reinforces existing racial disparities in stop, investigation, arrest and incarceration rates because of racist prejudices and even contributes to strengthen the unhealthy effects of racism on historically disadvantaged racial groups, like black people. (2019, 321)
Likewise, Buolamwini and Gebru have shown that for many of the widely used FRT systems:
Darker-skinned females are the most mis-classified group (with error rates of up to 34.7%). The maximum error rate for lighter-skinned males is 0.8%. The substantial disparities in the accuracy of classifying darker females, lighter females, darker males, and lighter males in gender classification systems require urgent attention if commercial companies are to build genuinely fair, transparent and accountable facial analysis algorithms. (2018, 1)
[2.2] FRT, like other machine learning/classifier systems, proceeds inductively based upon its training set. The problem is that early FRT systems were trained on data sets that consisted largely of faces of white males from the USA and Europe. Inductive approaches to learning, classifying, and reasoning are only as good as the data/corpora from which they are derived. Responses to the problems pointed out by researchers like Bacchini and Lorusso (2019) and Buolamwini and Gebru (2018) have been to compile and use better, more representative corpora in developing FRT systems, and to create algorithms that can recognize and “unlearn” bias present in their training data (see Kim et al. 2019)
[2.3] Of course music analysis does not work in the same way as machine learning algorithms or classifiers, but like FRT, music theorizing is also an essentially inductive practice, the core concepts of which are derived from a set of canonical works of the music of so-called “common practice period.” The music theory corpus has its origins in the nineteenth century, when music theorists like A. B. Marx, Hugo Riemann, and Heinrich Schenker established the tenets of formal, harmonic, and contrapuntal analysis that are still in use today. Their theories were based upon and illustrated with music from a small sample of German-speaking composers, most especially Beethoven. Their core analytic repertoire is also still with us today—manifesting most obviously in the continued study of Schenkerian analysis, but also in recent and influential work on harmony, voice leading, and small- and large-scale form. Two relatively recent examples of this scholarship include Caplin’s (1998) taxonomy of phrase-level formal function, and Hepokoski and Darcy’s (2006) treatise on sonata form.
[2.4] The problems of the WAM analytic canon, upon which our normative theories of harmony, voice leading, and form in the common tonal practice period depend, go far beyond the problems of the early FRT training data sets, as the WAM analytic canon is astonishingly small and astonishingly un-representative. First, there is its relatively small size. Schenker’s published works include discussions of 40 pieces/examples (Ayotte 2004), Caplin’s book has 288 examples, and Hepokoski and Darcy’s volume has 552 examples. While Caplin’s and Hepokoski and Darcy’s repertoires seem to be big, note that other music data sets are much larger. Daniel Harasim’s website (https://github.com/dharasim/MCR/wiki) contains a list of corpora for music analysis in a range of formats, and includes both symbolic encodings (e.g., text, MusicXML, KERN, MIDI) and real audio. Harasim’s site lists 42 corpora, of which 14 are compilations of pop, jazz, or folksongs (including both Western and non-Western folksongs), and 28 are collections of “classical” music, which ranges from monophonic chant to row forms in Schoenberg. Some of these corpora are modest in size—several hundred pieces or score excerpts—but others are extensive:
- The Yale-Classical Archives Corpus includes 8,980 pieces/movements from 1548 to the mid-20th century, providing over 12 million chords for harmonic sequence analysis (https://ycac.yale.edu/downloads).
- The Meerens Tune Collection (MTC-FS-INST-2.0) contains 18,618 pieces of instrumental and vocal Dutch folk music (http://www.liederenbank.nl/mtc/).
- The Essen collection of European folksongs presently contains over 20,000 songs and instrumental melodies (http://esac-data.org/).
- The Million Song Dataset is a product of the Echo Nest corporation (the.echonest.com), a subsidiary of Spotify, which, as its name suggests, contains metadata and access to audio for one million pop songs (http://millionsongdataset.com).
[2.5] The examples listed in Hepokoski and Darcy 2006 and Caplin 1998 do not broadly sample the music of the common practice period, nor even the more specialized sub-periods and genres that are the focus of their studies. Worse, perhaps, than the small size is that these samples are mostly comprised of the works of four composers: J. S. Bach, Haydn, Mozart, and (of course) Beethoven (henceforth “BHMB”). These four composers represent 62.5% of Schenker’s published analyses (Ayotte 2004) and 69.4% of the pieces mentioned in Hepokoski and Darcy’s book; note the percentage for the latter jumps to 96.3% when we consider only the musical examples. All of the examples in Caplin’s book are from Haydn, Mozart, and Beethoven, as for him—note his title—these three composers represent the “core repertory of the high Viennese classical style” (1998, 3; see also p. 52).(2) We thus should be honest, and note that when we say “music of the common practice period” we really just mean BHMB, with a few others thrown in, most typically Schubert, Schumann, and Chopin. Markus Neuwirth (2013) sums up the problem as follows:
First, there is the problem of the paucity of examples. The compositional output by Haydn, Mozart, and Beethoven, upon which far too many studies in the field of formal analysis rely, represents only the “tip of the iceberg” of the entire musical output from Vienna between 1770 and 1810, comprising perhaps less than 5% of that repertoire.
However, even more critical is the second problem, which concerns the representativeness of the chosen repertoire. This issue arises when the corpus selection is not made on a random basis, but is instead biased by prior value judgments that have determined which composers and works belong to the canon of the “true” masters. Are the formal features found in the works of Haydn, Mozart, and Beethoven representative of Viennese compositional practices as a whole, such that these features occur with about the same frequency in the music of other composers working in Vienna at around the same time? (Neuwirth 2013, 26)
[2.6] We do not know the answer to Neuwirth’s question, because we have yet to look at enough of the music of the contemporaries of Haydn, Mozart, and Beethoven in sufficient detail.(3) If we were/are truly interested in developing a sense of the tonal grammar and formal strategies of the eighteenth and early-nineteenth century common practice, we would pay attention to works by the most popular composers of that era, e.g., Handel (especially), Pepusch, Graun, Hasse, Jomelli, Viotti, Mehul, Cimarosa, Wagenseil, and Paisiello (see Weber 2006). In his 2013 dissertation, Neuwirth broadens the study of Viennese classical form to include the music of Koželuch, Pleyel, and Clementi, all of whom were contemporaries of and potential influences upon Haydn, and in so doing shows how various “exceptional” aspects of Haydn’s compositional practice were, in fact, commonplace.
[2.7] Rather than developing a true sense of the common practice, we have systems of formal analysis and approaches to tonality that are grounded upon the compositional idiosyncrasies of a handful of composers. What is more, the BHMB analytical corpus isn’t even a representative sample of the compositional output of Bach, Haydn, Mozart, and Beethoven. It privileges instrumental music, even though sacred music and opera were the dominant genres of the day. Bach’s cantatas, motets, and passions are largely absent, as are Mozart and Haydn’s masses and operas as well as Beethoven’s songs. Music for wind band (Beethoven), Baryton (Haydn), or organ (Bach) is also given little attention. To be fair, works in the formenlehre tradition like Hepokoski and Darcy (2006) and Caplin (1998) will tend to include more instrumental than vocal music, but our myopic fixation on sonata form and a limited assortment of phrase structures causes us to ignore the many other contexts that present other compositional problems and solutions (e.g., the da capo and double aria forms; variations in the brilliant style, potpourris, dramatic recitative, etc.).
Example 1. BHMB Representation in current theory textbooks
(click to enlarge and see the rest)
[2.8] Of course, even if we extend music theory’s analytic canon to include both a more representative sample of BHMB’s music and a good number of pieces by their contemporaries to make it more representative of the music of the late eighteenth and early nineteenth centuries, it would still be an almost exclusively white, male list. This becomes obvious when we look at recent editions of music theory textbooks and analysis anthologies, many of which have attempted to include a more diverse range of examples, especially by women composers (see Example 1).
[2.9] As can be seen in Example 1, our teaching repertoire is drawn from the traditional music theory/analysis corpus. Indeed, the works of seven composers—the “BHMB+” set plus compositions by Chopin, Schubert, and Robert Schumann—make up, on average, 70% of the teaching examples in the undergraduate harmony curriculum (London 2020). Drilling down deeper reveals that the repertoire largely consists of the same subset of pieces, including works such Bach’s C-major Prelude from Book I of the WTC, Beethoven’s F-minor Piano Sonata op. 2, no. 1, and Chopin’s E-minor Prelude, op. 28. This body of work, then, is even less representative than the above numbers initially suggest.
[2.10] A survey of these teaching texts also highlights the limited opportunities for the inclusion of works by women and BIPOC composers in repertoire from the eighteenth and nineteenth centuries. Notably, in Roig-Francolí (2003), the earliest textbook surveyed, 11.7% of the examples are by women and BIPOC composers, including two pieces by Joseph Boulogne. Clendinning and Marvin’s first edition (2005) only has three pieces by women composers in its examples from the CPP, one by Clara Schumann and two by Fanny Hensel. Their latest edition (2021) includes examples by eight women composers (11%), and Samuel Coleridge-Taylor’s Valse Bohémienne. Most of the gender and BIPOC diversity that we find in teaching and analysis anthologies is found in the music of the twentieth and twenty-first centuries, especially with the inclusion of examples from jazz, musical theater, popular music, and folksong genres, although this is uneven. Turek’s anthology (2007), for example, includes a narrow list of CPP composers—wherein the addition of Brahms and Tchaikovsky to the BHMB+ set accounts for 85% of all of the pre-twentieth century examples—leavened with a large list of jazz and musical theater tunes that lean heavily on the Great American Songbook. Of these tunes, though, only 13.7% are by BIPOC composers, and none are by women.
3. A Bevy of Biases
[3.1] Many reasons exist for the emphasis/over-representation of the music of BHMB in both our analytical and pedagogical repertoires. These include (a) the privileging of instrumental music over vocal music, a holdover of the “absolute” music “agenda” that emerged over the nineteenth century, (b) a bias toward piano music, as music theorists were and are often pianists, and (c) the use of music that is ready-at-hand. This last reason exemplifies the problem of convenience sampling, that is finding data, examples, or subjects that are readily available and/or familiar to the researcher. As Etikan et al. point out:
Although commonly used, it is neither purposeful nor strategic. The main assumption associated with convenience sampling is that the members of the target population are homogeneous. That is, that there would be no difference in the research results obtained from a random sample, a nearby sample, a co-operative sample, or a sample gathered in some inaccessible part of the population
. . . [but] In fact, the researcher does not know how well a convenience sample will represent the population regarding the traits or mechanism under research. What makes convenience samples so unpredictable is their vulnerability to severe hidden biases. (Etikan et al. 2016, 2)
[3.2] There is, of course, more to our reliance on BHMB than simple convenience, for it is a broadly held belief that masterworks by “master/genius” composers are the most proper (and perhaps only) objects worthy of study, with Beethoven as the paradigm case (Ewell 2020b). Our enshrining of certain pieces as masterworks might be thought of as an explicit bias, an overt and shared cultural preference regarding the status and aesthetic and cultural value of certain works. The institutions of classical music—conservatories, symphonies opera companies and their supporting infrastructure, arts funding agencies, and so on—rarely examine or question this explicit bias. Music theorists by and large are classically-trained musicians, and music theory’s traditional home is in the schools of music and conservatories where such musicians are trained. Entry into most graduate programs in music theory requires a substantial amount of music performance skills (keyboard skills, solfège, compositional ability in various forms of harmony and counterpoint, etc.). To gain admission to those schools and conservatories—the usual first step to becoming a music theorist—one has to practice, and indeed, practice a lot.
[3.3] As Ericsson, Krampe, and Tesch-Römer (1993) have noted, sustained, intensive practice is what is required to become an expert performer—and conservatories are in the business of producing expert performers. So, most musicians, including those who are music theorists, have an exceptionally high level of exposure (i.e., 10,000 hours) to a very limited range of repertoire. It is not surprising that one might harbor a very positive view of a repertoire that one knows so well and has dedicated so much time and effort to learn. Moreover, becoming a skilled musician—in any style, genre, or culture—carries with it the presumption that the music one has learned is of high cultural value. This is certainly true in the case of Western classical music, which we mark as “art” music, in distinction to “popular” or “vernacular” music. Thus, we have explicit positive biases toward the classical musical canon in general, and in many cases toward the BHMB corpus in particular, as those pieces—and especially the pieces studied in music theory classes—are the mainstays of the concert repertoire, at least for pianists and orchestral string players.
[3.4] Learning the standard repertoire for [your conservatory instrument of choice] offers you repeated encounters with one type of music—but not necessarily with others. And while most music students, both present and past, have wide-ranging musical interests as both listeners and performers (e.g., the classical guitarists who are active as rock or folk performers), the sustained exposure to the music of the CPP produces not only explicit biases, but also implicit biases. Implicit bias (or implicit stereotyping) was initially framed by Greenwald and Banaji (1995) within the context of implicit cognition: “an implicit C is the introspectively unidentified (or inaccurately identified) trace of past experience that mediates R. In this template, C is the label for a construct (such as attitude), and R names the category of responses (such as object evaluative judgments) assumed to be influenced by that construct” (1995, 5). Greenwald and Banaji note that attitudes can be favorable or unfavorable dispositions toward people, places, policies, and so forth, and that the responses can be preferences, value judgments, and actions. Greenwald and Banaji also note that “the identifying feature of implicit cognition is that past experience influences judgment in a fashion not introspectively known by the actor” (1995, 4–7).
[3.5] Since the publication of their landmark paper, Greenwald, Banaji, and their colleagues have published dozens of papers on studies of implicit bias, using various forms of their implicit association test (IAT). Through “Project Implicit,” they have tested over 20 million participants with the IAT (https://implicit.harvard.edu/implicit/blog.html; see also Greenwald and Krieger 2006). While the specific findings and the interpretation of IAT data have been the matter of much debate—see Jost (2019) and Gawronski (2019) for summaries—it is uncontested that implicit bias exists, that it is a product of our enculturation and exposure, and that it can and does affect our attitudes and behavior.
[3.6] We must, then, ask “how could implicit bias, derived from our life-long exposures to and positive enculturation with WAM in general and BHMB in particular, affect our attitudes toward other musics?” For the most important dimension for implicit cognition is that of familiarity: for the most part, the more familiar something is, the more we tend to like it (e.g., Schubert 2007). The less familiar something is, the less we are inclined to like and/or esteem it. The effect of unfamiliarity on our analytic judgments has been noted by Neuwirth in the way we tend to regard compositions by contemporaries of BHMB whose music is less familiar to us:
In the case of Kleinmeister compositions, deviations from what is regarded as the normative model are devalued, as are pieces which [rigidly] conform to that model. It is a no-win situation for the Kleinmeister: whatever option is chosen, the typical reaction of many analysts is either to regard the work in question as a premature manifestation of the full-fledged form, or to assume a failing on the part of the composer rather than specific aesthetic intentions. This suggests that in many cases, analytical judgment is implicitly (or unconsciously) guided by knowledge of the identity of the composer.” (Neuwirth 2013, 42)
Of course the very term Kleinmeister is pejorative, and—as Neuwirth has pointed out—the “little master” designation itself is a product of implicit bias (Neuwirth 2011, fn 31). For the most part, we don’t know the music of BHMB’s contemporaries, so our negative judgments of their work cannot logically be based on familiarity with it. For the most part, the simple reason we don’t value these works is because we don’t know them.
[3.7] One final source of bias concerns how we use the evidence we gather (or rather, do not gather) in support of our theories of harmony, melody, and form. Consider the following thought experiment: I give you the number sequence “2–4–6,” and I ask you to guess the rule that generates it. To assist in your guessing, you may give me other sequences, and I will tell you if they fit the rule or not. Most people will say “6–8–10” or some other sequence of even numbers, though a few might say “11–13–15,” These responses reflect an inference that the rule is “increasing even numbers” or “add 2 to each number in the sequence;” they are responses that conform to that rule. This thought process is symptomatic of confirmation bias: only choosing test cases that confirm your presupposition, rather than examples/cases that might disconfirm it. Whereas attempts at falsification, on the other hand, would include sequences like “10–8–6” or “7–11–13” (i.e., is it directionality? It is a sequence of a class of numbers? and so forth).
[3.8] The “2–4–6” example comes from Wason’s 1960 paper on the pitfalls of positive testing strategies, of only using cases that you expect will give you a “yes” answer to the question “do they fit the rule?” In Wason’s experiment, the rule to be inferred was simply “increasing numbers.” As Oswald and Grossjean point out:
Wason argues that their [the subjects’] error consisted of failing to test sets of three numbers that did not correspond to what was assumed to be the rule. Thus a sequence like “4–5–6” would have been an appropriate test. This is because it does not correspond to the rule assumed by the participant at this stage and yet it prompts a positive feedback (since it does correspond to the correct rule). Thus, participants’ assumptions about the rule would have been falsified. (Oswald and Grossjean 2004, 80).
When we test a hypothesis we also evaluate, if only implicitly, the cost of disconfirmation. The cost of disconfirmation in Wason’s number-guessing game is low, but in other contexts it can be much higher. If the cost of disconfirmation is high—for example, if it forces us to find fault with a friend, to abandon a pet theory, or to lower the esteem for composers we have previously valued and whose music we have extensively studied and practiced—then we are more likely to exhibit confirmation bias.
[3.9] With these motivationally-supported hypotheses, we are inclined to proceed in a confirmatory fashion:
A true confirmation bias seems to occur primarily when the hypotheses tested are already established, or are motivationally supported. In general, we may say that the confirmation bias consists in favoring expectancy-congruent information over incongruent information. This may happen in different ways: (a) memories congruent with the hypothesis are more likely to be accessed
. . . (b) undue weight is given to the importance of the congruent information . . . and (c) sources with information that could reject the hypothesis are avoided. (Oswald and Grossjean 2004, 93)
Music theories are motivationally supported by our aesthetic values and encultured beliefs. If we “know” that Beethoven and Mozart are master composers, rather than reject or modify a theory inductively derived from their music, we reject data that run counter to our well-established biases. Again, Neuwirth’s comments on how we regard the work of Kleinmestern continue to register as unsurprising. In a similar vein, it is noteworthy that in Hepokoski and Darcy’s theory of sonata form, there are only three (out of 80) musical examples that are not by Haydn, Mozart, and Beethoven, and that these three examples (by J. C. Bach, Scarlatti, and C. P. E. Bach) appear in the chapters on variant sonata forms, especially the “problematic,” Type 2 classification (Scarlatti and C. P. E. Bach).
[3.10] John Steinbeck, writing years before Wason, gives a fine account of the problems of displacing confirmation bias, even when we know better:
There is one great difficulty with a good hypothesis. When it is completed and rounded, the corners smooth and content cohesive and coherent, it is likely to become a thing in itself, a work of art. It is then like a finished sonnet or a painting completed. One hates to disturb it. Even if subsequent information should shoot a hole in it, one hates to tear it down because it once was beautiful and whole
. . . The things of our minds have for us a greater toughness than external reality. . . These mind things are very strong; in some, so strong as to blot out the external things completely. (Steinbeck and Ricketts 1941, 180–181)
Thus in music theory we all too often fail to acknowledge the various biases that lead to the construction of our analytic and teaching corpora. This includes implicit biases that come from our active enculturation as practicing musicians, explicit biases from broadly held aesthetic beliefs regarding the status of “great” composers and “masterworks,” and confirmation biases that are reinforced by our tendency to use only positive testing strategies and/or selective sampling when putting our theories in practice.
4. Overfitting to Small Corpora: The Fundamental Problem
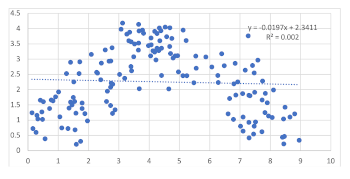
[4.1] Overfitting is a problem that can arise when one produces a model or theory based upon recurring patterns found in one’s data or corpus, and it is one of the bugbears of machine learning approaches in AI. Overfitting occurs when one constructs a model that is more complex than it needs to be to capture the pattern in the data, a pattern that is presumably related to some underlying structure (Abu-Mostafa 2012). To show the dangers of working with small data sets, I have constructed an illustration using various scatterplots as illustrations. Here, we may think of the points as pieces in the WAM corpus and trendlines as the models (i.e., theories of harmony, form, etc.).
Example 2. Plot of data generated from Y = X, with random noise added to x and y values
(click to enlarge)
[4.2] Example 2 presents some data along a very nice linear model. It should be: in this instance, the underlying structure was pre-designed as Y = X (a straight line), with some random noise added to the Y values of each X. The regression line (or trendline) is the “model” of the relationship between X and Y derived from the data; when one asks a graphing program to add a trendline, it computes the line that minimizes the collective distances between it and all the points in the data set. R2 is a specific measure of how close all of the points are to the regression line, and here it is also quite high.(4) It is possible to infer Y=X from this scatterplot, and since the data are well behaved, we have a very good “fit.” This, then, represents a case where a simple linear trendline is a fair representation of the underlying structure.
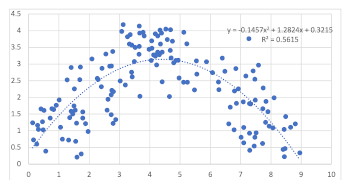
[4.3] Examples 3 and 4 illustrate a more complex pattern of data that goes up and then down. A simple linear model (Example 3) does not fit the data very well, while a quadratic model (Example 4) fits much better. Note the dramatic increase in R2 value. In machine learning and other contexts, one increases the complexity of the model by adding terms that substantially improve the fit. In the case of the data in Example 4, adding additional terms to the model/equation beyond the quadratic model will not improve the fit very much, if at all. This can be seen in terms of the increase in the R2 value of each additional fit. For the data in Example 3, adding a cubic term does not increase the R2 value at all, and polynomials of degree four (R2 = .6097), five (R2 = .6135), and six (R2 = .6236) are only marginally better.
Example 3. Plot of data generated from equations Y = X (for X = 0 to X = 4.5) and Y = X-9 (for X = 4.5 to X = 9), with random noise aided to X and Y values, with linear trendline (click to enlarge) | Example 4. Plot of data generated from equations Y = X (for X = 0 to X = 4.5) and Y = X-9 (for X = 4.5 to X = 9), with random noise aided to X and Y values., with quadratic trendline (click to enlarge) |
Example 5. Sparse subset of data from Example 2; linear trendline added
(click to enlarge)
[4.4] One would be hard-pressed to claim that the quadratic model in Example 4 is an example of overfitting. But note that it is, in fact, wrong. In fitting a regression line to this model, we presume there is only one continuous function that underlies the data, but in this case the “structure” to be discovered here was pre-designed to comprise the union of two straight line segments.
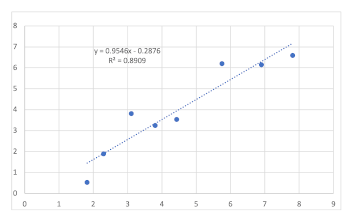
[4.5] Let us return to the case of Y = X. In Example 2, several points are marked with a different color. If we extract these points, we have the scatterplot given in Example 5. Example 5 is a “sparse” sample, and its trendline is a simple linear fit that is actually quite good (R2 = .8909). We might be bothered by the three points that lie some distance from the trendline. This is because we have forgotten that this data set is only a small sample from a much larger population. So there is a temptation to try and see if a more complex model will improve the fit to the data. Example 6 gives a quadratic fit, Example 7 a cubic fit, and Example 8 a fit with a polynomial of degree 6.
Example 6. Quadratic fit of data from Example 5 (click to enlarge) | Example 7. Cubic fit of data from Example 5 (click to enlarge) |
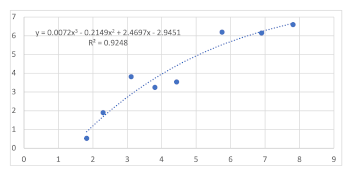
Example 8. Polynomial of degree 6 fitted to data from Example 5
(click to enlarge)
[4.6] While adding one or two (or even three or four) additional terms does not improve the fit very much, the regression line given in Example 8 is a nearly perfect fit, which in and of itself should rouse our suspicions. We might think this is the best model for our data, especially if we believe that there is something special or significant about this particular sample from our data population—if these were, for example, Mozart’s concertos. But remember, for this data set, the underlying structure our theory is attempting to capture is simply Y = X. In Example 8, we have not fitted our model to the underlying structure, we have fitted the model to the noise in our data. Even if one were to claim that the model is “bespoke,” a model intended only to address Mozart’s concertos, for example, it does not represent the broader background of compositional choices open to Mozart. In fact, it explicitly excludes/obscures them.
[4.7] Bad inductive theories arise from the perfect storm of (a) small data set/sample, (b) a belief that that particular sample is important/typical, (c) a desire to have a model that captures as many nuances in the data as possible (i.e., a “tight fit” between model and data), and finally (d) failing to reexamine the larger population to see if the model makes any sense (cf. Example 2). As noted above, music theory also tends to commit the sin of using the same data set for training and testing/verification. As a result, our theories always work; however, this strategy inevitably leads to overfitting. Hepokoski and Darcy’s (2006) elaborate taxonomy of sonata forms—with their five basic types, first and second level defaults and various counterexamples (“deformations”)—is a textbook example of overfitting, for all the reasons given above.
5. The Perils of Exemplars and Scripts
[5.1] Music theorists like canonical examples, as they are pedagogically useful and seemingly explain so much. One such piece is Beethoven’s Piano Sonata in F minor op. 2, no. 1, which Matthew BaileyShea (2004) has singled out as a case in point:
It is quite likely that no other form in the history of Western music theory has been so strongly associated with a single musical example as the sentence. Most forms are not defined by a single locus classicus; no one piece serves as the ultimate paradigm of sonata form, no single phrase represents the virtual embodiment of the period. When it comes to the sentence, however, one example is consistently privileged above all others: Beethoven’s Piano Sonata in F Minor, op. 2, no. 1, first movement, bars 1–8. (BaileyShea 2004, 5)
[5.2] As BaileyShea notes, the use of op. 2, no. 1 as the model for sentence form originates with Schoenberg (1967), with assists from Ratz ([1951] 1973) and Caplin (1998). It is excellent “one-stop shopping” for many attributes of the sentence: a 2+2+4 grouping structure, a relatively low degree of closure in bar 4, and so forth. But as BaileyShea also notes, using Beethoven’s theme as an ideal type masks the wider range of sentence forms, many of which he catalogs in his article. This leads BaileyShea to ask, “at what point do listeners begin to hear a passage as ‘sentential,’ and what do they expect to happen in such a passage?” (2004, 21). He goes on to say:
Because these types of repetition are ubiquitous in Western music, an extraordinarily large number of passages would elicit sentence expectations without producing normative continuations. In order to hear a specific passage as a “failed sentence” or “failed continuation” then, we need to separate those types of repetition that initiate sentential expectations from those that do not. Creating a theory that would account for such a distinction, however, is nearly impossible
. . . [for] any passage that begins with the statement of a brief musical idea and some form of repetition would immediately fall under the category of “sentence. (BaileyShea 2004, p. 22)
The real problem here, which follows from our fondness for exemplars and prototypes, is that Schoenberg, et al., treat the sentence form as a narrow script. It is more properly regarded as a plan, that is, as a constellation of more general and basic constraints on how melodies can unfold when they begin with the repetition of a basic idea.
[5.3] The distinction between scripts and plans was articulated by Schank and Abelson (1977) as part of early work in cybernetics, and its relevance for music analysis has previously been noted, especially in the context of schema theory (Gjerdingen 1988, 3–10; Narmour 1990, 32–35; Meyer 1989, 245–246.) Scripts and plans perform similar functions: they allow us to understand sequences of events, and hence provide a basis for prediction, action, and/or comprehension as similar event sequences unfold. Scripts are concrete, context-specific, and as Schank and Abelson note, “stylized” for their contexts. They use the example of ordering a meal from a menu to illustrate some of the essential features of scripts and scripted behaviors. As such:
A script
- is a structure that describes appropriate sequences of events in a particular context.
- is made up of slots and requirements as to what can fill those slots.
- handles stylized everyday situations.
- is not subject to much change, nor does it provide the apparatus for handling totally novel situations. (Schank and Abelson 1977, 41)
[5.4] By contrast, plans are more abstract. They involve more general information about how the various steps in a sequence of events can be related to each other and understood. Schank and Abelson define the term as follows:
A plan
- is intended to be the repository for general information that will connect events that cannot be connected by use of an available script.
- is made up of general information about how actors achieve goals.
- Thus plans are where scripts come from . . . The difference is that scripts are specific and plans are general. (Schank and Abelson 1977, 70–72)
[5.5] BaileyShea’s account of the sentence form makes clear that when one treats Beethoven’s op. 2, no. 1 as the model for a sentence, problems are bound to arise when other musical utterances go “off script”; these become variants or deformations that need to be explained away. But no explaining away is necessary if one regards the sentence as a more general plan that involves options for repetition, continuation, and closure. To put it in Caplin’s terms, the sentence is an essentially “loose” form, with a range of options for its unfolding (Caplin 1998, 255; see also BaileyShea 2004, 10–11). In expressly framing it in this manner, Caplin presents the sentence as a type of plan as opposed to a script. More broadly, while scripts, according to Schank and Abelson, can be executed in different ways (“slots and requirements as to what can fill those slots”), the use of privileged exemplars leads to two outcomes, both undesirable. One is script-based thinking in contexts where plans would be more appropriate, or else making those slots too restrictive within the context of a particular script.
[5.6] All this brings us to Hepokoski and Darcy’s Elements of Sonata Theory. Their book presents an elaborate taxonomy of a subset of pieces from the BHMB canon, a subset united by the concept of “rotational form,” an apt term coined by the authors to cover formal constructions that involve the repetition of a sequence of formal units. This view of form sounds very much like a plan, rather than a script. In line with this, at various points Hepokoski and Darcy properly note that sonata form is a flexible framework for the organization of musical ideas: they recommend that readers remain “cautious in reconstructing the internal anatomy and details of the formal aspects of musical genres
[5.7] While Hepokoski and Darcy appear to embrace plan-like thinking, overfitting and script-like thinking remain pervasive in their work; this problem is evident from the very subtitle of their book, “Norms, Types, and Deformations in the late 18th-Century Sonata.” First, Hepokoski and Darcy use (with some special pleading; see pp. 11 and 614–621) the term deformation to refer to variants from what they consider to be the normative or exemplary versions of sonata form. Those norms are the result of a long music-theoretic tradition of overfitting to small sets of privileged data points, which include the BHMB canon and subsets thereof (e.g., Hepokoski and Darcy’s “Type 5 Sonata” is essentially derived from Mozart’s concertos). As noted above, the only non BHMB musical examples in their sizable book are examples of variants and/or deformations. Second, they claim—based on a belief that one composes and listens “dialogically” relative to the norms of compositional practice—that one of the goals of their project is to enable modern listeners to be able to hear and appreciate those dialogs (2006, 9–13 and 603–610). However, as the quote above from Neuwirth (2013) points out, they have not done the analytical surveying required to establish what those norms are. Third and most significantly, they frame their elaborate taxonomy of sonata form types, subtypes, defaults (on multiple levels), and so forth as script-like, post hoc ergo propter hoc reifications of specific choices that Haydn, Mozart, and Beethoven made. They do so in the context of the rotational forms that all fall under the umbrella term “sonata form.”
[5.8] Music theory is right to acknowledge that music is created and understood against the background of normative practices. But thinking solely in terms of scripts is the “moral hazard” that comes from overfitting our theories to a small set of exemplars, exemplars that reflect our implicit biases and explicit beliefs regarding their value and importance.
6. Moving Forward
[6.1] At the 2011 SMT Annual Meeting, Brenda Ravenscroft organized a public debate over the continued use and privileging of the WAM canon in undergraduate theory curricula; it was titled “The Great Theory Debate: Be It Resolved
[6.2] In our remarks, Heather and I stressed the need for the greater relevance of an expanded canon for all of our students (both music majors and non-majors), and the practical value of including musical genres that twenty-first century performing musicians are likely to be playing in their professional careers. Critically, we neglected to emphasize the problems of diversity, equity, and inclusion that come with hewing to the traditional teaching repertoire. We should have. Poundie and Peter’s arguments affirmed the high artistic value of the music of the BHMB canon and our collective duty to preserve and present that canon to our students; its presumed ubiquity and familiarity; and, pragmatically, that we have well-developed tools for teaching and analyzing it. In the end, the large audience of music theorists in attendance agreed with them; Heather and I lost the debate.
[6.3] I am sure that many readers of this essay will be quick to point out that music theory is more than just what appears in our undergraduate textbooks, and that the volumes of JMT, Spectrum, MTO, and other journals are full of works on jazz, popular music, and non-Western music. That is true, but for most musicians, and certainly for most of the public, music theory is what we teach in the undergraduate classroom. As the 2011 debate demonstrated, we are very reluctant to move away from that core pedagogy. I think this is due, perhaps in large part, to the constellation of biases, implicit and explicit, that prevents us from considering alternative pedagogical repertoires, topics, and approaches (though see VanHandel 2020 for various ideas on how we might do so). There is also the problem of habit: we continue to teach this repertoire and the concepts derived from it “because we’ve always done it this way,” even though we know there are other repertoires and approaches that can serve us well in teaching our students how harmony, melody, rhythm, and form work.
[6.4] To be clear, I am not advocating for the elimination of BHMB from our analytic and teaching canons, for this is music that I know and love, and have loved sharing with my students for decades. But we must be clear eyed about how and why we inherited the BHMB canon from our music-theory forebears, and about the overt and covert values and biases that support our continued use and valuation of it. I hope readers of this essay will also acknowledge that many of our core concepts in music theory—from “metrical accent” and “harmonic dissonance” to “recapitulation” and “developing variation”—come from our deep engagement with the BHMB canon and the canon of theory literature that has emerged. While we can develop alternative approaches to functional harmony in popular music, or different modes of development in minimalism, or different theories of metrical accent to account for the rhythmic structure of Balkan and Sub-Saharan African musics, we must recognize the biases and conceptual baggage we carry with us when do so. We must be aware of these biases to the fullest extent possible, especially when we rely on our “analytic intuitions.” For far too often, intuition is simply prejudice by another name.
[6.5] Similarly, for the music of the common practice or any other music tradition we wish to come to know and understand, we should recognize the problems we face in coming to know it, problems that stem from our bad habits of using convenient rather than representative samples, relying on undersized corpora, overfitting to those corpora, and thinking in terms of scripts rather than plans. The methodological potholes that we have fallen into in our study of WAM from 1700–1900 can all too easily be replicated in our study of other musics, whether jazz, blues, pop, or world music.
[6.6] So, to repeat my earlier remarks, Phil Ewell’s address to the Society for Music Theory in the fall of 2019 was a not only a wake-up call for music theory to assess its whiteness and move toward greater equity, diversity, and inclusion in our discipline. It was also a wake-up call for us all to be better music theorists. Indeed, we cannot do the former if we do not do the latter.
Justin London
Department of Music
Carleton College
Northfield, MN 55057
jlondon@carleton.edu
Works Cited
Abu-Mostafa, Yaser. 2012. Learning from Data: Online Lectures on Machine Learning, Lecture #11, “Overfitting.” Video, 2:09. https://www.youtube.com/watch?v=EQWr3GGCdzwM.
Ayotte, Benjamin M. 2004. Heinrich Schenker: A Guide to Research. Routledge.
Bacchini, Fabio, and Ludovica Lorusso. 2019. “Race, Again: How Face Recognition Technology Reinforces Racial Discrimination.” Journal of Information, Communication and Ethics in Society 17 (3): 321–35. https://doi.org/10.1108/JICES-05-2018-0050.
BaileyShea, Matthew. 2004. “Beyond the Beethoven model: Sentence types and limits.” Current Musicology 77 (Spring): 5–33.
Briscoe, James R. 2004. New Historical Anthology of Music by Women. 2nd ed. Indiana University Press.
Buolamwini, Joy, and Timnit Gebru. 2018. “Gender shades: Intersectional Accuracy Disparities in Commercial Gender Classification.” Proceedings of Machine Learning Research 81: 1–15.
Caplin, William E. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford University Press.
—————. 2004. “The Classical Cadence: Conceptions and Misconceptions.” Journal of the American Musicological Society 57 (1): 51–118. https://doi.org/10.1525/jams.2004.57.1.51.
—————. 2017. “Fantastical Forms: Formal Functionality in Improvisational Genres of the Classical Era.” In Musical Improvisation and Open Forms in the Age of Beethoven, ed. Gianmario Borio and Angela Carone, 85–114. Routledge. https://doi.org/10.4324/9781315406381-6.
Caplin, William E., and Nathan John Martin. 2016. “The ‘Continuous Exposition’ and the Concept of the Subordinate Theme.” Music Analysis 53 (1): 4–43. https://doi.org/10.1111/musa.12060.
Clendinning, Jane Piper, and Elizabeth Marvin. 2005. The Musician's Guide to Theory and Analysis. 1st ed. W.W. Norton.
—————. 2021. The Musician's Guide to Theory and Analysis. 4th ed. W.W. Norton.
Diergarten, Felix, and Markus Neuwirth. 2019. Formenlehre. Ein Lese- und Arbeitsbuch zur Instrumentalmusik des 18. und 19. Jahrhunderts. Laaber Verlag.
Ericsson, K. Anders, Ralf T. Krampe, and Clemens Tesch-Römer. 1993. “The Role of Deliberate Practice in the Acquisition of Expert Performance.” Psychological Review 100 (3): 363–406. https://doi.org/10.1037/0033-295X.100.3.363.
Etikan, Ilker, Sulaiman Abubakar Musa, and Rukayya Sunusi Alkassim. 2016. “Comparison of Convenience Sampling and Purposive Sampling.” American Journal of Theoretical and Applied Statistics 5 (1): 1–4. https://doi.org/10.11648/j.ajtas.20160501.11.
Ewell, Philip. 2020a. “Music Theory and the White Racial Frame.” Music Theory Online 26 (2). https://doi.org/10.30535/mto.26.2.4.
—————. 2020b. “Beethoven Was an Above Average Composer—Let’s Leave It at That.” Music Theory’s White Racial Frame: Six Blogposts. https://musictheoryswhiteracialframe.wordpress.com/.
Ewell, Philip, Rosa Abrahams, Aaron Grant, and Cora Palfy. 2023. The Engaged Musician: Theory and Analysis for the Twenty-First Century. W. W. Norton.
Field, Andy. 2005. Discovering Statistics Using SPSS, 2nd ed. Sage Publications.
Gawronski, Bertram. 2019. “Six Lessons for A Cogent Science of Implicit Bias and Its Criticism.” Perspectives on Psychological Science 14 (4): 574–95. https://doi.org/10.1177/1745691619826015.
Gjerdingen, Robert O. 1988. A Classic Turn of Phrase: Music and The Psychology of Convention. University of Pennsylvania Press.
Gramit, David, ed. 2008. Beyond the Art of Finger Dexterity: Reassessing Carl Czerny. University of Rochester Press.
Greenwald, Anthony G., and Mahzarin R. Banaji. 1995. “Implicit Social Cognition: Attitudes, Self-esteem, and Stereotypes.” Psychological Review 102 (1): 4–27. https://doi.org/10.1037/0033-295X.102.1.4.
Greenwald, Anthony. G., and Linda H. Krieger. 2006. “Implicit Bias: Scientific Foundations.” California Law Review 94 (4): 945–967.
Harasim, Daniel. n.d. The Musical Corpora Register. Website. https://github.com/dharasim/MCR/wiki. Accessed April 24, 2021.
Hepokoski, James, and Warren Darcy. 2006. Elements of Sonata Theory: Norms, Types, and Deformations in the Late Eighteenth-century Sonata. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195146400.001.0001.
Hisama, Ellie M. 2000. “Life Outside the Canon? A Walk on the Wild Side.” Music Theory Online 6 (3). https://www.mtosmt.org/issues/mto.00.6.3/mto.00.6.3.hisama.html.
Jost, John T. 2019. “The IAT Is Dead, Long Live the IAT: Context-sensitive Measures of Implicit Attitudes are Indispensable to Social and Political Psychology.” Current Directions in Psychological Science 28 (1): 10–19. https://doi.org/10.1177/0963721418797309.
Kim, Byungju, Hyunwoo Kim, Kyungsu Kim, Sungjin Kim, and Junmo Kim. 2019. “Learning Not to Learn: Training Deep Neural Networks with Biased Data.” Computer Vision Foundation Proceedings: 9012–20. https://doi.org/10.1109/CVPR.2019.00922.
Kostka, Stefan, and Dorothy Payne. 2004. Tonal Harmony. 5th ed. McGraw Hill.
Kroll, Mark. 2007. Johann Nepomuk Hummel: A Musician’s Life and World. Scarecrow Press.
London, Justin. 2020. “What Should an Undergraduate Music Theory Curriculum Teach? (And, Alas, What Most of the Time We Don’t).” In The Routledge Companion to Music Theory Pedagogy, edited by Leigh Van Handel, 424–33. Routledge. https://doi.org/10.4324/9780429505584.
Maust, Paula. 2021. Expanding the Music Theory Canon. Website. https://www.expandingthemusictheorycanon.com/.
Meyer, Leonard. B. 1989. Style and Music: Theory, History, and Ideology. University of Chicago Press.
Narmour, Eugene. 1990. The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. University of Chicago Press.
Neuwirth, Markus. 2011. “Joseph Haydn’s ‘Witty’ Plan on Hepokoski and Darcy’s Elements of Sonata Theory.” Zeitschrift für Gemeinschaft für Musiktheorie 8 (1): 1999–200.
—————. 2013. “Recomposed Recapitulations in the Sonata-Form Movements of Joseph Haydn and His Contemporaries.” PhD diss., University of Leuven.
Oswald, Margit E., and Stefan Grossjean. 2004. “Confirmation Bias.” In Cognitive Illusions: A Handbook on Fallacies and Biases in Thinking, ed. R. Pohl, 79–96. Taylor & Francis.
Parsons, Laurel, and Brenda Ravenscroft. 2016. Analytical Essays on Music by Women Composers: Concert Music. Oxford University Press.
—————. 2018. Analytical Essays on Music by Women Composers: Sacred Music to 1900. Oxford University Press.
Ratz, Erwin. [1951] 1973. Einführung in die musikalische Formenlehre: über Formprinzipien in den Inventionen und Fugen J.S. Bachs und ihre Bedeutung für die Kompositionstechnik Beethovens. 3rd ed. Vienna: Universal.
Roig-Francolí, Miguel A. 2003. Workbook and Anthology for Use with Harmony in Context. McGraw-Hill.
Schank, Roger C., and Robert P. Abelson, 1977. Scripts, Plans, Goals and Understanding: An Inquiry into Human Knowledge Structures. Lawrence Erlbaum Associates.
Schoenberg, Arnold. 1967. Fundamentals of Musical Composition, edited by G. Strang and L. Stein. St. Martin’s Press.
Schubert, Emery. 2007. “The Influence of Emotion, Locus of Emotion and Fmiliarity Upon Preference in Music.” Psychology of Music 35 (3): 499–515. https://doi.org/10.1177%2F0305735607072657.
Steinbeck, John, and Edward F. Ricketts. 1941. Sea of Cortez: A Leisurely Journal of Travel and Research. Viking Press.
Straus, Joseph N. 1993. Music by Women for Study and Analysis. Prentice-Hall.
Turek, Ralph. 2007. Theory for Today's Musician. McGraw-Hill.
VanHandel, Leigh, ed. 2020. The Routledge Companion to Music Theory Pedagogy. Routledge. https://doi.org/10.4324/9780429505584.
Wason, P. C. 1960. On the Failure to Eliminate Hypotheses in a Conceptual Task. Quarterly Journal of Experimental Psychology 12 (3): 129–140. https://doi.org/10.1080/17470216008416717.
Weber, William. 2006. “The Rise of the Classical Repertoire in Nineteenth-century Orchestra Concerts.” In The Orchestra: A Collection of 23 Essays on its Origins and Transformations, ed. Joan Peyser, 361–85. Hal Leonard.
Footnotes
1. Ewell’s plenary session address is available on the SMT website. See the “Business Meeting, Awards, and Plenary” video, beginning at 2:14:08. https://www.youtube.com/playlist?list=PL7EdSIX7ZDUYCyceCvb8XrdSS3_tjEBB9.
Return to text
2. This is not just a problem for Caplin or Hepokoski and Darcy. Of the 28 classical corpora on Harasim’s website noted above, 11 are wholly dedicated to pieces by BHMB. The music of BHMB has a significant presence in many of the other corpora, for example, a corpus of all of the musical examples in the Kostka and Payne (2004) music theory textbook.
Return to text
3. In addition to the analytical work of Neuwirth (2013), Diergarten and Neuwirth’s (2019) handbook on musical form includes examples by Leopold Mozart, Corelli, J. C. Bach, C. P. E. Bach, Clementi, Vanhal, Rosetti, Koželuch, Platti, and Hummel, in addition to HMB. Musicologists have done better, as Kroll (2007) focuses on the music of Hummel and Gramit (2008) on Czerny. To be fair, Caplin and Martin (2016) do look at a few pieces by Hummel—though, tellingly, they do so in terms of their deviations from form-functional norms Caplin derives from the music of HMB.
Return to text
4. More precisely, R2 is based upon r, the Pearson product-moment correlation coefficient, which is a standardized measure of the covariance between two variables; it can range between
-1 and 1. A coefficient of 1, for example, is a perfect positive correlation, so that as one variable increases the other also does so by a proportionate amount. A coefficient of 0 means there is no linear relationship between the two variables. Squaring r gives R2, a measure in the amount of variability in one variable that is explained by the other. For an excellent and readable introduction to these statistical concepts, see Field (2005).
Return to text
5. This event was modelled after the “Intelligence Squared” debate series on public radio (https://www.npr.org/series/6263392/intelligence-squared-u-s).
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Lauren Irschick, Editorial Assistant
Number of visits:
12209