Three Audiovisual Correspondences in the Main Title for Vertigo
Scott Murphy
KEYWORDS: Bernard Herrmann, Saul Bass, Tonnetz, Lissajous, harmony, cross-domain, topology, narrative
ABSTRACT: Saul Bass and Bernard Herrmann provided the visuals and music, respectively, for the main title of Alfred Hitchcock’s 1958 movie Vertigo. These artworks correspond with one another in three ways. First, when aligning two dimensions of visual and pitch brightness, a portion of each artwork moves through this two-dimensional space using a similar path. Second, when arranging some of the tonal materials onto a certain space, these materials transform into each other using transformations similar to those that animate some of the visual designs. Third, under partial enharmonic equivalence, these pitch spaces curl into a partly-closed and partly-open shape that closely resembles manipulated visual forms whose looped closure is partially obscured. The first and third ways shed significant light on the film’s narrative, and the first way in particular parallels the film’s central dramatic form.
DOI: 10.30535/mto.28.1.6
Copyright © 2022 Society for Music Theory
0. Outline of the Article
[0.1] Saul Bass and Bernard Herrmann provided the visuals and music, respectively, for the main title of Alfred Hitchcock’s 1958 movie Vertigo. Much could be said about Bass’s visuals, or Herrmann’s music, or the following narrative of Vertigo independently from the others. However, the purpose of my article is to propose correspondences among these three artworks.
Section 1 of the article presents a notated harmonic and formal reduction of Hermann’s music and a summary of Bass’s images for Vertigo’s main title. Section 2 lays out multiple invitations and rationales for locating correspondences between Vertigo’s main title music, main title visuals, and narrative, which include the relevance of the Tonnetz, a specific array of pitch classes that makes proximate the constituents of consonant harmonies. Section 3 shows, using a homology between visual and musical brightness, how one particular orientation of the Tonnetz is especially appropriate for the first part of Bass’s main title. Section 4 argues that a progression of five of Herrmann’s chords through this specifically oriented Tonnetz matches Bass’s camera motions in the first part of the main title. Section 5 contends that the way these five chords transform into others on this version of the Tonnetz matches those transformations that animate some of the visual designs used in the second part of the main title. Section 6 demonstrates how, under partial enharmonic equivalence, this Tonnetz curls into a partly-closed and partly-open shape that closely resembles Bass’s manipulations of these same designs whose looped closure is partially obscured. Section 7 claims that the first and third correspondences—from Sections 1 and 3, respectively—illuminate elements of the film’s narrative content and form. Section 8 offers a short metatheoretical afterthought.
1. The Music and Visuals of Vertigo’s Main Title
Example 1. Herrmann, Vertigo, “Prelude,” reduction
(click to enlarge)
Example 2. Herrmann, Vertigo, “Prelude,” mm. 1–2
(click to enlarge)
[1.1] Example 1 displays a harmonic reduction and formal analysis of Bernard Herrmann’s main title music for Vertigo. This reduction lines up the chords with both the mensural notation of Herrmann’s original manuscript score, from which the reduction was made, and the chronology of the movie, shown numerically above and below the reduction, respectively.(1) My atypical use of first and second endings, as well as the letters attached to chordal enumeration, convey a sense of the prelude’s form: an A–B binary whose repetition is truncated, and with coda material labeled as C. The open noteheads provide a harmonic summary of this main title music, whereas solid noteheads synopsize melodic motion and thus show pitches that may not be in the concurrent chord. The pitch C5 is initially tangled up in the tripleted arpeggios, shown in Example 2, that appear on the top of the chords in the A and C sections, insinuating its chord-tone status. However, there are three good reasons to treat it as a non-chord tone, and for Example 1 to indicate all C5s accordingly with a solid notehead. First, it is the only note within the arpeggiations that is approached and left by step, as an upper neighbor to
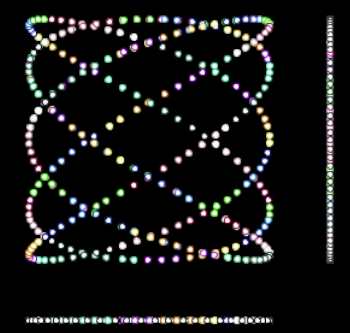
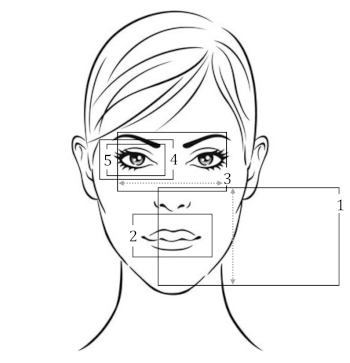
[1.2] Bass’s main title for Vertigo divides into two successive parts. The first part features a close-up of a woman’s face, over which the camera moves among five different stations and five different degrees of zoom, ending with a shot of the woman’s right eye that fills the frame. Loud brass statements of Herrmann’s chords A1b, A2, A3, and A4 and four title credits—“JAMES STEWART,” “KIM NOVAK,” “IN ALFRED HITCHCOCK’S,” “VERTIGO”—punctuate the completion of motion to Stations 2 through 5 of Bass’s camera, respectively. The second part of Bass’s main title involves slowly enlarging curvilinear forms with contrasting colors and designs centered in the frame, most rotating as well. The entire main title with both image and music can be viewed and heard at https://www.youtube.com/watch?v=Lvaahmgmz8w.
2. Motivations for Analyzing Vertigo’s Audiovisual Correspondences
[2.1] This article proposes three ways in which Herrmann’s chord progressions and Bass’s moving images for the main title parallel one another. These ways have value in a manner similar to the value of the corresponding audiovisual connections that I (2009) proposed for the main title collaboration between Herrmann and Bass for Hitchcock’s movie Psycho, released two years after Vertigo. First, it suggests some degree of authorial influence, however abstract. According to Herrmann, Bass animated his titles to the composer’s music for Psycho. Although the most comprehensive source on Vertigo’s production (Auiler 2000) has no information about which came first and whether one influenced the other, another source (Karamath 2001) claims that “Hermannn later scor[ed] to Bass’s visuals.” (45, 47) Second, as in my earlier study, these audiovisual connections, working in synergistic combination, substantiate Herrmann’s (1980, 132) claim for a main title’s primary function to both “set the pulse” and “set the drama” for the movie that follows.(4) I will propose that the first and third ways in which music and visuals correspond in Vertigo’s main title shed significant light on the film’s narrative, and the first way in particular parallels the film’s central dramatic form. These three ways involve technical, even fastidious, analysis. This statement is more than a caveat: while the discipline of music theory in particular tends to tolerate such complex descriptions more than other disciplines, this degree of precision itself is also relevant to how I connect Herrmann’s main title music to Vertigo’s narrative, as explained at the end of my article.
[2.2] However, before presenting these ways and their dramatic implications, I would like to list five specific aspects in orbit around Vertigo’s opening that motivate and corroborate the notion that the musical and the visual can closely correspond. In doing so, I wish to show that the very premise of an audiovisual analysis sympathetically resonates with an understanding of an especially close-knit relationship between sight and sound shared by both creators and receivers of Vertigo’s artistry.
[2.2.1] Like many before and after him, the literary scholar Jack Sullivan hears how “Vertigo opens with triplets spiraling in contrary motion” (2006, 222). A cross-domain mapping between these triplets, notated in Example 2, and a visualization of spiraling or spinning, like that of the shapes used in the second part of Bass’s main title, is at once quite natural and highly metaphorical. A projection of two-dimensional circular motion onto a single dimension—that is, a sine or cosine function—maps to motion in pitch register, while the continuous turning translates to continuous onsets in time. In standard Western notation, this resembles a wave-like oscillation.(5) Herrmann’s arpeggiations comply with a sinusoidal wave in particular: if measured in semitones, their outer intervals—the
Video Example 1. Demonstration of the making of a 5:3 Lissajous curve
(click to watch video)
[2.2.2] The curvilinear forms in Vertigo’s main title are Lissajous curves, named after the nineteenth-century French physicist Jules Lissajous (1822–1880) who, like other scientists of his day, was engrossed in the prospect of visualizing vibrations, including sounds. Two mirrors attached to two tuning forks at right angles to one another combine the sinusoidal functions of the two forks’ pitches into a two-dimensional loop that becomes more Arabesque-like the more complex the frequency ratio is. In one way, this is the inverse of spinning-becoming-arpeggiating: instead, waves extended in time collapse into a closed two-dimensional loop. Video Example 1 demonstrates in slow motion the making of a relatively simply Lissajous curve in which the two component pitches are in a 5:3 ratio, the ratio of a pure major sixth.(6)
[2.2.3] Bass did not create the Lissajous curves of Vertigo’s main title. Instead, he engaged John Whitney (1917–1995) for this task, although Whitney’s name does not appear in Vertigo’s credits. Whitney was not only a filmmaker who pioneered computer and digital animation, but he was also a composer who studied the twelve-tone technique and explored analogues for it and other musical structures and processes in the visual world. In the foreword to his book Digital Harmony: On the Complementarity of Music and Visual Art, he summarizes his artistic vision: “
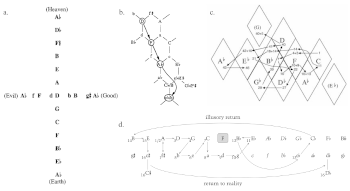
Example 3. Music-analytical Tonnetzen from (a) Lerdahl (1994, 2001) (b) Gollin (2000) (c) Harrison (2001) (d) Hoeckner (2005)
(click to enlarge)
[2.2.4] Herrmann’s music for Vertigo drips with the chromatic harmonic styles allied with Middle-European romanticism and postromanticism, particularly the music of Richard Wagner: both allusions to and quotations from Tristan und Isolde in particular occur throughout Vertigo’s score. In interpreting such music from this time period, some music scholars have found hermeneutic value in projecting its materials onto some geometric space. Example 3 compiles an selection of such analyses that appeared around the turn of the twenty-first century: Fred Lerdahl’s interpretation of the heaven-earth and good-evil axes in Wagner’s Parsifal (1994, reworked in 2001); Edward Gollin’s interpretation of Schubert’s wandering pilgrim (2000, 308–23); Daniel Harrison’s “resurrexit in tertio subdominanto” interpretation of Mahler’s Second Symphony “Resurrection” (2002, 137–38); and Berthold Hoeckner’s interpretation of Heine’s “Armesünderblum” in Schumann’s Dichterliebe (2006). These analyses and many others like them employ some sort of register-blind spatial arrangement of pitch classes, roots of triads, or tonics of keys in which perfect fifths are laid out along one axis, and major or minor thirds are laid out along another non-parallel axis: what is commonly labeled as a Tonnetz.
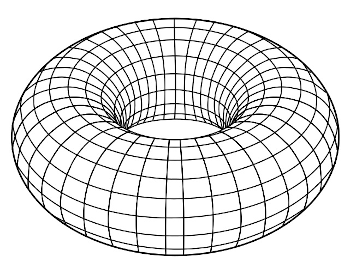
Example 4. A common three-dimensional depiction of the torus
(click to enlarge)
Video Example 2. Projection of descending perfect-fifth motion through a three-dimensional torus onto a plane, producing a Lissajous curve
(click to watch video)
[2.2.5] When enharmonic equivalence is imposed upon the Tonnetz, bending both its lines of perfect fifths and its lines of major or minor thirds into cycles, the result—now well known in music-theory circles—is a torus. Example 4 shows the common doughnut depiction of a torus embedded in three dimensions. Less well known is the close relationship between the torus and the Lissajous curve. Video Example 2 simulates some uniform motion—in this case, ascending perfect fifth motion—around the three-dimensional toroidal Tonnetz. If this uniform motion is projected onto a plane—like how an object moving in three dimensions might cast a shadow moving along a two-dimensional wall—one produces a close approximation of a Lissajous curve. It is sometimes said that music adds a third dimension to cinema’s two: perhaps Whitney’s spirals in Vertigo display the casting of this third dimension of music back onto the screen. Whitney’s spirals are more complex than the Lissajous curve generated during Video Example 2, because Whitney’s are based on polynomial parametric equations, instead of the monomial ones used in Video Example 1. However, this is consistent with how Herrmann’s music is more than just uniform motion—like ascending perfect fifth motion—around the Tonnetz.
3. Light to Dark: Lining up Two Dimensions of Cinematic and Pitch Spaces
Example 5. A portion of a “nonconformed” Tonnetz arranged by orthogonal equal-tempered perfect fifths and major thirds, with shading indicating degree of sharpness
(click to enlarge)
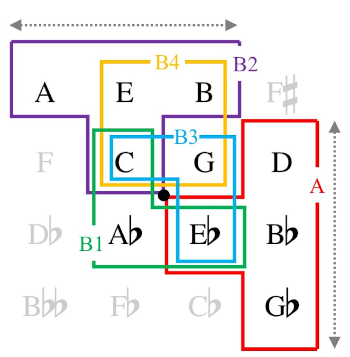
[3.1] In making my three audiovisual connections between Herrmann’s harmonic progressions and Bass’s moving images for Vertigo’s main title, I will also employ a version of the Tonnetz. This is not unprecedented: Kenneth Smith (2018) uses similar networks to interpret music from Vertigo. However, Smith’s visuals can withstand manipulability; in other words, they could be reoriented or reshaped and essentially serve the same function. Even the graphs used by Gollin, Lerdahl, Harrison, and Hoeckner cited earlier could be flipped, rotated, skewed, or otherwise transformed without altering their basic arguments, such as “one pitch is three-unit distances from another.” By contrast, the use of the Tonnetz in my analysis of Vertigo’s main title is as a precisely calibrated metric that cannot be so transformed without changing the analysis. I respectively map its two axes—the rising-perfect-fifth axis and the rising-major-third axis—to the left-to-right and down-to-top axes of the two-dimensional cinematic screen. Example 5 shows one example of a Tonnetz both oriented specifically as such and non-toriodal, “unconformed” (Harrison 2002) to any equivalences (beyond those involving octaves) and thereby made flat like a screen. The shading will be explained momentarily.
[3.2] This mapping may appear arbitrary and, worse, contrived. A correspondence of this type may remind the film scholar of the Russian director Sergei Eisenstein’s (1942, 173–216) study of audiovisual, or vertical, montage, in which, in the most famous example from the “Battle of the Ice” scene from Alexander Nevsky, he draws a literal two-dimensional correlation between the two-dimensional pages of Prokofiev’s notated score and the two-dimensional static cinematic images that the score accompanies. Critics like Theodor Adorno and Hans Eisler (2005 [1947], 153), Roy Prendergast (1992, 223–26), and Nicholas Cook (1998, 57–65) rebuked this kind of correlation, citing how the temporal and processual horizontal dimension of music notation fails to match the spatial and instantaneously perceived horizontal dimension of the filmic frame. Royal S. Brown (1994, 135–38) sides with Eisenstein, arguing both against the immediacy of the cinematic image’s perception and for an atemporal understanding of music’s structures, and validating the mapping of an up-down verticality in both spaces: higher in musical pitch maps to higher in the filmic frame.
Example 6. A portion of the “embodied Tonnetz” (Brower 2008)
(click to enlarge)
[3.3] My analytical use of the two-dimensional Tonnetz, rather than a two-dimensional notated score, as a parallel to the cinematic frame sidesteps the problem of temporal mapping in Eisenstein’s correspondences. Both the unconformed Tonnetz and the filmic frame can act as atemporal “grounds” upon which corresponding “figures” can move in time.(7) However, the Tonnetz, even the unconformed version, also apparently relinquishes the VERTICALITY image schema: what should be “up” on a Tonnetz? Candace Brower (2008) tackles this question from the perspective of cognitive science in general and conceptual metaphor theory in particular, resulting in an “embodied Tonnetz.” Example 6 displays a portion of her embodied Tonnetz, but, like Example 5, without conforming equivalence. For Brower, the verticality of the overtone series orients triads with their fifths above their roots and their thirds in between. Furthermore, metaphor theory posits that, on the conventionally oriented circle of fifths (matched to the twelve positions of the clockface), a pitch class thirty degrees (one hour) clockwise from another pitch (such as G from C) circle is “sharper” and “brighter” and therefore should be positioned “higher.” Brower maps the last two of these qualifiers to one another by citing “our experience of the brightness of the sky versus the darkness of the ground when turning our eyes upwards or downwards” (2008, 75).
[3.4] Additionally, she arranges the constituents of two triads or two keys in a parallel relationship (e.g., C major versus C minor) such that the sharper is both slightly above and to the right of the flatter. While the latter choice is arbitrary, the former choice is not. Placing C major higher than C minor on the embodied Tonnetz expresses a metaphorical height differential in two ways: in a closest registral realization, E in a C-major triad has a slightly faster pitch frequency than
[3.5] Despite their shared dark/bright parallels, Brower’s choice to otherwise differentiate the two axes of her embodied Tonnetz—the vertical axis conveys perfect-fifth relations of tension and relaxation, and the horizontal axis conveys semitonal relations of happiness and sadness—is made for good reason. Imagine if only the metaphor of “sharper” and “brighter” as “higher” were applied to both horizontal and vertical dimensions of her embodied Tonnetz.
Example 7. Vertigo, 0:30, shadow analysis
(click to enlarge)
[3.6] However, the visuals of the main title for Vertigo can. Bass illuminates the woman’s face with a single stationary light source well above but also slightly displaced from her center toward the left side of the woman’s face, or, equivalently, toward the right side of the cinematic frame. The angle of displacement is hard to measure precisely, as the shadows cast by facial protuberances—nose, lips, eyelashes—fall upon curved surfaces and are themselves angled or curved. On the still of Example 7, I approximate the angle to be 37 degrees, which is admittedly more than 14 degrees of Example 5’s skew. But the light is still farther up than it is to the woman’s left. Therefore, since Bass’s camera motions from station to station are mostly orthogonal to the cinematic frame, these motions clearly fall into one of two categories: horizontal motion that moves minimally toward or away from the light source, and vertical motion that moves considerably toward or away from the light source. Respectively, these two orthogonal motions correspond well to perfect-fifth motion, which metaphorically brightens or darkens by some minimal unit, and motion by some intervallic compound of n perfect fifths, which metaphorically brightens or darkens by n units. As the angle of Bass’s lighting is somewhat indeterminate, so should n also be. However, Bass’s videography captures contiguous parts of the woman’s face, as naturalistic depiction requires, and these parts progress continuously away from or toward the light source. Since Herrmann’s harmonies for Vertigo’s main title are built from perfect fifths and thirds, any correspondence between them and Bass’s camera stations will be best served by an n of 3, 3.5, or 4, because this generates a Tonnetz in which the constituents of tertian harmonies are likewise contiguous and continuous in their relation to the light source.
- An n of 3 produces a Tonnetz of orthogonal perfect fifths and minor thirds and a displacement angle of around 18 degrees (arctan of 1/3), like the graphs by Lerdahl and Hoeckner in Example 3, but flipped.
- An n of 3.5 produces a Tonnetz of triangulated perfect fifths, minor thirds, and major thirds and a displacement angle of 16 degrees (arctan of 1/3.5), like the graphs by Gollin and Harrison in Example 3, as well as the design Richard Cohn consistently employs in his 2012 book Audacious Euphony.
- An n of 4, as aforementioned, produces a Tonnetz of orthogonal perfect fifths and major thirds and a displacement angle of around 14 degrees (arctan of 1/4), like the graph in Example 5.(8)
[3.7] To summarize, in the first part of Vertigo’s main title, there are camera motions both minimally (right and left) and considerably (up and down) toward and away from the single light source. There are also harmonic progressions both minimally (perfect-fifth-related) and considerably (third-related) sharpward and flatward. The metaphor of musically-sharp-is-visually-bright suggests aligning the two dimensions of these two spaces, especially since the light source is at an angle that approximates the ratio between the minimal and considerable motions. It is important to recognize that cardinal directions like left or up, while mnemonically useful, are independent of this metaphorical alignment and my correspondences that rely upon it: the filmic image could be inverted or rotated without altering any of my arguments, which rely solely on how Bass’s camera and Herrmann’s chords are moving closer to or farther from something that is brighter.
[3.8] Theories of function corroborate a two-dimensional parametrization of musical sharpness and flatness. Minimal sharpward and flatward motion as transposition up and down by perfect fifth typically matches a unit functional change (usually dominant or subdominant to tonic, or vice versa) but no chromatic change, as perfect-fifth motion strays less, if at all, from a diatonic center. Third motion inverts the size of these two vectors: the most quintessentially chromatic moves between tertian harmonies use root motion by thirds. Yet, in Hugo Riemann’s theory of harmonic syntax, such motion best preserves harmonic function, as encapsulated in his parallel (e.g., Sp) and counterparallel (e.g., 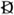 ) modifiers. Cohn has extended this idea to major thirds in particular, speculating that, for Romantic-era music, triads a major third apart belong to the same functional category (1999). Following this conjecture, I will use the n=4 Tonnetz orientation, because this supports the idea of breaking down any harmonic motion into pure functional changes and pure chromatic changes, matching how the mostly orthogonal camera motions can be easily broken down into minimal or considerable motions toward or away from the light source.
) modifiers. Cohn has extended this idea to major thirds in particular, speculating that, for Romantic-era music, triads a major third apart belong to the same functional category (1999). Following this conjecture, I will use the n=4 Tonnetz orientation, because this supports the idea of breaking down any harmonic motion into pure functional changes and pure chromatic changes, matching how the mostly orthogonal camera motions can be easily broken down into minimal or considerable motions toward or away from the light source.
4. Correspondence #1: Camera and Chord Progressions
Example 8. Five harmonies of Herrmann’s “Prelude” on a portion of a Tonnetz
(click to enlarge)
[4.1] All of Herrmann’s main title music uses only ten of the twelve pitch classes: pcs 1 (
Example 9. The five camera positions and zooms of the main title of Vertigo
(click to enlarge)
[4.2] Setting aside chronology for the moment, the union of the five camera stations in the first part of Bass’s main title—overlaid in Example 9 for immediate comparison—and the union of the five harmonies in Example 8 bear a strong resemblance. In both cases, both the brightest (upper right) and darkest (lower left) corners are skirted. The music avoids continuing from chord B2 or B4—chords with a B—to a chord with a functional
[4.3] The order in which these chords and stations progress in time also match to a significant degree. In both cases, the progression from the first to the second event is a minimally darkening motion, which happens to be toward the left in both Examples 8 and 9. For the image, the move from the side of the woman’s face to the tight shot of her lips is mostly lateral to the light source, but still away from it to a small degree. For the music, this means moving from the locally asserted tonic of
[4.4] Moreover, and independent of motions of root and camera, in both music and image the vertical extent starts at its maximum and then immediately narrows in this initial progression. Herrmann’s chord A embeds an augmented triad—a stack of two major thirds—that binds together in a single chord the broadest span between sharpest and flattest notes of all five chords, as shown in Example 8 with the vertical dotted double-headed arrow connecting
[4.5] The visual and musical progressions from the second to the third event of each also closely match. For the image, the move straight up from the woman’s lips to her eyes is a marked motion nearly directly, but not exactly, toward the light source. For the music, the
[4.6] Moreover, and independent of motions of root and camera, in both music and image the horizontal extent expands to its maximum when the third event is achieved. As aforementioned, Station 1 displays the greatest vertical span of the woman’s face. However, even though Station 1 is zoomed out the most, due to its placement of the woman’s face considerably off center, Station 1 does not show the most horizontal distance on the woman’s face. Rather, this maximum is saved for Station 3’s view of the woman’s two eyes, as shown in Example 9 by the horizontal dotted double-headed arrow connecting the left and right side of the frame. The woman’s left eye is somewhat more illuminated than her right; in fact, this station affords the best opportunity to witness horizontal contrast anywhere on the woman’s face. However, her two eyes are also mostly equidistant from the light source. Likewise, chord B2’s major ninth added to an A-minor triad is the one chord of the five most expanded in the functional dimension: it contains not only the usual root-as-tonic and fifth-as-dominant, but also a ninth(-or-second)-as-double-dominant. The vertical dotted double-headed arrow connecting the pitches A and B in chord B2 of Example 8 signifies this maximal bright-dark expanse along the fifth-based functional continuum. However, unlike chord A and its embedded augmented triad, this expansion is diatonic, lacking chord A’s chromatic vividness.
[4.7] Bass’s next two camera stations (4 and 5) and Herrmann’s next two harmonies (B3 and B4) do not emulate one another as closely as the preceding three of each. However, both harmonic and camera progressions slow down at this point, mostly hovering around territory already visited rather than relocating to new territory. In Bass’s video, Station 4 zooms in on the woman’s right eye, and Station 5 slightly zooms in further. On the one hand, chord B2’s farthest reach to the upper-left with the A—the pitch most coloristically bright but the most functionally dark (plagal)—matches Bass’s arrival at Stations 4 and 5, the part of the filmed face closest to the light source vertically but farthest from it horizontally. On the other hand, the progression from chord B3 (C-minor triad) to chord B4 (C-major-seventh chord) not only retreads a portion of the pitch content of chords B1 (
[4.8] The two progressions of five camera stations and five chords homologized with one another in Correspondence #1 take place largely at different times: the preceding chords A1–A5 accompany the five homologized camera stations, and the five homologized chords (A, B1–B4) take place only after the camera has settled into Station 5. While this temporal displacement may appear to be a setback for Correspondence #1, it plays a crucial role in how this correspondence relates to the narrative that follows Vertigo’s main title, which I will share at the end of my article.
5. Correspondence #2: Figure and Chord Rotations
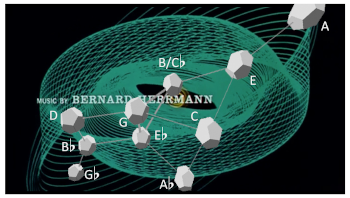
[5.1] By contrast, my second correspondence involves events more simultaneous in the second half of Vertigo’s main title: the chords A through B4—the same scrutinized for Correspondence #1—and Bass’s Lissajous figures. Nine such figures of different colors and designs follow one after the other on average every twelve seconds, usually overlapping each other a bit and each growing in size as if they are directly approaching the viewer from the center of the frame. Most have a rotational symmetry of two—that is, a 180° rotation along with the trivial 0° rotation preserve the shape of each—but two of them have a much higher degree of rotational symmetry (35, to be exact) and are therefore basically “circular.” Excluding one, these figures spin around this center: all of them counterclockwise, except one that spins clockwise. The spinning figures rotate at a speed of one rotation every six seconds, so they complete at least one rotation.
[5.2] Cohn (2012, 113) calls the group of three major triads and three minor triads that all share a single pitch class a neighborhood. For example, the triads of
[5.3] Chords A, B1, B2, and B3 also correspond in a different manner to the animated Lissajous curves via rotation as well as revolution. As shown on Example 8, chord A—the
[5.4] Likewise, chords B1 and B3—the
[5.5] I concede that this second observation of rotation is less distinctive: all major and minor triads look like L-triominos on the n=4 Tonnetz. I also concede that both pairs of chords could be equally geometrically interpreted as flips of one another as well as rotations of one another, since both the T-tetromino and the L-triomino are not chiral, which means that they are inversionally symmetrical. However, more distinctive is the fact that both rotations use the same fulcrum, indicated with a dot in Example 8 in between the pitch classes C and
- Chord A can be generated by first combining
E♭ with a note a perfect fifth brighter (B♭ ), then, from that note, adding the notes a major third both brighter (D) and darker (G♭ ). Chord B2 can be generated by first combining C with a note a major third brighter (E), then, from that note, adding the notes a perfect fifth both darker (A) and brighter (B). - Chord B1 can be generated by first combining
E♭ with a note a perfect fifth darker (A♭ ), then, from that note, adding a note a major third brighter (C). Chord B3 can be generated by first combining C with a note a perfect fifth brighter (G), then, from that note, adding a note a major third darker (E♭ ).(11)
[5.6] Lastly, the dot in Example 8 is located in the very center of the ten-pc pitch network, if the very center is defined either as the center of the smallest square into which this particular graph would be inscribed, or the middle of the network’s longest main diagonal, the minor-third chain from A to
[5.7] Chords B4 and B5 (
[5.8] As is well documented, enharmonic equivalences like these muddle the definitions of sharp, flat, bright, dark, and center upon which the first two correspondences have relied, rendering these concepts less usable. In fact, this is the reason that my first two correspondences have stopped just short of chord B5. Although the third correspondence will draw upon these equivalences that chord B5 instigates, chord B4 can still contribute to the second correspondence. As a major-seventh chord, which assumes the shape of a square on the n=4 Tonnetz of Example 8, it can be understood as a rotation of itself. This rotational invariance can be heard and conceived by choosing any note, and generating the rest of the notes using equal parts brightening and darkening intervals, and equal parts perfect-fifth and major-third intervals distributed crosswise. For example, to make chord B4, start with a C, then move by brightening major third (to E), brightening perfect fifth (to B), darkening major third (to G), and, to bring it full circle, darkening perfect fifth (back to C). To be sure, its pivot point—the spot between E and G on Example 8—is not the same as that which pivots chord A to B2, and B1 to B3—the spot between C and
6. Correspondence #3: Figure- and Pitch-Space Topologies
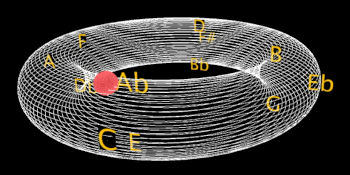
[6.1] Toward the end of my argument for the second correspondence, I proposed that the progression from chord B4 to chord B5 is the first progression in the main title to invoke an enharmonic synonym, specifically, B =
Example 10. A rendering of Example 8 with
(click to enlarge)
[6.2] However, I believe that, for an analysis of this music, such a default conversion goes too far. The graph atop Example 10 imposes the equivalence between the B of chord B4 and the
[6.3] I will articulate two such absences of this kind. First, the only two pitch classes of the ten in Herrmann’s prelude that span a perfect fifth or fourth but are not adjacent in Examples 8 or 10 are D and A. Herrmann’s choice and ordering of harmonies keeps these two pitch classes from forming any perfect-fifth-related bond, either functional between successive harmonies (one as dominant or subdominant to the other) or as consonant within a harmony.
Example 11. Recomposition of B section, with new bass note, chord-root analysis, and syntonic loop
(click to enlarge)
[6.4] Second, as mentioned earlier, Herrmann’s prelude is missing an F. Its subposition under chord B5, producing an F half-diminished seventh chord, would be extremely proper and conventional for reasons both less and more germane. Less germane to my third correspondence is how this F would produce, in its exact transposition, the famous “Tristan chord” that generally represents in microcosm the Wagnerian idiom Herrmann appropriates for this movie and a chord Herrmann specifically uses later in the movie, particularly when Judy first appears dressed as Madeleine to Scottie on the opposite end of a hotel hallway. More germane to my third correspondence is how this F would pull together the left and right sides of Examples 8 and 10 into a looped series of pitch classes (
[6.5] Accordingly, as shown with the still in the background of Example 10, Bass does not display Lissajous designs uniformly, which, in their standard form like that of Video Example 1, typically show a continuous curving line that closes into a loop. Rather, by shading their perimeters in particular and zooming in so much that they exceed the frame, Bass’s titles concentrate on central circularities while allowing the peripheral loops of the original Lissajous curves to fade into non-continuous tendrils or hooks, some cut off at a point by the edges of the screen. This hybridization of infinite cyclicity and finite linearity in Bass’s treatment of Whitney’s curves also appears in a similar fashion in the part-plane, part-torus Tonnetz atop the still of Example 10. Just as this network completes the shorter major-third loop but not the longer syntonic loop or even longer perfect-fifth cycle, the complete loops that the viewer sees most clearly in Vertigo’s Lissajous designs are small with a higher curvature and the broken or faded loops are larger with a lower curvature. The enharmonic equivalence of pitch class 11 puts this small major-third loop in the middle of the graph, with notes extending outward both in ascent and descent by perfect fifth away from it, with the ascending perfect-fifth side winnowing from
7. Correspondences with Vertigo’s Narrative
[7.1] The merger of central closed loop and marginal open hooks in both music and visuals suggests an uneasy amalgam of an imprisoning interior cycle and the longing for a sense of orientation. This amalgam readily describes both the plight and aspirations of Vertigo’s protagonist: although James Stewart’s Scottie is afflicted by acrophobia-generated vertigo through much of the interior of the film, the film begins briefly with him chasing a crook over San Francisco rooftops, before the harrowing event that produced his condition, and ends with him looking down from the bell tower of a mission church, now cured of his vertigo. This final shot of the film features an alternation between chords B1 and B4 with the same melodic notes from the prelude. The concluding B1-B4 succession—the last harmonic progression in the entire film—strips chord B4 of its seventh B, leaving a C-major triad to finish the movie. On its own, this
[7.2] This is not the first time that the B music is heard after the main title. Many interpreters call this music—the melodic presentation, often twofold, of the D-C-B-E treble pitches, plus the harmonies B1 through B4—the film’s “Love theme.” It appears throughout the film in conjunction with Scottie’s adoration of Madeleine, sometimes with slight adjustments to the harmonies, or lower-neighbor adornment of the second note (D-CBC-B-E), or both. For instance, Herrmann distributes five separate instances of this theme among an exudation of other love-associated musical ideas into the single cue entitled “Scene d’Amour,” in which Judy completes her transformation into the likeness of Madeleine, fulfilling Scottie’s obsession.
[7.3] My first correspondence anticipates this association. Bass’s visuals divide the main title into two successive parts: the camera motions across the woman’s face, and the Lissajous rotations. Herrmann’s music divides into two alternating parts: the A harmonies with the
[7.4] In a 2017 essay, Kevin Clifton hears multiple musical doubles in Herrmann’s main title for Vertigo, and relates them to the film’s “many double identities
[7.5] Contrary motions, voice exchanges, melodic repetitions, enharmonic respellings—these musical relationships certainly invite cross-domain mapping, but their relative frequency throughout Herrmann’s scoring in particular and Western music in general makes the mappings less distinctive. My audiovisual correspondences also resemble doubles, albeit between media instead of within a medium. Moreover, my close, even fussy, attention to details in arguing for these three correspondences is intended not only to achieve a relatively high distinctiveness, but also to strengthen the correspondence between the audiovisual correspondence and the film’s story.
[7.6] Just as the main title’s visuals (camera motions across a face, then rotating Lissajous figures) and music (A chords, then B chords) divide into two parts, Vertigo’s narrative divides into two parts. In the first part, Scottie’s old college acquaintance Gavin Elster hires Scottie to watch and record every detail of his wife Madeleine as she travels in a near-trance around San Francisco. Scottie falls in love with Madeleine, but she does not reciprocate, and she dies. In the second part, Scottie meets Judy, recreates her into the likeness of Madeleine, and realizes that Judy, by pretending to be Madeleine, conspired with Elster in the first part to cover up Elster’s murder of his actual wife. Judy reciprocates Scottie’s love, but then dies accidentally.
[7.7] I interpret Bass’s camera motions in the first part of Vertigo’s main title as reflecting Scottie’s behavior during the first part of Vertigo’s story: watching and recording every minute detail of Madeleine. Bass’s main-title camera stations parallel Scottie’s observation stations: restaurant, flower shop, art gallery, cemetery, San Francisco Bay. I interpret Herrmann’s harmonic progression in the second part of Vertigo’s main title (B chords) as reflecting Scottie’s behavior in the second part of Vertigo’s story: a re-creation of this detailed recording of Madeleine in a new form. With each harmonic shift among Herrmann’s main-title B chords—a slight fifth-based darkening, then a significant third-based brightening, and so forth—there increases the potential for realization that one has born witness to these motions before, but through the sense of sight, toward images held at a distance. However, recast in sound, these motions envelop the witness, reduce this distance to zero—physically, psychologically, and emotionally—and transfigure the original relationship. Therefore, as Herrmann asserted for the main title of Psycho, this two-part image-to-sound transformation within the main title of Vertigo sets the stage for the two-part Madeleine-to-Judy drama to follow.
8. Conclusion
[8.1] In this article, I have proposed three ways in which Bass’s and Herrmann’s contributions to the main title of Vertigo correspond with one another: through motion from one position to another within a space, through transformations of objects situated in this space, and through the particular topological contortion of this space itself. I have also suggested how these correspondences relate to Vertigo’s narrative. As aforementioned, one could analyze and interpret Bass’s main-title visuals, or Herrmann’s main-title music, or Vertigo’s narrative independently from the other artworks. Nonetheless, one point of view holds that analysis and interpretation of an artwork inherently involves other artworks, including those outside of the original medium. The literary critic Harold Bloom once claimed that “the meaning of a poem can only be another poem, a poem not itself,” (1973, 70) and the music theorist David Lewin (1986) recommended revising this to “the artwork can only be perceived in the making of another artwork, an artwork not itself” (381, paraphrasing), providing multiple examples in which the two artworks belong to different modes of expression. From this perspective, Herrmann perceived Bass’s visuals and Hitchcock’s film by making musical art, and both artists perceived Vertigo’s narrative by making musical and visual art. By extension, those seeking to better understand a multimedia work are well justified in perceiving Herrmann’s, Bass’s, or Hitchcock’s art by remaking in another manner of presentation—performing, recomposing, drawing, animating, re-enacting—not only Herrmann’s, Bass’s, or Hitchcock’s artwork but also the other accompanying artworks that were created in response to its perception. In an important way, multimedia gives us a readymade example of the kind of analysis that Lewin championed, one with re-creation at its heart.
Scott Murphy
University of Kansas
School of Music
1530 Naismith Dr Rm 220
Lawrence, KS 66045-3102
smurphy@ku.edu
Works Cited
Adorno, Theodor, and Hanns Eisler. 2005 [1947]. Composing for the Films. Continuum.
Auiler, Dan. 2000. Vertigo: The Making of a Hitchcock Classic. Macmillan.
Bamberger, Jeanne. 1986. “Cognitive Issues in the Development of Musically Gifted Children.” In Conceptions of Giftedness, ed. Robert J. Sternberg and Janet E. Davidson, 388–413. Cambridge University Press.
Blim, Dan. 2013. “Musical and Dramatic Design in Bernard Herrmann's Prelude to Vertigo (1958).” Music and the Moving Image 6 (2): 21–31. https://doi.org/10.5406/musimoviimag.6.2.0021.
Bloom, Harold. 1973. The Anxiety of Influence. Oxford University Press.
Brower, Candace. 2000. “A Cognitive Theory of Musical Meaning.” Journal of Music Theory 44 (2): 323–79. https://doi.org/10.2307/3090681.
—————. 2008. “Paradoxes of Pitch Space.” Music Analysis 27 (1): 51–106. https://doi.org/10.1111/j.1468-2249.2008.00268.x.
Brown, Royal S. 1994. Overtones and Undertones: Reading Film Music. University of California Press. https://doi.org/10.1525/9780520914773.
Brown, Stephen C. 2003. “Dual Interval Space in Twentieth-Century Music.” Music Theory Spectrum 25 (1): 35–57. https://doi.org/10.1525/mts.2003.25.1.35.
Clifton, Kevin. 2017. “The Anatomy of Aural Suspense in Rope and Vertigo.” In Partners in Suspense: Critical Essays on Bernard Herrmann and Alfred Hitchcock, ed. Steven Rawle and K. J. Donnelly, 39–94. Manchester University Press. https://doi.org/10.7228/manchester/9780719095863.003.0004.
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15 (1): 9–40. https://doi.org/10.2307/854168.
—————. 1999. “As Wonderful as Star Clusters: Instruments for Gazing at Tonality in Schubert.” 19th-Century Music 22 (3): 213–32. https://doi.org/10.2307/746799.
—————. 2004. “Uncanny Resemblances: Tonal Signification in the Freudian Age.” Journal of the American Musicological Society 57 (2): 285–323. https://doi.org/10.1525/jams.2004.57.2.285.
—————. 2012. Audacious Euphony: Chromaticism and the Triad’s Second Nature. Oxford University Press.
Cook, Nicholas. 1998. Analysing Musical Multimedia. Clarendon Press.
Cooper, David. 2001. Bernard Herrmann’s Vertigo: A Film Score Handbook. Greenwood Press.
—————. 2005. Bernard Herrmann’s The Ghost and Mrs. Muir: A Film Score Guide. Scarecrow Press.
Eisenstein, Sergei. 1942. The Film Sense. Translated by Jay Layda. Harcourt, Brace, and Company.
Gollin, Edward. 2000. “Representations of Space and Conceptions of Distance in Transformational Music Theories.” PhD diss., Harvard University.
—————. 2009. “Combinatorial and Transformational Aspects of Euler’s Speculum Musicum.” In Mathematics and Computation in Music, Vol. 37, ed. Timour Klouche and Thomas Noll, 406–11. Springer. https://doi.org/10.1007/978-3-642-04579-0_40.
Harrison, Daniel. 2002. “Nonconformist Notions of Nineteenth-Century Enharmonicism.” Music Analysis 21 (2): 115–60. https://doi.org/10.1111/1468-2249.00154.
Herrmann, Bernard. 1980. “Bernard Herrmann, Composer.” In Sound and the Cinema, ed. Evan William Cameron, 117–35. Redgrave Publishing.
Hoeckner, Berthold. 2006. “Paths Through Dichterliebe.” 19th-Century Music 30 (1): 65–80. https://doi.org/10.1525/ncm.2006.30.1.065.
Huron, David. 2001. “What is a Musical Feature? Forte’s Analysis of Brahms’s Opus 51, No. 1, Revisited.” Music Theory Online 7 (4) https://www.mtosmt.org/issues/mto.01.7.4/mto.01.7.4.huron.html.
Imbrie, Andrew. 1973. “‘Extra’ Measures and Metrical Ambiguity in Beethoven.” In Beethoven Studies, ed. Alan Tyson, 45–66. W. W. Norton.
Karamath, Joel. 2001. “Overtures and Psychotic Symphonies.” Eye: The International Review of Graphic Design 39 (10): 40–49.
Klumpenhouwer, Henry. 2002. “Dualist Tonal Space and Transformation in Nineteenth-Century Musical Thought.” In The Cambridge History of Western Music Theory, ed. Thomas Christensen, 456–76. Cambridge University Press. https://doi.org/10.1017/CHOL9780521623711.016.
Lehman, Frank. 2018. Hollywood Harmony: Musical Wonder and the Sound of Cinema. Oxford University Press. https://doi.org/10.1093/oso/9780190606398.001.0001..
Lerdahl, Fred. 1994. “Tonal and Narrative Paths in Parsifal.” In Musical Transformation and Musical Intuition: Essays in Honor of David Lewin, ed. Raphael Atlas and Michael Cherlin, 121–46. Ovenbird Press.
—————. 2001. Tonal Pitch Space. Oxford University Press.
Lewin, David. 1986. “Music Theory, Phenomenology, and Modes of Perception.” Music Perception 3 (4): 327–92. https://doi.org/10.2307/40285344.
—————. 1993. Musical Form and Musical Transformation: 4 Analytic Essays. Yale University Press.
Murphy, Scott. 2009. “An Audiovisual Foreshadowing in ‘Psycho’.” In Terror Tracks: Music and Sound in the Horror Film, ed. Philip Hayward, 47–59. Equinox Publishing.
—————. 2018. “Durational Enharmonicism and the Opening of Brahms’s ‘Double Concerto’.” In Brahms and the Shaping of Time, ed. Scott Murphy, 260–93. University of Rochester Press. https://doi.org/10.2307/j.ctvbtzpqg.13.
Prendergast, Roy. 1992. Film Music: A Neglected Art, 2nd ed. W.W. Norton.
Ross, Alex. 1996. “The Music That Casts Spells of Vertigo.” New York Times, October 6: 17–18.
Smith, Kenneth. 2018. “Vertigo’s Musical Gaze: Neo‐Riemannian Symmetries and Spirals.” Music Analysis 37 (1): 68–102. https://doi.org/10.1111/musa.12109.
Sullivan, Jack. 2006. Hitchcock’s Music. Yale University Press.
Whitney, John. 1980. Digital Harmony: On the Complementarity of Music and Visual Art. Byte Books.
Footnotes
1. The original manuscript is part of the Bernard Herrmann Papers collection at the University of Santa Barbara. Published reductions vary regarding details of pitch content. Dan Blim (2013) names chord A4, minus the recurrent high arpeggios of Example 2, the “Prelude” chord. His analysis of this chord notes how the absence of the pitch class D brings it just short of mirror symmetry, although Herrmann’s score calls for this note in the first trumpet and first oboe parts, even before it occurs again as part of the upper arpeggios in the following measure. In chord B2, Frank Lehman (2018, 154) has no B, although the pitch is sustained throughout this harmony in the third trumpet, second trombone, and vibraphone. This excision of the non-tertian B supports his observation that chords B1-B4 are isomorphic to an important four-chord progression in Hans Zimmer’s score for Inception, although he leaves in the non-tertian B of Herrmann’s chord B4, which also provides support for his isomorphism.
Return to text
2. As Kevin Clifton (2017, 44–45) astutely recognizes, these melodic seconds can be heard as horitontalizations of the harmonic seconds of D-C and
Return to text
3. Royal S. Brown (1994, 151) dubs the minor-major seventh as the “Hitchcock chord,” although David Cooper (2005, 39) recognizes Herrmann’s use of it before his partnership with Hitchcock.
Return to text
4. On the occasion of the 1996 theatrical release of a painstakingly restored Vertigo, Alex Ross (1996) wrote a review of Herrmann’s music, similarly claiming that, in the opening title sequence, “Herrmann has told us what the movie is about” (also quoted at the beginning of Smith 2018).
Return to text
5. As part of her study of the roles pattern matching and metaphor play in the production of musical meaning, Candace Brower (2000, 329) visually depicts the CYCLE image schema as both a closed circular directed path and as a sinusoidal waveform.
Return to text
6. To expound upon the structure of Video Example 1: each of two balls on the right and bottom of the video moves through a certain length of one-dimensional space using a sinusoidal function. The ball on the bottom moves through its length 5/3 more quickly than the ball on the right moves through its length. For example, at the 1.22-second mark, the ball on the bottom is at its most right, and the ball on the right is at its bottommost. At the 3.37-second mark, the ball on the bottom is at its leftmost, and the ball on the right is at its topmost. In between these times, the ball on the bottom has swept through its length five times, while the ball on the right has swept through its length three times. The ball in the middle then maps these two one-dimensional functions onto a two-dimensional space.
Return to text
7. David Lewin (1993, 46ff.), following Jeanne Bamberger (1986) uses the term “formal,” as opposed to “figural,” for a kind of spatial network representing this atemporal ground.
Return to text
8. This is also the orientation for Leonhard Euler’s Speculum Musicum (Gollin 2009), albeit with the major-third axis inverted from that of Example 5.
Return to text
9. Some scholarship (e.g., Cohn 2004) proposes that a diatonic default induces the interpretation of a semitonal interval, such as
Return to text
10. However, Herrmann does use this chord in very similar music later in the film. In the “Scene d’Amour,” Herrmann begins with chords B1 and B2 with the same melody above, but the bass note A has been removed from chord B2, leaving the notes C, E, and B, which together belong to the [015] Forte type and are a 90° rotation of chords B1 and B3.
Return to text
11. This manner of rendering a chord resembles Henry Klumpenhouwer’s (2002) spatial characterization of one form of nineteenth-century dualist thought: that the pitches of both major and minor triads can be generated from a source pitch using directed perfect fifths and major thirds. Dualists considered the source pitch as the root both for major and minor triads. My approach integrates this generative method with Brown’s (2003) system of spatial equivalences.
Return to text
12. Since Herrmann writes
Return to text
13. Something similar could be said of Blim’s (2013) mirrors and spirals: rotational forms, for example, are quite common in both Herrmann’s music and Western music. My use of the word “distinctive” here and earlier refers specifically to David Huron’s (2001) use of the word as signifying a “greater salience compared to occurrences in other artifacts.”
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Fred Hosken, Editorial Assistant
Number of visits:
8425