Klangfarbenmelodie in 1911: Timbre’s Functional Roles in Webern’s Opp. 9 and 10*
Matthew Zeller
KEYWORDS: Timbre, Texture, Klangfarbenmelodie, Progression, Anton Webern, Arnold Schoenberg
ABSTRACT: Anton Webern’s pre-World War I aphoristic works sometimes appear to defy comprehension, but through the lens of Klangfarbenmelodie organizing principles of this music come into focus. Klangfarbenmelodie is a multifaceted principle of musical organization. It is how Klangfarbenfolgen—timbral progressions—are structured into music. This article explores timbral progressions in Webern’s music and some of the types of timbre-based musical logic that organize them. Timbre and pitch are simultaneous, codependent, and symbiotic. With the notion of timbre as the totality of musical tone, this article examines how timbral-registral space is employed to compose timbral trajectories like expansions, contractions, and crossing lines. In addition to drawing out timbral lines, the analyses focus on how timbre helps delineate pitch constructs, timbre’s role in structuring gesture and theme, and various types of timbral symmetry. Rather than a shift away from pitch analysis, this article proposes a repositioning toward the inclusion of timbre in analytic discourses.
DOI: 10.30535/mto.28.1.9
Copyright © 2022 Society for Music Theory
1. Introduction
[1.1] For Anton Webern, “The ultimate principle in the presentation of a musical thought is comprehensibility” (1958, 22). Generations of scholars have sought structural determinants in Webern’s music in aspects of pitch, but through the lens of Klangfarbenmelodie, timbre also contributes to compositional comprehensibility. Arnold Schoenberg’s theorization of Klangfarbenmelodie in his treatise Harmonielehre was published in 1911. That same year, Webern showed works to Schoenberg hoping his teacher and friend would find Klangfarbenmelodie in his new compositions. Examining Webern’s works from 1911 reveals organizational principles based on timbre that help bring musical logic in Webern’s aphoristic works into focus.
[1.2] Timbre and pitch are simultaneous, codependent, and symbiotic. Every timbre contains pitch, whether definite or indefinite, and every pitch is perceived in a timbre. A common challenge to considerations of timbre as a functional parameter in music is the misconception that it might undermine pitch. Timbre cannot and does not negate pitch, but neither does pitch eliminate timbre as a salient aspect of music. Considering timbre as a central concept in analytic narratives only adds to the possibilities; it does not take anything away. The notion of timbre-music that Schoenberg articulated, and that Webern elevated and refined, had an enormous impact on twentieth-century composition. But as of yet, timbre has failed to make the same level of impact in analytic discourses. In this article, I seek a repositioning toward the inclusion of timbre in conjunction with other parameters. Analyses incorporating both timbre and pitch can provide a more thorough understanding of the music than either parameter is capable of alone, and it also creates new ways to consider pitch.
[1.3] Timbre and pitch may coexist relative to each other, yet most analytical approaches only take one (pitch) or rarely the other (timbre) into account. The analytical corpus of studies on Webern’s free atonal works is largely pitch centric.(1) As Allen Forte puts it, “Pitch is assumed to have been Webern’s primary concern as he composed this music, with other musical parameters being significant, but conceptually secondary” (1998, 5–6). While this is but one author’s comment, it is generally representative of many previous approaches. Yet, Webern’s letters during the pre-World War I atonal (pantonal) period refer to timbre as an artistic domain of his compositional discourse. Writing to Schoenberg on August 23, 1911, Webern exclaims, “I can hardly wait to show you [op. 9, nos. 2–5] and my seven orchestral ‘chamber pieces’ [including op. 10, nos.1 and 4]. What will you say to them? They consist of a change of colors [Wechsel der Farben] in sixteenth and thirty-second notes” (Moldenhauer 1979, 195).(2) Again, Webern highlights timbre in op. 9, nos. 2–5 in a letter to Alban Berg dated May 23, 1913: “You must look closely at the instrumentation. You have to imagine very precisely these mixtures and alterations of the various bowing possibilities (col legno, sul ponticello, naturale, etc.)” (191).(3) Webern’s concern for timbre is evident in these letters.
[1.4] It is unclear exactly when Webern learned of Schoenberg’s theorization of Klangfarbenmelodie, but it seems likely that by the summer of 1911 Webern either read about it in Schoenberg’s pre-publication drafts of Harmonielehre or that the two composers had discussed the idea. The manuscript of Harmonielehre was completed in 1910, and Webern had read at least a portion of it by July 6 or 7, 1911, perhaps earlier (Puffett and Schingnitz 2020, 131–32). Once it was published, Schoenberg received his copy on December 5, 1911, and showed it to Webern the following day (133). Nearly a month earlier, Webern wrote about Klangfarbenmelodie to his friend, the musicologist and conductor Heinrich Jalowetz:
Zehlendorf, November 12, 1911
To Heinrich Jalowetz
. . .
Schoenberg very much likes my essay about him. Likewise, my new compositions. He had a great impression of them. He even wants to write something about them. He thinks that they are already a melody of timbres! I am happy! (Webern 1999, 175)(4)
The joy expressed in Webern’s letter to Jalowetz indicates the importance of Klangfarbenmelodie to him at the time. Though it is difficult to establish when or in what manner Schoenberg and Webern may have discussed Klangfarbenmelodie, it is a relatively straightforward task to identify the possible pieces Webern showed to his teacher in Berlin in 1911. The candidates are those referred to in the letter of August 23, 1911, above: Sechs Bagatellen für Streichquartett, op. 9, nos. 2–5, and 5 Stücke für Orchester, op. 10, nos. 1 and 4, as well as five other short orchestral works that are not published.(5) Through detailed analyses of op. 9, nos. 4 and 5 and op. 10, nos. 1 and 4, this article demonstrates how timbre functions as an organizational parameter in these works’ musical structure. But before proceeding to analytically parsing Webern’s works, I first examine the concepts of timbre and Klangfarbenmelodie.
2. Concepts: Timbre, Klangfarbenmelodie, and Klangfarbenfolgen
[2.1] Analyzing timbral function in Klangfarbenmelodie works raises two foundational questions. What is Klangfarbenmelodie? And even before that: what is musical timbre?
[2.2] Identifying timbre seems easy: it is what makes a violin sound like a violin and an oboe an oboe. It is also what makes my violin sound different from your violin. On the other hand, defining timbre is far more complex. There is something enlightening in the intentional imprecision of Isabella van Elferen’s (2021, 72) explanation, “In its most basic definition, timbre is musical difference.” According to psychoacousticians Kai Siedenburg, Charalampos Saitis, and Stephen McAdams, “Roughly defined, timbre is thought of as any property other than pitch, duration, and loudness that allows two sounds to be distinguished” (2019, 1). Yet, timbre also covaries with pitch and loudness (McAdams 2019a, 50–52). McAdams puts it simply, “Changing the pitch or the musical dynamic also changes the timbre” (2019b, 221). Albert S. Bregman explains:
[I]f we create a synthetic timbre by copying the spectral envelope (the shape of the spectrum) of an oboe playing a middle C. . . the result sounds like an oboe. However, if we synthesize a tone an octave above or below the original by using the original tone’s spectral and temporal envelopes, the result will not sound much like an oboe. This means that there are changes in the spectrum and dynamics of an oboe that are locked together with changes of pitch. (1990, 484–85)
Psychoacoustics confirms what can be readily discerned in the ordinary experience of listening to instruments: the timbre of an instrument changes as the pitch changes. For example, the quality of pizzicato
[2.3] For the purpose of this discussion, timbre is the totality of a musical tone (or any sound) not including pitch class or duration. This definition differs from some previous definitions in four substantial ways. First, it includes articulation. Different types of articulation such as legato and staccato (etc.), accents, or instrument specific articulations—for example, various on-the-string and off-the-string bowings for the violin family—all translate to changes in playing technique that alter timbre since they affect the mechanics of sound production and the resulting vibrations. Expressive markings may also fall into this category if they impact playing technique. Second, it includes the contribution of loudness. A tone played loudly on a violin has a different perceived sound quality than the same pitch and duration played softly on that same instrument. The timbre of the instrument changes as playing force is modulated by the performer because the forces applied to the sounding mechanism change. In this way, loudness is also a type of articulation. Third, it takes spatial location into account. As location of a sound source changes relative to the listener, so does the perceived timbre. Even though the physical vibrations produced by the instrument may be identical in both locations, the sound waves’ transit to our ears is not.(6) Finally, and perhaps most importantly, this definition of timbre includes the registral aspect of pitch. It is necessary, here, to distinguish between pitch-in-register and pitch class. Pitch class is a relational convention based on octave equivalence applied to perceived fundamental pitches. The extent to which pitch class communicates information about an actual sounded tone and its perceived fundamental frequency is limited to the context of this relational system of classification. On the other hand, pitch-in-register describes aspects of the sounded tone and its perception by locating that pitch in the registral profile of its sounding timbre. As analysts, we can discuss pitch and timbre separately, but they always occur together in music. It is impossible to perceive a pitch without also hearing it in a timbre. Timbres can be perceived with a single fundamental, with multiple pitches as a multiphonic, or with indefinite pitch. Reuniting timbre with its registral attributes in analytic discourse offers the opportunity to create deep and rich musical interpretations.
[2.4] Musical tones (sounds) are never just one or another parameter; they always have the attributes of timbre, pitch (definite or indefinite), duration, loudness, and spatial location simultaneously. This understanding of the musical tone leads to the practical approach that a musical tone (sound) is a timbre that contains pitch (definite or indefinite) and lasts a duration. This view resembles Schoenberg’s understanding of tone production and perception as expressed in Theory of Harmony when he was theorizing Klangfarbenmelodie. According to Schoenberg:(7)
In a musical sound (Klang) three characteristics are recognized: its pitch, color (timbre), and volume.. . . the tone becomes perceptible by virtue of tone color, of which one dimension is pitch. Tone color is, thus, the main topic, pitch a subdivision. Pitch is nothing else but tone color measured in one direction. (1978, 421)
From the Helmholtzian scientific viewpoint that Schoenberg understood, a tone is the collective result of its partials, including the fundamental and its overtones. Since the partials are not perceived individually by the ear, they are heard in their totality as the tone’s timbre. The fundamental is parsed separately because of its position (and often its strength) relative to the other partials in the tone; therefore, a pitch is heard as part of the tone. Schoenberg’s view that pitch is a subdivision of timbre is entirely justified by his understanding of the actual phenomena of tone production and perception: timbre is the totality of the tone, the fundamental with all of its partials; pitch is only the fundamental.
[2.5] Though I view it from the opposite side of the same lens, the notion of the totality of the tone is what allows Alfred Cramer (2002) to consider timbre as an aspect of pitch. Cramer counters the historical view of timbre and pitch as separate and distinct aspects of the musical tone through interpreting Helmholtzian Klang theory to mean that timbres are “not attributes of discrete tones, and they are not distinct from pitch” (2–3). For him, timbre results from pitch, both from perceived fundamentals and unperceived attributes (13–28). Cramer extends Schoenberg’s reliance on the overtone series to find that the “coloristic contribution of a tone [is] a function of its pitch” (30). Considering timbre as a part of pitch allows Cramer to frame Klangfarbenmelodie as a harmonic principle. According to him, “Klangfarbenmelodie [is] harmony composed of reified overtones” (3n13). But Schoenberg also relates the overtone series to timbre as we commonly call it. Of the “more distant overtones” Schoenberg (1978, 20) writes, “Even if the analyzing ear does not become conscious of them, they are still heard as tone color.” He describes timbre as the “musical ear” processing the “impression” of a tone rather than attempting “direct analysis” (20). Though pitch as an aspect of timbre and timbre as an attribute of pitch view the totality of the tone from different angles, both approaches agree that in the case of Klangfarbenmelodie works, “Pitches in their compositions were meant to form elements of acoustic wholes, originating not as points forming designs with one another in pitch-space, but as elements in progressions of coloristic sonorities” (Cramer 2002, 32). In Schoenberg’s words, “The tone is the material of the music. It must therefore be regarded with all its properties and effects, as suitable for art” (1978, 20). In this article, I follow Schoenberg and consider pitch contained within timbre, once again allowing Klangfarbenmelodie to be framed through what Schoenberg calls “simply ‘tone color’” (1978, 421).
[2.6] For over a century, commentators have grasped at the “melody” portion of the term, describing Klangfarbenmelodie as timbres connected sequentially through time—but Schoenberg (1911, 471) refers to such successions as Klangfarbenfolgen (timbres-sequences or timbres-progressions), conveniently translated as timbral progressions. After considering the potential for a system of describing and organizing timbres themselves, similar to theories used for systematizing pitch, Schoenberg concludes, “
Now, if it is possible to create patterns out of tone colors [Klangfarben] that are differentiated according to pitch [Höhe], patterns we call ‘melodies,’ progressions, whose coherence (Zusammenhang) evokes an effect analogous to thought processes, then it must also be possible to make such progressions out of the tone colors [Klangfarben] of the other dimension, out of what we call simply ‘tone color’ [Klangfarbe], progressions whose relations with one another work with a kind of logic entirely equivalent to that logic which satisfies us in the melody of pitches [Klanghöhen].(10) (Schoenberg 1978, 421)
Klangfarbenmelodie is the notion of organizing Klangfarbenfolgen.(11)
[2.7] The canonical narrative of Klangfarbenmelodie has been shaped by two competing definitions: (1) a quasi-static pitch with transforming timbres, and (2) the fragmentary, pointillistic distribution of linear pitch material among different timbres. Both approaches are methods of creating timbral progressions. In other words, these “two strands of Klangfarbenmelodie” as Jennifer Iverson (2009, 144–91) calls them, are actually two different styles of presenting Klangfarbenfolgen. The two stylistic strands—transformational and fragmentary, historically referred to as “Schoenbergian” and “Webernian” respectively—develop from different ways of creating and combining timbral progressions. The two styles can be effectively illustrated through Ligeti’s approach as described by Iverson. Ligeti distinguishes between composition with timbres and composition of timbres. Iverson’s (2009, 157–58) investigation shows that when Ligeti taught composition with timbre he used Webern’s opp. 6, 10, and 29 to elucidate how timbre delineates structure, while he used Schoenberg’s op. 16, no. 3, “Farben,” to illustrate composition of mixed sound colors, or, as we now prefer, blended (emergent or augmented) timbres. As she explains, “Ligeti both received and propagated this bifurcated historical narrative” (156). The canonical domino effect was initiated, transmitted, and proliferated throughout the twentieth century. Reframing our understanding of these two approaches as strands of timbral progressions—that is, of -folgen rather than -melodie—opens the possibility of new ways to hear and understand Klangfarbenmelodie in this music.
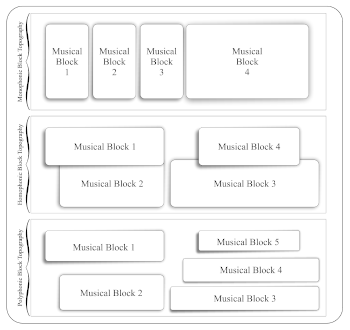
[2.8] This article explores timbral progressions in Webern’s music and some of the types of timbre-based musical logic he employs to organize them. New insights are possible by considering timbre in addition to pitch and building upon previous threads in the theoretical narrative such as chromatic aggregates, various types of symmetry, and wedge constructions. In addition to drawing out timbral lines, each of the subsequent analyses focuses on a different aspect of how timbre functions to provide structure and promote coherence and comprehensibility in Webern’s music. The analysis of Bagatelle no. 4 (op. 9) illustrates how timbre helps delineate pitch constructs such as chromatic aggregates, while that of the Fifth focuses on timbral lines and how they elucidate wedge constructions and inversional symmetry. Moving to op. 10, the analysis of Orchestral Piece no. 1 shows Webern’s use of retrograde symmetry to define form, and that of the Fourth explores timbre’s role in structuring gesture and theme. This investigation makes use of a new analytical apparatus to visualize analytical segmentations and stratifications in Webern’s music: block topography. Block topography arranges musical blocks—portions of music grouped according to salient analytical, compositional, or perceptual factors—into varying textures. The arrangement of musical blocks is organized into three topographical classifications:
- Monophonic block topography is the sequential presentation of musical blocks without overlap.
- Homophonic block topography is the simultaneous presentation of multiple musical blocks with a dependent foreground and background relationship.
- Polyphonic block topography is the simultaneous presentation of multiple musical blocks as independent lines or voices.(12)
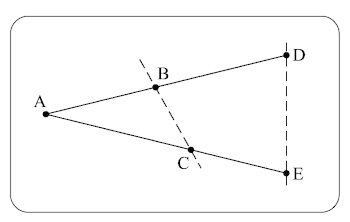
Example 1. Monophonic, homophonic, and polyphonic block topographies illustrating generic sample topographical arrangements of each type
(click to enlarge)
Example 1 shows generic sample configurations of the three topography types. In practice, block topographies are often complex and may be illustrated in mixed topographies as dictated by the music and the type of analysis undertaken. Block topography is not a method of deciding what gets analytically segmented, it is a method of visually depicting analytical choices. The boundaries of musical blocks may be determined through a variety of means such as traditional analytical categories, perception and auditory chunking, or any novel method.(13)
3. Timbral Considerations in Webern’s Op. 9 Bagatelles
[3.1] Throughout all six of Bagatelles, op. 9, there is an omnipresent elevation of timbre through playing technique. Above all, Webern’s extensive use of am Steg (sul ponticello) bowing is a concrete, physical move away from pitch primacy. Bowing at the bridge reduces the perception of the fundamental frequency in comparison to its overtones—so much so, that depending on the performer’s technique, a fundamental may not even be discernable.(14) Physicist Joe Wolfe (n.d.) has shown that the second, third, fourth, and sixth harmonics are much more prominent than the fundamental in at-the-bridge bowing. Patricia and Allen Strange describe it well: “The nebulous environment suggested by sul ponticello is created by the narrow boundary between a slight pitch and the production of a non-pitched timbre” (2001, 3). More accurately, bowing at the bridge can produce a timbre of indefinite pitch. Second, artificial and natural harmonics reduce the fundamental in favor of the much more prominent overtone sounded by the fingered node. Webern regularly employs artificial harmonics with resultant tones two octaves above the stopped fundamental. Pitches are still perceived, but compositional weight is placed on the timbre. If the pitch was all that Webern had wanted, there would be no need for the harmonics; the instruments could play the same absolute pitches in pure tones. The timbral contrast between tones in harmonics and those that are not draws attention to the shift in color. In the Bagatelles, harmonics help to elevate timbre to a compositionally salient position.
[3.2] Several other techniques also work to promote timbre’s saliency. Webern’s extensive use of mutes is a physical reduction of sound across many of its properties. When mutes are employed in music, the perception of pitch and duration are largely unaffected, but timbre is accentuated as a manipulated compositional parameter. Both Bagatelles analyzed below are performed entirely with mutes (mit Dämpfer). Playing at the fingerboard (am Griffbrett) also changes the spectral characteristics of the tone. It does not reduce or mask the fundamental in the same way playing at the bridge does, but it moves the sound away from prototypical unmodified arco tones. Tremolo de-emphasizes pitch by creating a constant state of acoustic attack, eliminating the more stable sustain portion of the tone’s ADSR (attack-decay-sustain-release) envelope. In combination with am Steg, tremolo at the bridge heavily masks the fundamental pitches sounded by the technique. Finally, Webern’s instruction an der Spitze—at the tip [of the bow]—shows the familiarity he had with string instruments and his insight into timbral control. By playing at the tip of the bow, its weakest point, additional bow pressure may be required from the performer. This increase in pressure also increases the amount of bow noise present at the beginning of each stroke. Playing at the tip is yet another, albeit more subtle, way to emphasize timbre.
[3.3] Many approaches to Webern’s op. 9 have struggled to make sense of the Bagatelles. In his 1932–33 lectures, Webern famously said, “About 1911 I wrote the ‘Bagatelles for String Quartet’ (op. 9).
4. Op. 9, No. 4
Example 2. Webern, op. 9, no. 4, first thirteen tones
(click to enlarge)
Example 3. Webern, op. 9, no. 4, Violin II, mm. 1–3
(click to enlarge)
[4.1] It is enlightening to begin this timbre-based study with a short discussion of pitch. Bagatelle no. 4 contains two aggregates of chromatic saturation governed by timbre and musical phrasing. There only two
Example 4. Webern, op. 9, no. 4, Blocks 1 and 2 texturally stratified in polyphonic block topography
(click to enlarge)
[4.2] Taking timbre into account, the composer’s notated phrasing, auditory streaming, and timbral progressions all dictate that Violin I’s am Steg
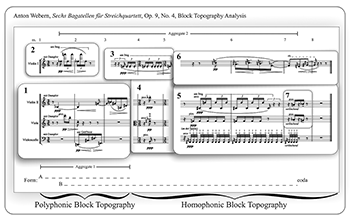
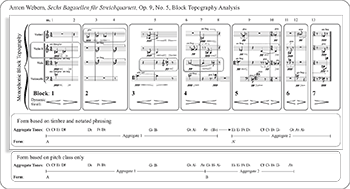
Example 5. Webern, op. 9, no. 4, block topography analysis
(click to enlarge)
Example 6. Webern, op. 9, no. 4, Blocks 3–4 in homophonic block topography
(click to enlarge)
Example 7. Webern, op. 9, no. 4, Blocks 5–6 in homophonic block topography
(click to enlarge)
[4.3] Timbre functions to promote Block 2’s independence from Block 1, and to connect it with the music to come. Throughout the work, Violin I is texturally stratified from the other three voices. Example 5 depicts the complete block topography of Bagatelle no. 4. The musical blocks are numbered in order of their entrance. The work’s mixture of polyphonic and homophonic block topographies is illustrated by simultaneous blocks that do not overlap (polyphonic) and those that do (homophonic). Blocks 1–2 retain their co-equal textural independence, but after that a foreground-background texture develops. Blocks 3–4 (mm. 3–5) combine to create a homophonic texture with am Steg portato foregrounded over the not-am Steg emergent timbre of pizzicato tenuto combined with harmonic tenuto marcato (Example 6). The two blocks also create a tetrachord of semitonal pitch class pairs: [
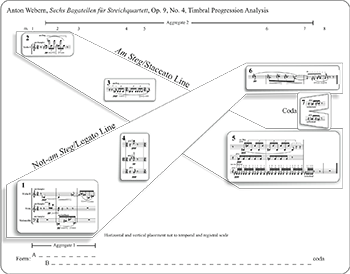
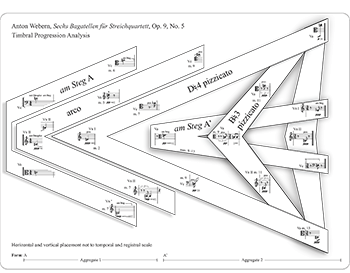
Example 8. Webern, op. 9, no. 4, timbral progression analysis
(click to enlarge)
[4.4] In Bagatelle no. 4, two crossing timbral lines emerge to dominate the texture. Slightly rearranging the orientation of the musical blocks illustrates the timbral lines and their registral trajectories (Example 8). Characterized by their timbres and articulations, the two contrasting lines are termed the “am Steg/staccato” and “not-am Steg/legato” lines. The am Steg/staccato line (Blocks 2, 3, and 5) is governed by its namesake timbre, but also includes pizzicato and arco staccatissimo harmonics. Its articulations involve an aspect of disconnectedness. The oscillating am Steg music, even though it is a slurred gesture, forms a cohesive timbral line with the repeated staccato tones for two reasons. First, bowing at the bridge aligns the oscillating gesture with the repeated staccato tones of Block 3 (mm. 3–5). Block 3 brings am Steg down from its upper reaches to a middle register, connecting the first violin in mm. 1–2 with the second violin in mm. 5–6. Second, the registral leap within the gesture separates the tones. Probably not coincidentally,
[4.5] The extended downward plunge of am Steg/staccato line is mirrored by its counterpart: the not-am Steg/legato line (Blocks 1, 4, and 6) which is characterized mainly by slurred arco in both natural (including am Griffbrett) and harmonic tones with occasional tenuto pizzicato and one instance of tenuto marcato harmonics. The not-am Steg/legato line mounts a drastic ascent from
Example 9. Webern, op. 9, no. 4, Block 7, coda combining pizzicato staccato and pizzicato tenuto
(click to enlarge)
Example 10. Webern, op. 9, no. 4, Block 7, coda as an expanding wedge
(click to enlarge)
[4.6] Connecting the am Steg/staccato timbral progression through the work helps unveil a coherent second aggregate. The form that emerges from this timbral reading of the work is a binary AB structure. Webern elides the B section with the A section by creating a type of symmetrical reflection between the end of the first aggregate (A section) and the beginning of the second (B section): the final two tones of the first formal section (Violin II arco
5. Op. 9, No. 5
[5.1] Having seen how timbre can help structure pitch, we turn to how it contributes to symmetry. Analytical investigations of symmetry in Webern’s music are plentiful.(20) As Kathryn Bailey (1991, 41) notes, Webern’s predilection for symmetrical constructions and their concealment are a vital part of his musical language. There are many kinds of symmetry in music. Types of pitch symmetry such as inversional or transpositional are often considered, but that does not preclude symmetrical constructions being composed of other parameters such as timbre or rhythm. In his study of Webern’s op. 11, Robert Clifford finds evidence of “Webern’s attention to symmetry, not so much in the pitch selection or aggregate groupings that many analysts have already noted, but rather in the registral dimensions and rhythmic placement of the musical events themselves” (2002, 199). Incorporating Clifford’s willingness to engage with symmetry outside traditional pitch approaches with Benjamin K. Davies’ (2007) insightful analytical approach of chromatic wedges allows us to come to a new understanding of how symmetry operates in Webern’s music. According to Davies, “Chromatic wedges do not form the material of op. 9 in any thematic or motivic sense. Rather, they are employed in what might be termed the structuring of tonal space: in short, they serve to configure the pitch-register field within which fully articulated textures coalesce” (29). He notes, “[A wedge] establishes connections, affinities, or latent symmetries that can be articulated or exploited in a variety of ways” (42). Of course, Davies has a traditional notion of pitch in mind, but since pitches are contained within timbres, this line of thinking can be extended to include the totality of the tone.
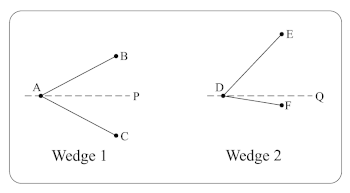
Example 11. Symmetrical and asymmetrical wedges
(click to enlarge)
Example 12. Transversal wedge pairings
(click to enlarge)
[5.2] Wedges are related to inversional symmetry, but they are not the same. In wedges, lines extend from or converge in a vertex—the point at which two or more lines, facets, or planes meet. Vertices bear resemblance to axes of symmetry, around which bodies rotate, but the two are not synonymous as wedges are not necessarily symmetrical. For instance, Wedge 1 in Example 11 is symmetrical about axis P, while Wedge 2 is not symmetrical about axis Q. Inherent in the two-dimensional wedges employed in music analysis is some sort of height differentiation in relation to the vertex. Of course, pitch height in reference to an axis of inversional symmetry is often employed. But since pitch-in-register is an aspect of timbre, there is also a registral-height dimension of timbre that allows for it to become a compositionally salient characteristic of wedge components through expanding or contracting registral manipulation of timbral pairs. As will be shown in the Fifth Bagatelle’s wedge expansions and contractions, Webern largely maintains timbral similarity between corresponding points, or transversal wedge pairs. (In geometry, a transversal is a line that intersects at least two other lines.) As used here, a transversal wedge pairing is the correspondence of two musical events that create an analytical coupling on opposite lines extending from or converging in a vertex. For instance, in Example 12 points B and C make a transversal wedge pairing, as do points D and E. Transversal pairings may be created through any musical parameter. They may be inversionally symmetrical through pitch, but they may also contain asymmetric pitch content if paired through other compositional means.
Example 13. Webern, op. 9, no. 5, timbral progression analysis
(click to enlarge)
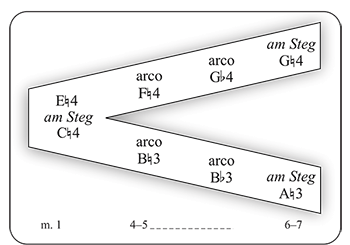
[5.3] As can be seen from an overview of the Fifth Bagatelle, timbral progressions—produced by am Steg, arco, and pizzicato—elucidate wedge constructions throughout the music (Example 13). Globally, there is a trajectory from containment to escape. Timbral lines create nested wedges that delineate the form and provide an avenue for comprehensibility in the music. The am Steg timbre traces two expanding wedges, the first symmetric, the second asymmetric. The two am Steg lines coincide with the formal divisions of the piece, and thus, are called the am Steg A and am Steg A’ lines. They are not a background, but they are the most consistent aural reference and have the narrowest range. The am Steg A line begins in m. 1 with
Example 14. Webern, op. 9, no. 5, block topography analysis
(click to enlarge)
[5.4] Moving to a more fine-grained analytical approach, the timbral lines and the wedges they articulate elucidate the connections, affinities, and symmetries of Webern’s musical logic. Bagatelle no. 5 unfolds in a monophonic block topography comprised of seven musical blocks (Example 14). Each block contains a complete aphoristic musical phrase consisting of a timbral idea, dynamic swell, and a unique tetrachord-based pitch construct. The result is a series of audibly distinct phrases presented sequentially, each expanding or contracting from the previous block.
[5.5] Block 1 (m. 1) establishes the foundation of the piece’s compositional strategy by encapsulating the arco melodic statement
Example 15. Webern, op. 9, no. 5, Block 1, timbral stratification with arco encapsulated within am Steg (click to enlarge) | Example 16. Webern, op. 9, no. 5, Block 2 with vertex tone, pizzicato (click to enlarge) |
[5.6] Block 2 (mm. 2–4.2) immediately provides the work’s vertex tone: the pizzicato Dn4 in Violin I (Example 16). After the silence that precedes it, the vertex tone’s isolation marks it as a salient moment. Block 2 implies a homophonic texture, with the pizzicato of Violin I foregrounded over tremolo at the bridge in Violin II and Viola. The pizzicato and the tremolo am Steg timbres maintain their textural stratification through timbral dissimilarity and asynchronous onsets. But Webern smooths the entrance of the tremolo am Steg through increasing the dynamic level of the pizzicato with the onset of the second timbre. As with the first phrase, the dynamic wave imparts an arch-like structure.
Example 17. Webern, op. 9, no. 5, Block 3 highlighting arco
(click to enlarge)
[5.7] Block 3 (mm. 4.2–5) is entirely in arco, the only block in the work in a single timbral profile (Example 17). At first, the arco line contributes to the am Steg A line’s chromatic expansion through
Example 18. Webern, op. 9, no. 5, Block 4 with arco timbres registrally encapsulating am Steg and post-phrase silence
(click to enlarge)
Example 19. Webern, op. 9, no. 5, am Steg A line
(click to enlarge)
[5.8] Block 4 (mm. 6–7) continues the timbral emphasis of the arco line and concludes the first formal unit with the final expansion of the am Steg A Line (Example 18). The most salient feature of Block 4 is the viola’s arco
[5.9] Here, we see the first divergence between a pitch-based reading of the form and one that accounts for timbre. An understanding of form based on pitch class and chromatic aggregates alone necessitates locating a formal division after the downbeat of m. 7. There are only two
Example 20. Webern, op. 9, no. 5, Blocks 5–6, varied repeat of Blocks 1–4
(click to enlarge)
[5.10] Block 5 (mm. 8–10) contains the most striking timbral event in the work—the ascending pizzicato glissando culminating in a sustained arco tone (m. 9)—but more than that, Blocks 5–6 recapitulate Blocks 1–4 in a varied repeat of the A section (Example 20). Bagatelle no. 5 makes use of an AA’ binary structure, rather than an AB pattern. In restarting the formal unit, Webern repeats nearly every element of the work’s beginning. The unique pizzicato Dn3 glissando to arco C#5 in the cello (m. 9) corresponds to the pizzicato
Example 21. Webern, op. 9, no. 5, Bn3 pizzicato line
(click to enlarge)
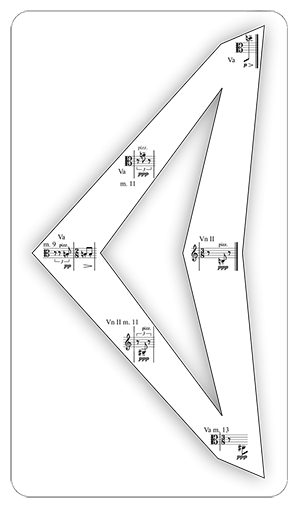
[5.11] Throughout the entire piece, only one tone is repeated in succession: the pizzicato Bn3 in the viola in mm. 9–10. Its repetition marks it as an important moment, and it becomes the vertex of a new pizzicato line that unfolds layers of both simultaneous and successive timbral symmetry. The wedge trajectories commence immediately with the simultaneous pizzicato tones in m. 11 and conclude with the final expansion of timbral-registral space in m. 13 (Example 21). Trading partners in a dance of metrically offset transversal pairs, the timbral symmetry is extended linearly. After the prominent repetition, the next pizzicato tones in the viola are
Example 22. Webern, op. 9, no. 5, Block 7, final expansion of the timbral lines
(click to enlarge)
[5.12] Block 7 (m. 13) offers the final expansion of the timbral lines and reiterates the foundational material of the movement, recalling the opening of both the A and A’ sections (Example 22). The block’s timbres are distributed in an alternating pattern:
D♮ 5 pizzicato (Viola)E♭ 4 am Steg (Violin I)B♮ 3 pizzicato (Violin II)E♮ 3 am Steg (Cello)C♯ 3 pizzicato (Viola)
The viola’s pizzicato
[5.13] In this Klangfarbenmelodie work, timbral lines impart coherence and comprehensibility. The
6. Op. 10, No. 1
Example 23. Webern, op. 10, no. 1, symmetrical form
(click to enlarge)
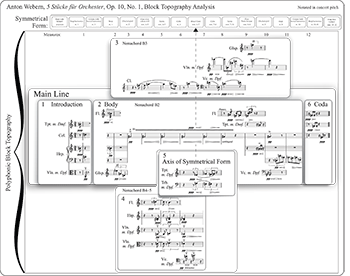
[6.1] In addition to the inversional symmetry explored through Bagatelle no. 5, timbre informs retrograde symmetry in Webern’s music. The First Orchestral Piece of Webern’s 5 Stücke für Orchester, op. 10, provides an excellent example—its form is symmetrical, articulated by timbre and defined around the timbral axis of the trumpet and trombone brass choir in mm. 6–7. Beginning in the middle facilitates an understanding of Webern’s timbral palindrome. Expanding outward from the form’s axis, the structural timbres on either side are: cello in mm. 7–8 and 6; violin in mm. 7–10 and 4–5; flutter-tongue flute in m. 8–9 mirroring the flute combined with the celesta trill in mm. 4–5; glockenspiel in mm. 9 and 2; harp in mm. 9 and 1; celesta augmented with bowed string harmonics in mm. 10 and 1; harp in harmonics in mm. 10–11 and 1; and the harp in m. 10 along with the trumpet in m. 12 mirroring harp combined with trumpet in the anacrusis (Example 23). The strings and brass instruments are muted throughout.
Example 24. Webern, op. 10, no. 1, block topography analysis
(click to enlarge)
[6.2] Exploring the work by expanding outward from the axis unveils multiple layers of symmetry. The work’s six musical blocks unfold in a polyphonic topography (Example 24). As usual, the blocks are numbered in order of their appearance; the block numbers themselves do not relate to the symmetrical unfolding. Block 5 is the brass choir axis of the work’s symmetrical form (mm. 6–7). Block 3 consists of clarinet in mm. 3–6, cello in mm. 7–8, and violin in mm. 7–10 along with glockenspiel’s
Example 25. Webern, op. 10, no. 1, Block 1, the introduction, part of the main timbral line
(click to enlarge)
Example 26. Webern, op. 10, no. 1, Block 2, the body, part of the main timbral line
(click to enlarge)
Example 27. Webern, op. 10, no. 1, Block 6, the coda, part of the main timbral line
(click to enlarge)
[6.3] Blocks 1, 2, and 6 form a monophonic chain that creates the main timbral line of the work and contains many of the form-bearing symmetrical partners. Continuing with the outward expansion, on either side of the cello (mm. 6 and 7–8) and violin (mm. 4–5 and 7–10), flutter-tongue flute and flute combined with celesta trill. This is the only instance where Webern does not use a direct timbral pairing. Instead, he employs timbral imitation. The combination of flute and celesta trill (mm. 4–5) emulates the timbre of flutter-tongue flute (mm. 8–9). The palindromic mirroring continues with the direct timbral pairings mentioned above ([6.0]). Only the glockenspiel’s augmentation of the violin (m. 9) rests outside the main line. Within this timbral line, each block is formally segmented by rests, resulting in an introduction, body, and coda. All three sections share a group of instrumental timbres and articulation techniques that promote coherence across the movement. The introduction (Block 1) is the opening
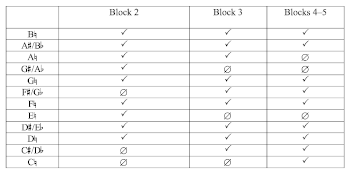
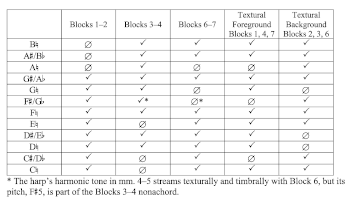
Example 28. Distribution of nonachords in Blocks 2–5 of Webern’s op. 10, no. 1
(click to enlarge)
[6.4] The pitch content of op. 10, no. 1 reinforces the work’s symmetry and segmentation into blocks. Perhaps most obvious, the introduction and coda highlight
7. Op. 10, No. 4
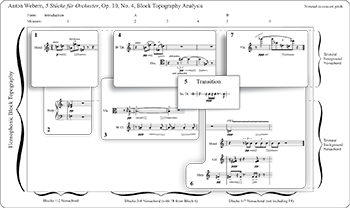
Example 29. Webern, op. 10, no. 4, block topography analysis
(click to enlarge)
[7.1] In addition to considering timbral progressions in the above works, thus far the analyses in this study have explored how timbre structures pitch (op. 9, no. 4), inversional symmetry (op. 9, no. 5), and retrograde symmetry (op. 10, no. 1). Lastly, we will explore timbre as a way of structuring gesture and theme. In his analysis of op. 11, no. 1, Clifford posits that “the shape of an established gesture took precedence over, and even influenced, Webern’s choice of specific pitches or register for a given chord or melody” (2002, 210). Neither Clifford nor I ignore pitch in our analyses, but the addition of timbre as a parameter that can structure gesture and shape enriches analytical possibilities. Clifford concludes by suggesting op. 11, no. 1 may have been “an early working out another type of symmetrical compositional technique, not of pitches or palindromes, but of gestures and shapes” (210). Extending this line of thought, the notion of timbre structuring gesture, and in turn theme, can be seen in Orchestral Piece no. 4, op. 10. Opus 10, no. 4 is only six measures long, yet it has provided fertile analytical ground for generations of scholars.(24) As abstract as the piece may seem, it is actually one of Webern’s most “old-fashioned” aphoristic works. It combines a clearly stratified homophonic texture with Webern’s typical symmetrical language. The form is binary with a short introduction (iAB). Through timbral similarity and dissimilarity, the work neatly partitions into formal segments and textural foreground and background in a homophonic block topography (Example 29).
[7.2] Blocks 1 and 2 (the anacrusis and m. 1) form the introduction. The mandolin provides the melody with the harp in accompaniment. Immediately, Webern establishes a melodic contour of two ascending dyads followed by a descending dyad. Viewing this “up-up-down” gesture is the primary thematic element of the piece, the mandolin’s melody is echoed in the foreground of each subsequent homophonic grouping. Blocks 3 and 4 (mm. 2–4) constitute the A section. The melody is in the trumpet and trombone (both muted), while the muted viola harmonic and clarinet carry the accompaniment. In Block 4, the trumpet has the up-up-, and the trombone answers with the -down. The up-up-down melody integrates as a musical block through timbral similarity, reinforced by repetition of the thematic gesture. Timbral dissimilarity segregates the brass instruments from their accompaniment in Block 3. In the background, the clarinet’s
Example 30. Webern, op. 10, no. 4, retrograde timbral symmetry (inexact)
(click to enlarge)
Example 31. Webern, op. 10, no. 4, crossing registers of textural layers
(click to enlarge)
[7.3] Returning to Block 5, the snare drum in m. 4 is the transition between the A and B sections and the only sound of indefinite pitch in the work. The A section is separated from the introduction by an eighth rest, and it is clearly partitioned from the B section with the same value. Only the sound of the snare drum penetrates the silence. Though not symmetrical in form, there are elements of retrograde timbral symmetry in Orchestral Piece no. 4. On either side of the snare drum axis are harp joined with mandolin, clarinet, and a solo string, though the symmetry is inexact with violin in its upper register mirroring viola harmonics (Example 30). The only non-direct pairing of timbres is the celesta matched to the brass instruments. Even though the form is not defined by these symmetrical timbres, the timbral pairings are consistent with Webern’s technique in op. 10, no. 1. Reinforcing this consistency, the register of Orchestral Piece no. 4’s textural layers cross, similar to the timbral progressions of Bagatelle no. 4 (Example 31). In mm. 2–4, the melody in the brass is registrally below the accompaniment of clarinet and string harmonics. Then, in mm. 5–6, the melody in the violin is in the traditional upper voice above an accompaniment in a lower register. Though symmetry appears not be the main compositional strategy here, the symmetrical timbral features are consistent with Webern’s musical language.
Example 32. Distribution of nonachords in Webern’s op. 10, no. 4
(click to enlarge)
[7.4] As in Orchestral Piece no. 1, here in no. 4, pitch nonachords reinforce the structures defined by timbre. Some previous analyses have focused on the hexachord created by the first three mandolin tones and the trichord in the harp to extrapolate structural formations.(25) However, that approach does not consider the work’s notated phrasing. The continuation of the mandolin line to its completion yields the more cohesive nonachord as the pitch unit.(26) Each of the three homophonic combinations of blocks (Blocks 1–2, 3–4, and 6–7) is assigned a unique nine-tone grouping. Furthermore, the stratified foreground (Blocks 1, 4, 7) and background (Blocks 2, 3, 6) layers each contain a collection of nine tones as well (Example 32). The harp’s harmonic tone in mm. 4–5 is unique in this work. It streams texturally and timbrally with Block 6, but its pitch,
[7.5] Pitch and timbre buttress each other. The nonachords reinforce the timbral groupings and textural stratifications that create the musical blocks. Structure is communicated through timbral and textural stratification and segmentation, with phrasing, dynamic shaping, and rests clearly demarcating transitional points. In this Klangfarbenmelodie music, gestural shape, timbre, and registral distribution logically convey the presentation of musical ideas.
8. Conclusions
[8.1] Webern’s Six Bagatelles for String Quartet, op. 9, and 5 Orchestral Pieces, op. 10, show the organization of timbral lines (Klangfarbenfolgen) into music structured through timbre (Klangfarbenmelodie). These works demonstrate that well-defined forms, symmetry, musical ideas like expansion and contraction, and lucid textures are all consistent aspects of the composer’s Klangfarbenmelodie works. Bailey calls Webern’s opp. 9 and 10 the “epitome of musical aphorism as it is generally understood—those wisps of music in which one ephemeral gesture follows another for no very apparent reason” (1997, 85). When examined through the lens of Klangfarbenmelodie, however, Webern’s ephemeral wisps convey well-articulated musical ideas. This article offers a new way to consider the interaction of timbre and pitch. Both of these aspects of the musical tone are capable of being the basis for musical logic. Pitch can be considered independently, as in traditional analytical approaches, or for its contributions to timbre as part of the totality of the musical tone. In some instances, readings of timbre and pitch reinforce and strengthen one another, and in others they offer evidence of conflicting interpretations. In both cases, Webern’s works explore some of the possibilities of timbre as a medium for artistic expression. With them, Webern takes concrete steps on Klangfarbenmelodie’s path to new music.
Matthew Zeller
McGill University
555 Sherbrooke Street West
Montreal, Quebec H3A 1E3
matthew.zeller@mcgill.ca
Works Cited
Archibald, Bruce. 1972. “Some Thoughts on Symmetry in Early Webern: Op. 5, No. 2.” Perspectives of New Music 10 (2): 159–63. https://doi.org/10.2307/832341.
Bailey, Kathryn. 1983. “Webern’s Opus 21: Creativity in Tradition.” Journal of Musicology, 2 (2): 184–95. https://doi.org/10.2307/763806.
—————. 1991. The Twelve-Tone Music of Anton Webern: Old Forms in a New Language. Cambridge University Press. https://doi.org/10.1017/CBO9780511552458.
—————. 1996. “Symmetry as Nemesis: Webern and the First Movement of the Concerto, Opus 24.” Journal of Music Theory 40 (2): 245–310. https://doi.org/10.2307/843890.
—————. 1997. “Berg’s Aphoristic Pieces.” In The Cambridge Companion to Berg, ed. Anthony Pople, 83–110. Cambridge University Press. https://doi.org/10.1017/CCOL9780521563741.007.
Bregman, Albert S. 1990. Auditory Scene Analysis: The Perceptual Organization of Sound. MIT Press. https://doi.org/10.7551/mitpress/1486.001.0001.
Busch, Regina. 1985–86a. “On the Horizontal and Vertical Presentation of Musical Ideas and on Musical Space (I).” Tempo 154 (Sep.): 2–10. https://doi.org/10.1017/S0040298200021434.
—————. 1985–86b. “On the Horizontal and Vertical Presentation of Musical Ideas and on Musical Space (II).” Tempo 156 (Mar.): 7–15. https://doi.org/10.1017/S0040298200022063.
—————. 1985–86c. “On the Horizontal and Vertical Presentation of Musical Ideas and on Musical Space (III).” Tempo 157 (Jun.): 22–26. https://doi.org/10.1017/S0040298200022312.
Chrisman, Richard. 1979. “Anton Webern’s ‘Six Bagatelles for String Quartet,’ Op. 9: The Unfolding of Intervallic Successions.” Journal of Music Theory 23 (1): 81–122. https://doi.org/10.2307/843695.
Clifford, Robert. 2002. “Multi-Level Symmetries in Webern’s Op. 11, No. 1.” Perspectives of New Music 40 (1): 198–215.
—————. 2005. “Perennial Questions.” Tempo 59 (234): 29–33. https://doi.org/10.1017/S004029820500029X.
Cramer, Alfred. 2002. “Schoenberg’s Klangfarbenmelodie: A Principle of Early Atonal Harmony.” Music Theory Spectrum 24 (1): 1–34. https://doi.org/10.1525/mts.2002.24.1.1.
Cohn, Richard. 1988. “Inversional Symmetry and Transpositional Combination in Bartók.” Music Theory Spectrum, 10th Anniversary Issue 10 (Spring): 19–42. https://doi.org/10.2307/745790.
Davies, Benjamin K. 2007. “The Structuring of Tonal Space in Webern’s Op. 9.” Music Analysis 26 (1/2): 25–58. https://doi.org/10.1111/j.1468-2249.2008.00273.x.
Delcombre-Monpoel, Marie. 1998. “L’Opus 10 de Webern.” Musurgia 5 (1): 35–49.
Deliège, Célestin. 1975. “Webern: Op. 10 No 4. Un Thème d’Analyse et de Réflexion.” Revue de Musicologie 61 (1): 91–112. https://doi.org/10.2307/928684.
Elferen, Isabella van. 2021. “Timbrality: The Vibrant Aesthetics of Tone Color.” In The Oxford Handbook of Timbre, ed. Emily Dolan and Alexander Rehding, 69–91. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780190637224.013.28.
Ferneyhough, Brian. 1995. Collected Writings. Edited by James Boros and Richard Toop. Harwood.
Forte, Allen. 1973. The Structure of Atonal Music. Yale University Press.
—————. 1998. The Atonal Music of Anton Webern. Yale University Press.
Haimo, Ethan. 1996. “Atonality, Analysis, and the Intentional Fallacy.” Music Theory Spectrum 18 (2): 167–99. https://doi.org/10.2307/746023.
Hanninen, Dora A. 2012. A Theory of Music Analysis: On Segmentation and Associative Organization. University of Rochester Press.
Hasty, Christopher. 1981. “Segmentation and Process in Post-Tonal Music.” Music Theory Spectrum 3 (1): 54–73. https://doi.org/10.2307/746134.
Hutchins, Carleen Maley, ed. 1997. Research Papers in Violin Acoustics 1975–1993. 2 vols. Acoustical Society of America.
Iverson, Jennifer. 2009. “Historical Memory and György Ligeti’s Sound-Mass Music 1958–1968.” PhD diss., University of Texas at Austin.
Johnson, Peter. 1978. “Symmetrical Sets in Webern’s Op. 10, No. 4.” Perspectives of New Music 17 (1): 219–29. https://doi.org/10.2307/832669.
Lachenmann, Helmut. 2003. “Hearing [Hören] is Defenseless—without Listening [Hören]: On Possibilities and Difficulties.” Circuit: Musiques Contemporaines 13 (2): 27–50. https://doi.org/10.7202/902272ar.
Lambert, Philip. 2000. “On Contextual Transformations.” Perspectives of New Music 38 (1): 45–76. https://doi.org/10.2307/833588.
Lewin, David. 1993. Musical Form and Transformation: 4 Analytic Essays. Yale University Press.
McAdams, Stephen. 2019a. “The Perceptual Representation of Timbre.” In Timbre: Acoustics, Perception, and Cognition, ed. Kai Siedenburg, Charalampos Saitis, Stephen McAdams, Arthur N. Popper, and Richard R. Fay, 23–57. Springer International Publishing. https://doi.org/10.1007/978-3-030-14832-4_2.
—————. 2019b. “Timbre as a Structuring Force in Music.” In Timbre: Acoustics, Perception, and Cognition, ed. Kai Siedenburg, Charalampos Saitis, Stephen McAdams, Arthur N. Popper, and Richard R. Fay, 211–43. Springer International Publishing. https://doi.org/10.1007/978-3-030-14832-4_8.
McAdams, Stephen, and Kai Siedenburg. 2019. “Perception and Cognition of Musical Timbre.” In Foundations in Music Psychology: Theory and Research, ed. Peter J. Rentfrow and Daniel J. Levitin, 71–120. MIT Press.
Metzer, Dave. 2006. “Modern Silence.” Journal of Musicology 23 (3): 331–74. https://doi.org/10.1525/jm.2006.23.3.331.
Moldenhauer, Hans, and Rosaleen Moldenhauer. 1979. Anton von Webern. Alfred A. Knopf.
Puffett, Kathryn, and Barbara Schingnitz. 2020. Three Men of Letters: Arnold Schönberg, Alban Berg, and Anton Webern, 1906–1921. Hollitzer Verlag. https://doi.org/10.2307/j.ctvzsmcwj.
Sallmen, Mark. 2003. “Motives and Motivic Paths in Anton Webern’s Six Bagatelles for String Quartet, Op. 9.” Theory and Practice 28: 29–52.
Schoenberg, Arnold. 1911. Harmonielehre. Universal Edition.
—————. 1975. Style and Idea: Selected Writings of Arnold Schoenberg. Edited by Leonard Stein. Translated by Leo Black. Faber and Faber.
—————. 1978. Theory of Harmony. 1911. Translated by Roy E. Carter. University of California Press.
Siedenburg, Kai, Charalampos Saitis, and Stephen McAdams. 2019. “The Present, Past, and Future of Timbre Research.” In Timbre: Acoustics, Perception, and Cognition, ed. Kai Siedenburg, Charalampos Saitis, Stephen McAdams, Arthur N. Popper, and Richard R. Fay, 1–19. Springer International Publishing. https://doi.org/10.1007/978-3-030-14832-4_1.
Strange, Patricia, and Allen Strange. 2001. The Contemporary Violin: Extended Performing Techniques. University of California Press.
Straus, Joseph N. 2014. “Total Voice Leading.” Music Theory Online 20 (2). https://doi.org/10.30535/mto.20.2.5.
Webern, Anton. 1958. “The U. E. Reader.” In Die Reihe, ed. Herbert Eimert and Karlheinz Stockhausen, vol. 2, Anton Webern.
—————. 1975. The Path to the New Music. Edited by Willi Reich. Translated by Leo Black. Universal Edition.
—————. 1999. Briefe an Heinrich Jalowetz. Edited by Ernst Lichtenhahn. Schott.
Wolfe, Joe. n.d. “Articulation and vibrato on the violin.” University of New South Wales. https://newt.phys.unsw.edu.au/jw/violinarticulation.html#sulponti.
Zeller, Matthew. 2020. “Planal Analysis and the Emancipation of Timbre: Klangfarbenmelodie and Timbral Function in Mahler, Schoenberg, and Webern.” PhD diss., Duke University.
Footnotes
* I would like to thank my two MTO reviewers, Jennifer Iverson and Joseph N. Straus, whose editorial comments led me to a stronger version of this article. I would also like to thank Robert Hasegawa, Stephen McAdams, Philip Rupprecht, and R. Larry Todd for providing feedback on early drafts of this article, as well as Mitch Ohriner and the MTO editorial team for initiating the non-anonymous collaborative review pilot program. This work was supported by the Analysis, Creation, and Teaching of Orchestration (ACTOR) partnership at McGill University, funded by the Canadian Social Sciences and Humanities Research Council (#895-2018-1023).
Return to text
1. Among others discussed below, previous analyses of Webern’s opp. 9 and 10 include those by Busch (1985–86a, 1985–86b, 1985–86c), Forte 1998, Haimo 1996, Johnson 1978, Lewin 1993, and Sallmen 2003.
Return to text
2. I thank Thomas Ahrend for assisting in the transcription of Webern’s letter to Schoenberg of August 23, 1911 (Arnold Schönberg Center, 21866). Ahrend also suggests that “auf 1/16, 1/32 Sechzehntel, Zweiunddreißigstel” may refer to an underlying beat rather than specific note durations as translated by Moldenhauer but finds both translations possible (email to author, April 3, 2021).
Return to text
3. Webern had not yet begun op. 9, no. 1 and 6 in May of 1913; those two movements were composed sometime between June 3 and July 10, 1913.
Return to text
4. “Schönberg gefällt mein Aufsatz über ihn sehr. Ebenso meine neuen Kompositionen. Er hatte einen großen Eindruck davon. Er will sogar darüber etwas schreiben. Er meint das sei ja eigentlich schon eine Melodie der Klangfarben! Ich bin glücklich!” Translation mine.
Return to text
5. Both opp. 9 and 10 have complicated gestations. Webern had begun op. 9/2–5 by August 7, 1911 and all four movements were complete by August 23, 1911 (Moldenhauer 1979, 190–96). Opus 9/1 and 6 were composed June 3–July 10, 1913. Opus 10/1 was completed on June 28, 1911 and op. 10/4 was completed on July 19, 1911. Opus 10/2–3 and 5 were composed September 6–October 10, 1913. Webern composed at least eighteen short orchestral movements during 1911–13, eleven of which are published: five as op. 10 (1911–13; Universal Edition, 1923), five as Orchestra Pieces, op. Posthumous (1913; Carl Fischer, 1971), and “O sanftes Glühn der Berge,” which became no. 3 of the Three Orchestral Songs (1913–14; Carl Fischer, 1968).
Return to text
6. For example, the offstage oboe at the beginning of the third movement of Hector Berlioz’s Symphonie fantastique (1830) has a different timbre than when it returns to the stage.
Return to text
7. “Am Klang werden drei Eigenschaften erkannt: seine Höhe, Farbe und Stärke.
Return to text
8. “
Return to text
9. “Welches System liegt diesen Folgen zugrunde?” (Schoenberg 1911, 471)
Return to text
10. Carter renders “melodies” in scare quotes in the second line; however, they are not in the original German. “Ist es nun möglich, aus Klangfarben, die sich der Höhe nach unterscheiden, Gebilde entstehen zu lassen, die wir Melodien nennen, Folgen, deren Zusammenhang eine gedankenähnliche Wirkung hervorrufen, dann muß es auch möglich sein, aus den Klangfarben der anderen Dimension, aus dem, was wir schlechtweg Klangfarbe nennen, solche Folgen herzustellen, deren Beziehung untereinander mit einer Art Logik wirkt, ganz äquivalent jener Logik, die uns bei der Melodie der Klanghöhen genügt.” (Schoenberg 1911, 471)
Return to text
11. A full exploration of the multifaceted meaning of Klangfarbenmelodie is outside the scope of this article. For a discussion of Klangfarbenmelodie as a concept as well as its implications as an organizational principle on the style of musical presentation, texture, and potential types of musical logic employed, one might consider my manuscript in preparation, “Klangfarbenmelodie, Style, and Idea: Timbral Function in Music.” For an early version of this work see Zeller 2020.
Return to text
12. Block topography bears resemblance to Kathryn Bailey’s (1991, 30–93) topographical arrangement of tone rows in dodecaphony. Row topography is a way of describing how tone rows are put together in the musical texture. Bailey lays out two types of row topography. What she calls “block [row] topography” and “linear [row] topography” are roughly analogous to monophonic block topography and polyphonic block topography, respectively (31).
Return to text
13. On auditory chunking see, for example, Bregman 1990 and McAdams 2019b. For examples of the array of factors that may govern musical segmentation, see Hasty 1981 and Hanninen 2012.
Return to text
14. For detailed discussions of bowed string acoustics see Hutchins 1997.
Return to text
15. As pitch-class sets, these tetrachords have the TC-property (See Cohn 1988, esp. 23–28 and Straus 2014); see Lambert (2000) for a discussion of this type of tetrachord in Webern’s op. 11.
Return to text
16. If forming a hexachord with the first six tones of the work, a decision would have to made between
Return to text
17. These are just a few of the possible pitch readings.
Return to text
18. Within this timbral reading of the first aggregate there are still a number of analytically attractive tetrachordal and hexachordal groupings available. For example, either of the latter two tetrachord groupings discussed above, or the hexachord sounded by the second violin (mm. 1–3) and, allowing for the repeated
Return to text
19. While 6:9:12 may be reduced to 2:3:4, the larger numerals reflect the actual division of rhythmic onsets per measure that Webern employs.
Return to text
20. For example, Archibald 1972, Bailey 1983, 1991, 1996, Clifford 2002, Davies 2007, and Lewin 1993.
Return to text
21. Albeit slightly removed, retrospective reinterpretation adds one more layer of support for the
Return to text
22. This brings to mind Christopher Hasty’s (1981) discussion of analytical domains in “Segmentation and Process in Post-Tonal Music.”
Return to text
23. In this way, Webern’s use of the harp in op. 10/1 is similar to the function it performs twenty-four years later in his arrangement of the Fuga (Ricercata) a 6 voci, no. 2 from J. S. Bach’s The Musical Offering BWV 1079 (1747).
Return to text
24. Notable analyses of Webern’s op. 10, no. 4 include those by Clifford 2005, Delcombre-Monpoel 1998, Deliè 1975, Forte 1973, 1998, Johnson 1978, Lachenmann 2003, Lewin 1993, and Metzer 2006.
Return to text
25. Notably, Lewin 1993 and Forte 1973, 1998.
Return to text
26. Advancing from the first nonachord, a chromatic aggregate is completed with the first three tones of Blocks 3 and 4 (
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Andrew Eason, Editorial Assistant
Number of visits:
10547