George Walker’s Piano Music: Traditional Forms in Tonal, Serial and Atonal Styles
Jack Boss
KEYWORDS: George Walker, piano music, atonality, serialism, sonata form, variations, referential collection, motivic development
ABSTRACT: Throughout his compositional career, George Walker dedicated himself to reimagining the traditional forms of tonal music, such as sonata and variations, in dissonant styles. This was a feat that Arnold Schoenberg (famously) declared to be impossible, at least for free atonal music; but Walker achieved it in the free atonal style as well as in his serial music. This article attempts to show how he did so, by presenting close readings of three piano pieces from Walker’s tonal, serial, and atonal periods: the first movement of the First Piano Sonata, Spatials, and the first movement of the Fourth Piano Sonata. Specifically, it considers the ways in which he uses pitch and pitch-class patterns (particularly referential collection progression and motivic variation), rhythm, dynamics, register, and tempo to simulate the various aspects of sonata and variation forms. For sonata form, this involves delimiting phrases and themes and creating senses of transition, retransition, and development; for variation form, it involves imitating the ways in which themes are preserved and varied by means of developmental processes. The results of this study will show that Walker’s music has much to teach us about how to recreate traditional forms in a dissonant harmonic language.
DOI: 10.30535/mto.28.3.2
Copyright © 2022 Society for Music Theory
Introduction
[1.1] George Theophilus Walker was a Black American pianist and composer who was born in Washington, D.C., in 1922 and died in 2018. He began his musical career with the intention of becoming a concert pianist, studying first at Oberlin and then with Rudolf Serkin at the Curtis Institute, and giving concerts around the United States and in Europe. But he ran up against a roadblock in the late 1940s: a number of performing-artist agencies refused to represent him, assuming that a Black pianist would be unable to attract an audience (Walker 2009, 72, 78; Hampton 1994, 56–60; Boe 1995, 13; Newson 1977, 26–28). Roosevelt Newson situates these difficulties in Walker’s performing career within the context of systemic racism in the United States in the early twentieth century, explaining that young Black instrumentalists were rarely given the opportunity to study with excellent teachers from an early age to develop their talents as classical musicians. Those few who did manage to develop their talent, like Walker, were treated as anomalies; many of them turned toward careers in jazz, where they felt more welcome (Newson 1977, 55–57).
[1.2] After trying unsuccessfully for a few years to find a manager, Walker shifted his focus toward composition (though he continued to concertize for the remainder of his career). He was one of the first students to enroll in the DMA degree program at the Eastman School in 1955, and though his program of study was in piano performance, he submitted his second Piano Sonata in lieu of a dissertation (Walker 2009, 91). After graduating from Eastman in 1957, Walker studied with Nadia Boulanger in Paris before beginning a long teaching career that took him to Dillard University, Smith College, the University of Colorado, and Rutgers University, among other schools. In 1996, he received the Pulitzer Prize in music for his work Lilacs for Voice and Orchestra.
[1.3] The evolution of Walker’s musical style can be divided into the same three categories that scholars typically use for the Second Viennese School composers Schoenberg, Webern, and Berg—tonal, atonal, and serial—but with the last two stages reversed. Much of what he wrote in the 1940s and 1950s is tonal on at least some level, but in 1961 he composed Spatials for piano, his only twelve-tone piece. According to interviews he did with Kevin Hampton, Walker “admitted that he found the strict application of the [twelve-tone] technique stifling artistically” (Hampton 1994, 138). Thus, within Spatials, he ordered the row unusually freely, and after finishing it turned toward a style that is almost completely freely atonal.
[1.4] Walker’s reversal of serial and atonal approaches, viewed in light of the Second Viennese School’s three-part style progression, is especially interesting for the reason that, throughout his career, he similarly remained committed to projecting the traditional forms of Western music through dissonant melodic and harmonic structures. As he himself said:
I have really been a strong advocate of traditional forms simply because they provide stability to a work. . . . I keep coming back to traditional forms because they provide a base from which I can incorporate new and more contemporary content into my music. In retrospect, I think I have shown a partiality to variation forms, sonata forms and fugues. (Baker 1978, 366)
It seems that Walker may have successfully avoided a central problem Schoenberg experienced when composing free atonal music, specifically an inability to write longer, traditional forms without recourse to functional harmony and its usual form-building properties. As Schoenberg put it in “Composition with Twelve Tones,”
Establishing functions demanded different successions of harmonies than roving functions; a bridge, a transition, demanded other successions than a codetta; harmonic variation could be executed intelligently and logically only with due consideration of the fundamental meaning of the harmonies. Fulfillment of all these functions—comparable to the effect of punctuation in the construction of sentences, of subdivisions into paragraphs, and of fusion into chapters—could scarcely be assured with chords whose constructive values had not as yet been explored. Hence, it seemed at first impossible to compose pieces of complicated organization or of great length. (1984, 217)
In my book Schoenberg’s Atonal Music, I point out that Schoenberg’s pre-serial atonal music contradicts this argument, in that it actually does find effective ways to execute formal functions of various kinds without recourse to tonal harmony (2019, 348–49). My purpose in this article is to show how Walker was likewise able to create sonata and variation forms convincingly and effectively in all three harmonic styles—tonal, serial, and atonal.
[1.5] To do this, I will examine Walker’s style development and his different ways of realizing traditional forms in light of three representative examples from his piano music. I will first consider the opening movement of the First Piano Sonata (1953, rev. 1991), a piece that overlays a background tonal structure with a surface syntax rooted primarily on progressions between referential collections.(1) Next, I will discuss the twelve-tone work, Spatials (1961), which creates six variations on its opening “statement” through repeating, retrograding, and sometimes transposing its row form, as well as through dyad invariances used as motives. In addition, the work uses what Hyde 1980 refers to as “secondary harmony” to create a large ternary structure over the whole cycle. Last, I will take up the opening movement of the Fourth Piano Sonata (1984). This is another sonata-form movement, but one that unmoors its dissonant chord progressions from the tonal framework they had elaborated in the First Sonata. Despite these three pieces’ divergent tonal, serial, and atonal styles, taken together they provide a wonderful example of how a composer can use means other than functional tonal harmony to project traditional forms, thus solving Schoenberg’s supposed dilemma.
First Piano Sonata, movement I
[2.1] Walker wrote his First Piano Sonata after returning from a concert tour of Europe, sensing that he needed a larger work with an American flavor for his recital programs. He says about it in his autobiography: “It occurred to me that the use of quartal harmony would also add some distinction to it” (Walker 2009, 81). Likely on this basis, the analytic literature on this sonata (which consists primarily of doctoral dissertations) routinely places emphasis on the interval of the perfect fourth as the constructive element.(2) There is evidence, however, that the importance of the fourth for this movement has been overemphasized. As Walker complained in his autobiography:
Contrary to the inaccurate statements made in several doctoral dissertations about the intervallic content, there is no consistency in the use of the interval of a fourth. (Where were the doctoral advisors for these students?) (Walker 2009, 81)
Walker goes on to explain that the sonata “integrates” fourths, thirds, and seconds “without having a predominance of one interval” (Walker 2009, 81). I will show that he does this by using sonorities rich in perfect fourth (and perfect fifth) intervals, such as 3-9 (027), 4-23 (0257), and 5-35 (02479) as starting and cadential points in phrases, then moving from them to more dissonant sonorities combining the smaller intervals of second, third, and tritone, and finally back again.(3) In this way, the assertions made by previous scholars about the importance of the perfect fourth, while in many respects correct, are refined by showing that sonorities built from fourths attain their importance not by occurring constantly without interruption, but by being used as starting and ending points for progressions involving a greater variety of chords.
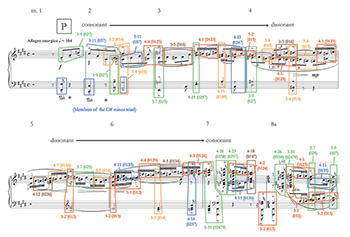
Example 1. Form chart for George Walker, Piano Sonata No. 1, I
(click to enlarge)
[2.2] Before continuing on to illustrate such progressions in detail, I need to address in what ways the first movement of the First Piano Sonata is functionally tonal. Example 1 provides a form chart. The first movement has a key signature of four sharps, corresponding to
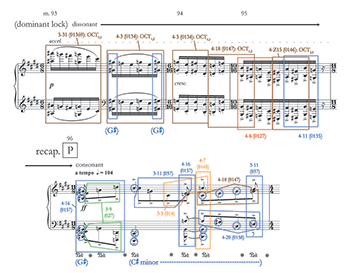
[2.3] The development area divides into a section based on P (mm. 48–78a) and one based on S (mm. 78b–92). Both of these sections emphasize E, in particular by casting it as a pedal point. The relative major is of course not an unusual place to begin a development in classical sonata form. By the time the development’s “dominant lock” section is reached at m. 93, however, E has given way to other pitches, including (but not primarily) the expected
Example 2. George Walker, Piano Sonata No. 1, I; mm. 1–8a, primary theme in the exposition
(click to enlarge)
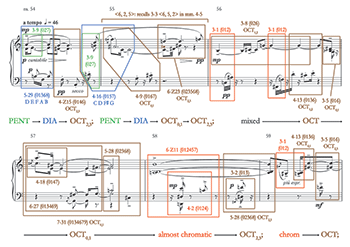
[2.4] Even though a functional-tonal skeleton underlies this work, much of the music that surrounds these emphasized tonal centers does not relate to it in traditional ways. Instead of iv-V-i or ii°-V-I progressions that structure phrases and sections, Walker alternates between two groups of set classes. One group consists of consonant set classes belonging to the pentatonic collection—the “quartal harmonies” that he mentioned in his autobiography—and diatonic collections; and the other consists of more dissonant subsets of the hexatonic, octatonic and chromatic/near-chromatic (i.e. “n-1” chromatic subset) collections.(6) These more dissonant sets have a greater prevalence of minor seconds and/or tritones in their interval contents; as opposed to the prevalence of perfect fourths and major seconds in the pentatonic collection or perfect fourths, major seconds and major/minor thirds in the diatonic collection. The P theme in Example 2 provides an illustration of alternation between pentatonic and more dissonant collections. The various referential collections are color-coded in this example: diatonic subsets (including the
[2.5] A more detailed view of Example 2 shows the perfect-fourth chord and the
[2.6] Moving forward, m. 3 and the downbeat of m. 4 create a mixture of consonance in the vertical dimension with dissonance in the horizontal. Pentatonic subsets that highlight perfect fourths and major seconds (3-7 (025) [011010], 4-23 (0257) [021030], and 3-9 (027)) sound as chords on first and third beats, while the lines connecting these chords make use of sets from chromatic, hexatonic, and octatonic collections that either prefer or include the minor second and/or tritone (4-4 (0125) [211110], 3-5 (016) [100011], 4-1 (0123) [321000], and 3-2 (013) [111000]). In the dissonant middle of the arch in mm. 4–6, however, both vertical and horizontal dimensions rely on more dissonant referential collections: the chords project hexatonic and chromatic sets 3-4 (015), 3-2 (013), 3-2 (013), and 3-3 (014),(9) while the lines focus on octatonic, hexatonic, chromatic, and almost-chromatic sets. (The pentatonic subset 3-7 (025) and diatonic subset 4-11 (0135) do show up briefly in these measures to break up the steady stream of more dissonant set classes.) Then at the cadence, the situation reverts mostly to the state of mm. 3 and 4: simultaneous pentatonic subsets progress to a more-dissonant 4-18 (0147) [102111] in m. 7, followed by all pentatonic subsets in m. 8. Walker’s use of the rhythmic gesture  |
| 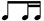
 to support consonant-dissonant harmony in m. 7 and consonant-consonant harmony in m. 8 supports hearing these two measures as cadential. These chords are linked by chromatic subsets 4-1 (0123) and 3-1 (012) and the almost-chromatic set 3-2 (013).(10)
to support consonant-dissonant harmony in m. 7 and consonant-consonant harmony in m. 8 supports hearing these two measures as cadential. These chords are linked by chromatic subsets 4-1 (0123) and 3-1 (012) and the almost-chromatic set 3-2 (013).(10)
Example 3. George Walker, Piano Sonata No. 1, I; mm. 21–28, end of “dominant lock” section and first phrase of secondary theme in the exposition
(click to enlarge)
[2.7] The total effect of the P theme, despite it strongly emphasizing
[2.8] In addition to its more relaxed rhythms and more straightforward functional-tonal nature, the S theme relies to a greater extent on consonant sonorities and stepwise melodic lines, as the prevalence of blue and green colors in Example 3 attests. One of the few places we do hear a dissonant sonority is in the “dominant lock” section. The octatonic subsets 4-18 (0147) and 5-32 (01469) that contain the
Example 4. George Walker, Piano Sonata No. 1, I; mm. 93–96, “dominant lock” and first measure of primary theme in the recapitulation
(click to enlarge)
[2.9] We next move forward to the measures that end the development section, shown in Example 4. Here we again see octatonic subsets being used to connote expectation in mm. 93–95. I have labeled this as “dominant lock,” even though
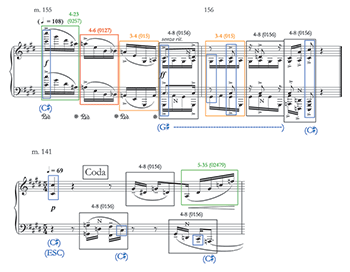
Example 5. George Walker, Piano Sonata No. 1, I; mm. 155–56, ending measures of coda, and m. 141, beginning of coda
(click to enlarge)
[2.10] I will close my detailed account of harmony in Walker’s early sonata with its final measures, shown on the top half of Example 5. Here the sense of a conclusive final cadence is conveyed by a strong tonal reference, the motion in the bass from repeated
[2.11] As a whole, Walker’s First Piano Sonata can be heard reinforcing the traditional form-defining powers of its underlying tonal progressions with new, extra-tonal ways of characterizing the different kinds of sections. Walker delimits themes and phrases within themes by arch forms created from referential collection progressions and the relative consonance and dissonance of their subsets. Furthermore, he augments the expectant quality of the “dominant lock” sections by the use of octatonic subsets in contrast to the subsequent pentatonic and diatonic subsets, and he projects the “cantabile” nature of the second theme by the use of more consonant referential collections in general. As I have shown, rhythmic, textural, dynamic, and articulative patterns also play important roles in the process. In the twelve-tone and freely atonal works I will consider next, a number of these methods of delimiting and characterizing formal sections will continue to impact musical structure in the absence of the usual tonal routines.
Spatials
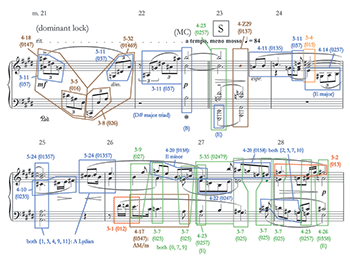
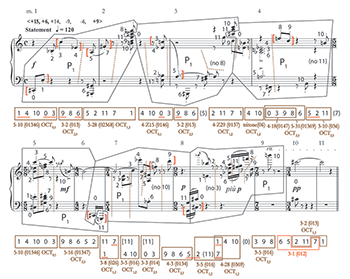
[3.1] Walker’s only twelve-tone work was composed in 1961 in response to his sense that “dodecaphony was acclaimed as the music of the avant-garde” (Walker 2009, 103). The composer’s autobiography says very little to put this statement into context; it doesn’t explain what he meant by “acclaimed” or what exactly motivated him to write this piece in the twelve-tone style. It could have been that in the early 1960s he was influenced by an early form of what Joseph Straus calls the “Myth of Serial Tyranny” (2009, 198–202), the notion that serial music was the dominant force in the American musical scene in the 1950s and early 1960s and that composers had to write in that style to be taken seriously.(13) At this point in his career, Walker was employed as a composition, theory, and piano professor at Smith College, and as an academic composer the pressure to try serialism may have been strong. Or perhaps Walker seized upon the notion of dodecaphony being acclaimed later, at the time of writing his autobiography, to provide justification for writing in the serial style. In any case, Walker’s response to “serial tyranny”—if that is indeed what it was—gave rise to an unusually well-formed and interesting piece of music. It consists of a “statement” (Walker’s name for the theme) and six “variations” and is composed such that the traditional theme-and-variation form is reimagined on at least two levels. Each of the six variations either presents a new form of the statement’s basic row or combines pitch and intervallic features of it in new ways; at the same time, the row form is continually varied within the statement and each of the variations. Each variation presents a single form of the row exclusively, cycling through it repeatedly until the end of the variation, so that there is no opportunity for a combinatorial relationship between different row forms happening simultaneously. The statement features the basic row P1, the first variation R1, the second variation P4, the third I1, and the fourth, fifth, and sixth P8.
Example 6. George Walker, Spatials, basic row in pitch classes and pitches (from mm. 1–2)
(click to enlarge)
[3.2] The basic row of Spatials is given in pitch classes in Example 6, along with the pitches used in its first appearance in mm. 1–2. Order positions, numbered from 0 to 11, are indicated in smaller type above the row’s pitch classes in the example.(14) (The order numbers will be highlighted in bold when they appear in the text.) The discussion below will make passing reference to examples 7-10, in advance of them being more carefully treated over the next few pages. In his autobiography, Walker claims that he “decided to compose a strict, serial work for piano” (2009, 103), but the row count of Spatials demonstrates that his creative impulses could not be constrained by strict row order for very long.(15) Already in the second presentation of P1 in mm. 2–3, there is a note missing (see Example 7), and small reorderings and omissions continue through Variation 3. With Variation 4, there are larger omissions (the initial statement of P8 begins on order position 5, and never presents 0–4: see Example 8). By the time the music reaches Variation 5, hardly any of the presentations of P8 are rendered in proper order (Example 9). Only in Variation 6 does Walker work his way back toward row order; he nearly achieves this at the end, only to cadence on a fragment using order numbers 1–4 of P8 (Example 10). Taken together, the six variations create a large ternary pattern that progresses away from row order through the course of the piece, then climaxing in Variation 5 before moving back in the direction of ordered row forms at the end. Not only that, but the row reorderings in Variation 5 are arranged so that they create the same set classes (mostly octatonic subsets) from non-contiguous row members as those set classes formed by contiguous row segments in the rest of the piece. This technique creates Martha Hyde’s (1980) “secondary harmony,” and adds another dimension to the work’s large ternary pattern: the same octatonic subsets featured as contiguous at the beginning and end are projected by different pitch-class combinations in the fifth variation, allowing for new transpositions of pitch-class motives to come to the fore. It is interesting to note in this regard that Walker created similar large ternary shapes in the variation movements of his piano sonatas by repeating the theme at the end: Roosevelt Newson describes this process in the second movement of the First Sonata and first movement of the Second Sonata (Newson 1977, 87).
Example 7. George Walker, Spatials; mm. 1–11 (statement)
(click to enlarge)
[3.3] Example 7 reproduces the statement section (theme) from Spatials, with a row count on the score above and a map of the pitch classes of P1 below showing the contiguous partitions induced by rhythm and register. P1 is stated six times in order (allowing for simultaneities), and almost every row ending overlaps with the beginning of the following row either through placement in the same chord or by means of two-note motivic grouping. Only the end of the third P1 in m. 4 is separated from the beginning of the next. In addition, every instance of P1 except for the first and fourth (mm. 5–6) is missing one note, causing a different order position to be absent in every row (see parentheses in the score above and pitch-class map below). Because of the row’s construction, and because of Walker’s habit of leaving out single notes and overlapping ends with beginnings, nearly every melodic fragment or chord consists of a contiguous or overlapping segment that creates a subset of some octatonic collection. For example, the first P1 partitions into a five-note melodic segment that projects 5-10 (01346) and is a member of OCT0,1. Next is a three-note segment belonging to 3-2 (013) and OCT2,3, and last we hear the last four row elements sounding as a high-register chord with the first element of the second P1, pitch class 1, to form 5-28 (02368), which belongs to OCT1,2. Continuing on through the pitch-class map, we observe that similar partitions (all contiguous, with some overlapping ones) form a host of other octatonic subsets—3-2 (013), 3-5 (016), 3-8 (026), 3-10 (036), 4-3 (0134), 4-Z15 (0146), 4-18 (0147), 4-28 (0369), 4-Z29 (0137), 5-10 (01346), 5-16 (01347), 5-28 (02368), and 5-31 (01369).(16) The octatonic collections that contain these sets alternate freely between the three possible transpositions. In mm. 5–7, Walker sustains the B4, order position 10 of the fourth P1, in the right hand, suggesting several non-contiguous overlapping partitions; but these also form octatonic subsets, such as 3-8, 3-5, and 3-3 (014). The only prominent harmonic element that does not belong to some octatonic collection occurs near the end of m. 8, a 3-1 (012) chromatic trichord formed by a non-contiguous partition.
[3.4] The octatonic collection in the statement of Spatials thus plays a very different role than it did in the First Piano Sonata. Rather than serving as a foil to the pentatonic collection, a relatively dissonant place to progress to within arch forms, the octatonic sound world here serves as the baseline condition from which the harmony hardly ever deviates. Phrasing in the statement section relies more on rhythm and, especially, contour; for example, several of the phrases are delimited by an upward rise to a staccato chord in the highest register (mm. 1–2 and 2–3 are particularly notable in this regard).(17) Subsequent analysis will show Walker’s preference for octatonic subsets continuing through the six variations. Likely for this reason, the developmental techniques that characterize each variation and distinguish it from the statement are, again, typically not harmonic ones. Instead, pitch motives that were highlighted in the statement will be brought back, sometimes transposed as well as undergoing rhythmic and other changes, and placed in new contexts. Eight of these motives are bracketed in red in the score of Example 7. Also, their pitch classes are underlined in the pitch-class map (also in red), showing that not all of them are created by adjacent notes in the row and that some result from overlaps between rows. Six of them, <
Example 8. George Walker, Spatials; mm. 40–45 (beginning of Variation 4)
(click to enlarge)
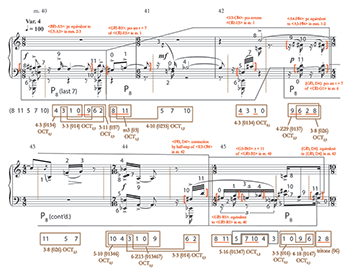
[3.5] Example 8 illuminates this motivic variation process together with octatonic harmonic consistency in the beginning of Variation 4, mm. 40–45. As I mentioned above, Variation 4 begins a string of three variations that use P8 as their source. In mm. 40–45, every segment of P8, be it contiguous or non-contiguous, projects an octatonic subset, many of them the same set classes as in the statement: 3-3, 3-5, 3-8, 4-3, 4-18, 4-Z29, 5-10, and 5-16. New set classes such as 3-11 (037), 4-10 (0235), and 6-Z13 (013467) do appear, but these are likewise octatonic, meaning that any harmonic variation that one might wish to posit is more a matter of individual chord types than collectional membership. As in the statement, the specific pitch-class sets of Variation 4 cycle freely through all three octatonic collections.
[3.6] Where an audible variation process does take place is in the treatment of two-note pitch motives belonging to interval classes 3 and 6, which are again highlighted in red in both the score and pitch-class map. The first salient dyad (emphasized through accent) is <
[3.7] In mm. 44–45 of Variation 4, a cluster of two-note motives appears that can be heard as repetitions or small changes to earlier elements of the same variation. The pickup notes to m. 45, <
Example 9. George Walker, Spatials; mm. 50–55 (Variation 5), row count and pitch-class map
(click to enlarge)
Example 10. George Walker, Spatials; mm. 50–55 (Variation 5), two-note motives
(click to enlarge)
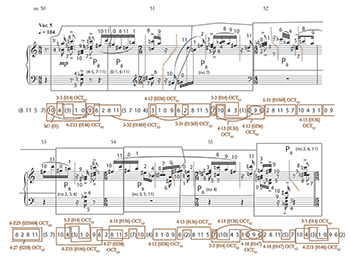
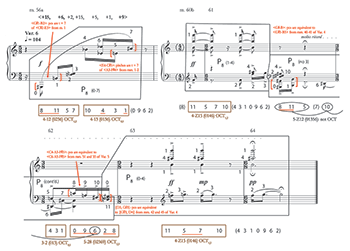
[3.8] This motivic process continues in Variation 5, together with the same strong emphasis on octatonic harmonies, but there the ways of drawing chords and motives from the row (still P8) become increasingly non-contiguous. Examples 9 and 10 respectively illustrate the row-count and pitch class map (Example 9) and some of the dyad motives (Example 10) of the full fifth variation. Already at the beginning in m. 50, Walker bypasses order positions 0–3 of P8, and fashions alternating chords from 4 and 9; 5, 7, and 8; 4, 5, 9, and 10; and 5, 7, and 8 again. While the artist can be seen moving beyond the “strict application of the twelve-tone technique,” the intervals and chords that result are all still familiar. The initial dyad is ic 1; it is followed by 3-3 (014), 4-Z15 (0146), and 3-3 again. Both set classes are also available as contiguous subsets of the row, 3-3 at order positions 7–9 (<6, 5, 2> in P1) and 4-Z15 at positions 1–4; the latter actually did occur in the statement at the end of m. 2 (<4, 10, 0, 3> of P1). Hence these chords at the beginning of Variation 5 qualify as “secondary harmonies.” We note that, even though Variations 1–4 had a few secondary harmonies, Variation 5 is almost totally dependent on them. Another appears immediately after in m. 50, where Walker brings together order positions 10 and 11 of the first P8 with positions 0, 1, 6 and 11 of a second one to yield the pitch class sequence <6, 2, 8, 3, 2, 11>. This is a marker of set-class 5-32 (01469), which is also available contiguously at order positions 6-10. The music presented throughout the rest of the variation features many non-contiguous and overlapping partitions of P8 (as well as a few contiguous ones) forming set classes 4-12 (0236), 5-31 (01369), 4-13 (0136), 6-Z23 (023568), 4-27 (0258), and 4-18 (0147). All of these can also be formed contiguously within the row and thus qualify as secondary harmonies.
[3.9] Another point to make about Variation 5 is that every one of its set classes is an octatonic subset, so the non-contiguous row partitions have little effect on the harmonic language of the piece: it remains firmly within the octatonic orbit. All three octatonic collections are again represented, though there is a significant emphasis on OCT0,1 at the beginning in m. 50, and again at the end in m. 55 as the same {0, 1, 4} and {4, 6, 9, 10} chords return. Although all the sets are octatonic in Variation 5, they are formed here by different groups of pitch classes because of the non-contiguous partitions. This treatment leads to the motivic changes that create the sense of variation here, as shown in Example 10. Of special import are the salient two-note motives belonging to ics 3, 4 and 6 that recall motives from the statement and earlier variations. Variation 5 begins with <A5, C6>, followed directly by <A4, C6>, marked with staccato and accents in the top voice at the beginning of m. 50. This recalls the similarly accented <
[3.10] In Example 10, numerous other motives are bracketed with brief texts describing at least one of their possible derivations. I will not discuss every one of these, but some of the simultaneous intervals that appear at the end of the variation in m. 55 are worth mentioning. The final P8 row form in m. 55b includes two pitch-class sets with normal form {4, 6, 9, 10} (order positions 4, 5, 9, 10) that are voiced as an ic 3 (minor third or major sixth) on top and an ic 6 on the bottom. Identical chords appeared earlier in Variation 5 at m. 50 and m. 53. The ic 3s can be traced back to numerous other sources earlier in the fifth variation as well, though their pitch classes, 6 and 9, also recall a prominent motive in m. 42b of Variation 4. The {4, 10} dyads on the bottom can be heard as varying the {2, 8} dyads in mm. 42b and 45b of Variation 4, as well as the {1, 7} motive in mm. 6–8 of the statement. Again, there is an intricate web of pitch, pitch-class, and intervallic dyads that relate in multiple ways to what came before, changing features of earlier motives as well as placing them in new contexts.
Example 11. George Walker, Spatials; mm. 56a and 60b–64 (Variation 6)
(click to enlarge)
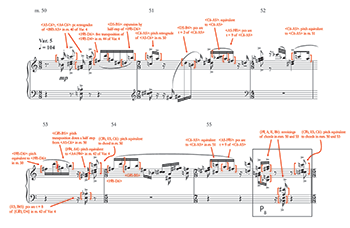
[3.11] Variation 6, the final section of Spatials, moves back in the direction of preferring ordered row forms. This can be seen in Example 11, which reproduces part of the first measure of Variation 6, m. 56a, and the last four measures plus pickup, mm. 60b–64. I discussed above how Variation 6 has a “rounding” function within Spatials. One way it does that is by returning to mostly contiguous partitions of the row, still P8. An even stronger allusion to the beginning is the ascending pitch arpeggio through P8 in m. 56a: although its ordered pitch interval sequence varies that of m. 1 in some of the middle intervals, both successions start <+15, +6> and end with <+9> (compare the beginnings of Examples 7 and 11).
[3.12] Though the row forms are mostly ordered in Example 11, none of them are complete; the closest is the P8 in mm. 61b–62, which contains all elements save order position 3. Still, the almost completely contiguous partitions of row fragments bring back octatonic tetrachords that had been created both contiguously and non-contiguously in previous variations, demonstrating how simple it is for the composer to derive the work’s harmonic vocabulary from contiguous segments of the row. The ascending arpeggio in m. 56 can be divided into discrete tetrachords 4-12 (0236) and 4-13 (0136), sets that were created both ways in Variation 5. In mm. 60–61, the focus turns to the 4-Z15 (0146) that occurs between order positions 1–4; it will return at the final cadence in mm. 63–64. 4-Z15 was present as a contiguous subset in m. 2 of the statement and a non-contiguous one in mm. 50, 53, and 55 of Variation 5. In between the two Variation 6 appearances of 4-Z15, in m. 61, a non-contiguous partition appears that yields one of the piece’s few non-octatonic (but still relatively dissonant) sets: specifically, order positions 0, 1, 2, 4 and 10 come together to create 5-Z12 (01356) [222121]. I hear this as a bit of anticipatory harmonic tension, given that it leads in m. 62 to two more octatonic subsets: 3-2 (013) as order positions 5–7 and 5-28 (02369) as 8–11, overlapping with 0 of the following P8. The piece then cadences securely in the octatonic realm with 4-Z15, as already mentioned.
[3.13] Because Variation 6 partakes almost exclusively of the same octatonic sound world as its predecessors, it falls to motivic relations again to accomplish the actual “varying.” A number of these dyadic motives are marked in red on the score of Example 11 as before. The opening <
[3.14] Unlike the First Piano Sonata, Spatials does not employ progression among referential collections as a harmonic device to delimit or characterize formal sections. Its music is overwhelmingly octatonic from beginning to end, which serves as a unifying factor. It is interesting to note that the octatonic harmonies are derived contiguously at beginning and end of the piece, and non-contiguously in Variation 5; but, in the end, the same set classes and kinds of set classes are produced through more complex partitions in the fifth variation (albeit by different groups of pitch classes). What exactly, then, makes these variations besides the fact that each of them varies some version of the source row, repeatedly and consecutively? In my understanding, it is the way each variation takes up and reworks dyad motives presented first in the statement, followed by further reworkings of the same motives. Each variation thus explores a new way of combining old motives and placing them in new contexts. In Spatials, Walker finds creative ways to simulate both the repetitive and developmental aspects of variation form, without the recourse to tonality he made use of in the First Piano Sonata.
Fourth Piano Sonata, movement I
Example 12. Form chart for George Walker, Piano Sonata No. 4, I (adapted from Boe 1995, 53 and 56)
(click to enlarge)
[4.1] According to George Walker’s autobiography, the Fourth Sonata was conceived in 1983 in response to a commission from Frederick Moyer (the pianist who premiered the work) and the Pew Charitable Trust (2009, 141). Dennis Boe characterizes the first movement as a clear instance of sonata form, and provides the chart adapted in my Example 12 (1995, 51–52, 53, 56). According to him, there are two exceptional features with respect to sonata form on display: first, the development presents new material, and second, rather than working with the exposition’s thematic material, the recapitulation is abbreviated to a presentation of the P theme only. In an interview with Boe, Walker commented on the creative license he felt writing in sonata form gave him:
To me, the great beauty of sonata form is the tremendous variety that it offers and the fact that you will never find two that are identical . . . for a while, I was sort of under the impression that you must make a statement of the first theme, a transition, a second theme, etc., but even in Beethoven, you find that he’ll repeat the first theme again before he goes on into the transition. (Boe 1995, 55–56)
Example 13. George Walker, Piano Sonata No. 4, I; mm. 1–6a (exposition’s primary theme, section A)
(click to enlarge)
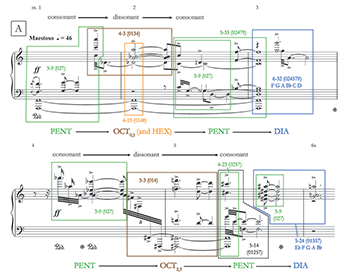
[4.2] Example 13 provides a score of the A section of the first theme, mm. 1–6a, with the subsets of various referential collections color-coded as before: green for pentatonic, blue for diatonic, orange for hexatonic, brown for octatonic, and red for chromatic. Later in the sonata movement, whole-tone subsets appear, which are colored purple. Boe places great emphasis on the importance of the pentatonic collection in his account of the A section:
In the first movement, the initial theme is stated primarily on the pitches of F G A C D in the first three measures and
A♭ B♭ C D E in measures 4–5. The pentatonic quality of the two combinations is obvious. (1995, 62)
However, as Boe himself points out, the composer disagreed with this assessment. He quotes Walker:
There is no relationship to the pentatonic scale. From an analytical point of view, you could make reference to pentatonic, but the notes that don't fit are important and change what you associate with pentatonic. They intentionally refute the pentatonic idea. (Boe 1995, 63)
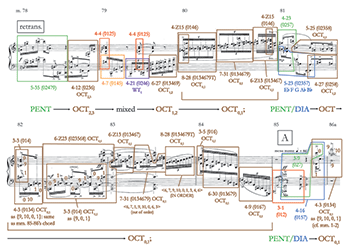
[4.3] Walker’s comment about notes “changing” or “refuting” the pentatonic collection leads to a more nuanced description of the harmonic pattern underlying the A section. Essentially, it consists of two phrases, both of which start within the pentatonic collection, gravitate toward more dissonant collections, move back to pentatonic, and finish with a subset of the major scale. As Example 13 shows, mm. 1–3 begins with {0, 5, 7}, which form 3-9 (027) [010020]; the
[4.4] The second phrase, mm. 4–6a, creates a similar pattern, with a few of the same set classes. Set 3-9 manifesting as {8, 10, 3} appears at the beginning of measure 4, but is soon followed by a “note that doesn’t fit,” the
[4.5] Like the P theme in the First Piano Sonata, the two phrases in this first part of P in the Fourth Sonata delimit themselves through patterns involving referential collections. The patterns that shape each phrase in the latter sonata work also form arches that move from consonant to dissonant and back to consonant—with one small difference being that the consonant material expands to diatonic subsets from pentatonic at the end of each phrase. An even more significant difference is that the Fourth Sonata uses referential harmony to shape the phrase in the absence of a tonal center: there is nothing like the First Sonata’s emphasis on its
Example 14. George Walker, Piano Sonata No. 4, I; mm. 6b–13a (exposition’s primary theme, transition and beginning of section B)
(click to enlarge)
[4.6] This piece’s lack of tonal function motivates the question of how a transition in an atonal sonata could be achieved, since a change of key is not possible. Boe’s form chart (my Example 12) labels mm. 6b–12 as a transition between the A and B sections of the P theme, and my Example 14 reprints that passage, together with a few measures from the beginning part of the goal, the B section. Harmonically, the piece abruptly shifts strategy from consonant-dissonant-consonant arches to an emphasis on the more dissonant collections, rich in half steps and tritones. First comes 3-1 (012), the chromatic trichord, then a long string of OCT2,3 subsets. These subsets are occasionally broken up by hexatonic trichords and tetrachords in mm. 7, 9, and 10, and supported by a sustained 3-3 (014) belonging to OCT0,1 in mm. 9–12. The B section enters in m. 12 with OCT2,3, so the shift to this particular collection six measures earlier can be understood as having a transitional function.
[4.7] Remarkably Walker also uses the order of his OCT2,3 subsets, as well as their gradually increasing size, to more sharply define these measures as transitional. Note that the 6-Z13 (013467) in the left hand at the end of m. 7 and the 7-31 (0134679) in the right hand in m. 8, though ascending in contour, do not simply ascend through OCT2,3. Instead, the first set jumps over a few notes and changes direction, <2, 3, 8, 9, 0, 11, 2>, and the second runs through seven notes in order, <3, 5, 6, 8, 9, 11, 0>, before skipping notes and changing direction, <5, 6, 9, 8, 11>. This development leads to the full presentation of 8-28 (0134679T) in ascending order in m. 9: <0, 2, 3, 5, 6, 8, 9, 11>. The music next backtracks in mm. 9b–11, presenting smaller subsets of OCT2,3 that decrease in size and descend as well as ascend. Upon reaching m. 12, we observe an ascending OCT2,3 that is almost completely in order except for one pair of notes: <8, 9, 0, 11, 2, 3, 5, 6>. The gradual buildup of ordered segments, together with the more obvious clues provided by the accelerando e crescendo, characterize this passage as moving forward toward its goal in m. 12.
Example 15. George Walker, Piano Sonata No. 4, I; mm. 26b–30 (exposition’s secondary theme)
(click to enlarge)
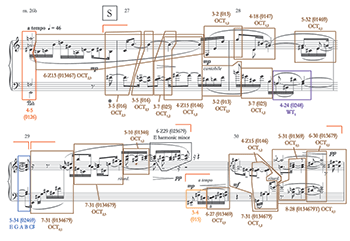
[4.8] Following repetition of the A and B sections of the first theme in mm. 18–25 and a shorter transition in m. 26, the brief second theme is introduced in mm. 27–30. This theme will not reappear in the recapitulation or development sections; however, there is a measure-long reference to it in the closing section of the exposition at m. 42. The S theme, together with a half-measure of the transition to it, is reproduced in Example 15. One notices that it does not seem to emphasize the dominant C or mediant
[4.9] Harmony also plays a role in shaping the design of these phrases. Like Spatials, just about everything is octatonic here, except for the ends of the first and second phrases. The first phrase introduces a whole-tone tetrachord in m. 28 into a texture that had consisted entirely of subsets of OCT2,3 and OCT1,2; it then cadences in m. 29 on set-class 5-34 (02469) [032221], which could be understood as a segment of the D major scale. Phrase two cycles through all three octatonic collections. Then, as it fades out near the end of m. 29, it wanders off into 6-Z29 (023679), which spells a segment of the E harmonic minor scale in this particular transposition. The third phrase has a different harmonic profile to go with its fade; after a 3-4 (015) trichord, it produces incrementally longer octatonic subsets in mm. 29b–30: 6-27 (013469), 7-31 (0134679), and finally the full 8-28.
Example 16. George Walker, Piano Sonata No. 4, I; mm. 54–59 (beginning of development)
(click to enlarge)
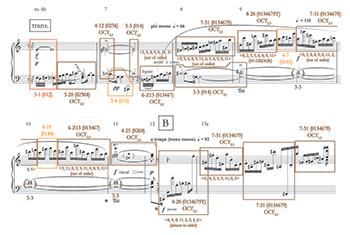
[4.10] After a fairly lengthy closing section, the development section of this sonata movement begins at m. 54. The first six measures are illustrated in Example 16. The composer himself had the following to say about the unconventional design of this area:
The development is really not a development of previous thematic material, but new material put into the location of what would be the development. (Boe 1995, 55)
It is true that the melodic and rhythmic ideas presented after m. 54 bear few obvious resemblances to either first or second theme. However, one can make the case that these measures do develop the progression of referential collections presented in the exposition . . . by condensing it. Example 16 illustrates a development of the harmonic progression of the previous music.
[4.11] The progression that occurs twice in mm. 54 and 55a is one of a perfect fourth chord opening out into a diatonic subset, and finishing with an octatonic tetrachord. The first time, 3-9 (027) continues into 5-29 (01368), and then 4-Z15 (0146); the second 3-9 leads to 4-16 (0157), which overlaps with 4-9 (0167). This pentatonic-diatonic-octatonic pattern varies and condenses that of the P theme’s A section, which had gone pentatonic-octatonic-pentatonic-diatonic, also twice (refer back to Example 12). Measure 55b then produces an OCT2,3 subset, 6-Z23 (023568), which is the same transpositional goal of the octatonic collection earlier seen in the transition between A and B sections in the P theme. The pitch-classes D5 and F5 at the top of this 6-Z23 can be heard as connecting up with the
Example 17. George Walker, Piano Sonata No. 4, I; mm. 78–86 (end of retransition and beginning of recapitulation)
(click to enlarge)
[4.12] The foregoing analysis has shown how Walker simulates thematic, transitional, and developmental functions in the Fourth Sonata without having recourse to the tonal relationships he relied on in the First Sonata. The last passage to consider will be the retransitional measures leading up to the abbreviated recapitulation, mm. 78–84, as well as the opening measures of the recapitulation, mm. 85–86. This music is given in Example 17. Here Walker uses not only referential collection progressions but also a specific pitch-class motive to create a retransition, anticipating the return of A. The passage falls into two phrases, mm. 78–80 and 81–84, each marked by a crescendo and an increase in rhythmic activity toward sextuplet, septuplet, octuplet, and nonuplet sixteenths and thirty-second notes. The beginning of the second phrase is also marked by a change in dynamics from forte down to mezzo-piano. Both phrases are centered around the same referential collection progression; however, the second extends the first. Measures 78–80 move from pentatonic (5-35) to OCT2,3, then through a mixture of collections in m. 79 to OCT1,2, and finally reach an OCT0,1 collection that sustains for all of m. 80. Measure 81 begins with a pentatonic set (4-23), just like the first phrase, then extends that into a diatonic 5-23 (02357), all this before finishing with two octatonic sets from different collections, OCT0,1 in the right hand and OCT1,2 in the left. The second phrase then settles into a longer string of OCT0,1 chords in mm. 82–84. Both progressions anticipate the sequence of referential collections that appears at the beginning of the recapitulation in mm. 85–86: pentatonic to diatonic to OCT0,1.
[4.13] Walker uses an even more salient device within the second string of OCT0,1 chords to anticipate the A section that is about to return. The music states the specific OCT0,1 pitch-class subset that will appear at mm. 85–86 and had appeared in the exposition at mm. 1–2, that being set 4-3 (0134) realized as {9, 10, 0, 1}. Measure 82a brings {9, 0, 1} together as a chord, then follows it with the sequence <0, 10, 1, 0>. Then, 0, 9, and 1 repeat for the rest of the measure as a bass ostinato. This music looks forward to the return of the recapitulation by highlighting and repeating parts of the specific chord that had originally “changed what you associate with pentatonic” at the piece’s beginning.
Conclusion
[5.1] In the analyses of these three piano pieces by George Walker, I have shown the means by which he reconstructs various formal functions of two traditional tonal formal types: sonata and variations. The opening movements of the First and Fourth Sonatas use progressions of referential collections—notably pentatonic and octatonic and the consonant and dissonant subsets resulting from them—to delimit phrases through arch forms. The early and late sonata movements also use motion from one referential collection to another, in addition to motion from unordered to ordered collections of the same kind, to simulate transitional function. Last, the Fourth Sonata creates a sense of development by condensing the progression of collections from the exposition and associating it with (mostly) new melodic and rhythmic material.
[5.2] Spatials, as a variation form realized by a twelve-tone style, takes a different tack. The octatonic collection provides harmonic consistency, though it is produced by contiguous row subsets at beginning and end and non-contiguous ones in Variation 5. The sense of variation is created in part by using different row forms for some of the variations, but mostly by working with salient dyad motives that are transposed, reordered, octave-complemented, and placed together in new combinations and new contexts.
[5.3] Most significant (and interesting to me) is the fact that Walker recreated the functions of these tonal forms using the traditional tonal reference points in the early sonata, but completely abandoned them in Spatials and the later sonata. It seems that for him, in contrast to what Schoenberg claimed, it was indeed possible to “replace those structural differentiations provided formerly by tonal harmonies” (Schoenberg 1984, 218) with the use of a twelve-tone row—or even without it, in a freer atonal style.
[5.4] Before closing, it is important for me to place the research I have just presented in the context of the important conversation about “whiteness” in music theory that Philip Ewell set in motion with his 2020 article, “Music Theory and the White Racial Frame.” I identify as a straight, white male, a senior member of the music theory community whose training (which culminated at Yale in the 1980s) comprised music-analytical methods of white origin. I also count myself as someone who at all stages of my career has actively recruited and mentored students of color. With this article I aspire to contribute to the broader conversation about rebalancing and shifting the racial frame of music theory by resisting the erasure of George Walker’s music from the music-analytical literature, among other ways.
[5.5] Having thus identified myself and my aspiration, I admit that this article on Walker’s piano music constitutes only a (very small) step. It studies the work of a Black American composer who clearly understood his music as contributing to the Western classical tradition. Prominent antiracist scholars are actively engaging with the idea of “assimilationism,” in which a Black person expresses the idea that his “racial group is culturally or behaviorally inferior, and is supporting cultural or behavioral enrichment programs to develop that racial group” (Kendi 2019, 24). Possibly, the reader could understand Walker’s music as contributing to such a program. In this regard, it is pertinent that Walker acknowledged his father, George Walker Sr., as his most important influence. Walker Sr. was a successful medical doctor who encouraged his children to develop a strong work ethic and to excel in academic activities—Walker Jr., for example, entered the Howard University Prep School when he was ten—as well as extracurriculars such as music and tennis. At least some of these academic and extracurricular activities were rooted in white culture. For example, Walker’s early musical training focused on piano performance, and although the repertoire he learned did include the Juba Dance of R. Nathaniel Dett, it centered mainly on the European canon, including a public performance of Beethoven’s Op. 13 piano sonata at the age of thirteen (Newson 1977, 16–20).
[5.6] But Walker’s own descriptions of his identity and aspirations as a composer do not paint a picture of letting himself be “taken in” or “absorbed” by the dominant white culture, to bring himself up to the level of white people and escape racism.(19) Instead, he seems to declare that he has taken hold of the Western classical music tradition and made it his own, because he sees value in it beyond socio-political spheres. At times, his language takes on an actively antiracist tone, pushing back against the systemic racism that has hindered the progress of Black classical musicians, such as conscious decisions by composition juries to exclude Black artists. The following passage from a New York Times interview is relevant in this regard:
As a matter of fact, I believe that music is above race. I am steeped in the universal cultural tradition of my art [italics added]. It is important to stress one’s individuality beyond race but I must do it as a black person who is aspiring to be a product of a civilized society. Recordings, like commissions, have been for the lucky few. The juries who make decisions are made up of white teachers—our teachers—and they consciously tend to recommend other whites. (Klein 1971, cited in Newson 1977, 60)
My goal, then, was to use white analytic approaches as illustrative tools here,(20) to show how successful Walker was in making the Western classical tradition his own as well as how intricate, ordered, complex, and beautiful his work in that tradition was. Through doing that, I hope to amplify the voice of a Black composer, as well as resisting scholars’ erasure of George Walker’s music from music history, analysis, and criticism. My attempt to do this in the way I have done seemed warranted given his own comments about both race and the classical tradition.
[5.7] Ewell (2020, [3.5]) and others have encouraged members of our field to look beyond the traditional Euro-centric ways of analyzing and discussing music that students of my generation were taught in graduate school, including the ones I use here: musical form, pitch-class set theory, and twelve-tone theory. This has created a challenge for many of us about how to move forward. Perhaps part of the solution is to listen to our students from other cultures as well as others with direct experience and knowledge of world culture, so that our work together becomes an exchange of ideas between equals combining a broader variety of perspectives. In this way, music theory may continue to blend Western and world-music approaches, including studies in which methods of organizing from world music illuminate Western theory in new ways.
Jack Boss
School of Music and Dance
1225 University of Oregon
Eugene, OR 97403-1225
jfboss@uoregon.edu
Works Cited
Baker, David. 1978. The Black Composer Speaks. Scarecrow Press.
Bernard, Jonathan W. 1997. “Chord, Collection and Set in Twentieth-Century Theory.” In Music Theory in Concept and Practice, ed. James M. Baker, David Beach, and Jonathan W. Bernard, 11–51. University of Rochester Press.
Boe, Dennis Leonard. 1995. “The Evolutionary Development of Compositional Technique and Style in the Piano Sonatas of George Walker: A Study of the Sonata No. 4 and Analytical Comparison of the Four Sonatas.” DMA diss., University of North Texas.
Boss, Jack. 2019. Schoenberg’s Atonal Music: Musical Idea, Basic Image, and Specters of Tonal Function. Cambridge University Press. https://doi.org/10.1017/9781108296991.
Ewell, Philip A. 2020. “Music Theory and the White Racial Frame.” Music Theory Online 26 (2). https://doi.org/10.30535/mto.26.2.4.
Forte, Allen. 1973. The Structure of Atonal Music. Yale University Press.
Hampton, Edwin Kevin. 1994. “George Theophilus Walker as Composer and Pianist: A Biography and Discussion of his Stylistic Evolution as Seen in Selected Works for Solo Piano.” DMA diss., University of Maryland, College Park.
Hanson, Howard. 1960. Harmonic Materials of Modern Music: Resources of the Tempered Scale. Appleton-Century-Crofts.
Headlam, Dave. 1996. The Music of Alban Berg. Yale University Press.
Hepokoski, James, and Warren Darcy. 2006. Elements of Sonata Theory: Norms, Types, and Deformations in the Late-Eighteenth-Century Sonata. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195146400.001.0001.
Hindemith, Paul. 1984. The Craft of Musical Composition. 4th ed. 2 vols. Translated by Arthur Mendel. Schott.
Hyde, Martha. 1980. “The Roots of Form in Schoenberg’s Sketches.” Journal of Music Theory 24 (1): 1–36. https://doi.org/10.2307/843737.
Jones, Everett. 2005. “Intervallic Coherence in Four Piano Sonatas by George Walker: An Analysis.” DMA document, University of Cincinnati College-Conservatory of Music.
Kendi, Ibram X. 2019. How to Be an Antiracist. One World Books.
Klein, Howard. 1971. “Overdoing ‘Benign Neglect’?” New York Times, March 7, 1971, sec. 13, 1. https://doi.org/10.1080/00396337108441236.
Levy, Janet M. 1982. “Texture as a Sign in Classic and Early Romantic Music.” Journal of the American Musicological Society 35 (3): 482–531. https://doi.org/10.2307/830985.
Newson, Roosevelt. 1977. “A Style Analysis of the Three Piano Sonatas (1953, 1957, 1976) of George Theophilus Walker.” DMA diss., Peabody Institute of the Johns Hopkins University.
Schoenberg, Arnold. 1984. Style and Idea: Selected Writings of Arnold Schoenberg. Edited by Leonard Stein. Translated by Leo Black. University of California Press.
Straus, Joseph N. 2009. Twelve-Tone Music in America. Cambridge University Press.
Walker, George. 2008a. Spatials. Lauren Keiser Music Publishing.
—————. 2008b. Sonata No. 4 for Piano. Lauren Keiser Music Publishing.
—————. 2009. Reminiscences of an American Composer and Pianist. Scarecrow Press.
—————. (1991) 2011. Sonata No. 1 for Piano. Rev. ed. Lauren Keiser Music Publishing.
Footnotes
1. Referential collections will be described in terms of their 3-, 4-, 5-, and 6-note subsets, which I will label according to the convention introduced by Forte 1973, the “Forte number,” in addition to the set’s prime form (3-2 (013)). Walker may not have been aware of the concept of pitch-class set when he wrote the First Piano Sonata in 1953, but it is important to notice that during and after his Second Sonata in 1957, he was strongly influenced by the “chemistry” system of Howard Hanson’s Harmonic Materials of Modern Music (Hanson 1960). As Jonathan Bernard (1997) has shown, Hanson’s analytic system was a forerunner to Forte’s notion of interval vector. Walker was a student in a seminar at Eastman devoted to testing out Hanson’s book, and the Second Sonata has been called “a direct result of what he learned in this class” (Newson 1977, 32).
Return to text
2. For example, Everett Jones: “Walker achieves unification in the First Piano Sonata by consistently using the interval of a fourth” (Jones 2005, 11). Or Kevin Hampton: “The logic of the traditional sonata-allegro form in the first movement is defined by his use of the interval of the perfect fourth” (Hampton 1994, 95). Or Dennis Boe: “The primary unifying principle to the work is the consistent projection of intervals of the fourth” (Boe 1995, 39).
Return to text
3. I would like to acknowledge my winter-quarter 2021 Post-Tonal Analysis class at the University of Oregon here, who helped me work out some of the following ideas about the form and harmonic progression of this movement in our class discussions of it.
Return to text
4. The terminology I use to describe the parts of sonata form in my first and third analyses is borrowed from James Hepokoski and Warren Darcy’s Elements of Sonata Theory (2006).
Return to text
5. I place “dominant lock” in quotation marks here because, though Walker does lock on to a particular chord at m. 20, it is not a simple dominant. (I will discuss the specifics of the section’s harmonic progression below.)
Return to text
6. What I call “n-1 chromatic subset” has also been recognized as a basic harmonic element in Berg’s music, a “1-cycle+ set,” by Dave Headlam. See Headlam 1996, 73.
Return to text
7. For readers unfamiliar with pitch-class set theory, the interval vector is a listing of 6 numbers representing the total number of occurrences of each “interval class” within a given set. Interval class 1 represents minor seconds and major sevenths (and their compounds). Interval class (“ic”) 2 corresponds to major seconds and minor sevenths, ic 3 to minor thirds and major sixths, ic 4 to major thirds and minor sixths, ic 5 to perfect fourths and perfect fifths, and ic 6 to tritones. The proposition I will make here is that interval vectors with relatively large second and fifth numbers can be considered more “consonant,” those with relatively large first and sixth numbers can be considered more “dissonant.”
Return to text
8. In this article, I will discuss a number of 3- and 4-note set classes that can be attributed to more than one referential collection. My strategy will be to assign them to one collection or another based on their immediate context in a given example. For instance, 3-3 (014) belongs both to octatonic (0134679T) and hexatonic (014589) collections. In Example 2, where it appears in close proximity to 3-4 (015), I labeled it as “hexatonic” and colored it orange. But in Example 16, where it appears in the midst of a large number of octatonic subsets, I will label it as “octatonic” and color it brown.
Return to text
9. Here, members of set class 3-2 are understood as “almost-chromatic” sets because of their prevalence of thirds and seconds and complete lack of perfect fourths.
Return to text
10. In this discussion my evaluation of various trichords and tetrachords as “consonant” or “dissonant” has depended mainly on the prevalence of major-second and perfect-fourth interval classes in the first kind of chord, as opposed to prevalence of minor-second and tritone interval classes in the latter kind. Another way to measure the relative consonance or dissonance of these chords would be Paul Hindemith’s “table of chord-groups” in the appendix of Hindemith 1984, vol. 1. In Hindemith’s table, groups I, III, and V can be understood as relatively consonant, while groups II, IV and VI are relatively dissonant (Within this larger division, I is more consonant than III, and II more consonant than IV). Of the set classes I have discussed so far, 3-11 constitutes category I, and 3-9, 3-7, and 4-23 all belong to category III. 3-5 and 4-18, because of their tritones, belong in Hindemith’s most dissonant category, IV. (Of course, my other “dissonant sets,” 3-3, 3-4, 3-1, 3-2, 4-1, and 4-4, are also members of category III, but I justify them as dissonant here on the basis of their prevalence of minor-second as opposed to major-second interval classes.)
Return to text
11. The change of texture in the latter half of m. 22 to the B in three octaves is another traditional way of signaling the end of the transition and beginning of the second theme in a sonata form, as Janet Levy (1982, 519) has pointed out.
Return to text
12. My convention for bracketing pitch classes and intervals in this article will be to use angle brackets for pitch-class or interval successions, and curly brackets for unordered pitch or pitch-class sets. I reserve square brackets for interval vectors, and parentheses for prime forms.
Return to text
13. Walker’s piece is not considered in Straus’s extensive catalogue of the diverse compositional approaches of American serial composers.
Return to text
14. This ordering is different (in its third discrete tetrachord) from the one given in Hampton 1994 (p. 137) but conforms better to the row presentations given in Walker’s “statement.”
Return to text
15. I am indebted to my colleague Timothy S. Pack of the University of Oregon for sharing with me his row count of Spatials, on which mine is based.
Return to text
16. Of course, some of the smaller subsets are not exclusively octatonic: 3-2 (013) and 3-6 (024) also belong to the diatonic collection, 3-6 (024) to the whole-tone collection, and so on. My justification for calling them “octatonic subsets” here depends on the larger context; they are surrounded by larger sets that answer only to that label.
Return to text
17. Walker’s tendency to give his phrases an ascending contour to some sort of climax at the end has also been discussed by Dennis Boe in his dissertation on the Fourth Piano Sonata (Boe 1995, 67–68). Boe describes a phrasing process called “expansion,” which begins with lower register and lighter textures and builds out incrementally into higher registers and heavier textures, with more dissonant harmonies.
Return to text
18. As in my analysis of the First Piano Sonata, the interval vectors with bold numbers are intended to show a shift of emphasis from major-second and perfect-fourth interval classes to minor-second interval classes and back again, corresponding to my characterization of mm. 1–3 as moving from consonant to dissonant sounds and back again.
Return to text
19. Webster’s definition of the intransitive verb “assimilate”: “to be taken in or absorbed” (from “assimilate,” Merriam-Webster, https://www.merriam-webster.com/dictionary/assimilate.)
Return to text
20. It is important to state here that even though I am using these analytical techniques as illustrative tools for Walker’s music, I do not consider them to be measuring devices for excellence, greatness, or beauty in music. There are myriad ways for music to demonstrate value that these tools do not address.
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
9259