Analyzing the Beat in Metrically Consonant Popular Songs: A Multifaceted Approach
David Geary
KEYWORDS: popular music, beat, rhythm and meter, drum feels, analysis
ABSTRACT: The beat is regularly defined as a song’s primary pulse layer and as a requirement for metric formation. Despite the beat’s familiarity, however, its precise characterization and analytical application is inconsistent in scholarship. In this article, I present a new approach to analyze the beat in popular songs with a consonant, clear, and unchanging quadruple simple meter. At bottom, I take the traditional view of the beat as a singular entity and reframe it a multifaceted phenomenon where different aspects of music can simultaneously, and at times variably, create a sense of metric primacy. My analytical system has three parts: the drum pattern layer, the absolute time layer, and the preferred pulse layer. Further, I introduce the term “interpretive flexibility,” a spin on interpretive multiplicity, to refer to metrically consonant popular songs with multiple options for the perceived beat. In the second half of the article, I apply the three-part system and interpretive flexibility to analyze the beat in popular songs with multiple drum feels and layered drum feels. The evolving sense of metric primacy in these songs is experientially engaging, helps express musical form, and parallels extramusical narratives.
DOI: 10.30535/mto.28.4.2
Copyright © 2022 Society for Music Theory
1. Introduction
[1.1] Most popular songs establish and maintain a consonant, clear, and unchanging quadruple simple meter, their rhythms inspiring an unambiguous set of isochronous and inclusive pulse layers.(1) This does not mean, however, that popular songs are metrically unengaging or uninteresting. Quite the opposite, meter provides a framework that grounds cognitive experience and guides physical movements. A central feature of this framework is the beat, which is regularly defined as a song’s primary metric layer (London 2012, 65; Danielsen 2006, 55; Iyer 2002, 398; Lerdahl and Jackendoff 1983, 21).(2) The beat is an essential component of metric theories, and it is also part of people’s everyday vocabulary to describe music. But its familiarity has led to some theoretical and analytical irregularities. One inconsistency arises when the beat is defined as a single pulse layer, but the parameters of the definition do not clearly indicate which of a song’s layers should be considered primary. Another inconsistency arises when two or more definitions identify the beat according to different musical characteristics, which can also result in classifying multiple metrical layers as primary.
[1.2] Rather than viewing these irregularities as irresolvable, I believe they pinpoint an opportunity for theoretical reconciliation and for analytical application. This article presents a new analytical method where these discrepancies are treated not as inconsistent or incompatible, but as different parts of a broader system. A fundamental characteristic of this broader system is that metric primacy is not viewed as a singular entity in which all evidence converges on a single pulse layer as the beat. Instead, it treats the beat as a multifaceted phenomenon where different aspects of music can simultaneously, and at times variably, create a sense of metric primacy. In many songs, these multiple methods of establishing metric primacy align at a single pulse layer. But other times they do not, resulting in a sense of metric primacy at multiple pulse layers concurrently. This article analyzes these multiple ways to establish metric primacy together. Not only is this approach more theoretically comprehensive, but it also actively pushes new analytical insights to the foreground. Instead of addressing all metric music, this new system is designed specifically for analyzing the beat in popular songs with a consonant, clear, and unchanging quadruple simple meter. This characterizes the majority of popular songs, and this system can therefore be applied effectively across genres and decades.
[1.3] Section 2 begins by describing the inconsistencies above in greater detail. I conclude by introducing the new analytical approach, and the system has three parts. First, a popular song’s drum pattern can create metric primacy at a pulse layer, which I call the drum pattern layer (DPL). Second, research shows that the metrical layer closest to 100–120 beats-per-minute (BPM) also tends to be the most salient, and I call this the absolute time layer (ATL). Third, a person’s perceived beat is different than the DPL and ATL. It involves subjectivity and interpretation, and people can choose to identify different metrical layers as primary. I refer to this as the preferred pulse layer (PPL). In many popular songs, the DPL, ATL, and PPL converge at a single pulse layer. But in other songs, they can create metric primacy at multiple pulse layers simultaneously. As a result, analyzing them together not only formally recognizes each one’s ability to create a sense of metric primacy, but also provides a framework for studying ways that the drum pattern layer, absolute time layer, and preferred pulse layer can interact dynamically in metrically consonant popular songs.
[1.4] With this three-part system established, Section 3 introduces a new term that guides my analyses in Sections 4 and 5. While interpretive multiplicity (Butler 2006) has been used to describe metrically dissonant or ambiguous music with multiple and competing interpretations for the perceived beat, interpretive flexibility refers to metrically consonant popular music with multiple preferred pulse layer options. I show that popular songs can have different degrees of interpretive flexibility, and I describe how people can personally navigate these metrically open passages. Finally, Sections 4 and 5 apply the three-part system and interpretive flexibility to analyze the beat in two musical contexts. Each section identifies a specific way that a song can shift its degree of interpretive flexibility while maintaining its quadruple simple meter. The first is changing between groove patterns with different drum feels and the second is changing between groove patterns with one drum feel and multiple drum feels.(3) These groove changes can be experientially engaging, help articulate musical form, and express extramusical narratives. Analyzing these songs with this article’s new approach fundamentally changes the analytical process and results.
2. The Beat: Existing Definitions and a New Approach
[2.1] There is a long and rich history of studying, theorizing, and analyzing rhythm and meter.(4) In general, rhythm is treated as the real-world timing of sounding musical events and meter is our perception and anticipation of those events (London 2012, 65).(5) One of the basic requirements for something to be considered metric is that there are at least two isochronous and inclusive pulse layers (Yeston 1976, 66) with a preference for three or more (London 2012, 16). Further, virtually all theories of rhythm and meter identify one of these pulse layers as the beat. “Meter is first and foremost grounded in the perception and production of a pulse or tactus [or beat]. The tactus establishes the continuity of musical motion; without it, no sense of meter is possible” (London 2012, 15). Scholars have adopted terms other than beat and tactus (Lerdahl and Jackendoff 1983), such as primary metrical layer (Krebs 1999), primary metrical level (Lester 1986), primary rhythmic level (Cooper and Meyer 1960), and referent time level (Jones and Boltz 1989).
[2.2] The beat’s significance is also recognized specifically in popular music scholarship. Iyer (2002, 398) says, “in groove-based music, this steady pulse [the beat] is the chief structural element.” And Danielsen (2006, 55) states, “in a groove, the rhythm triggers an underlying basic pulse, an internal beat that also forms the basis for how the gesture is in turn played. This internal beat is fundamental for playing, dancing, and listening—in short, for understanding the groove.” Whether it is about metric music in general or popular music in particular, there is agreement that the beat is important.
[2.3] A problem, however, is that there is not agreement about the beat’s precise definition, which has led to inconsistencies with its analytical application.(6) There are at least two types of discrepancies: internal and external. First, there are internal inconsistencies when a definition of beat says that one metrical level is primary, but the definition itself can lead to multiple plausible options. And if research acknowledges this mismatch and cites the role of interpretation, it does not play a meaningful part in the analytical framework. For instance, Lerdahl and Jackendoff (1983, 21, 74) say that the tactus is “the level at which the conductor waves his baton, the listener taps his foot, and the dancer completes a shift in weight
[2.4] London (2012) is another example, which describes beat preferences according to absolute time. “Metric entrainment can occur only with respect to periodicities in a range from about 100 ms to about 5 or 6 seconds. In addition, we may grasp a sense of beat or tempo in a subrange of 200–250 ms to about 2 seconds, although we have a preference for periodicities around 600 ms” (London 2012, 46). Reframed in terms of BPM, listeners can track periodicities between 10–600 BPM, are more comfortable performing the task between 30–240 BPM, and particularly prefer rates around 100 BPM. London also notes, though, that “given the wide range in which a tactus may be perceived (250–2,000 ms), it often is the case that there are several periodicities present in the musical texture, any number of which could be heard as a tactus” (London 2012, 33). Like Lerdahl and Jackendoff, London acknowledges the role of interpretation. But it does not play a meaningful part in his analyses of music with clear and isochronous meters.
[2.5] Second, there are external inconsistencies when definitions of beat say that different musical characteristics create a song’s metric primacy. This is particularly prevalent in popular music scholarship, where some definitions of beat elevate the drumset rhythm while other definitions elevate absolute time. Further, these one-dimensional definitions can also have internal inconsistencies. They can acknowledge other musical characteristics or the role of interpretation, but such concessions remain outside the theoretical framework and its analytical application.
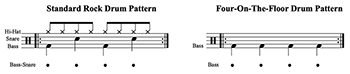
Example 1. The standard rock and four-on-the-floor drum patterns
(click to enlarge)
[2.6] Of all of popular music’s sounding components, the drums have the strongest influence on metric formation. Therefore, many scholars define the beat according to the drumset rhythm. Example 1 notates the two archetypal drum patterns that dominate American popular music. Each one has a specific rhythmic gesture corresponding to a pulse layer that has become marked as a significant, stylistic, temporal cue. To avoid confusion, I call this the drum pattern layer (DPL).
[2.7] The standard rock drum pattern is depicted on the left. Also called a backbeat or backbeat-driven pattern, its most basic design includes alternating bass drum and snare drum attacks at the DPL rate while the hi-hat performs a constant rhythm at the immediately faster pulse layer. Regarding the DPL, Temperley (2018, 69) says that “one particular level in a metrical structure is generally assumed to have privileged status—the tactus. Generally, it is very obvious which level is the tactus in rock, due to the conventional drum pattern.” Similarly, Butler (2006, 87) states that snare-drum backbeats “are so pervasive that this trait can be regarded as normative
[2.8] Since at least the 1970s, a repeating four-on-the-floor bass drum has often been recognized as popular music’s second foundational drum pattern. Shown on the right of Example 1, the bass drum “sounds out the same basic quarter-note pattern throughout most of the performance” (Butler 2006, 4). This drum pattern is particularly prevalent in electronic dance music (EDM) and other electronically produced genres. According to Zeiner-Henriksen (2010, 124–25), “if we grew up moving to music with a four-to-the-floor bass drum, moving becomes a likely affordance of this kind of music whenever we hear it later on, whereas, if we did not, this music may be meaningless or even annoying.”
[2.9] While the drums are important, other aspects of music influence metric formation. One of them is speed, or absolute time. Drawing on theories of embodiment, perception experiments, and corpus studies, some scholars define the beat according to a certain pace of periodicity expressed in terms of BPM. “It is a simple psychological and physical fact that we cannot tap our toes to just anything: if recurrent musical events occur at too great a temporal interval (if the beat is too slow) the rhythmic frame diminishes in salience; if the temporal interval is too small (if the beat is too fast) we will typically find some other way of organizing the events in order to create a meaningful rhythmic frame. More specifically, research on temporal acuity and judgment has demonstrated a significance for periodicities in the 600–700 millisecond [approximately 86–100 BPM] range” (Zbikowski 2004, 279). Iyer (2002) also characterizes the beat with absolute time, although he adopts a much wider BPM range. Drawing a parallel between “musical pulse (tactus)” and physical correlates like “heartbeat, sucking, chewing, walking, sexual intercourse, [and] head nod,” the beat can fall between 60–180 BPM (Iyer 2002, 393). More recently, de Clercq (2016) surveys absolute time’s influence on metric formation in popular music by describing classical theories of rhythm and meter, cognitive science research, perception experiments, corpus studies, and modern music production software. His overview results in the following conclusion: “Since I deal exclusively with meter and bar lengths in pop/rock music, I take 120 BPM to be the best available approximation of ideal tempo, given a time signature of
[2.10] Instead of identifying an optimal BPM rate or range, other scholarship studies how the beat’s speed has shifted in popular songs over the years. According to Schellenberg and Scheve (2012), the average tempo decreases from 116.4 BPM in songs from 1965–1969 to 99.9 BPM in songs from 2005–2009. Temperley (2018, 68–70) also notes a decrease in the average tempo of rock songs from the 1950s–1990s. Finally, White, Pater, and Breen (2022) compares the tactus of premillennial (1955–1997) and postmillennial (2015–2019) American popular music with two methods. The first method measures the tactus only within a set range of 70–140 BPM, which identifies a modest tempo decrease between the two corpora, from 103.91 BPM to 99.91 BPM. The second method measures the tactus according to the backbeat, which identifies a more dramatic tempo decrease from 119.53 to 91.07 BPM.
[2.11] Given the breadth of existing scholarship, any all-encompassing definition of the beat in popular music according to absolute time is overly simplistic. Nevertheless, 100–120 BPM appears to be a fairly agreeable range. For this paper, then, I define the absolute time layer (ATL) as the pulse layer closest to 110 BPM in songs with a quadruple simple meter.
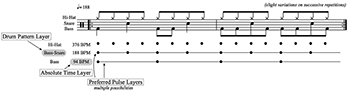
Example 2. “Billie Jean” (Michael Jackson, 1982), Introduction
(click to enlarge and listen)
[2.12] It is surprising that the internal and external inconsistencies above have not received closer scrutiny. One reason for the lack of attention may be that a more comprehensive definition or analytical system appears unnecessary, since a song’s drum pattern layer and absolute time layer are typically the same. Example 2 shows a straightforward example, Michael Jackson’s “Billie Jean.” The song’s buildup introduction (Attas 2015; Spicer 2004) begins with drums alone, performing an unambiguous and moderately paced standard rock drum pattern. The bass line joins next with steady eighth notes, followed by a synthesizer with chordal punctuations. Shown beneath the transcription, the DPL identifies the kick-snare alternation (Pearson 2019) at a rate of 117 BPM, and the ATL recognizes that this same metric layer is also the closest to 110 BPM. The two definitions lead to the same analytical result.
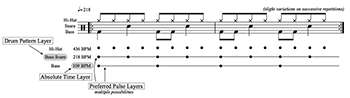
Example 3. “86” (Green Day, 1995), Verse 1
(click to enlarge and listen)
Example 4. “Dammit” (Blink 182, 1997), Verse 1
(click to enlarge and listen)
[2.13] But this is not always the case. There are many popular songs, as a whole or in a particular passage, where defining the beat as either the drum pattern layer or the absolute time layer results in identifying different metrical layers as primary. In these instances, adopting either definition says that one metrical level is the beat and that the other is not. One demonstrative musical context is songs with a fast DPL rate, which is a central characteristic of several popular genres such as metal, punk, punk rock, and pop-punk (Garza 2021; Pearson 2019; Waksman 2009). Examples 3 and 4 transcribe the drum patterns from the first verses of Green Day’s “86” and Blink 182’s “Dammit,” and they include the same beat annotations as Example 2 but with one addition. Shown beneath the staff, both songs have a DPL rate that is twice as fast as the ATL rate. In “86,” the DPL rate is 188 BPM and the ATL rate is 94 BPM. In “Dammit,” the DPL rate is 218 BPM and the ATL rate is 109 BPM.
[2.14] The two songs have consonant, clear, and unchanging quadruple simple meters. But they also have what de Clercq (2016) describes as a particular type of metric conflict. “In a double-time or half-time feel, therefore, the listener is presented with somewhat conflicting metrical information, in that there appear to be two viable metric levels for the perceived beat
[2.15] de Clercq’s quote about songs with a double-time feel recognizes the distinction between and significance of what I call the drum pattern layer, absolute time layer, and preferred pulse layer. But based upon his adopted definition, the ATL is the beat and the DPL and PPL are secondary rhythmic and perceptual observations. This is partially understandable given that his focus is musical form and not musical meter. Doll (2019) is similar. “Since the advent of rhythm ‘n’ blues and rock ‘n’ roll in the 1950s, popular music has tended to feature a clear backbeat, a regular emphasis often played on a snare drum that is typically interpreted by experienced listeners as beats 2 and 4 within a group of four. This practice has major consequences for how listeners decide which rhythmic level the beat occupies; however, there is also experimental evidence to suggest that listeners tend to associate beats with the rhythmic level closest to 120bpm” (Doll 2019, 7). Doll’s goal is to outline some of the practical issues in popular music analysis. But it leaves analysts without a practical solution.
[2.16] As I mentioned in the introduction, my primary goal in critiquing earlier scholarship is to highlight a theoretical and analytical opportunity. Theories of rhythm and meter acknowledge that metrically consonant, clear, and unchanging music can have multiple beat interpretations, and popular music scholarship recognizes that the drum pattern layer, absolute time layer, and preferred pulse layer are conceptually distinct and musically significant ways to define the beat. But there has yet to be an analytical method that moves beyond acknowledgement to a consistent and explicit framework in which the beat in popular music is analyzed according to the DPL, ATL, and PPL together. This article, therefore, formally adopts this three-part analytical approach. It takes the traditional view of beat as a single, primary pulse layer and replaces it with the idea that different aspects of music and the musical experience can simultaneously, and at times variably, create a sense of metric primacy. Not only is analyzing the DPL, ATL, and PPL together more comprehensive, informative, and inclusive compared to existing one-dimensional methods, but it also actively pushes new metric insights to the foreground of analysis. Among other things, it shifts the beat from a singular and often static phenomenon to one that is multifaceted, interactive, interpretive, and structural.
3. An Introduction to Interpretive Flexibility
[3.1] Before applying the three-part system to detailed analyses of popular songs, this section introduces a new term that functions as the general backdrop for Sections 4 and 5. I apply what I call interpretive flexibility to characterize music with a consonant, clear, and unchanging meter where more than one of its pulse layers can function as the perceived beat. I adopt the term interpretive flexibility because it is similar to, but distinct from, a related term: interpretive multiplicity. Interpretive multiplicity has been used to analyze music with dissonant, ambiguous, or changing meters where there are multiple and competing interpretations for the perceived
[3.2] The similarity between interpretive flexibility and interpretive multiplicity is the role of interpretation, which is reflected in the shared word “interpretive.” The difference is that for interpretive flexibility, interpretation is still present when a song has a clear metric framework. This is depicted with the word “flexibility” instead of “multiplicity.” If something is flexible, like a rubber band, it is a single object that has the capacity to change its shape in different contexts. Likewise, popular songs can have a clear metric framework—an unambiguous set of inclusive and isochronous pulse layers—and where someone chooses to interpret the PPL changes its experiential shape. Further, physical objects have different degrees of flexibility, which can also be connected to interpretive flexibility. Examples 2–4 indicate that some songs are likely to have a higher consensus at a single PPL (Example 2), which can be called a lower degree of interpretive flexibility, while other songs are more likely to have two or more PPL interpretations (Examples 3 and 4), which can be called a higher degree of interpretive flexibility.
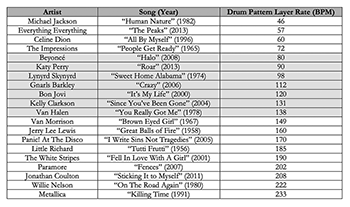
Example 5. Popular songs with a quadruple simple meter and standard rock drum pattern
(click to enlarge)
[3.3] Interpretive flexibility can be applied to any musical style, but the focus of this article is popular music. In principle, all metrically clear popular songs are interpretively flexible and have the possibility, however faint, of multiple preferred pulse layer interpretations. In practice, though, certain songs are more likely than others to have higher or lower degrees of interpretive flexibility. What determines a song’s flexibility is multifactorial, but the DPL rate may be the most influential. Example 5 is a list of popular songs with clear standard rock drum patterns and DPL rates.(11) The rates, however, are distributed fairly consistently from 46–233 BPM, and the songs likely have incremental, and perhaps irregular, differences in their degree of interpretive flexibility.
[3.4] While interpretive flexibility operates on a continuum, the relationship between a song’s drum pattern layer and absolute time layer can serve as a framework for classification. The songs in Example 5 are organized into three groups. Highlighted in gray, the middle group comprises songs in which the DPL and ATL are the same pulse layer, which occurs when the DPL rate is between 73.33–146.66 BPM.(12) The top group comprises songs in which the DPL is the pulse layer slower than the ATL, which happens when the DPL rate falls below 73.33 BPM. Alternatively, the bottom group comprises songs in which the DPL is the pulse layer faster than the ATL, which happens when the DPL rate is above 144.66 BPM. Again, these groups and BPM boundaries are not meant to be dogmatic. They are designed to function as a guide for when a song’s degree of interpretive flexibility shades from one to two preferred pulse layer
[3.5] Further, from top to bottom, the three groups in Example 5 correspond roughly, but not perfectly, with half-time, normal-time, and double-time drum feels (de Clercq 2017b; de Clercq 2016). According to de Clercq (de Clercq 2016, abstract), double-time feel and half-time feels are instances when “the drum pattern can be seen to exist on a metrical level above or below the primary beat level as implied by the time signature,” and a normal-time feel is when they exist on the same metrical level. Absolute time, melodic-harmonic content, and formal prototypes help determine a song’s drum feel, but de Clercq (2017b, 145) also acknowledges that “it is impossible to offer a set of definitive guidelines” to distinguish between, say, a double-time feel and a fast normal-time feel. As a result, the songs at the top of Example 5 may have a half-time feel or a slow normal-time feel, and the songs at the bottom may have a double-time feel or a fast normal-time feel. The purpose of Example 5, of course, is not which drum feel label best fits each song. Rather, it is to demonstrate the broader point that popular songs differ in their degree of interpretive flexibility, and the songs at the bookends are more flexible than those at the center.
[3.6] In songs with a high degree of interpretive flexibility, the likelihood of an individual favoring one preferred pulse layer interpretation over another is also multifactorial. But two of the more influential factors are stylistic familiarity and speed. First, people who are deeply familiar with popular music and its idiomatic features are likely to entrain to the DPL even as it moves to more extreme rates.(14) I use the term drum pattern layer preference to describe a preferred pulse layer selection that is based primarily on the DPL. In contrast, people who are not very familiar with popular music are less likely to weigh the drum pattern layer as heavily when selecting a preferred pulse layer. This difference is likely intensified when a song’s drum pattern varies from the generic realizations in Example 1 with modifications like rhythmic syncopation and instrumental substitutions, where discerning the drum pattern layer requires more style-specific knowledge. Danielsen (2010) describes the necessity of stylistic familiarity and what she calls music’s “virtual reference structures” for metric formation. “They are so important that if a listener fails to catch the ‘correct’ reference structure, he or she may actually hear a rhythm that is entirely different from the one intended” (Danielsen 2010, 19). Drum patterns and their DPL rates are among popular music’s most important virtual reference structures, and whether or not someone “catches” them can strongly impact their sense of meter.
[3.7] Second, speed is a heavily influential factor when determining a preferred pulse layer interpretation. The research referenced above demonstrates that people can identify the perceived beat in a wide but not limitless BPM range, 30–240 BPM according to London (2012) and 60–180 BPM according to Iyer (2002), and that people particularly prefer periodicities around 100–120 BPM (de Clercq 2016; London 2012; Zbikowski 2004).(15) I use the term absolute time layer preference to describe a preferred pulse layer selection that is based primarily on the ATL.
[3.8] An individual’s preferred pulse layer proclivities are multifactorial, dependent on both stylistic familiarity and speed. But in general, when a song has a high degree of interpretive flexibility, people are likely to favor a DPL preference or an ATL preference. Among other things, this can help clarify de Clercq’s quote above regarding the sense of “conflict” about the perceived beat in double-time feel grooves. In short, a person may or may not feel conflicted about their PPL interpretation. For example, in Panic! At The Disco’s “I Write Sins Not Tragedies,” some people will have a drum pattern layer preference, a PPL rate at 170 BPM, and other people will have an absolute time layer preference, a PPL rate at 85 BPM. Within those two groups, some people may experience conflict about where to place their PPL interpretation, feeling the pull of both a DPL and ATL preference. But other people may not have any personal uneasiness, feeling a strong DPL or ATL preference and no interest in the other.
[3.9] Because people may or may not feel uncertain about their PPL interpretations, I like to think of half-time feel and double-time feel grooves, or slow and fast normal-time feel grooves, as places with metric possibilities instead of places with metric conflict. Further, this article’s three-part system for analyzing the beat in popular music has helped me more quickly identify songs with a high degree of interpretive flexibility, and it has helped me imagine, try, and enjoy different ways to navigate metrically stable but interpretively open passages. Butler (2006) uses similar language to describe interpretive multiplicity in EDM. “Electronic dance music invites listeners to chart their way through an interpretively open soundscape in which ambiguous structuring and divergent metrical paths enable diverse experiences of time” (Butler 2006, 166). Half-time and double-time feel grooves are not identical to the music Butler analyzes. But their soundscapes are nonetheless inviting, and whether a person adopts a DPL preference or an ATL preference will create different experiences of time.
4. Changing Drum Feels
[4.1] In Section 2, I showed that the drum pattern layer, absolute time layer, and preferred pulse layer are conceptually distinct and musically significant ways to establish metric primacy, and that analyzing them together is more theoretically comprehensive and analytically illuminating than any one-dimensional approach. In Section 3, I introduced interpretive flexibility as an analogue to interpretive multiplicity, where metrically stable popular songs can differ in having one or two likely preferred pulse layer interpretations, which can invite different modes of metric engagement. These sections focused on individual groove patterns in order to establish the more general point that the beat is multifaceted, interactive, and interpretive even in a consonant, clear, and unchanging quadruple simple meter.
[4.2] Sections 4 and 5 pivot to analyzing popular songs with multiple groove patterns, where certain groove changes maintain the same set of isochronous and inclusive pulse layers, but they also shift the song’s three-part beat annotations and degree of interpretive flexibility. The result is metric constancy and variability together, and this article’s analytical approach highlights how the beat in these musical contexts can be experientially engaging, help express musical form, and parallel extramusical narratives. More specifically, Section 4 analyzes songs that include multiple drum feels, where groove patterns shift between a normal-time feel and a half-time or double-time feel. Section 5 analyzes songs that not only include multiple drum feels, but that also have individual groove patterns that layer two drum feels simultaneously. Each section begins with a generic example to introduce the groove change, demonstrate its impact on the three-part beat labels and degree of interpretive flexibility, and describe its experiential and interpretive openness. I then analyze popular songs that show how each type of groove change can be a single or recurring event.
[4.3] There are many studies of form in popular music, including typologies of sections and song structures (Nobile 2020a; Temperley 2018; de Clercq 2012; Covach 2005), more specific descriptions of sections and their formal functions (Barna 2020; Nobile 2019; Osborn 2013; Summach 2011), and demonstrations of how form can be ambiguous and interpretive (Adams 2019; de Clercq 2017a). This body of research references rhythm and meter to varying degrees. Biamonte (2014) provides an example of how they can be centered in formal analysis. She identifies how “metric dissonances in rock typically contribute to formal articulation at the phrase or section level” (Biamonte 2014, [7.1]). Like metric dissonances, the metrically consonant groove changes analyzed in the remainder of this article also contribute to formal articulations.(16)
Example 6. Normal-time feel to half-time feel groove change
(click to enlarge)
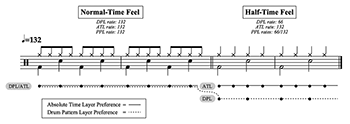
[4.4] While Example 5 above lists popular songs that maintain a single drum feel throughout—performing a half-time, normal-time, or double-time feel from start to finish—popular songs can also shift between drum feels as a way to create rhythmic, metric, and formal contrast. It is most often the case that a song will switch between grooves with a normal-time feel and either a half-time or double-time feel. Example 6 is an acontextual example of the former. A song can begin by establishing a clear metric framework as well as a normal-time feel groove through a standard rock drum pattern. At some point in the song, though, the groove can switch to a half-time feel by changing the drum pattern. The meter remains constant across the groove change in that its pulse layers continue without interruption or recalibration. But the musical events that happen at those pulse layers shift, which affects the sense of metric primacy. The DPL rate halves from 132 to 66 BPM, the ATL rate remains constant at 132 BPM, and degree of interpretive flexibility increases from one to two PPL interpretations.
[4.5] Whether it is this acontextual example or one of the popular songs below, analyzing this type of groove change with any one definition of beat is limiting. Focusing on just the halving DPL rate deemphasizes the passage’s metric consistency. Alternatively, focusing on just the constant ATL rate underplays the fact that there is a significant rhythmic change with metric implications. Finally, focusing entirely on individual PPL interpretations minimizes the sounding musical features that influence beat perception. As a result, the three-part beat labels are necessary in order to formally account for the different types of metric primacy at play simultaneously.
[4.6] The three-part beat labels also help identify the changing degree of interpretive flexibility from one to two PPL options. As mentioned in Section 3, some people may feel torn between the two PPL paths across the groove change—unsure about whether to adopt a DPL or ATL preference in the half-time feel groove—but other people may feel no uneasiness at all. The two interpretations can be more positively approached as different and equally available options for metric engagement.
[4.7] Another benefit of viewing Example 6 as perceptually open is that it provides an alternative to more traditional depictions of changing musical surfaces with multiple perceived beat interpretations. In short, analyzing the beat with anything less than a three-part approach forces an unnecessary sense of conflict onto the music and its perception. One of the most widely applied frameworks for describing listening preferences across a changing musical surface is Imbrie’s (1973) distinction between conservative and radical listeners. “In a conservative hearing the listener seeks to retain the previous pattern as long as possible against conflicting new evidence; in a radical hearing he immediately adjusts according to new evidence” (Lerdahl and Jackendoff 1983, 22–25).(17) Imbrie and others since have adopted the conservative-radical framework to analyze metrically dissonant music, including different interpretations of the beat (Kleppinger 2001, 66; Butler 2001, [9]; Horlacher 2000/2001, fn39). Ohriner (2019, 95) also references Imbrie’s approach in his analysis of groove class patterns in rap, though he replaces the terms with “persistent listening” and “adaptive listening.”
[4.8] With existing one-dimensional approaches to analyzing the beat in popular music, it is easy to imagine how Imbrie’s framework could be applied to Example 6. The normal-time feel groove has one PPL option, the half-time feel groove switches to two PPL options, and the two perceptual paths moving through the excerpt can be identified as conservative and radical. The problem, however, is that framing perceived beat interpretations based upon the drum pattern layer or based upon the absolute time layer leads to opposing views about which interpretation “retains the previous pattern” and which interpretation “adjusts according to new evidence.” For example, defining the beat in popular music as the absolute time layer, like many people do, would mean that an ATL preference across the groove change is conservative and a DPL preference is radical. But defining the beat in popular music as the drum pattern layer, like many people do, would mean that a DPL preference is conservative and an ATL preference is radical. Put differently, a DPL preference is conservative if stylistic familiarity is prioritized, while an ATL preference is conservative if speed is prioritized. My point is not that one of these prioritizations is correct and the other is incorrect. Instead, it is that removing the either-or mentality becomes possible when the beat is analyzed with the three-part system.
“Him and I”
[4.9] In musical practice, changing drum feels can be used flexibly in popular songs in terms of both frequency and genre.(18) Regarding frequency, a change in drum feel can be a one-time event to set apart an individual formal area. The bridge is one of popular music’s nonrecurring sections, and its formal location and function are fairly consistent. Bridges typically begin a popular song’s third formal rotation after two cycles of what Temperley (2011) calls verse-chorus units (VCUs), and they serve as a place of contrast compared to the rest of the song (Nobile 2020a, 106–115; Peres 2016, 148–152; de Clercq 2012, 70).
Example 7. “Him and I” (G-Eazy and Halsey, 2017), Postchorus 2 to Bridge
(click to enlarge and listen)
[4.10] Rapper G-Eazy and singer Halsey’s hit “Him and I” lyrically depicts a deeply committed couple, and the two perform alone for most of the song. With a normal-time feel, G-Eazy raps the verses, and Halsey takes over in the choruses and postchoruses. Example 7 transcribes postchorus 2 into the bridge, which includes the change in drum feel. In the postchorus, Halsey mixes a new vocal hook with the final line of text from the chorus. There is also a four-bar harmonic loop that runs throughout the rest of the song: Am–G–Dm–Em. Finally, the drums perform a slightly embellished standard rock drum pattern with a normal-time feel and a DPL rate of 88 BPM.
[4.11] In the bridge, Halsey and G-Eazy alternate singing and rapping every two bars, which is the only time in the song that they perform melodic material together. Harmonically, the four-bar chord loop is expanded to eight bars, performing the same progression but at half the speed. This parallels the change in drum pattern and the shift to a half-time feel.(19) The two-bar drum pattern in the postchorus is stretched to four bars in the bridge, an almost literal halving of the same rhythmic pattern.
[4.12] In terms of formal function, the switch to a half-time feel is the bridge’s primary element of contrast. In terms of metric experience, the bridge increases the degree of interpretive flexibility from one to two preferred pulse layer interpretations. The notably slow DPL rate of 44 BPM may motivate more people than usual to adopt an ATL preference, since the DPL preference pushes to our perceptual limits according to London (London 2012, 33). Nevertheless, I still find the slow PPL a metrically available and engaging option.
“Love or Let Me Be Lonely”
[4.13] Moving between two drum feels can also be a recurring pattern in a popular song. Like “Him and I,” these cyclical shifts still express formal function and musical narrative. But the repetitions also give people multiple opportunities to experientially engage the groove change. Perhaps the primary formal gesture in American popular music from the 1960s to present is the sense of trajectory across a verse-chorus unit—more specifically, building from verses to choruses. Songs can include additional sections within a VCU such as a prechorus or postchorus, but as Nobile puts it, “the interplay between verse and chorus is the song’s central guiding principle” (Nobile 2020a, 148). Temperley (2018, 160) lists some of the musical characteristics that distinguish the two sections. In comparison to verses, choruses tend to occur second, repeat its lyrics, thicken texturally, add backing vocals, and have a faster harmonic rhythm.
Example 8. “Love or Let Me Be Lonely” (Friends of Distinction, 1970)
(click to enlarge and listen)
[4.14] A change in drum feel is not a feature that typically differentiates verses and choruses, but it is an effective one. Example 8 depicts Friends of Distinction’s “Love or Let Me Be Lonely” with a form diagram and a transcription of the first four bars of verse 1 and chorus 1. The song has three cycles of verse and chorus, and the two sections differ according to all of the characteristics listed above. Verse 1 has a solo vocalist, who presents a relational ultimatum in the first line of text: “Love [me] or let me be lonely.” The harmonic rhythm is one chord per bar, and the progression uses chromaticism atop a pedal tone:
[4.15] Compared to verse 1, chorus 1 pivots both musically and lyrically. Vocally, the solo melody becomes a tightly coordinated four-part texture. Harmonically, the verse’s
“Slow Down”
[4.16] Selena Gomez’s “Slow Down” also features a recurring changes in drum feel, oscillating between a normal-time feel and half-time feel throughout the song. But its pattern of repetition is different than “Love or Let Me Be Lonely” in two ways. First, the switch from a normal-time feel to a half-time feel happens in most but not all of the choruses. Second, there is also a shift to a half-time feel in a subsection of the bridge, which makes it similar in some ways to “Him and I.” These differences highlight the commonplace of flexible song structures and formal functions in twenty-first century pop (Adams 2019; Peres 2016), and changing drum feels can be a salient tool for articulating form.
Example 9. “Slow Down” (Selena Gomez, 2013)
(click to enlarge, see the rest, and listen)
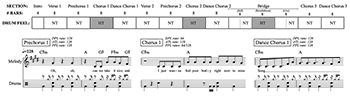
[4.17] Like most pop songs, “Slow Down” has three formal cycles. Shown at the top of Example 9, the first two are VCUs composed of verse, prechorus, chorus, and dance chorus. Adams (2019) describes the rhetorical functions of these sections as expository (verse), intensifying (prechorus), culminating (chorus), and celebratory (dance chorus). In popular styles without a dance chorus, the chorus is a VCU’s climactic section. In popular styles with a dance chorus, however, the chorus and dance chorus “represent culminating points, [but] they serve different expressive functions” (Adams 2019, 36). The chorus is a vocal climax, stating a song’s focal text, and the dance chorus is an instrumental climax, prompting physical movement and dancing (Barna 2020).
[4.18] In the first two VCUs, the drum feel helps set apart the choruses from the other sections. The top row of transcriptions in Example 9 shows the incipits of prechorus 1, chorus 1, and dance chorus 1. The prechorus continues the harmonic progression established in the song’s introduction: one bar of
[4.19] The third formal cycle begins with a bridge and ends with a final chorus and dance chorus. Peres (2016, 146–52) describes pop bridges as typically having two parts: an initial “fall” that recovers energetically from the preceding VCU, and a concluding “rise” that builds to a song’s formal highpoint. In “Slow Down,” however, the bridge includes an intervening eight-bar subsection that functions as a “dance-oriented breakdown” (Peres 2016, 147). The middle transcription in Example 9 shows the second half of the fall and the first half of the breakdown. The fall has a simplified version of the song’s initial chord progression, and a four-on-the-floor bass drum that accelerates rhythmically in the last two bars. The breakdown, then, continues melodically but differs instrumentally. The lyrics repeat, but the harmonies resume the axis progression and the drums switch again to a half-time feel. The result is a new metric feeling and formal function compared to what comes immediately before and after, and another section with an inviting and high degree of interpretive flexibility.
[4.20] Finally, “Slow Down” ends with a chorus and dance chorus. But the third and final iterations differ from the first two VCUs, serving as the song’s musical highpoint. The main difference between choruses 1 and 2 and chorus 3 is that the latter no longer has a half-time feel. Instead, chorus 3 begins by immediately performing the normal-time feel drum pattern that was previously reserved for the dance choruses. Not only does this change create contrast from the preceding formal cycles, but it also helps combine the formal functions of the final chorus and dance chorus. By introducing the normal-time feel drum pattern earlier, the physical climax of the previous dance choruses is shifted forward to the launch of the chorus.
5. Layering Drum Feels
Example 10. Normal-time feel to normal-time+half-time feel groove change
(click to enlarge)
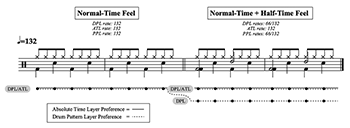
[5.1] Switching between a normal-time feel and a half-time or double-time feel is an effective way for popular songs to create metric variability in metric stability, changing aspects of the beat while maintaining a consonant, clear, and unchanging set of pulse layers. Example 10 shows another groove change that accomplishes this balance of variability and stability, and it too shifts the degree of interpretive flexibility, provides an opportunity for different modes of metric engagement, and can help express formal function and musical narrative. Like Example 6, it begins with a normal-time feel drum pattern. But rather than shifting to a half-time feel, Example 10 adds a half-time feel. This layering effect can be performed by a drummer on a drumset, but it is more common in popular styles when a song’s drum part is created with a digital audio workstation (DAW) or another kind of music technology, where artists and producers can add and remove parts with the click of a button.(22) When two drum feels are superimposed in a single drum pattern, their distinctiveness is normally projected through instrumentation. For instance, a snare drum can perform the normal-time feel backbeat and a clap sound sample can perform the half-time feel backbeat.
[5.2] As before, analyzing the beat in Example 10 and the songs below with the three-part approach formally accounts for the multiple, conceptually distinct, and musically significant types of metric primacy together. There is still a single and uninterrupted set of isochronous and inclusive pulse layers, and the ATL rate is 132 BPM throughout the groove change. The most notable difference, of course, is that the DPL doesn’t just shift from one pulse layer to another, but that it shifts from one pulse layer to two pulse layers: a DPL rate of 132 BPM to 66/132 BPM. The layered drum pattern also creates new possibilities for the preferred pulse layer. There is still an increase in the degree of interpretive flexibility from one to two PPL rate options in terms of BPM: 132→132 and 132→66. But there are also now three interpretive paths in terms of adopting an ATL preference or a DPL preference. Represented by the solid line, an ATL preference focuses on the pulse layer closest to 110 BPM throughout the excerpt: 132→132 BPM. But shown with dotted lines, a DPL preference can mean focusing on the normal-time feel attributes in both grooves (132→132 BPM), or it can mean focusing on the normal-time feel attributes in the first groove and the half-time feel attributes in the second (132→66 BPM). These three interpretive paths are, as Butler says, “diverse experiences of time” afforded by the layered drum pattern’s “interpretively open soundscape” (Butler 2006, 166). While people may gravitate instinctually towards one of these interpretations, they are also invitations to different modes of metric engagement.
“Symphony”
[5.3] Moving between groove patterns with one and multiple drum feels can also be a one-time or recurring event.(23) The first VCU of “Symphony” by Clean Bandit featuring Zara Larsson includes the song’s only layered drum feel, and it also has a normal-time feel groove pattern, a half-time feel groove pattern, and a groove pattern without drums. Larsson sings about a couple’s relationship in three parts: loneliness before having met, joyfulness while together, and incompleteness when alone again. These emotional stages map onto the three formal sections of verse, prechorus, and chorus. But they don’t map in that order, and the drums and the beat are integral in expressing the musical form and text trajectory.
Example 11. “Symphony” (Clean Bandit featuring Zara Larsson, 2018), Prechorus 1 to Chorus 1
(click to enlarge and listen)
[5.4] “Symphony” begins with the song’s thinnest texture. The introduction starts with just a synthesizer, which continues alone into verse 1 to support the vocal melody. In the verse, Larsson describes the pre-relationship stage with phrases like “before all I heard was silence” and “was solo singing on my own.” Shown in Example 11, prechorus 1 shifts musically and lyrically. In addition to introducing a bass line and new chord progression, the prechorus has the song’s first drum sound: a quiet woodblock performing a half-time feel backbeat rhythm. While it is not uncommon for a popular song to withhold the drums until partway through the first VCU, this instrument choice and the half-time feel are less common. Nevertheless, adding the woodblock in the prechorus functions as a textural accumulation compared to the drumless verse, and it makes the prechorus interpretively flexible where a DPL preference at 61.5 BPM and an ATL preference at 123 BPM are both available PPL options. The accumulation can also be linked to the text. Instead of describing the joys of being in a relationship, Larsson jumps ahead to describing the post-relationship emptiness with lines like “and when you’re gone, I feel incomplete.” Placing this relational stage in the prechorus, the in-between formal section that connects verses and choruses, reveals that the text is not progressing chronologically but qualitatively. To love and to have lost, the prechorus, is better than to have never loved at all, the verse, but is not as good as actively giving and receiving love, the chorus.
[5.5] The lyrics in chorus 1, then, describe the relationship itself, ending the first VCU as the emotional and musical highpoint. The focal section introduces more musical elements, including a new drum pattern. It is still a backbeat-only pattern, but it replaces the half-time feel woodblock with a normal-time feel snap. There is a clear progression from no drums in the verse, through a half-time feel in the prechorus, to a normal-time feel in the chorus. This also creates an evolving sense of the beat. Before the chorus, there is a sort of temporal misalignment while Larsson sings about the pre- and post-relationship stages. The ATL rate is constant at 123 BPM throughout the VCU, but the DPL rate is absent in the verse, and it is a different rate in the prechorus. In contrast, Chorus 1 is the first instance where the DPL and ATL align, creating a metric coordination that parallels the couple’s time together.
[5.6] Finally, the layered drum feel in “Symphony” occurs in bars 5–6 of Example 11. In some ways, it is a type of “turning the beat around” (Butler 2001), but the turn looks different. Instead of phasing in and out two groove patterns with different metric frameworks, “Symphony” superimposes two drum feels without disrupting the quadruple simple meter. The beginning of prechorus 1 has the half-time feel woodblock backbeat, the beginning of chorus 1 has the normal-time feel snaps backbeat, and the intervening bars 5–6 sound the 61.5 BPM and 123 BPM DPL rates together. In terms of its rhetorical effect, the layered drum feel momentarily takes on heightened intensification within a section of more general intensification (Adams 2019; Summach 2011).
“Firestone”
Example 12. “Firestone” (Kygo, 2015)
(click to watch video)
[5.7] Kygo’s “Firestone” featuring Conrad Sewell is a tropical house song that includes multiple layered drum patterns. The title, “Firestone,” means a stone that can withstand fire and great heat, or a piece of flint used to start a fire. Both usages are metaphorically appropriate, and the lyrics describe the coming together of two people—albeit in a much more physical and temporary capacity than “Symphony.” Its formal design is based upon EDM’s two-core model (Butler 2006). There are two rotations of verse, build, and core, and the first is preceded by an initial introduction. Example 12 provides a form diagram, incipits for most sections and subsections, and beat annotations. Beyond including multiple instances of a normal-time+half-time feel, “Firestone” also includes normal-time feel grooves, half-time feel grooves, and grooves without drums. In fact, the song is organized in such a way that no two adjacent sections have the same drum feel, and where the majority of sections also include internal drum pattern changes. The result is a constantly evolving musical texture and sense of the beat.
[5.8] The introduction of “Firestone” has two subsections that are arranged, like many popular songs, to build and create momentum towards the first verse (Attas 2015; Spicer 2004). It begins with an instrumental melodic hook performing a tresillo rhythm and a chordal accompaniment composed of mostly whole notes. Though texturally sparse, the first half includes enough rhythmic information to establish the song’s metric framework and an initial sense of the beat. The annotations show that there is no DPL rate, an ATL rate of 114 BPM, and two PPL rates of 57 and 114 BPM. In terms of the PPL options, the faster rate is based upon an ATL preference, but the slower rate fosters a better “compromise” between the faster melodic rhythm and the slower chordal rhythm (Lerdahl and Jackendoff 1983, 73).
[5.9] The second half of the introduction continues the melodic and harmonic layers from the first half and adds the song’s first drum pattern. The introduction’s buildup is not just accomplished through sonic densification, adding the drums, but it is also accomplished through metric intensification by what the drums perform. Rather than a straightforward normal-time feel or half-time feel, the second half sounds a layered normal-time+half-time feel drum pattern. The four-on-the-floor bass drum, the snaps and claps backbeats, and the hi-hat/tambourine project a normal-time feel and a DPL rate of 114 BPM. The pronounced snare drum backbeat, however, projects a half-time feel and a DPL rate of 57 BPM. The result is an evolving sense of metric primacy across the introduction’s two halves. They share the same ATL and PPL options, but the progression from no DPL to two DPLs is a salient shift that helps build to the verse.
[5.10] After the introduction, “Firestone” has two cycles of verse, build, and core. In both cycles, the verses depict the initial attraction between two people (“I’m a flame, you’re the fire / I’m the dark in need of light”), the builds express their coming together (“Our hearts are like firestones / And when they strike, we feel the love.”), and the cores replace the vocal melody with an instrumental motive. Presumably, the two people are together, the fire is struck, and words are no longer necessary.
[5.11] Both rotations musically parallel this extramusical trajectory. In the first, verse 1 returns to the song’s opening sparsity. The instrumental hook is replaced with Sewell’s vocal melody, the chords and their harmonic rhythm remain the same, and the beat annotations show the removal of the DPL. Then, build 1 includes a handful of changes to match the developing lyrics. First, there is a new chord progression that reverses the groove’s opening harmonic direction from Bm–A–G to G–A–Bm. Second, the harmonic layer also performs a different rhythm, replacing the slower whole notes in the verse with a more animated tresillo rhythm. Third, and like “Symphony,” build 1 adds a half-time feel drum pattern by reintroducing just the snare drum backbeat from the drum pattern in the second half of the introduction. These changes create another new set of beat annotations: one DPL rate at 57 BPM, one ATL rate at 114 BPM, and two PPL rates at 57 BPM and 114 BPM.
[5.12] Considering each section in the first formal cycle as a whole, verse 1 and build 1 lead to core 1 as the climax. But similar to the prechorus in “Symphony,” core 1 in “Firestone” has an evolving formal function within its overall formal function. It is an example of what Nobile (2019) calls an anti-telos chorus. The intensification throughout the verse and build creates anticipation for a climactic arrival at the onset of the core, but “Firestone” instead has a sudden and unexpected dissipation of energy. Shown in Example 12, core 1.1 sounds the instrumental melody without drums, removing a key element of cores and the physically engaging drum pattern rate. Nobile describes how an anti-telos chorus can remain subdued throughout—creating even greater anticipation for successive choruses—or it can rebuild in its later phrases. “Firestone” is an example of the latter. Core 1.2 adds the bass line and a four-on-the-floor bass drum rhythm, and core 1.3 introduces intermittent vocal interjections as well as more drum sounds to reinforce the normal-time feel—the snaps and claps backbeats, and the tambourine’s offbeat eighth notes.
[5.13] In terms of musical texture, core 1 is the formal highpoint of the first formal cycle, and core 1 also builds from its beginning to end. Analyzing the beat parallels this reading. Globally, “Firestone” is like “Symphony” in its progression from no drum pattern in the verse, through a half-time feel groove in the build, to a normal-time feel groove in most of the core. But core 1 also includes its own internal trajectory. The lack of drums in core 1.1 means no DPL, which I believe also maintains the possibility of both the faster and slower PPL options. The normal-time feel groove in core 1.2, however, creates the song’s first alignment between the DPL and ATL, and a likely higher consensus at the faster PPL.
[5.14] The second rotation of “Firestone” is similar to the first in its large-scale trajectory towards core 2 as the focal point, and in terms of having an anti-telos chorus. But there are also some textural and metric differences between the song’s two halves. Verse 2 begins, like verse 1, without drums, but it also includes moderate changes to the other instrumental parts. The most notable difference, not shown in Example 12, is the addition of a repeating bell-tone D in the piano that functions like a normal-time feel backbeat rhythm. The harmonic layer also adds a crescendoing tresillo rhythm to the slower rhythmic profile in verse 1. Verse 2 still has no DPL, but I believe these other rhythmic differences tip the degree of interpretive flexibility from two to one PPL option.
[5.15] Next, the build reintroduces the drums. But instead of sounding one half-time feel drum pattern like build 1, build 2 has three different versions of a layered drum pattern by adding elements throughout the section. Example 12 shows that build 2.1 starts with the normal-time feel and half-time feel backbeats as well as with intermittent hi-hat attacks. Build 2.2a then adds the four-on-the-floor bass drum, and build 2.2b layers in the remaining hi-hat/tambourine attacks. Texturally, there is a clear accumulation leading to core 2. In terms of the beat, there is a sense of consistency across the build’s three parts that is captured by the annotations: two DPL rates, one ATL rate, and two PPL rates. Yet, there is also an experiential difference between the beat in build 2.1, build 2.2a, and build 2.2b that is not represented in the annotations. While both DPLs are present and both PPL options are available across the build, I find that the process of adding more normal-time feel elements in the drum part increases the salience of the normal-time feel DPL and its PPL correlate.
[5.16] Finally, core 2 has the same textural and metric direction and destination as core 1, but it has a slightly different path. It begins with the same anti-telos chorus effect by removing the drums, and therefore also removing the DPL. But instead of reintroducing the drums in core 1.2, the four-on-the-floor bass drum rhythm enters four bars earlier in core 2.1b. Next, core 2.2a adds the bass synthesizer, as before, but core 2.2b adds an intermediary step of accumulation in the drum part that wasn’t part of core 1: introducing the offbeat hi-hat/tambourine eighth notes. Core 2.3 adds the final elements of the drum part, the normal-time feel backbeat rhythm. The textural accumulation across core 2 points to the third subsection as the song’s formal climax, and “Firestone” ends with a gratifying alignment between the DPL, ATL, and PPL.
6. Conclusion
[6.1] The beat is far from a one-dimensional, static, and ancillary musical phenomenon. First, it is multifaceted in that the drum pattern layer, absolute time layer, and preferred pulse layer are conceptually distinct and musically significant ways to establish metric primacy in popular music. Analyzing songs with all three together is more comprehensive and illuminating compared to existing approaches. Second, the beat is dynamic in that the relationship between the DPL, ATL, and PPL can differ between songs as well as throughout a song. Interpretive flexibility helps frame some of these relationships and guide analysis. Third, the beat is interpretive in that popular songs can have more than one preferred pulse layer. Passages with a high degree of interpretive flexibility can be more productively understood as places with multiple possibilities for metric engagement instead of places with metric conflict. Finally, the beat is an integral part of popular songs in that it regularly participates in expressing musical form and narrative. The analyses above show that groove changes can shift the sense of metric primacy, and that these metric movements work alongside other musical characteristics to project formal functions and text trajectory.
[6.2] A three-part approach to analyzing the beat in popular music has many benefits, but it is not meant to be unyieldingly formalistic. “Firestone” in particular demonstrates the need for an engaged analyst, since people may have different ideas about a passage’s three-part beat label. Further, this article’s analytical system is not meant to be conclusive. Two readily available next steps for research are to explore people’s actual listening preferences for the groove changes in Sections 4 and 5 through perceptual studies, and to extend a multifaceted approach to beat analysis to other repertoires.
David Geary
Wake Forest University
Scales Fine Art Center, M312
Winston-Salem, NC 27109
gearyd@wfu.edu
Works Cited
Adams, Kyle. 2009. “On the Metrical Techniques of Flow in Rap Music.” Music Theory Online 15 (5). https://mtosmt.org/issues/mto.09.15.5/mto.09.15.5.adams.html.
—————. 2019. “Musical Texture and Formal Instability in Post-Millennial Popular Music: Two Case Studies.” Intégral 33: 33–45. https://www.esm.rochester.edu/integral/33-2019/adams/.
Attas, Robin. 2015. “Form as Process: The Buildup Introduction in Popular Music.” Music Theory Spectrum 37 (2): 275–96. https://doi.org/10.1093/mts/mtv020.
Barna, Alyssa. 2020. “The Dance Chorus in Recent Top-40 Music.” SMT-V 6.4. http://doi.org/10.30535/smtv.6.4.
Biamonte, Nicole. 2014. “Formal Functions of Metric Dissonance in Rock Music.” Music Theory Online 20 (2). https://doi.org/10.30535/mto.20.2.1.
Butler, Mark. 2001. “Turning the Beat Around: Reinterpretation, Metrical Dissonance, and Asymmetry in Electronic Dance Music.” Music Theory Online 7 (6). https://www.mtosmt.org/issues/mto.01.7.6/mto.01.7.6.butler.html.
—————. 2006. Unlocking the Groove: Rhythm, Meter, and Musical Design in Electronic Dance Music. Indiana University Press.
Capuzzo, Guy. 2018. “Rhythmic Deviance in the Music of Meshuggah.” Music Theory Spectrum 40 (1): 121–37. https://doi.org/10.1093/mts/mty005.
Christensen, Thomas, ed. 2002. The Cambridge History of Western Music Theory. Cambridge University Press. https://doi.org/10.1017/CHOL9780521623711.
Cohn, Richard. 2014. “Meter Without Tactus.” Paper presented at the Society for Music Theory Annual Meeting, Milwaukee, WI.
Cooper, Grosvenor, and Leonard B. Meyer. 1960. The Rhythmic Structure of Music. The University of Chicago Press.
Covach, John. 2005. “Form in Rock Music: A Primer.” In Engaging Music: Essays in Music Analysis, ed. Deborah Stein, 65–76. Oxford University Press.
Danielsen, Anne. 2006. Presence and Pleasure: The Funk Grooves of James Brown and Parliament. Wesleyan University Press.
—————. 2010. “Here, There, and Everywhere: Three Accounts of Pulse in D’Angelo’s ‘Left and Right.’” In Musical Rhythm in the Age of Digital Reproduction, ed. Anne Danielsen, 19–35. Ashgate. https://doi.org/10.4324/9781315596983-2.
de Clercq, Trevor. 2012. “Sections and Successions in Successful Songs: A Prototype Approach to Form in Rock Music.” PhD diss., University of Rochester, Eastman School of Music.
—————. 2016. “Measuring a Measure: Absolute Time as a Factor for Determining Bar Lengths and Meter in Pop/Rock Music.” Music Theory Online 22 (3). https://doi.org/10.30535/mto.22.3.3.
—————. 2017a. “Embracing Ambiguity in the Analysis of Form in Pop/Rock Music, 1982–1991.” Music Theory Online 23 (3). https://doi.org/10.30535/mto.23.3.4.
—————. 2017b. “Swing, Shuffle, Half-Time, Double: Beyond Traditional Time Signatures in the Classification of Meter in Pop/Rock Music.” In Coming of Age: Teaching and Learning Popular Music in Academics, ed. Carlos Rodriguez, 136–67. Maize Books.
—————. 2021. “The Logic of Six-Based Minor for Harmonic Analyses of Popular Music.” Music Theory Online 27 (4). https://doi.org/10.30535/mto.27.4.4.
Doll, Christopher. 2019. “Some Practical Issues in the Aesthetic Analysis of Popular Music.” In The Routledge Companion to Popular Music Analysis: Expanding Approaches, ed. Ciro Scotto, Kenneth Smith, and John Brackett, 3–14. Routledge. https://doi.org/10.4324/9781315544700-1.
Garza, Jose M. 2021. “Transcending Time (Feels): Riff Types, Timekeeping Cymbals, and Time Feels in Contemporary Metal Music.” Music Theory Online 27 (1). https://doi.org/10.30535/mto.27.1.3.
Hanenberg, Scott J. 2020. “Using Drumbeats to Theorize Meter in Quintuple and Septuple Grooves.” Music Theory Spectrum 42 (2): 227–46. https://doi.org/10.1093/mts/mtaa005.
Hasty, Christopher F. 1997. Meter as Rhythm. Oxford University Press.
Horlacher, Gretchen. 2000/2001. “Multiple Meters and Metrical Processes in the Music of Steve Reich.” Intégral 14/15: 265–97. https://www.esm.rochester.edu/integral/14-15-2000-2001/14-15-horlacher/.
Hudson, Stephen S. 2022. “Bang your Head: Construing Beat through Familiar Drum Patterns in Metal Music.” Music Theory Spectrum 44 (1): 121–40. https://doi.org/10.1093/mts/mtab014.
Imbrie, Andrew. 1973. “‘Extra’ Measures and Metrical Ambiguity in Beethoven.” In Beethoven Studies, ed. Alan Tyson, 45–66. W. W. Norton.
Iyer, Vijay. 2002. “Embodied Mind, Situated Cognition, and Expressive Microtiming in African-American Music.” Music Perception 19 (3): 388–89. https://doi.org/10.1525/mp.2002.19.3.387.
Karpinski, Gary. 2000. Aural Skills Acquisition: The Development of Listening, Reading, and Performing Skills in College-Level Musicians. Oxford University Press.
Kleppinger, Stanley V. 2001. “Metrical Issues in John Adam’s ‘Short Ride in a Fast Machine.’” Indiana Theory Review 22 (1): 65–81. https://digitalcommons.unl.edu/musicfacpub/52/.
Kozak, Mariusz. 2021. “Feeling Meter: Kinesthetic Knowledge and the Case of Recent Progressive Metal.” Journal of Music Theory 65 (2): 185–237. https://doi.org/10.1215/00222909-9143190.
Krebs, Harald. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195116236.001.0001.
Kvifte, Tellef. 2010. “Composing a Performance: The Analogue Experience in the Age of Digital (Re)Production.” In Musical Rhythm in the Age of Digital Reproduction, ed. Anne Danielsen, 213–29. Ashgate. https://doi.org/10.4324/9781315596983-13.
Lerdahl, Fred, and Ray S. Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Lester, Joel. 1986. The Rhythms of Tonal Music. Southern Illinois University Press.
London, Justin. 2006. “Metric Fake Outs.” Excel spreadsheet. https://www.carleton.edu/people/jlondon/downloads-and-media/.
—————. 2012. Hearing in Time: Psychological Aspects of Musical Meter. 2nd ed. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199744374.001.0001.
Nobile, Drew. 2019. “Anti-Telos Choruses in Recent Pop.” Paper presented at the Society for Music Theory Annual Meeting, Columbus, OH.
—————. 2020a. Form as Harmony in Rock Music. Oxford University Press. https://doi.org/10.1093/oso/9780190948351.001.0001.
—————. 2020b. “Double-Tonic Complexes in Rock Music.” Music Theory Spectrum 42 (2): 207–26. https://doi.org/10.1093/mts/mtaa003.
Ohriner, Mitchell. 2019. Flow: The Rhythmic Voice in Rap Music. Oxford University Press. https://doi.org/10.1093/oso/9780190670412.001.0001.
Osborn, Brad. 2010. “Beats that Commute: Algebraic and Kinesthetic Models for Math-Rock Grooves.” Gamut: Online Journal of the Music Theory Society of the Mid-Atlantic 3 (1). https://trace.tennessee.edu/gamut/vol3/iss1/4 .
—————. 2013. “Subverting the Verse/Chorus Paradigm: Terminally Climactic Forms in Recent Rock Music.” Music Theory Spectrum 35 (1): 23–47. https://doi.org/10.1525/mts.2013.35.1.23.
—————. 2017. Everything in its Right Place: Analyzing Radiohead. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780190629229.001.0001.
Pearson, David. 2019. “Extreme Hardcore Punk and the Analytical Challenges of Rhythm, Riffs, and Timbre in Punk Music.” Music Theory Online 25 (1). https://doi.org/10.30535/mto.25.1.5.
Peres, Asaf. 2016. “The Sonic Dimension as Dramatic Driver in 21st-Century Pop Music.” PhD diss., University of Michigan.
Jones, Marie R, and Marilyn Boltz. 1989. “Dynamic Attending and Response to Time.” Psychological Review 96 (3): 459–91. https://doi.org/10.1037/0033-295X.96.3.459.
Richards, Mark. 2017. “Tonal Ambiguity in Popular Music’s Axis Progressions.” Music Theory Online 23 (3). https://doi.org/10.30535/mto.23.3.6.
Schellenberg, E. Glenn, and Christian von Scheve. 2012. “Emotional Cues in American Popular Music: Five Decades of the Top 40.” Psychology of Aesthetics, Creativity, and the Arts 6 (3): 196–203. https://doi.org/10.1037/a0028024.
Spicer, Mark. 2004. “(Ac)cumulative Form in Pop-Rock Music.” Twentieth-Century Music 1 (1): 29–64. https://doi.org/10.1017/S1478572204000052.
Summach, Jay. 2011. “The Structure, Function, and Genesis of the Prechorus.” Music Theory Online 17 (3). https://doi.org/10.30535/mto.17.3.2.
Temperley, David. 2011. “The Cadential IV in Rock.” Music Theory Online 17 (1). https://doi.org/10.30535/mto.17.1.8.
—————. 2018. The Musical Language of Rock. Oxford University Press. https://doi.org/10.1093/oso/9780190653774.001.0001.
Waksman, Steve. 2009. This Ain’t the Summer of Love: Conflict and Crossover in Heavy Metal and Punk. University of California Press.
White, Christopher W., Joe Pater, and Mara Breen. 2022. “A Comparative Analysis of Melodic Rhythm in Two Corpora of American Popular Music.” Journal of Mathematics and Music 16 (2): 160–82. https://doi.org/10.1080/17459737.2022.2075946.
Yeston, Maury. 1976. The Stratification of Musical Rhythm. Yale University Press.
Zbikowski, Lawrence. 2004. “Modelling the Groove: Conceptual Structure and Popular Music.” Journal of the Royal Musical Association 129 (2): 272–97. https://doi.org/10.1093/jrma/129.2.272.
Zeiner-Henriksen, Hans T. 2010. “Moved by the Groove: Bass Drum Sounds and Body Movements in Electronic Dance Music.” In Musical Rhythm in the Age of Digital Reproduction, ed. Anne Danielsen, 121–29. Ashgate. https://doi.org/10.4324/9781315596983-8.
Footnotes
1. Isochronous means that the pulses of each layer are regularly recurring and equally spaced (Krebs 1999, 22). Inclusive means that the pulses of a particular layer coincide with a pulse of every faster-moving layer (Krebs 1999, 29).
Return to text
2. This definition of beat is different than the term’s usage in hip-hop and rap, where the beat refers to “every musical layer except the vocals” (Adams 2009, fn7).
Return to text
3. Following Attas (2015), I use “groove” and “groove pattern” interchangeably to describe a song’s repeating instrumental accompaniment.
Return to text
4. For a historical overview of rhythm and meter, see the relevant chapters in Christensen (2002, 628–725).
Return to text
5. Hasty (1997) rejects this interdependent approach to rhythm and meter, preferring instead to treat “meter as rhythm.”
Return to text
6. Cohn (2014) also identifies the inconsistent treatment of primary beat in music-theoretical scholarship.
Return to text
7. Drum feels are described more in Section 3 below.
Return to text
8. Again, Lerdahl and Jackendoff (1983) and London (2012) acknowledge the role of interpretation in beat perception, but it is not a focal part of their theories and analyses. Karpinski (2000, 20) also mentions multiple perceived beat interpretations in music with a clear metric framework from a pedagogical perspective.
Return to text
9. See Hudson (2022, 129–30) for a similar characterization of multiple perceived beat options in metal music, as expressed through headbanging.
Return to text
10. See Krebs (1999) for a more detailed overview of metric consonance and dissonance.
Return to text
11. Example 5 is a personal compilation of popular songs. It was not taken from a particular source or corpus.
Return to text
12. This BPM range is determined by the DPL rate’s proximity to the optimal ATL rate in terms of BPM. In other words, 73.33 BPM and 146.66 BPM are both 36.66 BPM away from 110 BPM.
Return to text
13. Further, it is unlikely that a song’s degree of interpretive flexibility increases indefinitely and uniformly as a song’s DPL rate moves away from the optimal ATL rate of 110 BPM. This warrants further research that extends beyond the scope of this paper.
Return to text
14. A specific example is fans of metal music, which regularly has songs with fast DPL rates (Hudson 2022).
Return to text
15. London (2012, 64) also notes that a person’s preferential speeds for the perceived beat vary slightly throughout his or her life.
Return to text
16. Garza (2021) also studies drum feels (and prefers “time feels”), but his focus is not on the beat or form. Instead, he studies how different instrumental parts in contemporary metal music like the guitar, bass, and cymbals can “reinforce, clarify, or contradict a feel” that is established by the alternation of kick and snare (Garza 2021, [7]). Further, Garza adopts a one-dimensional definition of beat according to absolute time. “Time feels affect the way listeners perceive music metrically by maintaining a tempo while altering the frequency of the kick-snare alternation. As a result, feels make the music seem faster or slower while not actually affecting the speed of the beat” (Garza 2021, [5]).
Return to text
17. Imbrie (1973) does not provide explicit definitions for conservative and radical hearings.
Return to text
18. Regarding flexibility of decade and genre, songs with a change in drum feel include “25 or 6 to 4” by Chicago (1970), “Take On Me” by Aha (1985), “Easily” by Red Hot Chili Peppers (1999), “Big Girls Don’t Cry” by Fergie (2006), “Endeavours” by MitiS (2013), “Bang Bang” by Green Day (2016), “Egypt” by Bethel Music and Cory Asbury (2020), and “Good 4 U” by Olivia Rodrigo (2021).
Return to text
19. Lerdahl and Jackendoff (1983, 73–74) list harmonic rhythm as an influencing factor for tactus selection. de Clercq’s (2016) one analysis of an intra-opus change in drum feel is “Should I Stay or Should I Go” by The Clash (1982), where the drum pattern changes from a normal-time feel in the verses to a double-time feel in the choruses, but the song “retains the same harmonic structure, as well as most of the melodic structure” (de Clercq 2016, [3.2]). I have found that though changing drum feels are driven by the drum pattern, they can also involve other rhythmic, melodic, and harmonic shifts—all of which can impact the PPL. See also Garza (2021).
Return to text
20. Another popular song that uses a straight-four snare drum rhythm is “Satisfaction” by The Rolling Stones (1965).
Return to text
21. For more about tonal ambiguity, multiple tonal centers, and double-tonic complexes in popular music, see de Clercq (2021), Nobile (2020b), and Richards (2017).
Return to text
22. See Kvifte (2010) for an overview of DAWs, which also discusses the fuzzy boundaries music technology creates between recording, composition, and performance. See Butler (2006, 47–75) for a similar discussion about music technology and the fuzzy boundaries between producers, DJs, and audiences in EDM.
Return to text
23. While a change in drum feel occurs in popular songs across decades and styles, moving between groove patterns with one and multiple drum feels is more common in EDM and EDM-influenced genres due to their digital construction with DAWs and other kinds of music technology. There are songs, however, with drummers performing these types of groove changes on a drumset. Examples include “Unstoppable God” by Elevation Worship (2014) and “Before You Go” by Lewis Capaldi (2019).
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Lauren Irschick, Editorial Assistant
Number of visits:
14794