Reconstructing the Paris Conservatory’s Cours d’Harmonie 1812–1844: Discipline, Sources, Theory, and Method
Michael Masci
KEYWORDS: Paris Conservatory; partimento; Victor Dourlen; history of theory; music theory pedagogy; history of harmony
ABSTRACT: A growing body of scholarship on practical music theory traditions, and Italian partimento pedagogy in particular, has begun to shed light on the nature of harmony pedagogy prior to the development of functional tonal theory. The methods of the Italian schools were not adopted wholesale in Paris, but rather interacted with local pedagogies, resulting in an institutionally-specific approach to teaching harmony. In Paris, the study of written harmony relied on a contrapuntal method for polyphonically realizing and elaborating a series of canonic figures in the form of cadences (progressions); marches (sequences); modulations; broderies (non-harmonic tones), altérations (chromatic alterations); and pédales (pedals). This article reconstructs the basic catalog of the first four of these elements which served as the cornerstone of the harmony course at the Paris Conservatory across the nineteenth century. In addition, it illustrates how the incorporation of these elements within the institutional confines of the Conservatory resulted in both their distinctive pedagogical treatment and the advancement of a specific compositional method.
DOI: 10.30535/mto.28.4.4
Copyright © 2022 Society for Music Theory
1. Introduction
[1.1] A growing body of scholarship on practical music theory traditions, and Italian partimento pedagogy in particular, has begun to shed light on the nature of harmony pedagogy prior to the development of functional tonal theory.(1) As a historical matter, students in the conservatories of Milan and Naples—or, later, Paris—never learned that “I” ought to move to “ii6” or “IV” then onto “V7.” Research by Gjerdingen, Sanguinetti, and others has shown that, rather than relying on prescriptive concepts for harmonic function and root progressions, harmony pedagogy in eighteenth-century Italian conservatories proceeded by means of simple keyboard figures along with their subsequent, contrapuntal elaborations (Gjerdingen 2007, Sanguinetti 2012, IJzerman 2018). Students would internalize a catalog of these various patterns—or “schemata,” to borrow Gjerdingen’s characterization—which provided a cognitive foundation for elaboration in the form of semi-improvised keyboard exercises, or partimenti. Many of these partimenti and their constituent figures, along with other exercises in solfège and counterpoint, found their way to the Paris Conservatory in the early nineteenth century. As Cafiero and Gjerdingen have also shown, we can trace the transmission of these exercises by surveying French pedagogical materials, including harmony texts and keyboard manuals (Cafiero 2007, Gjerdingen 2014).(2)
[1.2] Yet the methods of the Italian schools were not adopted wholesale in Paris. Rather, the ultramontane theory interacted with local pedagogies, resulting in a unique and institutionally-specific approach to teaching harmony.(3) In Paris, the study of written harmony specifically relied on a contrapuntal method for polyphonically realizing and elaborating a series of canonic figures in the form of cadences (progressions); marches (roughly translated as “sequences”); modulations; broderies (non-harmonic tones, literally melodic “embroidery”); altérations (chromatic alterations resulting in non-diatonic sonority types); and pédales (pedals).(4) Yet of all these figures, it was the collection of “cadences et marches” that was most essential to the course, serving as the foundation for all subsequent techniques. This catalog of canonic figures and their related sonority types would be refined over decades, forming the basis of the discipline for much of the nineteenth century. In this article, following the model of previous partimenti scholarship, I reconstruct a preliminary catalog of these cadences, marches, and their contrapuntal elaborations that served as the foundation of the Conservatory harmony course in the early nineteenth century. More narrowly, I focus on the first iteration of the harmony course as created by the Conservatory’s inaugural cohort of faculty and students.
[1.3] This article also extends recent partimenti scholarship in two additional ways. First, I contextualize the Paris Conservatory’s particular brand of harmony pedagogy in its specific disciplinary and institutional setting, examining the various structures that constrained the study of harmony at the school. In particular, I trace the broad network of subdisciplinary courses, institutional procedures, and pedagogical texts that articulated and regulated the study of harmony. Methodologically speaking, understanding the relationship between the courses and textbooks that circulated within this structure, and how these relationships are reflected across different genres of harmony and composition texts, is essential to arriving at an accurate reading of the discipline and its textual sources; not all harmony treatises served the same purpose or implicated the same sorts of disciplinary relationships. (Additionally, tracing these relationships will also serve as an initial review of numerous unfamiliar music theoretical texts written in early nineteenth-century Paris.)
[1.4] Second, following the reconstruction of the catalog of figures that comprised the course’s music theoretical and pedagogical content, I propose a compositional method for putting this catalog of figures into practice. More practically, this method may be useful to today’s classroom teacher who is interested in adopting various historically informed pedagogies, whether Italian partimenti or French harmonie. More generally, this method points to an important analytic distinction. Namely, distinct from its music theoretical content, which outlined the formal definition and construction of fundamental sonorities, cataloged cadences et marches, etc., the course aimed to transmit a disciplined method for harmonizing progressively complex melodies and basses. This method taught students to move from sketch to complex realization through the deployment of increasingly elaborate sonorities and figures. As Gjerdingen describes, this method amounted to the musical equivalent of the beaux arts method that painters learned in the French academy (2020). Key to reconstructing this beaux arts method of harmony, then, is not only an analysis of the course’s basic catalog of cadences and marches, but also a consideration of how daily classroom exercises prompted students with specific and ordered tasks. As suggested above, the Conservatory harmony course and its text did not outline a linear process for harmonizing a bass in the manner of “chord x should move to chord y,” etc., which offers the tempting prospect, however inadvertent, of conflating a descriptive theory of harmonic syntax with a linear method for harmonizing a bass.(5) In recuperating a distinction between descriptive theory and practical method, this article attempts to take one step to reimagining how this beaux arts method may be brought to bear in the harmony classroom.
[1.5] Taken together, then, this article reconstructs the harmony course at the early Paris Conservatory from without as well as from within. I begin by considering the broad disciplinary structures of composition study at the Conservatory that constrained the workings of the harmony course, focusing in particular on the teachings and writings of the school’s initial cohort of faculty and students, among them Cherubini, Catel, Dourlen, and Leborne (Section 2). These faculty members’ work reflects the operations of a disciplinary network: a series of imbricated courses, administrative procedures, and texts that articulate the content and constrain the purview of the school’s harmony course. Tracing this structure reveals important course details and provides a key for interpreting extant texts and sources associated with the harmony course. Having established this broad disciplinary context, I then turn to a detailed examination of the course’s theoretical content and method, reconstructing the catalog of cadences and marches that served as its foundation (Section 3). For the sake of concision, the initial account of the harmony course offered here focuses on four primary types of figures that served as the pillars of the nineteenth-century discipline in Paris, namely those for cadences, marches, modulations, and broderies.
2. Reconstructing a Disciplinary Network: Structures, Sources, and Organization of the Cours d’Harmonie at the Early Paris Conservatory
[2.1] Institutional Structures
[2.1.1] During the nineteenth century, the Paris Conservatory administered the study of composition as a strict hierarchy of interrelated courses, coordinated by a network of administrative procedures for the admission, examination, and promotion of students.(6) The course in harmony played a central role in this structure. Jeunes aspirants in composition began their studies where all Conservatory students began, with a mandatory course in rudiments and solfège. After successfully completing the solfège course, students approved for composition study would then enter the year-long harmony course. Typically, this took the form of either an initial course in keyboard harmony followed by a course in written harmony, “harmonie écrite,” or a combined course in both written and keyboard harmony, “harmonie et accompagnement pratique.” From there, students progressed on to courses in counterpoint and fugue as well as lyric composition.(7) Admission to each of these upper-level courses was extremely competitive, with each successive course enrolling fewer students than its prerequisite. (8)
[2.1.2] Admission to any of the composition courses required the instructor’s permission as well as approval by the school’s director. Obtaining this permission was in no small part contingent upon a student’s success in the two-tiered selection process of annual exams and concours (competitions), which identified those students skilled enough to advance to the next level of study. For each course, the school’s independent examination committee would administer semester exams, on the bases of which they would admit selected students to the annual July concours. Exams and concours for written harmony courses included an unfigured bass, approximately seventy-five measures in length, and a melody, approximately sixty measures long, which were to be harmonized in four-part, vocal polyphony written in vocal clefs. Exams and concours for the combined course in written and keyboard harmony additionally included a figured-bass example to be executed at the piano at sight and, after 1879, a melody to be harmonized at the piano. The concours in harmony, as well as that in counterpoint and fugue, awarded up to two first prizes, two second prizes, and two or three accessits (or “runners-up”). Prizewinners in the concours received gifts of printed music or musical instruments of French manufacture. Arguably, however, the most significant award to be obtained from a first- or sometimes second-place finish in the harmony concours was admission into the upper-level composition courses.
[2.1.3] This strict hierarchical course administration, which governed a student’s advancement through the composition disciplines, also extended to faculty hiring and promotion. Similar to Neapolitan mastricelli, The Paris Conservatory employed répétiteurs, which is where most Paris faculty began their careers. Prize-winning students in harmony, for instance, often served as répétiteurs for the solfège course, where they accompanied solfège exercises from figured bass. Successful counterpoint students similarly served as adjuncts to professors in harmony, often lecturing to auditors. Along these lines, the first full-time post held by most junior faculty was often a professorship in solfège, with some then moving up the ranks to professor of harmony and, in select cases, to the rank of professor of counterpoint or lyric composition. The Conservatory’s preference for hiring and promoting former and prize-winning students meant that by the end of their careers, most composition faculty had traversed the same institutional path twice, first as students and then a second time as faculty. This practice established an important patronage system between professor and prized student, ensuring a longitudinal transmission of the institution’s particular approach to composition pedagogy, which, as a result, was slow to change and insulated from the external influence of other schools.
Example 1. Composition subdisciplines at the Paris Conservatory (École royale de musique et de déclamation), 1816–1865
(click to enlarge and see the rest)
[2.1.4] Despite the strict administration of the composition subdisciplines, the prescribed content of each course, along with the resulting relationships among the courses, underwent regular revision. Each of the Conservatory’s four primary administrations during the nineteenth century, headed by Bernard Sarrette (1795–1814), Luigi Cherubini (1822–41), Daniel Auber (1842–71), and Ambroise Thomas (1872–96), would rearrange the scope and content of the various composition courses and of the harmony course in particular.(9) When it came to the lower-level disciplines, a central concern was whether to treat harmony as a keyboard discipline—taught primarily as a course in extemporaneous realization of figured bass exercises and partimenti—or as a written discipline—taught primarily as a propaedeutic to counterpoint in which students would learn the basics of writing vocal polyphony. The Conservatory’s answer to these basic disciplinary questions changed over the course of the nineteenth century, resulting in a perennial repositioning of the harmony and counterpoint courses within the curriculum. Example 1 summarizes the various configurations of the composition subdisciplines, along with their instructors, under the various administrations.(10) As shown there, the 1830s witnessed a marked proliferation of courses associated with composition study. By 1835 the Conservatory offered multiple sections of “style, genre, and lyric composition;” two sections of counterpoint and fugue, each with a preparatory section; two sections of harmonie et accompagnement pratique, also with two additional preparatory sections; and a course on accompanying from figured bass. With regard to the harmony course, the most significant disciplinary change occurred in 1823 when Cherubini combined the courses in written harmony and keyboard harmony. The class in harmonie et accompagnement pratique would exist at the Conservatory until the two disciplines were formally separated once again, in 1878, into “harmonie” and “accompagnement au piano.” In addition, starting in 1840, the Conservatory reintroduced the course on written harmony that existed alongside the combined course.
Example 2. Selected list of harmony and counterpoint texts produced by Conservatory faculty, arranged by course, 1801–1870
(click to enlarge)
[2.1.5] The regular reconfiguration of the composition subdisciplines also brought with it a corresponding proliferation in official pedagogical texts approved for use at the Conservatory, both in number and in kind. As the types of composition courses multiplied, so did the genres of corresponding texts. For each new subdisciplinary course, given its specific purview and disciplinary positioning, a new genre of text was created. Example 2 summarizes some of the central texts produced by Conservatory faculty across composition subdisciplines between 1816 and 1870, with a marked increase in the production of texts occurring through midcentury. The swirl of generic language used in the texts’ titles provides a more nuanced map of the relationship between subdisciplinary courses compared to the otherwise strictly hierarchical administration of the composition subdisciplines. It helps reveal the specific ways in which the particular brand of harmonic theory being taught at the Conservatory—even as it was reorganized and presented in various textual and generic guises—circulated throughout numerous courses, crisscrossing various subdisciplinary territories and boundaries.
[2.1.6] Noting the recurrences of a few generic formulations in titling provides a helpful starting point for tracing the relationships among composition subdisciplines and their respective genres of texts. Perhaps the most common formulation is that of “harmonie théorique et pratique,” roughly “theoretical and practical harmony.” The term “théorique” in these titles often refers to the inclusion, within the text, of a formal exposition of the essential elements and principles of harmony, including definitions for rudiments such as meter, rhythm, intervals, chord construction, and chord qualities. Such material appeared in texts across all subdisciplines, often as a summary of definitions along with the rudiments of notation. Its use in combination with the term “pratique” refers to the equal inclusion of exercises in written harmony or keyboard partimenti, or both. Note that the use of the term “pratique” does not stipulate the nature of the practice described by the text, e.g., written polyphony or keyboard harmony; instead, it merely indicates that the text includes exercises of some sort. Thus, while Savard’s Études d’harmonie pratique is a collection of written exercises in a vocal, contrapuntal style lacking any formal exposition of harmonic elements, Bazin’s Cours d’harmonie théorique et pratique not only formally outlines the elements of harmony, but also includes both written and keyboard exercises. A related formulation is that of “harmonie et accompagnement,” indicating the inclusion of keyboard exercises, usually partimenti. Similarly, when “harmonie” is used exclusively, such as in Reber’s Traité d’harmonie, it often entails just that: written harmony with no keyboard partimenti. Last, some texts are referred to as “traités” while others are labeled specifically as “cours.” In many cases, the latter term carries with it very particular connotations, especially if the text had been approved for use at the Conservatory. Texts deemed suitable for use in the Conservatory’s composition courses meant that the text was constrained in terms of length as well as content. The material had to be able to be covered in nine months—the typical duration of the school’s courses—and its content had to conform to the Conservatory curriculum, preparing students for the semester exams and annual concours. A text described as a “cours” might therefore be more concise, obligated to eschew theoretical speculation regarding the origins of harmony, the nature of the fundamental bass, and the like.
[2.1.7] The changing conception of harmony as a discipline thus manifested itself in numerous ways across the Conservatory as the frequent renegotiation of disciplinary boundaries gave rise to a variety of theoretical and pedagogical works. Viewed as a whole, the specific music theoretical content distributed across non-congruent theoretical genres respectively associated with composition subdisciplinary courses points to a complex interaction between the disciplines’ practical content, the discursive, texted representation of those practices, and the various institutional structures and networks—including those of promotion, admission, and patronage—that regulated and circulated that content. It is this imbrication of practice, text, and institutional structure, I would suggest, that constituted the discipline of composition at the Conservatory. Amidst these shifting interactions, we can trace how relatively distinct configurations of these elements emerged and receded across the nineteenth century as they coalesced into relatively stable disciplinary systems.
[2.1.8] The first of these systems emerged during the founding years of the Conservatory, around 1801. The original faculty included Gossec, Méhul, and Cherubini, who served both as professors of composition and Inspectors of Instruction; Catel and Berton as professors of harmony; among the students were Dourlen, Leborne, and Panseron, who would themselves become future Conservatory faculty and authors of important texts. The close patronage relationships developed between this first generation of faculty and their students, buttressed by the longevity of the tenure of these faculty, along with the Conservatory’s preference for promoting former prize-winning pupils, transmitted a common disciplinary conception of harmony with its specific techniques and exercises. This particular conception of the harmony course would, given these porcesses of official transmission, transcend the school’s 1814 closure, reemerging to be cultivated under Cherubini’s directorship into the 1840s.(11) We can trace the broad workings of this disciplinary network, along with what it contended to be the proper content of the harmony course, by briefly tracing the single line of disciplinary transmission that runs through the writings of Catel, Cherubini, Dourlen, and Leborne.
[2.2] Sources and Structures of Transmission
[2.2.1] The Paris Conservatory’s first official harmony text came in the form of Charles-Simon Catel’s 1801 Traité d’harmonie. As a matter of genre, Catel’s treatise served more as a theoretical tract than a practical harmony manual. The Conservatory commissioned the work from Catel, the school’s inaugural harmony professor, in conjunction with ongoing curricular reforms at the school. These reforms charged Conservatory faculty with creating a series of elements texts for use in every discipline.(12) In accordance with this charge, the Traité outlines all the rudiments and procedures necessary for the study of harmony. Furthermore, as a theory of elements, Catel made sure to construct his work in a way that vouched for its intellectual rigor, organizing it loosely as a “demonstration” that deduced the elements of harmony from a handful of compositional procedures applied to basic, irreducible sonority types, in this case, so-called “natural” harmonies. Notably, as I will discuss below, the text significantly limits its initial chord catalog of natural harmonies, rejecting Rameau’s derivation of natural sonority types.(13) Yet while Catel’s text satisfied its institutional charge of being both formal and comprehensive, the work contained little in the way of actual figured and unfigured bass exercises, suggesting that the text was not primarily intended for classroom use; for our purposes, it fails to convey much information about the course’s practical day-to-day pedagogy. Instead, much of the earliest documentation regarding the actual practical application of these elements comes to us from the writings of one of Catel’s first students, Victor Dourlen.
[2.2.2] Dourlen served as the sole instructor of the men’s section of harmonie et accompagnement pratique from 1816–1842, spanning the entire combined tenures of Perne and Cherubini as school directors. Like most Conservatory faculty of his generation, Dourlen worked his way through the Conservatory’s ranks as one of the school’s earliest star pupils and then as a faculty member.(14) During his long tenure, Dourlen authored a number of harmony texts, with his first and arguably most significant contribution to the school’s harmony pedagogy coming during his initial post as Berton’s répétiteur. In that position, and in collaboration with Catel, he produced a collection of figured and unfigured bass exercises for daily classroom use. Aimé Leborne (1797–1866), who was enrolled in Berton’s 1812 course, would years later redact the exercise book he kept from Berton’s class and leave it to the Conservatory library. Leborne’s notebook records a trove of 151 dated exercises, one for each day of the course, composed by Dourlen and Catel. In addition to providing a comprehensive series of exercises, the notebook also provides an indispensable roadmap to the course, giving a highly detailed and day-to-day account of its overall organization and procedures (these to be discussed below). In addition, decades after his time as répétiteur, Dourlen would collect and supplement a number of the exercises he composed for Berton’s course as the basis of his own 1838 Traité d’harmonie. This subsequent collection was the first practical text in written harmony published by the Conservatory. As its generically mixed, full title suggests, Dourlen’s Traité d’harmonie contenant un cours complet tel qu’il est enseigné au Conservatoire de Paris (Treatise on harmony containing a complete course as taught at the Paris Conservatory) functions both as a theoretical “treatise,” reiterating the officially endorsed principles from Catel, and a “course” in harmony, containing exercises then in use in the harmony curriculum. Dourlen’s text was not only the first comprehensive “practical” treatise in written harmony produced at the Conservatory, but it was also the first to connect this content explicitly to the school’s official harmonic theory.(15)
[2.2.3] Beyond the comprehensive sources of Catel, Dourlen, and Leborne, other documentary evidence, in the form of exam and concours exercises, confirms essential details of the course’s practical and theoretical content. As described above, written harmony concours were composed and evaluated by members of an independent examination committee, not by individual harmony faculty; this ensured that instruction would conform to certain institutional standards and expectations. Cherubini was responsible for composing the majority of harmony concours exercises in the 1830s, followed by Leborne in the 1840s and 1850s. The concours exercises not only corroborate the contents of the harmony course—as we will see, select canonic figures studied in the course consistently appear in the concours exercises—but, given the role they played in student advancement, reflect what composition faculty viewed as being the most important techniques that were prerequisite to more advanced study in counterpoint.
[2.2.4] Taken together, Catel’s Traité d’harmonie, Dourlen’s Cours, and Leborne’s notebook, along with concours exercises by Cherubini, offer a relatively comprehensive picture of what the harmony course looked like at the early Conservatory. These sources constitute a network that operated in the following way: Catel’s text enumerates the officially approved elements of harmony study; Dourlen’s writings show how these elements were taught via a series of exercises in polyphonic writing; Leborne’s notebook reveals how they were structured in a course; and Cherubini’s concours pieces provide a succinct summation of the course outcomes. To gain further understanding of these relationships, we will next calibrate the lessons of Leborne’s notebook with the list of elements found in Catel’s treatise, tracing how they interacted in the form of Berton’s harmony course.
[2.3] Course Structure
[2.3.1] Conservatory regulations stipulated that the harmony course run for a roughly nine-month period from October through July, suspending just prior to the annual concours. The course convened three days a week, with each class meeting lasting four hours. In addition, and unlike courses in the other composition subdisciplines, the Conservatory’s official governing documents singled out the harmony course, initially stipulating that the course could last only one year and that students could not repeat it (though this latter prohibition would change under Cherubini’s administration). These restrictions meant that the course needed to be concise and instruction efficient. Judging from the contents of Leborne’s exercise book, Berton’s course was just that, treating each individual element of harmony as identified by Catel’s Traité with dispatch.
Example 3. Table of Contents from Catel, Traité d’harmonie
(click to enlarge)
[2.3.2] The elements enumerated in Catel’s text broadly consist of sonority types and compositional figures. Example 3 reproduces the table of contents from Catel’s treatise. Catel groups sonorities into two main categories: “harmonies simples” or “naturelles” and “harmonies composées” or “artificielles.” Catel treats so-called “natural harmonies” in Articles II-VI, including the major, minor, and diminished triads (or what the discipline would later categorize as “harmonies consonantes naturelles”), as well as dominant and diminished seventh sonorities (later, “harmonies dissonantes naturelles”). “Compound” or “artificial” harmonies, discussed in article VII, consisted of all other dissonant sonorities that required preparation.(16) Compositional figures then include those for cadences, marches, modulations, broderies, alterations, and pédales (Articles VII-XIII). In the context of the actual harmony course, however, certain sonorities were used in conjunction with the realization of all figures, whereas other sonorities were associated with only specific figures. For instance, broderies were applied to natural harmonies in order to produce artificial ones. Marches, by contrast, were taught in conjunction with all sonorities, natural and artificial. Thus, while sonority types do not map onto figures in a neat one-to-one manner, the specific, informal affinities between sonority types on the one hand and their attendant procedures and figures on the other constituted the overall course structure.
Example 4. Contents of Leborne’s Notebook for Berton’s Cours d’harmonie, 1812/13
(click to enlarge and see the rest)
[2.3.3] A simple analysis of the contents of Leborne’s notebook reveals these affinities—i.e., how specific sonority types are paired with their attendant harmonic figures—and the resulting course structure. Example 4 lists the notebook’s contents by topic and date of entry. Mapping Catel’s list of elements onto these entries, Berton’s course neatly divides into three trimesters. The first two trimesters, from October through April, address all the elements of harmony in Catel’s Traité. Though not explicitly indicated by Leborne or Dourlen, the first twelve weeks of study were dedicated to the study of natural harmony both consonant and dissonant, including triads, dominant seventh chords, half-diminished seventh chords, and fully diminished seventh chords; this material consisted of thirty written exercises in total. The next eleven weeks, an additional thirty exercises, were dedicated to the study of artificial harmony. This included all non-dominant-functioning dissonant sonorities using fourths, sevenths, ninths, and their practicable inversions, derived either through melodic elaborations (such as suspensions and passing tones), pedals, or chromatic alterations. The final trimester of the course introduced no additional elements, but rather focused on the realization of increasingly complex unfigured basses and melodies; it included an additional eighty-four exercises, two per class meeting, concluding with a series of “leçons de concours” to prepare students for the July competition.(17) The division between the course’s second and third trimesters is also indicated by the sources of the exercises in the notebook: all exercises for the first two trimesters, dealing with the basic elements of harmony, were composed by the course répétiteur, in this case Dourlen, whereas the exercises for the final trimester, which prepared students for the concours, were composed largely by a professorial faculty member, here Catel (with a few by Gossec).
Example 5. Lesson and exercise on inversions of seventh chords in Leborne’s notebook
(click to enlarge)
[2.3.4] Considering the elements portion of the course more closely, the first two trimesters were each internally divided into two primary units. This resulted in a four-fold division, with each division addressing a single primary sonority type: triads (weeks 1–4); dominant and diminished sonorities (weeks 5-12); diatonic seventh chords (weeks 12–16); and other diatonic, artificial dissonant harmonies, including fourths, ninths, and elevenths (weeks 17–23). The course generally addressed one specific harmony or its inversions per week, often introduced on a Wednesday (see bolded entries in example 4). For each new sonority, Leborne’s notebook contains a “lesson” that briefly illustrates the construction of the harmony under consideration, along with its corresponding figured-bass notation, followed by approximately three written exercises employing that sonority. Students would practice that particular sonority for each class meeting by copying or realizing in writing one figured or unfigured bass in both three- and four-part vocal polyphony. Reflecting the vocal conception of the contemporary discipline, all realizations were written in multiple vocal clefs rather than in keyboard style. Leborne’s entry on inversions of seventh chords and the initial figured bass exercise are given as Example 5.
[2.3.5] Examining the exercises for these four broad topic areas, we see that a particular harmonic figure is associated with each sonority type. The study of triads began the course by introducing consonant cadences et marches—i.e., the realization of cadences and sequences through the use of consonant (triadic) harmonies. The unit on dominant and diminished sonorities then extends these consonant figures by introducing procedures for modulations. The exercises on artificial dissonance, through applying techniques for suspensions and other “prolongations” to triads, derive a corresponding catalog of dissonant cadences et marches, while the final unit on ninths and elevenths introduces contrapuntal broderies, again applied to the initial set of cadences et marches. These pairings point to an important distinction between the harmonic theory and the course pedagogy. Remarkably, the course was not structured according to the theoretical deduction of elements as outlined by Catel. Rather, the course coordinated the elements found in Catel’s text in a particular order, based on practical techniques for the increasingly complex realization and elaboration of cadences and sequences.
3. Pedagogy and Method of the Cours d’harmonie
[3.1] Pedagogy and Method for Realizing “Cadences et Marches Consonants” (uses of triadic harmony)
[3.1.1] Given the overall course organization, let us now consider each of these central sonority types (triads, dominant sonorities, dissonant sonorities), and the cardinal figures associated with them, respectively (consonant cadences and marches, modulations, dissonant cadences and marches, and broderies/imitative counterpoint). For each pair, I will identify the central canonic contrapuntal figures as cataloged in the texts described above. I will then reconstruct a possible method advanced by the course for putting them into practice.
Example 6. Consonant cadences and marches (uses of natural consonant harmony/triads)
(click to enlarge and see the rest)
[3.1.2] Leborne’s notebook records a series of ten exercises demonstrating the consonant realization of cadences and sequences using natural consonant harmonies (triads), including root-position triads (weeks 1–3; exercises nos. 1–3) and triads in inversion (weeks 4–5, exercises nos. 4–10). Each exercise generally consists of three or four marches bookended by cadential figures. Appendix A, table A.1 collects the consonant marches used in these initial exercises. This series of canonic, root-position “marches consonantes” includes sequences comprised of bass motion by fifth, fourth, descending third, and by step (i.e., scales, ascending and descending).(18) Conservatory pedagogy classified sequences in terms of the initial interval and direction by which the bass moves (i.e., rising or falling fifth, fourth, etc.) and then how that basic progression steps (i.e., “marches” or steps) up or down the scale. Exercise no. 1 from Leborne’s notebook, reproduced as Example 6, illustrates the typical form.(19) The exercise begins with a marche of a rising fifth, ascending by step [M1], followed by arguably the most important marche in the catalog, that of a rising fourth ascending by step [M2].(20) The two are followed by a chain of root-position triads falling by third [M7]—a customary progression found in a number of contemporary harmony texts, and considered a marche within the Conservatory curriculum—leading to a final cadence. The next two exercises in Leborne’s notebook proceed in a similar manner, completing the catalog of marches recorded in Appendix A (table A1). This series of canonic, root-position “marches consonantes” includes sequences comprised of bass motions by fifth, fourth, descending third, and by step (i.e., scales, ascending and descending).(21)
[3.1.3] These sequences serve as the basis for many of the subsequent procedures, which entail the melodic (rather than harmonic) elaboration of these patterns, addressed by the course. This is precisely how the course approached inverted triads, namely as consonant melodic or basic contrapuntal elaborations of root-position sequences. The approach, in other words, does not emphasize what a given sequence would look like if one or more of its constituent sonorities were rendered in inversion, but rather how inverted sonorities could be used to “fill in” melodic gaps or create basic counterpoint, either in the bass or the melody of a consonant marche, enhancing the contours of individual lines. As such, we might refer to many of these devices, as I will here, as uses of “melodic sixths” or “contrapuntal sixths.”
[3.1.4] The harmony course focused on two primary uses of such contrapuntal sixths for elaborating the collection of consonant sequences: the chordal skip of an ascending third in the bass (5—), and the melodic 5-6 elaboration of an upper voice over a sustained bass note. The first of these is used to elaborate the bass of root-position sequences where the bass leaps by fourth or fifth, while the second is most often used in conjunction with scalar basses to produce a stepwise melodic elaboration of an upper voice. Example 6b (Leborne, no. 4) shows these melodic elaborations applied to some of the canonic marches. Consisting again of three different marches, the exercise begins with a sequence of falling fourths descending by third, though now elaborated with ascending chordal skips (5—) in the bass [M45-]. By contrast, the next two sequences introduce the melodic 5-6 elaboration applied to an ascending scale [M55-6] and to a descending scale in thirds [M85-6]. Subsequent exercises present the remaining series of root-position marches elaborated with similar melodic sixths (see Appendix A, table A2).(22)
[3.1.5] In addition to their role in the melodic elaboration of sequences, these melodic sixths, and the ascending bass skip (5—) in particular, are suggestive of one of the course’s most fundamental distinctions that figures prominently in its approach to cadences. As noted above, there is a fundamental distinction between marches where the bass rises by fifth and those where the bass rises by fourth. Filling in these contours with an ascending chordal skip produces two fundamental bass patterns: do-mi-sol and do-mi-fa (compare, for instance, [M15—] and [M25—]).(23) These two patterns act as the basis for the majority of the cadential figures used throughout the course. Cadential patterns found in Dourlen’s exercises are drawn from a table of cadences outlined in Catel’s treatise (1802, 39–40). Appendix C offers a reduced version of Catel’s extensive cadence catalog, illustrating the elaboration of two basic cadence types, an ascending pattern and a descending pattern. The ascending pattern either moves from a root-position tonic to the dominant via an initial chordal skip—do-(mi)-sol in the bass—leading to a cadential 6/4 on the dominant, or via a chordal skip landing on the pre-dominant [C1b,c]—do-(mi)-fa-sol in the bass—where the predominant supports a fifth or a sixth or both (i.e. figured bass 5-6). The ascending cadential patterns are thus corollary to the melodic uses of inverted sonorities identified above in the various marches. All ascending cadential patterns thus exhibit one of two bass patterns: either do-mi-sol or do-mi-fa-sol. By contrast, the descending cadential pattern, similar to [M7], falls from do by a chain of thirds to either fa or re in the bass before moving to the dominant, as in [C2].
[3.1.6] Last and perhaps most significantly, this melodic conception of inversion begins to reveal the broadly contrapuntal, and specifically species-based, conception of harmony as taught at the Conservatory. Notably, the three exercises on root-position sonorities rely exclusively on whole notes, establishing an initial association between figures for root-position sonorities and first-species textures. By contrast, the study of inverted triads introduces half-note diminutions, producing a rudimentary form of second species counterpoint. Crucially, however, the second species produced here is exclusively consonant; it does not allow for passing dissonances on the weak half note, but rather only consonant 5-6 melodic elaborations or consonant chordal skips. Similarly, the 5-6 elaboration produces a rudimentary fourth-species texture by introducing the syncope, a rhythmic feature that, as we shall see below, serves as an important device for realizing more complex dissonant figures. Initially, however, the fourth species produced here is exclusively consonant as well.
[3.1.7] Given this collection of figures for both cadences and sequences, I would like to consider a possible method for how to deploy them. In the broadest terms, the exercises in Leborne’s notebook served the larger curricular objective of preparing students to harmonize unfigured basses and melodies in an exam or concours setting. In reviewing Leborne’s notebook, a handful of foundational contours and patterns consistently emerge from the exercises on triadic harmony as particularly salient in developing and deploying an overall method in such a setting. For cadences, these contours include the ascending bass patterns with chordal skips (either do-mi-sol or do-mi-fa-sol) as well as the pattern of a bass descending in thirds through the pre-dominant before arriving at the dominant (do-la-fa-re-sol). For marches, stock contours include extended sequential passages where the bass leaps by fourth or fifth, again often elaborated with ascending chordal skips in the bass (5—), as well as extended scalar passages by step or by third, often elaborated with a melodic 5-6 figure in an upper voice. Harmonizing an unfigured bass required students to identify these contour types in a methodical yet flexible way in order to develop a polyphonic realization of the exercise, moving from an initial sketch to a complete harmonization. Methodologically speaking, certain bass contours only entailed one possible realization and therefore provide a solid starting point for approaching an exercise, whereas other contours could support multiple possible realizations and are therefore best handled at subsequent stages of the realization process. Using this fundamental distinction, we can begin to lay the foundation of an informal method for creating consonant, polyphonic harmonizations of an unfigured bass. The method prioritizes those figures that support unique realizations before moving to those more multivalent contours that can support multiple realizations.
Example 7. Method for consonant realization of cadences and marches (Leborne, Cours d’harmonie de Berton, 11–2, no. 9, mm. 1–21, redacted)
(click to enlarge and see the rest)
[3.1.8] Step 1. Realize ascending skips and sequences of fourths and fifths. Consider the ninth exercise from Leborne’s notebook (see Example 7). This exercise exhibits the standard form for harmony exercises: it consists of multiple sequential passages (mm. 1–3, 6–15) connected by cadential figures (mm. 17–19, 19–21). In scanning these passages, a few specific contours prominently emerge. In addition to the extended sequential passages, we can identify the use of ascending skips throughout. As described above, ascending skips in the bass support a single harmony and never a change in harmony and should therefore be identified with the figure 5—. Therefore, we can begin the harmonization by realizing the upper voices above these ascending chordal skips in the bass. Alternating with these measures, we see a series of whole notes that indicate an overall marche of falling fifths descending by step; this is a version of [M25-] in which the chordal skips in the bass act as melodic elaborations.
[3.1.9] Step 2. Realize cadential figures and elaborate sustained notes with melodic 5-6s. Turning to the remaining passages, the excerpt ends with two clear, canonic cadential figures, the first ascending through the pre-dominant and the second descending. In the academic style modeled here, whole notes in the bass rarely support a first-species melody, but more often signal the use of some sort of melodic diminution in an upper voice. As such, we can add a series of melodic 5-6 figures, producing syncopes in the melody over the primary sequences and resulting in a rudimentary fourth-species texture.
[3.1.10] Resumé. Taking these two previous steps together, then, we can identify four ordered methodological principles for realizing a consonant (triadic) harmonization of a bass consisting of canonic cadences et marches. They are as follows:
- Interpret and realize ascending skips as a change in inversion (5—)
- Interpret and realize sequences of fourths (or fifths) in root position
- Embellish sustained notes (whole notes) with a 5-6 melodic figure
- Identify and realize ascending and descending cadential figures
Having taken these steps, we can realize any outstanding figures that may support multiple harmonizations in an ad hoc manner (Example 7, step 3). Measures 1–3, for instance, contain a familiar chain of descending thirds in the bass that can support multiple harmonizations. Here, that span has been realized as supporting successive (though not parallel) sixths.
[3.2] Pedagogy and Method for Realizing Modulations (uses of “natural dissonances” or dominant sonorities)
[3.2.1] Following the first four weeks that treated the consonant realizations of cadences and sequences, the subsequent eight weeks of the course focused on realizing modulatory figures using “natural” dissonant sonorities, including the dominant seventh chord, half-diminished seventh chord, and fully diminished seventh chord (weeks 5–12, exercises 11–30). Leborne’s notebook illustrates the use of two primary figures in this regard: final cadences using root-position dominant sevenths and scalar patterns using inverted dominants (in today’s terms, so-called “linear dominants”). While these uses of dominant sonorities are familiar to us today, the study of modulatory figures was perhaps even more essential than we might imagine. Reflecting an eighteenth-century view of harmonic theory, Conservatory pedagogy understood every major or minor triad as a potential tonic, and by extension, every progression involving that triad as a cadence in that key (in French usage, “cadence” was synonymous with “progression” until Fétis).(24) From this perspective, modulation becomes a fundamental element of harmony study, as every progression is a potential modulation; constructing a modulation is therefore no more, or less, complicated than writing a cadence in a chosen key.
Example 8. Modulations (uses of dominant sonorities)
(click to enlarge and see the rest)
[3.2.2] As seen above, cadential patterns were limited to simple ascending or descending bass contours that often entailed a consonant chordal skip leading directly to the dominant, do-mi-sol, or to a pre-dominant do-mi-fa-sol or do-la-fa-re-sol. Accordingly, these patterns provided the basis for constructing modulations. As we can see from the first exercise on root-position dominant sevenths in Leborne’s notebook, Dourlen elides these simple cadential patterns, producing a suite of modulations to closely related keys (see Example 8a, mm. 11–24).
[3.2.3] The course approached inverted dominant sonorities in a similar manner, treating them primarily in their capacity for producing “modulations passagères” and scalar tonicization patterns in particular. Uses of inverted dominant seventh chords were determined by the scale degree found in the bass of each sonority and the scalar bass patterns that resulted from their combined use. Example 8b partially reproduces the demonstration from Catel’s treatise on the uses of inverted dominant sevenths. (The demonstration was commonplace in contemporary harmony texts, including those from which Catel’s text was compiled). In terms of scale degrees, the demonstration shows the following:
- A leading tone (ti) in the bass supports a first-inversion dominant seventh chord (6/5)
- The second scale degree (re), when moving by step—for instance, as a passing tone, do-re-mi—supports a second-inversion dominant seventh chord (+6) and fills in an ascending do-mi chordal skip in the bass (5—). The resulting do-re-mi is therefore harmonized 5-+6-6(25)
- The fourth scale degree in the bass, when descending by step fa-mi, supports the resolution of a dominant seventh in third inversion (+4/2).
Example 8b also illustrates the standard substitutions for inverted dominant sevenths using the fully diminished seventh chord. These substitutions occur according to the shared bass note found in corresponding inversions of dominant and diminished sonorities.
[3.2.4] Exercise no. 16 from Leborne’s notebook (Example 8c) illustrates how to apply these patterns, producing a number of tonicizations via the use of linear dominants. Measures 5–9, for instance, tonicize the relative minor simply by descending from the major tonic to the leading tone of the relative minor,
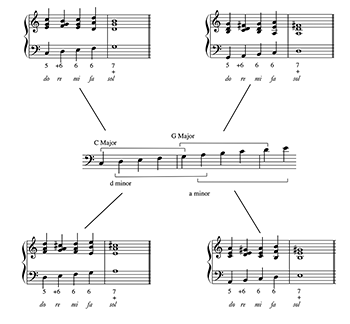
Example 9. Tetrachordal mutation within a major scale
(click to enlarge)
[3.2.5] Overall, the linear approach used here reflects an understanding of modulation as the simple, scalar mutation of melodic tetrachords in both major and minor keys. That is, all such tetrachords, when consisting of the first four degrees of a major or a minor scale, support the same sonority types. In C major, for instance, and as shown in Example 9, the major tetrachords built on the tonic and dominant, C-D-E-F and G-A-B-C, as well as the minor tetrachords built on the second and sixth scale degrees, D-E-F-G, or A-B-C-D, all represent do-re-mi-fa bass patterns in their respective, local key areas (again, any triad is potentially the tonic of a key). Passages using these melodic tetrachords in the bass, therefore, are all realized as supporting the same harmonization of a tonic expanded by its dominant (5-+6-6), transposed as the first three scale degrees of G major, D minor, and A minor.
Example 10. Method for Realizing Modulations (Dourlen, Traité d’harmonie, 26, no. 33, redacted)
(click to enlarge and see the rest)
[3.2.6] For the harmony student, learning to identify and realize modulations to closely related keys entailed the need to recognize two primary contours: root-position cadential patterns, often in sequence, and mutating tetrachords in a scalar bass. In regard to the former, this simply meant identifying cadential bass contours—such as the ascending do-mi-sol, do-mi-fa-sol, and the descending chain of thirds do-la-fa-re-sol, etc.—as they appear transposed to various keys. In regard to the latter, this meant identifying scalar patterns, and melodic tetrachords in particular, as they move through closely related major and minor keys. We can apply these techniques to Exercise no. 33 from Dourlen’s harmony treatise, reproduced here as Example 10, in order to construct an informal method for uses of dominant sonorities.
[3.2.7] Step 1. Realize inflected leading tones and bass suspensions. In exercises for dominant and diminished seventh chords, multiple chromatic inflections in the bass act as the most immediate prompts, indicating tetrachordal mutations. Chromatically raised notes in stepwise bass patterns frequently indicate leading tones resolving to a local tonic and support first-inversion dominant seventh chords (or root-position fully diminished sevenths, though they may also suggest a do-re-mi, as in m. 18). Similarly, bass suspensions indicate uses of a third-inversion dominant seventh (or a fully diminished seventh in second inversion) resolving to an inverted triad.
[3.2.8] Step 2. Realize do-re-mi’s. Next we can identify a series of major and minor tetrachords, interpreting them as scale segments in local keys. Each do-re-mi segment in the bass supports tonic expansion via an inverted dominant or diminished seventh chord (figured bass 5-+6-6).
[3.2.9] Step 3. Realize remaining cadential figures/final cadences using root-position dominant seventh chords. Having realized the linear dominant patterns, the remaining passages punctuate each phrase with cadential patterns using pre-dominant figures, mi-fa-sol-do, with and without cadential 6/4s. These occur in a minor, B minor, D major (deceptive cadence), and D minor.
[3.2.10] Resumé. Taken together, the steps here largely recast the three principles above for interpreting the harmonic implications of linear dominants in the bass—those for interpreting ti, re, and fa in the bass—as methodological prescriptions, including:
- Interpret chromatically raised notes as local leading tones (ti) that support a dominant seventh chord in first inversion or a root-position fully diminished seventh chord (ti supports 6/5 or 7)
- Interpret chromatically lowered notes as well as bass suspensions as a local fourth scale degree (fa) and as supporting a dominant seventh chord in third inversion or diminished seventh chord in second inversion (when moving fa-mi, fa supports a +4/2 or +4/3)
- For passages that suggest a do-re-mi, interpret the passing tone in the bass (re) as supporting a local dominant seventh in second inversion or a diminished seventh chord in first inversion, filling in a local do-mi chordal skip (re by step supports +6 or +6/5, do-re-mi supports 5-+6-6)
[3.2.11] These techniques, along with those for harmonizing final cadences, account for the majority of the excerpt. Before moving on, we note that the final step in this example (step 4), showing a final elaboration of the opening measures, points to an important feature of both the pedagogy and compositional method of the course—and again, one that reflects the Conservatory’s overall melodic and contrapuntal conception of the discipline. In particular, the final step of the realization here points to the combinatorial nature of many of the melodic figures used throughout the course. For instance, the sustained bass notes, do-re-mi, in mm. 1–3 support not only the 5-+6-6 associated with a tonic tetrachord, but can also support and be combined with melodic 5-6 elaborations commonly used over whole-note scalar patterns in the bass. This produces the syncope figure in the middle voice, the continuation of which prepares the dissonance over the pre-dominant. The combinatorial nature of a number of figures accounts for much of the increasing contrapuntal complexity of the realizations as the course moved forward.
[3.3] Pedagogy and Method for Realizing “Cadences et Marches Dissonantes” (uses of artificial dissonances)
[3.3.1] In nineteenth-century harmonic theory, the terms “artificial” or “compound” harmony—as opposed to “natural” or “simple” harmony—referred to all sonorities containing dissonances that required preparation (i.e., all dissonances not associated with the tritone of dominant-functioning sonorities).(26) The harmony course largely focused on three “compound” sonority types—fourths, sevenths, and ninths—along with their practicable inversions.(27) In addition, as we saw in regard to inverted triads, “artificial” dissonance was conceived largely as a melodic and contrapuntal device—rather than a harmonic one—available for elaborating cadences and marches through the use of both chordal dissonances and suspensions.(28) When applied to the set of canonic, consonant marches specifically, the procedures for realizing artificial harmonies result in a derived and corresponding series of “marches dissonantes” or “composées.” Given the sheer number of dissonant figures addressed by the course, it is not possible to discuss all of them here.(29) Instead, this account will summarize the broad music theoretical and pedagogical principles by which the course addressed the construction of dissonant figures, along with some of the more common sonority types resulting from their realization.
[3.3.2] Perhaps most fundamentally, the early harmony course distinguished between dissonances prepared over a bass ascending by fourth (descending by fifth), including seventh chords and their inversions, and those prepared over a bass ascending by fifth (descending by fourth), specifically the 5/4 sonority and its inversions. In terms of the basic contours discussed above, this means that cadentially, the ascending bass pattern do-(mi)-fa-sol and the descending bass pattern, do-la-fa-re-sol, support sevenths over the pre-dominant sonority, whereas the ascending bass pattern, do-(mi)-sol supports a fourth over the dominant. Similarly, a fourth may also be produced by delaying the resolution of a seventh over a bass that falls by fifth. This is particularly applicable to cadential passages where delaying the resolution of the chordal seventh of the dominant produces a fourth over the tonic (the so-called “tonic eleventh” or “onzième tonique”).
[3.3.3] With regard to marches, this means that sequential basses consisting of rising fourths or falling fifths, such as [M2] and [M3], may be elaborated with sevenths, whereas those consisting of rising fifths or falling fourths such as [M1] or [M4] support fourths. Table A3 (in Appendix A) applies this principle to the series of consonant marches from Table A1. In surveying the resulting marches dissonantes, we can also identify some additional broad principles for uses of compound harmonies. Scalar passages, for instance, may also support a chain of 7-6 suspensions as in [M57-6] or [M67-6] similar to the melodic 5-6 elaborations above. The table last reveals a final, important distinction between ascending and descending dissonant sequences. Given the requirement that dissonances resolve downward by step, only sequences that descend overall can accommodate both suspensions and “chordal” dissonances. By contrast, ascending marches can only support suspensions, and not chordal dissonances as an upward leap away from the resolved suspended tone—i.e., prior to movement in the bass or change in harmony—is the only means to accommodate the sequence’s overall upward motion in the upper voices. (Compare, for instance, the dissonant form of [M1] with that of [M3], or [M2] with [M4].)
Example 11. Dissonant Cadences and Marches (Uses of Artificial Harmony/Sevenths)
(click to enlarge and see the rest)
[3.3.4] Exercises nos. 35 and 45 from Leborne’s notebook illustrate a number of the figures that support the realization of sevenths and their inversions (see Example 11). Here we see the most common sequential uses of sevenths, including the marche of falling fifths descending by step [M37] as well as a chain of 7-6 suspensions elaborating a descending scale [M67-6]. In terms of inversions, the 6/5 is most commonly used to elaborate pre-dominant sonorities associated with cadential figures, ascending or descending, that move do-(mi)-fa-sol in the bass (Example 11b, m. 2, m. 21). By contrast, bass suspensions act as a prepared dissonance to support a third-inversion seventh chord resolving down by step to an inverted sonority. Last, this excerpt contains a central combinatorial marche in mm. 14–18. Here we see suspended bass notes prepared by a whole note. The syncope clearly supports a third inversion seventh chord, whereas the longer note values suggest that they support a 7-6 suspension. Taken together, this 7-6-2 figure supports an imitative realization in the soprano that uses a similar 7-6 suspension.
Example 12. Dissonant Cadences and Marches (Uses of Artificial Harmony/Fourths)
(click to enlarge and see the rest)
[3.3.5] By contrast, exercises nos. 46 and 49 (Example 12) demonstrate common uses of the 5/4 sonority and its inversions, the 5/2 and 7/4. As a pedagogical matter, many of the exercises in Leborne’s notebook emphasize the fundamental difference between contours associated with sevenths and those associated with fourths, placing patterns for each side by side. Exercise no. 46 (Example 12a) is instructive in this regard. In terms of marches, the rising fifth sequence [M1] that supports fourths (mm. 3–7) is juxtaposed with a sequence of falling fifths [M3] that supports sevenths (mm. 12–17). The exercise also features the “Pachelbel” sequence of falling fourths (ascending fifths), descending by third [M4] combined with 9-8 suspensions (mm. 18–23). In terms of inversions, exercise no. 49 (Example 12b) shows the first inversion of the 5/4, the 5/2. Similar to the 4/2, the 5/2 is prepared as a bass suspension followed by a downward resolution to an inverted sonority. In addition, the syncope is often prepared by a whole note supporting a 7-6 suspension or a 4-3 suspension (compare mm. 6–7 and 20–21). The difference in choosing between the two, again, has to do with the approach to the sustained note: if approached by a bass ascending by fifth or a skip, do-(mi)-sol, or by a resolving dominant seventh, then it will support an initial 5/4. If approached by a bass ascending by fourth, do-(mi)-fa, or descending by third, then it will support a 7-6 figure. As for inversions of the 5/4, the 7/4 often acts as a delay of the cadential 6/4, frequently indicating a protracted resolution over a double whole note (mm. 8–9). The 7/4 here resolves to a 6/4, followed by a 5/4 and finally to a 5/3.
[3.3.6] Given the variety of practicable dissonant harmonies, any attempt at a method beyond rote memorization might end up being ad hoc at best. In this case, it is important to take a broad approach, bearing in mind some of the basic contour types identified here and the respective dissonances they support. These include basic distinctions between bass contours ascending by fourth that support sevenths and those ascending by fifth that support fourths. Similarly, we should recall that marches that ascend overall, including scalar basses, can only accommodate suspensions and not “chordal” dissonances. In terms of the more granular details within these contours, for cadences, pre-dominant sonorities generally support sevenths, and sustained (whole) notes generally accommodate suspensions and their resolution (7-6, 4-3, etc., depending on how they are approached); bass suspensions, on the other hand, support a second of some sort, either a 4/2 or 5/2. With these broad principles in mind, let us turn to an unfigured bass exercise from Dourlen’s Cours d’harmonie.
Example 13. Method for the Dissonant Realization of Cadences and Marches (Dourlen, Traité d’harmonie, 44, no. 52, redacted)
(click to enlarge and see the rest)
[3.3.7] Step 1. Realize common sequences, add dissonances, and realize bass suspensions. In surveying the unfigured bass shown as Example 13, three primary sequential passages (mm. 8–13; 18–22; 25–30) as well as multiple bass suspensions (mm. 13–15) emerge as prominent contours. As seen above, all bass suspensions may be realized as supporting a second. In addition, we see that the bass suspensions in mm. 8–13 are incorporated into a larger sequence of rising fourths. As such, the sustained notes that serve to prepare the bass suspensions, approached from a fourth below, can support 7-6 suspensions. As indicated above, this sequence can support an imitative realization, as shown here in the soprano. Next, in regard to the final sequence (mm. 25–30), the chromatically raised notes suggest a sequence of dominant sonorities while, combinatorially, the approach to each raised note by ascending skip suggests motion between a root-position and first-inversion dominant seventh; recall from above that chromatically raised notes suggest ti and thus support a 6/5, while ascending skips support 5—. Lastly, we can suspend the chordal seventh of each dominant harmony as it moves to the chord of resolution, producing a chain of 4-3 suspensions. Again, the use of suspensions, rather than chordal dissonances, is necessary here as the overall sequence ascends by step.
[3.3.8] Step 2. Realize cadential passages and outstanding sequences. The opening measures contain an ascending tetrachord, do-re-mi-fa in C major, supporting a 5-+6-6-6 harmonization (mm. 1–2) leading to a cadence in F (mm. 3–5), immediately followed by a cadence returning to C major. In both cases we can elaborate the pre-dominant sonorities with sevenths and/or suspend the resolution of the dominant’s chordal seventh. Similarly, the excerpt closes with an ascending tetrachord in A minor, again suggesting a 5-+6-6-6 harmonization, followed by a sequence of rising fourths descending by step (a melodic inversion of [M1]) which can be elaborated with sevenths. These cadential passages, along with the sequences above, account for the majority of the realization. The final, outstanding sequence (mm. 18–22) is a bit more complex. The descending skips in the bass have been realized here as chordal skips (6—), leading to a series of 5/4-3 suspensions. Similarly, the root motion of descending fifths (G-C; B-E) suggests a sequence of dominant-tonic resolutions, though to inverted tonic triads (i.e., a series of avoided cadences).
[3.3.9] Resumé. We can thus identify some clear starting points for realizing a dissonant harmonization of a bass, beginning with:
- Realize bass suspensions as supporting seconds, either 4/2 or 5/2
- Realize marches for leaping basses, adding dissonances—sevenths or fourths—as appropriate
- For cadences, elaborate pre-dominant patterns, do-(mi)-fa, with a seventh; elaborate patterns that arpeggiate to the dominant, do-(mi)-sol, as well as the resolution of seventh chords, with a suspended fourth
- For sustained notes, add a 9-8, 7-6, or 4-3 suspension, depending on whether they are approached by ascending fourth or fifth
- Interpret outstanding passages, including sequences and stepwise bass motion, adding possible suspensions or chordal dissonances.
This is obviously not an exhaustive list, which makes the last principle perhaps the most important, as it points to the informal and compositional nature of techniques for realizing dissonant harmony. That is, techniques for dissonant harmony in particular and method more broadly understood as a deployment of informal techniques, at some point outstrips any appeal to clear, formal prescriptions. While contemporary harmony treatises exhaustively list and demonstrate the precise preparation and resolution of every practicable dissonance, such a list, on its own, may be methodologically useless without some general, practical principles for where to start. The above list attempts to articulate some of those principles.
[3.4] Pedagogy for Broderies and a Rudimentary Method for Imitative Counterpoint: Preparing for the Concours d’harmonie
[3.4.1] From the very first, the exercises in Leborne’s notebook reveal how Conservatory harmony pedagogy tied the realization of individual sonority types to specific contrapuntal species. Of all the topics addressed by the course, none more clearly and extensively reflect the Conservatory’s contrapuntal approach to harmony as the study of melodic elaboration and diminution than that of broderies. Broderies were taught as elaborations of previous canonic figures, and of marches in particular, as a means of introducing fourth-species (quarter-note) diminutions. Yet they also served as the means to introduce mixed-species writing and served as the basis for rudimentary techniques in both invertible and imitative counterpoint.
[3.4.2] In surveying Dourlen’s treatise, we can identify two broad categories of broderies: those that elaborate a single tone and those that connect two different tones. Appendix B collects the most common broderies addressed in the course. The “skip and return” example [B1a] is perhaps the most canonic, appearing as the first passing-tone figure introduced in multiple texts.(30) This figure elaborates individual whole notes and, as Dourlen illustrates, is ideal for elaborating sequences that include scalar patterns in a single voice as well as root-position sequences where the bass ascends by leap [B1c]; Dourlen also uses this pattern as an initial basis for imitative counterpoint.(31) As shown in this example, opportunities for imitative writing were generally signaled by the alternation of a specific broderie with a sustained note, constituting a marche. One additional broderie in this category deserves particular mention, namely that used for harmonizing a scalar, first-species (whole note) bass that supports melodic 5-6 figures [B1d-e]. This broderie consists of a lower auxiliary tone followed by a downward skip and is also frequently used in imitation.
[3.4.3] The next series of broderies in Dourlen’s treatise includes those that connect two different tones, as opposed to those that elaborate a single tone (Appendix B, example B2). Consistent with the conception of inverted sonorities as primarily melodic devices, these broderies, largely quarter-note diminutions and passing tones, fill in the various melodic intervals produced by common root-position marches. Dourlen addresses four primary marches in the following order: descending scale in thirds [M8]; rising fifths ascending by step [M1]; rising fourths ascending by step [M2]; and falling fifths descending by step [M3]. Dourlen elaborates the scale in thirds by adding passing tones to fill in all skips, both in the bass and upper voices. Again, the passing tones here create points of imitation between bass and soprano. Elaborations of sequences consisting of leaping basses ([M1], [M2], [M3]) result in extended scalar passages in a single voice or again, as indicated by the alternation of diminutions with whole notes, imitative writing between voices. The elaboration of the rising-fourths marche is particularly notable because the skip in the bass, when completed with a passing tone diminution, results in a florid rising and falling scalar bass.
Example 14a. Harmonic implications of common broderies (Dourlen, Traité d’harmonie, no. 71, redacted)
(click to enlarge)
Example 14b. Derivation of canonic dissonant broderie
(click to enlarge)
[3.4.4] In the second half of his treatise, Dourlen returns to the topic of broderies, showing the ready application of these figures to common dissonant marches in a series of unrealized figured basses. Example 14a reproduces exercise no. 71. The example includes a second figured bass below the original, added here to indicate the underlying marches and harmonies.(32) In scanning the overall contours of these exercises, we immediately recognize a number of familiar dissonant marches, including dissonant elaborations of [M2], [M3], [M4], [M6], and [M8], supporting the broderies described above for marches consonantes. Perhaps the most canonic broderie specific to dissonant harmony, however, is that associated with the descending scale in mm. 14-18. This is one of two canonic dissonant marches that use broderies in both an imitative and invertible manner (both dissonant broderies, along with their realizations, are given in Appendix B, example B2e and f). Here, as elsewhere, the alternation in the bass of the quarter-note diminution with a whole note suggests imitation in an upper voice. Example 14b shows a complete derivation and realization of this figure, based on a rhythmic augmentation of [M86/5], derived from a scale of descending thirds. Remarkably, this figure is thoroughly invertible, with any voice able to act as the bass, though it most often appears, as shown here, with the quarter-note diminutions producing imitation between the bass and soprano.
Example 15. Method for Interpreting Broderies and Completing a Concours d’harmonie (Cherubini, Concours d’harmonie, 1836)
(click to enlarge and see the rest)
[3.4.5] Understanding the harmonic implications of broderies was essential to developing a method for succeeding in the harmony concours. Concours exercises presented students with a highly elaborate surface of broderies, making the interpretation of their underlying marches a necessary initial step in the realization process. In approaching a concours exercise, then, it is helpful to bear in mind specific patterns and classes of broderies as well as some general principles for their use. In terms of individual patterns and classes of broderies, for instance, we should bear in mind the “skip and return” pattern as well as common elaborations of 5-6 marches, scales in thirds, marches by fourths and fifths, and the two common elaborations of dissonant marches. In working to distill this information down to a few central principles, we might therefore consider the following:
- Syncopes and skips: when interpreting and writing diminutions, generally group quarter notes separated by a skip into a single harmony, as the harmonic rhythm in academic exercises rarely exceeds the half note. Similarly, all bass suspensions support a 2.
- Extended scalar passages in a single voice generally indicate root-position marches, which may be deciphered by interpreting the first beat of each measure.
- Broderies alternating with whole notes suggest the opportunity to create imitative textures.
Taken together, these principles provide a workable starting point for interpreting the highly elaborate surfaces of concours exercises, such as the 1836 concours exercise composed by Cherubini and reproduced here as Example 15.
[3.4.6] Step 1: Interpret harmonic implications of broderies. In examining the bass, we can immediately identify four marches, three of which contain canonic broderies. In tracing the first note of each measure, we can observe that the extended scalar profiles of the broderies in both the first and final sequences reveal underlying root-position marches of rising fourths ascending by step (specifically [M2], indicated on the staff below the excerpt). By contrast, with respect to the interior sequence (mm. 29–39), the chromatically raised notes throughout suggest the use of secondary dominants applied to ascending skips (5—). The “skip and return” broderie, on the other hand, suggests an additional chordal-skip elaboration (5—) applied to the canonic marche [M3].
[3.4.7] Step 2: Realize marches, using broderies and imitative writing where possible. On the basis of the harmonic interpretation developed in step 1, we can begin to realize the various marches, including those that entail imitative uses of broderies. Furthermore, starting a realization by establishing points of imitation will create a framework on which to hang the surrounding measures of the realization. To begin, the marches in mm. 5–10 and 41–46, which make use of extended scalar, fourth-species diminutions, can support imitation. The sequence in mm. 29–39 suggests possible imitation as well, given the alternation of broderies with longer note values. Here, quarter-note broderies suggests a series of chordal skips, which is imitated in the soprano.
[3.4.8] The interior sequence in mm. 16–27 can support imitation as well, although it is not as evident, given the lack of a canonic fourth-species broderie that may be used as a motive. In addition, root motion by falling fifth is less commonly subject to elaboration; most of the broderies described above are more readily applied to root motion by fourth, either ascending or descending. Here, though, I have realized a second-species motive in imitation of a chordal leap of an ascending fourth in the soprano and alto. The bass of a falling fifth, descending by step, also suggests the use of the 5/4 coupled with a chain of 4-3 suspensions for added contrapuntal effect. The subsequent addition of quarter-note diminutions to these second- and third-species contours will help render the imitative nature of this passage more audible.
[3.4.9] Step 3. Realize cadential passages. The remaining cadential passages are by now familiar enough that we can include dissonant elaborations. The initial cadential passage establishes the key of C major, with opportunities for a number of dissonant sonorities. The final cadential passage similarly suggests a chain of dissonant sonorities. Here they have been interpreted as chordal dissonances, though they could just as easily support a chain of 7-6 suspensions resolving at the quarter note (see Step 4).
[3.4.10] Step 4. Elaborate. The final step adds fourth-species diminutions, particularly where such additions might contribute to the overall motivic imitation of the exercises. Here quarter- and eighth-note diminutions have been added to the interior sequences (mm. 16–27; 29–39) in order to bring out the second-species imitation.
[4] Conclusions
[4.1] The Paris Conservatory treated harmony as the practical study of techniques for the polyphonic realization and elaboration of a canonic series of cadences, marches, modulations, and broderies, each associated with uses of specific sonority types. The method most strikingly consisted of informal strategies for recognizing stock melodic patterns, contours, rhythmic species, and perhaps most particularly, melodic interval content. Thus, when it comes to interpreting a given bass’s implied harmonies, a number of the principles outlined above have to do with recognizing simple contours and interval patterns. It is largely possible to realize a serviceable harmonization of a bass given these broad indices alone. Subsequently, once the larger pattern or contour has been identified, the method consists of making a series of “either/or” determinations, often in combination depending on whether a consonant, dissonant, or modulatory realization is preferable, in order to develop a more detailed realization in a sort of “Beaux Arts” tradition. These overlapping, binary determinations can be understood as deriving in large part from the combinatorial nature of many figures. For instance, in this system every harmony supports either a fifth or a sixth (root position or inversion); every ascending cadence is either do-mi-fa or do-mi-sol; every marche is by fourth or by fifth; every suspension either a ninth, seventh or a fourth, etc. Given the number of informal strategies, I have not combined all the methods for the various sonority types into a single, twenty-step list. Rather, I have left them discrete so as to reflect the competing priorities and combinatorial strategies needed to realize a harmonization of any particular bass, as well as to acknowledge that most contours could be realized multiple ways.
[4.2] In comparison to current classroom pedagogies, the method here therefore does not appeal to functional or syntactic harmonic theory in many instances. It instead relies on what we might refer to as lower-level theory. For instance, it does not appeal to a theory of individual chords and their inversions, but rather simple interval patterns and melodic contours. While model syntactic progressions may nevertheless result from this method, a predetermined model for such progressions is not its primary means. Perhaps even more significantly, the method here uses complete figures—i.e., cadences—that may be realized multiple ways rather than individual sonorities chained together. This focus on complete figures—irreducible wholes—stands in marked contrast to methods that foreground the functions of individual chords, say in chorale-style harmonization, and may represent its most immediate advantage.
[4.3] A further benefit of the method developed in this article is its potential compatibility with current efforts to adapt partimenti techniques to the modern classroom. Notably, most of the recent research on partimenti has been focused on Italian keyboard traditions. Many of today’s undergraduate music students, however, lack the requisite keyboard skills to put many of those techniques, including the most basic ones, into practice. The method of the Paris Conservatory described here, however, was designed to work in tandem with “written” approaches to theory— including a focus on vocal polyphony—which increases the likelihood of it be readily mastered by today’s students. Furthermore, the exercises can be performed by groups of students in class, furthering another objective of the music theory classroom—namely sight singing—while also allowing students to hear what they have written.
Appendices
Appendix A: Catalog of Marches [PDF]
Appendix B: Broderies [PDF]
Appendix C: Cadences [PDF]
Michael Masci
SUNY Geneseo
Department of Music & Musical Theatre
Geneseo, NY 14454
masci@geneseo.edu
Works Cited
Barbati, Giovanna, and Guido Olivieri, eds. 2021. G. Francone: 10 Passacagli for Cello. HH Editions.
Bazin, François. 1857. Cours d’harmonie théorique et pratique. Escudier.
Cafiero, Rosa. 2007. “The Early Reception of Neapolitan Partimento Theory in France: A Survey,” Journal of Music Theory 51 (1): 137–59. https://doi.org/10.1215/00222909-2008-025.
Catel, Charles-Simon. 1802. Traité d’harmonie. Le Roy.
Cherubini, Luigi. 1847. Marches d’harmonie pratiquées dans la composition produisant des suites régulières de consonnances et de dissonnancees. Troupenas.
Choron, Alexandre-Étienne. 1808. Principes de composition des écoles d’Italie. August Le Duc.
Dourlen, Victor 1838. Traité d’harmonie. Prillip.
Fétis, François-Joseph. 1823. Méthode élémentaire et abrégée d'harmonie et d'accompagnement. Philippe Petit.
Gessele, Cynthia M. 1992. “The Conservatoire de Musique and National Music Education in France, 1795–1801.” In Music and the French Revolution, ed. Malcolm Boyd, 191–210. Cambridge University Press.
Gjerdingen, Robert O. 2007. Music in the Galant Style. Oxford University Press.
—————. 2014. “Harmony without Theory: Apprenticeship at the Paris Conservatory.” Paper presented at the annual meeting of the Society for Music Theory, Milwaukee, Wisconsin, November 6–9.
—————. 2020. Child Composers in the Old Conservatories: How Orphans Became Elite Musicians. Oxford University Press. https://doi.org/10.1093/oso/9780190653590.001.0001.
IJzerman, Job. 2018. Harmony, Counterpoint, and Partimento: A New Method Inspired by Old Masters. Oxford University Press.
Leborne, Aimé. 1866. Cours d’harmonie de Berton. Bibliothèque du Conservatoire Impériale de Musique.
Lester, Joel. 1992. Compositional Theory in the Eighteenth Century. Harvard University Press.
Masci, Michael. 2014. “Harmony as Practica: The Relationship of Tonal Theory to the Practical Study of Harmony Reconsidered.” Theoria 20: 5–38.
—————. 2023. Charles-Simon Catel’s Treatise on Harmony and the Disciplining of Harmony at the Early Paris Conservatory. Lexington.
Pierre, Constant. 1900. Le Conservatoire national de musique et de declamation: documents historiques et administratifs. Imprimerie Nationale.
Rubinoff, Kailan R. 2017. “Toward a Revolutionary Model of Music Pedagogy: The Paris Conservatoire, Hugot and Wunderlich’s Méthode de flûte, and the Disciplining of the Musician.” The Journal of Musicology 34 (4): 473–514. https://doi.org/10.1525/jm.2017.34.4.473.
Sanguinetti, Giorgio. 2012. The Art of Partimento: History, Theory, and Practice. Oxford University Press.
Savard, Augustin. 1853. Cours complet d’harmonie théorique et pratique. Maho.
Footnotes
1. A note on figured-bass symbols: the figured-bass symbols used here are those most commonly found in nineteenth-century French harmony texts. This includes the use of a slash (\) to indicate diminished intervals, diatonic or otherwise, and a (+) to indicate leading tones. Thus, for dominant sevenths, the figured-bass symbols for root position and its three inversions are: ![]() . In addition, these symbols are used whether or not the dominant seventh occurs naturally, given the key signature, or whether the note in the bass supports a secondary dominant. In other words, in this system accidentals are never—or at least very rarely—used to indicate dominant sevenths or diminished sevenths. For instance, in the key of G major, an A with a “+6” under it indicates a D7 chord in second inversion, while an C with a “+6” indicates the secondary dominant, F7, in second inversion. In the latter case, no additional accidentals are given to indicate the implied
. In addition, these symbols are used whether or not the dominant seventh occurs naturally, given the key signature, or whether the note in the bass supports a secondary dominant. In other words, in this system accidentals are never—or at least very rarely—used to indicate dominant sevenths or diminished sevenths. For instance, in the key of G major, an A with a “+6” under it indicates a D7 chord in second inversion, while an C with a “+6” indicates the secondary dominant, F7, in second inversion. In the latter case, no additional accidentals are given to indicate the implied
Return to text
2. Significant collections of Italian partimenti can be found in French harmony treatises and other pedagogical works, including Choron 1808, which sought to collect and transmit the teachings of Sala, and Fétis 1823, which, though less well known than his more famous harmony treatise, contains multiple exercises by Durante, Fenaroli, and Sala.
Return to text
3. Just as crucially, this adaptation, over the course of the nineteenth century in France, resulted in a popularization and simplification of the method for bourgeois consumption. The commodification of the French Traité d’harmonie by the middle of the nineteenth century resulted in a mere gloss on the Italian technique from which it partially derived. As Gjerdingen puts it, paraphrasing communication theory, French treatises served as a “simplified vector of grand generalization.” (2007, 173).
Return to text
4. I say “written harmony” specifically because at the Conservatory, the discipline of harmony was alternatively conceived at times as a written discipline or as a keyboard discipline. I will return to this issue below.
Return to text
5. As I explore elsewhere, a defining feature of American music theory pedagogy is its identification of descriptive models for harmonic syntax with a method for writing syntactic, functional progressions. This results in a primarily “left-to-right” method for composing harmonic progressions instead of the elaborative “beaux arts” approach offered by partimento study. See Masci 2014.
Return to text
6. For a detailed discussion, from the perspective of Foucault’s theory of disciplinarity, of the power dynamics of these administrative structures and the effect they had on knowledge production, see Masci 2014.
Return to text
7. In this context, “lyric composition” refers to the collection of genres appropriate to the lyric stage, which at this time included but was not limited to opera and comic opera. The ability of a student’s abilities in lyric composition was ultimately tested in the second round of the Prix de Rome, where students had to compose a lyric scene to a preapproved text by a poet from the Académie.
Return to text
8. Students were admitted to composition courses either as auditors or “élèves en exercice.” Reflecting the Conservatory’s role as a public institution, students admitted “en exercice” were required to participate in a number of public obligations, including annual public performances (“exercises”) and other ceremonial events. In any case, under Cherubini’s administration, enrollment in each of the two harmonie et accompagnement pratique sections was limited to ten élèves en exercice, with two additional sections open to an equal number of auditors. Counterpoint sections, however, enrolled only six students each, again with two sections intended for élèves and two for auditors, while three sections of lyric composition each enrolled four students and admitted no auditors.
Return to text
9. François-Louis Perne also served as the school’s director from 1816–1822 during the initial years of the Restauration. Following the Hundred Days and Napoleon’s second exile, the Conservatory was closed due to its origins as a Revolutionary institution, with many of its faculty, including Sarrette, Catel, and Gossec, forced to retire given their republican associations. Following its reintegration under the Ménu-Plaisirs du Roi, as the École Royale de Musique et de Déclamation, the school reopened under Perne’s sole directorship and underwent a period of extreme austerity. Fétis reports that the school had to burn old harpsichords for fuel during this period. It was not until Cherubini was named director that the school returned to its pre-1814 functioning and began to acquire its prominence as the modern institution for which it is widely known today.
Return to text
10. The information in the table here is drawn from the list of faculty rosters and courses in Pierre 1900 (415–30).
Return to text
11. The longevity of the Conservatory’s composition faculty during this period is remarkable. Cherubini would retire from the Conservatory in 1842, while Berton would occupy his position of professor of composition until his death in 1844. Dourlen, a former student of both Catel and Berton, would serve as the sole instructor of the men’s section of harmonie et accompagnement pratique from 1816 until his retirement in 1842. We might therefore consider the initial period of the discipline of harmony as coming to a partial close with the nearly simultaneous retirements of Cherubini and Dourlen and the death of Berton.
Return to text
12. Due to public criticism regarding its lack of productivity, particularly at the Opéra, the Council on Public Education charged the newly founded National Conservatory with a series of reforms. These reforms, initiated in 1799, included the creation of a series of elements texts, intended to establish curricular and pedagogical uniformity across disciplines. Catel’s harmony treatise was one such text. For further discussion of the reforms, see Gessele 1992, Rubinoff 2017, and Masci 2023.
Return to text
13. The adoption of Catel’s treatise significantly limited the influence of Rameau’s theories when it came to harmony pedagogy at the Conservatory. As commentators—including Choron and Fétis—remarked, the adoption of Catel’s text largely ended the influence of fundamental bass theory at the Conservatory. Perhaps most notably, Catel, unlike Rameau, did not include major or minor seventh chords in his fundamental chord catalog; there are no IV7 or ii7 chords in Conservatory music theory that are subsequently subjected to operations of inversion, etc. Instead, Catel derived dissonances beyond those associated with dominant sonorities from melodic elaborations.
Return to text
14. Dourlen won prizes in harmony (second prize, 1799), piano (accessit, 1801), and fugue (accessit, 1805). Dourlen was also one of the first winners of the Prix de Rome, taking second prize in 1804 and then the Premier Grand Prix in the following year—just the third year of the contest’s existence in the discipline of music composition. He began teaching at the Conservatory as répétiteur for the solfège course from 1800 to 1802, and later assumed the same role for Berton’s harmony course in 1812. When the Conservatory reopened as the École royale de musique et de déclamation in 1816, Perne appointed him professor of harmony, succeeding Berton upon the latter’s promotion to professor of composition.
Return to text
15. Remarking on the relationship between his treatise and that of his former teacher, Dourlen writes that he created his text in direct response to Catel’s not containing a sufficient number of examples and exercises. Dourlen goes on to recount that on a number of occasions, Catel had communicated to him his intention to produce a volume of exercises to accompany his treatise, though no such work had been completed upon his early and unexpected death. Having left no trace for the project, and recalling the support that Catel had lent him in his early career as a young composer, Dourlen felt it both appropriate and an homage to his former teacher to write his own volume, largely a series of figured and unfigured basses (1838, 1). Beyond the written exercises he provided for Berton’s that were recorded in Leborne’s notebook, no other documentation survives from Catel’s own harmony class. As such, Dourlen’s treatise provides the only extant account of how the Conservatory’s approved set of elements were put into practice in the context of actual courses during this period.
Return to text
16. Catel defines “natural harmony” as those that derive from the simple divisions of the monochord as well as those dissonant sonorities, such as the dominant seventh, that do not require any particular dissonance preparation. “Compound” harmonies were “artificial,” in that their dissonances derived from the artifice of various compositional procedures such as suspensions (Catel 1802, i). This conception diverges from traditional fundamental bass theory, which includes various diatonic seventh chords, such as major and minor sevenths, as fundamental harmonies.
Return to text
17. Though undated in terms of daily entries, the contents of Dourlen’s 1838 treatise corroborate this broad structure with remarkable consistency, with the overall organization of his cours closely resembling Berton’s from decades earlier: natural harmony —both consonant and dissonant—was covered first, followed by harmonie composée. The text covers all elements in the first two thirds of the text (exercises 1–65), presumably constituting the material for the first two trimesters of the course, while the remaining exercises (nos. 66–111), presumably two per class meeting, introduce no new elements. They instead focus on increasingly difficult, exam-quality pieces, including exercises in melody harmonization that, again, included examples by Catel and Gossec.
Return to text
18. In the Conservatory tradition, treatises by Langlé, Catel, and Dourlen consistently catalog scales as marches; the verb “marcher” means to step, hence the association with any scalar passages, including rule of the octave passages and sequences. As we will see below, the understanding of scalar passages as a form of sequence provides important material for contrapuntal elaboration, especially when it came to dissonant harmonies.
Return to text
19. It should be recalled that all exercises from Leborne’s notebook, while drawn from Berton’s course, were composed by Dourlen.
Return to text
20. For [M]-numbers (e.g., [M1], [M2], etc.) see Appendix A.
Return to text
21. In the Conservatory tradition, scales are consistently catalogued as marches in treatises by Langlé, Catel, and Dourlen. As subsequent discussion will clarify, the understanding of scalar passages as a form of sequence provides important material for contrapuntal elaboration, especially when it came to dissonant harmonies.
Return to text
22. The superscripts applied to M numbers indicate the figured-bass symbols, and thus the particular contrapuntal elaboration of the basic sequence. For instance, [M45--] indicates the sequence [M4] of a falling fourth descending by third elaborated with an ascending chordal skip in the bass.
Return to text
23. While French music theory uses fixed-do solfege, I will use moveable do throughout. This is common in recent partimento scholarship in order to indicate various figures and schema that appear in modulatory contexts. Perhaps the most common example of this is Gjerdingen’s “do-re-mi” schema.
Return to text
24. As Lester describes with respect to Rameau, any consonant chord acts as a tonic, while dissonances serve as an impetus for progression (1992, 116–19).
Return to text
25. As Gjerdingen has shown, of all the cadential contrapuntal schemata, the “do-re-mi” is perhaps one of the most foundational, acting as the source of extensive elaboration in common-practice repertory (2007, 77–88).
Return to text
26. These dissonances were “artificial” and not “natural” in that they derived from the artificial means of composition, such as suspensions and non-harmonic tones, and not from the “natural” vibrations of a sounding body, the divisions of a string, etc.
Return to text
27. To a lesser extent, the course also considers the tonic eleventh and various delayed arrivals on the dominant.
Return to text
28. French harmony pedagogy uses two terms in relation to dissonance preparation, “prolongation” and “retard,” that had evolved over time. In general, by the middle of the nineteenth century, prolongation or more specifically “chords by prolongation,” had come to refer to sonorities with prepared chordal dissonances, largely major and minor sevenths and their inversions as well as the major ninth; “retards” referred to suspensions, which in French pedagogy includes the 5/4 and its inversions. (See Bazin 1857 and Savard 1853) This distinction, however, was not widely recognized in the early part of the century. Catel’s Traité d’harmonie, the Conservatory’s first harmony treatise, for instance, defines the relationship between the two terms more broadly and as follows: “One may prolong one or several notes of a chord into the subsequent chord. The prolonged note (note prolongée) is a dissonance that must descend by one scale degree either over the given bass note or on the following chord. A prolongation is most often nothing more than a delay (retard) of a chord tone.” (Catel 1802, 21) Thus, for Catel, a “prolonged” note is simply a prepared dissonance that delays a chord tone, regardless of when it resolves. As such prolongation may result in either a chordal dissonance or a suspension depending on when it resolves. Dourlen’s 1838 treatise retains Catel’s definition, suggesting the broader definition was still in use as late as 1840.
Return to text
29. The history of the catalog of dissonant harmonies and figures addressed by the early harmony course attests to the polyglot Franco-Italian heritage of certain disciplines at the institution. The catalog may be traced back to the writings of Honoré Langlé (1741-1807), who studied in Naples under Cafaro. After his studies in Italy, Langlé returned to France in 1768, ultimately publishing his Traité d’harmonie et de modulation (dedicated to Cafaro) in 1795. The publication, possibly prompted by the founding of the Conservatory and the need for school texts, extensively lists all possible dissonances with respect to bass motions, resolutions, and accompanying consonances. The text would in turn serve as one of the models for Catel’s own Traité d’harmonie. Catel’s text, however, greatly reduces and simplifies number of figures found in Langle’s treatise, compiling them in a celebrated table. In the words of Choron, the principles of Catel’s theory “were prefigured by the school of Durante as well as attested to in Fenaroli’s pamphlet, Regoli per li principianti. . . but presented by Monsieur Catel in a more clear and concise manner.” It was Catel’s reduction of dissonant figures that then became the basis for the Conservatory’s course in written harmony. Additionally, for a comprehensive collection of marches dissonantes and their contrapuntal elaborations, the reader should consult Cherubini 1847.
Return to text
30. This is the first broderie to appear, for instance, in Choron 1808 as well as Fétis 1823.
Return to text
31. In regard to the latter, this is a function of the particular contrapuntal desideratum that leaps should not follow from stepwise motion in the same direction, i.e., that leaps change direction.
Return to text
32. I thank the anonymous reader of this manuscript for pointing out the use of similar cleffing devices to illustrate contrapuntal diminutions in Italian sources, including the counterpoint studies of Lavigna. Guido Olivieri has made a similar point in regard to Francone’s passacagli for cello (Barbati and Olivieri 2021). In this context, I would point out the broader novel uses of different clefs and system formatting when it came to matters of exemplarity in pedagogical works. In French accompaniment treatises, for instance, multiple treble clefs were used in a single system to show different hand positions for realizing figured basses; in theoretical treatises multiple bass clefs were used to illustrate fundamental bass progressions.
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
10204