Metric Modes and Fluid Meter in Mande Drumming Music*
James B. Morford and Aaron M. David
KEYWORDS: Africa, rhythm and meter, Mande, pulsation non-isochrony, microtiming, swing, groove
ABSTRACT: This article proposes a model that unites a broad range of performances of Mande drumming music within a single cohesive and fluid sub-beat metric framework. The framework categorizes musical performance in terms of two metric modes, each of which includes a set of metric cycles featuring non-isochronous pulsations. A novel feature of the proposed model that distinguishes it from previous research is that it frames metric non-isochrony in terms of the ranges for pulsation positions within a pulsation cycle. This approach is shown to be especially useful for analyzing and describing mechanisms of metrical change and transformation and for connecting seemingly distinct phenomena and repertoire.
DOI: 10.30535/mto.29.3.4
Copyright © 2023 Society for Music Theory
I. Introduction
[1.1] Over the last quarter century, scholars interested in the ways that music “swings” or “grooves” have afforded increasing attention to periodic non-isochrony within pulsation streams. Rather than relying on the sentiment that someone “just has to feel it,” music scholars have used a variety of computational strategies to measure and compare performances; this holds especially for case studies pertaining to specific musics associated with Africa and African diasporas (i.e., Polak 2010). Compelling evidence suggests that Mande drumming music is non-isochronous at the level of sub-beat pulsations, and that this non-isochrony is metric and structural rather than merely expressive (Polak 2022).(1)
[1.2] Scholars studying non-isochrony typically describe it in terms of relative durations of inter-onset intervals (IOIs) with values of Long, Medium, and Short (Neuhoff, Polak, and Fischinger 2017; London 2012). Periodic cycles emerge from combinations of these relative values, generating patterns such as Long-Short and Short-Medium-Long. This style of description has been broadly applied and has proven to be useful. We have found, however, that the IOI method of describing pulsation non-isochrony becomes cumbersome when trying to explain changes that commonly occur in Mande music. This article emerges in part from a desire to advance the discourse on metric transformation in Mande drumming performance, particularly with respect to pulsation positions and metric density. Rather than using IOIs, we categorize non-isochrony in terms of ranges for pulsation positions. This approach allows us to organize Mande drumming performances within a single and cohesive metric structure at the pulsation level that includes two metric modes. In this article, we argue that a modal perspective is better suited to facilitate understanding of how performances transform and how they relate to one another.
[1.3] In Mande music, onsets occur as if tied to a latent and malleable metric texture made up of pulsation cycles.(2) (This and other terms are defined in the glossary.) We adapt Arom’s (1991, 180) use of the term “pulsations” to mean metric units that may or may not be materialized as rhythmic parts of an isochronous or non-isochronous beat. Put another way, a pulsation is a duration of time in which a metrically defined onset can potentially occur. Pulsation cycles can be categorized according to the relative durations and positions of ranges for their constituent pulsations. These pulsation cycles are identifiable and predictable, but they are not static. They interact with and transform into one another, making up the underlying metric structure of Mande drumming music.(3)
[1.4] As stated above, we frame the pulsation cycles that make up the underlying metric background of Mande drumming performance in terms of the ranges of pulsation positions within a cycle. A pulsation cycle is somewhat analogous to what has been labeled a “metric timing pattern” or MTP (Neuhoff, Polak, and Fischinger 2017); however, pulsation cycles differ from MTPs in two critical ways. First, MTPs are defined in terms of repeated cycles of pulsation classes, themselves based on inter-onset intervals. We conceive of a pulsation cycle as a specific and repeating collocation, not of pulsation classes, or even of pulsation positions, but of pulsation position ranges. As detailed below, we classify pulsation cycles according to the quantity of pulsations in a single cycle as well as the relative positions of ranges for those pulsations.(4) Second, MTPs are restricted to describing the composite pulsation trains implied by an entire ensemble, whereas our formulation also includes individual manifestations of pulsation cycles.
[1.5] Polak asserts that the non-isochrony of pulsations within an MTP is neither a “participatory discrepancy” (Keil 1987), nor a mere “instance of departure for expressive variation” (Polak 2010, 149). The same holds true from a range-oriented pulsation cycle perspective. This is not to say that discrepancies and expressiveness are absent from Mande drumming performance. Rather, in agreement with Polak (2010), we find that expressive variations are individually or collectively applied to a temporal palette consisting of pulsations that are already non-isochronous by default.(5)
[1.6] A central concern of this paper is to address what we perceive to be an overemphasis on pulsation quantity in metric categorization. This concern extends beyond Mande music, as Africanist musicologists in general tend to consider rhythmic groupings as either binary or ternary, organizing music into either
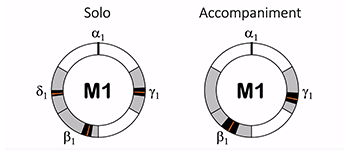
[1.7] For readers entirely unfamiliar with Mande drumming music, the following brief introduction to the basics of performance and instruments may be helpful. Mande drumming music typically includes a variative “lead” (often called “solo”) part and one or more accompaniment parts.(7) The lead part improvises and plays cues that signal other participants. Typically performed by one player at a time, musicians alternate taking this role during a performance. Accompaniment parts can include minimally variative ostinatos (often played across a variety of repertoire) as well as repertoire-specific variable patterns. While the concepts put forth in this paper may readily apply to instruments more broadly, we focus our attention on percussion instruments. Especially relevant in our analyses are djembes and dunduns. For more extensive discussion of these instruments and their developments, see Charry 2000 and Polak 2000.
[1.8] To our knowledge, no indigenous Mande terminology exists that directly identifies metric modes as we define them below. However, printed method books and instructional materials associated with internationally renowned musicians from Guinea and Mali describe non-isochronous pulsation positioning with words such as “feeling” and “warping” (Billmeier 1999, 110), the French term “sentiment” (Bénic and Noyer 2014, 8), and “drawing out” or “microtiming” (Konaté and Ott 1997, 34). In pedagogical materials developed alongside collaborators from Europe, Malian musician Sega Sidibé classifies music as belonging to one of three families, one featuring a quaternary (four-pulsation) pulsation cycle, and the others featuring their own distinct ternary (three-pulsation) pulsation cycles (Bénic and Noyer 2014). A similar formulation relating repertoire families to pulsation cycles can be found in Johannes Beer’s liner notes to Famoudou Konaté’s (1991) compact disc, Rhythmen der Malinke, where he identifies two categories of ternary rhythmic families categorized by a displacement of the second pulsation.(8)
[1.9] Errors in performance and their corrections can also provide insight into indigenous conceptions of music (Agawu 2003, 108–110). We have observed musicians using a variety of terms in response to pulsation position errors. These include calls to “pay attention to the time” or to the “tempo.”(9) Musicians also correct errors with encouragement to play “the other one” or “the other way.” References to an “other”—as opposed to “others”—suggests that the rhythmic conceptions of some indigenous musicians are consistent with our bi-modal model.
[1.10] This paper provides an alternative to the relatively static approaches that render many conventional theories of rhythm and meter insufficient for analyzing Mande music. In his study of stambeli music in Tunisia, Jankowsky (2013) argues that tempo increase often correlates with predictable pulsation position change. Jankowsky observes a specific “rhythmic elasticity” in stambeli music, featuring pulsations that move toward isochrony as tempo increases. Throughout this article, we argue that meter in Mande music is similarly fluid, with pulsation positions that also change predictably. Yet, pulsations do not necessarily move permanently, nor necessarily toward isochrony, nor only in response to tempo change.
[1.11] Thinking of meter as dynamic or fluid allows one to more readily connect seemingly distinct metric structures in Mande music. The non-isochronous timing patterns used in Mande music are not simply related by abstract relationships; they transform into one another in predictable ways during performance. Thinking in terms of a unified dynamic metric system allows us to better understand 1) transformations that occur in the course of a single performance; 2) relationships between different performances of the same piece; and 3) relationships between different pieces.
Materials/Corpus
[1.12] The materials explicitly analyzed in this article come from a variety of sources, including field recordings, commercial recordings, and publicly available recordings from open-access academic collections. We have elected not to restrict ourselves to a single isolated corpus of performances based on location, ethnicity, or instrumentation because our primary objective in this paper is to demonstrate relationships between pulsation-level metric structures in a variety of performance contexts. Further testing of our analytical propositions could benefit from a granular approach focusing on isolated practices in specific case studies recorded under controlled conditions.
[1.13] We surveyed dozens of recordings in search of examples of phenomena that are introduced and examined below. The corpus that we surveyed reflects our combined decades of practical experiences as performers, students, formal and informal researchers, and teachers of Mande music. After identifying potentially useful recordings, we selected specific examples based on a combination of factors, including general audio clarity, discernibility of parts, and ease of access for readers. Other potential examples were excluded because they were lacking in one or more of these features, or because we could not obtain what we consider to be reliable and ethical permissions for use. A full list of the examples in this paper can be found in Appendix 1.
[1.14] Each of the following parts of the article addresses a different aspect of our model for understanding microtiming in Mande drumming music. In Part II, we introduce a static view of pulsation-level metricity in Mande music by proposing analytical units called pulsation cycles; each of these is further categorized as belonging to one of two metric modes. In Part III, we push beyond the static view, applying the concept of metric mode as a framing device for understanding changes in pulsation quantity and in relative pulsation positions in the parts of lead musicians. In Part IV, we explore metric dynamism, demonstrating how collective change in pulsation position and quantity corresponds with a predictable sequence of metric transformations. Finally, in Part V, we discuss some of the rationales, implications, limitations, and potential extensions of the model and analytical approach introduced in this article.
II. Metric Modes
[2.1] The purpose of Part II is to present a basic description of pulsation organization in Mande drumming music. We begin by defining and classifying pulsation cycles. In addition, we explain our system for graphic representation and differentiate between pulsation cycles and metric modes. We last describe the three pulsation cycles that comprise each of the two metric modes in Mande music and an additional compound pulsation cycle.
Classifying Pulsation Cycles
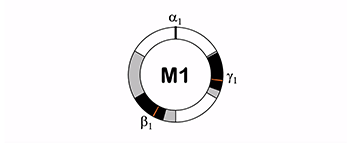
[2.2] Our classification terminology is based on the quantity of pulsations and the quality of pulsation range positioning within a cycle. The pulsation cycles in this model are constituted of two, three, or four pulsations. Each pulsation, moreover, maintains a unique categorical identity assigned according to relative metric hierarchy. In order of hierarchical importance (though not necessarily onset order), these pulsations are α (alpha), β (beta), γ (gamma), and δ (delta). When a pulsation cycle includes only α and β, we categorize it as binary (2). When a pulsation cycle includes only pulsations α, β, and γ, we call it ternary (3). Finally, we use the term quaternary (4) to describe pulsation cycles including α, β, γ, and δ.
[2.3] While, in colloquial terms, one might think of α as occurring on the beat, we define α as the first pulsation in a pulsation cycle.(10) This is advantageous for describing change in Mande music, as it does not require that repetitions of α generate isochronous beats. In a performance, α is not always identifiable by a single sonic or visual signal. Often, it emerges as a product of the following indicators: clapping; footfalls; dance movements; corrective gestures; the beginnings and endings of signals, rehearsed arrangements, and performances; verbal confirmation; and the existence of similar or identical phrases in other pieces that exhibit a clearly defined and emphasized α.
[2.4] In addition to pulsation quantity, pulsation cycles also exhibit quality, which is determined by the location of the smallest gap between pulsation ranges (rather than between onset positions). A pulsation cycle’s quality will be one of two types. When the shortest interval between two subsequent pulsation ranges in a pulsation cycle falls before β, we categorize that pulsation cycle as having a front-heavy (F) quality.(11) When it occurs after β, we categorize the pulsation cycle as back-heavy (B). We label pulsation cycles by combining their quality and pulsation quantity, using abbreviations as shorthand. For example, a binary pulsation cycle with back-heavy quality would be labeled a back-heavy two (B2). Similarly, a front-heavy pulsation cycle that is quaternary would be labeled a front-heavy four (F4).
Graphic Explanations
[2.5] Existing analyses of non-isochrony in Mande music foreground the relative durations of inter-onset intervals (IOIs), representing MTPs with structures such as Long-Short, Short-Medium-Long, and others (e.g., Polak 2010). Like standard notation, a description of non-isochrony built upon relative durations of IOIs is useful. However, it becomes unwieldy when addressing metric transformations that occur during performances. Our model responds to the problem of describing metric transformations by emphasizing the ranges of pulsation positions. Further discussion of our reasoning for this emphasis, and of how we determine specific pulsation range boundaries can be found in Part V of this paper.
[2.6] Although useful for representing rhythmic figures, staff notation is insufficient for communicating about the characteristics and transformations of non-isochronous pulsation cycles.(12) As such, we have developed a system of representing pulsation cycles using circular graphics with shaded bars showing the bounded ranges for pulsation positions.(13) We are aware that some scholars have criticized the use of new representational systems for rhythm in African musics on ethical grounds (Agawu 2003, 64–68). In response, we would maintain that the graphical system below is not used to transcribe rhythms; it specifically represents pulsation cycles, which are metric phenomena.(14)
[2.7] The graphics below feature a circle representing the duration of one pulsation cycle, with time flowing clockwise. Pulsation cycles begin with α, which always falls at the top of the circle. Because we define α as the beginning of a pulsation cycle, it is conceived of as a discrete moment and represented with a black bar. Each of the lower-hierarchy pulsations in a pulsation cycle falls somewhere within its own predictable range, shown as shaded areas.
[2.8] While moments of Mande music can be understood in terms of a single pulsation cycle, most performances include multiple pulsation cycles that occur either simultaneously between different parts, or serially within a single part. When considering general principles that apply to a wide range of people, performances, and pieces of repertoire, we find it useful to categorize Mande drumming music in terms of two metric modes that bear some resemblance to what London calls “metric types” (2012, 94). We refer to these two metric modes as Mode 1 and Mode 2, each of which includes three pulsation cycles. Pulsation α occurs at the beginning of the pulsation cycle, and the onset order of the remaining pulsations depends upon the metric mode of the performance. When necessary to avoid ambiguity, we add a sub-script 1 to Mode 1 pulsations and sub-script 2 to Mode 2 pulsations (e.g., δ1 or β2).
Mode 1 Pulsation Cycles
Example 1. Back-Heavy Two Pulsation Cycle
(click to enlarge)
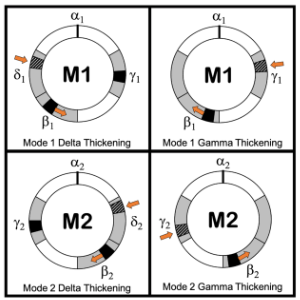
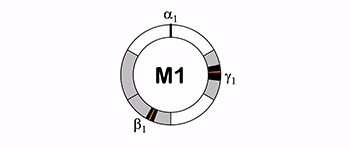
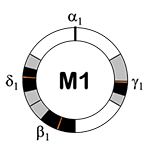
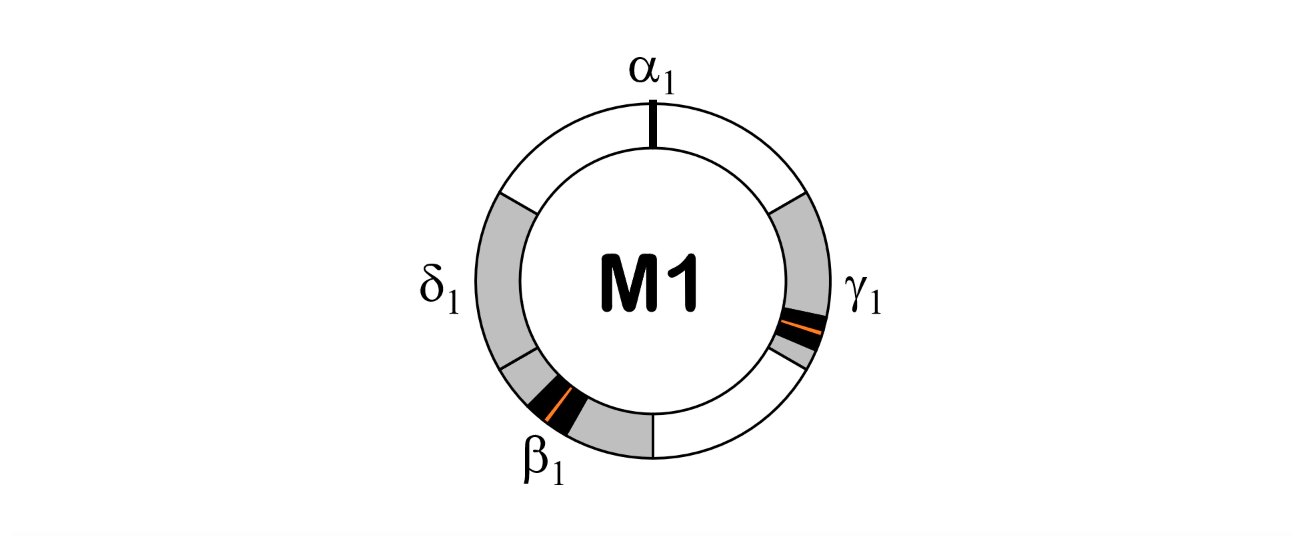
[2.9] Mode 1 includes three pulsation cycles: one binary, one ternary, and one quaternary. The binary pulsation cycle in Mode 1 includes two pulsations: α1 and β1. Again, we define α1 as the beginning of a Mode 1 pulsation cycle, α1 occurs at a fixed moment and not within an associated range. Pulsation β1 is second in the Mode 1 hierarchy, with a range from one-half to two-thirds of the duration of a full cycle between subsequent occurrences of α1. The shortest potential interval between pulsations is located after β1, making the pulsation cycle back-heavy. Thus, we call the Mode 1 binary pulsation cycle back-heavy two (B2); see Example 1.(15)
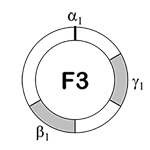
[2.10] Pulsation γ1 is third in the hierarchical order of the Mode 1 pulsations; it combines with α1 and β1 to generate the ternary pulsation cycle in Mode 1. Pulsation γ1 occurs between one sixth and one third of a pulsation cycle. This places γ1 second in terms of onset order, falling between α1 and β1. The shortest potential interval falls before β1, indicating front-heaviness, as illustrated in Example 2. We thus call the Mode 1 ternary pulsation cycle front-heavy three (F3).(16)
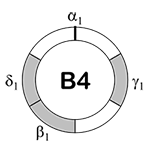
Example 2. Front-Heavy Three Pulsation Cycle (click to enlarge) | Example 3. Back-Heavy Four Pulsation Cycle (click to enlarge) |
[2.11] The quaternary pulsation cycle of Mode 1 features pulsation δ, which is fourth in both hierarchical order and onset order and occurs in a range between two thirds and five sixths of a cycle. This pulsation cycle is back heavy because the shortest potential interval falls after β1. Thus, we call the Mode 1 quaternary pulsation cycle back-heavy four (B4); see Example 3.(17)
Example 4. Mode 1 Pulsation Cycles in order of decreasing pulsation quantity from left to right
(click to enlarge)
Relationship Between Mode 1 Pulsation Cycles
[2.12] Back-heavy two, front-heavy three, and back-heavy four are all expressions of a more general Mode 1 performance. The common thread between the Mode 1 pulsation cycles is that α1 always begins the cycle and β1 always occurs between one half and two thirds of a cycle. These two pulsations form the B2 that is implied within all three pulsation cycles. Back-heavy two can thus be understood as the distillation or core of Mode 1, as shown in Example 4.
Mode 2 Pulsation Cycles
Example 5. Front-Heavy Two Pulsation Cycle
(click to enlarge)
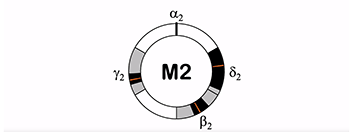
[2.13] Like Mode 1, Mode 2 includes binary, ternary, and quaternary pulsation cycles. The binary pulsation cycle of Mode 2 includes pulsation α2, which begins it, and β2, which falls in a range between one third and one half of the duration between subsequent occurrences of α2 (Example 5). Because the shortest potential interval between subsequent pulsations occurs before β2, we call the Mode 2 binary pulsation cycle front-heavy two (F2).(18)
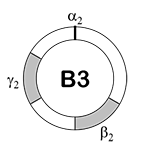
[2.14] In the Mode 2 ternary pulsation cycle, γ2 falls third in the onset order, occurring in a range from two thirds to five sixths of a cycle (Example 6).(19) This pulsation cycle is back-heavy because the shortest potential interval occurs after β2. We therefore call the Mode 2 ternary pulsation cycle back-heavy three (B3).
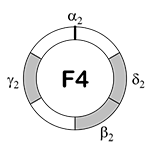
Example 6. Back-Heavy Three Pulsation Cycle (click to enlarge) | Example 7. Front-Heavy Four Pulsation Cycle (click to enlarge) |
[2.15] In the quaternary pulsation cycle for Mode 2, δ2 falls second in the onset order and can occur any time between one sixth and one third of a cycle (Example 7). This pulsation cycle is front-heavy because the shortest potential interval is located before β2. The quaternary pulsation cycle of Mode 2 is therefore called front-heavy four (F4).
Relationship Between Mode 2 Pulsation Cycles
Example 8. Mode 2 Pulsation Cycles in order of decreasing pulsation quantity from left to right
(click to enlarge)
[2.16] Front-heavy two, back-heavy three, and front-heavy four pulsation cycles are all expressions of a more general mode of performance that we call Mode 2. The common thread between the Mode 2 pulsation cycles is that β2 occurs between one third and one half of a beat cycle. When considered in isolation, the relationship between α2 and β2 is identical to the front-heavy two pulsation cycle. Front-heavy two is thus implied within all Mode 2 pulsation cycles (Example 8), and represents the core of Mode 2 performance.
Comparing and Contrasting the Two Modes
[2.17] Both Mode 1 and Mode 2 include three pulsation cycles, with the α-β relationship in the binary pulsation cycle serving as the common core for all pulsation cycles within each mode.(20) The pulsation cycles within a metric mode can occur simultaneously during a performance; however, pulsation cycles from the two metric modes are not blended. At any one moment, all competent performers play rhythmic material that is consistent with pulsation cycles from the same mode.
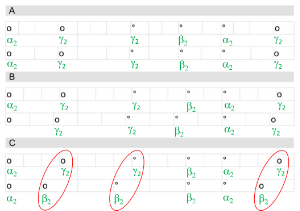
[2.18] The two metric modes differ from one another in a number of ways. First, the onset order of pulsations γ and δ is reversed in the two modes. Second, the qualities of pulsation cycles in the two modes are reversed in relation to their pulsation cardinality. That is, the binary pulsation cycle is back-heavy in Mode 1 (B2) and front-heavy in Mode 2 (F2). The ternary pulsation cycle is front-heavy in Mode 1 (F3) and back-heavy in Mode 2 (B3). Finally, the quaternary pulsation cycle is back-heavy in Mode 1 (B4) and front-heavy in Mode 2 (F4).
Example 9. Mode 1 and Mode 2 pulsation cycles
(click to enlarge)
[2.19] It is not necessarily possible to distinguish between Mode 1 and Mode 2 performance by the position of any single non-beat pulsation alone. For example, the ranges for γ1 and δ1 are identical to the ranges for δ2 and γ2, respectively. Yet, Mode 1 and Mode 2 performance can be distinguished from one another in terms of the ranges of β1 and β2. Example 9 shows that the range for β1, between one half and two thirds of a pulsation cycle, aligns with a gap in Mode 2 in which no pulsations occur. Similarly, the range for β2 aligns with a gap in Mode 1.(21)
[2.20] A final similarity between the two modes can be found in their rotational equivalence. Rotating a single pulsation cycle such that β is reframed as α (and vice versa) can produce the quantitatively equivalent pulsation cycle in the opposing mode. Therefore, for a given pulsation cycle, if β is perceived as the beat, the resulting pulsation cycle has the same quantity of pulsations but the opposite quality. For example, if β1 is perceived as occurring on the beat, then an F3 pulsation cycle can be perceived as a B3. This rotational equivalence at the level of the pulsation cycle extends to modal perception, such that if someone perceives β as occurring on the beat, then that person will perceive the entire performance as though it were in the other mode.(22)
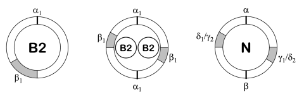
Neutral Pulsation Cycle
Example 10. Neutral Pulsation Cycle
(click to enlarge)
[2.21] It often occurs that performers treat two B2 cycles as a single beat; see Example 10. We call this compound quaternary pulsation cycle Neutral (N) because it manifests as modally ambiguous and as a kind of default. It is this compound cycle, and not isochrony, that represents “unswung” quaternary performance.(23) We have observed neutrality for this compound cycle when musicians refashion repertoire that is typically played in F4 or B4 to cater to the needs of novice students. In these cases, the pulsations are oriented not into isochrony, but into Neutral. The same often occurs when otherwise competent musicians who are not immersed in B4 or F4 performance adapt pieces to align with their own schemas for musical swing. Neutral features two equally short intervals between pulsation position ranges, with one located before β and one after β. Therefore, Neutral is neither back-heavy nor front-heavy. In Part IV below, we demonstrate how Neutral can transform into the quaternary pulsation cycles of either metric mode through changes in the metric background.(24) For this reason, it can be useful to think of Neutral as belonging to both modes or to neither mode, depending on the context.
III. Thinking Modally
[3.1] In Part II, we characterized the metric organization of Mande drumming music in terms of six pulsation cycles belonging to two modes. In Part III, we demonstrate the utility of an analytical orientation that foregrounds modes (rather than pulsation cycles) by focusing on changes in pulsation cycle cardinality by lead/solo musicians. Here, we focus on one particular kind of change that we call modal thickening, which we illustrate by means of analysis of various performances of the piece “Woloso.” To facilitate the discussion to follow, we preface the analysis by addressing the use of pulsation cycles within a modal perspective.
[3.2] Within more general metric modes, the pulsation cycles proposed in Part II can be understood as snapshots or landmarks that are useful as metric framing devices for a variety of combinations of voices (vertically) and at a variety of durational scales (horizontally). Thinking vertically, pulsation cycles can describe individual voices or combinations of two or more voices. A composite pulsation cycle combines the sounded notes and biomechanics (e.g., handing patterns) of multiple voices and parts. From this perspective, a composite pulsation cycle becomes synonymous with the individual pulsation cycle of highest cardinality among included voices. If, for example, any individual parts include γ but none include δ, then the composite pulsation cycle is treated as ternary.
[3.3] Thinking horizontally, analysts might work at the scale of a single pulsation cycle bookended by iterations of α, an ensemble thematic (melo-rhythmic) cycle, or even an entire performance. At perhaps the broadest scale, one might apply a pulsation cycle as a way to categorize a piece of repertoire in the abstract, but this risks oversimplification because pulsation cycles can change quite rapidly. Therefore, we treat composite pulsation cycles not as a baseline metric layer used to categorize a performance, but as temporary referents that help to describe metric change.
Modal Thickening
[3.4] In expressive variation, individuals can incorporate γ and/or δ when these pulsations were previously absent from their pulsation cycles. This process, which we call modal thickening (thickening) reinforces a performance’s modal identity, as it always incorporates γ and/or δ from the same mode as the previously established pulsation cycle.(25) Thickening can impact the cardinality of pulsation cycles in two ways. First, a musician introducing a new pulsation can change their own individual pulsation cycle. Second, thickening can change a composite pulsation cycle if the pulsation that is introduced was previously absent from all parts, destabilizing pulsation cardinality and reinforcing a performance’s modal identity.
Example 11. Delta and Gamma Thickening in Mode 1 and Mode 2
(click to enlarge)
[3.5] As detailed in examples below, thickening often corresponds with predictable changes in the position of β, depending on mode (Example 11). In Mode 1, β1 moves later in its range as gamma thickening changes a pulsation cycle from B2 to F3 (adding γ1). In Mode 2, β2 moves earlier in its range as gamma thickening changes a pulsation cycle from F2 to B3 (adding γ2). During delta thickening in either mode, γ and β can move within their respective ranges.(26) In Mode 1, β1 moves earlier in its range as delta thickening changes a pulsation cycle from F3 to B4 (adding δ1). In Mode 2, β2 moves later in its range as delta thickening changes a pulsation cycle from B3 to F4 (adding δ2).
“Hand-Over-Hand” Execution
Example 12. Hand-over-hand patterns in Mode 1 and Mode 2
(click to enlarge)
[3.6] Further insight into the metric perspectives of individuals may be gained by observing changes in “hand-over-hand” execution. Hand-over-hand execution occurs when musicians alternate hands for each consecutive pulsation within a pulsation cycle; such may be said to occur regardless of whether they sound every pulsation, perform ghost notes on them, or leave them unsounded (Example 12).(27) Because connections between handing patterns and pulsations are predictable in hand-over-hand execution, changes in handing can provide visual evidence of thickening.
[3.7] Gamma thickening requires a change from binary handing to ternary handing, while delta thickening requires a change from binary or ternary handing to quaternary handing.(28) As we demonstrate in the examples below, during thickening, pulsation and handing changes often precede the sounding of new pulsations. When pulsation positions change as described above and this change coincides with a change in handing, we consider thickening to have occurred, even when the new pulsations remain unsounded. In cases where we observe predicted pulsation movement but no change in handing can be observed, we consider thickening and pulsation position change alone to be indistinguishable from one another until notes are sounded on the newly introduced pulsations.
[3.8] To aid in identifying and understanding thickening (and, later, maturation), we refer to musical figures that we call “string phrases” or “strings.” The reason that strings are useful for understanding maturation is because changes in the type of string phrases often coincide with changes in the composite pulsation cycle during maturation. A string can begin on any pulsation and comprises every pulsation in a pulsation cycle sounded at least twice in an uninterrupted stream.(29) There are three types of string phrases, each corresponding with the quantity of pulsations in a pulsation cycle: binary, ternary, and quaternary. Binary strings consist of notes sounded on two consecutive cycles of α and β, beginning on either pulsation. Ternary strings consist of notes sounded on two cycles of α, β, and γ, beginning on any of these pulsations. Finally, quaternary strings consist of notes sounded on at least two cycles of α, β, γ, and δ, beginning on any of these pulsations.
[3.9] In the remainder of Part III, we identify and analyze specific examples of delta thickening in recordings of “Woloso” from the Interpersonal Entrainment in Music Performance (IEMP): “Malian Jembe” data set (Polak, Tarsitani, and Clayton 2019). Analysts typically classify “Woloso” as ternary, grouping pulsations into one of only three possible metric positions, which correlate to our ranges for α1, γ1, and β1. However, as demonstrated below, delta thickening in “Woloso” introduces notes in the predicted range for δ1 and results in the pulsation position change predicted for β1. This delta thickening, while changing pulsation cardinality, maintains metric consistency from a modal perspective. Therefore, thinking modally avoids the potential problems that emerge when attempting to classify a performance of “Woloso,” or even part of a performance, in terms of a single metric layer. The performances of “Woloso” analyzed below, for example, feature all three Mode 1 pulsation cycles. A modal perspective allows one to understand changes in pulsation cardinality and pulsation position without requiring categorical metric transformation.(30)
Method of Measurement
[3.10] The analyses presented throughout Parts III and IV frequently refer to specific pulsation positions. These positions were measured manually by examining the waveform using the digital audio editing software, Audacity. Temporal values for all onsets were measured using the earliest moment at which the new sound became visually apparent in the waveform. This introduced a level of subjectivity into the measurement, but nevertheless resulted in the ability to determine timing to within one millisecond on repeated measurement of the same onset.(31) We first calculated absolute inter-α durations for each example. In cases where no onset occurred on a particular α, the position for a hypothetical α was calculated by extrapolating from the two nearest iterations of α before it and the two nearest after it.(32) When all inter-α durations were calculated, we calculated the positions of other onsets in terms of the percentage of the inter-α duration into which they fell. In subsequent discussion, we typically refer to the mean when giving pulsation positions for a particular excerpt. Examples associated with those excerpts show the minimum, maximum, and mean for all pulsations, providing percent values in the captions.(33)
Delta Thickening in Woloso
Example 13. Timing profiles for the first delta thickening passage in “Woloso 1”
(click to enlarge and see the rest)
[3.11] The recording “Woloso 1” from the IEMP database—identified in Appendix 1 as Performance Example 1—features lead drummer Drissa Kone executing delta thickening several times, with the most pronounced cases occurring in three different passages.(34) In all of these passages, the introduction of δ1 is preceded by a change to quaternary handing. In the first passage, Kone begins playing ternary strings (α1+γ1+β1) with quaternary handing starting at 35.8 seconds (Audio Example 1).(35) Kone then plays notes on δ1 before transitioning away from quaternary handing. As predicted for delta thickening in Mode 1, β1 occurs earlier in its range here than during nearby ternary strings played with ternary handing (Audio Example 2).(36) The full timing profiles for this passage can be seen in Example 13.
|
Audio Example 1. “Woloso 1” passage 1 delta-thickening phrase |
Audio Example 2. “Woloso 1” passage 1 ternary string phrase |
Audio Example 3. “Woloso 1” passage 2
Example 14. Timing profiles for the second delta thickening passage in “Woloso 1”
(click to enlarge and see the rest)
[3.12] A second passage featuring delta thickening in “Woloso 1” includes a similar transition to ternary strings with quaternary handing beginning at 1m 33.7s (Audio Example 3).(37) Kone then plays notes on δ1, fully articulating the Mode 1 quaternary pulsation cycle (B4) through delta thickening. Kone ends this passage and transitions away from quaternary handing by playing a phrase that begins with β1 on his left hand. During this thickening, Kone again places notes earlier in the range of β1 than in a nearby phrase that does not include delta thickening (Example 14.)(38) This movement of β1 earlier in its range during delta thickening is consistent with (though less pronounced than in) the previous passage from “Woloso 1.”
Video Example 1. Moving graphic with audio demonstrating pulsation movement during the third delta thickening passage from “Woloso 1”
(click to watch video)
Example 15. Timing profiles for the first delta thickening passage in “Woloso 2”
(click to enlarge and see the rest)
[3.13] In the third passage from “Woloso 1” with pronounced delta thickening, Kone again performs ternary strings with quaternary handing beginning at 2m 23.1s.(39) He then plays notes on δ1. Kone transitions back to ternary phrasing in cycle 39.2, playing α1 of beat four with his left hand. The tempo is higher here (138 bpm) than in the first case of delta thickening (116 bpm), and yet the position change of β1 is proportionally similar when compared to the ternary string passage that precedes it; (Video Example 1).(40)
[3.14] A similar passage in “Woloso 2” from the IEMP database also featuring Drissa Kone on lead djembe —included in Appendix 1 as Performance Example 2— demonstrates a delta thickening that occurs across different performances (Example 15).(41) Beginning in cycle 31.1 (1m49s) at a tempo of 145 bpm, Kone changes to quaternary handing. He then plays δ1 in the second halves of cycles 32.2 and 33.1, and in both halves of cycle 33.2 (Audio Example 4). He ends the thickening by including an additional δ1 and departing from quaternary handing, all during cycle 34.1 (1m59s). As in Woloso 1, Kone places β1 earlier during this passage of delta thickening than in a nearby ternary string passage (Audio Example 5).
|
Audio Example 4. “Woloso 1” passage 1 delta-thickening phrase |
Audio Example 5. “Woloso 1” passage 1 ternary string phrase |
Example 16. Timing profile for extended second thickening passage in “Woloso 2”
(click to enlarge and see the rest)
Audio Example 6. “Woloso 1” passage 2 delta-thickening phrase
[3.15] A second passage from “Woloso 2” demonstrates how delta thickening occurs in more extended and sophisticated phrases; see Example 16. The above examples include phrases that are nearly identical to one another, with α1, γ1, and β1 in every beat cycle and δ1 included only during beat three. Cycles 24.1 (1m25s) through 26.2 (1m36s) of “Woloso 2,” however, feature distinct phrases, with δ1 occurring on beat one and beat two in addition to beat three (Audio Example 6).
[3.16] The above examples of thickening, while non-exhaustive, demonstrate the need to update pulsation grouping practices to include δ1 in further chronometric analysis of “Woloso.” While in this article we have restricted our discussion to “Woloso,” we have identified delta thickening in open-source recordings of other pieces, including “Suku” (Jacoby, Polak, and London 2021) and “Manjani” (London, Polak, and Jacoby 2017). In analyses published referencing these recordings, all pulsation cycles are treated as though they are essentially ternary. This results in notes that occur on δ1 being grouped together with β1. In existing analyses, the collective grouping of β1 and δ1 skews the average onset of β1 later than it should be because δ1 occurs after β1. We therefore advocate for (re)consideration of the metricity of δ in all performances, even if the composite pulsation cycle is not obviously quaternary during parts of the performance.
IV. Metric Transformation
Example 17. Full Maturation Sequence
(click to enlarge)
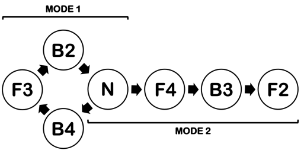
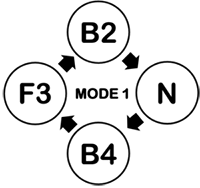
[4.1] In practice, the pulsation cycles and modes postulated in Part II of this article can transform into one another in a predictable sequence, and can thus be understood as part of a single unified metric structure that we call the maturation sequence (see Example 17).(42) In the present part, we address details and mechanisms of metric transformation between pulsation cycles and modes that generate the maturation sequence.(43)
[4.2] There are two principal kinds of metric transformations that contribute to the full maturation sequence: thinning and pulsation downgrading. Thinning applies to transformation between pulsation cycles within a mode, and it is largely analogous to the transformation of tempo-metrical type through layer reduction as described by Polak and London (2022) in the context of Dansa performance. A distinction is that thinning provides a more detailed account of transformations that occur in practice by also addressing the motion of pulsation positions, especially β. The second principal kind of transformation that we address, pulsation downgrading, applies to transformation between modes and involves categorical changes of pulsation identity. Both thinning and pulsation downgrading facilitate maturation in Mande drumming music.
Thinning
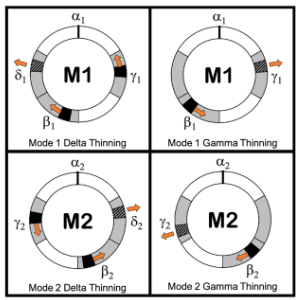
[4.3] In contrast to the previously discussed process of thickening, which introduces new pulsations, the process of thinning de-emphasizes the lowest-level pulsation in a pulsation cycle. This de-emphasis involves the lowest-level pulsation either moving earlier within its range or being omitted altogether.(44) In cases when the lowest-level pulsation is de-emphasized through omission, then thinning always includes movement of other (non-α) pulsations. In any case, a “thinned” pulsation cycle does not retain the timing profile of its precedent pulsation cycle, which is to say: pulsation omission alone does not constitute thinning. Pulsation position change coinciding with pulsation de-emphasis often corresponds with a change in handing. While lead players are the most likely to de-emphasize pulsations, other musicians may do so as well. As in thickening, an individual’s pulsation cycle serves as the referent from which thinning occurs. We identify two categories of thinning: gamma thinning and delta thinning. Gamma thinning involves de-emphasizing γ, while delta thinning involves de-emphasizing δ.
Example 18. Delta and Gamma Thinning in Mode 1 and Mode 2
(click to enlarge)
[4.4] Thinning corresponds with predictable changes in the positions of the thinned pulsation, the other non-beat pulsations, or both, as may be seen in Example 18.(45) During gamma thinning in Mode 1, if β1 moves at all, it moves earlier in its range; during gamma thinning in Mode 2, if β2 moves, it moves later in its range. During delta thinning in Mode 1, if β1 moves at all, it moves later in its range; if γ1 moves, it moves earlier in its range. During delta thinning in Mode 2, if β2 moves at all, it moves earlier in its range; if γ2 moves, it moves earlier in its range. Regardless of pulsation position change, we do not consider thinning to have occurred if γ is omitted and δ remains present, because γ is not the lowest-level pulsation in that case.(46) Despite their being implied above, we find the two following statements related to thinning and thickening crucial enough to make explicit. Put more plainly, they serve to highlight the necessary and sufficient conditions that define the relationships of handing, pulsation quantity and pulsation position change to thickening and thinning. First, not all cases of pulsation omission by an individual can be considered thinning even if accompanied by handing change, because thinning necessitates pulsation position change. Second, in thickening, the pulsation that is introduced through thickening need not actually be sounded, because pulsation position change and changes in handing can be sufficient to imply that thickening has occurred.
Maturation
[4.5] Maturation is an ensemble-wide tempo-related transformation of pulsation cycles through pulsation de-emphasis, perhaps thought of more simply as collective thinning.(47) Whereas individual thinning introduces vertical asynchronies between the thinned part and the rest of the ensemble due to pulsation position change, the process of maturation maintains vertical synchrony through the thinning of all parts. With pulsation position change as its defining feature, maturation typically also coincides with an increase in tempo as well as performer handing change in the case of two-handed instruments. The order of operations for maturation can vary between different pieces as well as between different performances of the same piece. For example, in one performance, tempo increase could prompt de-emphasis of a pulsation, followed by a handing change and repositioning of other pulsations. In another iteration, changing pulsation positions might lead to de-emphasis of the lowest-level pulsation, handing change, and then a subsequent increase in tempo.(48)
[4.6] In the simplest form of maturation, the hierarchically lowest-level pulsation in the pulsation cycle implied by the composite of all non-lead thematic cycles moves earlier in its range or is omitted entirely as that pulsation is de-emphasized. Notes on the other pulsations still sound, with these pulsations moving in predictable ways in their ranges similar to thinning (more on this in examples below). In certain pieces, however, accompaniment parts change entirely as performances mature. Relatively drastic changes in accompanying patterns during the maturation process can create the sense of a medley between discrete phases of a piece, rather than the gradual transformation of a rhythmic structure. During maturation, it is possible but not necessary that changes occur simultaneously between participants.
Maturation Examples
[4.7] In the present section, we describe four types of maturation using examples from live performances. We begin by demonstrating maturation within Mode 1 during a performance of Jondon. We then use a performance of Jelifoli to demonstrate how Mode 1 can mature in a circular manner. Third, we show that Mode 1 can also mature into Mode 2 with an example from Dansa performance. Last, we use an example of Goï performance to demonstrate maturation within Mode 2. Bibliographic information and links to audio or video recordings of each of these performances can be found in Appendix 1.(49)
Mode 1 Maturation
Video Example 2. Moving graphic with audio representing pulsation positions and omissions during the maturation of Jondon through Mode 1
(click to watch video)
[4.8] Our first example of maturation comes from a performance of Jondon—included in Appendix 1 as Performance Example 3—that features transformation within Mode 1, from a B4 to F3 in the full composite pulsation cycle and hinting at further maturation to B2. The performance features Birama Dambele playing lead dundun with bell. Accompanying musicians perform on dunduns with bells, as well as on tantango.(50) Over the course of this excerpt, the tempo gradually increases from 89 bpm to 100 bpm. Video Example 2 combines the following passages into a single moving graphic that visually represents the associated maturation along with the relevant audio.
[4.9] At the beginning of this video example, the presence of δ1 and the positions of the pulsations within their ranges help render the B4 composite pulsation cycle as evident. Dambele plays a phrase that marks a specific dance step on the lead dundun, performing four quaternary strings followed by an additional note on the subsequent α1 and γ1. During this passage, the tantango plays ternary strings. At 0m 18s, the lead dundun introduces phrases that, while still containing δ1, are sparser than the string phrases previously played. From 0m 38s–0m 57s, the lead dundun omits both δ1 and γ1, and then the tantango omits γ1 as well. Both musicians play binary strings and move β1 later in its range. Pulsation γ1 is then reintroduced in the lead dundun at 1m 00s and in the tantango at 1m 23s, and is placed substantially earlier in its range. From 2m 08s through the end of the excerpt, Dambele returns to a matured version of the first phrase in this example, now using ternary strings rather than quaternary strings. The omission of δ1 and changes in the positions of β1 and γ1, described above, are consistent with our predictions for delta thinning. Furthermore, this thinning is collective, maturing the ensemble within Mode 1 as the composite pulsation cycle transforms from B4 to F3.
[4.10] A passage from later in the same performance of Jondon hints at further maturation in Mode 1 to a B2 composite pulsation cycle in all parts. At this point in the performance, the tempo has increased to 135 beats per minute. All accompanying parts include only α1 and β1. The lead dundun de-emphasizes γ1 by including it less frequently than in previous passages and by placing β1 earlier in its range than the rest of the ensemble. Given these changes and the relatively high tempo of the performance, further maturation would require pulsation downgrading.
Pulsation Downgrading
Example 19. Transformation from Back-Heavy Two into Neutral through pulsation downgrading
(click to enlarge)
[4.11] When Mode 1 performance occurs at high tempos, two B2 pulsation cycles may begin to be treated as a single Neutral pulsation cycle through a categorical change in pulsation function that we call pulsation downgrading.(51) In colloquial terms, one can think of pulsation downgrading as a regrouping of two beats into a single beat, which cuts the tempo in half.(52) In pulsation downgrading, the α1 of every second pulsation cycle begins to function as a β. Pulsations previously functioning as β1 become γ or δ, as indicated in Example 19. We categorize the hierarchical change of α1 and β1 during pulsation downgrading as a type of pulsation de-emphasis, grouped conceptually with de-emphasis via pulsation omission or position change. As we demonstrate below, de-emphasis of α1 and β1 through pulsation downgrading facilitates additional pulsation position changes and further maturation. While subsequent pulsation position change may be the most solid evidence that pulsation downgrading has occurred, other practical indications of pulsation downgrading include a halving of the frequency of clapping, the abrupt doubling of the length of an accompanying part, a decrease in frequency of thickening, and the introduction of dance steps or musical phrases that are often performed in the same piece at faster tempos.
Intermodal Maturation from Mode 1 to Mode 1
Example 20. Mode 1 Maturation Sequence
(click to enlarge)
[4.12] Pulsation downgrading can allow Mode 1 performance to mature in a circular manner as two B2 pulsation cycles are regrouped into a single Neutral pulsation cycle, which now can further transform into B4 through pulsation position changes. In this case, the two-cycle α1+β1, α1+β1 becomes the single-cycle α1+γ1+β1+δ1 as the second, third, and fourth pulsations begin to emerge, and are therefore redefined, as lower-level pulsations in the metric hierarchy. The performance can then continue to mature through Mode 1, generating a circular maturation sequence as illustrated in Example 20.
Video Example 3. Moving graphics with audio representing pulsation positions during the maturation of accompanying parts in a Jelidon performance, “Nia Nia O,” from Mode 1 through Neutral and back into Mode 1
(click to watch video)
[4.13] The next example, from a recording of Jelifoli called “Nia Nia O” featuring lead djembe played by Ibrahima Sarr, demonstrates the performance of circular maturation of Mode 1. (See Appendix 1, Performance Example 4). “Nia Nia O” matures as the composite pulsation cycle of all non-lead parts transforms from F3 to B2, and then into Neutral through pulsation downgrading. The performance then proceeds to B4 through pulsation position change. Video Example 3 assembles a set of passages from the piece into a single moving graphic that tracks the associated maturation along with the relevant audio.
[4.14] At the beginning of the example, the composite pulsation cycle of all non-lead parts is F3 and the tempo is 128 beats per minute.(53) Both the dundun and tama accompaniment parts include only α1, γ1, and β1, while Sarr regularly includes δ1. Over the next 30 seconds, the tempo gradually increases to 136 bpm. At 0m 34s, a signal from the lead dundun initiates a period of increased activity and a further increase in tempo. At 0m 43s, the performance matures as all instruments omit γ1 and the accompaniment dundun part changes, transforming the composite pulsation cycle of the ensemble from F3 to B2. Two cycles of B2 are then reframed as a single quaternary pulsation cycle of Neutral through a pulsation downgrading that effectively halves the tempo from 146 bpm to 73 bpm. This downgrading is evidenced by the further maturation into B4 through pulsation position change.
[4.15] At 1m 01s, Sarr executes phrasing with increased rhythmic density, after which β1 (in the new, downgraded frame) moves later in its range. The ensemble gradually redoubles the tempo to approximately 146 bpm. At 2m 07s, Sarr plays phrases featuring α1, γ1, and δ1, while the remainder of the ensemble articulates β1. In doing so, the ensemble manifests a B4 composite pulsation cycle. At 2m 38s, Sarr ends the performance by playing a binary string phrase that is commonly used as to end Jelifoli and to begin and end other Mode 1 pieces that prominently feature F3.
[4.16] In the previous section, we demonstrated how Mode 1 performances mature from B4 to F3 using an example from Jondon. The current example of Jelifoli shows how performances mature from F3 to B2, undergo pulsation downgrading into Neutral, and arrive at B4 through pulsation position change. Taken together, these two performances illustrate ensemble transformation to and from all Mode 1 pulsation cycles, generating a maturation sequence that becomes cyclical through pulsation downgrading.(54)
Intermodal Maturation from Mode 1 to Mode 2
Example 21. Maturation from Mode 1 into Mode 2
(click to enlarge)
[4.17] In addition to the circular maturation of Mode 1, pulsation downgrading can also allow a performance to mature from Mode 1 into Mode 2. As in the previous section, this pulsation downgrading regroups two B2 pulsation cycles into a single Neutral pulsation cycle. In this case, however, Neutral transforms into the Mode 2 quaternary pulsation cycle, F4, through pulsation position changes. The two-beat cycle α1+β1, α1+β1 becomes the one-beat cycle α2+ δ2+β2+γ2 through pulsation downgrading (Example 21).
[4.18] The following example, taken from publicly available footage on Rainer Polak’s website and featuring performance of Dansa with Koly Sacko on lead dundun, demonstrates intermodal maturation from Mode 1 into Mode 2 (Appendix 1, Performance Example 5). The relevant excerpt from this example begins at 2m 31s with a starting tempo of 71 bpm. From here, the performance matures through Mode 1 as γ1 is omitted and the composite pulsation cycle of non-lead parts transforms from F3 to B2. At 2m 44s, the djembe accompanist abruptly changes to a new pattern that is double the length of the part from the preceding phase, suggesting that pulsation downgrading has occurred. The pulsation downgrading establishes a new tempo of 46 bpm and a quaternary (Neutral) composite pulsation cycle with pulsations α2+ δ2+β2+γ2.(55) The tempo from the downgraded perspective then increases to 60 bpm by 5m 35s.
[4.19] During the ten-second span from 5m 35s to 5m 45s, several changes occur that are consistent with the mechanisms of maturation outlined above. First, Sacko plays three variations of a signaling phrase. Each subsequent performance of the signaling phrase finds δ2 and γ2 occurring (on average) earlier in their ranges. During the second iteration of the signal, the dundun accompaniment part doubles in length, as an open tone is omitted and the bell pattern changes. At the same time, the djembe accompanist begins using quaternary handing, reinforcing the sense that pulsation downgrading has occurred. After the third signal phrase, Sacko plays every α2, reinforcing the new orientation and driving an increase in tempo to 95 bpm. By 8m 24s, the tempo stabilizes, and β2 has moved earlier in the accompanying dundun and djembe parts.(56)
Video Example 4. Moving graphic with audio representing pulsation positions during maturation from Mode 1 through Neutral and into Mode 2 in a performance of Dansa
(click to watch video)
[4.20] The tempo change, handing change, and pulsation de-emphasis that result from omission, position change, or pulsation downgrading combine to mature this performance from Mode 1 to Mode 2. F3 becomes B2 through the omission of γ1. B2 becomes Neutral through pulsation downgrading. Finally, Neutral becomes F4 through pulsation position change resulting from delta de-emphasis; see Video Example 4.
Maturation Through Mode 2
Video Example 5. Moving graphics with audio representing pulsation positions during maturation through Mode 2 in a performance of “Sunu”
(click to watch video)
[4.21] Our final example of maturation features a performance of “Sunu,” a piece within the larger performance genre, Goi, which is usually associated with a region known as Kaarta in southwestern Mali (see Appendix 1, Performance Example 6). Similar to Jondon in Mode 1, this example of “Sunu” demonstrates maturation through Mode 2 (Video Example 5).
[4.22] The example begins with an F4 composite pulsation cycle and a tempo of 83 bpm. Pulsation δ2 can be heard in the lead djembe part as well as in the accompanying djembe and dundun parts. At 0m 10s, the lead djembe performs a commonly occurring phrase featuring flammed figures on α2, β2, and the subsequent α2. The ensemble places β2 at nearly the center of its range with an approximate mean of 42% of a pulsation cycle, and this front-heavy 2 relationship between α and β solidifies that the performance is in Mode 2.
[4.23] The maturation of the ensemble ramps up at 0m 33s, after δ2 is included for the final time in the dundun accompaniment and the djembe plays a two-flam djembe phrase with β2 earlier in its range. At 0m 45s, he brings back the three-note flam phrase from 0m 10s, this time playing it three times and moving β2 earlier in its range. Between the second and third of these three-flams, the accompanist omits δ2 and begins using ternary handing, thinning the composite pulsation cycle from F4 to B3. The lead djembe reaffirms this change, playing a signal phrase commonly associated with other performances and repertoire featuring a B3 composite pulsation cycle in the non-lead parts. This initiates further pulsation position change across the ensemble that is consistent with delta de-emphasis. Along with this pulsation position change, the tempo increases to 150 bpm. At 1m 20s, the lead djembe plays a ternary string. Delta thickening remains present, and the lead djembe plays a signal phrase at 1m 35s that is typical of performances with a quaternary composite pulsation cycle. The three djembe players then alternate the role as lead, and the tempo increases to 170 bpm. At 2m28s, the lead djembe plays α2 and β2 again and again, articulating an F2 pulsation cycle in an extended binary string using binary handing. The example concludes with a relatively sparse signal phrase that is common to matured performances in Mode 2.
Example 22. Mode 2 Maturation Sequence
(click to enlarge)
[4.24] The above example matures within Mode 2, more than doubling in tempo from 83 bpm to 170 bpm as it does so; see Example 22. It begins with a quaternary composite pulsation cycle that matures from Neutral to F4 through pulsation position change. It then matures from F4 into B3 through further de-emphasis of δ2, including the omission of δ2 in all accompanying parts. Finally, the performance pushes toward the boundary between B3 and F2 as the lead players de-emphasize γ2, culminating in the use of a binary string as the final phrase.
Full Maturation Sequence
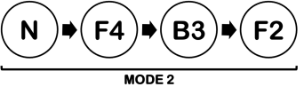
[4.25] Example 17, introduced above, incorporates the entire maturation sequence, including both Mode 1 and Mode 2, into a cohesive metric structure. This structure can be understood to comprise seven interrelated pulsation cycles in two connected modes. All of these pulsation cycles can serve as initial, final, or transitional composite pulsation cycles for a performance, with the exception of F2.(57) The least mature manifestations of both Mode 1 and Mode 2 feature Neutral composite pulsation cycles. From least to most mature, Mode 1 proceeds from N through B4, to F3, and finally to B2. From there, pulsation downgrading can group two B2 pulsation cycles into a single N pulsation cycle. Depending on the repertoire, this sequence can either cycle through Mode 1 again or move into Mode 2 through pulsation position changes. If moving on to Mode 2, the Neutral pulsation cycle will proceed through F4, to B3, and finally to F2.(58)
Sawtooth Maturation
[4.26] Some Mande drumming performances exhibit what we deem a sawtooth variety of maturation, achieved when maturation is preceded or followed by a sudden decrease in tempo and change in composite pulsation cycle. Sawtooth maturation enables participants to repeat the process of maturation again and again, generating alternating moments of high and low intensity. In our experience, sawtooth maturation occurs only in Mode 2 performance, alternating primarily between F4 and B3 composite pulsation cycles.(59) In these contexts, musicians often use two different signaling phrases, emphasizing F4 at slower tempos and B3 at faster tempo.
[4.27] As Parts III and IV of this article have illustrated, metric fluidity in Mande music manifests through commonly occurring expressive strategies and ensemble transformations. Thickening increases metric density. In practice, this increase acts as a ballast against the almost ubiquitous tempo increase that occurs in Mande drumming performance. A decrease in instances of thickening removes this ballast, allowing for tempo increase. Thinning further catalyzes tempo increase, resulting in ensemble transformation through maturation when done collectively. In the upcoming, final part of this article, we present some implications for existing scholarship and potential avenues for research based on the model outlined above.
V. Discussion and Implications
[5.1] A central aim of this paper is advocacy for the use of a modal perspective when analyzing metric change and transformation. Compared to approaches that foreground a single pulsation cycle or MTP, a modal perspective remains relatively stable during changes in tempo, pulsation position, and pulsation cardinality. Furthermore, by lessening the categorical emphasis on pulsation cardinality, focusing on metric mode allows for a consistent framework for comparing different pieces of repertoire as well as different performances of the same piece. In Parts II through IV, we proposed and applied a modal perspective of metric analysis in the context of Mande drumming music. In Part V, we highlight points of both contrast and resonance with prior research and identify applications and extensions of our model and methods that we believe to be potentially fruitful. We also expand on the rationale for some of the choices made in developing the concepts presented in this paper, and explore some of the implications of a modal perspective on meter.
Determining Pulsation Range Boundaries
[5.2] In Part II of this article, we proposed a set of pulsation cycles with the ranges for each pulsation defined in terms of two boundaries that are given as the proportion of the duration between subsequent iterations of α. The specific values for pulsation range boundaries emerged, first, from our own practice-based intuitions, and were further refined through comparison with empirical data (Polak 2010) and theoretical rationale. While an in-depth discussion of that rationale is beyond the scope of this paper, it is worthwhile to consider some contributing factors.
[5.3] The determinant for many of our pulsation range boundaries resonates with the work of composer and theorist Malcolm Braff (2015), who speculates that human perception limits the cardinality of a non-isochronous pulsation cycle. Specifically, Braff restricts viable pulsation cycles to those with maximum inter-onset duration ratios of two-to-one. Braff suspects that, when any inter-onset duration exceeds twice that of another within a pulsation cycle, the listener increases the perceived cardinality of the cycle by inserting an additional pulsation. While we are unaware of any empirical evidence that verifies this claim regarding perception, it resonates with our own experiences and with London’s formulations of “interpolated articulation” (2012, 36) and “well-formedness” (2012, 128). All but one of the range boundaries of the pulsation cycles proposed in Part II of this article are consistent with a two-to-one restriction for potential inter-onset ratios within adjacent pulsation ranges. For example, the late range boundary for β1 (at two-thirds of a cycle) coincides with the position at which the ratio of the IOIs between α1, β1 and the subsequent α1 reaches 2:1. Similarly, the early range for β2 coincides with the position at which the ratio of the IOIs between α2, β2 and the subsequent α2 reaches 1:2.
[5.4] The second of the range boundaries for β coincides with the perfect bisection of the inter-α duration into two isochronous segments. In the case of Mode 1, this bisection represents the early boundary for β1, and in Mode 2 it represents the late boundary for β2. Crossing over the bisection would result in a categorical change in the quality of the binary pulsation cycle from B2 to F2, or vice versa, making this boundary one that is modally definitional. Many of the other pulsation range boundaries in our proposed pulsation cycles (i.e., the late ranges for β1, γ1, and δ2 and the early ranges for β2, γ2, and δ1) coincide with isochronous ternary subdivision of pulsation cycles, even though this isochrony is not necessarily central to our rationale for boundary positions.
[5.5] One final consideration is the relationship between Neutral and range boundary positions. As discussed in Part IV, the Neutral pulsation cycle, in a sense, sits before the quaternary pulsation cycles of both modes. (To remind the reader, the Neutral pulsation cycle combines two B2 pulsation cycles, incorporating the ranges for β1 into each.) This places the late boundary ranges for γ1 and δ2 at one-third of a pulsation cycle and the late boundary ranges for γ2 and δ1 at five-sixths of a pulsation cycle. Thus, the late boundary ranges for γ and δ in both metric modes can be generated according to the Braff-esque 2:1 restriction on adjacent range boundaries described above, but also by observing the range boundaries of B2 and carrying them forward from Neutral through the maturation sequence.
Pulsation Alpha and Beat Non-Isochrony
[5.6] The conscious choice to frame α as the beginning of each iteration of a pulsation cycle provides a functional vantage point from which to orient toward and examine metric fluidity and transformation. Because we define pulsation cycles in terms of the duration bounded by subsequent iterations of α, our model does not rely on the presumption of beat isochrony. This is useful because, in practice, inter-α durations are often non-isochronous. Two of the most common ways we have identified that this kind of non-isochrony manifests in Mande drumming music are when 1) the gradual contraction of nominally-isochronous inter-α durations coincides with tempo increase, and 2) the rhythmic and metric structures interact with each other (Weede 2016), generating pairs of pulsation cycles with the same pulsation quantity and quality but inter-α durations that alternate between long and short. Additionally, there are instances of notes that appear to be associated with α being played noticeably later by lead musicians than by accompanists. Further work, likely including ethnographic data gathering, will be necessary to determine whether these notes are best understood as a kind of non-metric flammed note following α, an expressive variation intended to highlight the lead part note from otherwise shared onsets, or some other phenomenon.
Comparison to Other Range-Based Formulations
[5.7] Our model is distinct from but compatible with a number of previous range-centric formulations of meter. One of these is Danielsen’s (2018) conceptualization of “beat bins,” which articulates categorical identities based on onsets within particular boundaries. In part, Danielsen is concerned with describing vertical asynchrony, or asynchronous onsets being grouped together perceptually as belonging to the same beat. As expressed in this paper, our model of pulsation ranges allows for vertical asynchrony but is not highly attuned for understanding or describing the stability of any particular vertical asynchronies. Furthermore, whereas Danielsen appears to be most concerned with the establishment of a main beat, our model is better understood as hypothesizing pulsation range boundaries, predicting the direction of changes of onsets within those boundaries, and predicting the categorical transformation of one pulsation into another through pulsation downgrading. In the future, an attempt could be made to combine our model with Danielsen’s treatment of beat bins so as to allow researchers to account for vertical asynchronies in α when analyzing composite pulsation cycles.
Applications To and Connecting Between Other Musics
[5.8] In addition to applying to Mande drumming music, we believe our range-based modal model of meter could help analysts disambiguate phenomena in a variety of genres, including practices in Cuba, Balochistan, Eastern Mexico, and Brazil. For example, Benadon et al. (2018, 17) conclude that, in Cuban rumba guaguancó music, rhythmic materials “emerge from a deep blend of ternary and quaternary states rather than as conceptually segregated rhythmic dimensions.” Our model recognizes these materials simply as Mode 2 performance, collapsing quaternary (F4), ternary (B3), and binary (F2) states into a cohesive whole. Similarly, Stover (2009) describes rhythmic figures in rumba Columbia as being inflected from ternary toward quaternary or vice versa, existing between 16-pulsation and 12-pulsation subdivisions of four-beat units. Again, we find that all of the associated rhythmic phrases can be more simply framed as Mode 2 performance, with pulsation ranges providing stability and specificity to analysis of pulsation positions.
[5.9] In his study of music from Balochistan, Jean During (1990) explores pulsation groupings that he describes as being ambiguously between
[5.10] Another potentially fruitful application of our model is to music in Veracruz, Mexico. Son jarocho performance in this region appears to feature bimodal metricity that is quite similar to that found in the Mande region. In son jarocho, pieces can be identified as having one of two rhythmic feels or cadencias, with one called derecho (straight) and the other atravesado (crossed). Older and rurally trained son jarocho musicians sometimes maintain that the two cadencias are distinct, and that players who substitute one for the other when performing a particular piece are doing so in error (Nieto 2018). This is also the case in Mande drumming performance, where pulsation cycles from the two metric modes are not typically performed simultaneously. Having examined a number of different sones, we find that atravesado performance is similar or even identical to Mode 1 performance, and derecho is identical to Mode 2 performance. It is conceivable that bimodal metric systems with similar or identical pulsation position ranges could emerge in two different musical contexts independently from one another. However, additional non-musical links exist; these include the arrival of enslaved people from the Mande region in Veracruz (Sacolick 2016), the internal use of “Mandinga” as the name of a maroon community on the border of Veracruz and Oaxaca (Carroll 1977), and the longstanding maintenance of distinct ethnolinguistic identities and practices among enslaved African people and their descendants in Veracruz (Clark 2016). Given this evidence, we believe that analysis of son jarocho performance using our model and techniques could generate more compelling musicological support for specific African continuities in Veracruz beyond often-cited yet generic musical attributes such as polyrhythm or key patterns.
[5.11] While we find it plausible that there are lower limits on the ability for humans to perceive metricity based on absolute temporal values of inter-onset intervals, evidence from research on Brazilian samba music suggests that the lower limit for perception of metricity depends upon the relative positions of pulsations within a cycle. In one study, Haugen and Danielsen (2020, 358) have found that “the effect of tempo on the duration patterns. . . does not seem to be due to perceptual constraints like a lower limit of duration.” On that basis, Haugen and Danielsen (2020, 358) assert that the maintenance of metricity at inter-onset intervals that are far shorter than anticipated by previous scholarship on lower limits is due to a “specific samba ‘feel’” that must be maintained at all tempos.
[5.12] In the context of Mande drumming music, Polak and London (2022, 147) suggest that “tempo-metrical types are differentiated by various temporal thresholds for metric rhythm perception.” It is not, then, unreasonable to suggest that the kind of threshold-transcending tempo-independent categorical consistency observed in the “samba feel” remarked upon by Haugen and Danielsen might also apply to Mande drumming music.(60) We suspect that maintaining adherence to the ranges within a mode—along with its associated pulsation cycles—can allow rhythmic figures to maintain perceptual metric coherence even when inter-onset intervals are beyond the thresholds for metric perception predicted by existing experiments. We therefore advocate for further empirical analysis designed to explore the relationship between pulsation ranges and the lower limits for metric perception.
Closing Comments
[5.13] The model laid out in this paper can be thought of as both descriptive of and prescriptive for musical performance. It articulates how performances relate to one another and transform over time, and provides scholars with predictions that can be tested.. Throughout, we have intentionally avoided leaning into our assumptions regarding the psychology of participants, despite the fact that our experiences lead us toward speculative guesses regarding perception and performance. It is our hope that this paper will provide clarity to both practitioners and scholars by giving name to phenomena that regularly occur but typically go without comment. While the current paper is not primarily intended to be an instructional manual, and some aspects are presented in terms that prioritize technical precision for the sake of clarity, we hope that our model provides an intuitive way for teachers and learners to understand and communicate about timing in Mande drumming music. One of the most consistent problems that we have observed among non-immersed learners is that they fail to recognize large-scale interconnections between different moments, performances, pieces, and even genres. This results in the inability to display competence when circumstances require change or adaptation during participation. We hope that the framework and examples included above will enhance both the personal perception and pedagogical effectiveness of interested readers, whether scholars or practitioners.
Appendix 1: Performance Examples (Audio and Video)
Outdoor studio session featuring Drissa Kone on lead djembe, Sedu Balo on accompaniment djembe, and Madu Jakite on dundun. Recorded May 2, 2007 by Rainer Polak in Bamako, Mali
Outdoor studio session featuring Drissa Kone on lead djembe, Sedu Balo on accompaniment djembe, Madu Jakite on first dundun, and Antoine Traole on second dundun. Recorded May 3, 2007 by Rainer Polak in Bamako, Mali.
Performance Example 3 (Audio). “Jondon”
Field recording at an outdoor wedding ceremony featuring Birama Dambele on lead dundun with accompanying musicians on dunduns and tantango. Recorded January, 2011 by Aaron David in Gandéga, Kayes, Mali.
Performance Example 4 (Audio). “Jelifoli”
Commercial recording. Sarr, Ibrahima. 2008. “Nia Nia O (Rhythm Sandia).” Porte 386 Medina Coura. Fonti Musicali.
Outdoor studio session featuring Koly Sacko lead dundun, Toutou Sacko on accompaniment dundun, and Sambou Kante on djembe. Recorded February 2012 by Rainer Polak in Mahina, Mali.
Outdoor studio session featuring Bakary Dansogo, Jango Drame, and Vieux Diarra on djembes, with Moussa “Ba” Diallo and another unknown musician on dunduns. Recorded February 2013 by Aaron David in Tambacounda, Senegal.
Outdoor studio session featuring Sedu Balo on lead djembe, Drissa Kone on accompaniment djembe, and Madu Jakite on dundun. Recorded 2006 by Rainer Polak in Bamako, Mali.
Appendix 2: “Maturation” as Neologism
[A2.1] While we acknowledge that neologisms can sometimes be needless or obscuring, we find that the new term “maturation”—introduced in Part IV of this paper—is both necessary and useful for referring to ensemble-wide tempo-related transformations of pulsation cycles through pulsation position change and cardinality reduction. Because not all instances of maturation include changes in pulsation cardinality, and because we have not observed evidence suggesting that different degrees of maturation directly correspond with absolute tempos across pieces—or even in performances of the same piece—we find that existing terms such as “reduction in tempo-metrical type” (Polak and London 2022, 152) would require radical re-definitions to be applicable. In addition, use of the term “maturation” allows us to make connections between concepts such as maturation sequence, and sawtooth maturation, and to more easily group together modal elements. An additional benefit is that it helps clarify the similarities and differences between maturation within a mode and maturation between modes.
Example 23. Annotated reproduction of the impact of non-isochrony on consonance during hypothetical metric layer reduction of a “Sunun” dundun part from “Figure 3” of Polak (2020)
(click to enlarge)
[A2.2] A further distinction between maturation and existing conceptions of metric transformation can be understood through reconsideration of the analysis of “Sunu(n)” (see Appendix 1, Performance Example 7) presented in Polak (2020). Polak correctly asserts that greater consonance between individual parts at different stages of metric transformation can be achieved when pulsation non-isochrony is present; this is shown through comparison of the dundun accompanying pattern for “Sunu(n)” analyzed from the perspectives of quaternary and ternary cardinality in Figures 3A and 3B (Example 23). We would add that the non-isochrony must be modally consistent, and that “Sunu(n)” displays consistency within Mode 2, with the quaternary subdivision generating F4 pulsation cycles and the ternary subdivision generating B3 pulsation cycles. In Example 23, we have annotated Polak’s (2020) Figure 3 to include pulsation identity labels that are consistent with Mode 2 performance.
[A2.3] An advantage of thinking in terms of maturation emerges when applying pulsation identity labels to Polak’s Figure 3C. In his analysis, Polak demonstrates that the “melorhythmic identity” of the dundun part is lost when reducing pulsation cardinality from isochronous quaternary to isochronous binary while maintaining all onsets (2020, 27–28). Thought of in terms of maturation, melorhythmic identity depends on consistent association of onsets with particular pulsations, rather than the retention of all onsets. Maturation from F4 to F2 involves omitting all onsets on pulsations δ2 and γ2. In the case of the “Sunun” dundun part represented in Polak’s Figure 3, the second, third and sixth onsets would all be omitted in maturation through Mode 2. This generates a metrically consistent but rhythmically sparser part that maintains consonance even when onsets occur at the isochronous boundaries of pulsation ranges. Therefore, from the perspective of maturation, Polak’s Figure 3C profoundly changes the melorhythmic identity of the dundun part by categorically altering the pulsations associated with onsets on γ2 so that they fall on β2 instead, thus producing extreme vertical asynchronies. In sum, then, maturation can be distinguished from existing conceptualizations of metric transformation in part because it emphasizes the hierarchy of pulsations during changes in metric density.
Glossary of Terms
Back-heavy - a quality ascribed to pulsation cycles in which the shortest potential interval between subsequent pulsations is located after β
Delta thickening - the introduction of δ when δ was not previously present; often coincides with predictable movement of β within its range
Front-heavy - a quality ascribed to pulsation cycles in which the shortest potential interval between subsequent pulsations is located before β
Gamma thickening - the introduction of γ when γ was not previously present; often coincides with predictable movement of β within its range
Handing pattern (handing) - the pattern of repeated movement of a player’s hands on a two-handed instrument
Handing pattern, binary (binary handing) - hand-over-hand execution of a binary pulsation cycle
Handing pattern, quaternary (quaternary handing) - hand-over-hand execution of a quaternary pulsation cycle
Handing pattern, ternary (ternary handing) - hand-over-hand execution of a ternary pulsation cycle
Hand-over-hand execution - when a player alternates hands for each consecutive pulsation in a pulsation cycle, regardless of whether or not those pulsations are sounded
Isochronous - having metric units of equal duration; can apply at the level of pulsations or beats
Maturation - an ensemble-wide transformation from one pulsation cycle to another; typically coincides with tempo increase and handing change
Maturation sequence - the predictable sequence of pulsation cycles through which a performance can mature
Mode (Metric Mode) - a conceptual frame used to group related pulsation cycles into a single metric category
Neutral - a modally-ambiguous quaternary pulsation cycle that comprises two B2 pulsation cycles perceived as a single beat; represents “unswung” quaternary performance in Mande music
Non-isochronous - having metric units of non-equal duration; can apply at the level of pulsations or beats
Pulsation - a sub-beat level metric unit; a duration of time in which a metrically-defined onset can potentially occur
Pulsation cycle - a repeating colocation of metric pulsation ranges; bookended by adjacent iterations of α
Pulsation cycle, binary - a pulsation cycle containing only α and β.
Pulsation cycle, quaternary - a pulsation cycle containing α, β, γ, and δ
Pulsation cycle, ternary - a pulsation cycle containing only α, β, and γ
Pulsation de-emphasis - movement of the pulsation with the lowest hierarchical rank earlier in its range; or its omission; a component of thinning and maturation
Pulsation downgrading - regrouping of two beats into a single beat; halves the tempo; categorically changes pulsation identity
Pulsation hierarchical order - the order of pulsations according to their metric stability; in either mode: α, β, γ, δ
Pulsation omission - when notes no longer occur on a previously sounded pulsation; may or may not coincide with position change of remaining pulsations
Pulsation onset order - the sequence of pulsations in order of occurrence in a pulsation cycle; in Mode 1: α, γ, β, δ; in Mode 2: α, δ, β, γ
Pulsation position - the temporal location of a pulsation within its range
Pulsation range - the bounded range containing all possible locations for an onset associated with a particular pulsation
Quality - the distribution of pulsation ranges in a pulsation cycle; categorized in terms of the location of the shortest potential interval between subsequent pulsations (front-heavy, back-heavy, or Neutral)
Quantity - the number of pulsations in a pulsation cycle
Rotational equivalence - the resemblance of pulsation cycles in one mode to those in the other mode when β is perceived as the beat
Sawtooth maturation - maturation that is preceded or followed by a sudden decrease in tempo along with a change from a more mature to less mature composite pulsation cycle; allows for repeated maturation in Mode 2
String - a musical figure that occurs when every pulsation in a pulsation cycle is sounded at least twice in an uninterrupted stream
Thickening - the introduction of previously absent pulsations from the same mode as the established pulsation cycle
Thinning - the de-emphasis of the pulsation with the lowest metric hierarchy in a pulsation cycle
James B. Morford
University of Washington
jbmorford@gmail.com
Aaron M. David
ate7010@gmail.com
Works Cited
Agawu, Kofi. 2003. Representing African Music. Routledge.
Anku, Willie. 2000. “Circles and Time: A Theory of Structural Organization of Rhythm in African Music.” Music Theory Online 6.
Arom, Simha. 1991. African Polyphony and Polyrhythm. Cambridge University Press. https://doi.org/10.1017/CBO9780511518317.
Beer, Jonathan. 1991. “Liner Notes.” Liner Notes for Rhythmen der Malinké. Recorded by Famoudou Konaté. Museum für Völkerkunde Berlin (CD) MC 18.
Benadon, Fernando, Andrew McGraw, and Michael Robinson. 2018. “Quantitative Analysis of Temporal Structure in Cuban guaguancó Drumming.” Music & Science 1: 1–20. https://doi.org/10.1177/2059204318782642.
Bénic, Jean-Christophe, and Paul Noyer. 2014. Djembe Solos: Séga Sidibé. Play Music Publishing.
Billmeier, Uschi. 1999. Mamady Keita: A Life for the Djembe. Arun-Verlag.
Braff, Malcolm. 2015. “Diversity of Grooves: It’s all about da weight!” General Theory of Rhythm (blog). July 23. http://general-theory-of-rhythm.org/diversity-of-grooves-its-all-about-da-weight/.
Carroll, Patrick J. 1977. “Mandinga: The Evolution of a Mexican Runaway Slave Community, 1735–1827.” Comparative Studies in Society and History 19 (4): 488–505. https://doi.org/10.1017/S0010417500012032.
Charry, Eric. 2000. Mande Music: Traditional and Modern Music of the Maninka and Mandinka of Western Africa. University of Chicago Press.
Clark, Joseph MH. 2016. “Veracruz and the Caribbean in the Seventeenth Century.” PhD diss., The Johns Hopkins University.
Danielsen, Anne. 2018. “Pulse as Dynamic Attending: Analysing Beat Bin Metre in Neo Soul Grooves.” In The Routledge Companion to Popular Music Analysis, ed. Ciro Scotto, Kenneth M. Smith, and John Bracket, 179–89. Routledge. https://doi.org/10.4324/9781315544700-12.
Danielsen, Anne, Kristian Nymoen, Evan Anderson, Guilherme Schmidt Câmara, Martin Torvik Langerød, Marc R. Thompson, and Justin London. 2019. “Where is the Beat in that Note? Effects of Attack, Duration, and Frequency on the Perceived Timing of Musical and Quasi-musical Sounds.” Journal of Experimental Psychology: Human Perception and Performance 45 (3): 402-18.
During, Jean. 1990. “L'organisation Du Rythme Dans La Musique de Transe Baloutche.” Revue de Musicologie 76 (2): 213–25. https://doi.org/10.2307/947264.
Haugen, Mari Romarheim, and Anne Danielsen. 2020. “Effect of Tempo on Relative Note Durations in a Performed Samba Groove.” Journal of New Music Research 49 (4): 349–61. https://doi.org/10.1080/09298215.2020.1767655.
Jacoby, Nori, Rainer Polak, and Justin London. 2021. “Extreme Precision in Rhythmic Interaction Is Enabled by Role-optimized Sensorimotor Coupling: Analysis and Modelling of West African Drum Ensemble Music.” Philosophical Transactions of the Royal Society B: Biological Sciences 376 (1835): 20200331. https://doi.org/10.1098/rstb.2020.0331.
Jankowsky, Richard C. 2013. “Rhythmic Elasticity and Metric Transformation in Tunisian Sṭambēlī.” Analytical Approaches to World Music 3 (1): 32–61.
Keil, Charles. 1987 “Participatory Discrepancies and the Power of Music.” Cultural Anthropology 2 (3): 275–83. https://doi.org/10.1525/can.1987.2.3.02a00010.
Konaté, Famoudou, and Thomas Ott, in collaboration with Thomas Goldhahn, Bettina Kandé, Mohamed Mancona Kandé, Frauke Köhler, and Alexander Lück. 1997. Rhythms and Songs from Guinea. Translated by Bettina Kandé and Mary Staehelin. Institut für Didaktik populärer Musik.
London, Justin. 2012. Hearing in Time: Psychological Aspects of Musical Meter. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199744374.001.0001.
London, Justin, Rainer Polak, and Nori Jacoby. 2017. “Rhythm Histograms and Musical Meter: A Corpus Study of Malian Percussion Music.” Psychonomic Bulletin & Review 24 (2): 474–80. https://doi.org/10.3758/s13423-016-1093-7.
Neuhoff, Hans, Rainer Polak, and Timo Fischinger. 2017. “Perception and Evaluation of Timing Patterns in Drum Ensemble Music from Mali.” Music Perception 34 (4): 438–51. https://doi.org/10.1525/mp.2017.34.4.438.
Nieto, Alejandro Miranda. 2018. Musical Mobilities: Son Jarocho and the Circulation of Tradition Across Mexico and the United States. Routledge.
Polak, Rainer. 2000. “A Musical Instrument Travels Around the World: Jenbe Playing in Bamako, West Africa, and Beyond.” The World of Music 42 (3): 7–46. http://www.jstor.org/stable/41692764.
—————. 2010. “Rhythmic Feel as Meter: Non-isochronous Beat Subdivision in Jembe Music from Mali.” Music Theory Online 16 (4). https://doi.org/10.30535/mto.16.4.4.
—————. 2017. “The Lower Limit for Meter in Dance Drumming from West Africa.” Empirical Musicology Review 12 (3–4): 205–26. https://doi.org/10.18061/emr.v12i3–4.4951.
—————. 2020. “Wozu polychrone Pulsation? Funktionalistische Perspektiven auf metrische Strukturen in malischer Musik.” In Understanding Musics: Festschrift on the Occasion of Gerd Grupe's 65th Birthday, ed. Malik Sharif and Kendra Stepputat, 19–36. 1st ed. Shaker.
—————. 2022. “Non-Isochronous Metre in Music from Mali.” In The Oxford Handbook of Time in Music, ed. Mark Doffman, Emily Payne, and Toby Young, 252–74. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780190947279.013.22.
Polak, Rainer, and Justin London. 2014. “Timing and Meter in Mande Drumming from Mali.” Music Theory Online 20 (1). https://doi.org/10.30535/mto.20.1.1.
—————. 2022. “Tempo, Meter, and Form: An Analysis of ‘Dansa’ from Mali.” In Trends in World Music Analysis: New Directions in World Music Analysis, ed. Lawrence B. Shuster, Somangshu Mukherji, and Noé Dinnerstein, 143–59. Routledge. https://doi.org/10.4324/9781003033080-9.
Polak, Rainer, Justin London, and Nory Jacoby. 2016. “Both Isochronous and Non-Isochrononous Metrical Subdivision Afford Precise and Stable Ensemble Entrainment: A Corpus Study of Malian Jembe Drumming.” Frontiers in Neuroscience 10 (285). https://doi.org/10.3389/fnins.2016.00285.
Polak, Rainer, Simone Tarsitani, and Martin Clayton. 2019. “IEMP Malian Jembe.” Interpersonal Entrainment in Music Performance. OSF. https://www.doi.org/10.17605/OSF.IO/M652X. Accessed from https://osf.io/m652x/.
Rothstein, William N. 1995. “Beethoven with and Without Kunstgepräng: Metrical Ambiguity Reconsidered.” In Beethoven Forum IV, ed. C. Reynolds, L. Lockwood, and J. Webster. University of Nebraska Press: 165–93.
Sacolick, Robin. 2016. Transcendence and “Son Jarocho” as Practiced in the San Francisco Bay Area.” PhD diss., University of California, Santa Cruz.
Samarotto, Frank. 1999. “Strange Dimensions: Regularity and Irregularity in Deep Levels of Rhythmic Reductions.” In Schenker Studies 2, ed. Carl Schachter and Heidi Siegel. Cambridge University Press: 222–38.
Stover, Christopher D. 2009. “A Theory of Flexible Rhythmic Spaces for Diasporic African Music.” PhD diss., University of Washington.
Toussaint, Godfried T. 2020. The Geometry of Musical Rhythm: What Makes a “Good” Rhythm Good? Second edition. CRC Press, Taylor & Francis Group.
Weede, Oliver. 2016. “Polymetric Rhythmic Feel for a Cognitive Drum Computer.” In Proceedings from the 14th International Conference on Culture and Computer Science: 281–95. https://doi.org/10.48550/arXiv.1606.06197.
Footnotes
* This paper is the result of a multi-year collaboration between the authors, with initial theoretical foundations formulated by author David.
Return to text
1. Scholars of a variety of musics across the globe have also examined pulsation non-isochrony or swing ratios. A representative list of studies can be found in Neuhoff, Polak, and Fischinger (2017, 438).
Return to text
2. Mande music is not unique in this regard. While some of the metric features explored in this paper are globally unusual, others have analogues in other musics around the world.
Return to text
3. The existence of a kind of metric background leads us to favor a “divisive” approach to describing rhythm (Agawu 2003, 78). Emerging evidence, however, indicates that rhythmic phrases that produce contrasting metric cues can shape the underlying metric background in predictable ways (Weede 2016); this suggests that a combination of additive and divisive analysis is necessary for better understanding some performance practices.
Return to text
4. Our model is distinct from but accords with a number of previous range-centric formulations of meter. One of these is Danielsen's conceptualization of “beat bins” (2018), which articulates categorical identities based on onsets within particular boundaries. Danielsen is concerned with describing vertical asynchrony, or asynchronous onsets being grouped together perceptually as belonging to the same beat. As expressed in this paper, our model of pulsation ranges allows for vertical asynchrony, but is not especially tuned for understanding or describing the stability of any particular vertical asynchronies. Further research might attempt to combine our model with Danielsen’s treatment of beat bins in order to develop strategies for taking into account vertical asynchronies when analyzing composite pulsation cycles.
Return to text
5. While musicians in an ensemble may choose to play notes at any point in a pulsation’s range, competent non-lead players consistently play in consonant non-isochrony with one another. As such, lead musicians, more so than other musicians in an ensemble, exploit contrasting parts of pulsation ranges as an expressive tool.
Return to text
6. These two meters are sometimes expressed as
Return to text
7. In one sense, the words “Mande” and “drumming” categorize music at an arbitrary level of specificity. Any boundaries that might be drawn around certain peoples, places, or time frames will always be porous and shifting. We conceptualize Mande drumming music as a constellation of performance practices initially emerging among people living in and near the region of West Africa historically associated with the Mali Empire. This includes people identifying with or as part of a variety of ethnicities, nations, and linguistic subgroups (Charry 2000). While we restrict ourselves here to drumming music, we have found that the model described can be useful for understanding other instrumental and vocal musics, including contemporary popular song emerging from this region and its diasporas.
Return to text
8. Beer (1991) further suggests that sufficient displacement of the second pulsation toward the third pulsation within a ternary context generates quaternary figures, partially approximating what we articulate below as Mode 2 performance.
Return to text
9. Typically, non-native learners misinterpret the word “tempo” to mean the frequency of the beat. This can cause frustration among teachers and students alike when pulsation position change is necessary for competent performance.
Return to text
10. See paragraph 3.10 for additional detail regarding the assignment of α. Related discussion of pulsation position determination can be found in Polak, London, and Jacoby (2016).
Return to text
11. Composer Malcolm Braff identifies a similar quality in his theorization of non-isochronous tuplets, called “negative groove balance” (http://general-theory-of-rhythm.org/diversity-of-grooves-its-all-about-da-weight/).
Return to text
12. Because the metric background is both non-isochronous and fluid in Mande music, standard notation is also often inefficient for representing rhythmic figures. In future work, we intend to introduce alternate rhythmic notation systems for use in theoretical and pedagogical settings.
Return to text
13. The use of circular graphics as music transcription tools is not novel to this study. However, existing examples typically apply to rhythms rather than pulsation cycles (e.g., Anku 2000), omit non-integer pulsation non-isochony (e.g., London 2012), or do not include pulsation ranges outside of boundaries generated by binary and ternary isochrony (e.g., Toussaint 2020).
Return to text
14. We find London’s distinction of rhythm and meter useful here, wherein “rhythm involves the structure of the temporal stimulus, while meter involves our perception and cognition of such stimuli. . . an aspect of our engagement with the production and perception of tones in time” (2012, 4). Furthermore, we do not mean to imply that the style of graphic representation that we introduce in this paper applies only or especially to African musics. As we discuss in Part V, a range-based approach to analysis and representation might be fruitfully applied to any musics in which cyclic pulsation non-isochrony is observed.
Return to text
15. Back-heavy two (B2) is analogous to a Long-Short (LS) metric timing pattern (Polak 2010).
Return to text
16. Polak has presented several variations of front-heavy three, including short-medium-long (SML), Short-Flexible-Flexible (SFF) and Short-Long-Long (SLL) (e.g., Polak 2010).
Return to text
17. Back-Heavy 4 has no explicit equivalent in Polak’s publications, but is implied in Polak and London (2022) and could be represented as Long-Flexible-Flexible-Flexible (LFFF) or Long-Medium-Short-Medium (LMSM). We suspect that this pulsation cycle is globally unusual, but can be useful for explaining rhythmic phenomena observed in some places, including in Balochistan (e.g., During 1990).
Return to text
18. Front-heavy two has no equivalent in Polak’s publications on metric timing patterns, but could be represented as Short-Long (SL). Binary F2 string phrases can be found in a variety of Mode 2 repertoire, including Maraka, Sunu, Koredjouga, Ngri, Sogolon, Sungurubani, Djaa, Gidamba, Tiriba, and Kakilambe. In performances of all of these pieces, F2 strings can be heard in dundun patterns, djembe accompaniment patterns, bell patterns, or lead players’ signals and solo phrases.
Return to text
19. Polak has presented a variety of MTPs that are analogous to B3, including Long-Short-Medium (LSM), Long-Flexible-Flexible (LFF) and Long-Short-Short (LSS) (e.g., Polak 2010).
Return to text
20. These binary pulsation cycles, B2 and F2, occur quite commonly in Mode 1 and in Mode 2, respectively. A key distinction between the binary pulsation cycles across performances and repertoire is that F2 does not undergo pulsation downgrading and regrouping in the same way that B2 does. That is, as shown below, two B2 pulsation cycles are often grouped into a single quaternary pulsation cycle. There is no counterpart quaternary pulsation cycle combining two F2 pulsation cycles.
Return to text
21. These gaps can be observed in, for example, Polak, London, and Jacoby (2016, Fig. 4).
Return to text
22. In practice, we have observed rotational equivalence generating what London calls “conflicting cues” (2012, 100) associated with the phenomenon of “shadow meter” as noted by Rothstein (1995) and Samarotto (1999). This is most often encountered in performance contexts where unfamiliar participants are present. Sometimes, the conflicting cues resolve when a clear indication of ‘correct’ orientation–such as collective footfalls and hand-clapping–emerges. We suspect, however, that there are cases in which rotational equivalence has resulted in the divergence of a single piece of repertoire into two, with one variant retaining the same metric orientation as the original and the other stabilizing with a rotated metric orientation. In other words, some pieces appear to be susceptible to the shadow meter becoming the actual meter, and vice versa, across multiple iterations and contexts.
Return to text
23. Our model does not disallow pulsation isochrony altogether, as isochrony emerges at the boundaries of the pulsation position ranges for all pulsation cycles. Put another way, in music performed by competent participants, pulsation isochrony represents a case of extreme swing rather than the absence of swing.
Return to text
24. It is possible to identify the mode of Neutral performance through context clues, even without disambiguation in the metric background, in the bell patterns, accompaniment parts, signaling phrases, and relative pulsation emphasis.
Return to text
25. Polak and his collaborators describe a related phenomenon that they call “bifurcation” (Polak and London 2014: 101) or the “interpolation of Long subdivisions” (Neuhoff, Polak, and Fischinger 2017), in which the longest element in a metric timing pattern can be split into two elements.
Return to text
26. While we are confident in the movements of β based on our experiences and empirical confirmation, the movement of γ appears to be more complicated. We suspect that there are tendencies in the motions of γ during thickening, and these motions appear to depend on both the positions and movements of β and on the sounding of δ. Further computational studies might fruitfully be dedicated both to confirming or challenging the movements of β proposed in this paper, and to exploring the movements of γ.
Return to text
27. Some players diverge from hand-over-hand playing to maximize biomechanical efficiency. They sometimes use “alternating handing” in which the hands alternate for each sounded note, regardless of pulsation position within a cycle. At other times, musicians may begin each phrase with their dominant hand, regardless of pulsation position or which hand finished the previous phrase.
Return to text
28. For the sake of brevity, here and in the remainder of this document we shorten “hand-over-hand execution” to “handing.”
Return to text
29. Perhaps the most common use of string phrases is in the lead part during periods of intensified dance, often referred to by the French term echauffement (Charry 2000, 223). The term golobali, literally translatable as “period of much skin (playing),” referring to the materiality of the instruments, is used in Bamanankan. In Maninkakan, these periods and related string phrases are called donnasii, which can be translated as “seating of the dance.”
Return to text
30. The IEMP provides a table that includes time stamps for what they define as each metric cycle. For the sake of precision, we reference these specific cycle numbers in our analysis below. However, to allow for easier cross-checking against the available video recordings, we also provide the associated time stamps.
Return to text
31. In several instances, vertical asynchrony introduced uncertainty in determining the position of the sound on a pulsation through visual analysis of the waveform. When this occurred, the onset was re-checked by ear to verify its position in the waveform and confirmed to within one millisecond.
Return to text
32. The inclusion of hypothetical α onsets lowers the confidence in the output of further calculations. However, we determined that the cost of this lowered confidence was worth the gain in extending measurements across an entire excerpt. Furthermore, with the exception of moments of rapid tempo change, we observed no cases of actual inter-α onsets differing radically from one another across a limited excerpt.
Return to text
33. The min and max measurements represented in examples here generate empirical rhythmic onset ranges that are somewhat analogous to “beat bins” (Danielsen et al. 2019). These onset ranges can vary in absolute and relative duration, but exist within the consistent bounds of metric pulsation ranges.
Return to text
34. A file indicating cycles and timestamps for “Woloso 1” can be accessed at https://osf.io/rj4m7/.
Return to text
35. The beginning of this passage corresponds with ensemble cycle 7.2 as labeled in the IEMP database.
Return to text
36. This movement of β1 was calculated by isolating the raw onset timing data for jembe 1 from https://osf.io/fjwrk during the period of handing change, from 35.84452 seconds until 40.47971 seconds.
Return to text
37. The beginning of this passage corresponds with ensemble cycle 22.2 as labeled in the IEMP database. Some onsets listed in the IEMP data set did not align with any performed sound or hand motion by Kone at the indicated time in the associated video or audio recordings. These onsets were treated as recording errors and omitted from the analysis here.
Return to text
38. This ternary handing can most easily be seen in the phrasing between 2m12s to 2m19s, where Kone plays ternary strings.
Return to text
39. The beginning of this passage corresponds with ensemble cycle 36.2 as labeled in the IEMP database.
Return to text
40. These averages were calculated by the same method as above, and compared the delta thickening passage with a ternary string phrase performed beginning in cycle 34.2, about ten seconds earlier. The maximum and minimum β1 positions for the ternary passages were calculated to be approximately 60.2% and 57.8% of a pulsation cycle, respectively. For the delta-thickened passage, β1 was calculated at a maximum and minimum of approximately 55.6% and 53.5%, respectively.
Return to text
41. A file indicating cycles and timestamps for “Woloso 2” can be accessed at https://osf.io/gxqp5/.
Return to text
42. Recent publications on Mande drumming music by Polak (2020) and Polak and London (2022) use tree graphs to represent the consonance between metric layers that results from duration-categorical (especially Short and Long) pulsation non-isochrony in analyses of Sunun and Dansa, respectively. Despite our focus on position ranges rather than IOIs, our range-based model is not wholly incompatible with such representations; the full metric structure, including Mode 1 and Mode 2, could in fact be represented in a similar tree graph if it were supplemented with representations of ranges and of pulsation movement.
Return to text
43. Justification for the introduction for the new term, “maturation,” is explored in Appendix 2.
Return to text
44. During thinning, a de-emphasized pulsation sometimes appears to move so early that sounded notes fall outside of the pulsation range. We no longer categorize these notes according to their previous pulsation identity. We consider this a kind of “pulsation omission through de-emphasis.”
Return to text
45. These motions indicate interactions between sounded rhythms and the shape of the metric background, and can be understood as occurring in one of two ways. For example, in one interpretation, β moves toward a pulsation, causing that pulsation to be omitted. In the second interpretation, after a pulsation is omitted, β then moves to fill the temporal vacuum. Further research might focus on the possibility of determining which of these two interpretations is more likely to be correct.
Return to text
46. As stated above, analysts have not explicitly identified F2 as a metric pattern, despite the fact that its Mode 1 counterpart, B2, is central to their models. This is perhaps because F2 does not typically manifest as a composite pulsation cycle. However, thinning demonstrates another way that B2 and F2 parallel one another as metric phenomena: gamma thinning results in B2 in Mode 1 and F2 in Mode 2.
Return to text
47. While similar to the concept of “metric layer reduction” (Polak and London 2022), maturation does not always require the omission of a pulsation.
Return to text
48. We concur with Polak (2017) that tempo increase is a feature of nearly all Mande drumming performance. This tempo increase both drives and is driven by changes in pulsation position and pulsation quantity. As Polak and London (2022) demonstrate in the context of Dansa, a single piece of repertoire can feature tempo-dependent metric tranformations that are consistent across performances. However, we have observed that different performances of the same piece at the same tempo can feature different degrees of maturation.
Return to text
49. Our decision to italicize the terms Jondon, Jelifoli, Dansa, and Goï reflects their role in referring to styles or genres (caste-based or otherwise) that each include multiple distinct pieces of drumming repertoire.
Return to text
50. For descriptions of these instruments, their instrumental roles, and cultural contexts, see Charry 2000.
Return to text
51. While pulsation downgrading is hypothetically possible in either mode, we have only observed it to occur in Mode 1 performance.
Return to text
52. We acknowledge that pulsation downgrading is, in some regards, a socio-psychological or perceptual phenomenon. It is often evidenced by changes in footfalls of dancers or the frequency of clapping. Not all participants necessarily downgrade pulsations at the same moment, making this process gradual.
Return to text
53. The beginning of this example can be found at 6m 53s on the original track.
Return to text
54. While the performances here begin and end in F3, it possible that other performances in Mode 1 might begin or end in any of the relevant composite pulsation cycles, including Neutral.
Return to text
55. The modal identities of the pulsations in this Neutral pulsation cycle remain ambiguous until β changes positions and establishes a range. If β were to move later than the bisection of subsequent α pulsations, that would indicate transformation into Mode 1. In this case, β eventually moves earlier than the bisection of α pulsations, establishing its identity as β2 and indicating that a transformation into Mode 2 has taken place.
Return to text
56. Here, there is consistent vertical asynchrony between the bell and drum of Sacko’s lead dundun part, with the bell falling later than the drum every time that the two are struck on what might be considered to be the same pulsation. Measuring between initial peaks of the drum results in a β2 positioning of 45.8%, while measuring the bell results in a β2 positioning of 47.0% of a cycle. Further research might dedicate additional attention to the relationship between the position of a pulsation within its range and the vertical asynchrony between the bell and drum of a lead dundun player.
Return to text
57. While some performances feature gamma thinning to F2 by individuals, none of the performances we have witnessed include the entire ensemble omitting γ2 entirely, nor do any begin with an F2 composite pulsation cycle.
Return to text
58. It is conceivable that two F2 pulsation cycles could be grouped into a single quaternary cycle via pulsation downgrading, facilitating cyclical maturation in Mode 2 that is similar to what occurs in Mode 1. However, this does not appear to happen in practice. We suspect that there may be mechanisms that return a performance to Mode 1 from a high tempo in Mode 2, although further research is required in this area.
Return to text
59. Pieces commonly featuring sawtooth maturation include “Sob(g)oninkun” and “N’gri” (also called “Kirin”), both of which are associated with the Wasulu region near the intersection of the borders of Mali, Guinea, and Cote D’Ivoire. One example of what we consider to be sawtooth maturation can be found in Rainer Polak’s recording of a performance of “Sogoninkun.” In the program notes for this recording, he suggests that “it is interesting to note how in “Sogoninkun” the subdivision is seamlessly changed from quaternary to ternary and back, in the course of performance” (https://www.rainerpolak.de/field-recordings/video-footage/jembe/). We have also observed sawtooth maturation in Kutiro performance among Mandinka people in the Gambia.
Return to text
60. Haugen and Danielsen did not observe achange in pulsation quantity in samba that is analogous to what we observe as a part of the process of maturation in Mande drumming music. Nevertheless, the tempo-dependent transformations in relative pulsation position observed by Haugen and Danielsen (2020) suggest that it could be fruitful to seek examples of maturation in samba.
Return to text
Copyright Statement
Copyright © 2023 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
5714