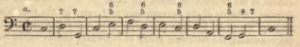Embedded Dissonance in Eighteenth- and Nineteenth-Century Harmonic Theory and Practice*
Karl Braunschweig
KEYWORDS: history of theory, dissonance, harmony, counterpoint, meter, Rameau, Kirnberger, Weber, Mozart, Chopin
ABSTRACT: Seeking to elucidate aspects of harmonic practice that originated in contrapuntal patterns, this article traces a specific set of voice-leading configurations in which the generative roles of dissonance, counterpoint, and harmonic progression are blurred. These configurations, originating in early eighteenth-century practice, feature upper-voice suspensions, which are notable for their interlocking qualities and for their compatibility with an extended range of thoroughbass patterns and bass motions (Harrison 2003). Segments of such patterns were partially assimilated into later compositional practice and appeared in treatises on fundamental-bass and scale-step systems of harmony, but these configurations revealed a degree of friction between counterpoint-based idioms and the emerging harmonic theories attempting to explain them according to singular principles. The continued appearance of these configurations in subsequent compositional practice raises the question of what aspects of dissonance and counterpoint have been both embedded in harmonic practice and increasingly subordinated to chord structure in the harmonic theories that stretch from Rameau to Schenker. This dialectical engagement between historical theory and compositional practice offers a critique of our inherited harmonic theories, exposing competing conceptions of dissonance and discrepancies over its autonomy relative to harmonic principles. Tracing this history also reveals that the essential connections among rhythm/meter, dissonance treatment, and harmonic progression that are clearly present in eighteenth-century practice—Kirnberger’s “rhythmic harmony” (Aldrich 1970)—become increasingly subordinated to harmonic principles in nineteenth-century theory. The historical path of embedded dissonance appears to exemplify Adorno’s notion of sedimentation, which offers several interesting disciplinary and aesthetic conclusions about harmonic theory.
DOI: 10.30535/mto.29.4.1
Copyright © 2023 Society for Music Theory
Introduction
[1.1] Many compelling moments in tonal music involve dissonant voice-leading configurations that have been derived directly from contrapuntal practice. While theorists today largely accept that many details of eighteenth- and nineteenth-century harmonic practice originated in such contrapuntal patterns, it has proven difficult to document this relationship within historical theory and practice. As a result, these configurations are frequently masked or obscured within analytic assessments. This is especially the case with a subset of these contrapuntal patterns in which suspensions coincide with a moving bass (and a chord change) and call into question their compositional origins and effects.
Example 1. Bach, Sinfonia in G minor,
(click to enlarge and listen)
Example 2. Chopin, Etude in C major, op. 10, no. 1, mm. 15–26
(click to enlarge, see the rest, and listen)
Example 3. Reduction of Chopin excerpt,
(click to enlarge)
[1.2] To illustrate, consider two contrasting passages. In Example 1, a descending octave progression in the upper voice (G5–G4) is eloquently realized with a series of dissonant 2–3 suspensions, which form an explicit counterpart to the imitation of the main arpeggiated figure. The prominence of these suspensions and the manner in which the bass seems to complement them both suggest that they are the primary agent of motion within the larger context of the phrase. In Example 2, a similar configuration is present but is embedded in a context that is on the surface not only far more vertical in textural profile but also more outwardly structured by customary harmonic progressions. However, a simple, three-voice reduction (Example 3) reveals a similar contrapuntal pattern at work and therefore also illustrates the changing harmonic contexts for such patterns: what may have originated as a 2–3 suspension chain becomes part of a modified Fonte schema, one that in this context completes a temporary digression to A minor.
[1.3] This raises a fundamental question, then, about how we should interpret such passages: are they generated by a contrapuntal suspension chain and subsequently harmonized or are they guided by harmonic progressions—or both? A quick and practical answer is of course both, but a more thorough answer must explore the shifts taking place between specific harmonic theories and should consider how these are reconciled within the historical record; it must also confront how we attribute a sense of origin and agency to events of a harmonic nature. As such, my study addresses some of the inherited assumptions within harmonic theory. My objective in this article is to demonstrate how a small collection of late seventeenth-century contrapuntal configurations—generated by 2–3 suspensions (or its 7–6 inversion) in the upper voices—have become embedded in idiomatic harmonic progressions within eighteenth- and nineteenth-century music, and how their presence becomes increasingly masked within harmonic theory. It is specifically within the differing contexts of harmonic theory, as well as their changing historical influences, that these configurations slowly became a kind of dormant metaphor.(1) In short, the theoretical history I am sketching here is (1) that the notion of embedded dissonance can account for the unique features of several common configurations in tonal harmony and (2) that the process of embedding was historically intertwined with a conception of increased autonomy for chords within harmonic theory.
Example 4. Common suspension chain and contrapuntal permutations; from Harrison 2003, 244, matched with excerpts from Handel, Chaconne in G major, HWV 435
(click to enlarge)
[1.4] Let us first pinpoint an initiating moment for this historical shift. In practice, certain contrapuntal patterns common in the repertoire around 1700 were subject to techniques of variation and generated small collections of related configurations. Several of these collections feature embedded dissonance as a motivating factor. In theory (as we will see shortly), the entry of the notion of the fundamental bass introduced the possibility for multiple harmonic meanings to arise, and eventually created the conditions for increased harmonic abstraction and autonomy. This friction between theory and practice, and between differing threads of harmonic theory, will be a guiding tension in the following historical sketch. As a starting point for illustrating practice, I rely on an insightful article by Daniel Harrison (2003), which offers an extended list of contrapuntal patterns in the music of Corelli and illustrates their compatibility with an extended range of basso continuo figures.(2) On the left-hand side of Example 4, staves A and 1 show a basic contrapuntal pattern and staves 2 through 5 (all to be combined with staff A) illustrate variants generated by embellishing bass motions. (The numbers enclosed in boxes index the passages in Corelli’s music corresponding to each row.) That these variants are related to a simple 7–6 prototype can be confirmed from practice rather easily. If we take one convenient instance, Handel’s well-known G-major Chaconne, HWV 435, we see that Var. 9 corresponds to Harrison’s line 1, Var. 10 to line 4, and Var. 11 to line 3 (see Example 4, right-hand side). The significance of Harrison’s list is that it binds at least five distinct variants together by suspension chain rather than by root or bass motion; in contrast, most modern approaches tend to classify solely by root progression. It is worth pointing out that Harrison’s variants are largely depicted in three-voice prototypes. This contributes to the sense in which they became embedded in fuller, four-voice harmonic practice.
[1.5] Segments of such patterns were partially assimilated into later compositional practice and appeared in treatises on fundamental-bass and scale-step systems of harmony; but, as we will see, these configurations revealed a degree of friction between a counterpoint-based practice and the emerging harmonic theories attempting to explain them according to singular principles. Ludwig Holtmeier describes this general historical path as follows, noting that this process was well underway even before overtly vertical conceptions appeared:
One is tempted to say—with all due caution—that at the beginning of the eighteenth century the linear significance [of thoroughbass figures] still predominates, and that thoroughbass or the understanding of thoroughbass becomes increasingly “verticalized” during the course of the century under the influence of Ramellian thinking. The one-sided vertical reading of the [nineteenth-century] German Harmonielehre is only a (radical) consequence of this development. (Holtmeier 2007, 9)
After outlining this shift within fundamental bass and scale step theories of harmony, this article takes a closer look at a specific set of these configurations—those featuring upper-voice 2–3 suspensions with harmonically moving bass—and explores what aspects of dissonance and counterpoint have been embedded in eighteenth- and nineteenth-century harmonic theory and practice. By way of conclusion, I will then return to harmonic theory to consider questions of metric placement and an emerging harmonic autonomy. In relation to prior research, my objective is to coordinate the findings of Harrison (2003) and Holtmeier (2007) and to extend this line of inquiry by focusing on several specific configurations and speculating about broad historical shifts.
A Double Meaning and an Emerging Shift in Harmonic Theory
Example 5. Suspension chain interpreted according to motion of the fundamental bass; from Rameau 1722, 242
(click to enlarge)
Example 6. “Colliding” dissonances within the motion of the fundamental bass; from Christensen 1993, 108
(click to enlarge)
[2.1] The unique condition for this shift toward an exclusively vertical conception of harmony lies in the multiplicity inherent in the configuration captured in Example 5, from Rameau’s Traité de l’Harmonie ([1722] 1971), at once a 7–6 suspension chain (at the level of the continuo bass) and a seventh-chord succession (at the level of the fundamental bass).(3) Although this multiplicity was already part of the practice of diminution within the thoroughbass tradition, Rameau’s conception of the fundamental bass authorized an explicit double meaning in theoretical terms, one that created conditions within which more profound shifts in harmonic theory could occur. It is significant that even though Rameau interprets this as generated by a chain of seventh chords, the practice of juxtaposing both basses on the page nevertheless provides a visual reminder of this double meaning. The fundamental bass asserts an origin for the passage but also explicitly recognizes the possibility of derivations, of variants, arising through contrapuntal practice. It is a double meaning embodied in the notation: the conceptual bass stands alongside the sounding bass but does not replace it. We should note that Rameau was keenly aware of the contrapuntal nature of the voice-leading underlying his newly conceived fundamental bass motion: as Thomas Christensen (1993) has pointed out, Rameau’s additional example in the supplement to the Traité (Example 6) included a mechanistic portrayal of colliding dissonances, in which the second of two consecutive 2–3 upper-voice suspensions (between letters A and B in the example) is rhythmically extended and resolves with the bass, defining the characteristic motion of the fundamental bass.
Example 7. Ambiguity arising from different contrapuntal settings of a suspension; from Remeš 2019, 77
(click to enlarge)
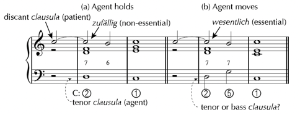
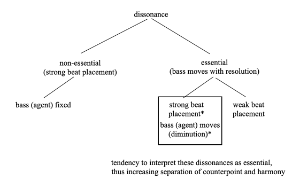
[2.2] The fact that the compositional diminution depicted in the Handel variations (Example 4, above) reveals the same double meaning as Rameau’s fundamental-bass interpretation thus adds a degree of complication to Kirnberger’s distinction between the categories of essential and non-essential dissonance, a distinction that has been firmly inscribed into harmonic theory ever since. While the basic distinction between them seems relatively unproblematic for most instances of dissonance (which fall neatly into one of the two categories), certain cases shown previously problematize it; specifically, in the dissonance chains depicted in Examples 1–3, the bass moves simultaneously with the suspension resolution, blurring Kirnberger’s categories. Remeš (2019) raises a similar ambiguity with Kirnberger’s types when considering eighteenth-century cadences: does the essential dissonance require a bass cadence or can it also be supported by a tenor cadence with diminution (Example 7)? In other words, recognizing a close relationship between configurations related by contrapuntal strands (rather than root motion) begins to complicate Kirnberger’s distinction and suggests that we might think of this ambiguity more accurately as two sides of the same coin, or a theoretical double meaning that models a singular but complex practice. Part of the reason for this ambiguity is that Kirnberger’s definition of the dissonance types relies not only on the motion of the bass but on metric placement. In his view, the suspension dissonance
must always occur on the strong beat of the measure and must resolve on the weak beat. In this way they are distinguished from the essential dissonance, the seventh, and those dissonances that arise from inversion of the seventh chord, which usually occur on a weak beat and resolve on the strong.(4)
Example 8. Kirnberger’s categories of dissonance revised to include mediating type
(click to enlarge)
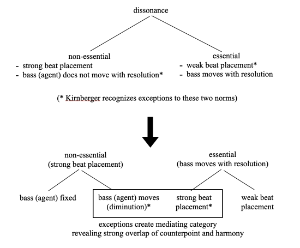
The ambiguous case above occurs when a strong-beat dissonance can be explained theoretically as both a suspension and a chordal seventh. We can, in fact, refine the situation further by pinpointing the fixed and flexible features of the dissonance categories. Thus, the diagram in Example 8 revises Kirnberger’s categories by indicating the overlapping region, the conjunction of strong beat placement and bass motion. This is the area I am exploring in this article.
[2.3] While some theorists (including Kirnberger) recognized these exceptions, there was nevertheless a tendency for harmonic theories to absorb this mediating category into the category of fundamental bass or root motion, leaving only a stationary bass for the definition of the suspension dissonance. In a broad sense, Rameau’s conception of the fundamental bass initiated a slow tendency for the harmonic progression category to absorb the mediating one; consequently, eighteenth-century theorists increasingly interpreted diminution of these dissonant contrapuntal patterns as harmonically motivated.
Example 9. Descending-fifth root motion depicted with embedded suspension chain, Weber 1832, 2: 251 (§263)
(click to enlarge)
Example 10. Descending-fifth root motion in voicings related by invertible counterpoint, Weber 1832, 2: 261 (§271)
(click to enlarge)
Example 11. Embedded suspension chain depicted as interlocking 7ths with Roman numerals, Richter 1860, 62
(click to enlarge)
[2.4] This trend continued in the nineteenth century. Weber, and later Richter, who we can take as representatives of scale-degree harmonic theory (Bernstein 2002), also presented examples suggesting the double meaning inherent in Rameau’s example, but largely replaced the separate fundamental bass notation with Roman numerals. While this might seem like an insignificant change, it nevertheless opened the door to a level of abstraction beyond the fundamental bass: while both the fundamental bass and the Roman numeral scale-degree are in a sense supplied by the imagination, the former asserts an explanation regarding its origin according to a deductive principle whereas the latter merely labels a position in a key, leaving largely unanswered the underlying reasons (contrapuntal, harmonic) for how chords are connected.(5) As a result, the introduction of Roman-numeral labels directs attention away from the voice-leading motivation for certain harmonic progressions toward how these chords assert a key center, and encourages conceptualizing chords as individual units. This shift is not absolute, however, because Weber’s examples in his Versuch do suggest that he was aware of standard voice-leading practices and the properties of invertible counterpoint. In Example 9, for instance, he analyzes the possibilities for descending-fifth root motion within a major key, marking with Roman numerals the motion from seventh chord to triad in each case; while dissonance resolution is still present—allowing the possibility of hearing these as embedded suspensions—Weber’s focus is on enumerating root motions within a key.(6) Example 10 depicts a similar progression in several different inversions. Thus, the change I am describing here is merely a shift in perspective, perhaps even a subtle one at first. Indeed, much of the abstraction occurred later in the history of theory, as Roman numerals became entrenched in the educational system.(7) Richter’s examples from his 1853 practical harmony treatise, Lehrbuch der Harmonie, similarly portray this configuration, maintaining the same voice leading but again summarizing the motion symbolically with Roman numerals (Example 11). Note the use of slurs to mark the preparation of each seventh, which shifts attention from the strong beat ones resembling suspensions and suggests reduced difference between strong and weak beat sevenths. In general, the scale-step approach to harmony in the influential publications of Weber and Richter allowed for the continued presence of contrapuntal patterns but tended to emphasize root motions and their Roman-numeral representation, a practice that slowly began to obscure such patterns within chord abstractions.
Example 12. Heinichen 1728, 179
(click to enlarge)
[2.5] Nevertheless, a particular thread within harmonic theory continued to acknowledge the generative aspect of contrapuntal patterns, and (to a certain extent) emphasized voice-leading and dissonance resolution as much as (or more than) root motion. In certain respects, this perspective could be said to originate with the Italian-influenced thoroughbass theory and practice codified (in the North) in Heinichen’s monumental treatise, Der General-Bass in der Composition ([1728] 1992). Specifically, Heinichen singles out configurations in which a syncopated dissonance (such as the fifth) can have several possible resolutions, all of which have very little to do with root progression or harmonic function. In Example 12, the
Example 13. Kirnberger (Beach and Thym) 1982, 95
(click to enlarge)
Example 14. Schenker 1922, 206
(click to enlarge)
[2.6] This perspective continued in Kirnberger’s work, even though he explicitly integrated Rameau’s fundamental bass into his explanations (reconciling some of the contradictions arising between thoroughbass practice and Rameau’s conception of the fundamental bass). In a prominent place in his Kunst des reinen Satzes, Kirnberger depicts the combined motion of suspension and moving bass more in terms of dissonance resolution than root progression; see Example 13, in which he explains each final chord as being a contrapuntal resolution of dissonance regardless of whether or not it involves a change of chord root. Significantly, Schenker retrospectively identified this contrapuntal independence as part of his “Bridges to Free Composition”—his groundbreaking effort to restore an awareness of the role of counterpoint in tonal harmony (Schenker 1922). I include his example here as a point of comparison (Example 14). To the extent that Schenker’s objective in his “Bridges” is to bring to light the counterpoint embedded in instrumental compositions, his insights are relevant here, specifically those regarding combinations of second- and fourth-species counterpoint. In these examples, the specific chord of resolution matters less than contrapuntal resolution and metric alignment.
Example 15. Embedded dissonance in three degrees of assimilation, Richter 1860, 104
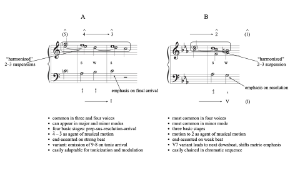
(click to enlarge)
[2.7] Example 15, from Richter 1860, is thus emblematic of the theoretical ambiguity resulting from these combined threads of harmonic theory in the mid-nineteenth century. Here three distinct upper-voice suspensions represent three degrees of assimilation. The first, the 9–6 in m. 2, is the most explicitly contrapuntal, retaining the overt character of a 9–8 suspension. The second, the 9–7 in m. 2 of the second progression, Richter interprets with two closely related fundamentals, thereby converting the ordinary 9–8 into a new harmonic motion. And the third, the cadential suspension in m. 3 of the first progression, represents the most harmonic of the interpretations, almost fully assimilated into the harmonic domain. Note that in Examples 12–15, the embedded dissonances retain the metric profile of ordinary contrapuntal dissonances, clearly defining strong and weak pulses (suspension and resolution) in all cases. The harmonic interpretation can simply be seen as an additional layer, mediating between theory and practice and the changing conceptions therein.
The Special Case of the Down3–Up2 Variant
Example 16. Various settings of a suspension chain with moving bass, annotated from Harrison 2003, 247
(click to enlarge)
[3.1] The down3–up2 variant of the descending-fifth sequence offers a special case of embedded dissonance because the contrapuntal shaping of the pattern is usually foregrounded: the suspension is (nearly) always placed on a strong beat and usually resolves to a triad on the weak.(9) This remarkable consistency even suggests that we might wish to define it in slightly different terms than as merely an inversion of a standard descending-fifth sequence.(10) Harrison’s summary example of this pattern is particularly clear (Example 16). This metrically aligned down3–up2 pattern closely resembles examples of dissonance treatment in seventeenth-century compositional treatises, as in the standard three-part voicing in Berardi’s Documenti Armonici of 1687 (Example 17).(11) It also maintained a lasting presence in eighteenth-century thoroughbass manuals, as can be seen in Gasparini’s L’Armonico Pratico al Cimbalo and Kirnberger’s Generalbass.(12) As was customary in four-voice thoroughbass style, Kirnberger presents three arrangements of the upper voices, placing the
Example 17. Berardi 1687, 151 (click to enlarge) | Example 18. Kirnberger 1781, II: 8 (click to enlarge) |
Example 19. Two versions of dissonant chord resolutions in the down3–up2 pattern; Weber 1832, 2: 252 (§263) and 2: 240 (§252)
(click to enlarge)
Example 20. Derivation of
(click to enlarge)
[3.2] This pattern continued to be presented as an idiomatic voicing (distinct from the root-position version) throughout the nineteenth century. In Example 19, Weber offers two versions of this pattern, both of which align the dissonances with strong beats. (Note that the slurs here simultaneously indicate suspension preparations and prepared sevenths, and that the analysis converts the actual
[3.3] Bach employs this pattern with some frequency in his keyboard works. Example 21 excerpts the opening of his three-part invention in E major, in which the pattern defines a two-measure hemiola, adding a degree of metric tension to the passage. Mozart features this down3–up2 variant prominently in his Piano Sonata K. 333 (Example 22), initially in the first movement and then in the final movement in a moment of recall during the cadenza-like passage.(15)
Example 21. Bach, Sinfonia in E major, BWV 792, mm. 1–7 (click to enlarge and listen) | Example 22. Two passages from Mozart, Piano Sonata K. 333, first movement (mm. 142–46) and third movement (mm. 189–92), vertically aligned with reduction (click to enlarge and listen) |
Example 23. Excerpt from Mozart, Mass in C minor, K. 427, “Et incarnatus est”; Salzer/Schachter 1969, 367
(click to enlarge)
Example 24. Mozart, Piano Sonata K. 545, first movement, mm. 18–21, with two alternative settings of a harmonized 2–3 series, from Holtmeier 2011, 315
(click to enlarge)
[3.4] As a brief digression, we can also take note of the similarity of these voice-leading patterns with additional contrapuntal types (various bass supports) that “accompany” such embedded suspension chains. For instance, suspended ninths frequently appear in a similar setting, with bass motion descending by third with the resolution, as in the Mozart passage in Example 23. The reduction from Salzer and Schachter (1969, 367) illustrates this important contrapuntal possibility. Holtmeier (2011, 315) refers to these as sequential ninths and identifies their implicit presence in the well-known Mozart K. 545 passage given in Example 24, which also reproduces his two alternative readings of this passage: on the one hand as strong-beat
[3.5] It is worth noting here that the prominent role of embedded suspensions in eighteenth- and nineteenth-century practice was also explicitly integrated into the partimento-based pedagogy that dominated the Italian conservatories. Nicholas Baragwanath (2011) traces the continued presence of the partimento/solfeggi pedagogy well into the nineteenth century, a tradition in which such embedded dissonance patterns played a significant role. Example 25 reproduces an exercise featuring an embedded 2–3 chain (harmonized with the down3–up2 variant) from Stanislao Mattei’s influential practical treatise (1827), and Example 26 reveals this same pattern underlying a famous passage in Puccini’s La Boheme.
Example 25. Mattei exercise from 1827 treatise in modern notation from Baragwanath 2011, 259 (click to enlarge) | Example 26. Excerpt from Puccini, La Boheme with reduction; Baragwanath 2011, 270 (click to enlarge) |
The Cadential Suspension and Two Idiomatic Configurations
Example 27. Four contrapuntal possibilities for “harmonizing” a 2–3 upper-voice suspension
(click to enlarge)
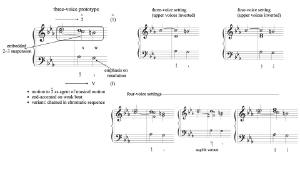
[4.1] Now let us consider some shorter configurations in more detail, those that combine an embedded suspension with a simultaneously moving bass, creating idiomatic harmonic progressions that we might informally think of as featuring “harmonized suspensions.” If we systematically arrange the contrapuntal possibilities for a bass supporting an upper-voice 2–3 leading-tone suspension according to an underlying seventh chord (Example 27), we can observe that the
Example 28. Exercise featuring cadential suspensions, in “Precepts and Principles” (originally in Niedt), Bach/Poulin 1994, 19
(click to enlarge)
Example 29. Embedded dissonance in the cadential suspension, Mozart, Piano Sonata, K. 310, first movement, mm. 43–49
(click to enlarge and listen)
[4.2] First, however, we should consider the cadential suspension figure as a simple yet pervasive case for the embedding process that occurs with the other configurations, a model that proves useful because its presence in eighteenth-century theory and practice is already well known. Recent studies (e.g., Diergarten 2015, Remeš 2019) have established important connections between thoroughbass concepts and practices between various regions of Europe and have offered a standard set of cadence types that were commonly recognized and used. Of these, the “composta” or compound cadence—typically defined as –– bass support for a cadential suspension (––)—appeared in treatises from Bonocini, Muffat, Niedt, Gasparini, and Walther, and was understood to have a degree of closure somewhere between the “long” cadence (
Example 30. Embedded dissonance appearing in Chopin, Nocturne, op. 48, no. 2, mm. 3–6, with hypothetical thoroughbass model
(click to enlarge and listen)
[4.3] As Felix Diergarten (2015) has demonstrated, this practice continued in the late eighteenth century, as can be seen in a representative example of the cadential suspension marking a final exposition cadence in Mozart’s Piano Sonata in A minor (K. 310). In this passage (Example 29) it first occurs as an embedded 2–3 and then is revoiced as 7–6 in the repetition; together these two statements signal the end of the exposition, and—following the conventions of sonata form—reappear in a similar passage at the end of the recapitulation in the home key.(19) This configuration becomes embedded in tonal practice in nineteenth-century music, as can be seen in Example 30, from Chopin’s F-sharp minor Nocturne, op. 48, no. 2, where it constitutes the basic progression harmonizing the stepwise descent in the upper voice (F#–E–D–C#) and is immediately repeated. The embedded 2–3 dissonance appears in the inner voices of the left-hand arpeggiation. A general way to frame the embedding process for the cadential suspension is to recognize changing cadential practices, which tend to favor stronger root motions (including tonicizations of the dominant), many of which use only chordal sevenths, going hand in hand with the use of effective voice-leading configurations in new situations. In practical terms, the cadential suspension became absorbed into the form of a pre-dominant seventh chord, which (no longer linked to the cadence) could appear anywhere within harmonic progressions.
Example 31. Embedded dissonance in the standard eighteenth-century cadential suspension
(click to enlarge)
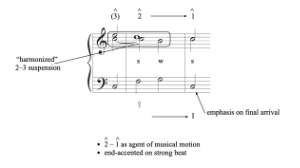
[4.4] Example 31 presents a three-voice prototype of the cadential suspension, with annotations noting the metric placement and “harmonization” of the embedded 2–3 figure, all of which animates – motion and an emphatic tonic arrival. The way in which the suspension dissonance became embedded in the cadential progression thus provides a model for the embedding process shaping two other configurations as well.
Example 32. Configuration A prototype and common settings
(click to enlarge)
Example 33. Mixed-species counterpoint, Fux 1725, 158, reproduced in Schenker 1922, 214
(click to enlarge)
[4.5] The first (configuration A) is a recurring idiom in which a segment of a 2–3 (or 7–6) suspension chain embeds into a familiar harmonic progression, one which tends to appear in thoroughbass sources under the topic of consecutive
Example 34. Contrapuntal configuration featuring consecutive (click to enlarge) | Example 35. Instances of Configuration A in pedagogical treatise of Mattei 1827, 8, 15, and 119 (click to enlarge) |
Example 36. Handel, Lesson 19, reproduced in Mann 1987, 24
(click to enlarge)
Example 37. Bach, Little Prelude, BWV 924, mm. 1–6; excerpt from analysis in Schenker (1921–1924) 2004, 142
(click to enlarge)
[4.6] The four-voice setting of configuration A commonly appeared in thoroughbass exercises and in genres directly derived from thoroughbass practice, such as the keyboard prelude. Example 36 reproduces one of Handel’s exercises for Princess Anne, and Example 37 shows a Bach passage familiar to theorists from Schenker’s foreground sketch in Der Tonwille [1921–24] 2004, an analysis that includes commentary explicitly acknowledging the prominent role of the consecutive suspensions. Both examples demonstrate the sequential potential of this configuration, one in the minor mode and the other in the major mode. The four-voice settings appearing in thoroughbass treatises of Kirnberger 1781 and Sechter 1830 (Examples 38 and 39) both feature sequential tonicizations, the latter extending to .(22) Note that both drop the final 9–8 suspension and thus begin to reveal how smaller segments have become embedded in harmonic practice, and how the metric and dissonance patterns become less dependent on the full suspension chain for their effect. It is important to remember that the consecutive
Example 38. Kirnberger 1781, Part 2, Fig. 25 (click to enlarge) | Example 39. Sechter 1830, 44 (click to enlarge) |
Example 40. Mozart, Piano Concerto, K. 488, second movement, mm. 1–12, with brief reduction
(click to enlarge and listen)
Example 41. Mozart, Piano Sonata, K. 311, first movement, mm. 48–52
(click to enlarge and listen)
[4.7] Configuration A is featured in numerous pieces by Mozart; here I will survey four different voicings and contexts. In Example 40, from the slow movement of his Piano Concerto in A major, K. 488, a three-voice setting appears as part of a sequence (not fully realized with
Example 42. Mozart, Piano Sonata, K. 310, second movement, mm. 46–47 (click to enlarge and listen) | Example 43. Mozart, Symphony no. 40, second movement, mm. 29–36, with reduction (click to enlarge and listen) |
Example 44. Configuration B prototype and settings
(click to enlarge)
Example 45. Heinichen 1728, 163
(click to enlarge)
[4.8] The second configuration (B) features an inner-voice 2–3 suspension supported by a
Example 46. Configuration B in Beethoven, Piano Sonata Op. 13 “Pathètique,” second movement; Salzer 1952, 151
(click to enlarge)
Example 47. “Secondary cadences” in down3–up2 pattern with embedded dissonance, Weber 1832, 2: 251 (§263) and 2: 259 (§269)
(click to enlarge)
Example 48. Richter 1860, 68
(click to enlarge)
[4.9] Three-voice settings of configuration B are far less common than the four-voice settings due to nearly obligatory presence of the sixth above the bass for the
[4.10] Configuration B appears somewhat frequently in the music of Chopin, who demonstrates a penchant for extending it through a chromatic sequence and for featuring its unique minor mode attributes. In his F-sharp minor Prelude, for instance, it initially embellishes a simple tonic-to-dominant motion in m. 1 and m. 2, and then subsequently guides a longer chromatic sequence (Example 49). Because the contrapuntal dissonance is typically hidden in the inner voices, I include reductions that rearrange the voices more explicitly. Chopin also features this sequential pattern in his F-sharp minor Mazurka (Example 50), this time with passing chords on the third beat of each measure.(25)
Example 49. Chopin, Prelude in F-sharp minor, op. 28, mm. 1–4, with two reductions (click to enlarge and listen) | Example 50. Chopin, Mazurka in F-sharp minor, op. 6, no. 1, opening measures, with reduction (click to enlarge and listen) |
Example 51. Koch 1811, 291
(click to enlarge)
[4.11] Interestingly, this sequential variant can be found as early as 1811 in a thoroughbass manual by Koch (Example 51), except that it appears with a reversed metric placement, one that exposes the embedding of dissonance within idiomatic harmonic progressions that convey metric autonomy.
Example 52. Summary prototypes and features of Configurations A and B
(click to enlarge)
[4.12] Having explored these realizations of configurations A and B in various sources, we can now draw some provisional conclusions about them within the broader context of tonal harmony (Example 52). Both embed upper-voice 2–3 suspensions within an idiomatic harmonic progression, yet the two differ considerably. Configuration A is the more flexible of the two, easily appearing in both major and minor modes and in three- and four-voice settings, all derived from a three-voice prototype. Configuration B, in contrast, is most common in the minor mode in four-voice settings (appropriately now represented by a four-voice prototype); it is also more complex in that it has a greater number of options for the voice-leading of the fourth voice. Within their typical compositional contexts, A tends to be end-accented on the final arrival of scale-degree 3 over tonic harmony, largely due to the active scale-degree 4 as the agent of musical motion; B tends to embellish an arrival of scale-degree 2 over dominant harmony, resolving on a weak beat, and—because of its incomplete tonal closure—offers the possibility of a variety of continuations, including a chromatic sequence (in which the suspension serves to break potential parallels in voice leading). While these prototypes are the most common instances of embedded dissonance, variants do appear in other contexts: for instance, other
Changing Priorities in Harmonic Theory
[5.1] As I mentioned above, my claim here is (1) that the notion of embedded dissonance can account for the unique features of several specific configurations in tonal harmony by foregrounding underlying counterpoint and (2) that the process of embedding went hand in hand with an increasing sense of autonomy for dissonant chords within harmonic theory. In several of the examples I have explored, we observed metric independence emerging within some harmonic sequences and embedded dissonance configurations as depicted in theoretical treatises. If we return to our historical starting point, we can observe that early eighteenth-century practice tends to follow contrapuntal norms in placing these dissonances on strong beats, but that a degree of metric flexibility does begin to appear with changing harmonic styles. As early as 1700, consecutive 7ths were not uncommon in the concertos and sonatas of Italian instrumental music (e.g., Corelli), and in the music of Bach we occasionally encounter sequences in which the metric disposition of the embedded dissonances is reversed from the contrapuntal norm.(26) A similarly ambiguous situation arose in the emerging theories of harmony, in which explanations were often framed in contradictory metric settings. We can also observe that, in general, both theory and practice demonstrated a tendency for settings of embedded suspension configurations (sequences and configurations A and B) to become increasingly independent of metric placement, a situation that introduced conceptual ambiguity into their compositional origins and motivations. This led eventually to an increased sense of autonomy for the chord as a basic harmonic unit, and an increased independence from meter, with which it had been previously integrated. These are no doubt broad generalizations—interpretations of the historical record that go beyond explicit evidence and attempt to probe deeper trends, ones that cannot always be empirically verified. But I believe that there is tremendous value in revealing the often-hidden conceptual shifts that have profoundly shaped our inherited understanding of tonal harmony. As such, this perspective affords new insight into historical theory and prompts important reflection on current pedagogical practices.
[5.2] In order to outline this historical shift it is once again helpful to recognize the multiplicity of possible dissonance realizations based on metric placement, bass motion, and diminution, with a mediating type explainable as both a suspension and harmonic progression: a suspension-generated dissonance that occurs on a strong beat (and which can resolve with contrapuntal bass motion) and a seventh interpreted harmonically that resolves with a chord change and that can occur with metric independence. Kirnberger notes that this mediating type can make identification difficult:
Usually it is easy to distinguish the seventh that is merely a suspension from the essential seventh, because the former never falls on a weak beat while the latter normally does. But when the essential seventh falls on a strong beat, as it sometimes does, it is more difficult to distinguish from the suspension.(27)
Example 53. Rule of the Octave in Kirnberger, Kunst, Chapter 4 (Beach 1982, 62)
(click to enlarge)
Example 54. Rule of the Octave in Rameau’s Traité, III (Rameau/Gossett 1971, 232)
(click to enlarge)
Nevertheless, his metric placement of dissonances generated by counterpoint is fairly consistent. Note his metric arrangement for the Rule of the Octave (Example 53), which deliberately places the inverted dominant seventh chord on a weak beat and which also places the ii
Example 55. Metric independence of “secondary cadences” in down3–up2 pattern with embedded dissonance, Weber 1832, 2: 252 (§263)
(click to enlarge)
[5.3] Scale-step theory, in contrast, gradually appears to attribute more metric autonomy to harmony; what appeared occasionally in Rameau’s work—the weakened metric position of the dissonance pattern—becomes in Weber’s more explicit.(30) In Example 55, the 2–3 suspension is embedded within two metrically opposed settings. The reversal seen here in the second setting suggests that Weber views them as interchangeable, which overtly obscures the contrapuntal pattern by diffusing the metric impact of the dissonance. This begins to demonstrate how the suspension figure was becoming embedded in Weber’s scale-step analysis, and how the scale-degree theory was partially obscuring its contrapuntal origin. Thus, even more than the common down5–up4 version of the harmonic sequence, this down3–up2 variant with its foregrounding of the dissonance in a strong metric position (and its resolution to consonant triads) captures the friction inherent in the harmonic embedding of dissonance when this metric association is upended.
Example 56. Jadassohn (1883) 1890, 71 (§41)
(click to enlarge)
Example 57. Ferdinand Hiller (1860) 1889, 15
(click to enlarge)
[5.4] That the
Example 58. Schoenberg, (1911) 1978, 84
(click to enlarge)
[5.5] The contradictory metric placements we have surveyed suggest the coexistence of different types of dissonance that exhibit considerable overlap. The strong-beat placement of dissonance followed by a change of bass and chord can be analyzed in two ways and reveals a compositional genealogy that can be traced along two different paths, one contrapuntal and one harmonic. While distinct, they nevertheless coexist in eighteenth-century theory and practice. By contrast, nineteenth-century theory, marked by the strong emergence of scale-step theory, continues this coexistence but casts additional emphasis on the harmonic generation of dissonance and begins to obscure the earlier contrapuntal origins of various prototypes. The end result of this tendency toward metric autonomy might be not the metric reversal of dissonance patterns but rather the complete removal of metric context, as depicted for instance in Example 58 from Schoenberg’s Theory of Harmony ([1911] 1978, 84), what we might consider the endpoint of the “long” nineteenth century. (Note how the marking of common tones replaces dissonance preparations.)
Example 59. Tendency of eighteenth- and nineteenth-century harmonic theory
(click to enlarge)
[5.6] If we return to a conceptual diagram of dissonance classifications (Example 59), we can depict this growing tendency by absorbing the mediating category into the domain of the essential (harmonic) dissonance. However, to focus solely on the distinction between a contrapuntal
[5.7] This paradigm shift also suggests an increased focus on individual chords rather than chord relationships and configurations (e.g., cadences and Rule of the Octave segments) as the basic harmonic units, a conceptual shift that leads directly to notions of chord derivation and the category of apparent chords. Decisive here is the scale-degree conception of harmony, which posits the chord as the basic unit (rather than the more integrated chord progression of Rameau’s fundamental bass) and presumes that any chord can move to any other chord.(32) This, in effect, severs the integral connection between progression and dissonance presupposed by Rameau. It is a subtle but far-reaching shift because Weber appeared to be aware of the interlocking sevenths in the descending-fifth sequence, a relationship only possible with the falling-fifth harmonic relationship. But because he asserts that in principle any chord can move to any other chord, dissonance in a sense becomes detached from harmonic progression—one can exist without the other without affecting the scale-degree interpretation (hence the notion of non-harmonic tones).
Example 60. Catel 1802, 56
(click to enlarge)
[5.8] Explanations of chord structure severed from contrapuntal antecedents thus open the door to chord derivation as a prominent theoretical tool. A vivid instance of derivation appears in Catel’s 1802 Traité d’Harmonie (Example 60). Here, he derives the idiomatic usage of the
Example 61. Prout 1889, 172
(click to enlarge)
[5.9] Along similar lines, in his early-twentieth century Harmony textbook (1889), Prout identifies an example from Haydn—a version of prototype B above—but views it as an inverted “dominant eleventh” chord with the ninth in the bass and the root omitted (Example 61), revealing the degree to which scale-degree harmonic theory had appropriated the tendency towards third stacking and conceived of complex harmonic events as entirely root generated. This marks one of the more extreme instances of linear factors being completely eclipsed by scale-degree theory’s singular conception of chord structure.(34)
[5.10] Tracing the reception history of these configurations in theory and practice leads to several additional observations, one of which is that the essential connection between meter, voice-leading, and harmonic progression clearly present in practice in the early eighteenth century becomes increasingly subordinated to singular harmonic principles in many nineteenth-century theories. The examples from Weber and Koch illustrate the metric reversal of the suspension accents, an inversion conditioned by the double-meaning inherent in the fundamental bass conception of harmony. We might say that the “rhythmic harmony” (Aldrich 1970) implicit in Kirnberger’s treatise (and explicit in his distinction between “essential” and “non-essential” dissonance) decreases in importance in subsequent harmonic theories.
[5.11] We might also conclude that harmonic analysis (as opposed to compositional theory) has the potential to obscure countrapuntal origins, even while most harmonic theories preserve some room for the presence of embedded counterpoint. In the era of harmonic theory, dissonance is reassigned a new role, which is to represent the new order of the tonal system, a system based on chord relationships rather than intervallic ones; while this point seems obvious, the deeper significance has to do with the fact that contrapuntal dissonance, while partially repurposed, also becomes a residue of an earlier paradigm, coexisting in sedimented form within the new paradigm. Thus, even within the new era of tonality in which harmonic theory carves out a new autonomy and agency for chord as the fundamental unit, which is largely independent of meter, there exists the quiet and often hidden presence of an earlier contrapuntal practice, now embedded in the new theory and practice.
[5.12] Dahlhaus once observed that theories that outwardly might be viewed as contradictory can be better understood as historically situated theories, a diachronic solution to a synchronic contradiction.(35) Adorno (1992) goes even further in his suggestive concept of sedimentation, which he illustrates most concretely in his book on Mahler and which I believe applies to the notion of embedded dissonance. If we view counterpoint as an autonomous domain in which voices are independent agents and in which harmony is largely a result of voice leading, then the emergence of different paradigms of harmonic theory reconfigure this domain by offering an expanded field of musical agents, each one historically sedimented on the previous: in fundamental bass theory, the perfect cadence and its variants become the primary model for harmonic progression; in Stufen theory, all of the scale steps (now identified by label and hence a name) gain a degree of autonomy, and a more complex table of progressions constitutes musical space; and in function theory, the three harmonic functions govern phrase syntax and tonal structure, even when represented by single scale degrees. In this new harmonic world, dissonance becomes simultaneously sedimented and appropriated—sedimented through accumulated practice, and appropriated by each agent in different ways, as chord member, as scale degree, as tonal function, each marked by a new metric autonomy. In short, dissonance is no longer solely governed by interval progression, and harmonic progression gains a new domain of autonomy, equal in influence to that of counterpoint. The tonal system (as an exclusively harmonic domain) thereby becomes a dominant force.
[5.13] Therefore, in a broader sense I suggest that we think of embedded dissonance as a renegotiation of musical agents and domains of autonomy within several different paradigms of harmonic theory. Schenker’s graphic notation, which incorporates figured bass, inner-voice contrapuntal patterns, and a structural assessment of harmony represents this composite process almost literally: one can read an analytic sketch not simply as representing the structural unfolding of a piece but as a snapshot in the historical dialectic of theory/practice. The path of embedded dissonance is thus the disciplinary negotiation of new foundations with established practices. Harmonic progressions and functions emerge as autonomous but have the history of contrapuntal patterns sedimented in them. The very identity of certain chords includes the embedding of dissonance.
[5.14] I wish to end by noting that, from my point of view, these insights are not merely theoretical speculation but also directly involve the listening experience. When we hear passages that feature these contrapuntal patterns, we can perceive both embedded dissonance and its history: these configurations are compelling not simply for their raw sound but also for their conceptual complexity, one in which history is embedded within theory.
Karl Braunschweig
Wayne State University
4841 Cass Ave., Suite 1321
Detroit, MI 48202
Works Cited
Adorno, Theodor W. 1992. Mahler: A Musical Physiognomy. Translated by Edmund Jephcott. The University of Chicago Press. https://doi.org/10.7208/chicago/9780226076300.001.0001.
Aldrich, Putnam. 1970. “’Rhythmic Harmony’ as Taught by Johann Philipp Kirnberger.” In Studies in Eighteenth-Century Music: A Tribute to Karl Geiringer on his Seventieth Birthday, ed. H. C. Robbins Landon and Roger E. Chapman, 37–52. Oxford University Press.
Bach, J.S.. [1738] 1994. J. S. Bach’s Precepts and Principles for Playing the Thorough-Bass or Accompanying in Four Parts. Translated by Pamela Poulin. Clarendon Press.
Baragwanath, Nicholas. 2011. The Italian Traditions & Puccini: Compositional Theory and Practice in Nineteenth-Century Opera. Indiana University Press.
Berardi, Angelo. 1687. Documenti armonici. Giacomo Monti.
Bernstein, David. 2002. “Nineteenth-Century Harmonic Theory: The Austro-German Legacy.” In The Cambridge History of Western Music Theory, ed. Thomas Christensen, 778–811. Cambridge University Press. https://doi.org/10.1017/CHOL9780521623711.027.
Catel, Charles-Simon. 1802. Traité d’Harmonie. Leduc.
Christensen, Thomas. 1993. Rameau and Musical Thought in the Enlightenment. Cambridge University Press.
Dahlhaus, Carl. 1989. Geschichte der Musiktheorie. Vol. 11, Die Musiktheorie im 18. und 19. Jahrhundert. Wissenschaftliche Buchgesellschaft.
—————. 2001. “Harmony, 4. Theoretical Study” Grove Music Online. https://doi.org/10.1093/gmo/9781561592630.article.50818
Damschroder, David. 2008. Thinking About Harmony. Cambridge University Press. https://doi.org/10.1017/CBO9780511482069.
Diergarten, Felix. 2011a. “‘The True Fundamentals of Composition’: Haydn’s Partimento Counterpoint.” Eighteenth-Century Music 8 (1): 53–75. https://doi.org/10.1017/S1478570610000412.
—————. 2011b. “Romantic Thoroughbass: Music Theory between Improvisation, Composition, and Performance.” Theoria 18: 5–36.
—————. 2015. “Beyond ‘Harmony’: The Cadence in the Partitura Tradition.” In What is a Cadence? Leuven University Press. https://doi.org/10.2307/j.ctt14jxt45.5.
Eybl, Martin. 1995. Ideologie und Methode zum Ideenschichtlichen Kontext von Schenkers Musiktheorie. Hans Schneider.
Förster, Emanuel Aloys. 1804. Anleitung zum General-Bass. Breitkopf and Härtel.
Fux, Johann Joseph. 1725. Gradus ad Parnassum. Johann Peter van Ghelen.
Gasparini, Francesco. [1708] 1963. L’Armonico Pratico al Cimbalo. Antonio Bortoli. Translated as The Practical Harmonist at the Harpsichord by Frank S. Stillings. Edited by David L. Burrows. Yale University Press.
Gjerdingen, Robert. 2007. Music in the Galant Style. Oxford University Press.
Groth, Renate. 1989. “Italienische Musiktheorie im 17. Jahrhundert.” In Geschichte der Musiktheorie, vol. 7, 307–79. Wissenschaftliche Buchgesellschaft.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music. The University of Chicago Press.
—————. 2003. “Rosalia, Aloysius, and Arcangelo: A Geneology of the Sequence.” Journal of Music Theory 47 (2): 225–72. https://doi.org/10.1215/00222909-47-2-225.
Heinichen, Johann David. [1728] 1992. Der General-Bass in der Composition. Narrative translation by George Buelow as Thorough-Bass Accompaniment According to Johann David Heinichen. Rev. ed. University of Nebraska Press.
Hiller, Ferdinand. [1860] 1889. Übungen zum Studien der Harmonie und des Contrapunktes. Du Mont.
Holtmeier, Ludwig. 2007. “Heinichen, Rameau, and the Italian Thoroughbass Tradition: Concepts of Tonality and Chord in the Rule of the Octave.” Journal of Music Theory 51 (1): 5–49. https://doi.org/10.1215/00222909-2008-022.
—————. 2011. Review of Music in the Galant Style, by Robert Gjerdingen. Eighteenth-Century Music 8 (2): 307–48. https://doi.org/10.1017/S1478570611000091.
—————. 2017. Rameaus langer Schatten: Studien zur deutschen Musiktheorie des 18. Jahrhundert. Georg Olms.
Hyer, Brian. 2002. “Tonality.” In The Cambridge History of Western Music Theory, ed. Thomas Christensen, 726–52. Cambridge University Press. https://doi.org/10.1017/CHOL9780521623711.025.
IJzerman, Job. 2018. Harmony, Counterpoint, Partimento. Oxford University Press.
Jadassohn, Salomon. [1883] 1890. Harmonielehre. Translated as A Course of Instruction in Pure Harmonic Writing. Breitkopf and Härtel.
Kaiser, Ulrich. 2013. Gehörbildung: Satzlehre, Improvisation, Höranalyse. Bärenreiter.
Kirnberger, Johann Phillip. [1771–79] 1982. Die Kunst des reinen Satzes in der Musik. Decker and Hartung. Translated as The Art of Strict Musical Composition by David Beach and Jurgen Thym. Yale University Press.
—————. 1781. Grundsätze des Generalbasses als erste Linien zur Composition. Hoffmeister.
Koch, Heinrich Christoph. 1811. Handbuch bey dem Studium der Harmonie. Hofmeister.
Lester, Joel. 1992. Compositional Theory in the Eighteenth Century. Harvard University Press.
Mann, Alfred. 1987. Theory and Practice: The Great Composer as Student and Teacher. W. W. Norton.
Martin, Nathan John. 2012. “Rameau’s Changing Views on Supposition and Suspension.” Journal of Music Theory 56 (2): 121–67. https://doi.org/10.1215/00222909-1650397.
Mattei, Stanislao. 1827. Pratica d’accompagnamento sopra bassi numerati e contrappunti. Ricordi.
Menke, Johannes. 2020. Kontrapunkt II: Die Musik des Barock. 2nd ed. Laaber-Verlag.
Muffat, Georg. [1699] 1961. An Essay on Thoroughbass. Edited by Hellmut Federhofer. American Institute of Musicology.
Perelman, Chaim and L. Olbrechts-Tyteca. 1969. The New Rhetoric: A Treatise on Argumentation. University of Notre Dame Press.
Prout, Ebenezer. 1889. Harmony: Its Theory and Practice. Augener.
Rameau, Jean-Philippe. [1722] 1971. Traité de l’harmonie. Ballard. Translated by Philip Gossett as Treatise on Harmony, Dover.
Remeš, Derek. 2019. “New Sources and Old Methods: Reconstructing and Applying the Music-Theoretical Paratext of Johann Sebastian Bach’s Compositional Pedagogy.” Zeitschrift der Gesellschaft für Musiktheorie 16 (2): 51–94.
Richter, Ernst Friedrich. 1860. Lehrbuch der Harmonie. 3rd ed. Breitkopf and Härtel. https://doi.org/10.31751/1015.
Rummenhöller, P. 1967. “Der deskriptive Theoriebegriff Gottfried Webers.” In Musiktheoretisches Denken im 19. Jahrhundert, ed. P. Rummenhöller, 11–17. Bosse.
Salzer, Felix. 1952. Structural Hearing. Vols. 1–2. Dover.
Salzer, Felix, and Carl Schachter. 1969. Counterpoint in Composition. McGraw-Hill.
Sanguinetti, Giorgio. 2012. The Art of Partimento: History, Theory, and Practice. Oxford University Press.
Schenker, Heinrich. [1921–24] 2004. Der Tonwille. Edited by William Drabkin. Oxford University Press.
—————. 1922. Kontrapunkt. Vol. 2. Universal Edition.
—————. [1926] 1996. The Masterwork in Music. Vol 2. Edited by William Drabkin. Cambridge University Press.
Schoenberg, Arnold. [1911] 1978. Theory of Harmony. Translated by Roy Carter. University of California Press.
Sechter, Simon. 1830. Practische Generalbaß-Schule, op. 49. Joseph Czerny-Witzendorf.
Weber, Gottfried. 1830–1832. Versuch einer geordneten Theorie der Tonsetzkunst, 3rd ed. Schott.
Compositions
Compositions
Bach, Johann Sebastian. 1853. Invention in E Major, BWV 792. Bach-Gesellschaft Ausgabe. Ed. Carl Ferdinand Becker, Vol. 3. Breitkopf and Härtel.
—————. 1853. Invention in G minor, BWV 797. Bach-Gesellschaft Ausgabe. Ed. Carl Ferdinand Becker, Vol. 3. Breitkopf and Härtel.
Chopin, Frédéric. 1894. Mazurka in F-sharp minor, op. 6, no. 1. Complete Works for the Piano, Vol. 2. Ed. Carl Mikuli. Schirmer.
—————. 1894. Nocturne in F-sharp minor, op. 48, no. 2. Complete Works for the Piano, Vol. 4. Ed. Carl Mikuli. Schirmer.
—————. 1894. Etude in C Major, op. 10 no. 1. Complete Works for the Piano. Vol. 7. Ed. Carl Mikuli. Schirmer.
—————. 1894. Prelude in F-sharp minor, op. 28. Complete Works for the Piano, Vol. 8. Ed. Carl Mikuli. Schirmer.
Handel, Georg Friedrich. 1858. Chaconne in G Major, HWV 435. Georg Friedrich Händels Werke. Vol. 2. Deutsche Händelgesellschaft.
Mozart, Wolfgang Amadeus. 1878. Piano Sonata in A Minor, K. 310. Mozarts Werke, Serie XX: Sonaten und phantasien für das pianoforte. Breitkopf and Härtel.
—————. 1878. Piano Sonata in D Major, K. 311. Mozarts Werke, Serie XX: Sonaten und phantasien für das pianoforte. Breitkopf and Härtel.
—————. 1878. Piano Sonata in B-flat Major, K. 333. Mozarts Werke, Serie XX: Sonaten und phantasien für das pianoforte. Breitkopf and Härtel.
—————. 1959. Piano Concerto in A Major, K. 488. Neue Mozart-Ausgabe, Serie V, Werkgruppe 15. Bärenreiter-Verlag.
Discography
Discography
Ashkenazy, Vladimir and the Philharmonia Orchestra. 1885 The Piano Concertos (Mozart 1959). London 443 727-2, 10 compact discs.
Koroliov, Evgeni. 2000. Inventions and Sinfonias (Bach 1853). Hänssler Bachakademie Edition 92.106, compact disc.
Krips, Josef and the Royal Concertgebouw Orchestra. 1996. Symphony no. 40. Mozart Complete Symphonies (Mozart 1880). Philips 454 097-2, compact disc 12.
Ohlsson, Garrick. 1989. The Complete Piano Works of Frédéric Chopin (Chopin 1895). Vol. 2, Preludes. Arabesque Z6629, compact disc.
—————. 1994. The Complete Piano Works of Frédéric Chopin (Chopin 1894). Vol. 6, Nocturnes. Arabesque Z6653-2, 2 compact discs.
—————. 1996. The Complete Piano Works of Frédéric Chopin (Chopin, 1895). Vol. 10, Etudes. Arabesque Z6718, compact disc.
Schiff, András. 1980. Mozart: The Piano Sonatas (Mozart 1878). London 443 717-2, 5 compact discs.
Footnotes
* I wish to thank Daniel Harrison for his insightful suggestions for the final version of this article, as well as to the anonymous reviewers for MTO, and to William Rothstein and Thomas Christensen for their valuable comments on an earlier version of this paper presented at the 2001 SMT annual meeting.
Return to text
1. Perelman and Olbrechts-Tyteca (1969, 405–10) insightfully discuss this aspect of metaphor as a valuable rhetorical tool, including the technique of “awakening” the metaphor through translation or recontextualization.
Return to text
2. Harrison (2003) traces these 2–3/7–6 chains through Fux to the Italian composer Tarquinio Merula (1595–1665), whose extensive use of this device in two-, three-, and four-part textures established the practice that would later be widely disseminated by Corelli and others. Harrison concludes that the 2–3/7–6 configuration became the default suspension type in this style (also encompassing the harmonic settings of 4–3 and 9–8 through an added lower voice), chains of which became the basis for Rameau’s notion of cadential prefixion ([1722] 1971, 83). Consequently, the present example is one of six from his article featuring various contrapuntal/harmonic settings of the 2–3/7–6 chain. See also Sanguinetti 2012 and Eybl 1995, especially the latter’s appendix of linear models, which includes various harmonic settings of upper-voice 2–3 (or 7–6) dissonance chains (154). Diergarten 2011a (65–67) similarly identifies a related set of contrapuntal possibilities relating to a passage in a Haydn Mass and resonating in contemporaneous treatises, and Lester 1992 (225) offers an interesting late eighteenth-century treatise example.
Return to text
3. Rameau claimed that the seventh represented the origin of dissonance within harmonic tonality (Christensen 1993, 123–29 and Holtmeier 2017, 38–39), but nevertheless recognized the suspension as distinct from chordal sevenths. The complex theoretical relationship between the two is thus related to the even more complex relationship between suspension and supposition in Rameau’s work (Martin 2012 and Damschroder 2008). As Martin argues, supposition is the broader category of the two: even though suspensions are conceptually distinct, they can be explained by supposition and therefore fit into a wider set of harmonic relationships (Martin 2012, 127).
Return to text
4. Kirnberger [1771–79] 1982, I, 72–73 (Beach and Thym 1982, 92): “Diese Dißonanzen müssen allezeit auf der guten Zeit des Takts eintreten, und auf den schlechten aufgelöset werden, und dadurch unterscheiden sie sich von der wesentlichen Dißonanz, der Septime, und denen, die aus Verwechslung des Septimen-Accords entstehen, welche meistentheils auf den schlechten Taktzeiten eintreten, und auf den guten aufgelöset werden.”
Return to text
5. Rameau’s fundamental bass explains harmony according to a scientific principle and accordingly makes normative claims regarding practice, Christensen 1993, 103–32; Weber’s scale-degree theory describes practice and only makes such claims based on description. See Bernstein 2002, 782–84, and Rummenhöller 1967.
Return to text
6. Weber’s examples occur in his Versuch (1830–1832), Volume 2 within his discussion of progression types, in which he distinguishes between those involving the “natural” motion involving dominant seventh chord to tonic triad (Hauptcadenz) and those that involve the other types of seventh chords resolving to triads a fifth below (Nebencadenzen), as well as the same fifth progressions with interlocking seventh chords. He also expresses his general disapproval of progressions in which seventh chords move to triads other than its fifth-related one.
Return to text
7. One could trace a similar process with the functional names that Rameau introduced in his later writings, which followed a similar process of abstraction in Riemann’s extended function theory. I will return to these observations at the end of this article; however, function theory will not figure into my discussion because it assumes a distinctly different view of dissonance within chord structures.
Return to text
8. This example is excluded from Buelow’s 1992 narrative translation.
Return to text
9. In fact, Kaiser (2013, 161) presents this version as the model and the root position as the variant in his exposition of the descending-fifth sequence. IJzerman 2018 maintains their independence, but notes that “The schema Third Down Second Up implies an alternation of
Return to text
10. I would even assert that, in the teaching of tonal theory, we would be well advised to note that the contrapuntal differences between the down3–up2 and the down5–up4 sequences might outweigh the harmonic similarities.
Return to text
11. Berardi’s example is cited in Groth 1989, 351–52 (vol. 7 of Geschichte der Musiktheorie). Groth notes that even though the musical practice of the second half of the seventeenth century favored a tendency toward harmonic sonorities, theorists such as Bononcini and Berardi nevertheless explained them according to linear norms, and that this linear conception persisted well into the eighteenth century. It might be worth pointing out that the down3–up2 version of this sequence lent itself more readily than the “root position” version to the thinner, three-voice texture that was more prominent in several early eighteenth-century genres (e.g., Corelli’s Trio and Violin Sonatas, Bach’s Inventions and French Suites).
Return to text
12. Gasparini ([1708] 1963, 54) provides only the figured bass for this progression but explains that the fifth above the bass is the dissonant tone that resolves down while the bass ascends by step or leap.
Return to text
13. In a separate example, Kirnberger (1781, II: 8) does include a version that places the
Return to text
14. Richter (1860, 173) states this explicitly in a chapter dedicated to three-voice writing; the beginning of his example is not shown here: “Der zehnte Takt zeigt einen Quintsextakkord scheinbar. Im Grunde ist die Quinte hier nichts Anderes, als der Vorhalt zur Quarte, die aber hier durch die Fortschreitung des Basses zur Terz wird. Vierstimmig wird auch dies deutlicher.”
Return to text
15. Although far less common, the down3–up2 variant can appear with dissonances on the weak instead of strong beats, as Mozart does in K. 310 near the end of the development section (mm. 70–73), an example that can be explained by the influence of the Prinner schema, with prominent parallel tenths in the outer voices on the downbeats.
Return to text
16. Holtmeier (2011, 315) defines these as “sequential ninths,” and directly attributes the model to Corelli (2017, 252). Menke (2020, 124) similarly connects this pattern to several related contrapuntal settings.
Return to text
17. These labels, like schema names (e.g., Prinner), are retrospective interpretations of musical units; authors of harmony treatises did not identify them explicitly as such, though the voice-leading profiles of configurations A and B can occasionally be found in their examples (especially in practical Harmonielehre types).
Return to text
18. The example in the “Precepts and Principles” slightly modifies Niedt’s original by placing both cadential suspensions on a downbeat. Niedt places one of them on a weak beat and reserves the strong beat for a subsequent 4–3 suspension. The role of the
Return to text
19. In the terms of sonata theory, the use of the cadential suspension here provides rhetorical emphasis for the EEC and ESC. Diergarten 2015 links Mozart’s use of cadence to the Partitura (and Partimento) tradition, particularly the use of the “compound cadence” at more conclusive formal positions (as compared to the “simple cadence”). In this particular sonata, Mozart’s use of the 2–3 suspension at the final formal cadences connects motivically to the broad and dramatic 2–3 dissonance series (repeated sequentially) that dominates the development.
Return to text
20. See, e.g., Muffat [1699] 1961, 26.
Return to text
21. See Gjerdingen 2007, 81, who documents a three-voice setting embedded as part of a Prinner schema in a work by Jean-Marie Leclair.
Return to text
22. See also Förster 1804, Example 112b.
Return to text
23. Recall also the previous discussion from Holtmeier 2011 of a voice-leading event that can be explained by derivation from two different models, suspension 9ths vs. sequential 9ths; see also Holtmeier 2017, 251–60.
Return to text
24. See also Schenker’s analysis in The Masterwork in Music II ([1926] 1996).
Return to text
25. See Felix Diergarten’s (2011b, 28) interpretation of this passage in the context of the practical partimento/thoroughbass practice, in this case, extending well into the nineteenth century in the hands of Chopin’s teachers and their manuals (e.g., Catel). Diergarten’s reading is similar to that of Felix Salzer, Structural Hearing (1952) vol. 2, 362. Both authors derive this passage from a 7–6 suspension chain; my reading differs only in a foregrounding of the accented
Return to text
26. See, for instance, Toccata, BWV 911, mm. 48–50, in which weak-beat
Return to text
27. Kirnberger [1771–79] 1982, I, 78 (Beach and Thym 1982, 97): “Insgemein ist es leicht, die Septime, die nur ein Vorhalt ist, von der wesentlichen zu unterscheiden, weil diese meistentheils, jene aber niemal auf die schlechte Zeit des Taktes fällt. Wenn aber die wesentliche Septime, wie bisweilen geschieht, auch auf die gute Zeit des Takts fällt, so ist sie schwerer von dem Vorhalt zu unterscheiden.”
Return to text
28. Note also that Kirnberger’s two
Return to text
29. See for example, Traité, IV, Chapter 13; additionally, he begins Book II by adding a fundamental bass to several examples from Zarlino’s Istitutioni Harmoniche, in which the characteristic suspension dissonance is always placed on a downbeat.
Return to text
30. In Rameau’s Traité, the weak-beat placement of dissonant tones with
Return to text
31. As Diergarten 2011b demonstrates, Hiller (the director of the conservatory in Cologne and personal friend of Chopin) was a central figure in the early nineteenth century whose practical harmony treatise (Hiller [1860] 1889) featured a substantial collection of partimenti exercises.
Return to text
32. Bernstein (2002, 783) cites Weber (1830, 2: 173) on this assertion, one which became fairly standard by the end of the nineteenth century; Harrison (1994, 1) cites Reger on this point, and even describes it as a “revolutionary slogan” of the generation of composers including Mahler, Strauss, and Schoenberg.
Return to text
33. Note the direct connection to Italian thoroughbass tradition through Choron and Fétis.
Return to text
34. To a certain extent, this reveals how scale-degree theory marks a certain loss from its fundamental bass inheritance, in that the consideration of fundamental bass motions had been severed from its relation to chord structure.
Return to text
35. Dahlhaus 2001: “The theory of fundamental progressions is primarily orientated to early eighteenth-century harmony (namely to the harmonic model of the sequence of 5ths), while the theory of functions, in common with Riemann’s doctrine of metre and rhythm, is developed from the music of Beethoven. It is thus to some degree not a case of competitive theories dealing with the same matter in hand, but of theses concerning different stages of a historical development” (section 4, “Theoretical Study,” final paragraph). See also, Dahlhaus 1989, 75–127.
Return to text
Copyright Statement
Copyright © 2023 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
6346