Out of the Blue: Preparing Proportions in the Old Hall Manuscript*
Philippa Ovenden
KEYWORDS: fifteenth-century music, inductio, meter, mensuration, notation, Old Hall Manuscript, performance, proportion, rhythm
ABSTRACT: The Old Hall Manuscript (OH, c. 1413–1419) is the largest and most complete surviving witness to English music of the early fifteenth century. The extraordinary notational complexity encountered in OH has led to doubt being cast on the performability of some of the repertory copied within this manuscript (Bent 1969, 172). Adopting an approach that places historical theory (Dygon [1510s–1530s] 2006; Willelmus [14th century] 1966) in dialogue with modern theories of musical meter (Cohn 2001; Krebs 1999) reveals that complex proportional changes (anything more complex than a 4:3 or 3:4 proportion) in OH are always introduced incrementally in a process that I term “proportional preparation.” From the perspective of performers and scribes who read their own parts sequentially directly from the manuscript, some of the most “virtuosic” (Bent 2022a) notational devices of OH can be seen as serving to make hard proportions easier to sing. The presence of proportional preparations in OH invites further consideration not only of this phenomenon in contemporaneous repertory, but also of the relationships between mensuration, meter, rhythm, notation, and counterpoint. Additionally, it opens a path to further interrogate whether historical composers and theorists possessed an innate or intuitive awareness for the kinds of cognitive constraints that are placed upon musicians during the performance of repertory that is technically demanding from the perspective of rhythm.
DOI: 10.30535/mto.29.4.4
Copyright © 2023 Society for Music Theory
Introduction
[0.1] Dated to c. 1413–1419 by Margaret Bent (2022b, 17–18), London, British Library, MS 57950 (the Old Hall Manuscript, OH) is the largest and most complete surviving witness to English music of the early fifteenth century. A luxurious manuscript of polyphonic repertory, OH contains Mass movements, motets, and other compositions by the prominent English composers of this period. A relative paucity of source materials has led the English music of the Middle Ages to be less studied than contemporaneous continental European repertories. Bent’s dissertation (1969), the complete edition of OH (Hughes and Bent 1969–73),(1) and further publications (Bent 2022a; Bent and Wathey 2022; Hughes 1965; Hughes and Bent 1967), have defined the field of study of this manuscript.
[0.2] Written in full (black) mensural notation, OH boasts an extraordinary range of mensural and proportional changes, coloration techniques, and canons. Along with the repertory of manuscripts such as Chantilly, ModA, and Turin, the repertory of OH sits at the apex of notational complexity of this period. A Gloria by Leonel Power (d. 1445) (fols. 17v–18r) and an anonymous Credo (fols. 62v–63r) are the only compositions of this period known to have survived that contain blue coloration.(2)
[0.3] The difficulty of the notational parameters in OH is considerable, leading to doubt being cast on the performability of the most complex pieces copied in OH (Bent 1969, 172). The present article places historical theory and repertory in dialogue with modern theories of musical meter to argue that the apparent difficulty of the temporal dimensions of the compositions copied in OH diminishes when proportional changes are analyzed sequentially, that is, as performers and scribes experienced them.(3) Because many medieval compositions are copied in separate parts, a performer’s and scribe’s horizontal perspective stands in marked contrast to that of an editor who is able to view all voices simultaneously and compare parts vertically. Employing a method in which the notation of individual parts is analyzed sequentially can allow an analyst to gain a better understanding of how performers and scribes assessed the difficulty of moving from one proportion to another. When a proportional change is compared against a default “global” (Stoessel 2010, 332) mensural background, it can appear to be more complex than it is when considered from a local perspective.
[0.4] I term the process in which proportions are introduced incrementally “proportional preparation.” The proportional preparations that are discussed in this article pertain solely to the temporal dimensions of mensural repertory and are thus distinct from other types of preparations encountered in early fifteenth-century compositions, such as the preparations of dissonances in counterpoint. In the repertory copied in OH, proportions that are far distant from the mensuration at the beginning of a section are prepared through a series of proportions that are more closely related and thus serve to smooth out the distance between the first and the last proportions in a sequence. Proportions are also sometimes prepared by long notes or rests that allow the reader to think about how they must count differently once a new proportion is introduced. Flexible notations, in which the same duration can be represented multiple different ways, occasionally prepare a proportion by drawing a reader’s attention to certain temporal units. Stone (2003, 186–89) has already observed this phenomenon, arguing that the use of coloration in Se j’ay perdu, copied in Oxford, Bodleian Library, MS. Canonici misc. 213 (Ob213, fol. 114r) prepares a proportion before its arrival is marked by a proportion sign, which Stone (2003, 187) compares to metric modulation.(4)
[0.5] The observations made in the following analysis support the claim that analyzing music manuscripts from the perspective of performers and scribes can shed light on the performability of repertory that editors might tend to judge quickly as excessively complex. Although medieval singers would probably have performed from memory (Busse Berger 2005, 198–251), there is evidence that they would have viewed manuscript notations in other contexts, such as for memorization (Smilansky 2011, 133) and for practice in conjunction with repeated listening (Greig 2003, 198), a practice that Bent terms “aurally-tempered looking” (2013, 253). As Stoessel (2012, 459) notes, some medieval repertory would have been studied by performers in the presence of composers, who would have guided them through their parts. Leech-Wilkinson (2003, 11) argues that some complex notations of the later fourteenth and early fifteenth centuries may be interpreted as written-in articulation, supporting the notion that such sources were employed for practice or performance. Bent’s evidence (2022b, 6) that OH was compiled for Thomas, Duke of Clarence (1387–1421), a younger brother of Henry V (1386–1422), whose chaplains included Leonel Power (d. 1445) (a composer who features prominently in OH), confirms that OH was compiled in proximity to composers.
[0.6] The analytical perspective adopted here supports Upton’s (2013, 35) hypothesis that the copying of late-medieval repertory leaves a material trace of the dialogue that likely took place between performers, scribes, and composers. Some notational devices in OH that appear “virtuosic” (Bent 2022a) may thus be explained as an attempt by scribes or composers to convey information extending beyond the parameters of pitch and rhythm. That some notations could have helped singers to navigate proportional changes does not negate the idea that the elaborateness or virtuosity of notations in OH can exceed the practical necessity dictated by performance.(5) What it does indicate is that some of the notational characteristics of this manuscript that appear arbitrarily virtuosic from the perspective of a modern reader may have been useful to historical professionals in ways that are not self-evident to modern analysts.(6) The apparent sensitivity of fifteenth-century scribes to the demands placed on performers singing difficult repertory provokes broader questions pertaining to historical understanding of human psychology.
[0.7] The article is divided into four parts. I begin by introducing mensural notation to a general readership and establishing definitions for mensural and proportional change. In Part 2, I draw on the work of Krebs (1987, 1999) to define and compare metrical and proportional preparation. Part 3 places Dygon’s ([1510s–1530s] 2006) theory of inductiones (a specific type of proportional preparation) and Torkesey’s triangle (Willelmus [14th century] 1966) in dialogue with Cohn’s theory of hemiola and the ski-hill graph technique (2016; 2001; 1992) to theorize the difficulty of a proportional change. The final part of the article analyzes two extraordinarily complex pieces, a Gloria by Byttering (fl. c. 1410–20, OH, fols. 13v–14r) and a Gloria by Power (OH, fols. 17v–18r), from the perspective of proportional preparation.(7)
1. Defining Mensural and Proportional Change
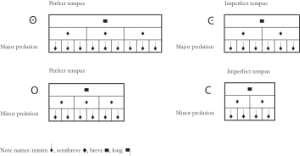
Example 1. The Four Prolations with minim equivalence
(click to enlarge)
[1.1] In contrast to modern notation, where notes are always duple by default, the notes of mensural notation may be duple or triple depending on the context. The components of mensuration are modus (the relationship of longs to breves), tempus (the relationship of breves to semibreves), and prolation (the relationship of semibreves to minims). Each component of mensuration can contain three of the next smaller note value (perfect modus, perfect tempus, major prolation) or it can contain two (imperfect modus, imperfect tempus, minor prolation).(8) The relationships between the four prolations are depicted in Example 1, which illustrates that the shared unit of measurement between the four basic mensurations is the minim. When the minim unit remains the same during a change of mensuration, “minim equivalence” is in effect. The equivalence between minims results in variable durations for longer notes while ensuring that there is a shared time unit between different mensurations.
Example 2. Imperfection coloration in an excerpt of the contratenor of an anonymous Credo
(click to enlarge)
[1.2] In OH, changes of mensuration are signaled by a combination of “intrinsic” signs (coloration, note patterns, dots) and “extrinsic” signs (mensuration and proportion signs) (Prosdocimus [1412] 1966, 130–32; Stoessel 2009, 182–83; Zazulia 2021, 126–29). The most common type of coloration is “imperfection coloration” (Bent 2022a, 77–78), which occurs when coloration renders a note imperfect that would be perfect in black ink. Coloration for imperfection also results in a change of mensuration. In OH, imperfection coloration is drawn in red ink. Imperfection coloration is shown in Example 2, which provides an excerpt of the contratenor of an anonymous Credo (fol. 59r) in which red ink renders semibreves imperfect. Marked by a mensuration sign, the mensuration of black notes is imperfect tempus with major prolation. The intervention of the red notes causes a change of mensuration to perfect tempus with minor prolation.
[1.3] In addition to changes of mensuration, OH features an extensive range of proportional changes. Proportional changes are signaled by a proportion sign or coloration and are distinguished from changes of mensuration because they do not retain minim equivalence (Bent 2022a, 79–80). The breakdown of minim equivalence that occurs during proportional changes naturally provokes the question of which time units should be compared. In later mensural theory, the prevailing time unit of a composition would be called the tactus or battuta. While the term tactus was first encountered only in the mid-fifteenth century (DeFord 2015, 54–55), evidence from Busse Berger (1993, 101) suggests that some early-mid fifteenth-century theorists would have placed the time unit that would later be called the tactus on the perfect semibreve. Notable among them are the Italian theorists Prosdocimus de Beldemandis (d. 1428) and Ugolino of Orvieto (d. 1452), and the English theorist John Hothby (d. 1487). Drawing on later fifteenth- and sixteenth-century repertory and theory, DeFord (2015, 51–52) theorizes a sixfold model of tactus that embraces physical and abstract temporal units. She argues for a “performance tactus” that corresponds to the physical motion of the counting body. Although the performance tactus can be associated with a number of temporal units, it is often aligned with the compositional tactus, “the time unit that serves as a standard reference for various aspects of rhythm,” including counterpoint, dissonance, and syncopation (51).(9) Typically, the compositional tactus is the semibreve or breve (82–83); DeFord also considers both the breve and the semibreve to be potential candidates for the performance tactus (110). Whether the breve or the semibreve is a more appropriate unit of comparison is contingent upon the context in which a proportional change takes place. For example, Busse Berger (1993, 55–56) observes that cut signs (e.g., or
), which can indicate a dupla (2:1) or tripla (3:1) proportion, imply breve equivalence.
[1.4] Stone (1996, 13; 1994, 178) argues that the term mensura or “measure” was used by medieval theorists to refer to the stable time units of compositions.(10) This would usually be the minim, but proportional changes compel the reader following the part to compare other time units, namely those of semibreves and breves. In some rhythmically and notationally complex compositions of the later fourteenth and early fifteenth centuries, a fixed time unit that prevails throughout a piece never manifests. This absence of a fixed time unit leads Stone to suggest that some compositions of the so-called ars subtilior were organized around abstract temporal units (1994, 290–91). Although the repertory of OH is in certain respects as complex as that discussed by Stone, Hughes (1965, 51) observed that the most complex pieces copied in OH lack the “haphazard” syncopations encountered in continental repertory due to proportionally related changes appearing “in isolated phrases.” In analyzing the repertory of OH, I compare notes of the same kind with one another. This practice was condoned by contemporaneous theorists (Busse Berger 1990, 109; Prosdocimus [1408] 1963, 218). Following Busse Berger’s and DeFord’s observations, I compare semibreves during proportional changes; that is, unless void or hollow coloration introducting a dupla or tripla proportion is employed, in which case I compare breves.
Example 3. Sesquialtera (3:2) proportion between black and red minims in the triplum of Damett’s Gloria
(click to enlarge)
[1.5] One of the most common types of proportional changes in OH occurs when red coloration is used to signal a sesquialtera (3:2) proportion (Bent 2022a, 79–80). Following medieval theory, I employ the Latin terms for proportions, I express proportions in terms of their time spans (rather than the number of notes that they contain), and I describe proportions in the order that they appear in a composition. A proportional preparation from the triplum of a Gloria by Damett (d. 1436/7) copied on OH, fol. 31v is provided in Example 3. The mensuration of black notes in the example is perfect tempus with minor prolation (marked by ), and red coloration introduces a sesquialtera (3:2) proportion at the level of the minim (there are two black minims for every three red minims). The mensuration for red coloration is therefore perfect tempus with major prolation but without equivalence between black and red minims; black and red semibreves are equal instead. Black minims are longer than red minims by one-third, as illustrated by the 3:2 ratio of the old proportion over the new.
2. Metrical and Proportional Preparation
Example 4. Krebs’s Example 2.3, illustrating pulse layers in “Innig” from Schumann’s Davidsbundlertänze Op. 6, No. 2, mm. 1–4 (1999, 24–25)
(click to enlarge)
[2.1] Harald Krebs (1987, 1999) has extensively theorized the process of how eighteenth- and nineteenth-century European composers smoothed out transitions between distinct temporal hierarchies. He terms this process “metrical preparation.” Krebs builds his definition of metrical preparation upon the concepts of meter, consonance, and dissonance. For Krebs, meter can be defined as “the union of all layers of motion (i.e., series of regularly recurring pulses) active within [a composition],” where layers of motion constitute “perceptible phenomena arising from the regular recurrence of musical events of various kinds.” Krebs’s procedure, which models the opening few measures of Robert Schumann’s Davidsbundlertänze Op. 6, No. 2 in terms of four metric layers, is illustrated in Example 4. The name of each layer describes how many eighth note pulses it encompasses. In this example, there is a “6-layer” (that is, a pulse that occurs every six eighth note pulses, i.e., every measure), a 3-layer formed by the dotted quarter note in the uppermost voice, and a 2-layer formed by the quarter note motion in the left hand. The pulse layer is the eighth note. The interactions of these layers are represented above the score.
[2.2] In Krebs’s terms, when interpretative layers do not line up, a “metrical dissonance” (1999, 29) occurs. Krebs (1999, 31–33) borrows the terminology of Peter Kaminsky (1989, 32) to discuss two types of metrical dissonances: “grouping dissonances” and “displacement dissonances.” There is a grouping dissonance in Example 4 (G3/2, 1 = ) and a displacement dissonance (D3+2, marked by the arrows).
[2.3] Whenever metrical dissonance appears following a period of consonance (full layer alignment), it introduces a sense of conflict against it. Depending on context, a composer may smooth out the transition between a metrical consonance and a metrical dissonance in a process termed “metrical preparation,” which Krebs defines as follows:
I refer to the more gradual manner of moving from consonance to dissonance by the term “preparation.” . . . Metrical preparation generally takes the form of the suggestion of an antimetrical layer by just one or two pulses — not enough pulses securely to establish a layer and a metrical dissonance, but certainly enough to prepare a later appearance of the dissonance. (1987, 87)
Example 5. Krebs’s Example 4.3, illustrating metrical preparation in Schumann’s “Préambule” from Carnaval, mm. 47–58 (1999, 88–89)
(click to enlarge)
Example 5 illustrates a metrical preparation discussed by Krebs (1999, 89) that occurs in “Préambule” from Carnaval by Schumann. From m. 54 onwards, the metrical hierarchy that is in alignment with the
[2.4] Krebs’s model of metrical preparation is highly pertinent to present discussion of fifteenth-century repertory, to the extent that it provides a framework for understanding that a new proportion may be hinted at by two or more units that are shared by the old and the new proportion. Nevertheless, readers should bear in mind that Krebs’s language of “consonance,” “dissonance,” and “preparation” would have been alien both to Schumann and his contemporaries, and the fifteenth-century composers discussed in this article. Moreover, the metrical structure of eighteenth- and nineteenth-century repertory differs from that of mensural compositions. The proportional preparations discussed in the remainder of this article are thus not metrical preparations in the modern sense of the term.
Example 6. A syncopation in the triplum of Bytterying’s Gloria
(click to enlarge)
[2.5] When a change of mensuration or proportion takes place, a misalignment arises between the time unit(s) of the new mensuration/proportion and the old. Medieval scribes and composers achieved simple misalignments through a process termed “syncopation” (syncopa, sincopa, sincopatio, etc.). In its basic medieval sense, a syncopation occurs when the parts of a perfection (or imperfection) are divided up by an intervening note that does not fit into a cycle of perfections or imperfections. A syncopation is completed when another note (or notes) intervenes that completes the broken perfection (DeFord 2015, 42–44). The disparate parts of the broken perfection are then regrouped, or “reduced” (reducuntur) (Misch 1972, 1–4). This process is illustrated in Example 6, which provides a textbook example of a syncopation in the triplum of Bytterying’s Gloria (fol. 13v). The mensuration of the example, which is left unsigned, is perfect tempus with minor prolation; perfect breve units are marked by the boxes. The beginning of the third breve unit of the example (marked by the first dashed box) begins with two minims but is left incomplete as a result of an intervening dotted breve, which divides or syncopates the breve unit. Following two more minims of the divided breve unit, a dotted semibreve and three minims fill out another breve unit; this further divides the syncopated breve unit, which is completed only at the end of the phrase by the arrival of two further minims (marked by the third dotted box).
[2.6] Medieval theorists also developed and extended the concept of syncopation to apply to the misalignments presented by mensural and proportional changes. Syncopation and proportional changes are conceptually related and in principle may be seen to overlap, because the disruption of time units that they initiate may be interpreted through the lenses of both division and regrouping. Some medieval theorists drew parallels between proportional change and syncopation (Rosa-Barezzani 2001). For instance, the anonymous author of the Tractatus figurarum (c. 1375) describes a practice termed traynour, a “more energetic manner” (fortior modus) than syncopation, in which special note shapes and/or coloration introduce changes of mensuration, resulting in breve rather than minim equivalence (Anonymous 1989, 100–101) (i.e., changes of proportion). John of Tewkesbury, writing in the Quatuor principalia musice (c. 1351), directly conflates syncopation and traynour (which he terms treyns); nevertheless, he condemns the practice.(11)
[2.7] Syncopations were viewed differently in medieval theory than their description in metric theory. Even though in modern metric theory syncopation tends to be regarded as a displacement of a time unit (as is seen in Krebs’s “displacement” dissonance) rather than the division and regrouping of a time unit, the technical resemblances between Krebs’s displacement and grouping dissonances and the medieval categories of syncopation and proportional change are unmistakable.(12)
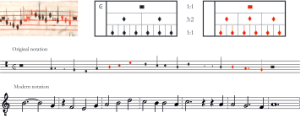
Example 7. Comparison of original and alternative notation in the cantus of Je ne puis avoir Plaisir (Chantilly, fol. 24r)
(click to enlarge)
[2.8] In the same way that metrical dissonances can be prepared through an intermediary step, proportional changes are, at times, prepared in mensural repertory by introducing a time unit that acts as an intermediary between an old and a new proportion. An example of a proportional preparation is found in the cantus of Je ne puis avoir plaisir, an anonymous virelai copied in Chantilly, fol. 24r (Example 7). Between caudated semibreves of
![]() and semibreves of
and semibreves of ![]() , there is a sesquialtera (3:2) proportional relationship. For every two caudated semibreves there are three imperfect semibreves. There is also a sesquialtera proportional relationship between dragmas
, there is a sesquialtera (3:2) proportional relationship. For every two caudated semibreves there are three imperfect semibreves. There is also a sesquialtera proportional relationship between dragmas of
![]() and minims of
and minims of ![]() . Two red semibreves immediately preceding the
. Two red semibreves immediately preceding the ![]() sign provide an intermediary step between these two proportions. Red semibreves are equivalent in duration to caudated semibreves. Note that this passage could have been notated differently by replacing the red semibreves with caudated semibreves (Example 7, alternative notation). The significance of the red semibreves becomes clear when they are thought of as divided into three minims, unlike the caudated semibreves, which are divided duply into dragmas (Stoessel 2002, 38). When the reader jumps directly between
sign provide an intermediary step between these two proportions. Red semibreves are equivalent in duration to caudated semibreves. Note that this passage could have been notated differently by replacing the red semibreves with caudated semibreves (Example 7, alternative notation). The significance of the red semibreves becomes clear when they are thought of as divided into three minims, unlike the caudated semibreves, which are divided duply into dragmas (Stoessel 2002, 38). When the reader jumps directly between ![]() and
and ![]() , they must traverse two simultaneous sesquialtera proportions. The red semibreves allow this process to take place in two steps: the reader of the part first traverses one sesquialtera proportion between dragmas and minims, and then a sesquialtera proportion between red semibreves and black semibreves. The red semibreves thus prepare perfect tempus with minor prolation by conceptually introducing the minim unit in advance of the
, they must traverse two simultaneous sesquialtera proportions. The red semibreves allow this process to take place in two steps: the reader of the part first traverses one sesquialtera proportion between dragmas and minims, and then a sesquialtera proportion between red semibreves and black semibreves. The red semibreves thus prepare perfect tempus with minor prolation by conceptually introducing the minim unit in advance of the ![]() mensuration sign.(13)
mensuration sign.(13)
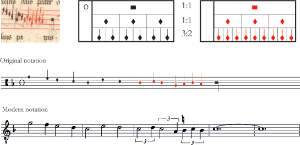
Example 8. Excerpt of the contratenor of Power’s Gloria showing the use of red ink to prepare a new mensuration
(click to enlarge)
[2.9] As illustrated in Example 8, which provides an excerpt of the contratenor of a Gloria by Power (fol. 20r), coloration sometimes prepares changes of mensuration. A sign marks imperfect tempus with major prolation at the opening of the passage before a
marks a change of mensuration to perfect tempus with minor prolation. (Minims and breves of
and
are equal.) Three red semibreves directly preceding
initiate perfect tempus with minor prolation before this mensuration is established by the mensuration sign. As before, this passage could have been notated differently by moving the mensuration sign before the three red semibreves and writing these notes in black ink (Example 8, alternative notation). The breve and minim that precede the three red semibreves—an example of remote imperfection in which the imperfect breve is reduced in length to five minims—provide a further opportunity for the singer to imagine the new imperfect semibreve unit.
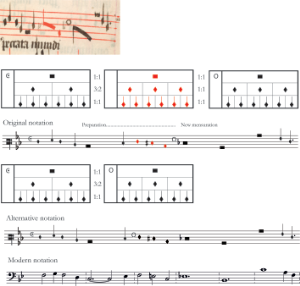
Example 9. Excerpt of a Gloria by Damett with transcriptions into score with modern and original notation
(click to enlarge and see the rest)
[2.10] In OH, changes of proportion are also, at times, prepared using coloration. Example 9, an excerpt of a Credo by Damett (OH, fols. 60v–61r), provides an example of a proportional preparation achieved through coloration. At the opening of the example, the mensuration of the black notes of the triplum is imperfect tempus with minor prolation, signaled by . Black breves of
and red void (empty) breves are in a sesquialtera (3:2) proportional relationship. Between black semibreves of
and the red semibreves of
, there is a subsesquitertia (3:4) proportional relationship. Readers may have already noted that the significance of the
sign is unclear since red coloration would be sufficient to indicate this proportion. Typically,
would be used to signal a sesquialtera (3:2) proportion (Stoessel 2010, 335), although it was also used for other proportions, such as 2:1, or to force a change of mensuration to imperfect tempus with major prolation. This logic has led Bent (2022b, 17) to suggest that this sign is “anomalous.” Damett’s Credo is also transmitted in Oxford, University College Library, MS. 192 (Ouc192), fol. 27a, part of a royal choirbook that Bent has argued was copied from OH. The copyist of this manuscript initially transmitted the sign but afterwards erased it, which indicates that the scribe of this source agreed that the sign was unnecessary.
[2.11] The red void coloration in the triplum is prepared by the rhythm of the contratenor. In the first part of this excerpt, the mensuration of black notes of the contratenor is imperfect tempus with minor prolation, but the black notes of the contratenor are twice as long as those of the triplum. A sesquialtera (3:2) proportion is introduced in the contratenor between black and red semibreves. The red coloration in the contratenor shares units with the red void coloration of the triplum and thus prepares its arrival: two red minims (or one red semibreve) of the contratenor equal one red void breve of the triplum. The red coloration in the contratenor also primes the singer of the triplum for the subsequent transition to the red coloration following the sign. Breves, semibreves, and minims are equal in the red coloration of the contratenor and the red coloration of
in the triplum. A singer of the triplum, hearing the gesture copied in red coloration in the contratenor, is audibly prepared to transition into the hierarchies represented by red void and red coloration.(14)
[2.12] A range of compositional parameters can help prepare mensural and proportional changes, even in the absence of a sounded, shared time unit. For instance, many proportions arrive after a long note or rest that introduces a pause, which affords singers the opportunity to prepare themselves for a new proportion. Contrapuntal parameters are also closely aligned with the temporal dimensions of fifteenth- and sixteenth-century compositions, which is to say, cadences provide unmistakable markers of the boundaries of temporal units and thus may be seen as an aural guide for notation (Bent 2013, 253; DeFord 2015, 101). While an examination of the relationships between counterpoint and notation in OH lies beyond the scope of this article, the approach adopted here invites further consideration of the relationships between the temporal and harmonic dimensions of late-medieval repertory more broadly.
3. Gauging the Difficulty of a Proportional Change
[3.1] Most of the proportional changes of OH are in sesquialtera (3:2) relationship. Complex proportions such as 9:2, 9:4, and 9:8 are always prepared by being introduced incrementally through a series of related proportions. Preparations such as these are conceptually similar to the preparations seen in Examples 8 and 9 in that they hint at proportional changes by placing shared units before the arrival of new proportions or by introducing new proportions with units that are closer to both proportions (even if units are not shared between them). Note that the practice of approaching a complex proportion incrementally, termed inductio (“induction” or “leading-in”), was discussed by three sixteenth-century English theorists, Richard Pace, Thomas Morley, and John Dygon. Pace briefly mentions the practice in his De fructu qui ex doctrina percipitur (1517), stating that inductiones are employed “maxima ingenii subtilitate” (with great subtlety) in British repertory.(15) Morley, on the other hand, is derisive of inductiones in his Plaine and Easie Introduction to Practicall Musicke ([1597] 1963, 136).(16) The most complete account occurs in Dygon’s Proportiones practicabiles secundum Gaffurium (1510s–1530s).(17)
[3.2] Proportiones practicabiles secundum Gaffurium elaborates Francinus Gaffurius’s account of the theoretical relationships among proportions. The sections that concern inductiones number among Dygon’s personal interpolations, which concentrate on issues that are encountered by performers. They are absent from Gaffurius’s original, which addresses theoretical questions. In Dygon’s words, inductiones occur in the following context:
Huic vero proportioni sextuple due, ut vides, inductiones sunt. prima sesquialtera. secunda tripla. quibus facile et vere hanc proportionem sextuplam mensurare queas.
This proportion sextupla has two inductiones, as you see. The first is sesquialtera, and the second is tripla. With these inductiones you can measure this proportion sextupla easily and truly. (Dygon [1510s–1530s] 2006, 76–77)
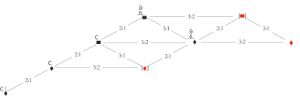
Example 10. Example of inductiones in Dygon’s Proportiones practicabiles secundum Gaffurium
(click to enlarge)
Dygon states that there are two different inductiones or ways of approaching a sextupla (6:1) proportion (Example 10). To sing six notes in the time of one, one may first sing a sesquialtera (3:2) proportion followed by a quadrupla (4:1) proportion, or a tripla (3:1) proportion followed by a dupla (2:1) proportion. This practice rests upon the assumption that singing 3:2, 2:1, 3:1 or 4:1 proportions before a 6:1 proportion is easier than singing six notes in the time of one directly, implying that there is a hierarchy of difficulty among these proportions.
Example 11. Dygon prepares a quadrupla sesquialtera (9:2) proportion using a sesquialtera (3:2) proportion and a tripla (3:1) proportion
(click to enlarge and see the rest)
[3.3] Dygon’s remaining examples are more complex. Dygon prepares several quadrupla sesquialtera (9:2) proportions via 3:2, 3:1, and 2:1 proportions. One of these is transcribed in Example 11 with a visual representation of the relationships between notes. The diagram shows that the sesquialtera (3:2) proportion simplifies the transition to the quadrupla sesquialtera (9:2) proportion as follows (when comparing semibreves): 9:2 = 3:2 + 3:1. In fact, the quadrupla sesquialtera proportion is reached even more gradually because Dygon first introduces a sesquialtera proportion between minims (m. 3 of Example 11). This maneuver allows for equivalence to be briefly maintained between void semibreves and red semibreves before a further sesquialtera proportion is introduced between red and void semibreves (m. 4). In essence, it provides a stepping stone to the quadrupla sesquialtera (9:2) proportion that arrives in m. 5. There is a tripla proportional relationship between the red semibreves in m. 4 and those in m. 5. In sum, this example supports the notion that Dygon regarded the proportions 3:2 and 3:1 as appropriate intermediary steps to a 9:2 proportion; it follows that he thought that these proportions were easier to sing.
[3.4] It should be remembered that Dygon completed his work over a century after the compilation of OH; thus, there is no evidence that the composers of OH would have thought about proportional preparation in terms similar to those of Dygon, nor would they have employed the term inductiones. It is possible, for instance, that composers simply found that introducing proportions incrementally sounded pleasing to the ear without giving heed to the difficulties faced by performers. Dygon, a theorist writing after the invention of tactus, may have been more preoccupied with promoting a stable temporal unit throughout a composition, even during the most rhythmically complex passages, thus compelling him to systematize a process that could have emerged unconsciously in practice. Moreover, although Dygon’s work is written in response to performance practice, many of his examples indicate that he was keenly interested in the mathematics of proportion, in and of itself. Dygon discusses a range of extraordinarily complex proportions that would not be encountered in practice. He forms these types of proportions between two voices simultaneously (Dygon [1510s–1530s] 2006, 102–3). Keeping these points in mind, Dygon’s comments nevertheless provide a useful framework for understanding the proportional changes in the repertory encountered in OH. Regardless of the conscious motivation of composers, all the complex proportions (recall that these exceed the complexity of a 4:3 or 3:4 proportion) encountered in OH are arrived at through a series of related proportions in a manner similar to the preparations that Dygon would term inductiones.
Example 12. Hemiola introduced via color of imperfection in the contratenor of Power’s Gloria
(click to enlarge)
[3.5] Continuing to the issue of why some proportions are more difficult to sing than others, it is helpful to turn to modern scholarship that discusses musical meter. Cohn (2001) has theorized a typology that distinguishes the degree to which pulse hierarchies or meters are “dissonant” with one another. The first category of dissonance Cohn describes is the well-known hemiola, which occurs when “a span of time is trisected in place of an anticipated bisection” (2001, 295). In the excerpt shown in Example 12, red ink introduces a change of mensuration that initiates what Cohn would term a hemiola. The mensuration at the beginning of the passage is imperfect tempus with major prolation, marked by . Coloration of imperfection results in a change of mensuration to perfect tempus with minor prolation.
Example 13. Visual representation of bisection of a breve unit by black, perfect semibreve pulse against trisection of the breve unit by red, imperfect semibreve pulse
(click to enlarge)
[3.6] Within Cohn’s framework, Example 12 incorporates a hemiola between the perfect semibreves of and the red, imperfect semibreves. The red semibreve pulses divide the span of the breve (six minims) into three parts, and in doing so trisect the breve span in place of the anticipated bisection by the perfect semibreve pulse of
. This process is illustrated in Example 13.
Example 14. Example 13 translated onto the ski-hill graph
(click to enlarge)
[3.7] The notes of this example are translated in Example 14 onto Cohn’s “ski-hill” graph, a “two-dimensional matrix” that visualizes the relationships between pulse hierarchies in terms of duple and triple units (2001, 301). To the left of Example 14, the breve pulse is bisected to form the perfect semibreve pulse-unit. The perfect semibreve pulse is trisected, resulting in the minim pulse-unit. To the right, the breve pulse-unit is trisected to form the red, imperfect semibreve pulse-unit. The red imperfect semibreve is bisected, resulting in the minim pulse-unit. The diagram also visualizes the 3:2 relationship between the black, perfect semibreve pulse and the red, imperfect semibreve pulse.
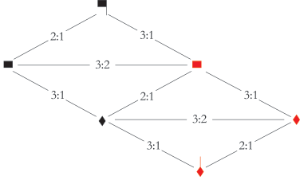
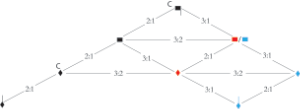
[3.8] The second category of dissonance that Cohn describes, termed “double hemiola,” (1992, 13) occurs when there are “3:2 conflicts at two adjacent levels of the metric hierarchy” (2001, 295). An example of a double hemiola from a Gloria by Power (fols. 17v–18r)—also to be discussed in a later section in more detail—is provided in Example 15. The modus of black longs is imperfect and the tempus of black breves is perfect: black and red breves and semibreves are in sesquialtera (3:2) proportion with one another.
Example 15. Excerpt of triplum of a Gloria by Power with transcription into modern notation (click to enlarge) | Example 16. Relationships between pulse hierarchies in Example 15 translated onto the ski-hill graph, excluding black minim pulse (click to enlarge) |
[3.9] The relationships between the notes of Example 15 are mapped onto the ski-hill graph in Example 16. Two 3:2 proportions occur concurrently between the pulses represented by the notes of the two diamonds. The long pulse is bisected by the black breve pulse (top left of the ski-hill graph) and is trisected by the red breve pulse (middle right of the graph). The red breve pulse is bisected by the black semibreve pulse (middle left of the graph) and is trisected by the red semibreve pulse (bottom right of the graph).
Example 17. Relationships between pulse hierarchies in Example 15 translated onto the ski-hill graph, including black minims
(click to enlarge)
[3.10] The proportional relationships of the excerpt in Example 16 are simplified in that black minims are excluded from this diagram. However, when the black minim unit is taken into consideration, a third 3:2 proportional relationship emerges between black and red minims, as shown in Example 17. For every two black minims there are three red minims, resulting in three layers of 3:2 proportions. Cohn terms a hemiola in which there are three or more 3:2 layers a “complex hemiola” (2001, 295). The third 3:2 proportion between the pulses associated with black and red minims can be seen in the bottom left of the diagram.
[3.11] Cohn’s model, which renders proportions visually, can aid greatly in understanding the complex proportional changes in OH. The distances between nodes roughly measure the effort or “psychological distance” required to jump to a proportion (Cohn 2016, 243). A proportion that is one “step” away from another, such as a 2:1 or 3:1 proportion, or a 3:2 proportion, which results from the combination of a 2:1 proportion and a 3:1 proportion, is easier to sing than any proportion that is farther away, such as a 4:3, 9:4, or 9:8 proportion, since the more complex proportions will necessarily entail navigating (implicitly) two or more adjacent 3:2 layers.
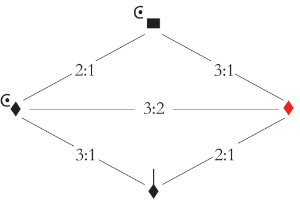
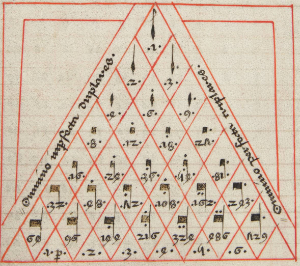
Example 18. Torkesey’s triangle as transmitted by Willelmus in Chicago, fol. 9r
(click to enlarge)
[3.12] Remarkably, Cohn’s model bears similarity to the popular late-medieval theoretical model of the English writer Johannes Torkesey (d. 1340?), who visualized the hierarchical relationships between notes in terms of duple and triple units (Cohn 2016, 240–43). An image of Torkesey’s triangle as transmitted by the English theorist Willelmus (fl. 14th century) is provided in Example 18.(18) The diagram is oriented differently from Cohn’s, in that the shortest notes are situated at the top of Torkesey’s triangle. However, both schematic approaches express relationships between temporal units in terms of 3:2 relationships, pointing towards a shared conceptual framework.
[3.13] The following analyses combine the elements of Torkesey’s triangle and Cohn’s ski-hill graph to visually represent inductiones in the repertory of OH. Of course, because the ski-hill graph was devised for modern repertory, it must be adapted to the music of the fifteenth century. For instance, Cohn’s ski-hill graphs represent the proportional relationships between pulses, or dimensionless points, in terms of 2:1, 3:1, and 3:2 relationships. Boone (2000, 32) and Maw (2004, 62n39) have observed that unlike the repertory of the eighteenth and nineteenth centuries for which Cohn theorized the ski-hill graph, the repertory of the fifteenth century was conceived not in terms of dimensionless points or pulses, but in terms of time spans. The notes that are depicted on the graphs below thus do not represent dimensionless points, but the spans of time represented by notes. In this respect, the diagrams below follow the model presented by Torkesey.(19)
4. Examples from the Old Hall Manuscript
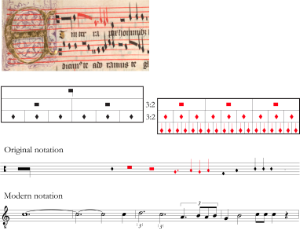
[4.1] Every proportion in OH that is more difficult than a 4:3/3:4 proportion—in Cohn’s terms a proportion that traverses more than two adjacent 3:2 layers (i.e., a “complex hemiola”)—is prepared with an inductio unless it appears after a cadence and/or held notes or rests, or in conjunction with a notational preparation that provides the singer with a gap to adjust to the new proportion. The analyses below aim to bridge medieval musicological scholarship and modern metric literature while advancing a model for analyzing proportional changes. First, reflecting the language of late-medieval theory, I compare proportions in terms of the ratios that exist between the same types of notes. For instance, a dupla sesquiquarta (9:4) proportion at the level of the semibreve may result from two adjacent sesquialtera proportions (3:2+3:2), also at the level of the semibreve. Second, following Cohn and Torkesey, I consider the degree of distance between proportions.
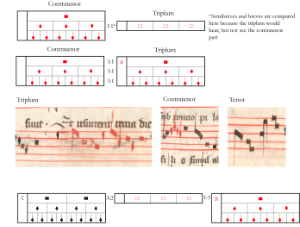
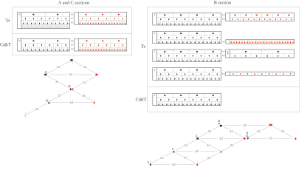
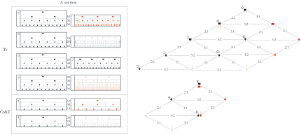
Example 19. Byttering’s Gloria, manuscript images
(click to enlarge)
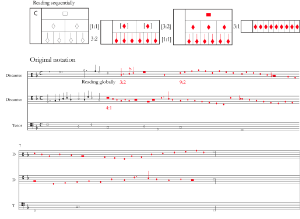
Example 20. Global relationships between proportions in Byttering’s Gloria, fols. 13v–14r
(click to enlarge)
Byttering’s Gloria, fols. 13v–14r
[4.2] In Byttering’s Gloria (fols. 13v–14r, see Example 19 for manuscript images), a sesquioctava (9:8) proportion is prepared through a series of simpler proportions. Like many items copied in OH, this composition is divided into three sections. The mensuration at the opening of the first and third sections is perfect tempus with minor prolation: the mensuration at the beginning of the third section is marked by ). The mensuration at the opening of the second section is imperfect tempus with minor prolation (marked by
). Void minims in the triplum in the A section equal half a minim. Brief passages of red sesquialtera coloration at the level of the minim occur in all voices in all three sections; note that red coloration of imperfection is also used at the level of the breve. In the B section, a series of proportions are introduced in the triplum voice. A
![]() sign marks a subsesquitertia (3:4) proportion between semibreves. Four semibreves of
sign marks a subsesquitertia (3:4) proportion between semibreves. Four semibreves of equal three of
![]() , and then red coloration introduces a new proportion. Understood globally, there is a sesquioctava (9:8) proportion between semibreves of
, and then red coloration introduces a new proportion. Understood globally, there is a sesquioctava (9:8) proportion between semibreves of and red semibreves. For every eight semibreves of
, there are nine red semibreves. In Aosta, Biblioteca del Seminario Maggiore, Cod. 15 (Ao, fol. 243v) this proportion is specified with a 9 proportion sign. The relationships between all proportions in this composition are visualized in Example 20 from a global perspective—that is, in relation to notes copied in black ink—and are mapped onto the ski-hill graph.
Example 21. Transcription into score of an excerpt of Byttering’s Gloria in original and modern notation
(click to enlarge)
[4.3] The passage of complex proportions in the B section is introduced incrementally in a manner that parallels Dygon’s inductiones. A transcription of this passage in original notation and modern notation is provided in Example 21, with grids that visualize the proportional relationships between notes when they are read sequentially. The organization of the proportions allows direct computation of the difficult sesquioctava (9:8) proportion between black semibreves of and red semibreves to be avoided; it does this by allowing the reader to proceed first through a subsesquitertia (3:4) proportion between black semibreves of
and
![]() , followed by a sesquitertia (3:2) proportion between black semibreves of
, followed by a sesquitertia (3:2) proportion between black semibreves of ![]() and red semibreves. The semibreves of
and red semibreves. The semibreves of ![]() may thus be said to prepare the sesquioctava proportion as follows: 9:8 (
may thus be said to prepare the sesquioctava proportion as follows: 9:8 ( → red) = 3:4 (
→
![]() ) + 3:2 (
) + 3:2 (![]() → red).
→ red).
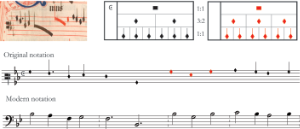
Example 22. Spans of time represented by the notation of the triplum of Example 21 represented on the ski-hill graph
(click to enlarge)
[4.4] A detail of the ski-hill graph in Example 20 is highlighted in Example 22. This graphic shows that it is easier to navigate the sesquioctava (9:8) proportion of to red via the semibreves of
![]() . This is because the hierarchy of
. This is because the hierarchy of ![]() (in the middle of the ski-hill graph) sits conceptually between the hierarchy of
(in the middle of the ski-hill graph) sits conceptually between the hierarchy of (left of the graph) and the hierarchy of the red notes (right of the graph). There are two adjacent 3:2 layers between the hierarchies of
(breves and semibreves) and
![]() . There are two between
. There are two between ![]() (breves and semibreves) and red coloration as well, but there are four between
(breves and semibreves) and red coloration as well, but there are four between and red coloration. Thus
![]() introduces an intermediary step between
introduces an intermediary step between and red.
[4.5] Although the subsesquitertia proportion between and
![]() is easier to sing than the sesquioctava proportion of the red coloration, it still represents a challenge because it traverses two adjacent 3:2 layers. The difficulty of the
is easier to sing than the sesquioctava proportion of the red coloration, it still represents a challenge because it traverses two adjacent 3:2 layers. The difficulty of the ![]() proportion is mitigated by compositional parameters. Namely, the proportional change follows a cadence (marked by the first arrow in Example 21) and is accompanied by held notes in the lower voices, which allow the ensemble to regroup. The return to
proportion is mitigated by compositional parameters. Namely, the proportional change follows a cadence (marked by the first arrow in Example 21) and is accompanied by held notes in the lower voices, which allow the ensemble to regroup. The return to after the conclusion of the red coloration is also attenuated by a cadence (see other arrow), and a long rest during which the singer of the triplum can think ahead to the return to
.
Power’s Gloria, fols. 17v–18r
Example 23. Power’s Gloria manuscript images; Courtesy of the British Library Board, Add MS 57950, fols. 17v–18r
(click to enlarge)
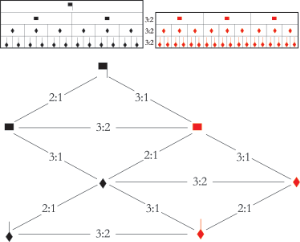
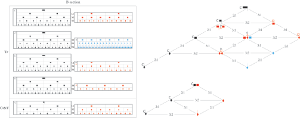
[4.6] Power’s Gloria (fols. 17v and 18r, see Example 23 for manuscript images) is one of the most notationally complex compositions in OH and features proportional coloration in all three voices. Representations of the proportional changes in this composition are analyzed from a global perspective in Example 24, with Example 25 translating the notation of the A and B sections onto the ski-hill graph. Similar to Byttering’s Gloria discussed in the previous example, the mensuration at the opening of the A and C sections of Power’s Gloria is perfect tempus with minor prolation. The mensuration at the opening of the B section is imperfect tempus with minor prolation.
Example 24. Visual representation of the notation of the A section of Power’s Gloria, fols. 17v–18r (click to enlarge) | Example 25. Visual representation of the notation of the B section of Power’s Gloria, fols. 17v–18r (click to enlarge) |
Example 26. Transcription in score of an excerpt of Power’s Gloria in original and modern notation
(click to enlarge)
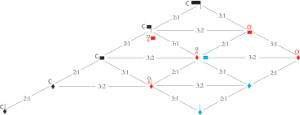
[4.7] In the triplum, three complex proportional changes are approached via inductiones. An excerpt of the B section that contains an inductio is transcribed into score and modern notation in Example 26. The mensuration of the first part of the passage is imperfect tempus with minor prolation, indicated by . Red coloration introduces a sesquialtera (3:2) proportion between black semibreves of
and red semibreves. Between black semibreves of
and blue semibreves of
there is a dupla sesquiquarta (9:4) relationship. When this passage is read sequentially, a direct transition to the dupla sesquiquarta proportion is avoided because there is a simpler, sesquialtera (3:2) proportional relationship between red and blue semibreves. The markings above the transcription illustrates that the red coloration prepares the blue coloration. Comparing semibreves, the proportional relationships of this passage are simplified as follows: 9:4 (
black →
blue) = 3:2 (
black → red) + 3:2 (red →
blue).
Example 27. Relative durations of spans of time represented by the notation of the triplum of Example 26 mapped onto the ski-hill graph
(click to enlarge)
[4.8] Mapping the notes of this passage onto the ski-hill graph (Example 27) is symptomatic of the red coloration (middle right of the ski-hill graph) being situated conceptually between black (left of the graph) and blue (bottom right of the graph), thus preparing blue. While there are three adjacent 3:2 proportions between the black and blue hierarchies, there are two between black and red, and there is one between red and blue. The red semibreve unit provides the best pivot between these hierarchies because it links the diamonds of black and blue.
[4.9] The proportional changes in this passage are further supported by cadential motion (see arrows in Example 26). Coloration visually delineates the cadences and phrase endings for a singer of the triplum, even if they focus only on their own part and fail to look at the cadential motion in the tenor and the contratenor. After the first cadence, the transition to blue is further eased by the held breves in the tenor and contratenor, which give a singer of the triplum freedom to navigate the transition between red and blue without having to fit in with the lower voices. At the second cadence, the alignment of the voices is reinforced through synchrony between coloration and counterpoint. Towards the end of this phrase, a sesquialtera proportion emerges between black and red notes in the tenor and contratenor; one red semibreve in the contratenor and tenor equals a blue breve in the triplum. Yet before the arrival of the red coloration in the contratenor and tenor, the ensemble transitions through a passage of extraordinarily intricate syncopations (marked in Example 27). The resulting alignment between the blue breves of the triplum and the red semibreves of the lower voices contrasts sharply with the disorder of the previous few breves, so much so that the auditory experience for an upper voice singer being jolted back into realignment with the remainder of the ensemble is almost comical.
Example 28. Transcription into score of an excerpt of Power’s Gloria in original and modern notation
(click to enlarge)
[4.10] Every complex proportion in this Gloria is introduced incrementally in a similar manner to the previous example. A further excerpt from the B section given in Example 28 illustrates this point. Although this thorny passage introduces several complex proportions, the section in its entirety is bookended by cadences (see arrows), which provide a rest for the singer of the triplum to gather themselves before and after they tackle the difficult proportional embellishments. The first proportion in this sequence is signaled by ![]() and red coloration. As Bent (2022a, 92) notes, the same sign is encountered in other compositions in OH, including two Credos by Power (68v–69r and fols. 70v–71r), the first of which has a black instead of a red 6. The difference in color does not seem to alter the significance of these signs. In the first Credo, a rubric is inserted that explains the significance of this sign: “in proporcione subsexquetercia capiendo talem figuram 6
and red coloration. As Bent (2022a, 92) notes, the same sign is encountered in other compositions in OH, including two Credos by Power (68v–69r and fols. 70v–71r), the first of which has a black instead of a red 6. The difference in color does not seem to alter the significance of these signs. In the first Credo, a rubric is inserted that explains the significance of this sign: “in proporcione subsexquetercia capiendo talem figuram 6 ” (this figure must be taken in subsesquitertia proportion) (OH, fol. 69r; Bent 2022a, 92). The explanation in this canon is also valid for Power’s Gloria, since there is a subsesquitertia (3:4) proportional relationship between black minims of
and red minims of
![]() . Bent states that the significance of the 6 is “not readily explained” (2022a, 88 n43), unless its purpose is indicating that there are six red full semibreves of
. Bent states that the significance of the 6 is “not readily explained” (2022a, 88 n43), unless its purpose is indicating that there are six red full semibreves of ![]() for every black long of
for every black long of . Indeed, 6 is usually employed to signal a sesquialtera proportion, as in Johannes Cesaris’s Se par plour, copied in Ob213, fol. 110r.
[4.11] Following ![]() , there is a brief passage of blue coloration that was originally copied in red void coloration. Black and blue semibreves are in dupla sesquiquarta (9:4) proportion. Bent (2022a, 92) rationalizes the original use of red void coloration in relation to a rubric in Power’s Credo (fols. 68v–69r), in which a canon instructs the reader to read red void notes in dupla sesquiquarta proportion. It is also possible that the scribe initially sought to introduce a tripla (3:1) proportion between
, there is a brief passage of blue coloration that was originally copied in red void coloration. Black and blue semibreves are in dupla sesquiquarta (9:4) proportion. Bent (2022a, 92) rationalizes the original use of red void coloration in relation to a rubric in Power’s Credo (fols. 68v–69r), in which a canon instructs the reader to read red void notes in dupla sesquiquarta proportion. It is also possible that the scribe initially sought to introduce a tripla (3:1) proportion between ![]() and red void (now blue) coloration, since for each breve, semibreve, or minim of
and red void (now blue) coloration, since for each breve, semibreve, or minim of ![]() there are three blue breves, semibreves, or minims. Reverting to blue promotes consistency between the use of coloration here and in the passage excerpted in Example 26, where black semibreves of
there are three blue breves, semibreves, or minims. Reverting to blue promotes consistency between the use of coloration here and in the passage excerpted in Example 26, where black semibreves of are also in dupla sesquiquarta proportion with blue semibreves. If this hypothesis is correct, this would indicate that the original copyist was thinking in terms of adjacent proportions, but that the scribe who reviewed the coloration was comparing proportions globally against the default of black full notation.
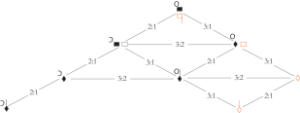
[4.12] Finally, Power introduces a new proportion with ![]() and red ink. Between black semibreves of
and red ink. Between black semibreves of and red semibreves of
![]() there is a sesquioctava (9:8) relationship. Power approaches the complex dupla sesquiquarta and sesquioctava proportions incrementally. A visual representation of notes when they are compared sequentially is provided in Example 28. Following the subsesquitertia (3:4) proportion between black semibreves of
there is a sesquioctava (9:8) relationship. Power approaches the complex dupla sesquiquarta and sesquioctava proportions incrementally. A visual representation of notes when they are compared sequentially is provided in Example 28. Following the subsesquitertia (3:4) proportion between black semibreves of and red semibreves of
![]() , there is a tripla (3:1) proportion between red semibreves of
, there is a tripla (3:1) proportion between red semibreves of ![]() and blue semibreves. Between blue semibreves and red semibreves of
and blue semibreves. Between blue semibreves and red semibreves of ![]() there is a subdupla (1:2) proportional relationship. Thus, the singer transitions through a series of easier proportions to traverse the two difficult proportional changes, as follows: 9:4 (
there is a subdupla (1:2) proportional relationship. Thus, the singer transitions through a series of easier proportions to traverse the two difficult proportional changes, as follows: 9:4 ( → blue) = 3:4 (
→
![]() red) + 3:1 (
red) + 3:1 (![]() red → blue); 9:8 (
red → blue); 9:8 ( →
![]() red) = 3:4 (
red) = 3:4 ( →
![]() red) + 3:1 (
red) + 3:1 (![]() red → blue) + 1:2 (blue →
red → blue) + 1:2 (blue → ![]() red).
red).
Example 29. Relative durations of spans of time represented by the notation of the triplum of Example 28 mapped onto the ski-hill graph
(click to enlarge)
[4.13] Both the dupla sesquiquarta and sesquioctava proportions of this passage would present a significant challenge to most singers. The ski-hill graph in Example 29 shows that one must traverse three 3:2 layers to reach the hierarchy represented by the blue notes (bottom center right of the graph) from that of the black notes of (left of the graph); one must traverse four 3:2 layers to travel from the hierarchy of the black notes of
to red notes of
![]() (right of the graph). Yet again, the order in which proportions arrive allows the most difficult proportions to be reached through a series of intermediary steps. Between the hierarchy of notes of
(right of the graph). Yet again, the order in which proportions arrive allows the most difficult proportions to be reached through a series of intermediary steps. Between the hierarchy of notes of and those of
![]() there are two adjacent 3:2 layers; between
there are two adjacent 3:2 layers; between ![]() and blue notes there are two, and between blue notes and those of
and blue notes there are two, and between blue notes and those of ![]() there are also two.
there are also two.
Example 30. Transcription into score of an excerpt of Power’s Gloria in original and modern notation
(click to enlarge)
Example 31. Relative durations of spans of time represented by the notation of the triplum of Example 30 mapped onto the ski-hill graph
(click to enlarge)
[4.14] In a final example from Power’s Gloria, a notational preparation is combined with inductiones to ease a transition to a new proportion. The passage in which this occurs is excerpted from the A section: it is transcribed in Example 30 in both modern and original note shapes. At the opening of the passage, the mensuration of black notes is perfect tempus with minor prolation. Two void breves introduce a dupla (2:1) proportion: for every black breve there are two void breves. In keeping with convention, the sign that follows initiates a sesquitertia (4:3) proportional relationship between semibreves. Finally, red void coloration introduces a tripla proportion. This passage is translated onto the ski-hill graph in Example 31. When semibreves are compared with one another (see alternative notation), the proportional relationships introduced by the various coloration and proportion types of this passage do not build up incrementally. There is a direct jump across two 3:2 layers between the hierarchies of
(middle right of the ski-hill graph) and
(left of the graph), followed by a jump back across three layers between
and red void coloration (bottom right of the graph).
[4.15] The void breves simplify this proportional jump. At face value, the void coloration appears redundant because void breves are equal to black breves of (see alternative notation in Example 30). The interjection of void coloration makes sense, however, when viewed as an instruction for the singer to compare breves. Counting breves rather than semibreves allows for the singer to traverse proportions that are less difficult. Instead of jumping directly to the sesquitertia relationship between semibreves of
and
, the singer navigates a dupla (2:1) relationship between breves of
and void breves. This is reinforced by the trochaic rhythm that precedes the void breves in the triplum, which also divides the breve in half (see red boxes in Example 30). The singer then traverses a 1:1 relationship between void breves and breves of
, followed by a sesquialtera relationship between breves of
and red void breves—as opposed to the dupla sesquiquarta relationship between black semibreves of
and red void semibreves. In other words, the proportional changes of 4:3 (
semibreve →
semibreve) + 9:4 (
semibreve → red void semibreve) become 2:1 (
breve → void breve) + 1:1 (void breve →
breve) + 3:2 (
breve → red void breve). The change of focus from the semibreve to the breve and, along with it, the subsequent simplification of these proportional changes, is marked by the void coloration.(20) Concurrently, the singer of the contratenor, in the course of navigating the void breves of the triplum, embarks on an extraordinarily challenging passage of syncopations, as marked in Example 30. The void breves may yet again be viewed as a visual marker of the beginning of this temporal disturbance. Unlike the previous examples, the return to black coloration of
after the red void coloration is not prepared, since these hierarchies are close together: for every three red void semibreves there is one black semibreve of
.
Conclusion
[5.1] Although the examples above may indicate that scribes and/or composers were aware of the cognitive demands placed on performers who sang complex repertory, it is by no means the case that all the notation in OH makes a performer’s task easier. An anonymous Credo (fols. 62v–63r) in fact presents one of the greatest notational challenges in early fifteenth-century repertory.(21) In other compositions, however, such as Power’s Gloria (fols. 17v–18r), notation appears to play a role in mitigating the difficulty of performing complex rhythms. It is possible that composers and scribes sought to cultivate a compromise between the difficulty of notation and rhythm, devising a set of creative means whereby these two parameters could be stretched to an apex of complexity without extending beyond the technical capacity of an expert singer. Amid the flurry of complex rhythms and notations encountered in this manuscript, short breaks are interspersed during which performers can rest and prepare their minds and bodies for the next challenge. The subtle interplay of notation and rhythm in OH reflects a sensitivity toward the technical limitations imposed by performance, but also toward the tremendous competency of the singers responsible for bringing the manuscript’s sounds forth. It can be assumed that this competency would have extended beyond that of any modern performer, since even the most able practitioners of historical performance enjoy less exposure to mensural notation than the most experienced singers of fifteenth-century England.
[5.2] The above analyses invite further investigation of proportional preparations in fourteenth- and fifteenth-century repertory more broadly, and an interrogation of Dygon’s claim that inductiones are more prevalent in English repertory. Because inductiones introduce complex proportions via simpler proportions, there is an implied hierarchy among the difficulty of proportions. The apparent alignment between Cohn’s model and the inductiones within OH prompts the question of whether fifteenth-century composers were aware of the cognitive constraints placed upon performers during complex proportional shifts.(22)
[5.3] Examining the temporal dimensions of compositions from the perspective of hypothetical performers demands a different set of tools and draws different conclusions than a study of a listener’s experience. While the stark contrast between the notational and visual layout of medieval manuscripts brings these differences into sharp relief, this observation is equally relevant to the broader corpus of Romantic-period repertory for which Krebs’s and Cohn’s models were devised. The above analyses aim to provide a path towards further historically and culturally situated analyses of performers’ experiences of the temporal dimensions of Early Music, and in particular a thorough longue durée examination of the relationships between mensuration, proportion, meter, and notation in this repertory.
Manuscript Sigla
| Ao | Aosta, Biblioteca del Seminario Maggiore, Cod. 15 |
| Chantilly | Chantilly, Musée Condé, MS 564 |
| Chicago | Chicago, Newberry Library, MS 54.1 |
| CtcO.3.38 | Cambridge, Trinity College Library, MS O.3.38 |
| ModA | Modena, Biblioteca Estense, MS α.M.5.24 |
| OH | London, British Library, MS 57950 |
| Ob213 | Oxford, Bodleian Library, MS. Canonici misc. 213 |
| Ouc192 | Oxford, University College Library, MS. 192 |
| Turin | Turin, Biblioteca Nazionale Universitaria, MS J.II.9 |
Philippa Ovenden
Pontifical Institute of Mediaeval Studies, University of Toronto
81 St Mary Street
Toronto, ON M5S 1J4
Canada
philippa.ovenden@aya.yale.edu
Works Cited
Adler, Israel. 1975. Hebrew Writings Concerning Music, in Manuscripts and Printed Books from Geonic Times up to 1800. G. Henle Verlag.
Aluas, Luminita Florea. 1996. “The ‘Quatuor principalia musicae’: A Critical Edition and Translation, with Introduction and Commentary.” PhD diss., Indiana University.
Anonymous. 1989. Tractatus Figurarum = Treatise on Noteshapes: A New Critical Text and Translation. Edited and translated by Philip E. Schreur. University of Nebraska Press.
Bent, Margaret. 1969. “The Old Hall Manuscript: A Paleographical Study.” PhD diss., Cambridge University.
—————. 1994. “Editing Early Music: The Dilemma of Translation.” Early Music 22 (2): 373–92. https://doi.org/10.1093/earlyj/XXII.3.373.
—————. 1995. “The Limits of Notation in Defining the Musical Text.” In L’edizione critica tra testo musicale e testo letterario: Atti del Convegno internazionale (Cremona 4–8 ottobre 1992), ed. Renato Borghi and Pietro Zappalà, 367–72. Studi e testi musicali; nuova ser., 3. Libreria musicale italiana.
—————. 2013. “Early Music Editing, Forty Years On: Principles, Techniques, and Future Directions.” In Early Music Editing: Principles, Historiography, Future Directions, ed. Theodor Dumitrescu, Karl Kügle, and Marnix van Berchum, 241–71. Brepols.
—————. 2022a. “Principles of Mensuration and Coloration: Virtuosity and Anomalies in the Old Hall Manuscript.” In Le notazioni della polifonia vocale dei secoli IX–XVII. Antologia, Parte Seconda: Secoli XIV–XVII, ed. Antonio Delfino and Francesco Saggio, 73–95. Edizioni ETS.
—————. 2022b. “Towards the Reconstruction of a Dismembered Royal Choirbook of the 1420s (RC).” In Fragments of English Polyphonic Music c. 1390–1475: A Facsimile Edition, ed. Margaret Bent and Andrew Wathey, 6–26. Stainer and Bell.
Bent, Margaret, and Andrew Wathey. 2022. Fragments of English Polyphonic Music c. 1390–1475: A Facsimile Edition. Stainer and Bell.
Boone, Graeme M. 2000. “Marking Mensural Time.” Music Theory Spectrum 22 (1): 1–43. https://doi.org/10.2307/745851.
Bray, Roger. 1995a. “Editing and Performing Musica speculativa.” In English Choral Practice, 1400–1650, ed. John Morehen, 48–73. Cambridge University Press. https://doi.org/10.1017/CBO9780511552410.004.
—————. 1995b. “Music and the Quadrivium in Early Tudor England.” Music & Letters 76 (1): 1–18. https://doi.org/10.1093/ml/76.1.1.
Busse Berger, Anna Maria. 1990. “Musical Proportions and Arithmetic in the Late Middle Ages and Renaissance.” Musica disciplina 44: 89–118.
—————. 1993. Mensuration and Proportion Signs. Oxford University Press.
—————. 2005. Medieval Music and the Art of Memory. University of California Press. https://doi.org/10.1525/california/9780520240285.001.0001.
Carter, Elliott. 1965. “The Time Dimension in Music.” Music Journal 23 (8): 29–30.
Cohn, Richard. 1992. “Metric and Hypermetric Dissonance in the Menuetto of Mozart’s Symphony in G Minor, K. 550.” Intégral 6: 1–33.
—————. 2001. “Complex Hemiolas, Ski-Hill Graphs and Metric Spaces.” Music Analysis 20 (3): 295–326. https://doi.org/10.1111/1468-2249.00141.
—————. 2016. “Graph-Theoretic and Geometric Models of Music.” In Mathemusical Conversations: Mathematics and Computation in Music Performance and Composition, ed. Jordan B.L. Smith, Elaine Chew, and Gérard Assayag, 237–55. World Scientific Publishing. https://doi.org/10.1142/9789813140103_0013.
—————. 2020. “Meter.” In The Oxford Handbook of Critical Concepts in Music Theory, ed. Alexander Rehding and Steven Rings, 207–33. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780190454746.013.9.
Collins, Henry Bird, Dom Anselm Hughes, and Alexander Ramsbotham, eds. 1933–1938. The Old Hall Manuscript. 3 vols. Plainsong & Mediaeval Music Society.
DeFord, Ruth. 2015. Tactus, Mensuration and Rhythm in Renaissance Music. Cambridge University Press. https://doi.org/10.1017/CBO9781107587717.
Desmond, Karen. 2018. Music and the moderni, 1300–1350: The ars nova in Theory and Practice. Cambridge University Press.
Dygon, John. [1510s–1530s] 2006. Proportiones practicabiles secundum Gaffurium. Edited and translated by Theodor Dumitrescu. University of Illinois Press.
Goldman, Richard Franko. 1957. “The Music of Elliott Carter.” The Musical Quarterly 43 (2): 151–70. https://www.jstor.org/stable/40374136.
Greig, Donald. 2003. “Ars Subtilior Repertory as Performance Palimpsest.” Early Music 31 (2): 196–209. https://doi.org/10.1093/earlyj/XXXI.2.196.
Heminger, Anne. 2018. “Music Theory at Work: The Eton Choirbook, Rhythmic Proportions and Musical Networks in Sixteenth-Century England.” Early Music History 37: 141–82. https://doi.org/10.1017/S0261127918000074.
Hughes, Andrew. 1965. “Mensuration and Proportion in Early Fifteenth Century English Music.” Acta musicologica 37 (1/2): 48–61. https://doi.org/10.2307/932338.
Hughes, Andrew, and Margaret Bent, eds. 1967. “The Old Hall Manuscript.” Musica disciplina 21: 97–147.
—————. 1969–1973. The Old Hall Manuscript. 3 vols. Corpus mensurabilis musicae, 46. American Institute of Musicology.
Kaminsky, Peter. 1989. “Aspects of Harmony, Rhythm and Form in Schumann’s Papillons, Carnaval, and Davidsbündlertänze.” PhD diss., University of Rochester.
Krebs, Harald. 1987. “Some Extensions of the Concepts of Metrical Consonance and Dissonance.” Journal of Music Theory 31 (1): 99–120. https://doi.org/10.2307/843547.
—————. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195116236.001.0001.
Leech-Wilkinson, Daniel. 2003. “Articulating Ars Subtilior Song,” Early Music 31 (1): 6–18. http://www.jstor.org/stable/3137917.
Maw, David. 2004. “‘Trespasser Mesure’: Meter in Machaut’s Polyphonic Songs.” The Journal of Musicology 21 (1): 46–126. https://doi.org/10.1525/jm.2004.21.1.46.
Misch, Imke. 1972. “Syncopa/Synkope.” In Handwörterbuch der musikalischen Terminologie, vol. 6, comp. Hans Heinrich Eggebrecht, 1–24. Franz Steiner Verlag.
Morley, Thomas. [1597] 1963. A Plain and Easy Introduction to Practical Music. Edited by Richard Alec Harman. W. W. Norton.
Ovenden, Philippa. Forthcoming. “Notation and Compositional Process in a Gloria by Leonel Power.” In European Music Notations in Theory and Practice, 1400–1600, edited by Paul Kolb. Brepols.
Pace, Richard. [1517] 1967. De fructu qui ex doctrina percipitur (the Benefit of a Liberal Education). Edited and translated by Frank Manley and Richard S. Sylvester. Ungar.
Pieragostini, Renata. 2013. “Augustinian Networks and the Chicago Music Theory Manuscript.” Plainsong and Medieval Music 22 (1): 65–85. https://doi.org/10.1017/S0961137112000198.
Prosdocimus de Beldemandis. [1408] 1963. “Tractatus practice de musica mensurabili.” In Scriptorum de musica Medii Aevi Nova series a Gerbertina, vol. 3, ed. Charles Edmond Henri de Coussemaker, 200–27. Olms.
—————. [1412] 1966. Prosdocimi de Beldemandis Opera, vol. 1: Expositiones tractatus practice cantus mensurabilis Magistri Johannis de Muris. Edited by F. Alberto Gallo. A.M.I.S.
Raz, Carmel. 2018. “An Eighteenth-Century Theory of Musical Cognition? John Holden’s Essay Towards a Rational System of Music (1770).” Journal of Music Theory 62 (2): 205–48. https://doi.org/10.1215/00222909-7127670.
Rosa-Barezzani, Maria Teresa. 2001. “Una rilettura di Le greygnour bien di Matteo da Perugia.” Philomusica 1 (1). http://dx.doi.org/10.6092/1826-9001.1.106
Schroeder, Eunice Mary. 1985. “Mensura According to Tinctoris, in the Context of Musical Writings of the Fifteenth and Sixteenth Centuries.” PhD diss., Stanford University.
Smilansky, Uri. 2011. “A Labyrinth of Spaces: Page, Performance and Music in Late Medieval French Culture.” In Ritual and Space in the Middle Ages: Proceedings of the 2009 Harlaxton Symposium, ed. Frances Andrews, 130–47. Donington.
Stoessel, Jason. 2002. “The Captive Scribe: The Context and Culture of Scribal and Notational Process in the Music of the Ars Subtilior.” PhD diss., University of New England.
—————. 2009. “The Interpretation of Unusual Mensuration Signs in the Notation of the Ars Subtilior.” In A Late Medieval Songbook and Its Context: New Perspectives on the Chantilly Codex (Bibliothèque du Château de Chantilly, MS. 564), ed. Yolanda Plumley and Anne Stone, 179–202. Brepols. https://doi.org/10.1484/M.EM-EB.3.2666.
—————. 2010. “Looking Back over the Missa L’Ardant desir: Double Signatures and Unusual Signs in Sources of Fifteenth-Century Music.” Music & Letters 91 (3): 311–42. https://doi.org/10.1093/ml/gcq059.
—————. 2012. “Revisiting Aÿ, mare, amice mi care: Insights into Late Medieval Music Notation.” Early Music 40 (3): 455–68. https://doi.org/10.1093/em/cas101.
Stoessel, Jason, and Denis Collins. 2019. “New Light on the Mid-Fourteenth-Century Chace: Canons Hidden in the Tournai Manuscript.” Music Analysis 38 (1–2): 155–203. https://doi.org/10.1111/musa.12116.
Stone, Anne. 1994. “Writing Rhythm in Late Medieval Italy: Notation and Musical Style in the Manuscript Modena, Biblioteca Estense, Alpha.M.5.24.” PhD diss., Harvard University.
—————. 1996. “Che cosa c’è di più sottile riguardo l’Ars Subtilior.” Rivista Italiana di Musicologia 31 (1): 3–31.
—————. 2002. “The Ars Subtilior in Paris.” Musica e storia 10 (2): 373–404.
—————. 2003. “Self-Reflexive Songs and Their Readers in the Late 14th Century.” Early Music 31 (2): 180–94. https://doi.org/10.1093/earlyj/XXXI.2.180.
—————. 2018. “Ars Subtilior.” In The Cambridge History of Medieval Music, vol. 2, ed. Mark Everist and Thomas Forrest Kelly, 1125–46. Cambridge University Press.
Tucke, John. 1993. A Case Study in Early Tudor Music Theory. Edited and translated by Ronald Woodley. Clarendon Press; Oxford University Press.
Tingley, George Peter. 1981. “Metric Modulation and Elliott Carter’s ‘First String Quartet’.” Indiana Theory Review 4 (3): 3–11. https://www.jstor.org/stable/24045947.
Upton, Elizabeth Randell. 2013. Music and Performance in the Later Middle Ages. Palgrave MacMillan. https://doi.org/10.1057/9781137310071.
Willelmus. [14th century] 1966. MS. Oxford, Bodley 842: Breviarium regulare musicae, edited by Gilbert Reaney; Anonymous, MS. British Museum, Royal 12. C. VI: Tractatus de figuris sive de notis, edited by Gilbert Reaney; Johnannes Torkesey, MS. British Museum, Royal 12. C. VI: Trianguli et scuti declaratio de proportionibus musicae mensurabilis, edited by André Gilles and Gilbert Reaney, Corpus scriptorum de musica, vol. 12. American Institute of Musicology.
Zayaruznaya, Anna. 2017. “Intelligibility Redux: Motets and the Modern Medieval Sound.” Music Theory Online 23 (2). https://doi.org/10.30535/mto.23.2.3.
Zazulia, Emily. 2021. Where Sight Meets Sound: The Poetics of Late-Medieval Music Writing. Oxford University Press. https://doi.org/10.1093/oso/9780197551912.001.0001.
Footnotes
* For their invaluable comments at various stages of the writing process, I am grateful to Margaret Bent, Jason Stoessel, Paul Kolb, Richard Cohn, Anne Stone, Anna Zayaruznaya, and an anonymous reader from MTO. I would also like to thank the participants of the Yale Medieval Song Lab for taking on the challenge of singing Power’s Gloria (fols. 17v–18r), and in particular Liam Hynes-Tawa and William C. Watson. This article was written with the generous support of the Jean-François Malle Fellowship from Villa I Tatti, The Harvard University Center for Italian Renaissance Studies. A related version of this research was presented at the conference New Perspectives in Fifteenth- and Sixteenth-Century Music Notations (May 4–7 2022), Alamire Foundation, Leuven and will be published in Ovenden (forthcoming).
Return to text
1. An edition of OH was also previously published by Collins et. al. (1933–38).
Return to text
2. Blue coloration is otherwise discussed only in theoretical treatises. See Adler 1975 (61); Bray 1995a (54); Bray 1995b (2–4); Heminger 2018 (148); Stone 2002 (387, 398–99); Tucke 1993 (68–69).
Return to text
3. Stoessel (2010, 332–33) has employed a similar method in the analysis of early fifteenth-century pieces by comparing proportional changes horizontally and cumulatively following the experience of a scribe. The approach employed here draws on the work of Bent (1994, 392; 1995; 2013, 270), who has argued for an analytical method that considers the experiences of hypothetical “native speakers” of mensural notation by gaining fluency through singing from facsimiles. It also develops Stone’s (2018, 1136–37) concept of a “written audience,” who can be singers or readers who sing or imagine a composition directly from a manuscript, and Desmond’s (2018, 212) concept of “experiential” mensuration.
Return to text
4. See n13 and Example 7 below for further discussion of this technique.
Return to text
5. Indeed, there are examples in OH in which notations make it more difficult for performers to execute a composition. The most comprehensive example of this is the anonymous Credo (fols. 62v–63v), a five-part notational canon that employs a wide range of proportions and coloration types.
Return to text
6. Stoessel and Collins (2019) also make this observation in relation to canon techniques of the fourteenth and early fifteenth centuries.
Return to text
7. Unless otherwise stated, notes are reduced 2:1 in all examples that include transcriptions into modern notation.
Return to text
8. For a list of note names, see Example 1. A long in perfect modus will not be perfect if it is “imperfected.” Imperfection occurs when a shorter note or notes is situated beside a longer note, such that the longer note (now imperfect) and the shorter note(s) together fill out the perfection.
Return to text
9. DeFord (2015, 106–7) notes that the performance tactus and the compositional tactus are nevertheless conceptually distinct. Whereas the compositional tactus is a “structural component,” the performance tactus is an “external time-keeping device” with which performers measure and interpret rhythms. The performance tactus is accessible only through secondary witnesses, such as theoretical treatises.
Return to text
10. For further discussion of the significance of the term mensura in the work of Johannes Tinctoris (d. 1511), see DeFord 2015 (51–52) and Schroeder 1985.
Return to text
11. “Quandocunque quatuor minimae separatim pronuntiantur . . . aequipollent brevi imperfectae de minori prolatione. Si enim tres aequaliter pronuntiantur, semibrevi de majori prolatione aequipollent. Tamen multi credunt unam esse mensuram, cum quis quatuor distinctas pronuntiat minimas, dummodo alius pronuntiat tres; in hoc enim decepti sunt, quia ratio eis contradicit, cum aequipollentia inter illas non est nec etiam talis aequipollentia in longis nec in brevibus, nec in semibrevibus invenitur. . . . Nam si ille idem in tanta velocitate tres pronuntiaret minimas quemadmodum et quatuor, aut remaneret pausa unius minimae, aut una illarum trium foret minor duas minimas continens. . . . Aequipollentiae enim supradictae atque reductiones musicam pronuntiandi difficultates causant; quae quidem difficultates, tractus gallice treyns, et sincope a multis nominantur.” “Whenever four minims are sung separately . . . they are equal to an imperfect breve of minor prolation. If three minims are sung equally, they are equal to a semibreve of major prolation. Many believe the measure to be one when someone sings four distinct minims the way another sings three. In this, they are deceived, for reason contradicts them, as these minims are not equal, nor are the longs, breves, or semibreves. . . . For if he sang three minims with the same velocity as four, a rest of one minim would remain, or one of those three would be a lesser [semibreve] containing two minims. . . . The above said equivalence and reductions make it difficult to sing music; these difficulties are named ‘tractus,’ by the French ‘treyns,’ and ‘syncopations’ by many.” Aluas 1996, 455, 703–704 (translation modified).
Return to text
12. Cohn (2020, 223) has previously observed his own “hemiola” type dissonance (an equivalent to Krebs’s grouping dissonance, to be discussed further below) “engages many of the same phenomenological processes as a syncopation” (Krebs’s displacement dissonance).
Return to text
13. As Stone (2003, 187) notes in her analysis of Se j’ay perdu, this parallels metrical modulation, a technique that has been theorized most prominently in the compositions of Elliott Carter (1908–2012), who defines the practice as “a procedure in which the tempo or ‘beat’ speeds up in an ordered manner between measures” (1965, 30). As Richard Goldman (1957, 161) notes, metrical modulation entails “going smoothly. . . from one absolute metronomic speed to another.” In metrical modulations, a principal time unit is subdivided into a greater or lesser number of parts. Equivalency between the parts is then altered to initiate an acceleration or a deceleration of the original, primary time unit. Consider, for instance, George Peter Tingley’s (1981, 4) Example 1, which analyzes a simple metrical modulation in the rhythm of the first violin in mm. 25–31 of Carter’s String Quartet No. 1.
Return to text
14. I briefly revisit this example at the end of the article in a discussion of Power’s Gloria (fols. 17v–18r). The apparent redundancy between red void breves and red semibreves following in the triplum (which are equal in duration) can be explained as a notational preparation.
Return to text
15. “Ceterum hoc ausim dicere, nostros Britannos musicos, maxima ingenii subtilitate [. . . ] illas quas vocant proportionum inductiones.” “If one looks into it closely, our British musicians have found with great subtlety of mind those things they call the inductiones of proportions” (Pace [1517] 1967, 64–65).
Return to text
16. Morley ([1597] 1963, 172) later provides an example of an induction without objection.
Return to text
17. As Dumitrescu (Dygon [1510s–1530s] 2006, 14–24) discusses, Dygon was a Benedictine monk at the monastery of St. Augustine in Canterbury. He probably studied music at the University of Oxford and later at the universities of Leuven and Paris. He would have benefitted from the flourishing intellectual environment of St. Augustine’s, where several music treatises were kept, and where he wrote several compositions. Curiously, his compositions do not reflect his theoretical interests in proportions.
Return to text
18. The transmission of the manuscript in which this diagram appears—Chicago, Newberry Library, MS 54.1 (Chicago), a miscellany of music-theoretical treatises copied by English Augustinian friars in Pavia before c. 1391—is discussed in Pieragostini 2013.
Return to text
19. A further caveat is that Cohn uses the ski-hill graph to represent hemiolas, which he describes in terms of metric “consonance” and “dissonance.”
Return to text
20. This pattern is also encountered in Damett’s Credo (fols. 60v–61r, Example 9). Direct computation of the subsesquitertia relationship between semibreves of and
is circumvented by three void breves, which invite the reader to compare breves. By comparing breves, the reader first traverses a sesquialtera proportion between breves of
and red void breves, followed by a tripla proportion between red void breves and red breves of
. This passage could thus have been notated differently by placing the
sign in front of the three red void breves and replacing these notes with red semibreves.
Return to text
21. This Credo differs from those of the examples discussed in this article. The challenges of reading it stem from a complex notational canon that occurs in addition to its idiosyncratic use of color of proportion.
Return to text
22. That historical music theorists may have had an awareness for facts about cognition that have subsequently been studied using the empirical method has been discussed by scholars such as Busse Berger (2005), Raz (2018), and Zayaruznaya (2017).
Return to text
Copyright Statement
Copyright © 2023 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
3307