Harmonic “Quality” and Set-Class Structure: Schoenberg’s Opus 19, No. 2 Reconsidered
Rajan Lal
KEYWORDS: Arnold Schoenberg, Anthony Pople, set-class, Alexander Scriabin, hexatonicism, octatonicism
ABSTRACT: This article focuses on one of the most discussed works in music-theoretical literature concerning tonal versus set-class organization, the second of Arnold Schoenberg’s Sechs Kleine Klavierstücke, op. 19. To advance a new understanding of how these two conceptual frameworks can be unified, I propose an intuitive notion of harmonic “Quality” inspired by a portion of Anthony Pople’s unfinished Tonalities project (2004). According to Pople, harmonic Quality derives from two sources: tritone intervals and seventh scale degree status. I argue that Quality can assist us in hearing Schoenberg’s overhaul of non-diatonic collections as articulating quasi-tonal tension-relaxation relationships, all within the context of a broader chromatic language. The analyses that follow suggest that Schoenberg favored a stable status for hexatonicism at the start and end points of op. 19, no. 2, a stability that is tied to its tonic-quality. The article then applies Quality to examine the outlier status of piece no. 6 within op. 19, Schoenberg’s moving tribute to Gustav Mahler written after the first five miniatures were conceived. The goal of this approach is to inject nuance into existing tonal versus set-class debates by thinking of Schoenberg as a composer of op. 19 no. 2 architectonically: as a collectional, set-class composer in terms of raw pitch resources, but also a composer handling such raw resources with a distinctly tonal intuition.
DOI: 10.30535/mto.30.1.4
Copyright © 2024 Society for Music Theory
1. A “Locus Modernus” of Atonal Music Theory
[1.1] From time to time compositions of extreme brevity and gestural irreverence capture the imagination of musicologists for many decades. And indeed here, from the mid-1960s till the present day, published music-theoretical literature is awash with studies of the second member of Schoenberg’s Sechs Kleine Klavierstücke, op. 19. Piece no. 2, a disarming, nine-measure musical aphorism, has not only captivated scholarly attention in terms of quantity of writings, but has played a key illustrative role in several landmark articles on post-tonal analysis (Travis 1966; Straus 1987; Lerdahl 1989). It has served as somewhat of a proving ground between proponents of extended tonal interpretations and those focused on set-class readings. Even more so than the sixth member of the op. 19 set, piece no. 2 can be said to represent a “locus modernus” of atonal music theory and analysis (Smith 2021b, 14).
2. Marrying the Tonal and Set-Class Perspectives
[2.1] The quantity of published literature on op. 19 no. 2 is matched by its variety. Jack Boss identifies a tripartite division in the scholarship (Boss 2019, 229–230), his demarcation falling into camps based on a) a broad interest in reduction and desire to view the piece’s final chord as a culmination, b) a view of the G–B dyad as a “reference set” and general focus on symmetrical tenets, and c) employment of conflict-resolution narrative(s) in tandem with harmonic or metrical analysis.(1)
[2.2] In addition to this three-part division, a binary one is possible for op. 19 no. 2: Is this work the product of extended tonal planning, where tonality holds status as a “guarantor of large-scale coherence” (Boss 2019, 4)? Or, does tonality manifest as a “specter” in this work, a limited “occasional expressive device,” thus implying that other viewpoints, particularly those related to set-classes, are better suited for shedding light on its overall coherence (Boss 2019, 4). This two-part division resonates with scholarly divides in literature concerning the whole op. 19 set, particularly pieces no. 3 and no. 6, as well as with broader debates surrounding Schoenberg’s middle, “atonal” period.(2)
[2.3] To further expound on these harmony-focused approaches—which largely set metrical and poetic concerns to the side—one branch of scholarship is concerned with quasi-Schenkerian thinking: it holds that opus 19 no. 2 is reducible to some form of primordial, likely highly extended tonal structure. By contrast, the other branch is more concerned with surface pitch organization: intervals, sets and referential collections for those sets in the musical foreground and what their interrelationships may be. I will henceforth refer to these two approaches as “tonal” and “set-class.” Despite their seemingly irreconcilable differences with regards to structural depth, the two approaches often align in terms of their rhetoric.(3) Both tend to stylize problem-solution dynamics into their frameworks and locate a sense of goal directedness in this work’s nine measures. Both agree that a sense of conclusion is felt at the piece’s final chord, be this through Schenkerian V–I (G to C) resolution (Travis 1966), constructional closure in satisfying all pitches of the aggregate through major third dyads (DeLio 1994, 32), or pure hexatonic “control” of the G–B dyad that makes up the work’s ostinato (Boss 2019, 238). Boss further fleshes out the process by adding the intermediary step of elaboration of a problem, following what Schoenberg would have referred to as “musical idea” (musikalische Gedanke) (see Schoenberg 1995; Heneghan 2018; Boss 2019, 238). Clearly, there is common ground between the varied tonal structural hearings, set-class analyses of this piece and the sense of ending engendered by m. 9.
[2.4] The convergence between the two viewpoints prompts us to note what each hopes to accomplish in a general sense. The tonal viewpoint pays attention to relative tension and relaxation at various moments in the piece, in essence keeping track of what is home and what is far from home. The set-class approach acknowledges a tighter mechanistic control over interrelated elements large and small. The question that will therefore be of greatest concern in this article is whether it is possible to show progression in terms of tension and release while acknowledging the work’s tightly wrought set-class organization. We shall thus seek to analyze opus 19 no. 2 in a way that a) assigns a general system of classification to its set-classes that elucidates their state of restlessness versus stability, and b) allows us to appreciate both its sense of progression and set-class architecture. These two facets, moreover, exist in a tightly bound relationship. I contend that the shared interpretation of op. 19, no. 2 across scholarly camps is not simply gestural (rhythmic and registral, as Morrison and DeLio argue, respectively) but also created by the intrinsic “Quality” of the harmonies Schoenberg employs. It is appreciation of the sonic characters created by Schoenberg’s harmonic choices within a broader chromatic field—as, for example, all twelve pitches of the chromatic aggregate are used by m. 9.1, with the final left-hand chord change (
3. Harmonic “Quality”
[3.1] To address the abstruse array of non-tonal pitch resources that make up opus. 19, no. 2, it will be useful to marry a tonal perspective with Boss’ pitch collection-based understanding (itself originating in Berger (1963) and later Van den Toorn’s (1983) scholarship devised for Stravinsky’s output).(4) As we do so, importantly, we need not (and should not) shift directly to any one specific tonal framework, historical or modern. Rather, we can shed fresh light on this work by viewing and hearing non-tonal, non-diatonic set-classes through different tonal means. To examine resources of the hexatonic, whole-tone and octatonic variety through this prism, we need to explore the intrinsic sonic characters that inhere in their subset constructions, a feature I will henceforth refer to as “Quality.” The method outlined below can be applied to any given set-class.
[3.2] In a series of highly imaginative theorizations for his unfinished Tonalities project, Anthony Pople proposed two criteria for what he termed the “Modal Quality” of linearized, scalar harmonies.(5) These criteria have recently received renewed attention within the context of Vasilis Kallis’s Scriabin studies (2022). To Pople, the key defining features of a pitch collection’s Quality include the nature of its seventh scale degree and its number of “housed” tritones (Pople 2004, 177).(6) I will now elaborate on these two criteria in turn.
[3.3] With regard to the nature of the seventh, Kallis explains
Pople introduced a qualitative distinction between non-diatonic modes, recognizing two Quality types, I-Quality (tonic-quality) and V-Quality (dominant-quality). The essential distinguishing criteria is to be found in a scale’s seventh scale degree and the harmonic structures it belongs to. The sonic Quality of the hexatonic scale, for example, is partially determined by its seventh scale degree (a major seventh above the tonic), which allows for the formation of characteristic structures on the scale’s ‘tonic’. . . [major seventh and minor-major seventh chords]. In the acoustic and [in prime form] octatonic scales, the seventh scale degree is lowered, forming an array of dominant-type chords on scale degree 1 (2022, 141–142).
Example 1. Characteristic Structures Formed on Scale Degree 1 and Various Nodal Points in Some Important Early Twentieth Century Collections
(click to enlarge)
Kallis hits upon an important consideration. In music that employs synthetic scalar collections, there is very often a sense of root centricity that is correlated with the nominal first scale degree of the sonority under consideration, or, for symmetrical scales, a root “feeling” related to one of their several “nodal” points (see 1985), each of which can act as a “tonic.” Thus, quite unlike Pople’s second criterion detailed below, the nature of the seventh scale degree cannot be accurately determined when expressing the set-class in question as raw Fortean data. To do so, attention must pivot to the musical surface, moving beyond the abstract musical space of ‘collection’ to the scalar voicing of that particular collection. Note that the hexatonic collection, set-class 6-20 (0, 1, 4, 5, 8, 9), in prime form indicates the presence of no seventh whatsoever. Nevertheless, this collection’s three pairs of chromatic dyads separated by minor third allow for the voicing of three possible major seventh intervals in the musical surface, each built upon a triadic nodal point. In essence, we extend the set up in our minds and conceive of its potential chordal sub-components; for example, (0, 1, 4, 5, 8, 9) contains three major seventh tetrads: (1, 5, 8, 0), (5, 9, 0, 4) and (9, 1, 4, 8). Thirds here are interchangeable, meaning our imagined chords could well be minor-major seventh tetrads. Regarding asymmetrical collections such as the diatonic, harmonic minor and acoustic, the relevant “formation of characteristic structures” often occurs on the first scale degree. Example 1 illustrates how a scalar viewpoint impacts perception of non-diatonic collections prevalent in early twentieth century music, offering just some possibilities for tonic- and dominant-quality chords situated on important scale degrees of the given collections.(7)
[3.4] Regarding the I-Quality major seventh, I take the view that a housed major seventh tetrad is really a major triad with an ingrained seventh appoggiatura left unresolved. (Pople’s writings, it should be noted, imply but do not explicitly lay bare such an understanding of major seventh scale degrees.) One might reasonably ask why the I-Quality major seventh scale degree itself does not point semitonally upward with its own drive to resolve, as the minor seventh does downward in Pople’s understanding of V-Quality harmonies. Indeed, though a sense of semitonal motion is without a doubt built into major sevenths, such “resolution” is to the first scale degree of the very same triad as that which is already present within a major seventh tetrad. Therefore, major sevenths do not create a sense of resolution to a new harmony, but rather a reinstatement of the prevailing harmony.(8) By contrast, a minor seventh scale degree maps most closely onto the V7 component of a V7–I resolution, where the goal harmony is not contained within the initial harmony. To summarize through tonal analogy: Cmaj7 → C Diatonic (therefore Cmaj7 manifests I-Quality), whereas C7 → F Diatonic (therefore C7 manifests V-Quality). Harrison notes the significance of the major seventh as a leading tone; this pitch produces the sense that scale degree 8 is a tonic (1994, 26). By contrast, the minor seventh provides an intrinsic need for resolution out of the tonic pitch space; it is, as Riemann and more recently Newton put it, a “characteristic dissonance” (Riemann 1895, 55; Newton 2022, 247).(9)
[3.5] Crucially, these differing seventh types carry their sonic footprints forward into post-tonal repertoire, where their tonal supporting chords typically fail to manifest. And, in post-tonal music, major sevenths and minor sevenths rarely resolve functionally as in tonality proper. Simply put, Pople’s theory abstracts such functional voice-leadings from their tonal context to indicate the respective stable/unstable qualities of major/minor sevenths, purely as listeners acquainted with tonality might hear them well beyond their older tonal contexts. The issue at hand is that the seventh type is a near-instantaneous artifact encoded on listeners familiar with the tonal tradition. It is one small portion of a rich network of tonal “schematic expectations” (Huron 2006, 419; Huron 2016, 135–141) that we can interpolate into post-tonal repertoire.
[3.6] Pople’s second criterion concerns the number of tritones within a sonority: just as with seventh scale degrees, hypothetical resolutions to hypothetical harmonies are key to determining harmonic Quality. For Pople, the number of tritone intervals “housed” in a collection directly influences its Quality tendencies (Kallis 2022, 141). To cite several well-known sonorities: the octatonic collection contains four tritones, the whole-tone three, and the acoustic collection two. All sonorities, to varying degrees of strength, offer multiple reminiscences of the characteristic tritone between the chordal third and minor seventh in a dominant seventh tetrad. As such, these three harmonies to various extents are V-Quality in Pople’s classifications (Pople 2004, 177). In Schoenbergian terms, we might say they are characterized by varying degrees of “vagrancy” (Schoenberg [1911] 1978, 238–67). By contrast, the hexatonic collection contains no tritones, and may thus be said to exhibit purely I-Quality. Unlike Pople’s first criterion regarding sevenths, the number of tritones can be determined with great ease using an interval vector. Here, critically, we are not talking about linear voice-leading, actual or implied. Rather, Quality considers the sonic character of potential voice-leading motions in light of the — potentially stacked — presence or absence of key intervals normally associated with instability in tonal music. The voice-leading potentials of tritones are abstracted alone as particular “rare-intervals” (see Browne 1981; Krumhansl 1990) that sound dominant-like to acculturated ears.
4. The Benefits of Understanding Collections through Quality
[4.1] The understanding of Quality outlined above can facilitate analyzing and perhaps even hearing post-tonal harmonic progressions as articulating quasi-tonal tension-relaxation relationships. It is true that Pople’s criteria offer us inert data in collectional isolation; however, the true utility of this approach emerges when we rank collections by their relative tendency towards I-Quality or V-Quality. Consider the case of a hexatonic harmony, perhaps voiced with major seventh and certainly no tritones, preceding an octatonic harmony. Here, it is possible to claim that the music presents a tonic-like sound world yielding to a much more dominant sounding one, relatively speaking, of course. Alternatively, if a whole-tone harmony (with minor seventh and three housed tritones) yields to an octatonic harmony (see above), then perhaps we may claim that the music’s dominant-like feel has increased, raising the level of harmonic instability. It should be emphasized at the outset that a Quality understanding is an entirely binary viewpoint.(10) It affords us an explanatory inroad into only the relative status of post-tonal harmonies, as listeners acquainted with the sonic trappings of tonality might view and hear them. The most convincing case studies for this model, as we shall see, occur when harmonies of differing Quality are localized to one another, closely adjacent and thus most facilitative of comprehension through sharp aural juxtaposition.
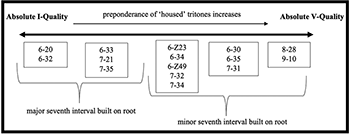
Example 2. Alexander Scriabin’s Post-Tonal Set-Class Repository: A Continuum from Absolute I-Quality to Absolute V-Quality
(click to enlarge)
[4.2] A useful way to illustrate how the concept of relative harmonic Quality may apply in analysis is to map set-classes that are characteristic to a particular repertoire on a continuum. Example 2 shows the results of this process in reference to the set-class repository of Alexander Scriabin’s late, post-tonal period, whose suitability for this present enquiry will soon become clear. The commonplace Scriabin collections by colloquial name and the Fortean interval vectors pertaining to their respective set-classes are shown below:(11)
[4.3] Major Seventh Characterized Sonorities, i.e., those that tend toward I-Quality:
6-20 (hexatonic collection) = 303630 = 0 tritones
6-32 (major diatonic hexachord) = 143250 = 0 tritones
6-33 (minor diatonic hexachord) = 143241 = 1 tritone
7-21 (only seven-note hexatonic superset) = 424641 = 1 tritone
7-35 (diatonic heptad) = 254361 = 1 tritone
[4.4] Minor Seventh Characterized Sonorities, i.e., those that tend towards V-Quality:
6-Z23 (acoustic/octatonic subset) = 234222 = 2 tritones
6-34A (Mystic Chord) = 142422 = 2 tritones
6-Z49 (octatonic subset) = 224322 = 2 tritones
7-32 (harmonic minor collection) = 335442 = 2 tritones
7-34 (acoustic collection/melodic minor ascending) = 254442 = 2 tritones
6-30 (octatonic subset) = 224223 = 3 tritones
6-35 (whole-tone collection) = 060603 = 3 tritones
7-31 (unequivocal heptad surrogate) = 3363333 = 3 tritones
8-28 (octatonic collection) = 448444 = 4 tritones
9-10 (acoustic-octatonic collection) = 668664 = 4 tritones
[4.5] Example 2 indicates that Scriabin’s harmonic resources exist on a broadly five-part spectrum, where hexatonicism at left entails a I-Quality extreme, and the octatonic collection and its sole nine-note superset (the acoustic-octatonic collection) at right represent a V-Quality extreme. Numerous other harmonies are situated in medial positions. Two points related to this continuum bear mention. First, supersets of a given set-class are almost always associated with relatively greater V-Quality; the inverse is true for subsets of a given set-class.(12) This trend occurs because higher set cardinality (i.e., greater tendency toward chromatic saturation) is correlated with greater number of housed tritones—and, indeed, generally greater preponderance of every interval. We can see this tendency at its clearest when sets become very large: a seven-note set cannot be tritone free, an eight-note set cannot have fewer than two tritones, a nine-note set has no fewer than three, etc. The only six-note sets that are tritone-free are set-classes 6-1, 6-8, 6-14, 6-20 and 6-32; that amounts to a mere six out of a possible 50 hexachordal set-classes.
[4.6] Second, the continuum shown in Example 2 is composer specific, meaning that it reflects characteristic voicings and spacings of an individual’s style. The reason that Scriabin is a useful case study at present amounts to his highly characteristic approaches to scalar voicing, spacing and orthography, especially in the late works. Scriabin rarely uses the hexatonic collection in prime form, but rather more typically in stacked thirds that articulate major seventh tetrads (Kallis 2015, 14; Kallis 2022, 147–155). This harmony is thus characterized in the continuum by its prominent I-Quality major seventh. The octatonic collection is always used by Scriabin in prime form, with half-step/whole-step gaps as its first two intervals, as opposed to whole-step/half-step gaps (Cheong 1993; Cheong 1993). This harmony is thus V-Quality minor-seventh-characterized in the continuum, with all its harmonic structures built up from its nodal points (see Example 1). Additionally, Scriabin uses the harmonic minor scale in its fourth mode, as an altered Dorian structure (with
5. Worked Analyses
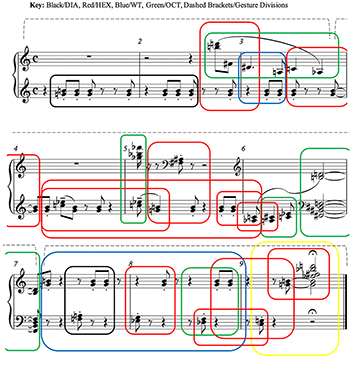
Example 3. Competing Pitch Collections in Schoenberg, op. 19, no. 2
(click to enlarge)
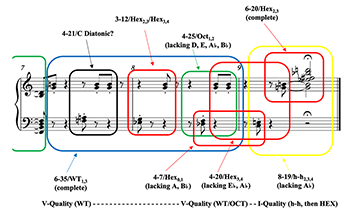
[5.1] Now that we have identified some possible tools with which to view post-tonal, non-diatonic pitch resources through a tonal prism, we turn our attention back to Schoenberg’s op. 19, no. 2. Curiously, despite having been written during Schoenberg’s middle period, this work uses several key sonorities also found within Scriabin’s late output discussed above. Indeed, Boss’s analysis (2019) pursues segmentation from the viewpoint that adjacent dyads can often be grouped together and that the hexatonic, whole-tone, octatonic and diatonic collections function as larger referential collections for smaller surface level harmonies. The following analysis largely concords with his in terms of this starting premise, although it intersperses several additional segmentations; many of these retain Boss’ referential harmony sizes, while others expand them.(14) Following DeLio 1994, I will use the term “gesture” (rather than phrase or section) to indicate the three subdivisions in the piece. Gesture 1 (Gest1) runs through mm. 1–3, exclusive of the final eighth note in m. 3; Gesture 2 (Gest2) runs from the last eighth note of m. 3 to the first eighth note of m. 7, inclusive; and Gesture 3 (Gest3) runs from the second eighth note of m. 7 to the work’s conclusion. Gest1 and Gest3 are symmetrical in duration (both 11.5 quarter note beats) about Gest 2 (13 quarter note beats), a feature demonstrated by the slight overspill of central dashed bracketing in Example 3.
[5.2] Example 3 serves primarily as a visual aid for identifying the presence of the four collections that Boss argues are salient in this work. While it omits performance directions and dynamics for neatness, it retains Schoenberg’s idiosyncratic accidentals and phrasings. Hexatonic presence is shown in red, whole-tone presence in blue, octatonic presence in green, and diatonic (specter) presence in black. Example 3 abounds with intentional overlaps of analytic segmentation. Indeed, the swift alternation of sonorities referable to different collections and the high degree of overlay between implied collections through shared subsets indicates that we are dealing with a sound world subject to not only a “high rate of pitch-class circulation” (Tymoczko 2011, 162–163), but a high rate of collectional circulation. However, this is rarely achieved through collections being presented in their complete forms; instead, smaller shards of these symmetrical structures arise. Though small sets are indeed most prominent, collections as large as nine notes can also be implied. In this latter category, the hyper-hexatonic (hereinafter “h-h”) final measure outlined in yellow will be commented upon at the close of the present analysis; Straus (1987, 9; 1990, 179) draws attention to the h-h subset 8-19 in this final measure during his critique of Travis; my own analysis will inject this octad with renewed interest.
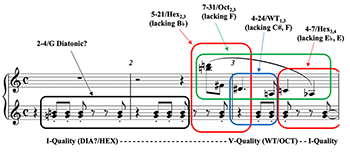
Example 4. Competing Pitch Collections in op. 19, no. 2, Gesture 1 (mm. 1–3)
(click to enlarge)
[5.3] The specific transpositions of the four governing collections for Gest1 are identified in Example 4.(15) After beginning with a major third diatonic “specter” that sounds plausibly referable to G diatonic, Gest1 quickly works its way into hexatonic space (Hex2,3) by mm. 2.4–3.1. A whole-tone intrusion (the odd WT1 collection) interjects by m. 3, a moment that Boss characterizes as an initial challenge for ownership of the G–B dyad (2019, 233). There is a resumption of hexatonic space almost immediately, but it is a new collection, Hex3,4, that gains traction by m. 3.3 to close Gest1. The right-hand melody that straddles (and facilitates) the harmonic hexatonic/whole-tone/hexatonic oscillation through mm. 2–3 articulates set-class 7-31, which expresses seven out of eight notes of Oct2,3. The only note extraneous to Oct2,3 within Gest1 is G, the root of the diatonic sound world most heavily alluded to in the opening left-hand ostinato. Were the G pedal within Gest1 to be replaced by F, then the entire passage would be purely Oct2,3.(16)
[5.4] The relative Quality of harmonies in Gest1 is the key to understanding how Schoenberg creates a sense of home followed by swift departure. The Hex2,3 subset, 5-21 (mm. 2.4–3.1) is articulated with a strong sense of I-Quality; it strongly expresses the major seventh scale degree
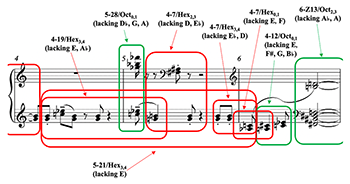
Example 5. Competing Pitch Collections in op. 19, no. 2, Gesture 2 (mm. 4–6)
(click to enlarge)
[5.5] Whilst Gest1 plays out a series of overlapping, rapidly shifting hexatonic/whole-tone/octatonic maneuvers, Gest2 is exclusively concerned with what Ross Edwards (2022) might term hexatonic/octatonic “emulsifications.” Example 5 illustrates the specific forms of each collection that appear within this second gesture. Three hexatonic collections are in play during Gest2. Hex2,3, which was articulated at the work’s outset with strong I-Quality, occupies a central position in m. 5, and indeed a precisely central position in the work more broadly. This collection is framed by Hex3,4 (the rival hexatonic home away from home in Gest1) through appearances of set-classes 4-19 (m. 4) and 4-7 (mm. 5.4–6.1). In addition, Hex3,4 articulates its own 5-21 horizontal structure in the left-hand part from mm. 4–6.1, inclusive. This 5-21 set, teasing a completely hexatonic melodic structure in the first two thirds of Gest2, mirrors the 7-31 melodic structure that was present in the closing stages of Gest1 in an almost complete octatonic context.(17) The two opening gestures counterbalance each other in this respect.
[5.6] Alongside the more general sense of hexatonic saturation, two major octatonic intrusions occur in Gest2. The first intrusion, at the outset of m. 5, articulates set-class 5-28 as a subset of Oct0,1, bringing a rival octatonic collection to Oct2,3 briefly to the foreground. The voicing of this chord is particularly striking from a Quality perspective. Always two tritones strong, 5-28 in this guise is voiced and spelled almost like an altered dominant seventh, with minor seventh scale degree
[5.7] By contrast, the octatonic intrusions within m. 6 are more substantive and exert a profound effect on the tensional shape of the miniature. Set 4-12 surfaces briefly, indicative of a continued-though-still-brief Oct0,1 presence.(19) Similar to the Oct0,1 writing in m. 5, this set is partly comprised of a hexatonic dyad; the A–
[5.8] These octatonic moments are the only unstable additions to a soundscape otherwise devoid of tritones. Sets 4-19 and 4-7, the two notable hexatonic subsets in Gest2, are tritone free and contain numerous instances where inverted major sevenths can be identified. For example, if one hears the 4-19 harmony of m. 4 with C as a tonic bass note—as a subdominant minor like that proposed by chord labelling analysis (Hicken 1980, 133)—then the C–
[5.9] In summary, Gest2 plays out an uneasy balance in which I-Quality hexatonicism predominates in terms of quantity of material, but V-Quality octatonicism characterizes the two most salient musical actions. That the G–B dyad is only ever subsumed within I-Quality hexatonic material is one indicator that this harmony has maintained some kind of tonic status—just as G alone remained excluded from Oct2,3 during Gest1 and B remained excluded from the nested tritones of the 7-31 octatonic melody in mm. 2–3.
[5.10] Intra-hexatonic and intra-octatonic conflicts emerge throughout this piece, as well. Hex3,4 establishes itself as a potential second I-Quality home by framing Hex2,3 material during Gest2, whilst Oct0,1 emerges as a brief competitor to Oct2,3 for the principal V-Quality counterweight within the work more broadly. Though it seems that by m. 7 that Oct2,3 has asserted its status as the principal V-Quality pitch space of the piece—largely by means of the tied half note duration of a formidable 6-Z13—the Hex2,3/Hex3,4 conflict remains undecided at the close of Gest2. Note that Hex0,1, which has not surfaced since m. 4 and will not emerge again until very close to the end of the piece, makes a fleeting appearance in the opening of m. 6. As if playing the role of mediator, this collection steps in to declare that the resolution of any Hex2,3/Hex3,4 interplay must wait.
Example 6. Competing Pitch Collections in op. 19, no. 2, Gesture 3 (mm. 7–9)
(click to enlarge)
[5.11] The collections of Gest3, within which two large-scale harmonic areas are present, are shown in Example 6. The first large-scale area is whole-tone in nature, recalling the material that manifested in four-note subset form in m. 3, now heard in its entirety. Yet rather than escalating what is already a feisty hexatonic/octatonic conflict, this whole-tone material summarizes several of the collectional relationships presented in Gest1 and Gest2. The first tetrad within WT1 space, set-class 4-21, is quite plausibly C diatonic in nature, further cementing the G–B dyad’s role as dominant in character in the piece to this point.(20) Had Travis’ tonal reading (1966) concerned itself with set-classes as well as extended Schenkerian intuitions, he might have viewed this 4-21 harmony as supportive of the final left-hand descent towards a C tonic. The four-note diatonic fragment proves to be a feint, however, nothing more than another of Boss’ tonal “specters”, and m. 8 diverts the listener into set-class 3-12, a harmony non-referable to diatonicism (alongside 3-1 and 3-3) but rather a key hexatonic resource. The particular augmented triad (Eb, G, B) employed in m. 8 is compatible with both Hex2,3 and Hex3,4, the two principal competitors for I-Quality hegemony in the work so far, efficiently tying together these two conflicting hexatonic sound worlds in three notes.(21) The final harmony shown enclosed within the WT1 blue outline occurs in m. 8.3–8.4, articulates the Oct1,2 set-class 4-25, a sonority replete with minor seventh scale degree and two nested tritones. By m. 8, Oct1,2 is the only octatonic collection left unuttered during the miniature; Schoenberg the completionist presents all possible octatonic V-Quality resources before the work’s conclusion.
[5.12] With V-Quality octatonicism having exerted its presence in all of its three forms across op. 19 no. 2, the pressing question at the work’s conclusion is whether V-Quality relents to I-Quality in a traditional tension-relaxation metanarrative. The answer to this question is yes, and spectacularly so. First, there is something of a staggered resolution, where the
[5.13] Eagle-eyed viewers of the coloring scheme utilized across Example 3 and Example 6 will note that yellow indicates the presence of hyper-hexatonic (h-h) material.(22) The 8-19 sonority of m. 9 falls one note shy from the complete h-h2,3,4 collection, a harmony that can be generated from combining the Hex2,3 and Hex3,4 collections (notably: the same two that have been competing heavily for supremacy in this work).(23) The h-h2,3,4 presence is generated by a threefold set of major seventh tetrads in op. 19 no. 2’s final measure. G major seventh and Eb major seventh tetrads occupy the right-hand. At the same time, a C major seventh tetrad plays out below them, allowing the G–B dyad to serve double duty, as the tonic and third of a I-Quality harmony in Hex2,3 and as the fifth and major seventh of another I-Quality harmony in Hex3,4.
[5.14] The note missing from set-class 8-19 in m. 9 that is needed to create complete h-h2,3,4 is
[5.15] The foregoing analysis has illustrated an inter-collectional dialog between hexatonic and octatonic collections across this miniature. The work’s tension-relaxation dynamic is created only in part through the gestural closure of the final left-hand descent through WT1 and the sense of rhythmic arrival on a strong third beat in m. 9.3. The more critical source of this dynamic stems from the character of the harmonies Schoenberg chooses within a broader chromatic soundscape. I-Quality is articulated firmly at the work’s outset, though is quickly dissolved through whole-tone and octatonic complications. The central gesture of the work introduces intrusions onto the soundscape that disrupt any defined sense of I-Quality stability, after which V-Quality tension is woven into the miniature’s fabric steadily through m. 6.3. The work’s conclusion is resoundingly I-Quality. This sensation emerges not only by means of the three interspersed I-Quality major seventh tetrads, but also from the unity between two of Schoenberg’s hexatonic collections (Hex2,3 and Hex3,4), with an outlier collection side-lined (Hex0,1) and octatonicism a distant past.
[5.16] A final issue to address beyond the inter-collectional interplay explored across the piece is the matter of intra-collectional interplay. On the octatonic side of the spectrum, brief moments of Oct0,1 in Gest2 and Oct1,2 in Gest3 erode the primary status of Oct2,3 as the piece’s principal V-Quality pitch space. WT1 arises as a non-hexatonic complication in m. 3, though by mm. 7–8, it becomes clear that whole-tone harmony was insufficient to act as a principal V-Quality agent. The role of WT1 is more to provide an over-arching sound world in which certain diatonic, hexatonic and octatonic subsets may nest, easing the transition from the highly V-Quality octatonicism of m. 6, through a slight decrease in V-Quality (both in the global collectional sense), all the way to the I-Quality of the work’s conclusion.
[5.17] There is a theoretical quirk to the whole-tone material in Gest3. WT1 is, in its entirety, more tritone-laden than the five or six-note octatonic chords within Gest2, and thus more fully exhibits V-Quality. Although the complete WT1 collection of mm. 7-8 nests three tritones (F-B,
6. I-Quality Opening and Closing Harmonies in the Op. 19 Set
[6.1] Several other members of Schoenberg’s op. 19 may similarly benefit from analysis from a Quality perspective, particularly when our eyes and ears focus on their opening and closing stages. These moments often articulate I-Quality harmony, be this hexatonicism or diatonicism. Somewhat more rarely, I-Quality major seventh scale degrees appear at salient start and end points within sets altogether more “chromatic” than the hexatonic and diatonic collections.(26) Examples 7, 8, 9, 10 and 11 catalog the opening and closing stages of pieces no. 1, no. 3, no. 4, no. 5, and no. 6, respectively, omitting performance directions and dynamics but retaining Schoenberg’s accidentals and phrasings, as before. Coloring schemes are also retained from earlier examples, with chromatic sets now shown in purple.
Example 7. Start-End Frame, Schoenberg, op. 19, no. 1 (m. 1/mm. 15–17)
(click to enlarge)
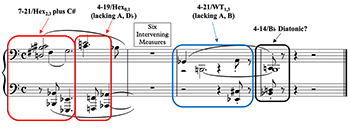
[6.2] Pieces 1, 2, 3, 4 and 5 either start or end or, more frequently, both start and end with I-Quality harmonies clearly articulated. Piece no. 1 (see Example 7) concludes with the B diatonic set-class 4-16, a collection with only one tritone but that articulates an incomplete E major seventh tetrad in the right-hand. This familiarly tonal trichord provides a right-hand inverted pedal harmony for nearly the last three full measures of the piece; the full right-hand part of mm. 15–17, moreover, articulates set-class 4-7 as a subset of Hex3,4, anchoring its ending to a sense of I-Quality through tritone aridity in this register. The left-hand part that plays out through mm. 15–17 fits almost entirely within Hex1,2. The exception is the B natural in m. 17, which is itself referable to the right-hand Hex3,4 collection, facilitating creation of a 4-19 vertical within Hex3,4 on the piece’s penultimate eighth note beat. The pitch structure of mm. 15–17 is almost entirely chromatic, in that two non-overlapping hexatonic collections (Hex1,2 and Hex3,4) are combined; only C natural from Hex3,4 is lacking to complete the aggregate. Even so, demarcation into two I-Quality hexatonic strata provides a particularly ingenious strategy that lends the close of op. 19, no. 1 a distinctive feeling of arrival.
Example 8. Start-End Frame, Schoenberg, op. 19, no. 3, (m. 1/mm. 8–9)
(click to enlarge)
[6.3] Piece no. 3 (see Example 8), a “photographic negative” of piece no. 2 according to Boss (2019, 238), opens with set-class 7-21. This is an extension of I-Quality Hex2,3 that is swiftly transformed into set-class 4-19, a subset of I-Quality Hex0,1. Note that in the 7-21 Hex2,3 sonority, D natural is spelled as a major seventh above the bass note
Example 9. Start-End Frame, Schoenberg, op. 19, no. 4 (mm. 1–2/mm. 12–13)
(click to enlarge)
[6.4] Piece no. 4 (see Example 9) opens with the characteristic I-Quality hexatonic signature of a minor-major seventh tetrad (
Example 10. Start-End Frame, Schoenberg, op. 19, no. 5 (mm. 1–3/mm. 14–15)
(click to enlarge)
[6.5] Piece no. 5 (see Example 10) also concludes with a major seventh harmony, though in a slightly different manner than in pieces 2, 3 and 4. Schoenberg’s left-hand part articulates a complete E-major triad in second inversion, while the right-hand simultaneously provides
[6.6] To summarize, Pieces 1, 2, 3, 4, and 5 start and end with I-quality harmony; this tendency is frequently achieved either by hexatonicism or diatonicism, or by a combination of both, with the major seventh scale degree marker from the major seventh tetrad (germane to both collections) serving as a key agent. Occasionally, as in the conclusion of piece no. 4, an altogether more chromatic set-class manifests, though the major seventh interval nevertheless remains easy to identify: A–
7. Schoenberg’s Op. 19, no. 6 as an Outlier in Terms of Quality
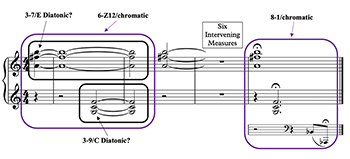
[7.1] Written approximately one month after the funeral of Gustav Mahler, the final member of the op. 19 set was added on June 17, 1911, roughly four months after the completion of the first five (Simms 2000, 85). This sixth miniature is discussed almost as often as op. 19, no. 2 and often along the same tonal versus set-class scholarly lines (Boss 2019, 248–251).(30) Yet the literature typically regards the final member of op. 19 as an outlier within the broader set.(31) This treatment makes sense in light of its later composition date and contrasting, funereal atmosphere. The piece is well known for its austere bell motifs and its increased tendency towards three-note diatonic harmonies, which readily combine to generate larger chromatic ones.
Example 11. Start-End Frame, Schoenberg, op. 19, no. 6 (mm. 1–2/m. 9)
(click to enlarge)
[7.2] Viewing this final piece through the lens of Quality reveals some profound harmonic differences with the other five members of op. 19. The two opening trichords articulated by the right and then left hands belong to diatonic set-classes 3-7 and 3-9, respectively (see Example 11); the latter is voiced quartally.(32) Both of these trichords articulate minor seventh scale degrees, with the 3-7 chord’s spelling suggesting an incomplete dominant seventh built on B. The 3-9 trichord expresses a G-F minor seventh; this harmony appears rather like an incomplete dominant seventh built on G awaiting the resolution of a 4-3 suspension. Both exhibit maximal V-Quality for trichords lacking tritones.
[7.3] The more chromatic set-class generated from the union of these two trichords is 6-Z12.(33) This hexachord, while containing two tritones (C-
[7.4] It is remarkable that the two trichords that form 6-Z12 in op.19, no. 6 are themselves some of the most straightforwardly and texturally bare diatonic harmonies of the set: sonorities to which one might hope to attribute a clearer sense of I or V-Quality. And yet, the combination of these diatonic harmonies into larger chromatic ones results in a profoundly novel approach to shaping Quality, one based on the co-presentation of seventh types. Piece no. 6 is also unique in the sense that its ending—which adds
8. An Ingenious Final Chord
[8.1] Previous discussion has already noted some similarities between pieces nos. 2 and 6 within op. 19; however, there are key differences. Set 8-1 is the most ambitious chromatic chord within op. 19; meanwhile, the closing 8-19 harmony of piece no. 2, which is tantalizingly close to complete h-h2,3,4, is the most ambitious of ends to any op. 19 member, staging three interlocking major seventh tetrad strata. Discerning readers will note two complications that 8-19 poses to Pople’s Quality model. First, as an eight-note sonority, 8-19 can never harbor any fewer than two tritones, which might lead one to identify it as having partially V-Quality status in a manner akin to the Mahler memorial. I would respond to this suggestion by noting that two tritones are the least possible in an eight-note set and that just half (14 out of a possible 28) of eight-note sets include this lowest number of tritones. 8-19 can thus fairly be said to rate as having a high degree of tritone scarcity. Furthermore, the two tritones nested within 8-19, C–
[8.2] 8-19 poses a second complication, one that Quality can help us resolve. The major seventh built up from C, the lowest of three interlocking such tetrads in m. 9, also interacts with the
[8.3] Together, the character of Schoenberg’s harmonic structure, voicings, and performance directions combine to make the most compelling segmentation, from a both set-theoretical and aural perspective, one that foregrounds Hex2,3. As such, this moment can be regarded as close in effect to Schoenberg’s notion of “floating tonality” (schwebende Tonalität) (see Schoenberg [1911] 1978, 383–384): two hexatonic collections tussle for prime status within a broader h-h context, with one unequivocally winning out in Quality terms against that more background set governance. One could say that there is a reciprocal relationship between the tonic- or dominant-quality of a passage and the specific tones within a collection that the passage affirms as home. This relationship occurs because hexatonic (and octatonic) collections are particularly saturated with triadic (and tetrachordal) nodal points that scaffold equivalent harmonies to stable or unstable chords within diatonic, functional tonality.(35)
9. Conclusions
[9.1] When ending their works, composers seeking to extend and eventually abandon tonality in the twentieth century often deferred to the very resource they sought elsewhere to put aside. Scriabin’s Prometheus (op. 60, 1910) concludes in a resounding, resplendent diatonic
[9.2] Before now, no one has explained Schoenberg’s use of the hexatonic collection as a home sonority in op. 19 no. 2, and his attraction to major sevenths and relatively tritonally arid harmonies in the openings and conclusions of the op. 19 set more broadly. This paper argues he may have done so because of this collection’s natural capacity to act as a vessel for the I-Quality sound world that musicians traditionally associate with home tonics within diatonic tonality. Hexatonicism does not contain any of the tritones or minor seventh intervals that characterize dominant-sounding harmonies in tonal music, and indeed it is these more traditionally unstable intervals that arise in the interior of op. 19 no. 2 and in its siblings composed on the same day. The first five members of op. 19 were all written on February 19th, 1911, “in a headlong manner with a minimum of reflection” (Simms 2000, 85). This is a description that correlates well with our sense of these works playing out a natural, pre-existing intuition based on tonal Quality within their wider atonal, chromatic soundscapes. When the “tonal clock struck midnight,” tension and release did not turn “into a pumpkin” (Newton 2014, 1), but continued to inform aspects of Schoenberg’s approach towards deciding where his non-diatonic pitch resources would sit within piece structures.
[9.3] And now again for the age-old question: Tonal oder atonal? The answer for op. 19 no. 2, and indeed the op. 19 set more broadly, is both: tonal and set-class organization may be said to hold sway over musical structure. However, tonality does not merely manifest through small, familiar tonal objects as “occasional expressive devices,” such as an ostinato dyad or final, stepwise descent towards C. Rather, tonal intuition continues to play into the character of the harmonies Schoenberg employs within his broader chromatic language, allowing us to hear and analyze his hexatonic, octatonic, whole-tone, hyper-hexatonic and more chromatic harmonies as playing out quasi-tonal tension-relaxation relationships. Perhaps this is the reason why tonal analyses of op. 19, no. 2 and set-class analyses of op. 19 no. 2 can both locate a sense of closure in this miniature’s concluding measure; both viewpoints have a common ground.
[9.4] It also does not matter greatly whether Schoenberg knowingly composed op. 19, no. 2 with set-class motives/basic shapes or extended tonal intuitions in mind, nor whether he was actively pondering the different types of thirds or the larger collections that are synthetically constructible from them. From the standpoint of reception, Pople’s model of harmonic Quality opens the door to how listeners acquainted with tonality and its tensional trappings may apprehend Schoenberg’s middle period sound world at its most aphoristic, its most austere, without detracting in any way from the chromatic innovations of the composer. We can understand set-classes and non-diatonic collections as quasi-tonal objects through their relative tendencies towards dominant or tonic-quality, perhaps most intuitively by examining their differing sevenths and relative tritone saturations at the musical surface as well as through set-class abstraction.(37) As composers sought to break with tonality, it seems logical that some of its aural trappings would be retained even when its deep-level status as a “guarantor of large-scale coherence” (Boss 2019, 4) had gently dissipated.
[9.5] Of course, a natural friction arises between the understanding of Quality presented in this article and the high rate of pitch-class circulation that is characteristic of Schoenberg’s middle period. We ought to expect such friction when tackling Schoenberg through the lens of non-diatonic sonorities more accustomed to scholars of Stravinsky, Bartók, Scriabin, Messiaen and others. This is all the more so when viewing these sonorities not as collections in the almost inert sense, but as linearized scalar harmonies that can scaffold differing seventh types and numerous residual chords from tonality proper. Schoenberg’s op. 19 harmony, it must be admitted, is not nearly as scalar—and not nearly as organized into discrete units with clear, complete collectional identities—as Pople’s method is designed for. We can nevertheless shed light on the organization and the soundscape of this music with a sensitive application of Pople’s method, proceeding forward while acknowledging that its ebbs and flows between relative I and V-Qualities are of a higher rate than that of other twentieth-century composers. The ultimate goal of my approach is not to solve the question of “tonality versus set-class;” it is rather, to inject nuance into this existing debate by thinking of Schoenberg as a composer of op. 19 no. 2 architectonically, as a collectional, set-class composer in terms of raw pitch resources, but also a composer handling such raw resources with a distinctly tonal intuition. The music he felt compelled to create, a true product of a musical mind experiencing art at the cusp of the twentieth century, looks back at and echoes the past at the very same time as it strives forward.
Rajan Lal
Gonville & Caius College
University of Cambridge
Trinity Street, Cambridge
CB2 1TA, United Kingdom
rsl34@cam.ac.uk
Works Cited
Ayrey, Craig. 1998. “Berg’s ‘Warm Die Lüfte’ and PC Set Genera: A Preliminary Reading.” Music Analysis 17 (2): 163–76. https://doi.org/10.2307/854436.
Baker, James. 1980. “Scriabin’s Implicit Tonality.” Music Theory Spectrum 2 (1): 1–18. https://doi.org/10.2307/746177.
—————. 1986. The Music of Alexander Scriabin. Yale University Press.
—————. 1990. “The Limits of Tonality in the Late Music of Franz Liszt.” Journal of Music Theory 34 (2): 145–73. https://doi.org/10.2307/843836.
Bailey, Katherine. 1997. “Berg’s Aphoristic Pieces.” In The Cambridge Companion to Berg, ed. Anthony Pople, 83–110. Cambridge University Press. https://doi.org/10.1017/CCOL9780521563741.007.
Barkin, Elaine. 1981. “(a song of ing).” In Theory Only 6 (1): 40.
Berger, Arthur. 1963. “Problems of Pitch Organization in Stravinsky.” Perspectives of New Music 2 (1): 11–42. https://doi.org/10.2307/832252.
Boge, Claire. 1992. “Poetic Analysis as Part of Analysis Pedagogy.” In Theory Only 12 (3–4): 47–67. https://doi.org/10.1016/0026-0657(92)90761-3.
Boss, Jack. 2014. Schoenberg’s Twelve-Tone Music: Symmetry and the Musical Idea. Cambridge University Press. https://doi.org/10.1017/CBO9781107110786.
—————. 2019. Schoenberg’s Atonal Music, Musical Idea, Basic Image, and Specters of Tonal Function. Cambridge University Press. https://doi.org/10.1017/9781108296991.
Browne, Richmond. 1981. “Tonal Implications of the Diatonic Set.” In Theory Only 5 (6): 3–21.
Buchler, Michael. 2001. “Relative Saturation of Interval and Set Classes: A New Model for Understanding Pcset Complementation and Resemblance.” Journal of Music Theory 45 (2): 263–343. https://doi.org/10.2307/3653442.
Caplin, William. E. 1984. “Moritz Hauptmann and the Theory of Suspensions.” Music Theory Spectrum 28 (2): 251–69.
Cheong, Wai-Ling. 1993. “Orthography in Scriabin’s Late Works.” Music Analysis 12 (1): 47–69. https://doi.org/10.2307/854075.
—————. 1996. “Scriabin’s Octatonic Sonata.” Journal of the Royal Musical Association 121 (2): 206–28. https://doi.org/10.1093/jrma/121.2.206.
DeLio, Thomas. 1994. “Language and Form in An Early Atonal Composition: Schoenberg’s Opus 19, No. 2.” Indiana Theory Review 15 (2): 17–40.
Dunsby, Jonathan. 2004. “Anthony Pople, 1955–2003: An Appreciation.” Twentieth-Century Music 1 (2): 277–83. https://doi.org/10.1017/S1478572205000150.
Edwards, Ross. 2022. “Setting Mystical Forces in Motion: The Dialectics of Scale-Type Integration in Three Late Works.” In Demystifying Scriabin, ed. Vasilis Kallis and Kenneth Smith, 196–222. Boydell and Brewer. https://doi.org/10.1017/9781800104181.012.
Eriksson, Tore. 1986. “The IC Max Point Structure, MM Vectors and Regions.” Journal of Music Theory 30 (1): 95–111. https://www.jstor.org/stable/843410.
Forte, Allen. 1963. “Context and Continuity in an Atonal Work: A Set-Theoretic Approach.” Perspectives of New Music 1 (2): 72–82. https://doi.org/10.2307/832105.
—————. 1973. The Structure of Atonal Music. Yale University Press.
—————. (1988). “Pitch-Class Set Genera and the Origin of Modern Harmonic Species.” Journal of Music Theory 32: 187–270. https://www.jstor.org/stable/843436.
Greenbaum, Matthew. 2009. “Dialectic in Miniature: Arnold Schoenberg’s Sechs Kleine Klavierstücke Op. 19.” Ex Tempore 14 (2): 51–52.
Guck, Marion. 1977. “A noir – à miroir: Past Senses Reverses Nests (A Priori?).” In Theory Only 2 (10): 29–34.
Hanson, Howard. 1960. Harmonic Material of Modern Music. Appleton-Century-Crofts.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music. The University of Chicago Press.
Hatten, Robert, 1994. Musical Meaning in Beethoven. Indiana University Press.
Heneghan, Áine. 2018. “Schoenberg’s Sentence.” Music Theory Spectrum 40 (2): 179–207. https://doi.org/10.1093/mts/mty030.
Hicken, Kenneth. L. 1980. “Tonal Organization in Schoenberg’s Six Little Piano Pieces, Op. 19.” Canadian University Music Review 1: 130–46. https://doi.org/10.7202/1013738ar.
Hindemith, Paul. 1945. The Craft of Musical Composition. Book I. Translated by Alfred Mendel. Associated Music Publishers.
Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. MIT Press.
—————. 2016. Voice Leading: The Science Behind a Musical Art. MIT Press.
Kallis, Vasilis. 2015. “Pitch Organization in Scriabin’s Tenth Sonata.” Music Analysis 34 (1): 3–46. https://doi.org/10.1111/musa.12039.
—————. 2022. “Demystifying the Mystic.” In Demystifying Scriabin, ed. Vasilis Kallis and Kenneth Smith, 134–57. Boydell and Brewer. https://doi.org/10.1017/9781800104181.009.
Kopp, David. 1995. “On the Function of Function.” Music Theory Online 1 (3). https://mtosmt.org/issues/mto.95.1.3/mto.95.1.3.kopp.html.
Krumhansl, Carol. L. 1990. “Tonal Hierarchies and Rare Intervals in Music Cognition.” Music Perception: An Interdisciplinary Journal 7 (3): 309–24. https://doi.org/10.2307/40285467.
Lee, Ji Yeon. 2023. “The Arrival 6/4 Chord in Wagner’s Die Walküre: Types, Function, and Dramatic Meaning.” Music Analysis 42 (3): 363–411. https://doi.org/10.1111/musa.12219.
Leichtentritt, Hugo. 1951. Musical Form. Harvard University Press. https://doi.org/10.4159/harvard.9780674430754.
Lerdahl, Fred. 1989. “Atonal Prolongational Structure.” Contemporary Music Review 4 (1): 65–87. https://doi.org/10.1080/07494468900640211.
Lester, Joel. 2008. “Rameau and Eighteenth-Century Harmonic Theory.” In The Cambridge History of Western Music Theory, ed. Thomas Christensen, 753–77. Cambridge University Press. https://doi.org/10.1017/CHOL9780521623711.026.
Lewandowski, Stephan. 2010. “‘A Far Higher Power’: Gedanken zu ideengeschichtlichen Vorgängermodellen der Pitch-Class Set Theory.” Tijdschrift voor Muziektheorie 15 (3): 190–210.
Lewin, David. 1982–1983. “Transformational Techniques in Atonal and Other Music Theories.” Perspectives of New Music 21 (1–2): 335–48. https://doi.org/10.2307/832879.
McKee, Eric. 2005. “On the Death of Mahler: Schoenberg’s Op. 19, No. 6.” Theory and Practice 30: 121–51.
Morrison, Charles. 1992. “Syncopation as Motive in Schoenberg’s Op. 19, Nos. 2, 3, and 4.” Music Analysis 11 (1): 85–90. https://doi.org/10.2307/854304.
Newton, Neil. 2014. “An Aspect of Functional Harmony in Schoenberg’s Early Post-Tonal Music.” Music Analysis 33 (1): 1–31. https://doi.org/10.1111/musa.12018.
—————. 2022. “An Investigation into Intrinsic and Extrinsic Function in Vagrant Harmonies.” Music Analysis 41 (2): 243–65. https://doi.org/10.1111/musa.12189.
Parks, Richard. 1989. The Music of Claude Debussy. Yale University Press. https://doi.org/10.2307/j.ctt1xp3t7b.
Pople, Anthony. 1997. “Early Works: Tonality and Beyond.” In The Cambridge Companion to Berg, ed. Anthony Pople, 53–82. Cambridge University Press. https://doi.org/10.1017/CCOL9780521563741.006.
—————. 2004. “Using Complex Set Theory for Tonal Analysis: An Introduction to the ‘Tonalities’ Project.” Music Analysis 23 (2–3): 153–94. https://doi.org/10.1111/j.0262-5245.2004.00201.x.
Quinn, Ian. 2006. “General Equal-Tempered Harmony (Introduction and Part I).” Perspectives of New Music 44 (2): 144–58. https://doi.org/10.1353/pnm.2006.0010.
—————. 2007. “General Equal-Tempered Harmony: Parts 2 and 3.” Perspectives of New Music 45 (1): 4–63. https://doi.org/10.1353/pnm.2007.0016.
Riemann, Hugo. 1895. Harmony Simplified: or, The Theory of Tonal Functions of Chords. Translated by Heinrich Bewerunge. Augener.
Russ, Michael. 2004. “‘Fishing in the Right Place’: Analytical Examples from the ‘Tonalities’ Project.” Music Analysis 23 (2–3): 195–244. https://doi.org/10.1111/j.0262-5245.2004.00202.x.
Russ, Michael, and Jonathan Cross. 2004. “Editorial: An Introduction to Anthony Pople’s ‘Tonalities’ Project.” Music Analysis 23 (2–3): 147–52. https://doi.org/10.1111/j.0262-5245.2004.00200.x.
Schoenberg, Arnold. (1911) 1978. Theory of Harmony. Translated by Roy E. Carter. Faber.
—————. (1948) 1999. Structural Functions of Harmony. Edited by Leonard Stein. Faber.
—————. 1995. The Musical Idea and the Logic, Technique and Art of its Presentation. Translated and edited by Patricia Carpenter and Severine Neff. Columbia University Press.
Simms, Brian. 2000. The Atonal Music of Arnold Schoenberg 1908–1923. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195128260.001.0001.
Smith, Kenneth. 2020. Desire in Chromatic Harmony: A Psychodynamic Exploration of Fin de Siècle Tonality. Oxford University Press. https://doi.org/10.1093/oso/9780190923426.001.0001.
—————. 2021a. “Diatonic Refraction through Metatonal Spaces.” In Music with and after Tonality: Mining the Gap, ed. Paul Fleet, 182–204. Routledge. https://doi.org/10.4324/9780429451713-9.
—————. 2021b. “The Enigma of Entropy in Extended Tonality.” Music Theory Spectrum 43 (1): 1–18. https://doi.org/10.1093/mts/mtaa021.
Smith, Kenneth, and Vasilis Kallis. 2022. “Scriabin and Music Analysis: The Search for the Holy Grail.” In Demystifying Scriabin, ed. Vasilis Kallis and Kenneth Smith, 269–81. Boydell and Brewer. https://doi.org/10.2307/j.ctv24tr735.19.
Stein, Deborah. 1976. “Schoenberg’s Opus 19, No. 2: Voice-Leading and Overall Structure in an Atonal Work.” In Theory Only 2 (7): 27–43.
Straus, Joseph. 1984. “Reviewed Work(s): The Music of Igor Stravinsky by Pieter C. van den Toorn.” Journal of Music Theory 28 (1): 129–34. https://doi.org/10.2307/843455.
—————. 1987. “The Problem of Prolongation in Post-Tonal Music.” Journal of Music Theory 31 (1): 1–22. https://doi.org/10.2307/843544.
—————. 1990. Remaking the Past: Musical Modernism and the Influence of the Tonal Tradition. Harvard University Press. https://doi.org/10.4159/harvard.9780674436336.
—————. 2016. Introduction to Post-Tonal Theory. 4th ed. W. W. Norton.
Taruskin, Richard. 1985. “Chernomor to Kashchei: Harmonic Sorcery; or, Stravinsky’s ‘Angle.’” Journal of the American Musicological Society 38 (1): 72–142. https://doi.org/10.2307/831550.
Travis, Roy. 1966. “Directed Motion in Schoenberg and Webern.” Perspectives of New Music 4 (2): 85–89. https://doi.org/10.2307/832217.
Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Utz, Christian, and Thomas Glaser. 2020. “Shaping Form: Performances as Analyses of Cyclic Macroform in Arnold Schoenberg’s Sechs kleine Klavierstücke, Op.19 (1911), in the Recordings of Eduard Steuermann and Other Pianists.” Music Theory Online 26 (4) https://doi.org/10.30535/mto.26.4.9.
Väisälä, Olli. 1999. “Concepts of Harmony and Prolongation in Schoenberg’s Op.19/2.” Music Theory Spectrum 21 (2): 230–59. https://doi.org/10.2307/745863.
Van den Toorn, Pieter. C. 1983. The Music of Igor Stravinsky. Yale University Press.
Von Massow, Albrecht. 1993. “Abscheid und Neuorientierung – Schönbergs Klavierstück Op. 19, 6.” Archiv für Musikwissenschaft 50 (2): 187–95. https://doi.org/10.2307/931190.
Warren Williams, Edgar, Jr. 1985. “A View of Schoenberg’s Op. 19, No. 2.” College Music Symposium 25: 144–51.
Whittall, Arnold. 2003. “Anthony Pople Remembered.” Music Analysis 22 (3): 24952.
Whittall, Arnold, and Jonathan Dunsby. 1988. Music Analysis in Theory and Practice. Yale University Press. https://doi.org/10.1111/j.0262-5245.2003.00185.x.
Yavorksy, Boleslav. 1908. Materials and Notes on The Structure of Musical Speech. Muzgiz.
Footnotes
1. Respectively, Boss’ camps contain the following studies: a) Hicken 1980; Lerdahl 1989; Vaisala 1999; Lewandowski 2010, b) Forte 1963; Stein 1976; Guck 1977; Whittall and Dunsby 1988, 125–126, c) Warren Williams 1985; Morrison 1992; DeLio 1994; Greenbaum 2009. Boss’ own 2019 reading falls into the third group, composing out the basic narrative of oppositions present in DeLio, Warren Williams and Greenbaum’s studies through expansion to larger referential collections. Additionally, Barkin 1981 and Boge 1992 approach the miniature through the lens of “analytic poetry” (Boss 2019, 234), whilst Utz and Glaser (2020) have recently explored the op. 19 set more broadly, shifting from score-based analysis to performance studies doctrine.
Return to text
2. Broadly, this binary viewpoint concatenates Boss’ second and third scholarly camps and sets them in counterpoint with his first. “Specter” refers to Boss’ understanding that tonality appears (or rather, reappears) in Schoenberg’s output around 1908, “in a much more limited role” (Boss 2019, 4), in contrast to serving as a force that articulates large-scale coherence.
Return to text
3. To my mind, the key difference between a quasi-Schenkerian, tonal approach and a set-class approach to op. 19 no. 2 is one of foreground/background architectonics. In an understanding predicated on competing sets and their referential collections, surface pitches are taken to be indicative of background governing structures. An octatonic subset implies fuller collectional presence, for example. On the quasi-Schenkerian hand, surface pitches are but composings-out (perhaps inflections or alterations) of deeper fundamental structures. One understanding thus progresses from a surface-to-depth viewing in which the deeper level is numerically greater than surface harmony size, whilst the other understanding progresses from a surface-to-depth viewing where the deeper level strips away surface harmony size (harmonies are but surface events subsidiary to deeper prolongations). In these terms, the two approaches would seem irreconcilable.
Return to text
4. Here, I echo assertions in Boss 2019 that analyses of Schoenberg’s atonal works ought to wear “atonal und tonal” hats (40).
Return to text
5. Attempts to define the intrinsic sonic character of harmonies are many and varied. Hanson (1960) proposes a theory of “great categories” in which there are prototypical sonorities of every cardinality in six genera pertaining to each interval class. Eriksson’s (1986) concept of an interval class “max point structure” yields similar results to Hanson (Quinn 2006, 134). A similarity viewpoint may lead to certain assumptions; for example, Forte (1988) and Parks’ (1989) respective theories of pitch-class set genera might lead us to expect that set-classes belonging to one single genus lie “near to one another in quality space” (Quinn 2006, 115). Quinn’s own work (2006; 2007) springboards from David Lewin’s first and last publications to propose compellingly the concept of a “Fourier Balance” in addressing numerous different types of “chord quality”.
The understanding of Quality proposed by Pople and adopted in this article differs from these scholars in that its only quantifiable element concerns number of housed tritones. Moreover, the understanding of Quality offered here is scalar in that it acknowledges differing seventh types at the musical surface, not harmonies, chords or set-classes in more abstract musical space. Thus, Pople’s method has much more in common with theorists who have taken explicitly intervallic approaches toward sonority classification: Yavorskian ‘modal rhythm’, Kholopovian ‘hemitonicism’, etc. However, the most notable predecessor in this regard is Paul Hindemith (1945), who offers a six-part harmonic classification based on tension-release properties, also using tritones and seventh types as arbiters. Similarities to Quality further abound in that Hindemith would describe an increase in dominant-quality through the fluid lens of Gefälle (gradient) and assumes pitch centricity in all his evaluations. Differences include that Hindemith factors in second types as well as sevenths (a rejection of mod-12 set theoretical thinking), a two-voice contrapuntal framework and acoustic considerations. Because the present article is concerned with tension and relaxation in a quasi-tonal sense, a continuum in one dimension, from tonic-quality to dominant-quality, is sufficient, rather than the more multi-category approaches noted above.
Return to text
6. For a detailed insight into Anthony Pople’s legacy and the unfinished Tonalities project, see: Whittall 2003; Pople 2004; Russ and Cross 2004; Russ 2004; Dunsby 2004. The Tonalities software, Pople’s guide to getting started with Tonalities, an archive of score extracts encoded by Pople and an archive of extracts encoded by Russ with associated commentaries may be located through the following University of Huddersfield Archive: https://research.hud.ac.uk/tonalities.
Return to text
7. Regarding asymmetrical collections, one might rightly ask why root centricity is articulated up from scale degree 1 and not any other scale degree. For instance: Why not build pandiatonic harmonies on the fifth of the diatonic scale? The answer to this question is that while such structuring is possible, this article addresses music that has departed the chord-within-scale architecture of functional tonality. Pople and Kallis assume that root centricity is correlated with the nominal root tone used to identify the given scale, i.e., Cac has a quasi-C centricity in an abstract scalar sense.
Regarding symmetrical collections, structures can of course be built up from bass notes that are not nodal tones. Thus, case-by-case sensitivity is required to see if such tones denature the Quality framework proposed here. It is worth noting that the hexatonic collection has no opportunity to be V-Quality, in any voicing, nor does the whole-tone collection regarding I-Quality. The octatonic collection can be voiced as if major seventh-characterized, but its tritonal ubiquity pushes against any true I-Quality sound.
Return to text
8. This classic view, set in contradistinction to those of Rameau and later Schenker, dates back to the eighteenth-century writings of Johann Philipp Kirnberger on “essential” and “nonessential” dissonance, where the “dissonant [here major] seventh is a genuine constituent of the [triadic] harmony” (Caplin 1984, 255).
Return to text
9. Notions of the minor seventh (in a dominant seventh tetrad) being particularly indicative of characteristic dissonance are also found in Rameau’s writings (Lester 2008, 762; Kopp 1995) and in those of Gottfried Weber (Kopp 1995).
Return to text
10. It is not my position to make assertions about the three Riemannian functions in any general sense, nor to explore the relationship between extrinsic function and intrinsic Quality in the present paper. This would demand consideration of the relationships between self-, local- and global-referentiality of harmonic objects.
Return to text
11. For a fuller breakdown of Scriabin’s stockpile of preferred sonorities and the varied dates of their entry into scholarly literature, see Smith and Kallis 2022 as well as Kallis 2022.
Return to text
12. In Example 2, the only instance in Scriabin’s set-class continuum where a superset is not of greater V-Quality than its notable subsets occurs through the acoustic collection, set-class 7-34, and its two notable subsets, set-classes 6-Z23 and 6-34A; the latter is the Mystic Chord. 6-Z23 is also an octatonic subset, so maintains the trend of lesser V-Quality in relation to 8-28.
Return to text
13. Number of housed tritones can be considered relative to the size of the set-class under consideration; this nuanced view can be expressed terms of a “proportional saturation vector”, as developed in Buchler 2001. I do not explore this avenue in the present article because Schoenberg’s op. 19 no. 2 does not deal with a great range of cardinalities; overwhelmingly, sets from a four to six-note size are those under consideration.
Return to text
14. For the most part, Boss’s 2019 analyses “avoid sets larger than hexachords” (Boss 2019, 40). My analysis remains similarly sparing in that I will not remark upon the acoustic-octatonic sonority built on B (set-class 9-10) during the entirety of m. 6, nor will I treat the issue of complements.
Return to text
15. Henceforth, specific transpositions of the hexatonic and octatonic collections are identified by Hexa,b and Octa,b, where subscripts a and b indicate the first two pitch classes in the given scale in normal form, where C = 0. Whole-tone collections are identified by WTx, where subscript x indicates the starting pitch class of the given scale in normal form, where C = 0. This nomenclature is outlined in Straus 2016, 257.
Return to text
16. It is possible to conceptualize this passage is through the lens of octatonic-diatonic “interpenetration,” as developed in Van den Toorn 1983. I do not assume this approach here considering the thorough critique Joseph Straus presents of interpenetration: virtually any harmony, particularly harmonies of a large size can be discussed as “diatonic interpenetration of an octatonic context” (Straus 1984, 132).
One could segment Gest1 along the grounds of mm. 1-3.2 as one unit; this yields set-class 6-31 (G, A, B, D,
Return to text
17. One could quite rightly grouse about my grouping of the G–B dyad that concludes m. 5 with the
Return to text
18. Schoenberg’s writings are awash with commentary on the dual interpretation of vagrant chords such as that here enunciated by 5-28. See, for example, the possibilities for the augmented 6-5 chord in Schoenberg [1911] 1978 (245–247) and the discussion of vagrant harmonies and their “multiple meaning” in Schoenberg [1948] 1999 (44–47). In Structural Functions of Harmony ([1948] 1999), Schoenberg draws attention to the fact that several vagrant harmonies belong to multiple “tonalities” or “regions” correspondent to the triadic structures that lay nested within the symmetrical collections discussed in the above analysis.
Return to text
19. Because 4-12 is a subset of all but one eight-note set-class (8-23, Forte’s so-named “diatonic octad”), and because the octatonic set 8-28 is a superset of almost half of all four-note set-classes (13/29), I would not say that the feeling of Oct0,1 is in any way strong here in set-theoretical terms (in addition to the fleeting presence of 4-12 in a gestural sense).
Return to text
20. One could also group together the F–A and
Return to text
21. The
Return to text
22. Henceforth, each h-h collection will be identified by h-ha,b,c notation, where subscript a, b and c refer to the three starting pitch classes of the specific transposition in normal form, where C = 0.
Return to text
23. Hyper-hexatonicism can be generated by combining two hexatonic collections that already share three pitches. Combining two hexatonic collections that do not already share half their pitches generates the chromatic aggregate.
Return to text
24. There is a third reason as well, one that ties into the G HM reading of mm. 1–3 detailed in endnote 16; the
Return to text
25. This is a reciprocal relationship in terms of reasoning because h-h pitch structure can only arise, from standalone hexatonic contexts, by combining hexatonic collections that are already half invariant. If Hex0,1 was to play any role in the final chord, then we would be talking about chromatic saturation much more akin to the close of op. 19, no. 1.
Return to text
26. I will henceforth determine set-classes as “chromatic” through two criteria; both criteria must be fulfilled to satisfy the distinction. Firstly, if at least half of the pitches in the set can be arranged in consecutive half steps, i.e., set-class 3-1 is a subset of a given six-note set in that it makes up at least half of its constituent pitches. Secondly, if the set-class in question resists easy classification through other scalar means. The h-h collection is not a chromatic set in both the first and second senses; even though 9-12 nests three forms of set-class 3-1, these cannot be arranged in consecutive half steps that sum to at least half the notes of the set. Moreover, 9-12 has a colloquial name that we may use for easier identification.
Return to text
27. The effect might even be heard as an expanded “arrival” second inversion chord to end the piece, a phenomenon with precedent ranging from Beethoven to Wagner (see Hatten 1994; Lee 2023). The effect here is, however, heard as relative I-Quality stability, not the instability usually heralded in a functional context by a ![]()
Return to text
28. See Boss 2019, 240–245, for compelling analysis of the interior of piece no. 3.
Return to text
29. It is relevant that Berg also employed hyper-hexatonicism as an agent of closure in two key works written closely to Schoenberg’s op. 19. The first work to employ such harmony at its close is the final member of Berg’s Vier Gesänge, op. 2 (1910); here 8-19 arises as the sum of two chords articulating a highly chromaticised
Return to text
30. For a set-class viewpoint on op. 19 no. 6, see Forte 1963 and Forte 1973 (96–100). For more tonal viewpoints on op. 19 no. 6, see Leichtentritt 1951 (444–45) and Hicken 1980. As with op. 19 no. 2, tonal viewpoints rarely agree on a given key or tonic for op. 19, no. 6 (Boss 2019, 249).
Return to text
31. Quite unlike the other members of op. 19, scholarship surrounding piece no. 6 is, understandably, more laden with programmatic elements related to Mahler’s death (Von Massow 1993; Lewin 1982–1983; McKee 2005).
Return to text
32. 3-7 in this context could belong to the G, D, A or E diatonic collections, while 3-9 in this context is one degree more ambiguous, being potentially referable to the C, F,
Return to text
33. For Forte (1973, 100) 6-Z12 forms “a kind of motto for the composition” on account of its thorough K and Kh relations to other sonorities.
Return to text
34. The most comparable opening to piece no. 6 within op. 19 occurs in the upbeat to m. 1 of piece no. 1, where the similarly chromatic set-class 5-3 (A, B, C, G,
Return to text
35. A hexatonic collection contains three pitches separated by major third that can support a major triad, minor triad, I-Quality major seventh tetrad (set-class 4-20) and I-Quality minor major seventh chord (set-class 4-19A). An octatonic collection contains four pitches separated by minor third that can each support a major triad, minor triad, V-Quality dominant seventh tetrad (set-class 4-27) and V-Quality V
Return to text
36. See: Baker 1980, Baker 1986, INLINE CITATION, for examples on Scriabin and Liszt.
Return to text
37. The approach espoused in this article is profoundly different from that of residual tonal functions presented by Newton (2014); to clarify, I am not looking for literal discharges of unstable tritones. I would also not suggest that the collections identified in the present analysis manifest as dominant or tonic pitch spaces in any functionally tonal sense, certainly not in the extended “extrinsic” manner proposed in Newton 2022. The understanding of Quality outlined in this article is much more akin to Newton’s notion of “intrinsic” harmonic function (Newton 2022, 248), though I see its closest bedfellow in the literature to be Smith’s kinetics-inspired approach towards charge and discharge initiated by different non-diatonic collections (see Smith 2020, Smith 2021a), such is its scalar orientation.
My approach is distinctly Yavorskian (Yavorsky 1908) in that it privileges tritone instabilities above augmented triad instabilities. Newton acknowledges tritone instability, as Pople and I do, but adds the augmented triad into the arsenal of Schoenberg chordal vagrancies (Newton 2014, 3-4). I do not adopt this view at present because the hexatonic collection, composed of two augmented triads with roots one half step apart, is articulated at structural start and end points which we traditionally associate with harmonic stability in op. 19. Moreover, given the normative status of hexatonic collections in the music of the Second Viennese school, free atonal and serial, it seems curious to assign augmented triads that together yield hexatonic construction a degree of instability akin to that articulated by more tritonally populous sets.
Return to text
The understanding of Quality proposed by Pople and adopted in this article differs from these scholars in that its only quantifiable element concerns number of housed tritones. Moreover, the understanding of Quality offered here is scalar in that it acknowledges differing seventh types at the musical surface, not harmonies, chords or set-classes in more abstract musical space. Thus, Pople’s method has much more in common with theorists who have taken explicitly intervallic approaches toward sonority classification: Yavorskian ‘modal rhythm’, Kholopovian ‘hemitonicism’, etc. However, the most notable predecessor in this regard is Paul Hindemith (1945), who offers a six-part harmonic classification based on tension-release properties, also using tritones and seventh types as arbiters. Similarities to Quality further abound in that Hindemith would describe an increase in dominant-quality through the fluid lens of Gefälle (gradient) and assumes pitch centricity in all his evaluations. Differences include that Hindemith factors in second types as well as sevenths (a rejection of mod-12 set theoretical thinking), a two-voice contrapuntal framework and acoustic considerations. Because the present article is concerned with tension and relaxation in a quasi-tonal sense, a continuum in one dimension, from tonic-quality to dominant-quality, is sufficient, rather than the more multi-category approaches noted above.
Regarding symmetrical collections, structures can of course be built up from bass notes that are not nodal tones. Thus, case-by-case sensitivity is required to see if such tones denature the Quality framework proposed here. It is worth noting that the hexatonic collection has no opportunity to be V-Quality, in any voicing, nor does the whole-tone collection regarding I-Quality. The octatonic collection can be voiced as if major seventh-characterized, but its tritonal ubiquity pushes against any true I-Quality sound.
One could segment Gest1 along the grounds of mm. 1-3.2 as one unit; this yields set-class 6-31 (G, A, B, D, D♯, F♯), lacking only C to form the complete G harmonic major collection. A pitch structure referable to G HM is reinforced by the appearance of C in m. 3.3, though is quickly destroyed by the appearance of A♭ in m. 3.4 (which creates set-class 8-18 if viewed in tandem with G, or 7-31 within Oct2,3 if viewed as a chromatic replacement for G). Perhaps, there an argument here for an interplay between G HM and Oct2,3, practiced through scalar maximal intersection, with 7-31 symptomatic of what Tymoczko terms the “subset technique” and a view to enhancing voice-leading efficiency (Tymoczko 2011, 341–348). No further relationships of this nature manifest in Gest2 or Gest3 of op. 19 no. 2, so these scales remain in the category of standalone observation.
My approach is distinctly Yavorskian (Yavorsky 1908) in that it privileges tritone instabilities above augmented triad instabilities. Newton acknowledges tritone instability, as Pople and I do, but adds the augmented triad into the arsenal of Schoenberg chordal vagrancies (Newton 2014, 3-4). I do not adopt this view at present because the hexatonic collection, composed of two augmented triads with roots one half step apart, is articulated at structural start and end points which we traditionally associate with harmonic stability in op. 19. Moreover, given the normative status of hexatonic collections in the music of the Second Viennese school, free atonal and serial, it seems curious to assign augmented triads that together yield hexatonic construction a degree of instability akin to that articulated by more tritonally populous sets.
Copyright Statement
Copyright © 2024 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Lauren Irschick, Editorial Assistant
Number of visits:
4861