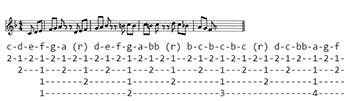Loud Rests and Other Strange Metric Phenomena (or, Meter as Heard)
Justin M. London
KEYWORDS: meter, rhythm, accent, parameter, perception, cognition, entrainment, ontology, dynamic model of meter
ABSTRACT: This is an excerpt from a work-in-progress, portions of which will be read at the 1993 meeting of the Society for Music Perception and Cognition. In order to give an adequate account of “loud” rests, metric articulations, and meter's propulsive character (as noted by theorists such as Berry and Zuckerkandl), a dynamic model of meter is proposed. In framing this model a brief overview of theoretical strategies for metric models is given. The dynamic model regards meter as a listener-generated framework for the understanding musical time. The theoretical implications of the dynamic model are discussed, as it challenges traditional notions of meter as “part of the music,” that is, as musical parameter with the same ontological status as pitch, loudness, timbre, texture, and rhythm.
Copyright © 1993 Society for Music Theory
Introduction
[0] Note: The three musical examples in the .gif file, while helpful, are not absolutely necessary for comprehension of this article; verbal descriptions of the salient features of each example are given in the text. Also, there are several citations to the author’s dissertation in the following article which are the natural outcome of the close relationship between the essay below and the dissertation, the former being an extension of some ideas already explored in the latter.
[1] Cooper and Meyer have noted that the downbeat of measure 280 in the first movement of Beethoven’s “Eroica” symphony “must be the loudest silence in musical literature.”(1) This moment, where triple meter has at last been re-established following an extended duple-vs.-triple conflict (in measures 250–75) is unequivocally striking, a moment whose poignancy and power is immediately felt.(2) But what exactly happens on the downbeat of measure 280? First and foremost, does something happen, or is it the absence of something which strikes us so profoundly? But if something does happen, what kind of thing is it?
Example 1. “accented” rest
(click to enlarge)
Example 2. Metric articulation within the span of a held note
(click to enlarge)
[2] The downbeat of measure 280 in Beethoven occurs in an incredibly
rich musical context—as there are not only metric intrigues here,
but also a nexus of motivic, phrasing, tonal, and formal events—and
thus it may be helpful to consider the metric issues in a simpler
context, and so I have composed the following two (and admittedly banal)
examples. [Example 1 and Example 2]. In Example 1 we have another “loud”
downbeat, though one not as markedly loud as measure 280 in the Beethoven
example. Following a clear antecedent phrase in
[3] The quick answer to such questions is, of course, “because one hears a beat or a downbeat in these cases.” But what exactly is meant by “hearing a beat?” I am quick to add that to come up with adequate definitions for “beat” and ”downbeat” is no easy task, as the work of theorists past and present will attest. Since beats and downbeats are “primitives” in most metric theories, these questions ultimately drive us down the slippery slope to ask “what is meter?”
The Physicist and the Musician Look at Musical Parameters
[4] Meter is often regarded as one of the parameters of music, an
aspect of musical structure (or to put it another way, a dimension
of musical description) that taken together with pitch, duration,
timbre, articulation, dynamics, and texture allows for a thorough
account of a musical event. Kramer puts it most boldly: “Meter is
not separate from music, since music itself determines the pattern
of accents we interpret as meter
| The MUSICIAN | The PHYSICIST |
| Pitch | Frequency of waveform |
| Rhythm | Duration in microseconds of event |
| Timbre | Shape of waveform |
| Articulation | Envelope of waveform |
| Loudness | Amplitude of waveform |
| Meter | (????) |
While these pairs of terms are not merely synonymous, they do show to serve how the physical attributes of sound inhere in the various musical parameters (for example, the physicist’s understanding of frequency is stated in terms of cycles per second of periodic vibration, and even if she takes octaves into account by mapping the frequencies onto a logarithmic scale, this is still quite different from the notion of “pitch” which defines tones relative to some scale or tuning context). And I hasten to add that these features are interdependent, especially those of timbre, articulation, and loudness. But where is meter for the physicist?
[5] Well, meter has something to do with musical time, so one might place meter under rhythm, as the term “rhythm” is admittedly vague. For clearly “rhythm” is more than just the duration of single notes/events; it also involves patterns of durations (i.e rhythmic groups), and patterns of patterns, and so forth. Perhaps meter can be subsumed under rhythmic grouping, that is, a special kind of temporal patterning.(4) We will allow our physicist, with help from a friendly, nearby music theorist, to consider meter to be a special kind of periodicity present in the music, one which is based on hierarchically regular isochronous durations.
[6] We give our physicist the following example [Example 3], where the duration of each pitch is an 8th note, and each rest two eighth notes (rests are indicated by (r)), at a tempo of a quarter-note = 100:
c-d-e-f-g-a (r) d-e-f-g-a-bb (r) b-c-b-c-b-c (r) d-c-bb-a-g-f
(N.B. “b”=
c-d-e-f-g-a (r) d-e-f-g-a-bb (r) b-c-b-c-b-c (r) d-c-bb-a-g-f
2-1-2-1-2-1-2-1-2-1-2-1-2-1-2-1--2-1-2-1-2-1-2-1-2-1-2--1-2-1-
2---1---2---1---2---1---2---1----2---1---2---1---2----1---2-
1-------2-------1-------2--------1-------2--------1-----
1---------------2----------------3----------------4-----
[7] So, the physicist can assign a unique label each note/event based
on its position within the hierarchy of periodicities (for example,
the “a” which starts the second rhythmic/motivic group can be labelled
as occurring at “1.2.1.2,” that is, Measure #1, 2nd half-note span of
Measure #1, first quarter-note span of 2nd half note, 2nd
eighth-note-span of first quarter-note). But (again, leaving the
time-span versus time-point question aside for the moment) what does
the physicist have? Is it meter? More to the point, what can the
physicist do with her periodic recognition? Well, along with a
particular pitch, duration, waveform, articulation, and dynamic, she
can now give each musical event a location (e.g. 1.2.1.2) relative
to the other events in this
[8] Our unhappy theorist has read a bit of psychology; he knows that when we listen to a periodically regular stimulus (to speak in psychological terms for a moment), psychological experiment has shown that we tend to respond by “entraining” our perceptions; that is, we tune our rates of attending to the rhythms present in our environment. As a result of this entrainment, we anticipate the occurrence of future events. We also seem to have particular range of sensitivity (whether learned or innate is another question) for attending to periodicities, what psychologists have termed “natural pace” or “preferred tempo” which falls in the range of 60–120 beats/minute.(6) Given these cognitive proclivities, we would expect that not only is meter used to give a location to previous events, but also to anticipate the location of future musical events. Furthermore, the presence of this projected/anticipatory framework can and at times does affect our interpretation of the ensuing musical events. Thus, to assuage his displeasure, our unhappy theorist turns to the current literature to see if his colleagues have provided an account of meter which can accommodate both the physicist’s periodicity and the psychologists entrainment.
Theoretical Strategies for Defining Meter
[9] There are three broad strategies for defining meter and metric accent: (a) one may divide time spans into smaller chunks, and then sub-divide the chunks, and so forth, with meter as the fallout of this segmentation process; (b) one may have an emergent hierarchy of time points independent of (though still interdependent with) concomitant durations; or (c) one may have an ordered series of time points (that is, counting patterns) whose accent is not hierarchically determined by “external” factors, but rather whose generative process itself gives rise to a modest time-point hierarchy.(7) In the previous paragraphs our physicist used the first strategy to determine the meter in Example 3. The end product of all three strategies is a set of temporal locations for musical events—either the “edges” of real durations, or time-points apart from durational phenomena. But if we assume that meter is crucially linked to our cognitive process, then we must ask which of these three strategies is best suited to the way(s) we actually deal with musical structures in our real-time listening experience—in other words, meter-as-heard.
[10] The first observation one might make regarding meter-as-heard is that we can differentiate two distinct phases of metric cognition. The first phase involves the initial recognition/discovery of the metric context, as happens either (a) at the very beginning of the piece, or (b) when we find ourselves thrown into a piece in medias res (as when we turn on the radio to the middle of a symphony or blues song). The second phase involves the continuation of an established context. The cognitive tasks are very different in these two phases. The first involves a rather high processing load, as every event an equal amount of metric significance (or potential significance). At the same time the listener is searching to find the most salient parameter(s) for metric information. Fortunately, in this first phase normally we are not trying to re-invent the metric wheel, as it were, but rather simply trying to match the initial series of musical events to a small number of metric archetypes.(8) Once the meter has been recognized the cognitive load drops considerably. Now the listener is entrained and needs relatively little information to maintain the metric pattern. Indeed, as is well known, we will continue to maintain the chosen pattern even when confronted with a fair amount of contradictory information (e.g. an extended passage of syncopation, or a series of stressed weak beats, etc.). In order to break or shift an established metric pattern we must be presented with a strong and continuing series of cues in order to achieve a metric reconfiguration.
[11] While all three metric strategies listed above may be used as means for metric recognition/ discovery—that is, during the first phase of metric cognition—one realizes that the first two strategies create problems in the second phase of metric cognition in that they allow only for the retrospective hearing of metric patterns. In the case of time-span segmentation this limitation is readily apparent, for one cannot begin sub-dividing a time span until its duration is complete. For the hierarchically-minded time-span segmenter this becomes an especially acute problem, for if the determination of the beat is determined by the partitioning of the measure, one must first have the location of the downbeats. But if the downbeats are determined by the partitioning of the next-larger span, then one must wait—and so on, and so on—and thus one does not know the location of the first beat (if a top-down partitioning plan is rigorously followed) until the piece is over (!). The problem is alleviated somewhat if we employ the second strategy and consider meter to be a hierarchy of time points built from the bottom up. Here we can (usually) read the lowest level of subdivision “right off the surface,” as it were. As soon as periodicities emerge we can retrospectively (but relatively quickly) tag particular moments at higher levels, such as the beat. Downbeats remain a potential problem, however, in that one is always looking backward for cues which mark a higher-level metric articulation.(9)
[12]. Fortunately, there is a fairly simply solution to the problem of retrospective metric hearing, and that is to combine a model of meter as hierarchic patterning of time-points with a knowledge of metric templates and our proclivities for entrainment—in other words, let’s tap our feet and count along. In counting along, we not only mark locations for events as they occur—we also anticipate the locations (and musical salience) of future events. This is a dynamic model of meter which assumes that meter is an active part of the listening process. It is the listener who, once the meter has been recognized, creates the “generative process that gives rise to a modest time-point hierarchy.” This assumption is admittedly restrictive, in that meter, for the most part, requires known archetypes. Similarly, since metric hearing is assumed to be a form of temporal entrainment, it demands that metric patterns be largely isochronous.(10) However, the dynamic model accords nicely with the simulations of metric attention proposed by Gjerdingen, where events at metrically important locations are assumed to be of greater structural importance, as well as Clarke’s experimental studies of metric perception, which use known metric patterns along with two basic durational categories (long vs. short) to account for a wide variety of rhythmic phenomena.(11)
The Ontological Status of Meter
[13] If we adopt the meter-as-counting-time-point-patterns model, we have made some rather far-reaching commitments regarding meter’s ontological status. Under this framework meter is a listener-generated construct that is intertwined with the musical surface. Meter is not “part of the music” in the same way that pitch, timbre, and duration are. This commitment may be more troubling for some theorists than others, and to explain (at least in part) this uneasiness I will arbitrarily divide my colleagues into two groups, the “structuralists” and the “phenomenologists.”
[14] The structuralist regards music as existing “out there,” apart from the listener, and thus treats our listening and cognition experiences as our efforts to understand these external sound objects. Given this assumption, meter as I have defined it is a particular kind of response to a particular kind of sound stimulus. As such, meter would then seem to be in the same basket as our other responses to sonic stimuli, such as feelings of sadness, surprise, or pain (if the music is unbearably loud), evoked remembrances, and so forth. This stimulus-response approach to meter, with its behaviorist overtones, is justifiably suspect. By contrast, the phenomenologist regards musical structure(s) as the product of the interaction between a sound object and our cognitive faculties; she disdains the notion that music qua music is only an external sound object, separate from the listener. For her the meter-as-counting model is more plausible. While meter is not part of the sound object, it nonetheless may still be regarded as “part of the music.”(12) Meter is neither a parameter like pitch or timbre, nor is it part of a nested measuring of durational patterns and/or periodicities. It is something that is heard and felt. And this is of course why the physicist has so much trouble with meter, for physics is not phenomenology. The physicist’s job is to describe the structure of physical objects in the world. Understanding our interaction with those objects is beyond the scope of the physicist’s mission—at least if we stay above the quantum level.
[15] The dynamism of the meter-as-actively-counting-time-point-patterns explains how and why we hear loud rests and metric articulations, as well as meter’s propulsive character. In most cases our self-supplied metric articulations go unnoticed because most of the time they are redundant: metric articulations at the levels of the downbeat, beat, and beat-subdivision(s) tend to be phenomenally present somewhere in the musical texture. What makes the Eroica example so striking is the absence of that redundancy just where we expect it the most. For at the very moment where we expect the culmination of a tissue of musical processes, all we get is the “default” articulation of the downbeat as we count along. With so much riding on that moment, the little metric “click” we hear/create in our heads is deafeningly loud indeed. In other cases, such as Example 2, the metric clicks are not so loud, but they nonetheless may be heard. A few theorists, most notably Berry and Zuckerkandl, have at length described meter’s propulsive character.(13) Here is Zuckerkandl’s aptly-worded account:
A measure, then, is a whole made up, not of equal fractions of time, but of differently directed and mutually complementary cyclical phases.. . . With every measure we got through the succession of phases characteristic of wave motion: subsidence from the wave crest, reversal of motion in the wave trough, ascent toward a new crest, attainment ofthe summit, which immediately turns into a new subsidence—a new wave has begun. (168)
He goes on to comment that:
Now we see the wrong-headedness of the doctrine that musical time, that is, the grouping of beats into measures, springs from differentiation of accents. There is no need for externally derived accents in order to distinguish weak and strong beats from one another and thus establish the metrical pattern. It is the wave released by the regular succession of marks in the time flux that in each case emphasizes the beat which falls on “one”; brings all the beats between “one” and “one” into a group. The theory that the metrical pattern depends upon accentual differences confuses cause and effect. It is not a differentiation of accents which produces meter, it is meter which produces a differentiation of accents. (168–69)
If meter were a partitioning of time-spans or a hierarchy of time points it would be difficult to see why meter should have such propulsive properties, but these properties are the natural fallout of a dynamic model. Indeed, under such a model it seems difficult to avoid such properties.
[16] Embracing a dynamic model of meter is not without theoretical cost. First and foremost, one must confront the ontological considerations of meter noted above. If meter is still “part of the music,” it is no longer phenomenally part of musical sounds and structures in the same way as pitch, timbre, dynamics, articulation, and duration. Since meter is based upon known archetypes, it is a facet of musical listening that is acquired, rather than innate (though metric hearing probably does not depend on formal training)—and so the theorist becomes interested in how we acquire such skills. As part of our cognitive matrix for musical experience, our metric sensibilities would also appear to be bound up with our other kinesthetic activities, and thus that too becomes an area of interest. One is also perhaps ruling out a number of structures that are often listed under the rubric of meter as non-metric phenomena, i.e.“mixed meters” (where there is no substantially continuing metric pattern, but only a succession of ever-changing metric notations) and thoroughly irregular meters (as contrasted from the modestly irregular meter noted above). And of course, the dynamic approach to meter creates large (and perhaps insoluble) problems for hypermeter—but that is another paper.
Justin M. London
Carleton College
Department of Music
Northfield, MN 55057
jlondon@carleton.edu
Footnotes
1. Cooper, Grosvenor, and Meyer, Leonard. The Rhythmic Structure of
Music, Chicago: Phoenix Press (1960): 139.
Return to text
2. Cooper and Meyer (op. cit.) view this moment as the culmination of
an extended anacrusis, the moment of thesis following an 8 mm. arsis.
While I would not describe mm. 272–79 as an extended anacrusis, as I
feel it is an inappropriate application of a phrase-level phenomenon
to higher structural levels, nonetheless I agree with Cooper and
Meyer's characterization of the essential rhythmic feel of the passage.
Return to text
3. Jonathan Kramer, The Time of Music, New York: Schirmer Books,
(1988): 82.
Return to text
4. The author is well aware of the fact that rhythmic groups consist of
patterns of duration, that is, of time spans, versus metric patterns
which may be viewed as an ordering of time-points. I do not wish to
imply here that I regard meter as a time-span phenomenon (as will be
made clear below). It has also been posited that metric patterns need
not be isochronous, especially on higher metric levels (see Kramer, op.
cit., Ch. 4). For the moment, let us allow our physicist to struggle
toward meter as best she can, with an admittedly over-simplified metric
model.
Return to text
5. The physicist's metric labels function as a temporal index for each
event—but one could also give an equally-useful index (at least for a
physicist) by simply labelling each event at the 8th-note level as
1,2,3,4,5,6,7
Return to text
6. For a detailed overview of psychological research in these areas
see Justin London, “The Interaction Between Meter and Phrase Beginnings
and Endings in the Mature Instrumental Music of Haydn and Mozart,” Ph.D.
Diss., U. of Pennsylvania (1990), Ch. 1, and David Butler, The
Musician's Guide to Perception and Cognition New York: Schirmer (1992).
Return to text
7. Given the scope of this essay I wish to avoid specific critiques
of other recent work in metric theory. Also, several fine overviews
of current work in metric theory are available elsewhere; see Fred
Lerdahl and Ray Jackendoff, A Generative Theory of Tonal Music,
Cambridge, MA: MIT Press (1983), esp. Chs. 2 and 4; Jonathan Kramer,
op. cit., Ch 4; and Justin London, op. cit., Chs 1 and 5.
Return to text
8. The number of metric archetypes is quite small: binary or ternary
patterns of beats, and simple versus compound subdivisions of those
beats. Moreover, I would posit that listeners have a store of
durational and pitch/durational templates which fit into the metric
archetypes. And so, for example, our anacrustic figure in example 3
involves the matching of a pitch-durational sequence (sol-la-ti-do
in even durations) into a limited number of metric possibilities. If
the notes are assumed to be subdivisions of the beat (a reasonable
assumption given the notion of natural pace) then the metric
recognition task boils down to simple versus compound subdivision—that
is, if do is the downbeat, then are the beats quarters or dotted
quarters? Furthermore, in actual performance (that is, by a human
player as opposed to a “deadpan” realization on a synthesizer) it is
likely that timing and dynamic cues within the sol-la-ti anacrusis
would indicate simple or compound time; see, for example, Eric F.
Clarke, “Categorical Rhythmic Perception: An Ecological Perspective"
in Action and Perception in Rhythm and Music, ed. Alf Gabrielsson,
Stockholm: Royal Swedish Academy of Music (1987): 19–33.
Return to text
9. Downbeats are, by definition, metrically-accented beats. Yet there
are a considerable number of problems with the notion of an accented
beat, for how do phenomenal properties, such as length, loudness,
contour salience, tonal emphasis, etc. inhere in a time-point? While
it is clear that these parametric differences can and do give rise to
rhythmic accent, how can one connect these to a nearly durationless
instant? Well aware of these problems Wallace Berry has spoken of
downbeats as “iterative impulses” (Structural Functions in Music,
2nd ed., Mineola: Dover Publications (1987): 327) and Kramer has
approached metric accent as an “accent of initiation” (op. cit.,
p.86). The problem here is that in order to recognize that something
has been initiated, it must endure for a while (and the higher the
structural level, the longer one must wait), and thus metric
accents—if they are accents of initiation—can only be tagged
retrospectively.
Return to text
10. Two comments regarding these restrictions: first, I stress/repeat
that the known archetypes are not “2/4,” “3/4,” “6/8,” “12/8” but rather
a matrix of “duple or triple” orderings for three to four layers of
time points. Thus one could “build” a template for a new or unusual
metric pattern even if one had not experienced it before. Second,
and following from the first, by “largely isochronous” I mean that
most (but not necessarily all) layers of the metric pattern be
isochronous. One can entrain to a pattern which encompasses some
irregularity. For example, Dave Brubeck's jazz standard “Blue Rondo
al a Turk” is based on a complex meter of 2+2+2+3/8, where the
8th-note level is isochronous, the downbeat level is also isochronous,
but the intermediate “beat” level is not. Nonetheless, once the
pattern is recognized, one can tap along to the “limping” meter quite
nicely.
Return to text
11. Robert O. Gjerdingen, “Meter as a Mode of Attending: A Network
Simulation of Attentional Rhythmicity in Music,” Integral 3 (1989):
67–91; Eric F. Clarke, op. cit.
Return to text
12. Of course, she now has another problem, and that is to confront
the different kinds of “phenomenological fallout” that the interaction
between the sound object and the listener may generate. For clearly
one would not want to put meter and remembrances of things past (as
triggered by hearing “our song”) in the same cognitive/phenomenological
basket.
Return to text
13. Wallace Berry, op. cit., and Victor Zuckerkandl, Sound and
Symbol, translated by Willard R. Trask, New York: Pantheon Books,
1956.
Return to text
Copyright Statement
Copyright © 1993 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Natalie Boisvert, Cynthia Gonzales, and Rebecca Flore, Editorial Assistants
Number of visits:
4850