Toward a Semiotic Evaluation of Music Analyses

[1] Semiotics, which describes the structure of meaning, is grandly comprehensive in scope. Umberto Eco's Theory of Semiotics, for example, defines a “sign” as “everything, that, on the grounds of a previously established social convention, can be taken as something standing for something else” (Eco 1976, 16; page numbers parenthesized below refer to the same work); Barthes's writings approximate “a translinguistics which examines all sign systems with reference to linguistic laws” (30); and others' refer to a “logic of culture” (26–28) not specifically linguistic. Yet supporting these transdisciplinary ambitions lies a well-developed foundation for discussing some important problems of specifically musical philosophy and aesthetics.

[2] A question that has dominated most such discussions is “What does music mean?” (It motivates earlier important studies by Coker, Meyer, and Cone as well.) Scholars' responses have explored the analogies between various modes of music cognition and various types of semiosis. (The diversity of these applications can be observed in McCreless 1988, Hatten 1989, Brooks 1980, Micznik 1989, and Agawu 1991). Far fewer studies analyze the various types of discourse about music, in order to answer the question “What do the signs we use to analyze music mean?”; yet this is an easier question to answer, and more pressing, for it seems essential that as professional interpreters of music we should constantly evaluate the accuracy and efficacy of the discourse we use. Jean-Jacques Nattiez (1990) has recently classified various types of analysis with respect to Molino's tripartition. He attributes the differences among analyses of the same piece to the symbolic nature of the musical act and the analytical act; however his work to date has not concentrated on any particular type of discourse. A more promising precedent for a semiotic analysis of musical discourse is Dunsby and Stopford's contrastingly technical and ecumenical essay (1981), which shows how Schenkerian analysis qualifies as a semiotic system by identifying the combinational system of counterpoint as its basis for signification.

[3] To understand better why evaluating music analysis is important, and how semiotics can help, let us review some essentials of Eco's theory, which is the most recent, explicit, and comprehensive. Eco regards signification as arising from the correlation of two distinct formal systems (see his Table 6, p. 53). A syntactic system is “a set of signals ruled by internal combinatory laws . . . an interplay of empty positions and mutual oppositions” (36). A semantic system consists of “a set of possible communicative contents” (37), typically a culturally-determined set of notions about the continuum of experience (76– 78). Each cultural unit in the semantic system “‘exists’ and is recognized insofar as there exists another one which is opposed to it.” (73) That is, semantic and syntactic systems are not distinguishable by their structure; both systems “can subsist independently of any sort of significant or communicative purpose, and as such may be studied by information theory or by various types of generative grammars.” (38) Rather they are distinguished by their respective functions in signification. A sign (or, more properly, a sign-function) arises every time “an element of an expression plane [is] conventionally correlated to one (or several) elements of a content plane.” (48) Syntactic systems serve as expression planes, and semantic systems serve as content planes in signification. The expression and content are called sign-vehicle and sememe (or meaning), respectively, and their correlation is called denotation. “The meaning of a sign-vehicle . . . is a semantic unit posited in a precise ‘space’ within a semantic system.” (84) A code is a collection of sign-functions linking a syntactic system with a semantic system. It “establishes the correlation of an expression plane (in its purely formal and systematic aspect) with a content plane (in its purely formal and systematic aspect)” (50), and so determines “that a given array of syntactic signals refers back . . . to a given ‘pertinent’ segmentation of the semantic system.”(36–37) Connotation arises from the “superelevation of codes” when a “signification [is] conveyed by a previous signification,” that is, when “the content of the former signification (along with the units that conveyed it) becomes the expression of a further content,” by means of a distinct connotative code (55). That is, connotation always entails the existence of a further, formally structured semantic system. Moreover, each sign-vehicle “possesses certain syntactical markers (such as Singular, Count etc.) which permit its combination with other sign-vehicles.” These syntactical markers locate the sign-vehicle by its positions and oppositions within the syntactical system to which it belongs. The particular contexts or circumstances in which the sign-function arises also affect its meaning; “a sign-function is established by the code between a given set of semantic markers and a given set of syntactic markers, both taken as a whole . . . The sign-function is not a marker to marker correlation; therefore the sign-function is not established on the grounds of a strict and ‘natural’ homology between the two functives, but is the result of an arbitrary coupling.” (92)

[4] Eco's theory of sign-function as a correlation of two formal systems asserts that all our models of music have a common significational structure. The codes of music analysis correlate concepts, determined by the conventions of our culture, with the psychophysical quantities of music. By studying how we correlate musical quantities with the terms and concepts of various kinds of music analysis, we can achieve several worthwhile goals. Since a semiotic analysis of any particular mode of music representation entails a structural analysis of theoretical concepts, it helps to refine their meaning. We can also recognize how some historically important types of musical discourse are indeed analytical, even though they are not quantitative, or otherwise structured in a way normal to our contemporary culture. We can better recognize similarities and contrasts among different modes of analysis. And we can define more precisely the limits of any particular analytical approach. To illustrate these purposes, I will treat three contrasting types of music analysis—mathematical, graphical, and literary—as semiotic systems.⁽¹⁾

[5] The first type of music-analytical discourse we shall consider is the mathematical one, incorporating the integer model of pitch applied by Babbitt and others to atonal and twelve-tone music (Rahn 1980). The semiosis in this model is simple, as befits an introductory example, but it is instructive nonetheless. The integers constitute the expression plane (the syntactic system), and pitches belong to the content plane (the semantic system). The code correlates the two system so that each integer conventionally denotes a distinct pitch. The algebraic structure of the integers is tremendously useful in describing the combinational resources of the equal-tempered pitch system. But Rahn (1980, 19) warns of a “numerological fallacy” lurking in this code: “we must carefully determine the limits of similarity between integers (with their structure) and pitches (with their possible structures).” Describing the model semiotically facilitates the determination of those limits.⁽²⁾ (a) Sign-functions are not reflexive; hence integers denote pitches, but not vice versa. The integer code does not enable set theorists to experience numbers when they hear pitches.⁽³⁾ (b) The integer code is an arbitrary convention in several senses. Other integers beside 0 could denote C1, as most theorists recognize. But the assignment of larger integers to pitches of greater fundamental frequency is also an arbitrary convention, according to which positive difference denotes ascent. Moreover semiotics helps us recognize that there is a strong cultural component to this code: it arose in a positivist, male-dominated academic culture that values certain qualities of discourse over others. (c) Since the content plane, the pitches, is actually a segmentation of the continuum of experience, and since this segmentation of experience is culturally determined, the code is only valid with respect to certain Western art music. Furthermore it expresses a particular listening competence with respect to that repertoire, in that the integer 0 denotes whatever we perceive to be “C1” about all the possible timbral and combinational manifestations of that pitch. (d) Although integers are often used in mathematical models to denote intervals as well as pitch, a denotation of pitches does not entail a denotation of intervals. The difference of integers is integers (this fact is essential to their group structure), but the distance between pitches is not pitch. Moreover the two percepts are different to the extent that we may cognize intervals but only dimly perceive pitch as such. So when we use integers to denote intervals we are using another distinct and arbitrary code. An explicit distinction has been made, to my knowledge, only by David Lewin (1977), who developed a model for pitch which encodes many of the intervallic properties we associate with pitch without actually labeling them with integers—that is, without invoking the integer code normally used. (e) Generalizing (d), not all the properties (in fact, none of the properties) of the integers necessarily denotes properties of pitches. In semiotic terms, not all the markers that determine the syntactic place of an integer with respect to the other integers correspond to semantic markers that locate a pitch with respect to other pitches. That is, not all syntactic markers for integers have musical meaning. Conversely, pitches as we experience them in actual music take on additional semantic markers by their position in segments. Although we obviously have internal codes for tunes, for progressions, and for climaxes, the integer code has so sign-functions for these. Series and sets of integers seem inadequate as sign-vehicles for such pitched temporalities in particular, for they do not possess enough syntactic diversity to account for essential aspects of our perception.

[6] Let us analyze another mode of music discourse semiotically. Graphs are often used to represent musical structure. On the surface many of these notations appear quite divergent in design and execution, with respect to their underlying theory (Agawu 1989) or their representational intent (Hamel 1989). From a semiotic standpoint, however, they are quite similar, because they all correlate graphical objects with musical objects. More exactly, every graphical music notation incorporates a code that apportions the elements of a graphical system—its graphical objects, their graphical features, and their geometrical relation in the two-dimensional plane—to the elements of a musical system—its events, their musical features, and their relation in various musical dimensions.

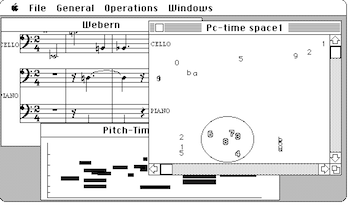
[7] Among many graphical representations the similarities of semiotic structure run even deeper than this general observation implies. As an illustration, consider Example 1, which presents three different graphical encodings of a piece by Webern. These representations appear dissimilar, but they share some common notational conventions that engage the two essential syntactic markers for a graphic—its shape and its position on the page. In all the representations shown here, a positioned shape denotes a distinct sonic event in the piece, as characterized by pitch, instrument, time of attack, and duration. The shape itself signifies some property—such as duration or pitch class—of the sonic event that distinguishes it from others. The various shapes are positioned in each space primarily according to the convention that lower-pitched events appear towards the bottom and later-attacked events appear towards the right of the page. This convention is ubiquitous to the extent that when we see any shapes vertically aligned, we assume that the corresponding music events are attacked simultaneously. Similarly we assume that horizontal proximity signifies temporal and registral contiguity. In the pitch-class representation shown in the Example, and in the simple-score representation, an additional positioning convention is adduced to place events played by the same instrument in the same horizontal stratum on the page. In the score there are also additional, orienting graphical shapes—staves, bar lines, and clefs—and the vertical position of each event within any given stratum is modified further according to the conventions of common music notation. In all these conventions, then, we observe a hierarchy. The three representations all share some basic positioning conventions, but the more elaborate ones embellish or add upon the simpler ones. Notice that this code does not correlate graphics objects with sound events; rather it correlates the geometric relations among the graphics objects with musical relations among the sound events.

[8] Our description of graphical analyses as a hierarchy of conventions which correlate graphical symbols (and relations) with musical events (and relations) suggests an efficient way to program a general-purpose graphical music analysis system for a computer using new object-oriented computer languages (Roeder and Hamel 1989). The semiotic distinction between the syntactic system and the semantic system is achieved by realizing musical events and graphical symbols as two distinct systems of objects, as symbolized in Figure 2b. In the music-object system, musical events are represented by their basic psychoacoustical properties, but they have no graphical characteristics. Related music objects belong to a data structure called a piece. In the independent graphics-object system graphical objects are represented by their basic geometric properties, but they have no musical referent. Related graphics objects belong to a data structure called a graphics space, and each different-appearing display instantiates a distinct class of graphics space. The graphics objects of each graphics space, then, are the expression plane that may signify the music contents of a piece. The sign-function that correlates these graphics-objects with music-objects is an algorithm that translates the properties and relations of the music objects into properties and relations of the graphics objects in the graphics space. Our observation that some graphic representations hold certain significational conventions in common is realized, according to the principles of object-oriented programming, by defining all graphics spaces in an inheritance hierarchy, such that each space, along with its objects, may inherit some of the properties of other spaces and their objects. This inheritance manifests the semiotic code that the complex and simple graphical representations share relative to music. The hierarchical definition of graphics space makes explicit the assumptions underlying each graphic representation—the semiotic code that apportions graphics objects to music objects, and geometric relations to musical relations—helping the analyst to evaluate the musical meaning of any graphical relations the representation reveals.

[9] The last mode of analysis to be evaluated as a system of signification is the literary mode of musical criticism emergent during the Romantic era. Many recent studies have attempted to define processes in Romantic music that are analogous to narrative strategies (Newcomb 1987; Daverio 1990). But less attention has been given to how Romantic music criticism, as text, might relate to the music to which it refers. Robert Schumann's reviews of his contemporaries' music would seem to be likely candidates for such consideration. But several problems arise when we try to understand these writings as music analysis. Narrative theory does not apply satisfactorily to them because they lack an explicitly narrative structure. Rather the reviews typically describe pieces by presenting a sketchy image, or a static scene lacking temporal development, plot, and sometimes even action. Another well-known problem arises in determining what aspects of the music, if any, these images signify. Natural language is very complex semiosis—Eco describes it as a “system of interconnected codes” (91) in which “ the cultural units are very seldom formally univocal entities, and are very frequently what logic calls ‘fuzzy concepts’” (82). Words and the images they immediate denote are ordinarily so rich in connotative implications, and require so many markers for their disambiguation that many modern analysts tend to disdain literary modes of musical discourse as too imprecise.

[10] However, semiotic theory suggests special conditions under which such prose could meaningfully represent music. Sign-functions arise to the extent that the sign-vehicles constitute a unambiguous syntactic system, that is, to the extent that they are arranged in clear patterns of positions and oppositions. If the images can be construed as constituting an unambiguous system, then they—and the relations they connote—may more readily function as the expression plane for a musical content. Restricting and schematizing images curtails their ambiguity and thereby enhances their denotative clarity as sign-vehicles.

[11] Remarkably, some of Schumann's imagistic critical prose does approach the constrained syntax essential to signification. A good example is the set of images he invents for Schubert's Deutsche Taenze und Ecossaisen, Op. 33. (Readers should refer to the scores of the dances in, e.g., DeVoto 1992, and to Strunk's fairly accurate translation in Schumann [1836] 1965, 103–104.) Regarding them together, we can observe special characteristics of both the music and the prose. Schumann's review presents ten images in the context of a masked ball—a highly conventionalized social affair in which the masqueraders cut themselves off from their everyday contexts and place themselves in an wholly different, stylized one, in order to act out their repressed inner desires. These ten little scenes, stripped by this restrictive context of any extraneous connotations we might otherwise attribute to them, polarize, as sign-vehicles, along various dimensions of relationship. Schubert's German dances are tokens of a similarly restricted, stylized genre, in which small contrasts of texture, harmony, phrasing, and accent, cut off from the larger continuities in which they normally participate, are magnified.

[12] This structural mimesis suggests that each of Schumann's scenes corresponds, in some ways, to the sequentially corresponding dance in Schubert's set. It also suggests that Schumann's aphoristic prose signifies not the content and process within each dance, but rather the semantic-structural position of each dance with respect to the set as a whole. Indeed when we compare the first ten dances to each other certain musical polarities are apparent. In the interest of space I will focus just on the most immediately apprehensible differences of harmonic vocabulary, registral span, and loudness among these dances, although it proves equally valid—and interesting—to contrast their more elaborate characteristics of texture, and motivic development.

[13] The tables in Example 2a show some musical dimensions in which oppositions can be defined, and indicate by number where the dances are positioned with respect to each other between the extremes in each dimension. The first table compare the dances by how far apart their independent outer voices get; Dance 8 keeps the voices closest together, while Dance 1 has the widest span (except for Dance 3, in which the extreme span arises from a nonstructural doubling of the bass at the cadence). The second table groups the dances according to how the dynamics change. Dances 6 and 4 keep a constant loudness; Dances 8, 2, 10, 5, and 7 move away from, then return to, a single dynamic; and Dances 1, 3 and 9 finish at a different dynamic from where they start. The third table ranks the dances according to their harmonic complexity. At one extreme are shown those dances, such as 8 and 2, that simply alternate tonic and dominant. Dances listed in the middle of the chart exhibit more diverse, but still diatonic, harmonies. Dances located towards the other extreme display more elaborate harmonic techniques, such as tonicization of secondary triads (Dances 1 and 10), accented non-chord tones (Dance 5), beginning and ending in different keys (also Dance 5), and use of distinctively chromatic chords (Dances 6 and 10).

[14] Within Schumann's text the sign-vehicles polarize as well along various connoted dimensions. The number of characters in each scene varies from solo to pairs to crowds, as shown in the first table in Example 2b. The second table ranks the scenes according to the amount of action in them. Scene 6, in which a hussar stands at attention, has the least action; a number of scenes combine speech with a little action; and, shown at the other end of the scale, are scenes 3 and 9 in which there is clear action without speech. Also evident among the characters in the scenes are distinctions of social class. Some persons are from the country; at the other social extreme are knights or nobility associated with the court; and some characters are anonymous masks.

[15] Schumann's scenes constitute an analysis of Schubert's music to the extent that the two distinct systems correlate. Most generally, of course, the prose asserts the musical unity of the first ten dances by representing them all as scenes within a single social affair. An analogous thread of continuity may be heard in the common-tone links between successive dances: the initial pitch of each waltz belongs to the tonic triad of the preceding one. Also the pitch D6 recurs, often as a registral high point, in many of these dances. The dances also obviously share a number of motives, some of them (such as quarter-eighth-eighth-quarter) common to the genre, and some (such as the F5-D5 motive prominent in Dances 3, 6, and 7, and also important in Dances 9 and 10) more specific to this set.

[16] But much more specific correlations are evident between the prose and the music, as indicated by the parenthetical additions to the titles of the tables in Example 2b. The number of characters Schumann places in each scene correlates with the maximum interval between the structural outer voices during the corresponding dance. The type of action in each scene correlates with the ways dynamics are shaped in each dance. The social class and the demeanor the characters in each scene, which parallel each other, correlate with the degree of harmonic complexity in the corresponding dance. Opposition along the axes for images correlates with opposition along the corresponding axes for music. For instance, scenes 1 and 2 contrast strongly with respect to the number and type of characters, action and tone. Dances 1 and 2 also contrast strongly: the widest span of dance 1 is much greater than that of dance 2, it is much more complex harmonically, and changes dynamics in a much different way. Scenes that are similar in some imagistic dimensions, such as 2 and 8, correspond to dances that are similar in the correlated musical dimensions. Some scenes and dances, such as 6, are consistently near the extremes in their respective dimensions, while others, notably 10, occupy various positions with respect to the others in different dimensions. It is important to realize that the review does not correlate specific images themselves with specific musical events, as a naive program description might try to do.⁽⁴⁾ Rather, just as geometric relations connoted by arbitrary graphic shapes may signify musical relations, the relations connoted by Schumann's images signify musical relations.

[17] An interesting question of pragmatics arises in this connection. Why did Schumann choose to give one of his most extensive literary descriptions to this particular, relatively generic set of short pieces? Certainly he was not incapable of what we would regard as technical commentary. His famous early essay on Berlioz's Symphonie fantastique (Schumann 1946, 164– 188) contains a detailed and occasionally scathing critique of individual chords, voice leading, counterpoint, harmony, tonal plan of movements, phrase lengths and symmetries.⁽⁵⁾ In some respects, though, that essay lacks comprehensiveness: Schumann discusses textural aspects, rhythmic goals, and larger patterns of dynamics and accent only obliquely or not at all, because the theoretical terminology was lacking. One motivation, then, for employing literary structure would be to get at oppositions for which there were not any commonly accepted or easily understood theoretical terms.

[18] Another motivation is suggested by the special properties of Schubert's dances. We have seen that using images to signify music works best under two reciprocal conditions: that the connotations of the images are constrained by the overall scene in which they appear; and that the musical relations are few enough and well enough defined. Too many images, too many connotations, or too many musical relations would cause the semiosis to become incomprehensible under the sheer multiplicity of correlations. In the case of Schubert's music, the constraints of the dance genre permit the structural features of these dances to be heard in a system of positions and oppositions that could not arise in the immensely varied, elaborate processes of large-scale symphonic works. These restricted pieces are better suited than symphonies for imagistic analysis. And the unity and structure of the dance set as a whole were more easily, more correctly—and perhaps more fully—signified by such a correlation of images than by elaborate technical description.

[19] The semiotic properties of literary analysis permit a critical evaluation of music as well as do other more technical modes of music analysis. For example, earlier in the article that contains this scene, Schumann faults some waltzes of Thalberg (Op. 4) for being “too transparent . . . and eternally tonic and dominant, dominant and tonic” (Schumann [1836] 1965, 103). Would not some of Schubert's harmonically and rhythmically simple dances, such as the second or eighth, receive similar condemnation? Our semiotic analysis of Schumann's review helps us realize that he was criticizing not merely the properties of the waltzes in isolation but their relations to each other as part of a system. His aesthetics valued collections, like Schubert's, in which simple pieces were set in opposition to more complex pieces, over uniformly simple sets like Thalberg's.

[20] Schumann renders other aesthetic judgments by the abrupt close of his review. Certainly there are elements of closure in the tenth dance that might have motivated closure in the text. Contrary to all previous junctions between dances, the tonic triads of dances 10 and 11 share no common tones. The tenth dance, like the first dance, spans 24 bars rather than the usual 16. Its recapitulates some of the sequential progressions of dance 1, and provides the first return of the A tonic. (Schumann was very sensitive to unity of key, as we know from his review of Chopin's Op. 38 Ballade (Schumann 1946, 143), and the only technical term he uses in his otherwise imagistic analysis is the key designation “A major”.) In the text, Florestan's abrupt departure comes at the moment when the scene he is declaiming provides elements of recapitulation and closure. Like the end of the first scene, the tenth scene reports spoken dialogue after a crowd (referred to in scene 9). And the Ursuline's reply—“I would rather not speak, to be understood”— is both a commentary on the scene, like the wigged man's comment in the first dance, and, perhaps, an expression of the futility of expressing music with words. In this light Schumann's termination of the review at this point can be understood as a subtle criticism of the remainder of the set of dances. At this point in the literary analysis the semiotic correlation seems to have reached saturation; continuing to add images would create too many new relations and confound the significance obtained by restricting them. Schumann insinuates analogously, by the correlation of text to music, that the later dances add too many new relations, spoiling the “point of highest enjoyment” created by the closures of the tenth dance, and threatening the musical unity of the entire set.

[21] In each of the three semiotic systems examined in this paper, a code is established whereby aspects of musical structure are signified by the structures of another system—the relations of graphical shapes and locations, mathematical structures, or images connoted by language, appropriately restricted by context. These examples substantiate the semiotic view that all our analyses of music are mediated by codes. Music cannot have meaning purely in its own terms, because purely syntactical, self-referential terms have no significance. To contemplate music as pure structure, without a code correlating it to some content plane, approaches the desperate situation in Kafka's works, as read by Gershom Scholem, “in which revelation appears to be without meaning, in which it still asserts itself, in which it has validity but no significance” (Benjamin and Scholem 1989, 142).

[22] We conclude, from this semiotic perspective, that music theorists must play an imperative and active role as a music semioticians. Theorists create and codify systems by which music can be represented and analyzed, that is, by which music can be understood to have significance. It may happen in our quest that we will invent systems that misrepresent music, especially those aspects of musical structure for which we have no alternative codes, such as texture and rhythm. Indeed every music-theoretical system, like other semiotic systems, “can be used in order to lie” (Eco 1976, 7). Accordingly we must continue to evaluate the representations and structures we invoke, and identify the limitations of analytical paradigms that are accepted by tradition, convention, or default.

John Roeder
University of British Columbia
School of Music
6361 Memorial Road
Vancouver, B.C. V6T 1Z2 CANADA
jroeder@unixg.ubc.ca

Works Cited

Agawu, V. Kofi. 1991. Playing with Signs. Princeton: Princeton University Press.

—————. 1989. “Schenkerian Notation in Theory and Practice.” Music Analysis 8/3: 275–302.

Benjamin, Walter and Gershom Scholem. 1989. The Correspondence of Walter Benjamin and Gershom Scholem: 1932–1940. Ed. Gershom Scholem. Trans. Gary Smith and Andre Lefevere. New York: Schocken Books.

Brooks, William. 1980. “Competenza Maledetta.” Perspectives of New Music 18: 11–45.

Daverio, John. 1990. “Reading Schumann By Way of Jean Paul and His Contemporaries.” College Music Symposium 30/2: 28–45.

DeVoto, Mark, ed. 1992. Mostly Short Pieces. New York: Norton.

Dunsby, Jonathan and John Stopford. 1981. “The Case for a Schenkerian Semiotic.” Music Theory Spectrum 3: 49–53.

Eco, Umberto. 1976. A Theory of Semiotics. Bloomington: Indiana University Press.

Hamel, Keith. 1989. “A Design for Music Editing and Printing Software Based on Notational Syntax.” Perspectives of New Music 27(1): 70–83.

Hatten, Robert. 1989. “Semiotic Perspectives on Issues in Music Cognition.” In Theory Only 11(3): 1–10.

Lewin, David. 1977. “A Label-Free Development for 12-Pitch-Class Systems.” Journal of Music Theory 21/1: 29–48.

Mazzola, Guerino. 1990. Geometrie der Toene. Basel: Birkhaeuser.

McCreless, Patrick. 1988. “Roland Barthes's S/Z from a Musical Point of View.” In Theory Only 10/7: 1–24.

Micznik, Vera. 1989. Meaning in Gustav Mahler’s Music : a Historical and Analytical Study Focusing on the Ninth Symphony. Ph.D. diss. State University of New York at Stony Brook.

Nattiez, Jean-Jacques. 1990. Music and Discourse. Trans. Carolyn Abbate. Princeton: Princeton University Press.

Newcomb, Anthony. 1987. “Schumann and Late Eighteenth-Century Narrative Strategies.” 19th Century Music 11/2: 164–174.

Rahn, John. 1980. Basic Atonal Theory. New York: Longman.

Roeder, John and Keith Hamel. 1989. “A General-Purpose Object- Oriented System for Musical Graphics.” Proceedings of the 1989 International Computer Music Conference. San Francisco: Computer Music Association. Pp. 260–263.

Schumann, Robert. 1965 [1836]. [Dance Literature]. Trans. by Oliver Strunk in Source Readings in Music History, Volume V: The Romantic Era. New York, Norton.

—————. 1946. On Music and Musicians. Ed. Konrad Wolff; trans. Paul Rosenfeld. New York: Pantheon Books.

Footnotes

1. Nattiez (1990, 19–28) identifies what he perceives to be a contradiction in Eco's theory of codes—between a closed, synchronic system of signification and an open diachronic process of communication—that render it insufficient for distinguishing the poietic and esthesic dimensions of semiosis, a distinction that is the primary concern of Music and Discourse. (He classifies music analyses into six categories according to how they engage these dimensions (139–143)). I am not concerned here with how meaning varies from one analysis to another, nor with the tripartition, but with the more modest goals stated in this paragraph, which I believe are accessible through the kind of structural analysis of meaning that Eco describes. Nevertheless, from this restricted perspective I do pursue an agenda suggested by Nattiez: to “interrogate the different methodologies practiced in music analysis” (238), and so to augment his brief characterizations of “impressionistic” (161), “formalistic” (163), and graphic (165) modes of music analysis.
Return to text

2. Mazzola 1990, a recent mathematical music theory, explicitly positions the integer model within Molino's semiotic tripartition.
Return to text

3. On the other hand, the sign-function correlating integers with pitch does not preclude another semiotic system in which pitches denote integers. A composer I know remembers his bank-card identification digits by the tune they denote. But such reflexivity is not a necessary property of the original semiosis.
Return to text

4. However, Schumann did seem to hear other short dances by Schubert in nearly in same terms: “Once, when I was playing a Schubert march, the friend with whom I was playing gave the following answer to my question whether he had not seen certain very special forms before him: ‘Yes! I felt I was in Seville more than a hundred years ago, amid promenading Dons and Donnas, with their trains, pointed shoes, daggers, etc.’ Strange to say, our visions were alike, even to the name of the city.” (Schumann 1946, 182)
Return to text

5. The review as a whole aims to treat “the four points of view from which a work of musical art can be surveyed: that of form (the whole, the separate movements, the section, the phrase); that of musical composition (harmony, melody, texture, style, workmanship); that of the special idea which the artist intended to represent, and that of the spirit, which governs form, idea, material” (164).
Return to text

Copyright Statement

Copyright © 1993 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.