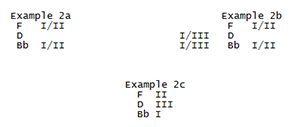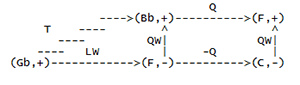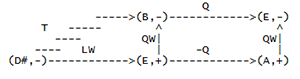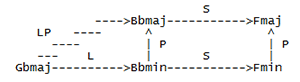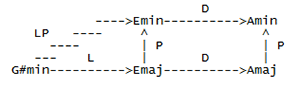Some Remarks on the Use of Riemann Transformations

[1] In this paper I suggest revisions to an analytical methodology developed in Lewin 1987, 1992 and Hyer 1989. Their work draws upon certain themes in Riemann”s writings in order to construct procedures for investigating harmonic relationships in Wagner, procedures that also engage transformational approaches to analysis. My revisions also refer explicitly to Riemann”s writing, but they refer to an earlier stage in his career, and in particular to his Skizze einer Neuen Methode der Harmonielehre (Riemann 1880).

I. Chord Models and Chord Transformations

[2] Hyer (1989) develops a group of transformations on triads from a collection of four relations generally associated with Riemann”s work: parallel, relative, leittonwechsel, and dominant. Lewin (1987, 1992) begins with a somewhat larger number of basic transformations. A few originate in Riemann (parallel, relative, leittonwechsel). Others (mediant, submediant) are adapted from other theorists. And still others (slide relation) are constructed by Lewin himself.

[3] Example 1 investigates how these transformations interact with the triads or klangs they relate. Example 1a is a network of three arrows labelled with Riemann transformations, and three nodes containing klangs. The relationship between C major and E minor is interpreted as leittonwechsel (L), defined by Lewin as a transformation on triads that maintains the two pitches that form a minor third (mod 8ve), and moves the remaining pitch one semitone so as to form another triad (1992, 49). The network interprets the relationship between E minor and G major as an instance of the relative transformation (R), which maintains the two pitches that form a major third (mod 8ve), and moves the remaining pitch a whole tone so as to form another triad. The arrow that extends from C major to the G major is labelled with the subdominant transformation (S), which transposes a klang by a perfect fifth up. The network suggests the following functional equality: L followed by R yields S.

[4] Aside from node content, the network given in example 1b is very similar to the network in example 1a. Both networks have leittonwechsel and relative labels on corresponding arrows. But while the arrow on example 1a that extends from C major to G major is labelled with the subdominant transformation (S), the corresponding arrow on example 1b (extending from A minor to D minor) is labelled with the dominant transformation (D), which transposes a klang up a perfect fifth down. The network in example 1b, contrary to the network in example 1a, suggests that L followed by R yields D.

[5] The difference bothers me because the difference (and other similar differences in the system) is brought about by separating dualist chord models from dualist transformations (leittonwechsel, relative) and then using those transformations in conjunction with functions or relations (dominant, subdominant, submediant, mediant) derived from fundamental-bass conceptions of chord structure. My point here is not that Hyer and Lewin have been unfaithful to the wishes of Riemann. My point is that technical properties of leittonwechsel and relative transformations—in particular the property that they are their own inverses— induce what amounts to a dualist relationship between major and minor chords. For instance, as one examines the values and arguments on the relevant function table of the leittonwechsel transformation, one sees that in general the transformation changes the modality of a major triad to its parallel minor and transposes a major third up, while it changes the modality of a minor triad to its parallel major and transposes a major third down. The reversal of direction that accompanies the reversal in modality is the imprint of dualist thinking. The imprint is indelible: the only way to avoid the dualism is to redefine the transformation so that its function table reverses the modality of a triad and transposes it a certain directed interval regardless of modality. But that would simply turn leittonwechsel either into Lewin”s SUBM (submediant) transformation or into his M (mediant) transformation, depending on the chosen directed interval.

[6] I have not faulted Hyer and Lewin with having misrepresented Riemann”s work because I do not count that as a fault, and because there is a sense in which an uncomfortable juxtaposition of dualist and non-dualist thinking is a prominent characteristic of Riemann, particularly of his later work: the well-known contemporary critique of Riemann in Belinfante 1904 makes this very point. In fact, it could be fairly argued that in what follows it is I who will be misrepresenting Riemann. My own distortions (as far as I can tell) involve projecting a particular ideational structure on Riemann”s transformations (as they appear in the Skizze einer Neuen Methode der Harmonielehre), and then appropriating the transformations for analytical purposes other than those discussed by Riemann, who seems most interested in using transformations to chart out the topographies of his Dur-Moll and Moll- Dur systems. Following Lewin and Hyer, I will be interested in extending the use of Riemann”s transformations to seek out repetitions of harmonic patterns, which are then presented as motivic.

[7] Accordingly, my proposed revision of the analytical methodology involves firstly turning away from non-dualist transformations adapted from dominant, subdominant, mediant, and submediant relations, and secondly identifying in Riemann 1880 a less conflicted group of transformations.

[8] Since the transformations I shall be discussing do compel a dualist conception of triads, it will be worthwhile to establish at least the dominant features of such a view. But because Riemann”s own explanation of chord dualism is premised on the existence of harmonic undertones, I shall use an alternative yet functionally equivalent explanation, developed from Hauptmann”s discussion of major and minor triads (1853, 25–35).

[9] Hauptmann assigns three “functions” to pitches that constitute major and minor triads: unity (Einheit); duality or separation (Zweiheit); union (Verbindung). The three functions are labelled respectively I, II, and III for reference, and are assigned to triad members according to two rules:

1) I and II form a perfect fifth (mod 8ve);
2) I and III form a major third (mod 8ve).

The rules stipulate that only the pitch that acts as I or the Einheit participates in both the perfect fifth (mod 8ve) and the major third (mod 8ve) relationships.

[10] Example 2 distributes the three symbols I, II, III among the pitches that form a major triad. Example 2a calculates which two pitches may be assigned I and II under the first rule above. Since the formalism asserts only that I and II form a perfect fifth, a perfect fourth, or one of their compounds, we cannot determine the assignment of function labels beyond what is shown in the example: F is either I or II; B♭ is also either I or II. To decide which is I and which is II, we need to carry out rule 2. Example 2b calculates which pitches may be assigned I and III under the second rule above. Since the formalism asserts only that I and III form a major third, a minor sixth, or one of their compounds, we cannot determine the assignment of function labels beyond what is shown in the example: B♭ is either I or III; D is also either I or III. But by combining the results of the rule assignments in examples 2a and 2b, we know that Bb must be I: only B♭ participates in a perfect fifth (mod 8ve) relationship and a major third (mod 8ve) relationship. If B♭ is I, F must be II, and D must be III.

[11] Examples 3a, 3b, and 3c carry out on a minor triad the procedures for assigning the functions I, II, and III. Example 3a calculates which pitches may be assigned I and II under the first rule above. Since the formalism asserts only that I and II form a perfect fifth, a perfect fourth, or one of their compounds, we cannot determine the assignment of function label beyond what is shown in the example: F is either I or II; B♭ is also either I or II. To decide which is I and which is II, we need to carry out the second rule. Example 3b calculates which pitches may be assigned I and III under rule 2. Since the formalism asserts only that I and III form a major third, a minor sixth, or one of their compounds, we cannot determine the assignment of function beyond what is shown in the example: F is either I or III; D♭ is also either I or III. But by combining the results of the rule assignments in examples 3a and 3b, we know that F must be I: only F participates in a perfect fifth (mod 8ve) relationship and a major third (mod 8ve) relationship. And if F is I, B♭ must be II, and D♭ must be III.

[12] Comparing the assignment of function labels in minor triads and major triads, Hauptmann analyzes the constitutive perfect fifths and major thirds as intervals directed upwards: in major klangs the two intervals extend respectively from I to II and from I to III; in minor klangs the two intervals extend respectively from II to I and from III to I. In major klangs, says Hauptmann, the pitch that acts as I has a perfect fifth and major third, while in minor klangs the pitch that acts as I is a perfect fifth and major third.

[13] Under Hauptmann”s explanation, a dualist model organizes aural sensations in roughly the following way: When listening to a triad, pick out a major third or its inversion, and pick out a perfect fifth or its inversion; when you do, you will become aware that one pitch in the triad member is overdetermined, and thereby seems more prominent than the others. By way of contrast, a fundamental bass model organizes sensations in roughly the following way: When listening to a triad, reorganize it so that it takes up the smallest registral space and so that only thirds and fifths are formed; assign prominence to the lowest pitch and take note of the quality of the third between that pitch and the next lowest. And a figured bass model organizes aural sensations in roughly the following way: When listening to a triad, concentrate on the lowest-sounding pitch, and assign it prominence; imagine a third and a fifth above the lowest pitch (the qualities of which are determined by a contextual diatonic collection); pitches that do not lie a diatonic third or fifth above the prominent pitch are momentarily displacing the pitches that do. The degree to which figured bass and fundamental bass protocols have been hypostatized by theorists (to the extent that many will claim that one or the other defines more or less the response end of a reflex arc) is something worth worrying about.

[14] In the course of this paper we shall represent klangs as ordered pairs. The first element defines Hauptmann”s I-function or Einheit (not the Grundton). The second element defines the klang”s modality. “+” represents a major (or over or super) klang, or a “positive” Einheit Hauptmann calls it. “-” represents a minor (or under or sub) klang, or a “negative” Einheit. The klangs in examples 2c and 3c are respectively represented as (B♭,+) and (F,-).

II. Schritts and Wechsels

[15] Having established the relevant chord model, we can now investigate appropriate transformations. We begin by examining Riemann”s Schritts, the first of two classes of transformations he presents in Skizze einer Neuen Methode der Harmonielehre. Quintschritt (abbr. Q) transposes a klang by the directed interval that extends from I to II. In the case of (C,+), where C functions as I and G as II, the relevant interval is a perfect fifth up. Accordingly, Q(C,+) = (G,+). In the case of (C,-), where C functions as I and F as II, the relevant interval is a perfect fifth down. Accordingly, Q(C,-) = (F,-), i.e., a B♭ minor triad.

[16] Gegenquintschritt (abbr. -Q) transposes a klang by the directed interval that extends from II to I. In the case of (C,+), where G functions as II and C as I, the relevant interval is a perfect fifth down. Accordingly, -Q(C,+) = (F,+). In the case of (C,-), where F functions as II and C as I, the relevant interval is a perfect fifth up. Accordingly, -Q(C,-) = (G,-). Q and -Q are inverse-related transformations.

[17] Terzschritt (abbr. T) transposes a klang by the directed interval that extends from I to III. In the case of (C,+), where C functions as I and E functions as III, the relevant interval is a major third up. Accordingly, T(C,+) = (E,+). In the case of (C,-), where C functions as I and A♭ functions as III, the relevant interval is a major third down. Accordingly, T(C,-) = (A♭,-).

[18] Leittonschritt (abbr. L) transposes a klang by the directed interval yielded by the composing the relevant directed intervals of Q and T. In the case of (C,+), the composition of Q (a perfect fifth up) and T (a major third up) produces a major seventh up. Accordingly, L(C,+) = (B,+). In the case of (C,-), the composition of Q (a perfect fifth down) and T (a major third down) produces a major seventh down. Accordingly, L(C,-) = (D♭,-).

[19] Ganztonschritt (abbr. G) transposes a klang by twice the directed interval that extends from I to II. Hence, G = Q2. In the case of (C,+), where C functions as I and G as II, the relevant interval is two perfect fifths up, viz., a (compounded) whole tone up. Accordingly, G(C,+) = (D,+). In the case of (C,-), where C functions as I and F as II, the relevant interval is two perfect fifths down, viz., a (compounded) whole-tone down. Accordingly, G(C,-) = (B♭,-).

[20] Kleinterzschritt (abbr. K) transposes a klang by the directed interval that extends from II to III. In the case of (C,+), where G functions as II and E functions as III, the relevant interval is a minor third down. Accordingly, K(C,+) = (A,+). In the case of (C,-), where F functions as II and A♭ functions as III, the relevant interval is a minor third up. Accordingly, K(C,-) = (E♭,-).

[21] Riemann only discusses these six schritts. Following the pattern established by the pair quintschritt/gegenquintschritt, we can define four more schritts: gegenterzschritt (abbr.-T), gegenleittonschritt (abbr. -L), gegenganztonschritt (abbr. -G), and gegenkleinterzschritt (abbr. -K), which will be inversely-related to terzschritt, leittonschritt, ganztonschritt, and kleinterzschritt respectively. Two others, which we shall call identity (abbr. I) and tritonusschritt (abbr. R) are generated by demands of group structure. Appendix I lists all twelve schritts, and provides paradigms for each. Those not explicitly defined by Riemann are given in angle brackets.

[22] The names of the transformations help us remember their particular effect: an X-schritt transposes by the magnitude X (where X is a German interval designation) in the direction determined by the operand: major (or over) klangs extend X upwards; minor (or under) klangs extend X downwards. Gegen-X-schritt may be taken either to reverse the direction of X, or to replace the magnitude X with its inverse. Accordingly, X-schritt and gegen-X-schritt are inverses. Kleinterzschritt and its gegen-form are the only schritts that do not follow the pattern: one needs provisionally to take kleinterz as signifying a major sixth.

[23] Schritts combine according to the following rule:

Xschritt*Yschritt = (X+Y)schritt

In other words, summing the directed intervals of composed schritts (and reducing any compounds) yields the appropriate product schritt. For example, Composing K and T in the context of major klangs yields -L, since a major sixth up (the directed interval by which K transposes major klangs) and a major third up (the directed interval by which T transposes major klangs) sum to a minor ninth up, a compound of a minor second up (the relevant directed interval by which -L, the inverse of L, transposes major klangs). Composing K and T in the context of minor klangs still yields -L, since a major sixth down (the directed interval by which K transposes minor klangs) and a major third down (the directed interval by which T transposes minor klangs) sum to a minor ninth down, a compound of a minor second down (the relevant directed interval by which -L, the inverse of L, transposes minor klangs).

[24] Since schritts are quantities that combine under simple addition, the group is commutative: in general X*Y = Y*X.

[25] But schritts only relate klangs of the same genus. Wechsels, the second class of transformations presented in Riemann 1880, relate klangs of opposing genera.

[26] Seitenwechsel (abbr. W) inverts a klang about I (or about I and I). The transformation reflexively maps the major klang and the minor klang whose I-functions are executed by the same pitch. In other words, it exchanges “positive” and “negative” forms of the same Einheit, so that W(C,+) = (C,-), and W(C,-) = (C,+). Seitenwechsel appears in Goetschius 1917 (114) as his “stride relation,” defined as “a perfect fifth downward from any major keynote, and upward from any minor keynote, with a change in mode.”

[27] The remaining wechsels may be construed as the composition of some schritt and seitenwechsel. Terzwechsel (abbr. TW) transposes a klang by the directed interval that extends from its I to its III, that is, applies terzschritt, and then inverts the result around its I, that is, applies seitenwechsel. One might then understand the designation “terzwechsel” as an elision of “terzschrittseitenwechsel.” Terz(schritt) only affects the first element of an order pair; (seiten)wechsel only affects the second element. In the case of (C,+), TW(C,+) = W(E+) = (E,-); in the case of (C,-), TW(C,-) = W(A♭,-) = (A♭,+). TW is functionally equivalent to Lewin”s and Hyer”s relative transformation (abbr. R), and may be alternatively defined as the inversion of a klang about I and III.

[28] Leittonwechsel (abbr. LW) is the composition of leittonschritt (L) and seitenwechsel (W). In the case of (C,+), LW(C,+) = W(B,+) = (B,-); in the case of (C,-), LW(C,-) = W(D♭,-) = (D♭,+). LW may be alternatively defined as the inversion of a klang about II and III.

[29] Riemann defines three more wechsels: quintwechsel (abbr. QW), ganztonwechsel (abbr. GW), and tritonuswechsel (abbr. RW). Quintwechsel is functionally equivalent to Lewin”s and Hyer”s parallel transformation (abbr. P), and may alternatively defined as inversion of klang about I and II. Six more wechsels are constructed by extending the idea of composing gegenquintschritt, kleinterzschritt, gegenkleinterzschritt, gegenleittonschritt, gegenterzschritt, and gegenganztonschritt in turn with seitenwechsel. Appendix II lists all twelve wechsels, and provides paradigms for each. Those not defined explicitly by Riemann are given in angle brackets. Appendix III provides rules and relevant examples for combining the twenty-four schritts and wechsels given in the first two appendices. The group is simply-transitive: in particular, for any two klangs j and k, there exists a unique member of the schritt-wechsel group S such that S(j)=k. The analytical use of groups with the property are considered in Lewin 1987.

III. Analysis

[30] Examples 4 and 5 investigate some possibilities of schritts and wechsels by using them as arrow labels on network analyses of two excerpts from Wagner”s Ring. Both networks are developed from analyses recently presented in Lewin 1992: Example 6 is based on Lewin”s figure 3b, which studies the harmonic structure of the Valhalla theme as it appears in Das Rheingold sc.2; Example 7 is based on Lewin”s figure 4b, which studies the harmonic structure of the same theme as it appears in Die Walkuere, act II, sc. 2. The networks are not exactly as they appear in the cited figures in Lewin 1992. The networks that appear in examples 6 and 7 were designed to have the same node-and-arrow configurations, viz., to contain the same number of nodes and arrows, with corresponding arrows extending in the same direction, while Lewin”s figures were constructed to serve other analytical purposes that did not require identical node-and-arrow configurations. In any case the divergences from Lewin”s figures are slight and the networks in examples 6 and 7 are well-formed according to standards of the relevant methodologies.

[31] The nodes in examples 6 and 7 are filled with triads construed according to the fundamental bass model, and are represented by the relevant fundamental bass and an indication of the third”s quality. The arrow labels are Lewin”s designations: L represents leittonwechsel; P, parallel; S, subdominant; D, dominant. LP represents the composition of L and P. Comparing the left sides of example 6 and 7, we see that they are identical except for node content, and are thus strongly isographic structures. The right sides of examples 6 and 7 are not identical: while the node and arrow configurations are the same, the corresponding arrow labels are different. The transformations L and LP on the left side of both networks invoke dualism on the relevant nodes. (P is neutral with respect to chord model.) Traveling to the right side of each network, one is constrained by the transformations S and D to adopt a non-dualist conception of major and minor chords, to shift from Riemann to Rameau. Accordingly the B♭ major/B♭ minor nodes in example 6 and the E major/E minor nodes in example 7 are ideational pivots that need to be conceived within both frameworks.

[32] Example 4 adapts example 6 to conform to the present methodology: harmonies are represented by the dualist ordered pair format, and arrows are relabelled with the appropriate schritt or wechsel. Only leittonwechsel appears on both example 6 (as L) and example 4 (as LW). Quintwechsel (QW) replaces parallel (P), and terzschritt (T)—which uses as its paradigm the directed interval the extends from I (G♭) to III (B♭) in the (G♭,+) klang—replaces LP, the composition of L and P. Quintschritt (Q) and its inverse, gegenquintschritt (-Q), transformations premised on the interval between I and II, replace the two S arrow labels.

[33] Example 5 carries out similar changes on example 7. Comparing examples 4 and 5, one sees that the corresponding arrow labels are strictly identical. The shift from the analysis in examples 6 and 7 to the analysis in examples 4 and 5 allow us then to assert a strong isography between the harmonic relations in two Valhalla themes. With respect to node content, one could assert that the network in example 4 is a positive or major form of the network in example 5.

[34] I will not pretend that schritt and wechsel transformations are the only way to establish a link between the two Valhalla themes. One could replace L and LP on example 6 by Lewin”s submediant transformation (SUBM) and the composite transformation SUBMP respectively, and replace L and LP on example 7 by Lewin”s mediant transformation (M) and the composite transformation MP respectively, thereby shifting the networks entirely into the discourse of fundamental bass theory. Corresponding arrows on example 6 and 7 would then be labelled by inverse-related (Rameau-) transformations.

APPENDIX I
Schritts

<Gegenleittonschritt> [-L]
(C,+) → (D♭,+); (C,-) → (B,-)

Ganztonschritt [G]
(C,+) → (D,+); (C,-) → (B♭,-)

<Gegenkleinterzschritt> [-K]
(C,+) → (E♭,+); (C,-) → (A,-)

Terzschritt [T]
(C,+) → (E,+); (C,-) → (A♭,-)

Gegenquintschritt [-Q]
(C,+) → (F,+); (C,-) → (G,-)

<Tritonusschritt> [R]
(C,+) → (F♯,+); (C,-) → (F♯,-)

Quintschritt [Q]
(C,+) → (G,+); (C,-) → (F,-)

<Gegenterzschritt> [-T]
(C,+) → (A♭,+); (C,-) → (E,-)

Kleinterzschritt [K]
(C,+) → (A,+); (C,-) → (E♭,-)

<Gegenganztonschritt> [-G]
(C,+) → (B♭,+); (C,-) → (D,-)

Leittonschritt [L]
(C,+) → (B,+); (C,-) → (D♭,-)

APPENDIX II
Wechsels

<Gegenleittonwechsel> [-LW]
(C,+)↔(D♭,-)

Ganztonwechsel [GW]
(C,+)↔(D,-)

<Gegenkleinterzwechsel> [-KW]
(C,+)→(E♭,-)

Terzwechsel [TW]
(C,+)→(E,-)

<Gegenquintwechsel> [-QW]
(C,+)→(F,-)

Tritonuswechsel [RW]
(C,+)→(F♯,-)

Quintwechsel [QW]
(C,+)→(G,-)

<Gegenterzwechsel> [-TW]
(C,+)→(A♭,-)

<Kleinterzwechsel> [-KW]
(C,+)→(A,-)

<Gegenganztonwechsel> [-GW]
(C,+)→(B♭,-)

Leittonwechsel [LW]
(C,+)→(B,-)

APPENDIX III
Rules for Combining Schritts and Wechsels

Xschritt * Yschritt = (X*Y)schritt
Q*L = Q+L = R

Xschritt * Ywechsel = (X*Y)wechsel
Q*LW = (Q+L)W

Xwechsel * Yschritt = (X*-Y)wechsel
QW*L = (Q-L)W = -TW

Xwechsel * Ywechsel = (X*-Y)schritt
QW*LW = (Q-L) = -T

Henry Klumpenhouwer
University of Alberta
Edmonton, Alberta T6G 2C9
userklum@mts.ucs.ualberta.ca

Copyright Statement

Copyright © 1994 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.