Types and Applications of P3,0 Seventh-Chord Transformations in Late Nineteenth-Century Music
Samuel Reenan and Richard Bass
KEYWORDS: Harmony, Chromaticism, Neo-Riemannian Theory, Parsimonious Voice Leading
ABSTRACT: The expression P3,0 refers to one class of parsimonious voice-leading transformations between seventh chords introduced in a 1998 article by Jack Douthett and Peter Steinbach as Pm,n (Journal of Music Theory 42 (2): 241–63). In addition to tones that may be held in common, the subscripts indicate the number of voices that move by half step (m) or whole step (n) in connecting one seventh chord to the next. P3,0 designates a transformation in which one of the chord members is held in common while each of the other three moves by half step. P3,0 transformations produce some of the most striking chromatic harmonic progressions in the late Romantic repertoire. This study focuses on aspects of P3,0 transformations that include
Copyright © 2016 Society for Music Theory
I. P3,0 in the Context of Neo-Riemannian Voice-Leading Transformations
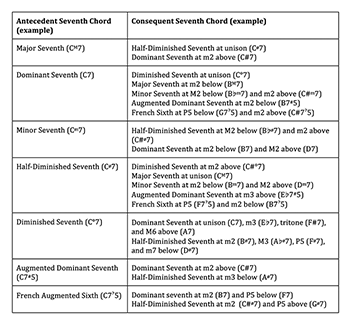
[1.1] P3,0 refers to one class of parsimonious voice-leading connections between seventh chords introduced in an article by Jack Douthett and Peter Steinbach (1998) as Pm,n. In addition to common tones that may be held between the two chords, the subscripts indicate the number of voices that move by half step (m) or whole step (n) in progressing from one chord to another. Thus, the smaller the sum of m and n, the more parsimonious the connection, and the more closely related the two chords are from a neo-Riemannian perspective. P3,0 indicates a relationship between two seventh chords in which holding one tone in common and moving each of the other three by half step will transform one chord into the other.
[1.2] Numerous other studies of voice-leading transformations in nineteenth-century chromatic harmony appeared around the time Pm,n was identified and in the years since. A comprehensive survey of these investigations is not practical here, but it is useful to note that studies of transformations based on such common-tone-plus-stepwise voice leading tend to fall into three general categories, as listed below:
- Triadic transformations, usually among major and minor triads, or set class 3-11 (037); see Cohn 1996, Cohn 1997, and Kopp 2002.(1)
- Seventh-chord transformations among chord types of the same set class, especially dominant and half-diminished, or set class 4-27 (0258); see Lewin 1996, 205ff., Childs 1998, and Callender 1998.
- “Cross-type” transformations among:
- triads and seventh chords; see Capuzzo 2004, Hunt 2007, and Hook 2007;(2) or
- triads or seventh chords of non-equivalent set class; see Douthett and Steinbach 1998 and Tymoczko 2011, 284ff.(3)
[1.3] These and related studies typically construct Tonnetze or similar networks to illustrate how specific kinds of voice-leading transformations create discernible, logical pathways through harmonic spaces.(4) Frequently, the networks presented have been limited to transformations among consonant triads, and only a small percentage of these studies have sought to explore through analysis how transformational voice-leading interacts with voice-leading associated with traditional harmonic practice. Steven Rings, for instance, has observed that a neo-Riemannian analysis often “[begins] with the most chromatically exceptional moment in the piece and [moves] outward from there to construct a broader interpretation” (2011, 492). In these cases, considerations of key and harmonic syntax are undervalued in favor of tonally neutral chord networks.(5)
[1.4] One of the advantages of revisiting Pm,n is that it is inherently generic. That is, while it has potential for the construction of networks and associated graphs (as Douthett and Steinbach so effectively demonstrate), it also possesses the flexibility to operate independently of such networks, and in ways that facilitate the analysis of music that blends tonally unencumbered voice-leading transformations with tonal harmonic syntax.
[1.5] Regarding transformations in the second and third categories above, Pm,n is particularly attractive for its applicability to a large number of seventh-chord connections involving parsimonious voice leading and chords of either the same or different set classes. To date, however, analytical studies that examine seventh-chord connections from this perspective have tended to focus on transformations with specific subscript values. Douthett and Steinbach, for example, explore only P1,0 and P0,1 among chords of different set classes (dominant/half-diminished sevenths and minor sevenths) and P2,0 among chords of a single set class (dominant/half-diminished sevenths). The P3,0 relationship has not been discussed in any detail as a specific transformation class, yet it holds considerable interest in its ability to account for a variety of seventh-chord successions in late nineteenth-century music. The role it plays within the host of common-tone and chromatic voice leading paradigms developed as a means of extending the range of harmonic relationships beyond the routines of the Classical style.
[1.6] Our article reconsiders this particular transformation from an analytical perspective. This entails an explanation of how P3,0 relates to other transformation classes and to traditional harmonic practices, and an identification of specific P3,0 types and their properties based on details of the voice-leading motions that connect one seventh chord to another. The larger part of our study is concerned with the ways in which P3,0 transformations operate within harmonic structures from the late nineteenth-century repertoire.
II. Types and Notation of P3,0 Relationships
[2.1] Although P3,0 transformations do occur in some traditional harmonic progressions, they also occur in ambiguous or unstable situations that at least temporarily suspend tonal centricity. The harmonic characteristics of specific P3,0 transformations depend on the chord types involved and the chromatic movement of the voices in relation to one another, as explained in the following discussion.
Table 1. Types of Parallel P3,0 Transformations
(click to enlarge)
Table 2. Types of Contrary P3,0 Transformations
(click to enlarge)
Table 3. P3,0 Notation
(click to enlarge)
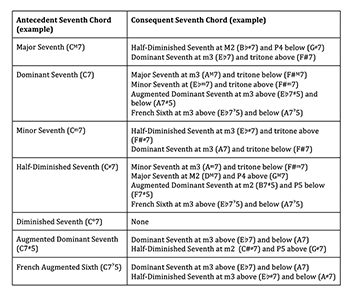
[2.2] The possible relationships between the antecedent (first) and consequent (second) harmonies produced by P3,0 are numerous and diverse, and in every instance the transformation results in a change of chord quality.(6) In fact, all P3,0 transformations belong to the “cross-type” category; the set class is always changed. They can also be divided into two groups according to the nature of the motion among the three moving voices: those in which the semitonal steps are in parallel motion, and those in which one voice moves contrary to the other two. The possible seventh-chord relationships belonging to the “parallel” P3,0 group are given in Table 1, while the “contrary” transformations are shown in Table 2. The set of objects represented is limited to the most common seventh-chord types associated with nineteenth-century tonal practice: major (M7), dominant (7), minor (m7), half-diminished (ø7), diminished (°7), augmented dominant (7
[2.3] Whereas none of the transformation types represented in Tables 1 and 2 connects seventh chords that are diatonically related, some do correspond with familiar chromatic harmonic relationships, such as the common-tone diminished seventh that embellishes a dominant seventh harmony (e.g., C°7–C7 in F major), and the normative resolution of a French sixth to a dominant seventh (e.g., C7
[2.4] Almost all of the chord-quality relationships between the antecedent and consequent harmonies are the same regardless of whether the transformation belongs to the parallel or contrary group, but they differ in terms of the relationships between the chord roots. A notable exception is the diminished seventh chord, as none of the other chord types are associated with it as a direct result of contrary P3,0 transformations. Contrary motion in this situation necessitates that the interval between two moving voices either expands or shrinks by a whole step, as those two voices shift by one semitone each. Because three of the four voices move by semitone in the P3,0 transformation, there must be one pair of adjacent voices that undergoes a whole step expansion or shrinkage. The stacked intervals that make up a dominant seventh and half-diminished seventh chord are all either minor or major thirds (and an inverted major second between the root and chordal seventh). A whole-tone expansion or contraction of any of these intervals due to contrary semitone motion would result in at least one interval that is not a minor third. Since the diminished seventh chord is a set of symmetrically stacked minor thirds, it cannot be achieved by application of the contrary P3,0 transformation.
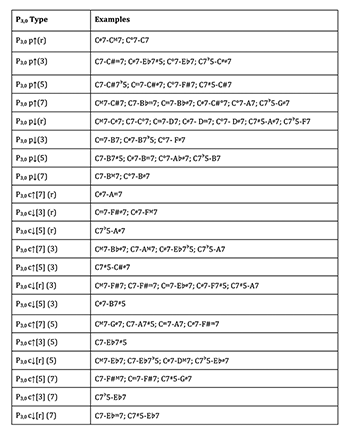
[2.5] Table 3 presents a model for the analytic notation of specific types of P3,0 transformations. Three factors determine the form and function of these transformations: 1) the relative interaction and direction of the voice leading, in either parallel or contrary motion; 2) the chord factor of the common tone between the antecedent and consequent harmonies; and 3) the chord factor of the independent chord tone opposing the other moving voices in a contrary P3,0. A parallel P3,0 depends only upon factors 1 and 2, while a contrary P3,0 is controlled by all three. Table 3 presents two related methods of notation for the distinct P3,0 types.
[2.6] Contrapuntal motion from the antecedent to the consequent chord is indicated by a lowercase “p” in parallel motion and “c” in contrary motion. Immediately following that is an arrow identifying the direction of the three moving voices for parallel types or the majority direction for contrary types. The remainder of the parallel P3,0 notation is a letter or number in parentheses indicating the chord factor (root, third, fifth, or seventh) of the common tone, based on its position in the antecedent chord.(11) The contrary P3,0 has an additional notation in square brackets preceding the common-tone factor, indicating the chord factor of the voice that moves in opposition to the other two voices (and thus opposite to the direction of the arrow). This table lists the specific analytical notation for each transformation type described in Tables 1 and 2.(12) For example, the parallel motion P3,0 that relates C7 to
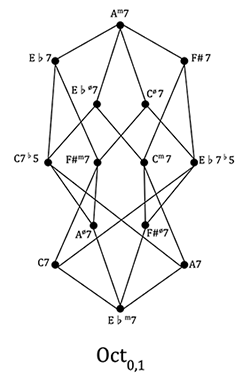
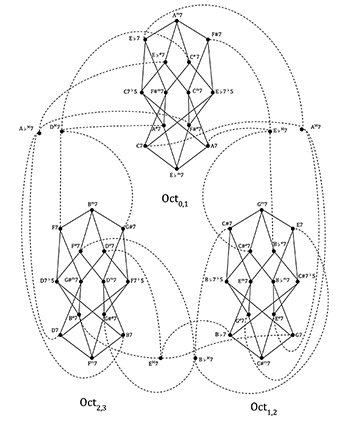
Example 1. An OctaCrystal network formed from contrary P3,0 transformations acting on subsets of the Oct0,1 set
(click to enlarge)
Example 2. A partial Power Crystals graph, showing some of the contrary P3,0 transformational “bridges” between the closed OctaCrystal networks
(click to enlarge)
[2.7] A remarkable property of the P3,0 transformation is that its voice leading is the complement of that for P1,0 and, in the abstract, it has a close relationship to Douthett and Steinbach’s “OctaTowers” and “Power Towers” graphs.(13) The respective qualities of the antecedent and consequent seventh chords achieved by P3,0 and P1,0 are the same, although they differ in the relationship between the chord roots and, of course, pc content. Similarly, the octatonic relationships implied by P1,0 are also relevant for P3,0, such that many of the seventh-chord combinations form octatonic subsets. Of particular interest are the contrary P3,0 transformations, because they form clear octatonic networks and connections between these networks when applied systematically to tertian tetrachordal sets. Thus the Power Towers and OctaTowers of Douthett and Steinbach can be constructed in a similar form for contrary P3,0 transformations, with different chord roots. Illustrations of these structures are provided in Examples 1 and 2. Analogous to the OctaTowers is Example 1, the “OctaCrystal” formed by the contrary P3,0 transformation when applied to (0258), (0268), and (0358) prime-form tetrachords within the Oct0,1 set. Among these tetrachord types, the OctaCrystal is a closed network;(14) however, if major sevenths and augmented dominant sevenths are incorporated, “bridges” between octatonic sets are formed, and a complete “Power Crystals” network can be constructed, demonstrating the connections among all three octatonic sets. A partial version of this Power Crystals graph is given in Example 2.(15) This network shows major seventh chords as bridges between the OctaCrystal P3,0 networks with dashed lines.
[2.8] Another consequence of the similarity between P3,0 and P1,0 is the possibility of reversing chord-quality transformations by combining the two. For example, a P3,0 that connects a dominant seventh to a minor seventh with a tritone-related root, or P3,0 c↓[r](3), may be coupled with a P1,0 moving the third of the minor seventh up by half step to yield a larger-scale connection between two dominant sevenths separated by a tritone , or P3,0+P1,0→P2,0. This type of compound transformation is employed in the Romantic repertoire as a compositional tool that allows for connections between distantly related seventh chords of the same quality (as in Franck’s Piano Trio in D Major, op. 2, discussed in Part III below, and Wagner’s Prelude to Tristan und Isolde, discussed in Part IV).(16)
III. Examples of P3,0 in Nineteenth-Century Repertoire
[3.1] Applications of the P3,0 transformation can be sorted into three basic groups. The first of these consists of parsimonious voice leading that coincides with a traditional harmonic paradigm; the second contains P3,0 transformations constructed as a compound of additive semitonal motions; and the third is made up of novel, non-functional progressions, conceived entirely in terms of voice-leading parsimony and usually with no discernible relation to traditional harmonic syntax.
Table 4. Comparisons of P3,0 between dominant and diminished seventh chords
(click to enlarge)
[3.2] The most common progressions in the first category are the embellishment of a dominant seventh harmony by a common-tone diminished seventh chord, and the conventional progression of a French sixth as a pre-dominant leading to a dominant seventh, as noted in Part II above. In both of these cases, the semitonal motion is parallel. The procedure for a common-tone diminished seventh is the voice-leading complement of a P1,0 transformation from dominant seventh to diminished seventh a half step above (e.g. C7–
Figure 1a. P3,0 in established harmonic paradigms: Strauss, Das Geheimnis op. 17, no. 3, mm. 1–3
(click to enlarge)
Figure 1b. P3,0 in established harmonic paradigms: Franck, Quatrième Trio op. 2, mm. 71–82
(click to enlarge)
Figure 1c. P3,0 in established harmonic paradigms: Scriabin, op. 11, no. 2, mm. 7–12
(click to enlarge)
Figure 2a. P3,0 usage in the combination of successive semitone shifts: Strauss, “Die Zeitlose” op. 10, no. 7, mm. 7–14
(click to enlarge)
Figure 2b. P3,0 usage in the combination of successive semitone shifts: Harmonic reduction of “Die Zeitlose,” mm. 8–13
(click to enlarge)
Figure 2c. P3,0 usage in the combination of successive semitone shifts: Balakirev, 10 Songs (1895-96) no. 4, mm. 27–28
(click to enlarge)
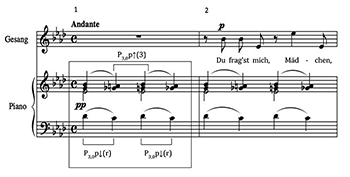
[3.3] Figure 1 illustrates three characteristic uses of P3,0 that fall into this first category. The opening of Richard Strauss’s “Das Geheimnis” op. 17, no. 3 in A-flat major (Figure 1a) serves to establish the mood of the 1888 piece and the evasive nature of its topic. It consists of a common-tone diminished seventh chord that alternates with a third-inversion dominant seventh harmony. The P3,0 p↓(r) transformation that introduces the C diminished seventh on beat two is then reversed to become P3,0 p↑(3), as it returns to the
[3.4] The passage from Franck’s Piano Trio op. 2, shown in Figure 1b, obfuscates the B-minor tonality in measures 71–79 through the P4,0 oscillation between two diminished seventh chords with
[3.5] Figure 1c (Scriabin’s Prelude op. 11, no. 2, measures 7–12) features an abundance of stepwise voice leading, including motion from a French sixth to a dominant seventh in measures 8–9. Whereas the pitch classes of this P3,0 transformation correspond to those of a traditional Fr+6 to V7 progression in D minor, there is nothing else in this passage to suggest that tonality, and even the ultimate key of the prelude, A minor, is not strongly represented at this point in the piece. Whereas the harmonic content is reminiscent of tonal practice, in this musical context the progression is more usefully understood as a chromatic voice-leading transformation.
[3.6] Figure 2 illustrates the two most common forms of compound semitone motions that result in P3,0. The excerpt from Richard Strauss’s “Die Zeitlose” op. 10, no. 7 shown in Figure 2a demonstrates the P2,0+P1,0→P3,0 paradigm as a means of text painting. The first eight measures clearly express the tonality of G major as the text describes a bucolic pasture of saffron flowers; however, coinciding with the key signature change in measure 9 is a shift in the mood of the text, which discloses the flowers’ poisonous nature. At this point, the voice leading in the piano part becomes exclusively stepwise and principally semitonal. As indicated in the harmonic reduction of Figure 2b, measures 8–9 contain a P2,0 transformation from C7 to Cø7 followed by the half-step descent (P1,0)
[3.7] An excerpt from the beginning of Mily Balakirev’s song “Kogda volnuyetsya zhelteyushchaya niv” (When the Yellow Cornfield Waves), shown in Figure 2c, embodies a similar harmonic procedure that departs from conventional tonal practice in favor of semitonal voice leading. The increase in energy indicated by the Poco più animato marking begins with a parallel P3,0 common-tone diminished seventh in the piano in measure 27, followed by P1,0 transformations on each of the next three beats that effect a reversal of the P3,0 and return to the initial G7 harmony. The two intermediate vertical harmonies are Gø7 on beat 4 of measure 27, and a French sixth (G7
[3.8] The most harmonically striking types of P3,0 transformations are those creating connections between harmonies related in ways that do not coincide with any progression associated with tonal practice, despite the fact that the individual chords involved are tertian constructions that have the potential to behave functionally. Progressions of this sort frustrate established expectations and force an interpretation that is apart from, even though it may also share space with, tonal writing. Both parallel and contrary P3,0 transformations carry the potential for many such connections, including those between tonally unrelated dominant and minor seventh chords, major seventh and dominant seventh, or French sixth and dominant seventh, which are among the progressions considered below.
Figure 3a. Parallel P3,0 transformations in non-functional progressions between dominant and minor seventh chords: Strauss, “Die Verschweigenen” op. 10, no. 6, mm. 5–15
(click to enlarge)
Figure 3b. Parallel P3,0 transformations in non-functional progressions between dominant and minor seventh chords: A harmonic reduction of Rachmaninoff, “Duma” op. 8, no. 3, mm. 21–25
(click to enlarge)
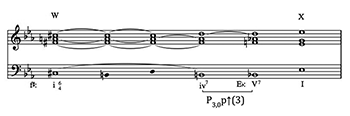
Figure 3c. Parallel P3,0 transformations in non-functional progressions between dominant and minor seventh chords: Liszt, Ce qu’on entend sur la montagne S. 95, rehearsals W–X
(click to enlarge)
[3.9] A common Romantic-era implementation of parallel P3,0 in novel harmonic progressions connects dominant and minor sevenths with root relationships that are either tonally distant or unrelated to the surrounding tonal context. The connection generated by the P3,0 p↑(7), for example (namely C7–
[3.10] Another relationship involving dominant and minor seventh chords, but one that lacks potential tonal implications, is shown in Table 3 as P3,0 p↑(3) connecting C7 and
Figure 4a. Instances of parallel P3,0 in pairings other than dominant and minor sevenths: A harmonic reduction of Wolf, Genialisch Treiben, mm. 39–47
(click to enlarge)
Figure 4b. Instances of parallel P3,0 in pairings other than dominant and minor sevenths: Liszt, “Ich Liebe Dich” S. 315, mm. 22–29
(click to enlarge)
[3.11] Two less common forms of the parallel P3,0 transformation are illustrated in Figure 4. The first of these is an excerpt from Hugo Wolf’s “Genialisch Treiben.” The final phrase of text (“es ist ein Nichts/und ist ein Was”) presents a contradiction perhaps more metaphysical and complex than the other dualisms in the poem (namely “earnest/jest,” “love/hate,” “this/that”). In this passage, the musical setting (measures 39–47) utilizes three repetitions of the P3,0 p↑(7) shift from major seventh to dominant seventh, as indicated in the harmonic reduction given as Figure 4a. Initially, these transformations are in sequence, until a deviation in measure 43. Subsequently, another P3,0 relates
[3.12] The fourth musical phrase from Liszt’s “Ich liebe dich” is shown in Figure 4b. In this song, each line of text begins with the titular phrase, followed by a reason for, metaphor about, or description of the power of love. This fourth line of text, “ich liebe dich durch einen Zauberbann,” is the only part of the poem that invokes the supernatural, as the poet’s love is attributed to some magical power. Liszt’s setting of these words initially incorporates a common-tone diminished seventh via P3,0 p↓(r), from B7 to
Figure 5a. Contrary P3,0 transformations in non-functional progressions between dominant and minor seventh chords: Balakirev, 10 Songs (1895–96) no. 4, mm. 1–2
(click to enlarge)
Figure 5b. Contrary P3,0 transformations in non-functional progressions between dominant and minor seventh chords: Rachmaninoff, “Duma” op. 8, no. 3, mm. 28–29
(click to enlarge)
Figure 6a. Other instances of Contrary P3,0: Strauss, Elektra op. 58, mm. 16–19
(click to enlarge)
Figure 6b. Other instances of Contrary P3,0: Liszt, “Der du von dem Himmel bist” S. 279, mm. 5–9
(click to enlarge)
[3.13] Contrary P3,0 transformations produce chord progressions that are more diverse and often more harmonically progressive than their parallel counterparts. The two excerpts shown in Figure 5 exemplify contrary P3,0 connections between dominant and minor seventh chord types, with different chord root relationships. The opening of the Balakirev song in Figure 5a features a connection between chords with tritone-related roots (
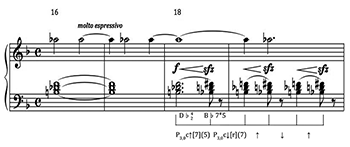
[3.14] Two less common examples of contrary P3,0 are given in Figure 6. The first of these involves the connection between a dominant seventh and augmented dominant seventh whose roots are related by a minor third. This excerpt is from the early portion of Strauss’s opera Elektra op. 58, from 1908 (Figure 6a). Each of the chords (
IV. Analytic Applications: The Opening of Wagner’s Prelude to Tristan und Isolde and Strauss’s “Ruhe, meine Seele!”
[4.1] The preceding discussion deals with examples from the repertoire that exhibit P3,0 transformations of various types, and it focuses on the explication of mostly localized, chord-to-chord connections. This final section seeks to demonstrate some ways in which these transformations operate within and contribute to larger musical structures.
[4.2] The opening of the Tristan Prelude has been fertile ground for numerous efforts at explaining its tonal and harmonic content, including approaches based on harmonic function, sequential construction, linear-motivic structure, or even pitch-class set organization.(17) It has also been an attractive example for neo-Riemannian analysis based on parsimonious voice leading, especially as it exhibits Douthett and Steinbach’s P2,0-type transformations in the sequential passage consisting of the first eleven measures.(18) Further aspects of the harmonic content of this passage, however, can be elucidated by considering P3,0 relationships as well.
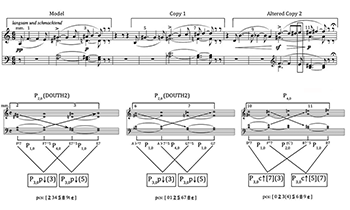
Figure 7. P3,0 analysis of the opening sequence of the Tristan Prelude, mm. 1–11
(click to enlarge)
[4.3] The opening harmonic sequence of the Prelude is given in Figure 7a, with a harmonic reduction showing the chords formed by the four voices sounding simultaneously in Figure 7b. The sequence is made up of a model followed by two copies in ascending-third transpositions. As David Lewin points out, P2,0 relationships exist between the half-diminished (“Tristan”) chord on the downbeat of measure 2 and the dominant seventh at the end of the model (indicated above the staff in Figure 7a), and also between the Tristan chord and each of the initial and final chords of both copies. The same relationship obtains between the initial and final chords of the first copy, but it does not continue in the altered second copy, where the half-diminished chord at the beginning and the dominant seventh at the end are P4,0-related, having no pitch classes in common.(19) Parsimonious voice leading is clearly the driving force of the harmony in this passage, but P2,0 does not offer an entirely consistent explanation for its construction.
[4.4] As indicated at measure 10 of Figure 7a, there is an added symmetrical triadic harmony (C augmented) in the second copy. The pitch class sets of the model and the first copy each consist of two chromatic tetrachords related at T6. The second copy, however, constitutes a complete octatonic collection plus one additional note⎯the E of the augmented triad that has no precursor earlier in the sequence. The deviations from the pattern that occur in measures 9–11 seem to indicate that there is motion through the sequence toward this second copy of the sequence, a perspective illustrated by the annotations beneath the reduction in Figure 7b that identify P3,0-related chords resulting from the combination of successive semitonal movement. The embedded P3,0 architecture is retained in the second copy, but the added augmented triad forces the transformation to shift from the parallel to the contrary variety. The implications of the overlapping P3,0 analysis are multifaceted. First, because there is no precedence given to any particular chord within each three-measure statement, it is possible to account for both the half-diminished sevenths and the French sixths in the passage. Also, the preservation of the overlapping P3,0 organization in measures 9–11 retains the prevalent common-tone and semitonal relationships from the previous statements in the otherwise altered second copy. As for the pitch-class sets employed in the three-measure statements, the shift to contrary P3,0 in measures 9–11 is also responsible for the introduction of the octatonic collection.
[4.5] A characteristic of many contrary P3,0 transformation types (and few of the parallel variety) is that the combined pitch-class content of the antecedent and consequent chords produces a nearly complete octatonic collection. One of the diminished seventh chords contained in the octatonic set of the second copy in measures 9–11 is B°7, which, as Cohn demonstrates, pervades the entire sequence (Cohn 2012, 150). The four pitch classes of that harmony are the only common tones retained in the model and both copies. Finally, as indicated by the arrows in the harmonic reduction, each of the two pairs of P3,0-related seventh chords shares a single but different common tone; these notes, taken together, induce a voice exchange between the soprano and tenor voices. In the final, altered statement in measures 9–11 (with the contrary P3,0 and inserted augmented triad) the voice exchange between the soprano and tenor differs from the others in that it has a slight rhythmic realignment of the notes that are exchanged. Many significant attributes of the model Tristan-chord progression are preserved in measures 9–11, in large part as a consequence of the overlapping P3,0 transformations.
[4.6] It is possible to imagine several alternatives to measures 9–11 of the Prelude, but none would be as satisfactory as the original because it would entail either a failure to conclude on B7 as necessary preparation for the V7 of A minor that resolves deceptively to VI in measure 17, or a failure to retain the pitch classes of B°7 as common tones throughout the three iterations of the sequence, while still preserving the voice exchange that is an essential characteristic of the construction. The overlapping P3,0 relationships result from the integration of semitonal voice leading and a voice exchange that provides the harmonic structure for the passage as a whole. Alterations to the progression in measures 9–11 create deviations within that structure in order to develop new seventh-chord relationships that maintain the same contrived attributes, in this case the pitch classes of B°7 as common tones.
Figure 8. Karl Henckell, “Ruhe, meine Seele!”
(click to enlarge)
Figure 9a. Strauss, “Ruhe meine Seele!” op. 27, no. 1, mm. 1–4: P3,0 transformations and octatonic organization
(click to enlarge)
Figure 9b. Strauss, “Ruhe, Meine Seele!”: harmonic reduction and analysis
(click to enlarge)
Figure 10. Strauss, “Ruhe, Meine Seele!”
(click to enlarge and see the rest)
[4.7] Whereas the opening of the Tristan Prelude contains P3,0 relationships that are embedded within its series of seventh-chord sonorities and overlap with other relationships (especially P2,0), Strauss’s “Ruhe, meine Seele!” op. 27, no. 1 (1895) is remarkable for its employment of P3,0 as an explicit procedure for generating chord-to-chord successions, as well as for the delineation of formal divisions in the piece. This song has been cited in earlier studies for its lack of conventional formal structures and its often ambiguous tonal orientation. Based on its text (given in Figure 8), it is possible to view the song as five melodic phrases ending with a semicolon, period, dash, or exclamation point (Hain;” “Sonnenschein.” “schwillt.” “Not—” “bedroht!”).(20) The musical segments corresponding to these divisions, however, do not provide similarly strong tonal-harmonic punctuation. Marie Rolf and Elizabeth Marvin write, “If a phrase has beginning, middle and end, it is difficult to find one complete phrase in all of ‘Ruhe, meine Seele!’” (Rolf and Marvin 1990, 72). In this work, parsimonious voice leading is the principal harmonic procedure, while traditional tonal syntax assumes an ancillary role.
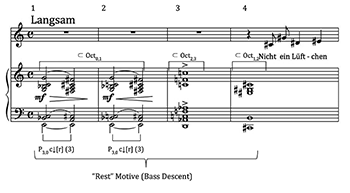
[4.8] The opening four measures of “Ruhe, meine Seele!” act as a microcosm of the motivic and voice-leading procedures developed later in the work. This progression, shown in Figure 9a, is remarkable at the outset for the contrary P3,0 transformation connecting C7 and
[4.9] Another feature of the opening four measures has to do with its pitch-class content. The opening C7–
[4.10] A harmonic reduction and audio example of the complete song are given in Figure 9b; the score is provided in Figure 10. As the harmonic reduction indicates, parsimonious seventh-chord transformations are pervasive in this work (with P3,0 most prominently represented), and progressions with tonal implications are sparse until the end, where C gradually emerges as the harmony associated with the repose that is the central idea of the text.(21) Momentum towards C begins to accumulate in measures 34–35, with an authentic resolution of A7 to D (ii). A cadential progression toward C minor ensues, but the resolution is thwarted when the expected tonic is replaced with C7 (V7/iv) at measure 39, and the opening (C7–
[4.11] In between the fleeting progressions associated with tonal procedures (e.g., the circle-of-fifths segment in measures 4–13 and some isolated chord pairs in measures 26–32) there are additional P3,0 transformations of the parallel variety. One example occurs after measure 14, where a P4,0 (B7–C7) obliterates the preceding circle of fifths and then moves to Gm7 (P1,1) at measure 16. The ensuing progression employs two iterations of the P3,0 p↓(r) type (Gm7–A7–
[4.12] This study seeks to codify aspects of P3,0 voice leading in a pragmatic way that encourages their incorporation into analyses focused on harmonic procedures associated with nineteenth-century chromaticism. Like most investigations based on neo-Riemannian transformations, the approach is limited in its ability to proffer all-encompassing explanations of complete tonal-harmonic constructions; rather, it serves as an effective resource for acquiring a deeper understanding of certain aspects of harmony in this repertoire not adequately addressed through traditional methods. The frequent appearance of P3,0 transformations and relationships in works by a variety of composers, and especially those occurrences that represent extraordinary departures from established practice, indicates that there is value in considering the various roles P3,0 may assume in local and larger-scale structures as it combines with other kinds of parsimonious voice-leading transformations and, especially, in the ways that all these procedures cohabitate with the routines of tonal harmony. The short analyses presented above represent some initial possibilities, and further study would in all likelihood uncover other ways in which such interactions take place, and how they cooperate in the creation of non-traditional types of musical coherence.
Samuel Reenan
Eastman School of Music
Theory Department, 26 Gibbs St.
Rochester, NY 14604
sreenan@u.rochester.edu
Richard Bass
University of Connecticut
Department of Music, U-1012
Storrs, CT 06269-1012
richard.bass@uconn.edu
Works Cited
Bass, Richard. 1996. “From Gretchen to Tristan: The Changing Role of Harmonic Sequences in the Nineteenth Century.” 19th-Century Music 19 (3): 263–85.
Callender, Clifton. 1998. “Voice-Leading Parsimony in the Music of Alexander Scriabin.” Journal of Music Theory 42 (2): 219–33.
Capuzzo, Guy. 2004. “Neo-Riemannian Theory and the Analysis of Pop-Rock Music.” Music Theory Spectrum 26 (2): 177–99.
Childs, Adrian P. 1998. “Moving beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords.” Journal of Music Theory 42 (2): 181–93.
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15 (1): 9–40.
—————. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their ‘Tonnetz’ Representations.” Journal of Music Theory 41 (1): 1–66.
—————. 1998. “Square Dances with Cubes.” Journal of Music Theory 42 (2): 283–96.
—————. 2000. “Weitzmann’s Regions, My Cycles, and Douthett’s Dancing Cubes.” Music Theory Spectrum 22 (1): 89–103.
—————. 2012. Audacious Euphony: Chromaticism and the Consonant Triad’s Second Nature. Oxford University Press.
Douthett, Jack and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42 (2): 241–63.
Gollin, Edward. 1998. “Some Aspects of Three-Dimensional Tonnetze.” Journal of Music Theory 42 (2): 195–206.
Hook, Julian. 2002. “Uniform Triadic Transformations.” Journal of Music Theory 46 (1–2): 57–126.
—————. 2007. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29 (1): 1–39.
Hunt, Graham. 2007. “David Lewin and Valhalla Revisited: New Approaches to Motivic Corruption in Wagner’s Ring Cycle.” Music Theory Spectrum 29 (2): 177–96.
Hyer, Brian. 1989. “Tonal Intuitions in ‘Tristan und Isolde.’” PhD diss., Yale University.
Kopp, David. 2002. Chromatic Transformations in Nineteenth-Century Music. Cambridge: Cambridge University Press.
Lewin, David. 1982. “A Formal Theory of Generalized Tonal Functions.” Journal of Music Theory 26: 23–60.
—————. 1987. Generalized Musical Intervals and Transformations. Yale University Press.
—————. 1996. “Cohn Functions.” Journal of Music Theory 40 (2): 181–216.
Rings, Steven. 2011. “Riemannian Analytical Values, Paleo- and Neo-.” In The Oxford Handbook of Neo-Riemannian Music Theories, ed. Edward Gollin and Alexander Rehding, 487–511. Oxford University Press.
Rolf, Marie and Elizabeth Marvin. 1990. “Analytical Issues and Interpretive Decisions in Two Songs by Richard Strauss.” Intégral 4: 67–103.
Santa, Matthew. 2003. “Nonatonic Systems and the Parsimonious Interpretation of Dominant-Tonic Progressions.” Theory and Practice 28: 1–28.
Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Modern Practice. Oxford University Press.
Footnotes
1. Important precedents for the studies listed here are Lewin 1982 and Hyer 1989.
Return to text
2. This category is prefigured to an extent in Douthett and Steinbach 1998 and Santa 2003; the term “cross-type” comes from Hook 2002 and Hook 2007. For Hook, cross-type transformations involve a change in pc-set cardinality (e.g., a triad becoming a seventh chord). Here, a more generalized usage of “cross-type” refers primarily to transformations that change the set class, either by cardinality or by prime form.
Return to text
3. Of particular interest are the graphs and discussions of “OctaTowers” and “Power Towers” in Douthett and Steinbach 1998, 255–57. In Tymoczko 2011, single semitone motions produce cross-type transformations, which the author then interprets as accumulating towards transpositions of a dominant seventh chord.
Return to text
4. See, for example, Cohn 1998 and Cohn 2000.
Return to text
5. In the latter portion of his study of Schubert’s Impromptu in G-flat Major (500ff.), Rings finds it necessary to abandon the distinctive properties of seventh chords by subsuming them into a network based solely on triadic content; he does this in an effort to create a context in which tonal-harmonic syntax and transformational networks can be considered side by side.
Return to text
6. This property of P3,0 stands in marked contrast to P2,0, in which dominant and half-diminished seventh chords (set class
Return to text
7. It would be possible to add other chord types to the set of objects in the tables, but doing so would greatly increase the number of P3,0 types with practically no relevance for analysis of the repertoire examined in this study. Such additions would include the mM7 (minor triad with major seventh), AM7, and the dM7. Three other combinations of triad plus seventh are transpositionally equivalent to other types already noted: md=dm (half-diminished seventh), Md=mm (minor 7), and Ad=mM. A similar situation arises with the French sixth sonority: using the (026) trichord (e.g., C–E–
Return to text
8. Sum class is determined by adding together the pitch-class numbers of the chord. For example, the sum class of C7 is 0+4+7+10= 9 (mod 12). Set classes of a particular cardinality have either an even or odd sum class and, as explained below, this determines which set classes can be transformed into others via a specific Pm,n class such as P3,0.
Return to text
9. In Childs 1998, for example, P2,0 transformations leave the sum-class parity unchanged and are used to form networks within the transpositions and inversions of set class 4-27.
Return to text
10. Another way of explaining this would be to consider the “parsimonious voice leading sum,” or PVLS, as defined in Santa 2003 (a variation of the DVLS proposed in Cohn 1998), of each transformation. PVLS is essentially the mod-12 magnitude difference between sum classes of the antecedent and consequent chord in a transformation; for parallel P3,0, PVLS = 3, while for contrary P3,0, PVLS = 1. This means that the P3,0 transformation imposes an odd number shift in sum class, necessitating a switch in the parity of the sum class from even to odd or vice versa (even + odd = odd; odd + odd = even).
Return to text
11. For the purposes of the present study, the chord root is generally determined by stacking the tetrachord as a tertian seventh chord in root position. For symmetrical pc sets, namely the diminished seventh and French sixth (7
Return to text
12. Employing a notation based in part on identifying chord factors enables the analyst to describe the motion of each individual voice within a given chord-to-chord motion. However, the dependency on tertian spelling obfuscates the inversional relationships between certain transformations. In particular, when the roots of the antecedent and consequent chords are different, the inverse of a given P3,0 transformation is rarely a simple flip of the direction of the arrow in the notation described here. For instance, motion from C7 to
Return to text
13. The term “voice-leading complement” refers to a relationship between two transformations such that the moving voices are mutually exclusive; for example, Bø7→ B°7 (A moves to
Return to text
14. In the case of the contrary P3,0 OctaCrystal, the PVLS (see note 10 above) of each branch is 1. The branches are independent, such that two successive iterations of a contrary P3,0 can connect two P2,0-related seventh chords, with a composite PVLS of 0 (i.e., C7–
Return to text
15. For clarity, some of the possible connections (including all cases where an augmented dominant seventh chord connects two OctaCrystals in a similar manner to the major sevenths shown) are omitted in the Power Crystals graph provided. Comprehensiveness in this situation would result in an unwieldy and unnecessarily complex graph.
Return to text
16. Among seventh-chord transformations including strictly semitonal voice leading, P2,0 and P3,0 have the largest number of possibilities, especially with regard to those involving contrary motion. There exists a parallel P3,0 transformation that is the voice-leading complement for every P1,0, as well as the full set of contrary P3,0 transformations. Parallel P4,0 is trivial in that it is limited to semitonal transposition of the same chord type, and only a limited number of possibilities exist for contrary P4,0 (major→major, major→minor, minor→minor, dominant→half diminished, and, perhaps most interesting, French sixth→augmented dominant).
Return to text
17. That which is considered to be the “opening” may be limited to the first three measures, which contain the “Tristan chord” and its progression (perhaps via a French sixth) to a dominant seventh harmony, or it may extend as far as measure 17, where the same dominant seventh resolves (albeit deceptively) to the work’s first consonant triad.
Return to text
18. See especially the discussions in Lewin 1996, 207–9; Cohn 2000, 101; and Cohn 2012, 149–57.
Return to text
19. For one interpretation of the altered aspects of this sequence, see Bass 1996, 279–84.
Return to text
20. Strauss’s setting replaces the period after “schwillt” with another exclamation point in measure 25, and replaces a comma (perhaps an editorial error) with a period after “Ruhe” in measure 31.
Return to text
21. Whereas Figure 10 identifies various Pm,n transformations, specific types are noted only for P3,0 in order to elucidate its importance in the harmonic structure of the piece. The motivic stepwise bass descents are indicated by brackets above the lower staff in the reduction.
Return to text
Copyright Statement
Copyright © 2016 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Cara Stroud, Editorial Assistant
Number of visits:
16403