The Individual Tone and Musical Context in Albert Simon’s Tonfeldtheorie
Michael Polth
KEYWORDS: tonality, harmony, voice leading, Tonfeldtheorie, Albert Simon, Bernhard Haas, Schenker, Schoenberg
ABSTRACT: Albert Simon’s analytical approach, or Tonfeldtheorie, is applicable to most compositions of the late nineteenth and early to mid-twentieth centuries. Pitch fields are not based on voices or voice leading; instead, individual pitches are understood as elements of a particular pitch field. The identity of pitches is partly defined systematically, partly through the sound material itself, that is, by material aspects that determine respective concrete, sensually experienceable properties. Compositions, then, are analyzed as aggregates of timbrally defined individual notes whose material identity reveals their membership in structures.
DOI: 10.30535/mto.24.4.15
Copyright © 2018 Society for Music Theory
1. Introduction
[1] There are at least three perspectives from which musical-theoretical approaches to tonality may be undertaken, namely the “historical,” the “systematic,” and the “philosophical.” A primarily historical point of view seeks to explain what the notion of tonality meant for the composer or the historical listener of the period. From the systematic perspective, tonality may be construed as a cognitive or communicative system requiring the identification and explication of general rules that can be validated empirically. In the philosophical point of view, the object “tonality” may be considered as partly undisclosed, in the sense that some tonal phenomena have hitherto not been fully explored, and so the task at hand is to uncover phenomena that represent forms of tonality. While most analytical studies share aspects of all three perspectives, one of them usually leads the line of argument and determines the methodological direction of the study. Albert Simon, the creator of Tonfeldtheorie (the theory of pitch fields), adopted a philosophical approach. Although his model resembles systematic theories at first glance, its primary objective is to guide the reader—who is addressed as a listener—into a hitherto unknown world of tonality and to raise awareness of new musical relationships. It is important to bear this aspect in mind for the following detailed discussion of one specific aspect of Simon’s theory, namely the meaning of the Einzelton (single tone).
[2] In European and especially in German music theory, Albert Simon’s theory of pitch fields (Tonfeldtheorie) has elicited great interest ever since attention was brought to it by Bernhard Haas(1) in his 2004 book Die neue Tonalität von Schubert bis Webern: Hören und Analysieren nach Albert
2. What are pitch fields?
[3] Pitch fields are structured inventories of tones. The principles according to which they are structured are the intervals fifth and third. A pitch field is based on the concatenation of fifths or of fifths and thirds.
Example 1. Fifths rows (Quintenreihen)
(click to enlarge)
[4] Pitch fields that are exclusively composed of fifths are called fifths-rows (Quintenreihen), which have at least three and no more than nine notes—see Example 1. The names of the fifths-rows are derived from the number of tones involved: the tri-tone has three notes, the tetra-tone four, and so on, through the ennea-tone, which has nine. With regard to interval content, one finds that a pitch field contains all intervals of the next smaller one—for example, the hexa-tone F to E contains the penta-tone F to A—plus a new interval. The new interval always arises between the first and last tone of the series. Thus, in the hexa-tone F to E, as in the penta-tone F to A, the following intervals are found: fifth (e.g., F–C), major second (e.g., F–G), minor third (D–F) and major third (F–A), but the hexa-tone also contains the minor second E–F. In the hepta-tone F to B, the augmented fourth F–B would constitute the new relation. The respective interval contents of a pitch field, in particular the interval of the “corner tones,” characterize the pitch field and render it recognizable in the context of a composition.
Example 2. “Function” (Funktion)
(click to enlarge)
[5] Two further categories of pitch fields are defined. The pitch field “function” consists of four perfect fifths whose roots are lined up in order of minor thirds—see Example 2, first system. On this basis, major and minor triads can be formed in the interval of minor thirds—see Example 2, second system. The category “function” owes its name to the concept by Riemann and systematically (that is, cyclically) completes it. While Riemann recognizes only five alternatives to C major as T: the parallel t (C minor) and the relatives Tp (A minor), TP (A major), tP (
Example 3. “Construct” (Konstrukt)
(click to enlarge)
[6] The category “function,” with its array of fifths separated by minor thirds, is a form of “symmetrical” octave division—as is the category “construct,” which consists of three fifths in intervals of major thirds—see Example 3, first system. Both types of pitch fields have a state of completeness—due to their eight or six tones, respectively—that the fifths-rows do not possess (the penta-tone is not more complete than the tetra-tone; no fifths-row with three to eight tones is an incomplete ennea-tone). The respective lower notes of the fifth intervals are regarded as (equivalent) roots in function and construct, while fifths-rows do not, on their own, form any root tones without context.
[7] As mentioned previously, the musical-theoretical description of these inventories of tones is by no means new; pitch fields are known from other contexts under other names. For example, medieval diatonicism derived from the sequence of fifths, or the pentatonic, as frequently found in Debussy’s compositions, was already described by Albert Jakobik as a fifths-row in 1977. Arranged linearly, the tones of a “function” produce a half tone–whole tone scale and, arranged harmonically, yield a chord cycle that comprises minor thirds. The scale was described by Olivier Messiaen as “Mode 2,” and the harmonic cycle was termed “axis system” (Achsensystem) by Ernö Lendvai (1971). The pitch field “construct” also corresponds to Richard Cohn’s “hexatonic collection” (Cohn 1996). Similar observations can be found in Richard Taruskin’s book on Stravinsky (Taruskin 1996).
3. Claim and methodology of pitch-field analysis
[8] With his theory of pitch fields, Simon lays claim to a theoretical account of the fundamental principles of musical relationships in compositions from the period between approximately 1850 and 1945. To speak in terms of fundamental principles of musical relationships is to assert that the categories one proposes describe nothing less than the (implicit) musical understanding of many (if not all) composers within the period in question, as reflected in their compositions. This claim poses a challenge for analytical practice: pitch fields must be found in nearly all compositions and in all places. If a theory with such a claim is to stand, the application of the categories must follow clear principles, the observations must be conclusive, and the results must yield more than generalities, which would border on insignificance. The analytical rules, with only three types of pitch fields at their disposal, must be flexible enough for application to a variety of compositions and compositional styles and yet sufficiently precise to follow the individual characteristics of a composition. How does Simon proceed to accomplish this?
[9] The principles of analysis, evident from the examples given by Bernhard Haas, are based on preliminary aesthetic decisions that, in turn, reflect a particular understanding of how the author believes that pitch fields can be incorporated “in” a composition. The resulting variety of possibilities for the compositional structure to articulate pitch fields can indeed pose quite a difficulty for the reader.
[10] Generally, pitch fields, like the structures of Schenker, can occur in different layers, so that they can sometimes be distributed over many measures in a composition, and, furthermore, tones from different pitch fields can sound at the same time. In other words, relations are assumed without their condition of possibility in pitch fields having been determined beforehand (in Schenker, the structure must follow principles of diatonicism and counterpoint): How can a sound form the unity of a pitch field with other sounds located at a distance, when it is surrounded by sounds of yet other pitch fields? What is the musical difference between simultaneous sounds that belong to the same field pitch and those that belong to different pitch fields?
[11] With his propositions on how to apply pitch fields in analysis, Simon touches upon the very core of the problem that confronts all musical-theoretical approaches of this kind, namely that most compositions were hardly composed for the purpose of theoretical reflection. It is very rare that a work can be seen from the perspective of pitch fields in simple and immediate ways (as, for example, is the case in Liszt’s late piano composition R. W. Venezia). This discrepancy between the simplicity of the proposed categories and the complexity of the compositions can be analytically surmounted in two ways: Either the author curtails the claim of the theory and confines it to the explanation of those phenomena for which the categories evidently do work, or the author stands by the claim, as Simon does, and instead strives to answer the complexity of the compositional circumstances with complexity of the analyzed structure (Gefüge).
Example 4. Franz Schubert, Piano Sonata D. 960, first movement, mm. 115–117, in: Cohn 2004, 301
(click to enlarge)
[12] Pitch-field analysis proceeds according to the latter course described above. The implications of this direction become especially evident when Haas’s analyses are compared to those analyses, widespread in contemporary American musical theory, concerned with music from the period around 1910. Of all these approaches, which include, for instance, the transformational theory of David Lewin and the pitch-class set theory of Allen Forte, the neo-Riemannian approach of Richard Cohn, initially developed to deal with late-Romantic music, may be fruitfully applied to the later repertoire as well. Cohn describes a “hexatonic system,” which is a structure corresponding to Simon’s concept of the “construct.” Cohn finds this structure in numerous examples that could also be the object of pitch-field analysis, such as Schubert’s last piano sonata—see Example 4.
[13] This is not the place for a detailed discussion of Cohn’s undoubtedly important and insightful approach. The aim here is merely to point out that from Simon and Haas’s perspective, Cohn’s analysis of hexatonic systems emphasize local chord successions or neighboring triads; this represents a pre-determined methodological limitation that Simon and Haas are not ready to accept, so as not to restrict the scope of analytical possibilities. In turn, this reluctance to exclude any analytical possibilities from the outset can be traced to their endeavor to pursue pitch analysis as a means of compositional analysis (rather than as an explanation of individual harmonic phenomena). From Simon’s perspective, if finding pitch fields were solely limited to neighboring chords, arriving at an interpretation of a composition as a whole could not be accomplished.
[14] In contrast to Cohn, Haas offers only a few musical-theoretical reflections. His analytical decisions are presented in the form of diagrams, with only minimal commentary or explanation (in this, Haas seems to follow Simon).(3) He records relationships between tones as they occur, but for whose condition he has no explanation (to have no explanation does not mean: to act subconsciously or without knowledge of the categories and principles at work). That Haas and (probably also) Simon shy away from musical-theoretical remarks may be due to the fact that they worked (or in Haas’s case, still work) as interpreters for whom a tonal relationship is established by becoming audible in performance, not by its scientific justification. Indeed, the reason German musical theorists are continually drawn to Simon is that many of his analytical suggestions are musically convincing, and, given that, it seems promising to search for underlying structures in his interpretations of musical relationships a posteriori.
[15] Haas’s analysis of Arnold Schoenberg’s Klavierstück op. 19, no. 6—to be examined below—is bound to surprise the newcomer to pitch-field analysis, because a clear reference between the cohesion of the tones to the pitch fields and the musical syntax (regarded as relationships in general) is not recognizable at first. The difficulty in finding this connection has to do, first of all, with the layers to which the composition’s pitch fields are assigned. Similarly to Schenkerian analysis, there are few background pitch fields, but more numerous ones in the middleground and foreground. Likewise as with a Schenkerian background, the Hintergrund tones of the pitch field that articulates the piece’s totality, are distributed over several measures of the piece (usually in groups). The tones of pitch fields in the middleground and foreground, which mediate between the tones of the background pitch fields, are more likely to be heard in the immediate listening contexts.
[16] The distribution of the tones of a pitch field to distant measures recalls Schenker’s idea of prolongation by composing-out. Pitch fields in the background (or on layers close to the background) are thus composed out by pitch fields on more foregrounded layers. According to Schenker, however, prolongation follows rational ideas and is contingent on an underlying seven-note diatonic scale (major or minor), and counterpoint. Such conditions cannot be found in Haas’s analysis, and moreover they would not apply to much music composed after 1909, because diatonicism and counterpoint were no longer the basis of composition. Instead of diatonicism, the chromatic scale of twelve tones became the material of music considered modern. Counterpoint, understood as the regulation of the compositional structure by the distinction between consonance and dissonance, had been largely suspended as the basis of compositional structure since the late nineteenth century.
[17] Moreover, one of Schenker’s central principles is that if pitches form a structure, they belong to a “voice.” Understood as a musical-theoretical category, “voice” is one of the conditions under which structures can emerge; the unity of pitches as a structure presupposes the more fundamental unity of the pitches as a voice. The voice coincides with its own irreplaceable variety of pitch cohesion, based on a Western understanding of music that goes back at least as far as the Middle Ages. One of the most important characteristics of this form of cohesion is that pitch sequences within a voice are understood not as a series of many different individual notes, but as the movement of a single note through pitch space; “classical” polyphonic composition is based on such movements. Voice is thus seen as essentially connected to the temporal sequence of pitches, but not necessarily to linearity. Linearity represents only one option for the treatment of voices, albeit a prominent one.
[18] As is well known, the term “voice” in Schenker refers not only to the individual voices or parts in the score, but also to events in the middleground and background. Schenker thus transfers a prominent understanding of pitch connections from the actual sounding lines to their structures. As a result, even two pitches that appear at some distance from each other in a composition can be heard as the progression of a single pitch to a different scale degree if they belong to a voice in the middleground or background.
[19] Haas never tires of emphasizing that tonality based on pitch fields knows no voices. What does that mean? To avoid misunderstanding, let me state that this certainly does not mean that he believes that there are no voices in the scores of the late nineteenth and early twentieth century. Furthermore, it does not signify that the notion described above, wherein a single pitch moves between different scale degrees, is necessarily incompatible with pitch-field music.
[20] Instead, the notion of absence of voices relates to the constitution of pitch-field tonality. For example, the pitch field known as “function” consists of eight pitch-classes gathered according to a particular rule. If such a function appears within a composition, its ideal-typical manifestation is eight individual pitches appearing in eight different places. It is not necessary to hear a single note proceeding through the eight pitches of the function in the way that the fifth-progression constitutes a traversal of five different scale degrees. A note that appears later expands the pitch field by a further element, but it does not continue the preceding one (as the notes in a voice would continue from one another).
[21] This circumstance has far-reaching methodological consequences. With the exclusion of the voice, one loses a central category of musical context, and thus also of analysis. Accordingly, there are no rules in pitch-field theory that correspond to the rules of composing-out in Schenker. But, if so, what evidence can the analyst use to support the argument that pitches located far apart belong to the same pitch field, or—conversely—that the linked pitches of a motif, a melody, or a chord belong to different pitch fields?
[22] In order to examine the “rules of prolongation,” it is expedient to recall Simon and Haas’s intention: to help other performers play a composition conclusively with their analyses. An interpretation is conclusive, if every detail is embedded in a meaningful context. Therefore, the main focus of the analyses is to present every detail as a partial moment of a comprehensive context. In doing so, the analyses indicate a way for the performer to hear and thereby play these details. Based on these insights, the relevant question for these analyses is: To which performance does Haas want to guide us?
4. Analysis: Schoenberg, Klavierstück op. 19, no. 6
[23] Haas proceeds from the specific tonal characteristics of the events (tones and harmonies), which he seeks to describe adequately by means of structural interpretation. These characteristics must not be regarded as inherent, that is, as if they had been created naturally. Rather, they are evoked by the analysis itself, as, conversely, they also inform the analysis. There is a reciprocal relationship between theory and tonal characteristics. The properties of the events indicate how, for example, simultaneous sounds (simple intervals, harmonies) are to be interpreted.
4.1. Harmonies
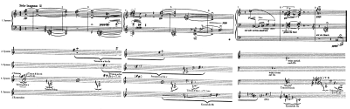
Example 5. Schoenberg, Klavierstück op. 19, no. 6, with analysis by Bernhard Haas (2004)
(click to enlarge)
[24] The question of how simultaneously sounding tones form a harmony is raised by Haas on a fundamental level. Whereas in Cohn’s analyses, for example, triads are presupposed as given units, in Haas’s one must determine each individually from the piece, that is, decide if and how events converge to a harmony. In op. 19, no. 6, there is clear indication of the difference between the first and the second harmony: The second chord (m. 1.3) can be heard as compact (inter alia due to the narrow position of its elements) and can therefore be regarded as a single “chord” of two fourths—see Example 5. The first one (upbeat to m. 1), on the other hand, can be perceived as heterogeneous because of the greater distance of the lower tone from the two upper ones. The analysis invites us to regard the harmony as composed of an upper fourth and a further tone A4.
[25] The divergence of notions of whether simultaneous sounds constitute one event or two events is reflected in the structure of the pitch fields. The compact, closed second chord itself forms a pitch field, a tri-tone F–C–G—see System 4 in Example 5. In the first harmony, however, the upper fourth belongs to the tri-tone B–
4.2. Intervals
[26] A remarkable detail, characteristic of Schoenberg’s new and unusual compositional direction after 1909, is the octave
4.3. Cohesion
[27] The conception of how tones can belong together in a pitch field is quite ambitious. In the first harmony, the fourth
4.3.1. Symmetry
[28] The tetra-tone and the penta-tone, which is entangled with it, are analogous: in both the systematically determined first note (A or
4.3.2. Tonal similarity – material shaping
[29] In principle, tones that belong to one pitch field, because they are involved in a structured context, can acquire certain musical characteristics that they do not possess outside of the specific context or in other contexts. Such characteristics, however, must be supported by further compositional features.
[30] Sometimes it is timbre that determines the identity of a pitch field. Or perhaps one should not call it timbre, but rather the concrete material shaping of a pitch. This shaping can be applied to a note in a piano piece through any manner of techniques that influence the attack and the tone: dynamics, articulation, and even pitch, provided that register also determines the character of a note. In the case of the above-mentioned tri-tone
[31] It is this common characteristic that enables the tones to be related to each other. They are of the same kind, with equal extrinsic properties. Because their identity is ensured, they can stand apart from each other in the flow of time. The pitch field that they form has a period of validity from the first note to the last. It would, however, be difficult to claim that with the first tones tension is introduced that the final tone resolves.
4.4. Hierarchy–background–prolongation
[32] Pitch fields are assigned to different layers (“System” in Example 5). One of the fundamental principles of this order of layers is the idea that the background, which articulates the composition as a whole, consists of twice twelve tones. This means that although a single pitch field can never cover all twelve notes of the chromatic scale, but certain combinations of similar pitch fields can consist of exactly twelve notes. Twelve tones can be formed by two complementary constructs, or (in the case of fifths-rows) by four tri-tones, three tetra-tones, or two hexa-tones. The total of the twelve tones would be articulated in each particular way by the respective combination of pitch fields. Aesthetically, it is not this abstract total that is decisive, but the concrete characteristics of the tones involved, which result from the respective articulation by pitch fields.
[33] When Simon speaks of “twice-twelve tones” in the background, he means that the form of the entire composition is determined by the fact that two different articulations of the twelve-tone total are presented and put into a chronological relationship. Since every articulation of the tones by pitch fields evokes certain characteristics of the tones involved, the form of a composition would thus be determined by the contrast of two groups of tones with two different types of properties. Every pitch appears in two properties just as the two properties are formed by the same twelve pitches.
[34] In Schoenberg’s Klavierstück op. 19, no. 6, the twice-twelve tones of the background are given, in the first instance, by occurrences of Constructs IIa (expressed as two augmented triads: G–B–
[35] The “melodic” and the “harmonic” constructs occupy the middle register of the piano, while some tri-tones are located in the extreme registers. The tri-tone F–C–G forms the first-level deep event. The next deeper event, the seventh E2–D3, supplements the tone A4 from the very beginning. Deeper than this seventh is only the aforementioned tone
[36] Haas notes that in each case, the tri-tones that are an augmented fourth or diminished fifth apart are constructed analogously. The tri-tones F–C–G and B–
[37] As mentioned previously, the tones of the pitch fields in the middleground mediate between those in the background. This mediation is not the same as a Schenkerian prolongation, although I used the terms middleground and background to describe it. The mediation adds new notes to the tones of the background pitch fields, thus forming new pitch fields. Thus the tetra-tone in mm. 2–4 connects the fourth (of the tri-tone B–
5. Conclusion
[38] It would, nevertheless, be a grave misunderstanding of pitch-field theory to think of it as a system constructed analogously to Schenkerian theory, that is, as theorizing the same kind of connection, layer formation, and composing-out—except with pitch fields instead of linear progressions, unfolding, etc. This would mean overlooking a fundamental difference: the identity of pitches is defined systemically by Schenker for the most part, but in Simon’s approach it is defined partly systemically and partly by the sound material. In Schenker, a note acquires its identity almost exclusively by belonging to a structure; it is more or less subsumed under this structure. For Simon, however, notes signify more than simply elements of pitch fields; their identity comes not only from belonging to a pitch field, but also from material aspects that determine their respective properties, which are concrete and can be perceived through the senses. This means that pitch-field theory is especially well-suited for analyzing compositions from historical periods in which timbre as an identity-defining element can be presupposed. Pitch-field theory views late nineteenth-century and early twentieth-century compositions as aggregates of timbrally defined individual notes whose material identity can precisely reveal their cohesion to structures—a cohesion that turns out to be far looser than is the case with Schenkerian structures. I would argue that this view put forth by pitch-field theory largely captures the compositional situation around 1900.
Michael Polth
Institut für Musikforschung Mannheim
Staatliche Hochschule für Musik und Darstellende Kunst Mannheim
polth@o2online.de
Works Cited
Bodamer, Konstantin. 2011. “Albert Simon—ein ungarischer Autor.” Zeitschrift der Gesellschaft für Musiktheorie 8 (2). <http://www.gmth.de/zeitschrift/artikel/639.aspx>
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15 (1): 9–40.
—————. 2004. “Uncanny Resemblances: Tonal Signification in the Freudian Age.” Journal of the American Musicological Society 57 (2): 286–323.
—————. 2012. Audacious Euphony: Chromaticism and the Triad’s Second Nature. Oxford University Press.
Haas, Bernhard. 2004. Die neue Tonalität von Schubert bis Webern. Hören und Analysieren nach Albert Simon. Noetzel.
—————. 2011. “Zu zwei Bartók-Analysen von Albert Simon.” Zeitschrift der Gesellschaft für Musiktheorie 8 (2).<http://www.gmth.de/zeitschrift/artikel/640.aspx>
Jakobik, Albert. 1977. Claude Debussy oder Die lautlose Revolution in der Musik. Würzburg.
—————. 1971. Béla Bartók: An Analysis of his Music. Kahn & Averill.
Polth, Michael. 2006. “Tonalität der Tonfelder. Anmerkungen zu Bernhard Haas ›Die neue Tonalität von Schubert bis Webern. Hören und Analysieren nach Albert Simon‹.” Zeitschrift der Gesellschaft für Musiktheorie 3 (1): 167–178. <http://www.gmth.de/zeitschrift/artikel/210.aspx>
Schild, Johannes. 2010. “ . . . zum Raum wird hier die Zeit.‹ Tonfelder in Wagners Parsifal.” In Funktionale Analyse. Musik – Malerei – Antike Literatur. Analyse Fonctionelle. Musique – Peinture – Littérature classique. Kolloquium/Colloque Paris, Stuttgart 2007, ed. by Bernhard Haas und Bruno Haas, 313–373. Olms.
Simon, Albert. 1983. “Béla Bartók: ›Secondes mineures – septièmes majeures‹ (Mikrokosmos, VI/144).” Schweizerische Musikzeitung/Revue musicale suisse 123: 82–86.
Taruskin, Richard. 1996. Stravinsky and the Russian Traditions: A Biography of the Works through Mavra. 2 vols. University of California Press.
Footnotes
1. Bernhard Haas studied with Albert Simon from the spring of 1994 until Simon’s death in 2000. Classes took place very irregularly—but when they did, the sessions were almost endless. The focus was usually on harmonic analysis; they sat at the piano, discussing music with the scores in front of them. Haas relates that Simon’s remarks were more like a course in harmonic theory; Simon especially liked to poke fun at interpretations of functional theory and present his own readings.
Simon recorded his analyses in the form of diagrams, but Haas saw very few of them—Simon only showed them to him on one or two occasions. At the time, Simon was working on a written formulation of his approach and entertained the idea that Haas might make fair copies of his diagrams for the planned book project. This portentous book has not been published to this day, however. Haas was only afforded brief glimpses of the typescript but based on his accounts we know that it was quite thick and was written in English. About its state of completion, let alone any concrete content, nothing is known. In other words, whatever insights Simon arrived at beyond what he shared in his lessons will remain unknown for the time being. One should not rule out the possibility that his estate holds some surprises in store.
To date, all subsequent publications on this subject have built upon Haas’s study. Most authors are primarily interested in a basic understanding of pitch field theory and assess the methodological propositions offered in terms of their potential use value. Until now, there have only been very few attempts to develop the theory further, rework it, or integrate it into other, more comprehensive approaches. Among those music theorists who have not only engaged with pitch field theory but also apply it as a method for uncovering forms of experience, some see the potential of this approach less in the transmittal of Simon’s surviving observations than in the insights afforded by Haas’s analyses of Simon. For Haas is concerned with far more than simply the harmonic classification of sounds. In the following, all general references to Simon’s theory will relate to the form disseminated by Haas.
Return to text
2. The only published text by Simon himself is Simon 1983. Haas 2011 gives an account of two unpublished analyses that are archived in the Paul Sacher Foundation in Basel. With respect to influences of Hungarian music theory, see Bodamer 2011. Good introductions to analysis via pitch fields are Polth 2006 and Schild 2010.
Return to text
3. On the reasons for relying on Haas, including issues of accessibility of manuscripts, see again notes 1 and 2.
Return to text
Simon recorded his analyses in the form of diagrams, but Haas saw very few of them—Simon only showed them to him on one or two occasions. At the time, Simon was working on a written formulation of his approach and entertained the idea that Haas might make fair copies of his diagrams for the planned book project. This portentous book has not been published to this day, however. Haas was only afforded brief glimpses of the typescript but based on his accounts we know that it was quite thick and was written in English. About its state of completion, let alone any concrete content, nothing is known. In other words, whatever insights Simon arrived at beyond what he shared in his lessons will remain unknown for the time being. One should not rule out the possibility that his estate holds some surprises in store.
To date, all subsequent publications on this subject have built upon Haas’s study. Most authors are primarily interested in a basic understanding of pitch field theory and assess the methodological propositions offered in terms of their potential use value. Until now, there have only been very few attempts to develop the theory further, rework it, or integrate it into other, more comprehensive approaches. Among those music theorists who have not only engaged with pitch field theory but also apply it as a method for uncovering forms of experience, some see the potential of this approach less in the transmittal of Simon’s surviving observations than in the insights afforded by Haas’s analyses of Simon. For Haas is concerned with far more than simply the harmonic classification of sounds. In the following, all general references to Simon’s theory will relate to the form disseminated by Haas.
Copyright Statement
Copyright © 2018 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor
Number of visits:
8530