| | ||||||||
| | ||||||||
Volume 9, Number 2, July 2003
Copyright © 2003 Society for Music Theory
Alfred Cramer*The Harmonic Function of the Altered Octave in Early Atonal Music of Schoenberg and Webern: Demonstrations Using Auditory Streaming |
KEYWORDS: Schoenberg, Webern, Saussure, Strindberg, auditory sceneanalysis, auditory streaming, atonality, expressionism, altered octave,major seventh, minor ninth, masking, fusion
ABSTRACT: I present synthesized sound examples of several atonal expressionist excerpts to illustrate the effect of the altered octave as a sonority. Psychology, linguistics, and literature about 1900 suggest that early atonal expressionist music of Schoenberg and Webern may consist of a polyphony audible as coalescing and dividing sonorities. I argue that ideas about sound perception gathered together by A. S. Bregman under the rubric ofauditory scene analysis provide a way to conceptualize such polyphony,and I propose that the altered octave is a harmonic element crucial inproducing the coalescences and divisions.
Submission received June 2002
[1] Scientists, philosophers, writers, and artists at the beginning ofthe twentieth century were preoccupied by the empiricist realization thatthe stimuli reaching the senses were not orderly in themselves but werea messy mass of lines and noises, as were the thoughts in the mind whichresponded to those stimuli.(1) These empiricists believed that the orderlyappearance of the environment was simply an interpretation formed by groupingthose messy stimuli in conventional ways. As Figure 1 shows, the linguistFerdinand de Saussure, for example, pictured both the "plane of sound"entering the ear (A) and the "plane of thought" of the hearer (B) as composedof many small, simple noises or ideas, representing both as streams ofshort, overlapping contours.(2) (Saussure's dashed lines represented divisionsinto words--in effect they were rationalizations allowing the relationof thought to sound. The contours of thought interacted with the contoursof sound to produce a kind of interference pattern represented by the dashedlines, through which linguistic representation emerged.) William James,likewise, viewed the "stream of consciousness" as the sum of innumerableneural activations; each of these had a simple rising and falling contour,but when added together in a particular way their sum amounted to complexthoughts.(3)
Figure 1. Saussure's "plane of vague, amorphous thought" (A) and "the equally featureless plane of sound" (B)

[2] Many artists at the beginning of the twentieth century aspired tobe conscious of the processes by which the mind organized perceptions.The dream plays of August Strindberg had plots intended, as Strindbergput it,
toimitate the incoherent but ostensibly logical form of our dreams...Working with some insignificant real events as a background, the imaginationspins out its threads of thoughts and weaves them into new patterns...The characters split, double, multiply, dissolve, condense, floatapart, coalesce. But one mind stands over and above them all, themind of the dreamer; and for him there are no secrets, no inconsistencies,no scruples, no laws.(4)
During the years when their atonal style was takingshape, Schoenberg and his circle were enthralled by Strindberg's dreamplays,(5) and if the closing words of Schoenberg's Harmonielehreare to be believed, Schoenberg aspired to a dreamlike effect in his ownmusic. There Schoenberg speculates about Klangfarbenmelodie, a spiritualmusic that "will bring us closer to the illusory stuff of our dreams."(6)
[3] If Schoenbergian atonal expressionism is indeed meant to accessthe dream state, one should be able to interpret it in terms of turn-of-the-twentieth-centuryconceptions of the mind. Saussure, James, and Strindberg were alike inconceiving of thought as a spinning-out and weaving-together of threadsof ideas, a stream in which discrete ideas flow together and then eddyapart. Is it possible to interpret atonal expressionist music as a streamof sound resembling such a stream of thought? Following James and Saussure,one might seek ways in which the individual voices stream together; followingStrindberg, one might look for ways in which harmonic sonorities divideinto separate melodic lines which then coalesce again in new combinations.(7)
[4] Such division and coalescence would provide a point of comparisonbetween atonal expressionism and the tonal common practice that Schoenbergand his students discarded. Much tonal music involves an equilibrium betweenthe perception of tones individually and as fused members of chordal sonoritiesor melodic lines. The nineteenth-century theory of the Klang--whichviewed the distinct tones of musical chords as reifications of the normallyinaudible partials of a single complex tone--captured the sense that atriad could be perceived as a whole or as a collection of individual tones.Atonal expressionist harmony rarely features the triads of tonality, andits voices should not be expected to combine with the clarity found incommon-practice tonality. But in atonal music, several seemingly distinctvoices may concertedly produce a striking color, or a blended group oftones may decompose into interesting melodies. In a recent article I arguedthat Schoenberg meant his word Klangfarbenmelodie to refer to amodern analog to the Klang in which expressionistic harmony couldbe understood in terms of the variety of tone colors that could emergewhen individual tones fused together into sonorities.(8) I suggested thatthe altered octave (the major seventh or the minor ninth) is crucial ingiving many atonal chords this psychoacoustic property. In the presentarticle I demonstrate this function of the altered octave using aural examples.
[5] My discussion focuses on the formation of cohesive sonorities thatemerge as subdivisions of a musical texture. I pursue it in terms of recentresearch into auditory scene analysis (ASA). Over the past three decades,a number of psychologists and musicians have investigated a problem mostextensively articulated by Albert S. Bregman: How does the auditory systemparse complex stimuli into simple sound objects (auditory streams)that correlate with the objects producing the sounds (the objects formingthe "scene" around the listener)?(9) This question is closely related tothe basic puzzle of early twentieth century empiricists: how do the innumerablemessy noises of the world somehow come to make sense, and to resemble reality,as they pass through the mind? The recent studies of ASA offer a relativelysuccessful account of how people hear sounds in terms that would have beenrecognizable in the early twentieth century.
[6] Thus, in this article I interpret the altered octave in the contextof ASA in order to suggest that early atonal expressionist compositionsare constructed to promote the coloristic blend of separate voices. I approachmusical surfaces in terms of perceived psychoacoustic groupings of varioustones, using synthesized audio examples and graphic illustrations to illustratethe kinds of groupings that arise. The latter are modeled on the "schematicspectrographs" used by Bregman to illustrate the way the mechanisms ofASA tend to group complexes of sound into integrated perceptual objects.
[7] ASA is "the process whereby all the auditory evidence that comes, overtime, from a single environmental source is put together as a perceptualunit."(10) Using the processes of ASA, the mind is able to hear, for example,the sounds uttered in a statement by a single person as belonging together,and it is able to distinguish that utterance from the many other soundsheard at the same time. Sounds grouped together through ASA have a qualityof perceptual coherence. Experimental studies designed to pinpoint exactlywhat ASA does include tests of auditory stream segregation, the phenomenon in which a series of consecutive tones appears to be split into two separate streams. For example, in Figure 2a, listeners perceive the tones to be linked in a single stream, with the result that they hear a galloping rhythm. But if tone B is moved to a pitch further away from A and C as in Figure 2b, ASA produces two distinct perceptual streams. This is indicatedexperimentally by the fact that the tones' rhythmic placement with respectto each other is perceived entirely differently: listeners can tell thatone stream contains a faster rhythm than the other, but they cannot hearthe galloping rhythm. The words "over time" are in Bregman's definitionof ASA are key. Consecutive tones in a series are more likely to split into separate streams if they move in a faster tempo. Thus, if Sound 2a is slowed down, it is possible for the listener to hear continuity between tones A, B, and C, as in Figure 2c.(11)
[8] When a single environmental source emits sound waves at various frequencies simultaneously, the psychoacoustic grouping together of the various component tones (as well as the separating of sounds that do not belong to the same source) is most strongly influenced by factors with a temporal dimension: If several tones rise or fall simultaneously in pitch or volume, they are likely to be grouped together; and if they have simultaneous onset they are also likely to be grouped together. If a series of tones is repeated over time, groupings are strengthened and ambiguity diminished. One major non-temporal factor promotes grouping: Groups of complex tones fuse insofar as their "combined spectral content conforms to a single hypothetical harmonic series." In pairs of complex tones, it happens that this occurs when their frequencies "are related by simple integer ratios."(12) Perfect unisons (1:1), octaves (2:1), fifths (3:2), and fourths (4:3) fuse strongly; thirds (5:4 and 6:5) fuse, but somewhat less strongly. About 1890, the psychologist Carl Stumpf claimed that such fusion, determined by simple frequency ratios, was the same phenomenon as consonance, and his understanding has held its grip ever since.(13) This factor functions in the dimension of pitch, not time. But temporal cues can undo this: if a harmonic partial begins earlier, or if its frequency is the same as that of an immediately preceding tone so that it seems to belong to an ongoing stream, it may be heard as separate from the other constituents of the harmonic partial-tone series. I summarize the factors promoting fusion and segregation in Table 1.(14)
Table 1. Factors in auditory stream integration and segregation | ||
| Simultaneous tones | ||
| factors favoring fusion | factors opposing fusion (favoring stream segregation) | |
|
| |
| | ||
| factors favoring stream integration | factors favoring stream segregation | |
|
| |
[9] ASA's perceptual grouping or segregation is rarely absolute. Individual tones may appear weakly grouped, individually discernible but with a sense of linkage, or so strongly grouped that there is no conscious awareness of the actual sounds of the individual tones, merely a sensation of their timbral effects on the global sound. Competition between different possible perceptual groupings can produce uncertainty. In the sound represented in Figure 3a, the simultaneous onset of tones B and C makes them likely to fuse almost into a single perceived sonority characterized by its own timbre. In Figure 3b, however, the pitch proximity of tone A to tone B makes it easier to hear continuity between A and B, while the tendency to hear B and C fused is correspondingly weakened. In Figures 3c and 3d, a fourthtone D is added to produce a stream between C and D. Since hearing a streambetween tones C and D is inconsistent with hearing tones B and C in thesame stream, it becomes harder to hear fusion between B and C, althoughin Figure 3c it is still possible to experience B as a timbral coloringof C. In Figure 3d, B is easily captured into the stream of A, and it ismuch more difficult to hear fusion of B with C.
[10] Auditory scene analysis is applicable to common-practice musicin that a melody occurs when successive tones are integrated into a singleauditory stream,(15) and in that tonal harmony is organized so that thosesimultaneities that are strongly integrated are consonances. Common-practicecomposers, in this view, treat dissonances (that is, simultaneities involvingcomplex frequency ratios or sensory roughness) in such a way as to separatethe dissonant tones into separate streams, so that they will be integratedonly weakly or not at all. Common-practice voice-leading, rhythmic features,and other choices reinforce the tendency of simple harmonic ratios (orrather, the tendency of the overtone series) to cause fusion.(16)
[11] But this serendipitous conformity of sensory consonance to featuressuch as voice-leading is not at work in atonality. Nor need it be. Sensoryconsonance is not synonymous with fusion, even though it stems from thesimple frequency ratios that are also implicated in the fusion of the overtoneseries. Sensory consonance is merely one factor promoting integration,and sensory dissonance is not in itself a factor opposing integration ashas often been supposed. Bregman emphasizes this distinction between consonanceand fusion. He notes that sensorily dissonant tones may fuse, and whenthey do so, the resulting dissonance must be understood as a timbral feature.(17)On its face, Schoenberg's argument in his Harmonielehrethat the higher overtones must be treatedas consonances suggests that he viewed consonance as synonymous with fusion:the overtone series, his reasoning went, generates both consonance andfusion. But in the end, Schoenberg's purpose was to argue that any combinationof tones--traditional consonances as well as traditional dissonances--couldfuse. Schoenberg rejected the claim (common in his day) that the firstsix partials of the harmonic series dictate the primary chords, arguinginstead in favor of a music in which any combination of tones might betreated as a harmonic unit.(18)
[12] My claim is that in their early atonal music Schoenberg and hisstudents learned to treat the altered octave as such a harmonic unit. Iargue that its psychoacoustic nature lets it function as a unified sonority.In this respect it is analogous to the common-practice major triad, whichfuses when its various overtones conform to one harmonic series. I suggest,however, that rather than than organizing the music functionally the waytriads do, the altered octave suggests an organizing resemblance between expressionistmusic and the conception of thought described at the start of this essay.Along with temporal ASA factors and, to some extent, traditionally fusingintervals such as the major and minor third, the altered octave is oneatonal tool in the creation of constantly changing subgroupings withinthe musical texture.(19)
[13] The tones of an altered octave may be said to fuse, but in a different manner fromthe fusion of traditional consonances. Integration occurs in this classof "sensory dissonances" (in Schoenberg's terminology, "remote consonances")because of the masking produced when two frequencies are within a criticalbandwidth of one another. According to the understanding that began totake shape in the 1960s, in the inner ear, the frequencies of tones aretransduced as excitations at particular positions along the length of thebasilar membrane, which then sends signals of these excitations to thebrain. When two tones activate positions on the basilar membrane closeto one another, one masks the other. This masking is substantial when theactivated positions are within about 1 mm of each other (at the bottomof the bass-clef staff, this means the frequencies are within about a fifthof each other; at the top of the treble, about a half step). The distancein pitch at which such masking takes place is known as the critical bandwidth.When two frequencies are within a critical bandwidth, the hearing has difficultyresolving them.(20)
[14] Whether because of neural properties inherent in the masking orbecause the critical band coincides with intervals at which beats are maximally"rough," the critical band is associated with a dissonant "color." Thegreatest roughness occurs when one partial is near the edge of the other'scritical band. When partials are well within each other's critical band(i.e. very close in pitch), there is little roughness; it is almost asif they coincided exactly. Figure 4 gives an approximate representationof the masking involved in various intervals, with a lower tone in middletreble register such as g1. For traditional consonances suchas the M3 and P5, several partials of each tone are not masked, and manyof those that are masked are so close in frequency that they do not producesensory dissonance. The augmented 4th presents little more masking thanthese consonances, but a greater degree of roughness. In the minor 2nd,masking and dissonance are both high. It is difficult to hear the two complextones separately from each other.
Figure 4. Critical band interactions of intervals. Long dark lines representpartials of a pitch in mid-treble register, such as g1. Shortdark lines represent the partials of tones at the specified interval abovemid-treble pitch. Shaded bands represent critical bands.
|
|
|
|
|
|
|
P5 | M3 | A4/d5 | m7 | M7 | m9 | m2 |
<less< criticalband masking >more> | ||||||
[15] Intervals such as the minor 2, minor 9, and major 7 are highlynon-fusing; but I contend that, in early twentieth-century expressionism,the difficulty of perceptually resolving individual tones in these highlymasked intervals is a substitute for fusion. Like fusion, such maskingcan unite several tones into a single perceptual object. (Much other musicfrom the twentieth century also uses traditional dissonances for this purpose.)Schoenberg and Webern, searching for coloristic variety in the progressionfrom one sonority to another, used the characteristic beating and roughnessof the altered octave as a color structurally equal to the colors of thetraditional consonant intervals. Used in this fashion, the color of analtered octave would no longer merely connote tension requiring resolution.
[16] The following informal demonstrations illustrate the interplay of streaming and altered-octave masking. There are two possible ways to hear the sequence F-sharp - B-flat - F-sharp (Sound 5). It can be heard as an integrated stream as inFigure 5a, or segregated into two streams as in Figure 5b. To me, it is easier to hear the singlestream shown in Figure 5a than to hear the two streams of Figure 5b, althoughthe latter is also possible. But when a continuous G is added an alteredoctave below the F-sharp (Sound 6), my hearing changes. It is still possible to hear F-sharp and B-flat in a single stream as in Figure 5a, but it becomes easier to hear the F-sharp in a separate stream from the B-flat, by hearing the F-sharp and G as a single sonority separate from the B-flat (Figure 6).
[17] This integration of F-sharp with G may be partly due to the fact that the two tones begin simultaneously. Yet the effect remains if the order of the F-sharp and the B-flat is reversed. I findFigure 7a to be a more persuasive representation of my hearing ofSound7 than Figure 7b; yet when G is added (Sound8), I perceive the F-sharp as a coloration of the G, and above this sonority I hear a stream of pulsing B-flats (Figure 8).
[18] In this case, it may be suggested that the G captures the F-sharp more than itcaptures the B-flat because G is closer to F-sharp than to B-flat. Butwhile this may be a factor, the parsing remains the same when the G isplaced above the other two tones. This is heard in Sound9, seen in Figure 9, and inSound 10, seen in Figure 10. (For comparison, hearFigure9 without g1; Figure 10without g1.) I can only conclude that the altered octave is responsible for the sense of integration.
| Figure 9 | Figure 10 |
| Sound 9 |without g1 | | | Sound 10 | without g1 | |
[19] Clearly these demonstrations of this sort can be heard in various ways, and certainly any conclusions drawn from them must remain tentative at least until more formal experimental study. The masking effect of the altered octave is less ambiguous, though, in chords with more tones--for example, in the series of sonorities found in Example 1 ([GIF] [Scorch]), the end of Webern's quartet movement, op. 5, no. 5, from which the previous demonstrations are abstracted. In this passage the first violin leaves and rejoins the underlying sonority. As with the previous demonstration, the changes in sonority can be investigated by means of fast repetition, in which changing degrees of masking and fusion are manifested as auditory stream segregation. The exaggerated comparisons resulting from high-speed repetitions reveal aspects of the sonority that present themselves as subtle but palpable shifts at the music's actual tempo. In measure 24, the first violin's F-sharp has a different sense of belonging to the underlying sonority than the B-flat. The F-sharp has an altered-octave relationship with the viola's G, but the B-flat does not have an altered-octave relationship with any element of the sonority. In addition, the F-sharp is probably significantly masked by the 2nd violin's C. When the F# is quickly alternated with the B-flat as in Figures11 and 12, the B-flat stands out from the sonority, but the F-sharp blends in.
[20] In Sound 12 at this speed, I hear the F-sharp as part of the sonority that includes the three lower tones, and it is difficult for me to "hear" that in fact the F-sharp begins later than the three other tones. Beneath the B-flat I hear a single sonority; the passage sounds more like Figure 13a than like Figure 13b. No doubt because the F-sharpis masked partly by the C and C-sharp in addition to the F-sharp (noneof which masks the B-flat as strongly), this effect is much stronger thanthe corresponding effect in the earlier demonstration (Sound 7). It may be suggested that the F-sharp appears to belong to the underlying tones not because of critical-band masking but because the example is played too quickly for a stream to be heard incorporating B-flat and F-sharp (as in Figure 7a). As a result, one might argue, an interpretation such as the one illustrated in Figure 13b is heard but mistakenly represented as in Figure 13a. The point, though, is not that at a certain speed B-flat and F-sharp are segregated into separate streams with the result that it is difficult to recognize their temporal relationship. Rather, what is interesting is that when such segregation takes place, the B-flat stands out while the F-sharp is folded into the tones below it. That is, accompanying the b-flat, one hears a sonority made up of the four tones of Figure 13c, instead of hearing a sonority that sounds like Figure 13d.
[21] As might be expected, the integration of the F-sharp but not theB-flat is even stronger when the cello's F is added to the sonority;Sound14a andSound 14b confirm this.
[22] This means, of course, that five tones are heard together as a sonority as in Figure 14c.
[23] Altered-octave masking accounts for the integration of the F-sharp, but other phenomena such as registral distance play roles as well. B-flat stands out partly because it is in a much higher register than all of the other tones, and if it is replaced in the sonority by B-natural as in Figure 15, the B-natural stands out at least as much. The increased interval--F-sharp- B-flat to F-sharp - B-natural--increases the tendency for stream segregation,making the B-natural stand out, despite that the B-natural forms an alteredoctave with the C-natural.
[24] The informal experiments just discussed suggest that it should be possible to perform the passage in such a way as to bring out the connections shown in Figure 16. Belowthe analysis I have given a drawing showing each sound-object as a lineor stream. Separate streams are represented by separate lines, and integratedsounds are represented by single or touching lines. As the figure shows,when the three upper instruments enter, the cello's F may at first be heardseparately, but as the chord is held the F-sharp blends in, changing thetimbre emerging from the chord. The violin moves to B-flat, again splittingthe mixture into two sonorities. The next gesture begins with the F-sharpalone in the violin (mirroring the cello's earlier isolated low F). Whenthe other instruments join, the violin stays in its own stream. In thefinal gesture, the violin again begins as part of the underlying sonority,moving later to B. At actual tempo, these streams are not clear-cut, butthey represent a subtle partitioning in the harmonic stream. A particularlynuanced performance might even succeed in using the F-sharp to establishthe first violin in a blend that is maintained even when the violin changespitch, so that the violin's motion to B-flat and B produces a change incolor of the continuous sonority, not a splitting of the sonority.
| Figure 16 |
| Sound 16 | |

|
[25] Stream- and color-creation cannot simply be inferred from the score. The fusing of sonorities depends greatly on balance between voices and on other factors in performance. The divided cellos' accompaniment near the beginning of Example 2 ([GIF] [Scorch]), Schoenberg's orchestral song "Seraphita,"op. 22, no. 1 (1913), is a case in point.(21) Theopening diminished fourth in the inner voices expands to a perfect fourthand finally a tritone (Sound 17c). Ifthese intervals can be heard as single sound objects, the passage may beheard as an evolving succession of colors. Their simultaneity indeed promotesperceptual integration, but the fact that they move only in similar motion,not parallel motion, does not. Whether the effect of evolving color isachieved depends on the playing of the altered octaves in the outer voices.
[26] If the outer voices are played loudly enough, they mask the inner voices of chord 3, as in Figure 17a (where vertical lines with arrows indicatethat the inner voices seem to "belong" to the outer voices). Because eachinner voice is masked by a different outer voice, the inner voices' ownintegration is minimized. (Sound 17a(i);the effect is strengthened further in Sound 17a(ii).) Chord 3 will then consist of two sonorities. (The decreasing integration is indicated by the thicker vertical line in chord 1, the thinner line in chord 2, and the line's disappearance in chord 3.) On the other hand, if the outer voices are quieter, they are masked by the inner voices, as in Figure 17b. The altered-octave shimmer steadily accruing to the innervoices adds to the evolving color of the inner voices' own integration.Thus, the inner voices of chord 1 are heard as simply a major third (withthe outer voices forming their own, separate, sonority). As the inner voicesmove to chord 2, a new color emerges not only because the inner voicesnow form a perfect fourth but also because this pair of tones is now coloredby the altered octave of the lowest voice. Finally, the color of the augmentedfourth of chord 3 is enhanced as a second altered octave is contributedby the highest voice. (Hear this effect in Sound17b(i), and more strongly in Sound17b(ii).)
Figure 17. Schoenberg, "Seraphita," op. 22, no. 1, mm. 2-3, cellos after Cramer, "Klang and Klangfarbenmelodie," p. 29 | |||||
| Realizations of Example 2 / Figure 17: | |||||
<<< more like Figure 17a | more like Figure 17b >>> |
| |||
|
| ||||
[27] Parallel motion between tones increases their fusion. Composersseem to find this principle useful for increasing the perceptual coherenceof sonorities with a moderate but not overwhelming tendency to fuse. Thus,in both common-practice and early atonal music, major and minor thirdsfrequently appear in parallel motion; and altered octaves often appearin parallel motion in early atonal music. In Webern's orchestral piece op. 6, no. 1, mm. 2-4 (Example 3 [GIF] [Scorch]), parallel motion fuses the top threetones of the first two tetrachords; in the second chord an altered octave captures the bottom tone as well; and parallel motion fuses the bottom three tones of the third chord. As is shown in Figure 18a, this leavesa low C and a high C free, and in Sound18a these tones stand out. But the Cs are not entirely free; theyform altered octaves with the B of the French horn, as shown in Figure18b (hearSound 18b(i) orSound18b(ii) with simultaneous onset of horn and cellos). In the demonstrations,the Cs are less prominent when the horn's B is sounding than when it isnot--another way of saying that the Cs start and end as colorations ofthe B, flowing from the B into the stream of chords and back. During thesethree chords, altered octaves are the key to associative relationshipsin which the melodic lines "split, double, multiply, dissolve, condense,float apart, coalesce" like characters in a Strindberg dream play.
| Figure 18 | |
18a. | 18b. |
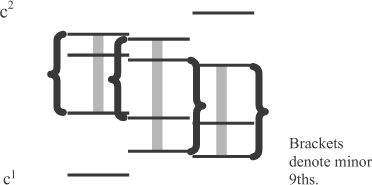 |  |
[28] Although this example shows a clean and simple use of the combination of parallel motion and altered octaves, most instances are not as neat. Altered octaves are often small details in complex, ornate progressions; and there are cases in which the use of the altered octave appears to be a governing principle even though its effect is difficult to precisely hear or predict.Example 4 from later in Op. 6, No. 1 illustrates sucha case. Here the d - a - c-sharp - b-flat - b line played by the fluteand oboe may function as a compound melody, an instrumental line dividedinto two perceptual objects through the auditory streaming created by relatively wide melodic intervals. Each "voice" of the compound melody joins another voice of the texture through altered octaves; in a sense, the separate components of the compound melody are harmonically dependent on (that is, coloristically related to) different voices elsewhere in the polyphony.
[29] For the first four notes, the high notes are introduced in altered-octaverelationships to the triplet melody of the clarinet, bassoon, and pizzicatocellos; the lower tones are related to the B-flat and A of the solo cello.The fifth note, B, fulfils the convergent implications of the compoundmelody while providing an altered-octave anchor for the newly-entered horns(whose opening pitches, incidentally, alternate in altered-octave relationshipswith the flute-oboe and the solo cello lines). If it were this simple,the oboe-flute line would be fully explainable in terms of its colorationsof, alternately, the cello solo and the clarinet-bassoon-cello lines. Butthe altered-octave harmonies are brief, lasting only until one voice orthe other moves to a new pitch, and many other factors are at work. InSound 19a, the altered octaves are hard to hear as such. They become a biteasier to hear in Sound 19b, in whichrubato lengthens the durations of altered octaves. Several possible interpretationsmay be competing: hearing the flute-oboe line as one melody or two; hearingit as a perceptually salient melody or as a series of colorations appliedto other voices; hearing the altered octave for its acoustic impact orfor other properties of ic1.
[30] Auditory scene analysis has been promoted for its ability to explaintraditional musical elements such as melody and counterpoint. In this articleI have drawn on it for a different reason: its ability to move the discussionof harmony beyond the categories implied by such traditional terms. Movingbeyond the traditional categories was a chief purpose of Schoenberg andWebern, evident in Webern's claim that their music ushered in a new eraof polyphony (which he called "a new interpenetration of music's materialin the horizontal and the vertical"),(22) evident in Schoenberg's claimthat in modern music the vertical and horizontal were unified,(23) andevident in Schoenberg's claim that the new sonorities might be explainednot in terms of the traditional dimensions of Klang-based harmonyand melody but in terms of a fusion called Klangfarbenmelodie. Myanalyses speak to all of these, positing that in the Viennese School'spolyphony, sonorities of varying color merge and separate, so that at anygiven moment the total sound is articulated into perceived groupings, muchthe way a melody over time is articulated into perceived groupings.
1. Judith Ryan, The Vanishing Subject: Early Psychology and LiteraryModernism (Chicago: University of Chicago Press, 1991).
Return to text
2. Saussure, Cours de linguistique générale, ed. CharlesBally, Albert Sechehaye, Albert Riedlinger; trans. as Course in General Linguistics by Roy Harris (LaSalle, IL: Open Court, 1986), 110.
Return to text
3. William James, Principles of Psychology (Cambridge, MA: Harvard University Press, [1890] 1983), 269-73.
Return to text
4. August Strindberg, "Author's Note" to A Dream Play, in AugustStrindberg, Selected Plays, ed. and trans. Evert Sprinchorn (Minneapolis:University of Minnesota Press, 1986), 646.
Return to text
5. To note a few bits of evidence: The first proper name in Schoenberg'sHarmonielehreisthat of Strindberg, cited as a "thinker who keeps on searching" (Schoenberg.Harmonielehre,trans. as Theory of Harmony by Roy C. Carter [Berkeley: Universityof California Press, 1978], vi, 2). At a gathering in 1909 or 1910, whenMahler suggested that Schoenberg should have his students read Dostoyevsky,Webern, who had been reading Strindberg's dream plays, retorted, "Please,we do have Strindberg" (Willi Reich Alban Berg, trans. CorneliusCardew [New York: Harcourt, Brace & World, 1965], 30-32; Hans and RosaleenMoldenhauer Anton Webern: A Chronicle of His Life and Work [NewYork: Knopf, 1979], 108-9). Berg told Schoenberg in a letter of December23, 1911 that he and Webern considered Schoenberg to be Strindberg's musicalcounterpart (Juliane Brand, Christopher Hailey, & Donald Harris, eds.TheBerg-Schoenberg Correspondence: Selected Letters [New York: Norton,1987], 61).
Return to text
6. Schoenberg, Theory of Harmony, 422.
Return to text
7. I have explored early twentieth-century conceptions of mind as a basis for understanding the Second Viennese School's early atonal music in Cramer, Music for the Future: Sounds of Psychology and Language inWorks of Schoenberg, Webern, and Berg, 1908 to the First World War(Ph.D. dissertation, University of Pennsylvania, 1997), 45-57, 297-401.
Return to text
8. That is to say, I asserted that the common usage of the word Klangfarbenmelodiedoes not reflect Schoenberg's intention in coining it. Cramer, "Schoenberg'sKlangfarbenmelodie:A Principle of Early Atonal Harmony," Music Theory Spectrum 24/1(Spring 2002): 1-34.
Return to text
9. Albert S. Bregman, Auditory Scene Analysis: The Perceptual Organizationof Sound (Cambridge, MA: MIT Press, 1990).
Return to text
10. Albert S. Bregman, "Auditory Scene Analysis: Hearing in ComplexEnvironments," in Thinking in Sound: The Cognitive Psychology of HumanAudition, ed. Stephen McAdams & Emanuelle Bigand (Oxford: OxfordUniversity Press, 1993), 11.
Return to text
11. This demonstration is based on experiments by van Noorden, reportedin Leo P. A. S. van Noorden, "Minimum differences of level and frequencyfor perceptual fission of tone sequences ABAB," Journal of the AcousticalSociety of America 61 (1977): 1041-5. Other demonstrations along theselines may be heard in Albert S. Bregman and Pierre A. Ahad, Demonstrationsof Auditory Scene Analysis (Compact Disc with booklet. Montreal: PsychologyDepartment, McGill University, 1995; distributed Cambridge, Mass.: MITPress).
Return to text
12. David Huron, "Tone and Voice: A Derivation of the Rules of Voice-Leading from Perceptual Principles," Music Perception 19/1 (Fall 2001):1-64 [18-19].
Return to text
13. Huron, "Tone and Voice," 19.
Return to text
14. For a good introductory summary of the factors involved in auditory streaming and fusion, see Huron, "Tone and Voice," 1-21.
Return to text
15. For a discussion of a possible neural process by which what is commonly called "melody" can be understood in terms of auditory scene analysis, see Robert O. Gjerdingen, "Apparent Motion in Music?" Musical networks:Parallel distributed perception and performance (Cambridge, MA: MITPress, 1999): 141-73; revision of "Apparent Motion in Music?" MusicPerception 11 (1994): 335-70. A slightly different interpretationof the perceptual significance of auditory scene analysis is presentedin Lerdahl, Tonal Pitch Space (Oxford and New York: Oxford UniversityPress, 2001), 81-82.
Return to text
16. Bregman discusses the significance of ASA to music in Bregman,Auditory Scene Analysis: The Perceptual Organization of Sound,Chapter 5: "Auditory Organization in Music."
Return to text
17. See Albert S. Bregman, Auditory Scene Analysis: The PerceptualOrganization of Sound, 488-9 onthe timbral consequences of fusion in music and 511 on dissonance as atimbre.
Return to text
18. Schoenberg, Theory of Harmony, 20-1. I discuss this passagein Cramer, "Schoenberg's Klangfarbenmelodie," 9-10.
Return to text
19. For another application of auditory scene analysis principles to early atonal expressionism, see Fred Lerdahl, "Spatial and Psychoacoustic Factors in Atonal Prolongation,"Current Musicology 63 (1999): 7-26,much of which is restated with more complexity in Lerdahl, Tonal PitchSpace, chapter 8.
Return to text
20. Huron, "Tone and Voice," 14-18.
Return to text
21. Much of the following analysis, including the analytical diagram, is drawn from Cramer, "Schoenberg's Klangfarbenmelodie," 28-29.
Return to text
22. Anton Webern, The Path to the New Music, trans. Leo Black(Bryn Mawr: Theodore Presser, 1963), 35.
Return to text
23. Schoenberg, "Composition with Twelve Tones (1)," Style and Idea,ed. Leonard Stein, trans. Leo Black (Berkeley: University of CaliforniaPress, [1975] 1984), 220.
Return to text
Copyright © 2003 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
prepared by
Brent Yorgason, Managing Editor
Updated 05 July 2003