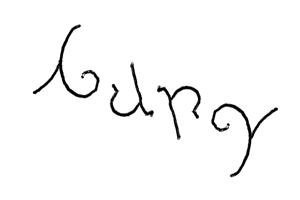Ambiguity: Another Listen
Gary S. Karpinski
for Steve
KEYWORDS: ambiguity, ambigrams, meter, tonality, analysis, pedagogy, Steve Larson
ABSTRACT: This article is an homage to the late music theorist Steve Larson, who passed away quite unexpectedly last year. Among his many talents (and he had many) was a remarkable ability to create ambigrams, which are constructed using ambiguous figures that can be interpreted in two different ways. An ambigram can be read the same way in two different orientations (often right-side-up and upside-down, but other orientation pairs are sometimes used). This article takes the notion of ambiguity at the heart of the ambigram concept and examines it in music. In addition to paying tribute to Steve Larson's delightful mind, the paper explores how metric and tonal ambiguity affect music analysis and pedagogy—two disciplines that were important to Steve throughout his career.
Copyright © 2012 Society for Music Theory
The consciousness of good intentions disdains ambiguity.
—Alexander Hamilton (Hamilton 1787)
I was looking for a name like The Crickets that meant two things,
and from Crickets I got to Beatles.
—John Lennon (The Beatles 1964)
1. A Gift
Figure 1. An ambigram of ”Gary“ (after Steve Larson)
(click to enlarge and rotate)
[1.1] I met Steve Larson in the late 1980s at a College Music Society summer Institute for Music Theory Pedagogy in Boulder, Colorado. One day at lunch, he grabbed a napkin and wrote my first name in some elaborate script, then pushed it across the table to me. I glanced at the napkin, and as I did so he rotated the figure so that down was up and left was right. It still read “Gary.” What had been a G now served as a Y. The A had become an R. And the last two letters underwent analogous complementary transformations. Unfortunately, I have no idea what became of that napkin over the years, but I recently attempted to produce something like it in my own hand, which you see in Figure 1.
[1.2] What Steve had done on the fly was to create an ambigram of my name—a figure containing shapes that may be interpreted in two different ways depending on orientation and context. Note, for example, how you reinterpret parts of the “G” when they’re inverted and placed at the end of the graphic. For instance, the decorative upstroke to the G takes on an essential role as part of the fork in the Y.
[1.3] Steve had made a personal ambigram just for me. This essay is a small attempt to repay him for this delightful little gift, by making some very personal observations about ambiguity in two perceptual domains—visual and aural.
2. Ambigrams and Multistable Perception
Figure 2. Steve Larson’s ambigram of his own name
(click to enlarge and flip)
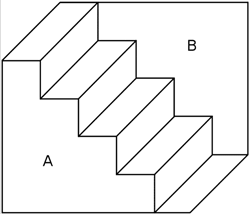
Figure 5. Schroeder stairs
(click to enlarge and rotate)
[2.1] Steve had a habit of making these ambigrams (or at least did so when I was around). He seemed to enjoy the unique challenges posed by each new name, word, or phrase he’d tackle. Figure 2 shows an ambigram he made, which viewers interpret as his name when read as shown, or reversed as in a mirror.(1)
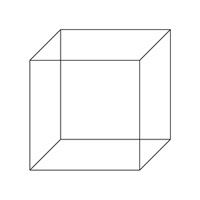
[2.2] At the heart of the ambigram concept is ambiguity—the principle that something can be perceived in two or more mutually-exclusive ways. One of the purest forms of ambiguity is multistable perception, in which a single stimulus can be reinterpreted without any change to the stimulus itself (unlike the ambigram, which must be reoriented in some way). Classic examples of multistable perception include the Necker cube (Figure 3) and the duck-rabbit (Figure 4).
|
Figure 3. A Necker cube (click to enlarge and animate) |
Figure 4. “Welche Thiere gleichen einander am meisten?” (1892): the first published image of a duck-rabbit (click to enlarge) |
[2.3] Another such illusion, one more appropriate for our current discussion, is the Schroeder stairs, shown in Figure 5. Most viewers tend to interpret this image as a set of stairs one could climb, moving from the lowest step on the right to the highest one on the left, with wall A towards the front and wall B towards the back. But it’s also possible to see this as perhaps the underside of a set of stairs, with wall B towards the front and wall A towards the back. However, if you rotate the image that the bottom is now at the top, you’ll find it easy to see wall B towards the apparent front of the image.
[2.4] Cognitive psychologists use the term multistable perception because it indicates that our perception of such stimuli can be stable in more than one percept. It’s important to note that this is not the same as vagueness. It’s not as if we can’t quite figure out just what the duck-rabbit is. It’s either a duck or a rabbit.(2) Likewise, the shapes in a well-drawn ambigram should leap off the page as specific characters—for instance, a G or a Y—and should not leave us scratching our heads.
[2.5] In the narrowest of construals, ambiguity is an either-or proposition. The prefix “ambi” comes from the Latin for “both.” As such, in words like “ambivalent” and “ambidextrous,” it refers to two, and only two, states. The kinds of musical ambiguities I’ll be exploring here are of this variety. But it’s important to acknowledge that the idea of ambiguity can encompass stimuli for which there are more than two interpretations, each of which is stable and competing with the others. For example, Justin London (2004, 86) allows for “two or more plausible and determinate patterns” [emphasis mine]. Nonetheless, he does distinguish between the ambiguous and the vague; in the latter condition, he says “no determinate pattern ever emerges.” Kofi Agawu (1994, 90) makes a similar distinction: “While an ambiguous musical situation is one that enables the analyst to specify two (or more) alternative meanings, a vague musical situation is presumably one in which the meanings are not sufficiently well-formed to be specifiable.”(3)
3. Metric Ambiguity
Audio Example 1. Camille Saint-Saëns,
Symphony no. 3, mvt. 2, beginning
Figure 6. Camille Saint-Saëns, Symphony no. 3, mvt. 2, as I hear it
(click to enlarge)
Figure 7. Camille Saint-Saëns, Symphony no. 3, mvt. 2, as notated
(click to enlarge)
Audio Example 2. Ludwig van Beethoven,
Piano Concerto no. 1 op. 15, mvt. 3, beginning
Figure 8. Ludwig van Beethoven, Piano Concerto no. 1 op. 15, mvt. 3, beginning (without bar lines and metric beaming)
(click to enlarge)
Figure 9. Ludwig van Beethoven, Piano Concerto no. 1 op. 15, mvt. 3, beginning
(click to enlarge)
[3.1] In my personal experience, this kind of multistable perception is most palpable in music when attending to the meter of certain pieces while listening without the score. For example, listen to the beginning of the second movement from Saint-Saëns’s Third Symphony (Audio Example 1). Like the Schroeder stairs, this is an ambiguous stimulus: We could perceive it as in Figure 6 (the way I always hear it, despite decades of musical training and more than a passing acquaintance with the score), or we could hear it the way Saint-Saëns wrote it and the way everyone plays it, as in Figure 7.
[3.2] But I simply have great difficulty hearing it the way Saint-Saëns intended. I spent a good ten years of my career conducting new-music ensembles on both coasts, navigating some of the most intricate rhythmic and metric challenges contemporary composers could throw at a conductor, but were I to stand in front of an orchestra to conduct Saint-Saëns’s Third, it’s likely I’d damage both my reputation and that of the orchestra.
[3.3] The cognitive process at work here is the inference of the interactions among multiple levels of pulse—in musical terms, where to place the beat or the downbeat. Another of my personal bugaboos appears without bar lines and metric beaming in Figure 8. (A recording of this passage can be found in Audio Example 2.) My wife introduced me to the Beethoven piano concertos shortly after I met her more than thirty years ago. I’d known the Beethoven symphonies well, but—for whatever reason—was not familiar with his piano concertos. When she played a recording of the first concerto for me, I flinched when we’d gotten no more than a few seconds into the third movement. I heard the beginning of the movement as you see in Figure 9a, starting on a downbeat. But by the time it got to the fifth measure, I shuddered. Something was wrong. Up was down. Left was right. Beethoven’s notation appears in Figure 9b. Clearly, he’d been thinking this way from the get-go, and the musical figures in measures 4 and 5 nestle nicely into that metric groove. On the other hand, my groove got disturbed by the time we reached that point, and I found myself shifting suddenly into placing the beats on notes I’d previously thought were off-beats.
[3.4] Like the duck-rabbit, Necker cube, and Schroeder stairs, these metric stimuli are not vague—they are multistable. It’s not that we can’t feel the pulse, just that it could be either here or there. This strikes me as a beat-level version of Bill Rothstein’s (2008) “German” meter and “Franco-Italian” meter. Like many North American musicians, I think I tend towards a “German” approach to such stimuli, placing my mental downbeats at the beginnings of phrases. But the Franco-Italian gives precedence towards placing downbeats at cadences, at the ends of phrases. As Rothstein points out, these “represent two different ways of listening. Which way a listener chooses to hear is surely a matter of acculturation, but there is much to be gained by being able to listen either way” (150). One might argue that, at the beat level, the composer’s notation should settle the matter. But in contexts like Saint-Saëns’s Third and Beethoven’s first piano concerto, I’m afraid I come in like a German and go out like a Frenchman every time I hear these passages, the composer’s authority be damned.(5)
Audio Example 3. Antonín Dvořák,
Slavonic Dance op. 46, no. 1, measures 2–17
Figure 10. Antonín Dvořák, Slavonic Dance op. 46, no. 1, measures 2–9
(click to enlarge)
[3.5] Metric ambiguity is also at the crux of the hemiola. When I was fifteen years old, I played in a district orchestra in southeastern Pennsylvania. During the first rehearsal, we read through Dvořák’s Slavonic Dance op. 46, no. 1. (The melodic line for the first eight measures is shown in Figure 10a; the first sixteen measures can be heard in Audio Example 3.) Within moments of commencing, I put my French horn in my lap and stared. Either the orchestra wasn’t following the conductor, or they’d hired the worst conductor in the world for this long weekend. Of course, it turns out that hemiola is a central “trick” of these triple-meter dances, and the first sixteen measures of op. 46, no. 1, sound in
[3.6] Agawu (1994) argues that musical ambiguity is “quickly ‘disambiguated’ in concrete musical situations” (90) and that theory itself (and analysis based on theory) resolves all ambiguities (107). Bruce Campbell (1985, 193) claims that “ambiguity in music does not really exist” and that a “powerful analytical system” will “resolve any and all [such] matters.” However, I find that these personal metric hobgoblins haunt me—playfully—every time I encounter them. I can bring to bear all the analytical tools I’ve learned in nearly forty years of studying music theory, and all the interpretive skills I learned in my years as an instrumentalist and a conductor, and I still undergo mind-bending readjustments as I move suddenly from one percept to another in response to the musical ground shifting under my feet. It’s as if I vacillate between the roles of Andrew Imbrie’s (1973) “conservative” and “radical” listeners. As Peter Smith (2006, 59) concludes, “the sum total of the process of hearing a motive that keeps switching meanings may indeed produce ambiguity.”
[3.7] Peter Martens (2011, 433) notes that “since individual listeners engage with musical meter in different ways, ambiguity of tactus should be an expected feature of any audience’s response to metrical music.” Indeed, it seems that some composers intentionally play with our perceptions of ambiguous elements. Deborah Stein (2005, 77) asks us to consider “whether the lack of clarity might be purposeful, whether the composer is using musical ambiguity as part of a compositional design,” and Michel Imberty (2011, 10) is more emphatic in concluding that “ambiguity often arises as a consequence of the desire of the composer to create an expressive effect or tension outside the syntax in the corpus of rules.”(7)
4. Ambiguity of Pitch Collections and Tonality
[4.1] In the pitch domain, as Carl Schachter (1990, 165) notes, “the same note, chord, or melodic succession will ‘mean’ different things in different surroundings.” Allen Cadwallader (1988, 59) makes an even broader claim: “The pitches of the tonal system are themselves inherently ambiguous; their meaning and function depend upon context.” David Temperley (2007) investigated the ambiguity of several 4-, 5-, and 6-member diatonic subsets in tonal works by various composers, concluding that “composers seem to have appreciated the ambiguity of these sets and exploited it in interesting ways” (37).
Audio Example 4a. Pitch classes 0 and 6 in D-flat major
Audio Example 4b. Pitch classes 0 and 6 in G major
Figure 11. The tritone sub
(click to enlarge)
[4.2] One of the simplest examples of this kind of ambiguity surrounds the tritone (or, more accurately, interval-class 6). Its diatonic membership is ambiguous: It can belong to one diatonic collection, and to the diatonic collection at T6. Any two pitches that form interval 6 can be interpreted as scale degrees and in one major key or and in the major key a tritone away. For example, pitch classes 0 and 6 in
[4.3] Interestingly, another slightly more complex ambiguity involving the tritone occurs in jazz, one of Steve’s other passions. The tritone substitution calls for the dominant to be replaced with a chord a tritone away—the so-called “flat II” chord. This is typically done with major-minor seventh chords, which results in a nifty bit of reinterpretation involving the interval of a tritone itself. Figure 11 shows a dominant-seventh chord in C (in ![]()
5. Pedagogical Implications
Audio Example 5. Benward,
Unit 1, Melody 1a, dictation 28
[5.1] In teaching aural skills, ambiguity of both pitch and meter can play important roles. For example, another departed friend of mine recorded hundreds and hundreds of dictation melodies for his textbooks; you can hear his voice at the beginning of Audio Example 5. That’s Bruce Benward introducing and playing melodic dictation number 28 from Unit 1 of his book Ear Training: A Technique for Listening (2010, 3).
[5.2] If students are to listen to that melody without any other context—without preparatory beats or counting, without a “key-establishing” scale or progression, or without a meter sign, key signature, and starting pitch printed for them on the page—then it’s truly ambiguous with regard to both key and meter. The pitches—
Audio Example 6. Benward,
Unit 1, Melody 1a, dictation 21
[5.3] Similarly, those ten notes shape themselves into no easily discernible meter. Instead, what students hear is an isochronous string of pitches. The rhythms are rather ambiguous with regard to meter (although a case could be made that the contour of the first six pitches makes triple meter more likely). However, certain other dictation melodies are such chameleons as to defy any definitive metric interpretation. For example, listen to the melody in Audio Example 6. What meter did you hear? Benward’s Instructor’s Edition prints it as quarter notes in
[5.4] Most aural-skills textbooks take one of several solutions to the problems of tonal and metric ambiguity. One is to print cues for students. In the pitch domain, this usually takes the form of printing a key signature and a starting pitch. In the temporal domain, we often see a meter sign, bar lines, and a rhythm for the first note.
[5.5] Another solution is to play certain extramusical cues before or during such melodies. Tonal bearings are usually established through the sound of a scale or chord progression before the dictation begins. Metric orientation is often provided through counting the beats of a preparatory measure, and sometimes through clapping, tapping, or some other metronomic sound during the dictation. But these extramusical cues obviate the need for students to learn some of the very fundamental listening skills they should be developing early in their training. The real solution is to excerpt or compose dictation materials that are unambiguous with regard to both key and meter.(8)
6. Inversion
[6.1] Most ambigrams involve the act of inverting, rotating, or reversing a figure so that its elements can be reinterpreted in a new orientation. In Western music, there are different kinds of inversion, including tonal inversion (in which interesting modal substitutions occur, such as Phrygian for major) and real inversion (in which there’s a literal swapping of ascending and descending interval patterns).
[6.2] One of the tenets of post-tonal theory is that pitch-class sets equivalent under real inversion should bear the same label. Thus, for example, sets (0137) and (0467) are both “instances” of set class 4-z29, because they are equivalent under the TnI operation. But there are those who are troubled by the idea that those two sets (and other inversion-pairs) are equivalent to the point that they should be called “the same thing.” In particular, Richmond Browne (1974) and George Perle (1989) railed against this procrustean approach to categorization. Browne was especially critical of the idea of inversional equivalence except in the most explicit of compositional circumstances. He wrote of his “disbelief that anyone can really discriminate between presented instances of inversional equivalents, unless the configuration of the presentation very strongly emphasizes the inversional relation” (404). It wasn’t until thirty years after Browne’s review that anyone thought to test this empirically. Art Samplaski (2004) asked a simple, commonsensical question: “If Tn/I-relatedness is a reasonable means of categorizing sonorities, do trained listeners actually hear these relationships?” (546). He ran a test of trained musicians from the Indiana University School of Music, including fourteen so-called “expert” listeners of post-tonal music (graduate students in composition, and one faculty member). He tested to see if they identified similarity between transposed and inverted instances of pc sets presented only aurally. His unequivocal conclusion: “No support for the salience of TnI relatedness was found. Instead, participants appeared to focus on the pitch height of equivalent voices or the ordered location of interval type between voices” (553). He went on to conclude that “the inverted forms of pc-set classes can be considered ‘top-heavy’ owing to the presence of small intervals
Figure 12. An inverted-face illusion
(click to enlarge and rotate)
[6.3] It seems that the way we process elements when they’re inverted is not necessarily to think of them as inversions at all. An inverted-face illusion demonstrates just this in the visual domain. Consider Figure 12 (reported in Barribeau 2012 and elsewhere). To most viewers, the image of the three women should seem OK. But now click the figure so that the image is right-side-up. You’ll notice that the elements of the eyes and mouths have been inverted while leaving the other elements uninverted. When the entire image is upside-down we register the small uninverted elements without much perturbation—a mouth is a mouth, eyes are eyes. But when these elements are inverted in situ, they’re uncannily disturbing. To me, these elements are powerfully analogous to Samplaski’s top- and bottom-heaviness, and Browne’s direct mappings between major and minor triads. Perhaps features of pitch sets do not lend themselves easily to inversion in pitch space any more than features of faces do in the visual domain. It could be that inversional equivalence is one of the “lingering remnants from a failed Arts Revolution of the past century” to which William Thomson (2010, 46) refers in critiquing serialist doctrine. This applies to tonal music as well. Samplaski dealt with post-tonal pitch collections, but Schachter (1996, 337) refers to “tonal music, with its gravitationally charged pitch space” as “non-commutative.” In other words, descending motion does not make the same connotations, does not have the same affect as ascending motion does. It’s obvious that Steve Larson’s (2012) concept of “physical gravity”—one of his musical forces—accounts for this phenomenon.
7. Vertical Space as Metaphor
[7.1] The very act I’ve been engaging in, assuming a cross-domain equivalence between pitch and vertical space, is so inescapable in our culture and so stubbornly entrenched in the way we musicians think about pitch, that it’s difficult for us to think about this as an arbitrary metaphor. We speak unremittingly about “low” pitches and “high” ones without giving this a second thought. In fact, most Western sources define pitch in these terms. The Oxford Dictionary of Music (2012) calls pitch “the location of a sound in the tonal scale, depending on the speed of vibrations from the source of the sound, fast ones producing a high pitch and slow ones a low” [emphasis mine]. Many fundamental music-theory textbooks begin with this metaphor. For example, the first sentence in Gary White’s (2011, 1) book Music First! is as follows: “The term pitch refers to the ‘highness’ or ‘lowness’ of a musical sound.” The second sentence in Joe Straus’s (2008, 1) Elements of Music reads, “A pitch is a musical sound at some particular point along the continuum from the lowest to the highest audible sound.” I thought about defining pitch in some other terms in the manuscript for a fundamentals book I’m currently writing, but abandoned this idea because of the ease with which I could appeal to this ubiquitous metaphor.
Figure 13. The actual and visual contours in Anton Webern, Variations op. 27, mvt. 2, beginning
(click to enlarge)
[7.2] We represent pitches in notation on the page using the vertical dimension as a visual representation of this metaphor. In doing so, we see “ascending” and “descending” passages, we refer to “upward” and “downward” leaps, and so on. We are so accustomed to this that when notation violates this metaphor, we are disturbed. I’ll never forget the first time I encountered the score to the second movement of Webern’s op. 27. I was about twenty years old, and—although I managed to follow the notation well enough—I couldn’t shake the discomfort caused by the many disagreements between the audible contour of the pitches and their relative positions on the page. Figure 13 shows the first six pitches of this movement. Of the first five directions caused by the relative “height” between adjacent pitches, the first three are flat-out “wrong” on the page: Down becomes up, up becomes down, and then same is up. The unsettling feeling we get from such violations is visceral evidence of how deeply the vertical pitch metaphor is entrenched in our minds.
[7.3] The so-called “Stroop effect” elicits an analogous unsettling feeling. To experience this, play Video Example 1 and name the color in which each word is printed. Don’t read the words, just the color in which they appear. Then play Video Example 2 and do the same thing—name the color in which each word is printed, not the word itself.(10) The incongruity in the second set of stimuli between the meanings of the words and the colors in which they’re rendered creates a cognitive burden, making it difficult to perform the task at speed.(11) This is analogous to the incongruity between the contour of the pitches in pitch space in the Webern and their contour on the printed page. We expect the vertical dimension on the page to be a reasonably direct mapping of the vertical pitch metaphor we hold so dear.
|
Video Example 1 (click to view video) |
Video Example 2 (click to view video) |
[7.4] But—despite how strongly we might feel about it—there is nothing “correct” about this metaphor. Some might argue that “higher” pitches correspond to “higher” frequencies,(12) but this is only a happy coincidence. The vertical metaphor for pitch was firmly ensconced in Western culture for centuries before the correspondence between frequency and pitch was discovered. In fact, it’s somewhat surprising that we didn’t adopt “long” and “short” (from divisions of the monochord or the length of organ pipes), or perhaps “left” and “right” (from the positions of keys on keyboard instruments). There is nothing inherently “low” or “high” about pitch in the human experience. According to Zohar Eitan and Renee Timmers,
cross-cultural anthropological studies. . . indicate a diversity of connotations for pitch. In different cultures and historical eras, pitch polarity was not designated as “high” vs. “low” but rather by “light” vs. “heavy” [in Liberia]. . . “sharp” vs. “heavy” (ancient Greek music theory), “small” vs. “large,” used in Bali and Java, as well as among Kpelle and Jabo in Liberia. . . “young” vs. “old” (Suyá people of the Amazon basin. . . ) or “weak” vs. “strong” (the Bashi people of central Africa) (2010, 406).
And the ’Are’are people of the Solomon Islands take the cake: They use the word “siho” (which means “to go down”) for what we would call “higher” pitches, and the word “hane” (which means “to go up”) for what we would call “lower” pitches. According to Hugo Zemp (1979, 14–15), this metaphor seems to have grown out of their use of panpipes, on which players move down to go towards the treble register, and up to go towards the bass.
Audio Example 7a. The “falling bells” audio illusion
Audio Example 7b. The first and last pitches of the
“falling bells” illusion
[7.5] Nevertheless, even our ingrained Western up-down metaphor for pitch is not as straightforward as it might appear at first blush. Consider the so-called “falling bells” audio illusion, which you can hear in Audio Example 7a. In that recording, pitch class falls with each iteration, but the Shepard tones are filtered so that we hear mostly low octaves at the outset, and then the filter is gradually raised as the illusion progresses.(13) Many of us focus intently on the pitch classes, tracing their apparent downward motion, while perhaps only secondarily noticing the rise in overall register. But by the time this illusion has seemed to “descend” an octave in pitch-class space, the register has moved up several octaves. Listen to just the first and last pitches in the illusion in Audio Example 7b, then listen again to the entire illusion in Audio Example 7a and note how the register rises while the pitch classes fall.
Figure 14. M.C. Escher, Ascending and Descending, detail
(click to enlarge)
[7.6] The “falling bells” illusion shows that there are at least two different factors at work in the ways we perceive pitch as a vertical dimension. On the one hand, pitch classes in close proximity trump subtle changes in register. On the other hand, the gradual buildup of registral change creates a cumulative effect that’s quite striking. So while we hear the pitch classes as descending, we eventually hear the register ascending. To me, this is analogous to the Penrose-stairs illusion, made famous in M. C. Escher’s lithograph Ascending and Descending, a detail of which you see in Figure 14. I’m not the first scholar to draw parallels between the Penrose illusion and Shepard tones, but the falling-bells illusion is aurally equivalent to viewing Figure 14 while riding in a gradually ascending elevator.
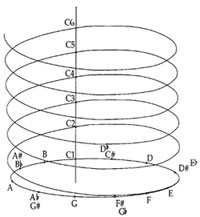
Figure 15. Pitch spiral (or “chroma helix”), after Butler (1992, 53)
(click to enlarge)
[7.7] We can visualize this using the pitch spiral shown in Figure 15. A Shepard tone presents all the instances of a pitch class across all audible octaves at once, an example of which is represented by the vertical line that’s drawn up the backside of the spiral, from below C1 through C6 and beyond. At the beginning of the falling-bells illusion, the sound is filtered so that we’re hearing more of the lower instances of the pitch classes. As the illusion progresses, the filter is gradually shifted upwards so that we’re hearing more of the higher instances. This means that there can be at least two different vertical dimensions to pitch—one in pitch-class space and the other in overall register.
[7.8] In conclusion, I’d like to say that many of these ideas have opened up lines of inquiry and surprising conclusions I hadn’t dreamed of until recently. I wouldn’t have thought about most of this had Steve Larson not handed me an ambigram that day. Thank you, Steve!
Gary S. Karpinski
University of Massachusetts Amherst
Amherst, MA 01002
garykarp@music.umass.edu
Works Cited
Agawu, Kofi. 1994. “Ambiguity in Tonal Music: A Preliminary Study.” In Theory, Analysis, and Meaning in Music, ed. Anthony Pople, 86–107. Cambridge: Cambridge University Press.
Barribeau, Tim. 2012. “These Upside Down Portraits Demonstrate The Bizarre Thatcher Effect.” PopPhoto.com June 19, 2012 http://www.popphoto.com/news/2012/06/these-upside-down-portraits-show-thatcher-effect (accessed July 12, 2012).
The Beatles. 1964. Hear the Beatles Tell All. Ve-Jay PRO 202, LP.
Benward, Bruce and J. Timothy Kolosick. 2010. Ear Training: A Technique for Listening. Revised 7th edition. Boston, MA: McGraw-Hill, 2010.
Browne, Richmond. 1974. Review of The Structure of Atonal Music, by Allen Forte. Journal of Music Theory 18, no. 2: 390–415.
Butler, David. 1992. The Musician’s Guide to Perception and Cognition. New York: Schirmer Books.
Cadwallader, Allen. 1988. “Foreground Motivic Ambiguity: Its Clarification at Middleground Levels in Selected Late Piano Pieces of Johannes Brahms.” Music Analysis 7: 59–91.
Campbell, Bruce. 1985. Review of Beethoven’s Compositional Choices: The Two Versions of Opus 18, No. 1, First Movement, by Janet M. Levy and Leonard B. Meyer. Journal of Music Theory 29: 187–97.
Chambers, Deborah, and Daniel Reisberg. 1992. “What an Image Depicts Depends on What an Image Means.” Cognitive Psychology 24: 145–74.
Dunsby, Jonathan. 1981. Structural Ambiguity in Brahms: Analytical Approaches to Four Works. Ann Arbor, MI: UMI Research Press.
Eitan, Zohar, and Renee Timmers. 2010. “Beethoven’s Last Piano Sonata and Those Who Follow Crocodiles: Cross-Domain Mappings of Auditory Pitch in a Musical Context.” Cognition 114: 405–22.
Escher, M. C. 1960. Ascending and Descending. Lithograph.
“Falling bells.” Mighty Optical Illusions. http://www.moillusions.com/2006/05/audio-optical-illusions.html (accessed February 11, 2012).
Hamilton, Alexander. 1787. Federalist no. 1. [The Federalist Papers]
Imberty, Michel. 2011. “Music, Linguistics, and Cognition.” In Music and the Mind: Essays in Honour of John Sloboda, ed. Irène Deliège and Jane W. Davidson, 3–16. Oxford: Oxford University Press.
Imbrie, Andrew. 1973. “‘Extra’ Measures and Metrical Ambiguity in Beethoven.” In Beethoven Studies, ed. Alan Tyson, 45–66. New York: W. W. Norton.
Karpinski, Gary S. 2000. Aural Skills Acquisition. New York: Oxford University Press.
Larson, Steve. 2012. Musical Forces: Motion, Metaphor, and Meaning in Music. Bloomington: Indiana University Press.
Lewin, David. 1986. “Music Theory, Phenomenology, and Modes of Perception.” Music Perception 3: 327–92.
London, Justin. 2004. Hearing in Time. New York: Oxford University Press.
MacLeod, Colin M. 1991. “Half a Century of Research on the Stroop Effect: An Integrative Review.” Psychological Bulletin 109: 163–203.
Martens, Peter. 2011. “The Ambiguous Tactus: Tempo, Subdivision Benefit, and Three Listener Strategies.” Music Perception 28: 433–48.
Penrose, Lionel. 1958. “Impossible Objects: A Special Type of Visual Illusion.” British Journal of Psychology 49: 31–33.
Perle, George. 1989. “Pitch-Class Set Analysis: An Evaluation.” Journal of Musicology 8: 151–72.
http://www.oxfordmusiconline.com/subscriber/article/opr/t237/e7960 (accessed May 30, 2012).
“Pitch.” 2012. In The Oxford Dictionary of Music, 2nd ed. rev., ed. Michael Kennedy. Oxford Music Online,
http://www.oxfordmusiconline.com/subscriber/article/opr/t237/e7960 (accessed May 30, 2012).
Rothstein, William. 1994. “Ambiguity in the Themes of Chopin’s First, Second, and Fourth Ballades.” Intégral 8: 1–50.
—————. 1995. “Beethoven with and without Kunstgepräng’: Metrical Ambiguity Reconsidered.” Beethoven Forum 4: 165–93.
—————. 2008. “National Metrical Types in Music of the Eighteenth and Early Nineteenth Centuries.” In Communication in Eighteenth-Century Music, ed. Danuta Mirka and Kofi Agawu, 112–59. Cambridge: Cambridge University Press.
Samplaski, Art. 2004. “The Relative Perceptual Salience of Tn and TnI.” Music Perception 21: 545–59.
Schachter, Carl. 1990. “Either/Or.” In Schenker Studies, ed. Hedi Siegel, 165–79. Cambridge: Cambridge University Press.
—————. 1996. “Schoenberg’s Hat and Lewis Carroll’s Trousers: Upward and Downward Motion in Musical Space.” In Aflame with Music: 100 Years at the University of Melbourne, ed. Brenton Broadstock et al., 327–41. Parkville, Australia: Centre for Studies in Australian Music.
Shepard, Roger. 1964. “Circularity in Judgments of Relative Pitch.” Journal of the Acoustical Society of America 36, no. 12: 2346–53.
Smith, Peter. 2006. “You Reap What You Sow: Some Instances of Rhythmic and Harmonic Ambiguity in Brahms.” Music Theory Spectrum 28, no. 1: 57–97.
Stein, Deborah. 2005. “Introduction to Musical Ambiguity.” In Engaging Music: Essays in Musical Analysis, ed. Deborah Stein, 77–88. New York: Oxford University Press.
Straus, Joseph. 2008. Elements of Music. 2nd edition. Upper Saddle River, NJ: Pearson Prentice Hall.
Stroop, John Ridley. 1935. “Studies of Interference in Serial Verbal Reactions.” Journal of Experimental Psychology 18: 643–62.
Temperley, David. 2007. “The Tonal Properties of Pitch-Class Sets: Tonal Implications, Tonal Ambiguity, and Tonalness.” In Tonal Theory for the Digital Age, ed. Walter B. Hewlett, Eleanor Selfridge-Field, and Edmund Correia, Jr., 24–38. Stanford, CA: Center for Computer Assisted Research in the Humanities.
Thompson, Peter. 1980. “Margaret Thatcher: A New Illusion.” Perception 9: 483–84.
Thomson, William. 1983. “Functional Ambiguity in Musical Structures.” Music Perception 1: 3–27.
—————. 2010. “Serialist Claims Versus Sonic Reality.” Empirical Musicology Review 5: 36–50.
“Welche Thiere gleichen einander am meisten?” 1892. Fliegende Blätter 97: 147.
White, Gary. 2011. Music First! 6th edition. New York: McGraw-Hill.
Zemp, Hugo. 1979. “Aspects of ’Are’are Musical Theory.” Ethnomusicology 23: 5–48.
Footnotes
1. Thanks go to Sonja Rasmussen and Caitlin Snyder for supplying this image.
Return to text
2. Lewin (1986) addressed the mutual exclusivity of duck and rabbit (see especially pages 370–71). Consult Chambers and Reisberg 1992 for more on such ambiguous figures.
Return to text
3. Compare this with Temperley’s (2007, 28) definition of ambiguous pitch-class sets: On the one hand, he says that “the ambiguity of a set is simply the degree to which it clearly implies a single key, or is equivocal between two or several keys,” but on the other, he says that the pc-set [C–
Return to text
4. Note that, although Saint-Saëns labeled only two movements in the score, many recordings list four movements (due to the internal divisions within the two), so that the passage in question here would occur at the beginning of the third movement.
Return to text
5. I would like to thank Jason Hooper for his keen observation that these beat-level ambiguities are analogous to Rothstein’s “German” and “Franco-Italian” meters.
Return to text
6. The best summary of all these types of metric ambiguities is in London 2004.
Return to text
7. Similarly, Dunsby (1981, 1) attributes to Brahms a conscious attempt to create “a functional ambiguity, giving his music its typically elaborate and complex character.” See also Thomson 1983 and Rothstein 1994 and 1995.
Return to text
8. See Karpinski 2000 for discussions of metric ambiguity (79–80), tonal ambiguity (84–85), and extramusical cues (92–98) during dictation.
Return to text
9. This illusion was first reported in print in Thompson 1980. It is sometimes dubbed the “Thatcher illusion” or the “Scheibe illusion.”
Return to text
10. I apologize to readers with color vision deficiencies. There are similar tests using animals, locations, and other prompts (many of which are available online), but the color test is the classic one.
Return to text
11. John Ridley Stroop reported his seminal experiments in Stroop 1935. For a survey of literature on the Stroop test, see MacLeod 1991.
Return to text
12. On the other hand, others might argue that there is nothing inherently “high” about “larger” numbers, either.
Return to text
13. For an introduction to Shepard tones, see Shepard 1964.
Return to text
Copyright Statement
Copyright © 2012 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by John Reef, Editorial Assistant
Number of visits: