“What can they have to do with one another?”: Approaches to Analysis and Performance in John Cage’s Four2 *
Drake Andersen
KEYWORDS: John Cage, indeterminate music, performance
ABSTRACT: In this study, I evaluate the sonic possibilities of John Cage’s Four2 (1990) by comparing existing performances of the piece with alternate renditions generated computationally and by hand specifically for this analysis. Four2, one of Cage’s Number Pieces, is fully determinate with respect to pitch, instrumentation and overall duration, but affords the performer the flexibility to choose the durations of specific sounds through time-bracket notation. The differences in the musical results between various performances, both real and virtual, prompt a discussion of the performance practices of the piece both as outlined by Cage and as understood by scholars and performers. Accompanying this text is a computer program with which readers can edit and play back their own interpretations of Four2.
Copyright © 2017 Society for Music Theory
1. Introduction
[1.1] The time-bracket notation that John Cage employs in his Number Pieces permits performers to produce different renditions of a given composition by choosing the position and duration of sounds within a flexible time range.(1) These works, from late in Cage’s career, are typically fully determined with respect to pitch, dynamics, instrumentation, and total duration. However, their relative flexibility and Cage’s own poetics of non-intention have inhibited analytical discussion of sonic relationships, even though the possible variation of the sounds themselves is highly regimented.(2)
[1.2] In this study, I analyze the sonic relationships in one such piece, Four2 (1990) for mixed chorus, by approaching the work from three interpretive perspectives: a Monte Carlo simulation of many (virtual) performances of the work; real-world performances; and four imagined performances, designed intuitively by the author to reflect distinct interpretive priorities embodied by four invented conductors.(3) These divergent strategies produce characteristic results that emphasize competing—and sometimes contradictory—concerns in the performance of Cage’s Number Pieces. Taken as a whole, they contribute to a more complete account of the musical possibilities of Four2.
[1.3] First, I describe the methodology of the Monte Carlo simulation and summarize the data obtained therein to establish some characteristic likelihoods in the piece. In the next section, I introduce each of the fictional conductors’ interpretations through a score-like transcription and brief analytical narrative. These interpretations were generated by the author to illustrate specific possibilities within the piece. Many aspects of them are statistically unlikely, but are included here to provide a more comprehensive understanding of what is possible in a performance of Four2. The simulation data and fictional conductors’ performances are then evaluated alongside real-world performances, transcribed from commercially available recordings.
[1.4] This comparative approach responds to Judy Lochhead’s suggestion to “[approach] the music from the perspective of what performers do,” as well as concerns expressed by Alexandre Popoff regarding how to account for differences between computational simulations and live performances of Cage’s Number Pieces (Lochhead 1994, 241; Popoff 2013, 20, 24). The live performances vary in some ways from the simulated performances; accordingly, I proceed with a discussion of the performance practice of Four2, and the Number Pieces in general, in order to account for some of the differences. The variety of performance practices in use suggests broader questions about the extent and meaning of indeterminacy in the Number Pieces, which I address in the concluding section.
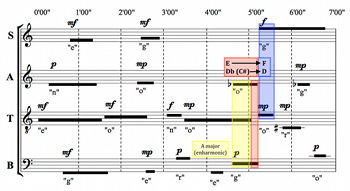
Example 1. Soprano Part of Four2
(click to enlarge)
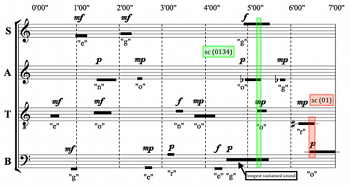
[1.5] Example 1 gives the soprano part of Four2. The soprano part consists of three sounds, each positioned within a unique time bracket. Cage’s time-bracket notation specifies two windows of time for each sound: one in which each sound may begin and one in which each may end.(4) The first bracket, consisting of an F4 sung on the vowel “e,” allows for the sound to begin anywhere between 0’00” and 1’00” from the start of the piece, and for the sound to end anywhere between 0’40” and 1’40”. This means that, for example, an 80-second sound beginning at 0’10” and ending at 1’30” would be permissible, as would an 8-second sound beginning at 0’51” and ending at 0’59”. In other words, the time-bracket notation allows for a wide range of durations.(5)
[1.6] A unique feature of these brackets is the overlap between the starting and ending windows—in this case, between 0’40” and 1’00”. This internal overlap allows for greater sonic indeterminacy, permitting, for instance, the flexible placement of sounds of extremely short duration, and avoiding an intermediary interval of obligatory sound between the starting and ending intervals.
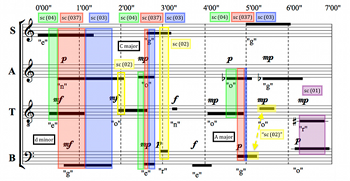
Example 2. A Transcription of the Time-Bracket Structure of Four2
(click to enlarge)
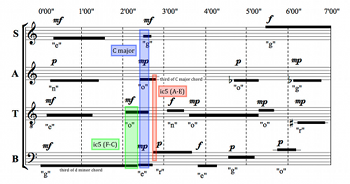
[1.7] Example 2 is a transcription of the twenty time brackets of the four parts in Four2 into a score-like format, using solid horizontal lines to represent individual sounds. Phonemes and dynamics are also included for each sound. As the legend below the score explains, the starting interval of any given time bracket extends from the leftmost edge of the black line to the right edge of the internal overlap box in the middle of each line. The ending interval of any given time bracket extends from the left edge of the internal overlap box to the rightmost edge of the black line.
[1.8] Often the time brackets of two successive notes in the same part overlap externally, such as the first two notes of the tenor part. In the transcription above, when these notes are different, it is generally clear visually where the two brackets begin and end. However, the last two notes of the alto part overlap externally on the same pitch (
2. Computational Simulation of Four2
[2.1] Cage’s Number Pieces have rarely been analyzed in detail for two primary reasons: their scores represent a multiplicity of possible performances in which sounds’ order and duration can vary widely, and a teleological analytical narrative seems to contravene Cage’s description of his indeterminate works and what we know of his compositional process. I will address the latter concern in the conclusion of this article; regarding the former, the Monte Carlo simulation provides a potential solution.
[2.2] Using this technique, virtual performances of Four2 are obtained by computationally determining the random variables (i.e. the starting and end points of the sounds) corresponding to Cage’s notated constraints. Popoff 2013 advocates this approach:
By averaging over a large number of realizations (which is achieved through a computer program running the determination of the parts repeatedly) we can access the probability distributions of each pitch-class set over time, thus turning the Number Pieces into stochastic processes. By doing so, we solve the problem posed by Haskins and Weisser of coping with all the possibilities offered by the Number Pieces. (Popoff 2013, 3)
[2.3] I have carried out a Monte Carlo simulation of over one thousand virtual performances of Four2; however, before discussing the results, I will raise a few specific points regarding the methodology. First, I created a specialized random value generator using Max software. Complete performances of the piece were generated as lists of time values (corresponding to the beginnings and endings of sounds) using the interval of a second as both the generative grain and sampling rate, since this is the smallest unit of subdivision in Cage’s notation. As each performance lasts exactly seven minutes, each simulation contains 420 data points, each corresponding to one second of the performance.
[2.4] Truly random selection of values within the (overlapping) starting and ending brackets of each sound means that, in a computational environment, a sound could end before it begins. To avoid this paradox, the software chooses a starting point first, then tests randomly-selected ending points, rejecting and discarding any that precede the starting point in time. The entire “performance” is then tested for any external overlaps, and if any are found, the entire performance is discarded and a new performance is generated in its place.
[2.5] Additionally, in the software I have established that a sound is equally likely to begin or end at any time during a given bracket—in other words, amongst many performances of the work, the distribution of each bracket approaches uniformity. This random (uniform) approach may be contrasted with that of Popoff 2013, in which a Gaussian curve is used to distribute starting and ending points within the time brackets.(6) This approach emphasizes the center of each starting and ending bracket and “gives less prevalence to sound events occurring at the very beginning or end of their time interval” (Popoff 2013, 5). The random approach I am employing emphasizes all parts of each bracket equally, enriching the analysis with a wider variety of possible results.
Example 3. Prevalence of All Pitch Class Sets in All Simulations, Organized by Set Class
(click to enlarge)
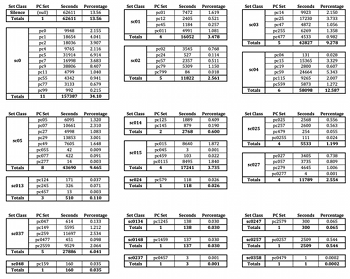
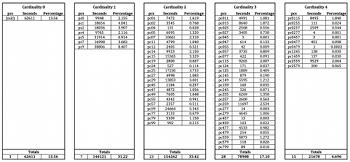
[2.7] Example 3 displays all of the pitch-class sets (pc sets), including multisets, obtained in 1099 simulations of Four2, organized by set class (sc). The raw number of seconds during which each set class sounds, added together in all simulations, is displayed in the column to the right of the pc set. The rightmost column displays the prevalence of each set compared to the others (of any cardinality) as a percentage. The percentage is obtained by dividing the raw number of seconds by 461,580, the total number of data points amongst all simulations (1099 simulations multiplied by 420 data points per simulation). The total number of values and total percentage per set class is displayed at the bottom of each box. The boxes display the set classes in Forte order from left to right and top to bottom.
[2.8] The single most prevalent pitch-class set is the null set—silence—which occurs 13.6% of the time amongst all simulations. The least prevalent pitch-class set is {0479}—an instance of sc (0358)—which occurs only once, or approximately 0.0000022% of the time. Between these two extremes lies a varied collection of sonorities, with 21 of 49 possible set classes of cardinality 0‑4 represented. Hünermann observes that, “[t]he increased probability of traditional harmonic content rests upon the simplicity of pitch material and the reduction of density” (Hünermann 2014, 612). Indeed, there are only seven distinct pitch classes available in the piece: the D-minor diatonic collection minus B-flat, plus the raised seventh degree written as both
Example 4. Prevalence of All Pitch Class Sets in All Simulations, Organized by Cardinality
(click to enlarge)
[2.9] Example 4 presents the same data as Example 3 organized by (multiset) cardinality: the number of active voices, even when two voices are singing the same pitch class concurrently. Thus {0115} reflects a cardinality of 4, even though in normal form it would be reduced down to the cardinality-3 set {015}. Comparing the total percentages in the lower-right cells of each column shows that the piece is silent approximately 13.6% of the time (about 57 seconds per simulation), one voice is sounding 31.2% of the time (about 2’11”), two voices 33.4% of the time (about 2’20”), three voices 17.1% of the time (about 1’12”), and four voices just under 5% of the time (about 20 seconds). This data helps illustrate the sparseness of the music: in a composition with four parts, textures of two or fewer parts are heard over 75% of the time.
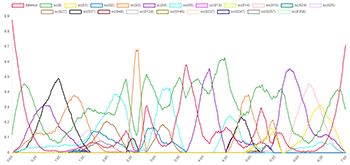
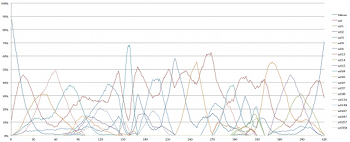
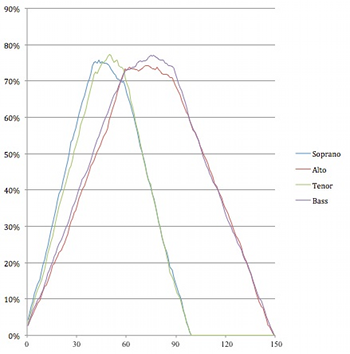
[2.10] Example 5 depicts the prevalence of each set class obtained in the simulations of Four2 graphically over time, using lines of different colors to represent each of the 21 set classes listed in Example 3. In Examples 3 and 4, prevalence is expressed as a proportion of the total duration of the piece; the graphs in Example 5 demonstrate how prevalence changes over time during a performance of the piece. The horizontal axis represents time (in seconds) and the vertical axis expresses the percentage of simulations in which a given set is sounding at a given time. For instance, in the opening seconds of the piece, almost 90% of the simulations are silent. Example 5a is an interactive graph for which individual lines representing set classes can be toggled on and off by clicking on the set name in the legend at the top of the graph. Example 5b is a still image giving all 21 set classes; Examples 5c and 5d depict only sets of cardinalities 0–2 and 3–4, respectively, for legibility.
Example 5a. Prevalence of Set Classes Over Time in Simulations of Four2 (click to enlarge and interact) Example 5c. Prevalence of Set Classes Over Time in Simulations of Four2 (click to enlarge and interact) | Example 5b. Prevalence of Set Classes Over Time in Simulations of Four2 (click to enlarge) Example 5d. Prevalence of Set Classes Over Time in Simulations of Four2 (click to enlarge) |
Example 6. Prevalence of Set Class (03) Over Time
(click to enlarge)
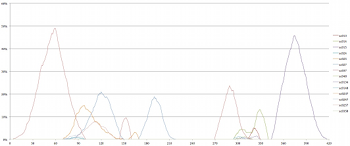
[2.11] As Example 3 demonstrates, many of the set classes in Four2 may be constituted by several different pitch class sets. Example 6 depicts all of the instances of a single set class—sc (03)—over time. In the simulations of Four2, sc (03) was formed by five different pitch-class sets which, because of the presence of duplicate pitch classes, reflect three distinct pitch-class pairings. Over the course of the piece, four distinct peaks can be ascertained: pcs (25) and (255), pcs (47) and (477), pcs (14), and a return to pcs (25). The vertical axis displays the prevalence of each particular pitch-class set (as a percentage) in relation to every other pitch-class set obtained among the simulations at each unit time (in seconds).
[2.12] In addition to the prevalence of diatonic harmony in Four2 already discussed, writers have remarked specifically on the strong potential for triadic harmony. Hünermann describes “an undeniably consonant sound environment circling around d minor,” through which, in relation to the chromatic material in the final minutes of the piece, “the listener may well perceive (and Cage at least facilitates) a teleological harmonic process” (2014, 612). While a discussion of “perception” is beyond the scope of this study, the simulation data provides a quantitative description of the prevalence of triads within the piece.
Example 7. Prevalence of Set Class (037) Over Time
(click to enlarge)
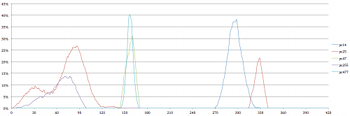
[2.13] Example 7 depicts the prevalence of sc (037) over time. As before, the lines of different colors represent different pitch-class sets that form triads in this piece. There are three distinct instances of sc (037): pcs (259) and (2559); pcs (047) and (0477); and pcs (149), corresponding to D minor, C major and A major triads, respectively. The first and third peaks (D minor and A major) are much more prevalent—both in the percentage of simulations containing these triads and in their duration—than the middle peak (C major), and the first and second can be formed by all four voices simultaneously, while the third cannot.
[2.14] While there are many intervening sonorities to consider as well, taken in isolation the data in Example 7 supports Hünermann’s assertion that D minor is central to the harmony of Four2. If we combine the data in Examples 6 and 7, we can also verify that the progression of triads roughly conforms to a recognizable harmonic progression: a strong emphasis on D minor in the first two minutes; a shorter and weaker appearance of a related triad (C major); a strong dominant function (A major); and a return to D minor—not with a triad, but through the D–F dyad that peaks at around 330 seconds (5’30”) as depicted in Example 6. I make no claims with respect to the composer’s intention here—the data merely indicates that these results are likely if the piece is performed many times with the time brackets determined at random.
[2.15] Scholars have acknowledged that the presence of triads like these in many of Cage’s late works—particularly the Number Pieces—is striking, though there is disagreement on how to account for them in the context of Cage’s longstanding rejection of familiar harmonic patterns.(7) Setting aside this dispute for the moment, I simply wish to assert that the triads’ prevalence and arrangement in Four2 is remarkable and, for this reason, I will employ the triads as reference points for much of the analytical narrative of the fictional conductors’ interpretations. By identifying prevalent sonorities such as these triads, the interpretations of the four conductors can be more effectively contrasted—specifically by evaluating the extent to which each interpretation conforms to statistical likelihoods or contravenes them. Analysis of other parameters of the simulation data, such as density, additional sonorities, and a more general discussion of consonance and dissonance, are folded into a discussion towards the end of the study comparing the conductors’ interpretations and real-world performances.
3. Four Conductors and Four Imagined Performances
[3.1] Given the musical possibilities ascertained from the simulation data, I invented four conductors with complementary aesthetic priorities, assigning each a name—Acuta, Metera, Soportia and Varia—and a collection of preferences, which are summarized at the beginning of each analytical narrative below. Amongst the four, many of the preferences are directly oppositional—for instance, Soportia has a preference for full textures, whereas Acuta has a preference for sparse textures. These oppositions were conceived intentionally so that the conductors’ respective (virtual) decisions in a given analytical moment might most dramatically illuminate the potential differences in musical outcomes.
[3.2] I imagined a performance that reflects each conductor’s unique priorities and determined the time brackets of each performance accordingly. These imagined interpretations were generated by hand and not culled from the simulations. I want to emphasize that in generating each interpretation I chose the placement and duration of the sounds of each part intentionally, with an awareness of the other parts, and have thus consciously deviated from the typical performance practice of Cage’s indeterminate works, in which the parts are determined independently of one another. This methodology is a heuristic intended to portray a range of possibilities within performances of Four2.(8)
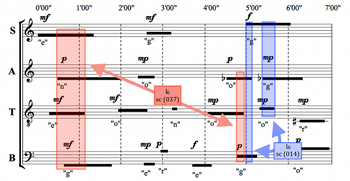
4. Soportia’s Interpretation of Four2
Example 8. Soportia’s Interpretation of Four2
(click to enlarge and listen)
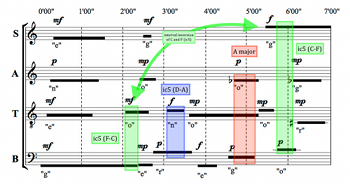
[4.1] Soportia seeks an interpretation that emphasizes a constant, underlying harmony. She prefers to carefully prepare changes in harmony step by step, building slowly. She avoids silences, as well as sudden changes in sonority. It follows that Soportia will want to sustain each of the three triads as long as possible. Her interpretation and a MIDI realization of it are given in Example 8 and Audio Example 1. In her interpretation, the constituent pitches of the opening D-minor triad—corresponding to each part’s first sound—enter one by one, in order from low to high. The D-minor sonority is established through this pyramid figure within the first twenty seconds and is sustained in four voices for about a minute.
Example 9. C Major and Surrounding Fifths (Soportia)
(click to enlarge)
Example 10. A Major and Surrounding Fifths (Soportia)
(click to enlarge)
[4.2] As the D-minor chord disintegrates voice by voice, the bass’s sustained F2, the chordal third, provides continuity when the tenor’s C4 enters above, preparing the C-major harmony to follow via an exposed fifth that echoes the ic5 formed by A–D in the previous triad. Example 9 highlights these events. The C-major triad then assembles itself amongst the four voices and disappears in similar fashion to the previous D-minor triad, with the third of the chord again sustained the longest after the triad has sounded. This E4 in the alto is joined by A3 in the bass around 2’45”, producing another open fifth.
[4.3] The A3 in the bass is taken up by the tenor and, between the two voices, is sustained for nearly two and a half minutes. This A occurs in a familiar register, recalling the tenor’s opening pitch and suggesting a potentially drone-like continuity throughout the interpretation. Sounding alongside this A are first a D (in the tenor), then an F (bass), and then an E (bass), echoing the previous progression from the D-minor triad to the sound of ic5. This time, E and A are joined by a
[4.4] Just as the bass F at the beginning of the piece provides continuity against changing harmony in the other parts, the soprano F here provides continuity against the
Example 11. Possibilities for Sustained Drones on A and F
(click to enlarge)
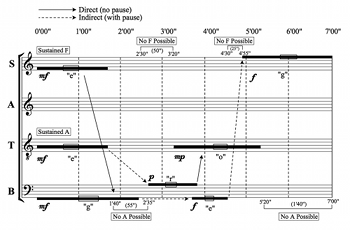
[4.5] Soportia’s interpretation emphasizes two particular sustained tones, A and F, which are the two most prevalent notes (by duration) amongst the composition’s time brackets for all parts. In fact, as Example 11 illustrates, it would be possible to sustain an A drone in the same register nearly throughout the entire piece between the tenor and bass, with gaps necessary only from 1’40” to 2’35” and from 5’20” to the end of the piece (7’00”). In other words, by using the full duration of the time brackets containing the pitch A, one could perform the seven-minute piece so that only 2’35” of it did not have an A sounding in the background.
[4.6] A similar feat could be achieved with the pitch F, which could be sustained between the bass and soprano for the entire duration apart from 2’30” to 3’40” and a brief pause from 4’30” to 4’55”, for a total gap of only 1’35”. Example 11 gives both of these possibilities, using solid lines to show where time brackets may be overlapped without a pause, and dotted lines to indicate a link across a gap in which the given pitch is not present.
[4.7] Soportia’s interpretation balances continuity of these two pitches with other concerns, such as harmony. Sustaining the F and A too long potentially results in a number of dissonant intervals, particularly seconds, which she aims to avoid. Soportia nevertheless makes use of both possible direct (i.e. overlapping) voice exchanges—a marked contrast with Acuta, for example, who avoids these drone possibilities by making these particular pitches noticeably short in duration, as demonstrated below.
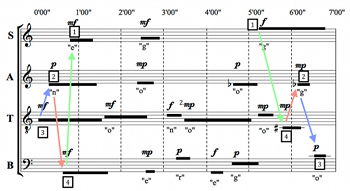
5. Acuta’s Interpretation of Four2
Example 12. Acuta’s Interpretation of Four2
(click to enlarge and listen)
[5.1] Acuta prefers unsettled, pointillistic musical textures. She emphasizes moments of silence and harmonic ambiguity, and often draws attention to discontinuities and transformations of harmony, destabilizing static sonorities when possible. Her version and a MIDI realization are given in Example 12 and Audio Example 2.(9)
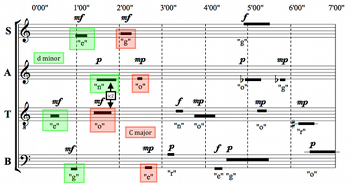
[5.2] Because Cage’s time brackets allow for a wide range of possible durations for the sounds within, there are numerous options for short patterns in which no two sounds overlap. Acuta considered, but ultimately rejected, such an interpretation in favor of a balance between pointillism and certain satisfyingly dissonant verticalities. At first glance, Acuta’s interpretation most strikingly differs from Soportia’s in the greater amount of silence. Additionally, the triads that were so clearly expressed in Soportia’s interpretation are significantly obscured. After a long opening silence, the tenor voice produces the first sound on A3. Following a pause, the bass and soprano enter on F2 and F4, respectively, overlapping slightly as, according to the time brackets, 1’00” is both the latest time at which the soprano may begin singing and the earliest that the bass may stop.
Example 13. Destabilization of Opening D-Minor Sonority (Acuta)
(click to enlarge)
Example 14. Emphasis on ic1 at the End of the Piece (Acuta)
(click to enlarge)
[5.3] The alto’s D4, the root of the D-minor triad, begins after another pause and after the entrance of the tenor’s second sound, a C4, further destabilizing the opening harmony (Example 13). This reordering is statistically unlikely, but possible because the starting interval of the time bracket for the alto’s D ends at 1’30”, while the time bracket for the tenor’s C begins at 1’25”. The dissonant second formed between them—which also defuses the perception of an F-major triad—is sustained much longer than any sound heard so far.
[5.4] The C–D dyad gives way to another pause, after which the constituent tones of the C-major triad sound one by one, interspersed with silences. Around 4’30”, the longest sustained sound of the piece—E3 in the bass—begins, above which the notes
[5.5] There are a number of relatively dissonant harmonic options at this point in the piece, including an augmented triad between the soprano’s F5, the alto’s
6. Varia’s Interpretation of Four2
Example 15. Varia’s Interpretation of Four2
(click to enlarge and listen)
[6.1] Varia relishes in revealing chains of transformations in music. She likes to follow labyrinthine pathways through scores in search of echoed intervals and buried cycles. The logic within her interpretations is rigorous, but often resides at a deeper, abstract level, often requiring several hearings to fully grasp it. Her interpretation and a MIDI realization are given in Example 15 and Audio Example 3.
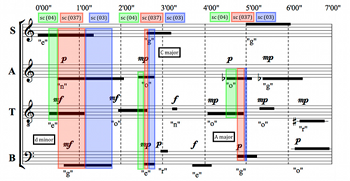
[6.2] Varia’s interest in intervallic patterns leads her to notice that in the simulation data, the opening D-minor triad is typically preceded by the major third F–A and followed by the minor third D–F. Even though there are three pitch classes—D, F, and A—available amongst the opening time brackets of each part, the pitches are not equally likely to sound at all times. First, the time brackets for the soprano and tenor, and the alto and bass, are different, resulting in different concentrations of sounds at different times. Secondly, both the soprano and bass begin on the pitch class F; therefore, that note is more likely to be sounding at any given time than the others.
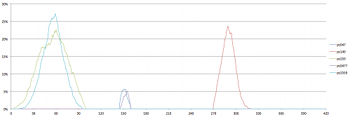
[6.3] As Example 16a illustrates, all of the brackets begin at 0’00”, but the total length of the bracket for the soprano and tenor is 1’40”, whereas the total length of the bracket for the alto and bass is 2’30”. It follows that the soprano and tenor’s first sounds (F and A, respectively) can potentially last from the beginning of the piece until 1’40”. This means that in all simulations, the initial sounds are concentrated within this window. By contrast, the time brackets for the alto and bass’s first sounds (D and F) last until 2’30”, meaning that their sounds are distributed over a broader time interval, and the internal overlap—which statistically represents the highest concentration of sounds—occurs later in time.
Example 16a. First Four Time Brackets of Four2: Transcription of the First Time Bracket for Each Part (click to enlarge) | Example 16b. First Four Time Brackets of Four2: Prevalence of Notes in the First Time Bracket for Each Part in Random Simulations (click to enlarge) |
[6.4] Thus, while all of the pitch classes are available in the first minute and a half of the piece, the alto’s D and the bass’s F will be skewed to arrive later on average, since their time bracket extends beyond that of the soprano and tenor. Example 16b displays the randomly determined results of these opening time brackets in the simulations, measuring the percentage of simulations that contain each part’s first note along the vertical axis. The data in Example 16b clearly illustrates the difference in time between the peaks of the two pairs, as well as the progression from A and F to D and F.
Example 17. Flowchart of Likely Harmonic Progression from 0’00” to 1’30”
(click to enlarge)
Example 18. Progressions from sc (04) to sc (037) to sc (03) (Varia)
(click to enlarge)
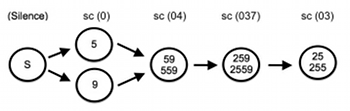
[6.5] Example 17 represents this data as a flowchart.(10) This flowchart—derived from the prevalence data above—depicts the first minute and a half of a typical performance of the piece, during which time the computational simulations tend to progress from silence to a single note, to sc (04) (via pcs 59 or 559), to sc (037) (via pcs 259 or 2559), to sc (03) (via pcs 25 or 255). By generalizing this observation into a progression from sc (04) to sc (037) to sc (03), Varia considers whether a similar pattern can be applied to the other two triads. Example 18 illustrates the solution she employs in her interpretation for each triad—which is just one of many possible solutions.
[6.6] In order to create a parallel structure around the C-major triad, Varia delays the G4 in the soprano as long as possible (the latest possible entrance time is 2’40”) and sustains the C4 in the tenor as long as possible (the time bracket ends at 2’40”), so that the C is sounding and the G is not when the alto enters with E4 at 2’25”. The alto’s E4 is then sustained as the soprano and bass enter on G (both relatively late within their respective time brackets), followed by the departure of the C. Varia’s interpretation maximizes the duration of each step in the progression, but it must all be coordinated within a relatively short time interval, as the (identical) time brackets containing the alto’s E4 and the bass’s G2 last only 25 seconds, between 2’25” and 2’50”. The intricacy of this timing reflects the C-major triad’s relative fragility, compounded by the mere 15-second potential overlap between the tenor’s C4 and the alto’s E4. This instability is especially vivid in Example 7, which depicts the low prevalence and short duration of the C-major triad relative to the D-minor and A-major triads in the simulations.
Example 19. Expanded Intervallic Progression About Each Triad (Varia)
(click to enlarge)
[6.7] The final triad—A major—can also be made to fit Varia’s pattern, as the first constituent tone is A3 in the tenor (appearing just after 4’00”), which Varia follows with
[6.8] For D minor, this next step occurs between the alto’s D and the tenor’s C; for C major, she engineered sc (02) between the soprano’s G and the bass’s A. For A major, a verticality between the tenor’s D and the bass’s E (around 5’15”) is not possible, but a listener could be guided to link them, especially considering their registral proximity (shown with a double-headed dotted arrow in Example 19). The C-
Example 20. I6-related Trichords (Varia)
(click to enlarge)
[6.9] At the end of piece, Varia ensures the presence of two instances of sc (014),
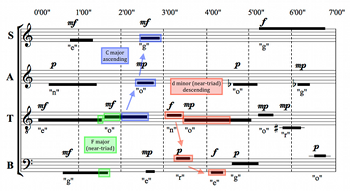
7. Metera’s Interpretation of Four2
Example 21. Metera’s Interpretation of Four2
(click to enlarge and listen)
Example 22. Registral Order of First and Last Four Sounds (Metera)
(click to enlarge)
Example 23. Near-Triads and Arpeggiations (Metera)
(click to enlarge)
Example 24. Quasi-Cadential Figure (Metera)
(click to enlarge)
[7.1] Metera prioritizes orderly, symmetrical structures of duration and harmony. She seeks balance in her interpretations, avoiding what she considers to be dramatic or overwrought climaxes or abrupt shifts in texture. A transcription and audio realization of her interpretation are given in Example 21 and Audio Example 4.
[7.2] Metera’s approach to the triads is generally to emphasize them as harmonic markers throughout the piece, but she takes care to integrate them into a parallel symmetrical structure that takes registral contours into account . The D-minor opening of her interpretation unfolds from the center outwards, with the voices entering in registral order of 3–2–4–1. This registral order is reversed for entrances of the last four sounds, resulting in a pattern of 1–4–2–3 for the soprano’s F5, the tenor’s
[7.3] Metera’s symmetrical framing may suggest to the listener the possibility of an explicitly defined center point, and Metera has indeed articulated the center through the D4 in the tenor, which enters just after 3’00”. This pitch recalls the root of the opening chord, but Metera makes sure to draw our attention by preceding it with the only silence of the piece. Additionally, the descent to A3 via the bass (subsequently taken up by the tenor) inverts ascent at the opening from the tenor A to the alto D in both pitch and register. Metera’s interpretation bridges the space between the first and third triads by agogically accenting the A3 in the tenor that is shared by both chords. This choice also serves to defuse the potentially “teleological” shape of the piece (in favor of a symmetrical structure) through continuity of both pitch and register.
[7.4] Throughout the piece, additional near-triadic moments are emphasized, such as the F-major near-triad between the bass and tenor around 1’35”, and the D-minor near-triad from about 3’00” to 4’30” (highlighted in Example 23). Where triads are not possible (as in these moments and others), Metera still emphasizes relatively consonant intervallic subsets of triads, such as thirds, fourths, fifths, and octaves.
[7.5] Metera integrates the D-minor near-triad even further by relating it to the second triad—the C-major chord—through the contours of her registral entrance structure. The C-major chord is arpeggiated in ascending registral order (with the exception of the bass’s G, which duplicates the soprano), and moments later the D-minor near-triad is arpeggiated in descending registral order, albeit without a full triadic verticality.
[7.6] The most distinctive feature of Metera’s interpretation is the quasi-cadential figure from about 5’05” to 5’35” highlighted in Example 24. The tenor’s sustained A3 is joined by
8. Real-World Performances of Four2
Example 25. Transcription of Houston Chamber Choir (ECM New Series)
(click to enlarge and listen)
[8.1] Having produced possible performances of Four2 by design and by computational simulation, I will now compare the results of these approaches with existing performances of the composition.
[8.2] Examples 25, 26, and 27 are the author’s transcriptions of three commercially available recordings of Four2: the Houston Chamber Choir conducted by Robert Simpson for ECM New Series in 2015, and two recordings (labeled “Version 1” and “Version 2” in the CD booklet) by Ars Nova Copenhagen for Mode Records in 1999.(11) These recordings are Audio Examples 5, 6, and 7, respectively. In addition, I reviewed four recordings available on YouTube—all of which appear to be live recordings—and one other commercially available recording.(12) Of the four YouTube recordings, three include both audio and video documentation of the performances, which is helpful in ascertaining some aspects of the performance practice, as will be discussed below.
Example 26. Transcription of Ars Nova Copenhagen, Version 1 (Mode) (click to enlarge and listen) | Example 27. Transcription of Ars Nova Copenhagen, Version 2 (Mode) (click to enlarge and listen) |
[8.3] In the three transcriptions, the opening D-minor triad is sustained for at least thirty seconds, but the other triads discussed above appear with less frequency. The C-major triad appears in both Ars Nova recordings, but not in the Houston Chamber Choir recording; the A-major triad is only heard briefly in the second Ars Nova recording and the Houston Chamber Choir recording. I will return to a discussion of harmonic considerations later, but first I will examine the distribution of densities in these recordings.
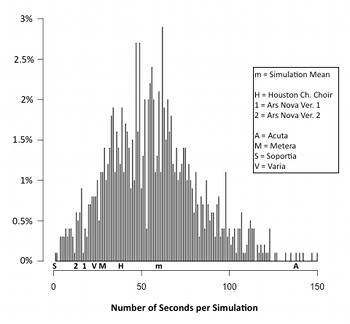
Example 28. Comparison of Distribution of Densities (by Number of Vocal Parts) in the Monte Carlo Simulations, Fictional Conductors’ Interpretations, and Selected Recordings of Four2
(click to enlarge)
Example 29. Comparison of Distribution of Densities (by Number of Vocal Parts) in the Monte Carlo Simulations, Fictional Conductors’ Interpretations, and Selected Recordings of Four2
(click to enlarge)
[8.4] Example 28 compares the distribution of densities (by number of active vocal parts) in the three commercial recordings of Four2 transcribed above to the four fictional conductors’ imagined performances and the statistical mean, maximum and minimum values obtained from the random simulations. (The extrema obtained from the simulation data do not reflect mathematical limits; additional simulations would likely slightly expand the ranges.)
[8.5] It is immediately clear from the data in Example 28 that the recordings deviate from the distributions that might be expected based on the random simulations. All three recordings exceed the proportion of three- and four-voice textures typical of the simulations; likewise they all fall below the average amount of silence and single-voice textures. This apparent preference for fuller textures is exemplified by Ars Nova’s performances in particular. In their second version, the proportion of three-voice textures easily exceeds that of any individual simulation, while their first version exceeds all but one of the simulations in its proportion of three-voice textures.
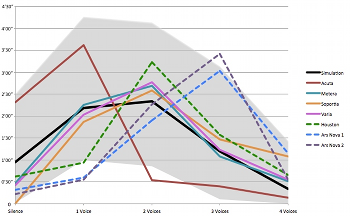
[8.6] Example 29 recasts the information in Example 28 graphically using line segments to link and juxtapose the prevalence of each cardinality—measured in total time on the vertical axis—amongst the recordings, the imagined conductors’ interpretations, and the simulation average. Each line represents what I will refer to as the density profile of a given performance. The gray shadow represents the area between the highest and lowest durations obtained for each cardinality amongst the simulations. Points on the density-profile lines that fall outside of the gray area—such as the prevalence of two-voice textures for the fictional conductor Acuta and the prevalence of one-voice textures for all three recordings—reflect values that were not once encountered in over one thousand random virtual simulations and, based on an expectation of a completely random determination of the time brackets, can be understood as statistically unlikely outliers.(13)
[8.7] Example 29 illustrates the difference in prevalence between the randomly generated simulation data, for which one- and two-voice textures are most common, and the commercial recordings, which skew towards two- and three-voice textures. It bears emphasizing that in a typical performance of Four2, the distribution of density is not directly selected by performers; it is contingent upon the confluence of choices made by performers in determining their own vocal parts, and choices made by the other performers in determining theirs independently. Furthermore, as the interpretations of the fictional conductors Metera, Soportia and Varia make manifest, performances with similar distributions of density can be constituted in strikingly different ways.
[8.8] Each density profile in Example 29 has a single peak, indicating the most prevalent density level over the course of a given performance. Although there is considerable variation among the versions, no performance has silence or a four-voice texture as the most prevalent density level. Furthermore, the peak for each density profile represents the line’s only change in direction (i.e. from increasing to decreasing prevalence values). This results in a generally concave (downward) bell shape—a shape emphasized by the use of lines in this figure, rather than bars or points.
[8.9] The consistent bell shape of the density profiles reflects the unlikeliness of simultaneous changes between two or more voices, a characteristic feature of Cage’s time brackets in general. In Four2, this is ensured by a variety of factors, including the independence of each time bracket and the fact that each contains a single sound. Assuming the brackets are determined randomly, one-voice textures typically move through two-voice textures to reach three-voice textures, and so forth. Therefore, as Example 29 demonstrates, the prevalence of a given cardinality will typically be closer to the prevalence of adjacent cardinalities than to more distant cardinalities. This is especially true regarding the peak cardinalities for each density profile. This suggests that the density profile of a performance of Four2 may be shifted left or right, but the bell shape of the line will persist.
[8.10] Popoff asserts that while Cage’s time-bracket structure “[allows] flexibility in its realization, it guarantees an overall regular behavior” when considered statistically, and indeed it would be logical to conclude that the random determination of a certain configuration of time brackets and sounds would produce consistent results over many trials (Popoff 2011, 227). The consistency of the bell shape of the density profiles and the statistical preference for one- and two-voice textures obtained from the simulation data can be regarded as deep properties of Four2, although in practice, these aspects are clearly far from guaranteed.
Example 30. Average Density of Voices in Simulations of Four2 Over Time
(click to enlarge)
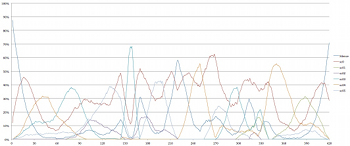
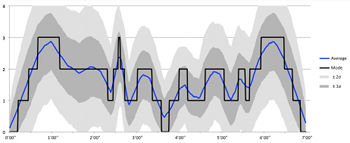
[8.11] Another method of characterizing the density of Four2 is to consider the average change in cardinality over time within a performance. Example 30 illustrates the average density of voices in the simulations over time, with a blue line indicating the running mean and a black line indicating the mode (the cardinality that appears most often) for each second of the work. The dark gray area indicates values that fall within the first standard deviation (± 1σ, which according to a common rule of thumb for normally distributed data, accounts for about 68% of the data); the lighter gray area indicates values that fall within the second standard deviation (± 2σ, which accounts for about 95%).
[8.12] A technical statistical analysis is beyond the scope of the present study, but the inclusion of the average, mode, and standard deviation is intended to provide a more nuanced account of how likely various cardinalities might be throughout the piece. For instance, between about 1’10” and 2’15”, the most common density in the simulations is a two-voice texture, but the running average suggests a decrease in the number of voices likely to be heard over time, with two- and three-voice textures taken together as most common at the beginning of this passage, and two- and one-voice textures more common at the end. Points at which the gray region is widest suggest the broadest variety of cardinalities, while narrower points suggest a focus around a particular cardinality.
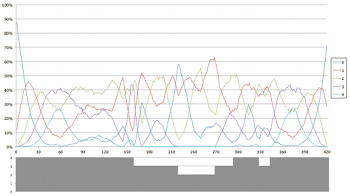
Example 31. Prevalence of Density of Voices Over Time in All Simulations
(click to enlarge)
[8.13] While Example 30 provides a useful summary of general changes in density over the course of a performance of Four2, its reliance on the average cardinality at any given time obscures the relationships between the discrete cardinalities of the individual simulations. Example 31 depicts the relative prevalence of each cardinality over time amongst the simulations in the line graph above, while the gray graph below indicates the number of time brackets available. Time brackets that overlap within a single part are counted as a single bracket, since only one can sound at a time.
[8.14] Example 31 shows that the most prevalent cardinality at any given moment is always overtaken by the line of an adjacent cardinality. For example, throughout the first minute of the piece the texture expands stepwise via a progression from silence as the most prevalent texture to a one-voice texture, a two-voice texture, and a three-voice texture. The various lines’ complementary peaks and troughs in response to one another are evident. A comparison with the full time-bracket structure depicted in Example 2 demonstrates that the lines become especially volatile when time brackets are shorter, or when multiple time brackets’ edges correspond (such as the moment around 2’30”–2’40” [150–160 seconds elapsed]). Interestingly, the relationship between density and the number of time brackets available is not so clear-cut. Although there is a time bracket available for each part for most of the piece, four-voice textures are never the most prevalent density level, reaching only second place around 1’00” and 6’15”.
[8.15] Although several writers have remarked on the importance of silence in the Number Pieces, the scarcity of silence amongst the recordings is notable.(14) Remarkably, among the eight recordings reviewed, only the YouTube recording of the Ensemble de Exploración Vocal de los Andes contains an internal silence (i.e., a silence anywhere between the first and last sound of the piece). Although there are a limited number of recordings available for evaluation, the lack of internal silences is unusual considering that over 98% of the random simulations contain internal silences. Furthermore, the aggregated simulation data in Example 31 indicates a clear statistical preference for silence over all other possible sonorities around 3’40”.
Example 32. Histograms of the Prevalence of Cardinalities in Simulations, with Recordings and Fictional Conductors’ Interpretations Superimposed
(click to enlarge and see the rest)
[8.16] Representing the density data obtained from the simulations as a series of histograms facilitates a more nuanced comparison with the distribution of density of the recordings and the fictional conductors’ interpretations. Example 32 comprises five histograms, each of which depicts the percentage of the simulations that exhibit each of the five possible cardinalities for a given number of seconds. Superimposed onto these results are the values from Example 28 for each of the recordings and the four imagined performances by the fictional conductors.(15)
[8.17] The histograms in Example 32 further illustrate the bias towards fuller textures in the recordings discussed above. Ars Nova’s second version, for instance, contains 33 seconds of four-voice textures—the fewest among the three transcribed performances—but Example 32e makes clear that this is still a surprisingly high value. Over half of the simulations include less than 20 seconds of four-voice textures, and about 17% have no four-voice textures at all.
[8.18] All five distributions in Example 32 exhibit a disproportionately long tail to the right of the center of the data, a phenomenon called a positive skew.(16) The distribution for four-voice textures (Example 32e) is especially skewed compared to the others, while cardinalities of 1 and 2 are the least skewed (Examples 32b and 32c). The extent to which a distribution is skewed with a longer tail to the right corresponds to an expectation that in future performances, a wider range of outlier values will be encountered above the mean than below it. This is shown in Example 29 by the relationship of the gray area to the simulation mean (the black line): the gray area is larger above than below it.
[8.19] Example 32e, the histogram depicting the distribution of four-voice textures, has the most unusual shape of the five, owing to the large proportion of simulations without any four-voice textures (represented by the leftmost vertical bar). According to the data in Example 28, four-voice textures are the least prevalent density level in the simulations; the average simulation has just twenty seconds of four-voice textures.
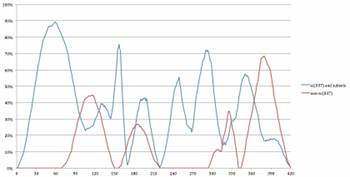
Example 33. Prevalence of (037)-Related Sets and Non-(037)-Related Sets in the Simulations Over Time
(click to enlarge)
[8.20] Using averages obtained from the simulation data allows one to evaluate areas of higher and lower density in a typical performance of Four2. The same methodology can be used to ascertain the contour of other musical qualities, such as dissonance. The variety of measures of dissonance available to analysts underscores the importance of choosing a contextually appropriate metric; here I have chosen to contrast the prevalence of triadic and non-triadic harmonies. Example 33 displays the average composite prevalence over time in the simulations of sc (037) and its subsets—sc (03), sc (04), sc (05) and sc (037)—in blue, and all other sets in red. The prevalence of silence and sc (0) are omitted since the concept of vertical consonance and dissonance is predicated on the relation of at least two different pitches.(17)
[8.21] Example 33 makes clear that there are four moments in which non-(037) sets are more prevalent than (037)-related sets: from 1’37”–2’06”, 2’48”–3’02”, 5’16”–5’29”, and 6’04”–7’00” (the end of the piece). The first dissonant moment can be attributed to the potential sc (02) dyads between the soprano’s G and the bass’s F or the tenor’s A, or between the tenor’s C and the alto’s D. The second dissonant moment results from the bass’s A and the G of the soprano. The third and fourth moments result from a variety of potential dissonances, including half-steps between the bass’s E and the soprano’s F, and the
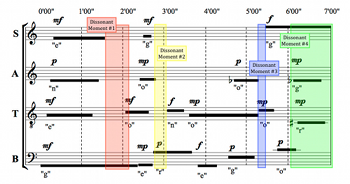
Example 34. Soportia’s Interpretive Response to Dissonant Moments
(click to enlarge)
[8.22] The three recordings offer little contrast with respect to these dissonant moments; while there is variation in the duration of the dissonances, no recording avoids any of them entirely. By returning to the fictional conductors’ interpretations, I hope to illustrate the variety of possible responses to these moments more vividly. Example 34 uses colored boxes to draw attention to the ways in which Soportia navigates these moments. In the first, second and third moments, she responds to the dissonance-favoring conditions by thinning out the texture, in each case to a single sustained pitch for at least part of the time interval—but not all the way to silence, which would contravene her musical preferences. In the minute or so preceding the fourth moment, faced with a strong prevalence of dissonant combinations, Soportia sustains one note for continuity (the soprano’s F5), and cues the other sounds against it, one by one. After 6’00”, she sustains the alto’s
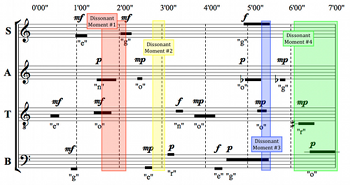
Example 35. Acuta’s Interpretive Response to Dissonant Moments
(click to enlarge)
[8.23] By contrast, Example 35 demonstrates that Acuta responds to these moments by balancing individual dissonances with silence, reflecting her preference for sparse textures. For instance, the first dissonant moment contains three different tones, including a sustained sc (02) between the tenor’s C and the alto’s D, while the second moment is completely silent. The third moment sets two highly dissonant semitonal dyads, E–F in the bass and soprano and
[8.24] As noted above, the most striking harmonic incursion is the
9. Performance Practice of Four2
[9.1] Just as the computational simulations and the fictional conductors’ interpretations generated by hand produced an array of diverse results, there are many factors that might produce differences between real-world performances. In this section, I discuss the performance practice of Four2 and the Number Pieces in general, in order to appropriately contextualize the analytical methodology and interpret the differences between the performances.
[9.2] Cage’s ideal performance practice is not entirely clear, as a number of writers have noted (Popoff 2010, 79; Haskins 2004, 271–2; Piekut 2011, 47–9; Lindau 2014, 27–8). Broadly speaking, however, his intention in employing the time-bracket notation seems to have been to ensure spontaneous decision-making that maintains the independence of each part (Weisser 2003, 191; Weisser 1998, 166–67). Cage’s Number Pieces, like his other works that combine techniques of chance and indeterminacy, allow both the composer and the performer to access a multiplicity of unfamiliar possibilities—to turn one’s mind “in the direction of no matter what eventuality,” in Cage’s famous phrase (Cage 1961, 39).
[9.3] Popoff notes that Cage’s time brackets frame duration as an abstraction to be accessed by the performer only indirectly, contingent upon the performer’s choice of starting and ending points in the moment: “in the framework of a time-bracket, a sound is defined by its starting and ending time and all the perceptual qualities of the sound such as duration or repartition in time are defined a posteriori” (Popoff 2011, 222). Unlike what Popoff refers to as the “discrete time of classical music measured in beats,” in which the beginning of a sound is often synchronized with the end of the previous sound, the starting and ending points of sounds within time brackets exist independently of one another as time values elapsed from the beginning of the composition (Popoff 2011, 222). In this way, conventional expressive gestures related to duration such as rubato and metric accents are rendered meaningless.
[9.4] Despite the unique qualities of the time-bracket notation, the realization of Cage’s priorities of spontaneity, independence of the parts, and non-intention are greatly shaped by choices made by the performers (Popoff 2010, 77, 80; Haskins 2004, 245–46, 271). An article on Cage’s choral music intended for prospective performers observes that the piece is often performed without a conductor, and that section leaders may cue the changes (John 2012, 69–70). As with many of Cage’s works, the use of a timekeeping device—whether stopwatches synchronized throughout the ensemble or a digital display visible to all—is typical (John 2012, 69; Haskins 2004, 9; Weisser 1998, 87).
[9.5] The video recordings of performances of Four2 on YouTube, in contrast with John’s observation above, all involve conductors, yet suggest a variety of approaches regarding the conductor’s role. In some cases, such as Carlos López Puccio conducting the Estudio Coral de Buenos Aires, conductors are clearly cueing the performers. In other instances, such as the Soundstreams performance conducted by Kaspars Putniņš ,the conductor seems to merely be indicating the passage of time, presumably leaving the decisions to the section leaders. Occasionally, the conductor’s cue seems to cause multiple parts to begin, end or change sounds simultaneously, such as in Puccio’s performance at 2:37. This kind of coordination suggests a predetermined interpretive strategy. In other performances, two successive sounds within a single part are often audible simultaneously, suggesting that the performers are transitioning from one sound to another independently, rather than as a section. This seems to occur at 1:11 in the performance by the Latvian Radio Choir conducted by Sigvards Klava, when the sopranos’ second sound, G4, begins but the sopranos’ first sound, F4, is still clearly audible. This performance technique in particular seems to contravene Cage’s prefatory instruction in the score that each sound should have a single beginning and a single end.
[9.6] Mark Steighner, who as choral director of the Hood River Valley High School commissioned Four2 from Cage, indicated that in performances he conducted he acted as a timekeeper and allowed section leaders to cue the beginnings and ends of each bracket independently (Steighner 2016). As conductor, Steighner would indicate intervals of fifteen seconds while each section leader cued their section—arranged in a circle—with eye contact or a head nod (Steighner 2016). This practice seems to resonate with Cage’s desire for the sections to determine their parts independently, yet in Cage’s correspondence with Steighner, he suggested that the conductor “may specify the beginnings and ends of tones but hopefully without gestures visible to the audience” (Steighner 1991). In the same letter, Cage advises that “touch may be useful between section members for cues.”
[9.7] Thomas Kiørbye, the manager of Ars Nova Copenhagen, drew a clear distinction between preparing for a live performance of Four2 and preparing the Mode recording. According to Kiørbye, Ars Nova Copenhagen has performed the piece live many times, and for those performances the time brackets are determined spontaneously by the individual sections. He acknowledges, however, that even though they did not agree to a plan in advance, through many rehearsals and performances “we may have developed a route through the piece which we found worked well so that the performances may not have been all that different” (Kiørbye 2016). Brent Baldwin, who conducted a performance of Four2 as the artistic director of Austin-based Panoramic Voices, similarly reported that there were “certain elements/sequences that we fell into throughout the rehearsal process” (Baldwin 2016).
[9.8] For the Ars Nova Copenhagen recording, in order to “make a point of demonstrating how the piece can end up sounding differently depending on the choices made by the performers,” the ensemble “pre-designed two versions meant to be as different from each other as possible” within Cage’s constraints (Kiørbye 2016). In our correspondence, Mark Steighner confirmed my observation that few performances of Four2 seem to take advantage of the possibility of internal silences. Based on his experiences preparing the work for performance, Steighner observed that one of the most difficult aspects of this piece for singers is audiating pitches after long silences. It is certainly plausible that this particular obstacle might have discouraged performers from including silences in their interpretations. Steighner’s interpretations, as he recalls, typically included internal silences but, unfortunately, were not recorded (Steighner 2016).
[9.9] The full textures and lack of silences in real-world performances of Four2 may simply reflect some performers’ aesthetic preferences for full textures or, more generally, an inclination to fill the sonic space. Cage asked performers to accept silence as part of his compositions, but if these recordings are any indication, performers may be hesitant to sing too little or enter too late in a bracket. In an interview with Mark Gresham, Cage observed that the things he asks of the performers in Four2, such as sustaining very long sounds and making choices about when to begin and end within the time brackets, “might have been difficult for their minds, but not for their capacities” (Kostelanetz 2003, 95–96). Elsewhere, regarding another of the Number Pieces, Cage acknowledged that “it is very difficult for performers to do so little” (Haskins 2009, 332).
[9.10] Even if performers approached the piece with the intention of producing unfamiliar or random results, it is well established that humans are poor random number generators (Popoff 2011, 223). Furthermore, because musically salient qualities of performance such as duration, density, and harmony are accessed only indirectly by performers through their choice of when to begin and end each sound in their own part only, performers’ ability to intentionally shape these qualities is limited, whether in pursuit of familiar or unfamiliar outcomes. For example, although Kiørbye indicated that the two Ars Nova recordings were intended to be “as different from each other as possible,” the analysis above suggests that in many respects they are remarkably similar.
[9.11] The difficulties imposed by the Number Pieces have occasionally inspired performers to invent novel performance paradigms. For a 2000 recording of 103 with the Janacek Philharmonic Orchestra, conductor Petr Kotik, who often worked with Cage, flipped coins to randomly determine the starting points of each of the 103 performers’ time brackets, and then generated parts based on the pre-determined starting points, leaving the ending points to the discretion of the performers. (Popoff 2010, 79; Haskins 2004, 271–72). Other writers have recognized the potential for technology to mediate performance of Cage’s music of this period.(20) In one instance, a recording of several of Cage’s Number Pieces was produced by having a single performer record multiple parts to be overdubbed in the studio (Popoff 2010, 79; Haskins 2004, 271). This approach would certainly eliminate any possibility of performers listening to one another and interacting musically, which Cage opposed to the extent that performers listening to one another and determining their time brackets in coordination might introduce intentional and familiar musical patterns.(21) While both approaches lack spontaneity, the (partially) random method used in the recording of 103 has the additional merit of embodying non-intentionality not only in the aggregation of the parts, but also at the level of each individual part. Furthermore, in contrast with the overdubbed recording, it is a viable strategy for live performance.
[9.12] As Popoff notes, achieving the fullest multiplicity of results from the Number Pieces without recourse to special accommodations (such as those described above) seems contingent upon the actions of an “ideal performer” whose choices would be “purely random and devoid of any bias,” or in Cage’s words, exhibit non-intention (Popoff 2010, 77). He goes on to observe that human performers are “very unlikely to act completely at random,” offering as an example the possibility that a “performer might choose to play the sounds so as to achieve a specific harmonic result with other performers” (2010, 77).
[9.13] One can easily imagine a performance in which performers project their expectations of what Cage’s music should sound like through their interpretive choices, or, as Kiørbye noted above, a performance in which the ensemble has become accustomed to taking a particular route through the piece. In addition to maligning what he considered to be undisciplined or incorrect performances, like many composers Cage actively disseminated his tastes and preferences by corresponding with performers, attending rehearsals, supervising recording sessions of his music and participating in performances himself. (22) The difficulties in achieving a performance without any sort of bias have led to the consensus view summarized by Elizabeth Ann Lindau: “the freedoms of indeterminate music are often described as deceptive, or as tests of a performer’s discipline and seriousness” (Lindau 2014, 19–20).
[9.14] In both theory and practice, Cage’s “ideal performer” remains elusive. Like Lindau and other scholars who are reassessing the fundamental terms of Cage’s project, performers of Cage’s works, often embroiled in what Lindau (after Lipsitz) terms “creative misunderstandings,” consistently challenge the descriptions of non-intention provided by Cage and his collaborators, both intentionally and inadvertently (Lindau 2014, 21 and 31). The versions of Four2 I have assembled for this study represent a spectrum of interpretive intentionalities by design: from the lack of intention in the random computational simulations to the highly intentional fictional conductors’ interpretations. In juxtaposing such different versions of the piece, my hope is to reconcile the multiplicity of performance practices in circulation with the multiplicity of musical results obtained.
[9.15] Appendix 1 gives an original software program with which readers can edit and play back their own interpretations of Four2, generate random interpretations, or access and manipulate one of the fictional interpretations. This software is intended to provide an additional venue in which to explore the multiplicity of possible musical results of the piece. It is a standalone application developed in Max/MSP compatible with both Mac OS and Windows.
10. Conclusion
[10.1] Cage famously theorized the radical independence of the acts of composing, performing, and listening from one another (1961, 15). Many writers have seized on this partitioning as fundamental to understanding Cage’s work, with some insisting that it precludes any kind of analysis that goes beyond a mere description of the compositional process. William Brooks, for instance, asserts that “when we impose an analysis—we violate Cage’s intention; we make his work conventional” (2014, 545). Brooks goes on to acknowledge that “the result might be entertaining, beautiful, or illuminating, but we put it there, not the creator” (545).
[10.2] I submit that while analysis is ultimately an intentional act, the clear patterns, tendencies, and relationships in Four2 suggest that Cage had specific musical results in mind, even if these results constitute a range of possibilities more than any single realization. James Pritchett, in his early study, insists that “[t]he frameworks for Cage’s chance systems were crafted with an ear towards what sorts of results they would produce,” arguing that “[the fact] that he chose one set of questions over another was purely a matter of taste and style” (Pritchett 1993, 4). Other writers have gone further, identifying the ways that Cage “tinkered with his chance-determined structures to achieve [certain sounds]” (Piekut 2011, 47). Benedict Weisser suggests that each Number Piece “deliberately aspires to be different” and describes Cage’s “growing interest in hearing a ‘result’ within certain boundaries” as he was composing the Number Pieces (Weisser 2003, 206 and 210).
[10.3] By analyzing this composition, I have merely sought to identify some of these “boundaries.” The analysis of an indeterminate work is a unique opportunity to discover both what is possible, and what else is possible—in other words, what typically results from the situation that Cage delineates, and how widely the results might vary in outlier performances. By acknowledging Cage’s musical preferences, and the fact that he upheld them in ways that seemed to contradict his stated methods and goals, we productively denude his work of its aura of impenetrability and encounter, as if for the first time, its architecture and its moving parts.
[10.4] In the course of defending the analysis of Cage’s works, Rob Haskins acknowledges that “any analytical description of his music can never account for the multiplicity of connections that exist, in part because those connections did not originate with the composer himself” (2009, 335). Yet a rigorous analysis of a work like Four2 uncovers a wealth of potential connections that, as Hünermann reminds us, “are subject to Cage’s compositional decisions, even if the details emerge from chance operations” (2014, 612). By returning to the two primary objections to the analysis of Cage’s compositions—the works’ inherent multiplicity and Cage’s compositional principle of non-intention—we may untangle these seemingly contradictory observations.
[10.5] Cage’s scores each set in motion a unique network of sounds, relationships, and decisions to be made that, while not always predictable in their results, are often aurally recognizable as a given composition, and in practice are treated as such. As Popoff has argued, the statistical approach is uniquely well suited to explicating the multiplicity of Cage’s Number Pieces because it treats the differences among multiple performances as complementary statistical probabilities (Popoff 2013, 3). By describing these possibilities in terms of the language of tonal harmony (or any other system), we do “impose an analysis,” but we do so in a way that is productive and consistent with contemporary music-theoretical scholarship, in which proof of a composer’s intention is not typically required to legitimize an empirical observation.
[10.6] In any case, Cage’s music offers a singular opportunity for performers to make musical decisions they would not be presented with in other works. By considering Four2 from the perspective of the performer in this study—in the guise of existing recordings, computer-simulated performances, and the interpretations of four invented conductors—I hope to have dramatized the multiplicity of the composition. However, as Hünermann argues, “chance,” like multiplicity, “does not just happen; it can only exist within a system, a surrounding order that is always produced by the composer” (2014, 599). Even though each performance of Four2 comprises dozens of individual determinations, each decision point is axiomatically contextualized by the composition. Indeterminate works like Four2 may admit a wider range of musical results than other compositions, but even these results’ latitude can be evaluated and understood in a broader musical context.
Appendix 1
Appendix 1 gives an original software program with which readers can edit and play back their own interpretations of Four2, generate random interpretations, or access and manipulate one of the fictional interpretations. This software is intended to provide an additional venue in which to explore the multiplicity of possible musical results of the piece. The software is a standalone application developed in Max/MSP which can be downloaded for Mac OS or Windows by following the instructions below.
Mac OS
Click here to download a ZIP file containing the application for Mac OS. Double-click the ZIP file to unzip it and double-click on the file CAGE-FOUR2.APP. Depending on the settings on your computer, you may have to CTRL+click to open the file. After the interface loads, click the button labeled “Instructions” in the lower-left corner of the interface for more information. A second smaller window labeled “Max” may also open; you can disregard any messages that may appear here.
System Requirements: OS X 10.5 or later and 1 GB RAM
Windows
Click here to download a ZIP file containing the application for Windows. Double-click the ZIP file to unzip it and double-click on the file CAGE-FOUR2.EXE within the folder. After the interface loads, click the button labeled “Instructions” in the lower-left corner of the interface for more information. A second smaller window labeled “Max” may also open; you can disregard any messages that may appear here.
System Requirements: Windows 7 or later and 1 GB RAM
Drake Andersen
The Graduate Center, City University of New York
365 Fifth Avenue
New York, NY 10016
dandersen@gradcenter.cuny.edu
Works Cited
Baldwin, Brent. 2016. Personal communication to author, November 22, 2016.
Brooks, William. 1982. “Choice and Change in Cage’s Recent Music.” In A John Cage Reader: In Celebration of His 70th Birthday, ed. Peter Gena and Jonathan Brent, supplementary ed. Don Gillespie, 82–100. C. F. Peters.
—————. 2014. “In re: Experimental Analysis.” Contemporary Music Review 33 (5/6): 539–55.
Cage, John. 1961. Silence. Wesleyan University Press.
Dohoney, Ryan. 2014. “John Cage, Julius Eastman and the Homosexual Ego.” In Tomorrow is the Question: New Directions in Experimental Music Studies, ed. Benjamin Piekut, 39–62. University of Michigan Press.
Gresser, Clemens. 2014. “Structured Silence as a Compositional Idea in Some of Cage’s Number Pieces.” Contemporary Music Review 33 (5/6): 580–96.
Hammersley, J. M. and D.C. Handscomb. 1964. Monte Carlo Methods. Methuen.
Haskins, Rob. 2004. “’An Anarchic Society of Sounds’: The Number Pieces of John Cage.” PhD diss., Eastman School of Music.
—————. 2009. “On John Cage’s Late Music, Analysis and the Model of Renga in ‘Two.’” American Music 27 (32): 327–55.
—————. 2010. “John Cage and Recorded Sound: A Discographical Essay.” Notes 67 (2): 382–409.
Hünermann, Tobias. 2014. “‘Back from Weather Which Had Been Reached to Object’: John Cage’s Number Pieces Two (1987) and Four2 (1990).” Contemporary Music Review 33 (5/6): 597–615.
John, Emily. 2012. “The Choral Music of John Cage.” The Choral Journal 53 (5): 66–76.
Kiørbye, Thomas. 2016. Personal communication to author, November 21, 2016.
Kostelanetz, Richard. 2003. Conversing with Cage. Routledge.
Lindau, Elizabeth Ann. 2014. “Goodbye 20th Century!: Sonic Youth Records John Cage’s ‘Number Pieces.’” In Tomorrow is the Question: New Directions in Experimental Music Studies, ed. Benjamin Piekut, 15–38. University of Michigan Press.
Lochhead, Judith. 1994. “Performance Practice in the Indeterminate Works of John Cage.” Performance Practice Review 7 (2): 233–41.
Piekut, Benjamin. 2011. Experimentalism Otherwise. University of California Press.
—————. 2013. “Chance and Certainty: John Cage’s Politics of Nature.” Cultural Critique 84: 134–63.
Popoff, Alexandre. 2010. “John Cage’s Number Pieces: The Meta-Structure of Time Brackets and the Notion of Time.” Perspectives 48 (1): 65–82.
—————. 2011. “Indeterminate Music and Probability Spaces: The Case of John Cage’s Number Pieces.” In Mathematics and Computation in Music: Third International Conference, MCM 2011 Proceedings, Paris, June 15–17, 2011, 220–29. Springer.
—————. 2013. “John Cage’s Number Pieces as Stochastic Processes: A Large-scale Analysis.” arXiv:1311.5853v1.
—————. 2015. “A Statistical Approach to the Global Structure of John Cage’s Number Piece Five5. In Mathematics and Computation in Music: Fifth International Conference, MCM 2015 Proceedings, London, June 22–25, 2015, 231–36. Springer.
Pritchett, James. 1993. The Music of John Cage. Cambridge University Press.
Sluchin, Benny and Mikhail Malt. 2012. “A Computer Aided Interpretation Interface for John Cage’s Number Piece Two5.” Paper presented at Actes des Journées d’Informatique Musicale (JIM 2012), Mons, Belgique, May 9–11, 2012, 211–17.
Steighner, Mark. 1991. Unpublished correspondence with John Cage, January 31, 1991.
—————. 2016. Personal communication to author, November 12, 2016.
Weisser, Benedict. 1998. “Notational Practice in Contemporary Music: A Critique of Three Compositional Models (Luciano Berio, John Cage, and Brian Ferneyhough).” PhD diss., The City University of New York.
—————. 2003. “John Cage: ‘. . .The Whole Paper Would Potentially Be Sound’: Time-Brackets and the Number Pieces (1981–92).” Perspectives of New Music 41 (2): 176–223.
Discography
Discography
Cage, John. 1999. The Complete John Cage Edition, Volume 18: The Choral Works 1. Vocal Group Ars Nova, conducted by Támas Vetö. Mode 71. CD.
—————. 2013. Mythes Étoilés. Latvian Radio Choir, conducted by Sigvards Klava. B00F3RJ6HS. CD. (https://www.youtube.com/watch?v=IxSAhnzZXfE)
—————. 2015. Rothko Chapel. Houston Chamber Choir, conducted by Robert Simpson. ECM New Series. CD.
“Four2, de John Cage, por el Estudio Coral de Buenos Aires.” YouTube video, 7:16. Posted by “Bahia Cesar,” August 19, 2016. https://www.youtube.com/watch?v=P7Gj-rCFz0w. (Estudio Coral de Buenos Aires conducted by Carlos López Puccio in 2016).
“’Four 2’ John Cage. EEVA.” YouTube video, 7:09. Posted by “eevavocal,” October 30, 2011. https://www.youtube.com/watch?v=-skB08-CUwY. (Ensemble de Exploración Vocal de los Andes conducted by Carolina Gamboa Hoyos in 2011)
“John Cage - Four2 for SATB choir (1990).” YouTube video, 6:54. Posted by “not looking for New England,” July 17, 2016. https://www.youtube.com/watch?v=BxFIYBrPBpc. (RIAS Kammerchor conducted by Florian Helgath in 2015)
“Soundstreams presents ‘Four2’ (1990) by John Cage.” YouTube video, 7:06. Posted by “Soundstreams,” July 30, 2013. https://www.youtube.com/watch?v=oz-2G7GTlY8. (consortium of Canadian and Latvian choirs conducted by Kaspars Putniņš in 2012)
Footnotes
* I am grateful to Joseph Straus, Philip Lambert, Nils Vigeland, and the two anonymous reviewers for their valuable comments on earlier drafts of this essay.
Return to text
1. Cage composed a series of forty-seven works, from 1987 until his death in 1992, characterized by “radical simplicity” of content and the use of time-bracket notation (Weisser 2003, 191). These compositions are known as the Number Pieces because their titles refer to the number of parts and the order in which each piece was composed. For instance, Four2 is the second piece for four parts in the series. For more on Cage’s Number Pieces (and his time-bracket notation in general), see Weisser 2003, Haskins 2009, and Pritchett 1993, 199–204.
Return to text
2. For a typical argument against “evaluative” analysis of Cage’s works, see Brooks 2014.
Return to text
3. A Monte Carlo simulation is a computational technique in which random sampling is used to model the behavior of systems that are complex or otherwise difficult to predict. Random sampling is typically repeated over many trials to produce better results. In this case, Cage’s time-bracket structure is randomly determined by the computer over many trials. For a concise and general introduction to this technique, see the first three chapters of Hammersley and Handscomb 1964.
Return to text
4. For a detailed discussion of Cage’s time brackets and the compositional process for Four2, see Hünermann 2014.
Return to text
5. To produce sounds lasting for longer than one’s breath allows, in the performance directions Cage suggests that performers within the same section may stagger breathe while treating each choral part as a whole.
Return to text
6. While Popoff employs a Gaussian distribution in his 2013 study, he uses a uniform distribution in an earlier article in order to project a Cagean ideal of “full randomicity” that is “devoid of any bias” (Popoff 2010, 70). Although using different flavors of randomness might seem to introduce an additional (and unnecessary) variable, Popoff asserts that “the results of the analysis of the Number Pieces do not depend on a large scale on the distribution chosen for the realization of the time brackets” (Popoff 2013, 5). For a comparison of different distributions and their potential to reflect human decision-making processes, see Popoff 2011.
Return to text
7. See Haskins 2004, 138–64; Weisser 2003, 200–1; and Brooks 1982, 94–8. See also Weisser 2003, 191 for a more general discussion of the ways in which the Number Pieces diverge from Cage’s previous compositions.
Return to text
8. My purpose in projecting these defined musical priorities is illustrative and not intended as a model of performance practice. However, alternative approaches to the performance of Cage’s Number Pieces—such as Sonic Youth’s recordings, in which the performers interpret Cage’s instructions rather freely, explicitly frame the performance as an improvisation, and at times intentionally seek to achieve specific musical results—potentially represent a “compelling new performance practice,” according to musicologist Elizabeth Ann Lindau (2014, 15). Although some argue that such performances are not “correct,” many performances and recordings of Cage’s Number Pieces are facilitated by subtle (or not-so-subtle) workarounds, as will be evident in the discussion of performance practice below (Lindau 2014, 20).
Return to text
9. Actua’s interpretation begins with about thirty seconds of silence; this silence is preserved in the MIDI rendition.
Return to text
10. This flowchart is modeled after a representation of transitions between pitch-class sets in Popoff 2013, 18–19.
Return to text
11. My transcriptions reflect the elapsed time of the recordings, but because each recording is less than seven minutes in duration, it is possible that the starting point of a given recording does not correspond to 0’00” of Cage’s time-bracket structure. Because of this uncertainty, these transcriptions cannot be compared directly with Cage’s seven-minute time-bracket structure (as illustrated in Example 2). In any case, they do provide a general sketch of the succession of musical relationships, and the uncertainty does not affect the distributions given in Example 28.
Return to text
12. These recordings are listed in the discography at the end of this article.
Return to text
13. Because the fictional conductors’ interpretations were generated by hand specifically for the purposes of this study, my analysis here focuses on comparing the recordings and the simulation data, which were conceived independently of one another. I will note, however, that I analyzed the density distributions of the fictional conductors’ interpretations only after they were complete, and did not subsequently alter or revise them.
Return to text
14. For example, see Gresser 2014 and Haskins 2004, 10.
Return to text
15. The histograms in Example 32 can also be thought of as vertical cross sections of the data in Example 29, with vertical relationships between the different density profiles from bottom to top now expressed from left to right.
Return to text
16. These observations were verified using the statistical computing software R (https://www.r-project.org/).
Return to text
17. This method is a useful heuristic, but is obviously not without flaws. Inevitably included with the category of sc (037)-related set classes (and thus treated as equivalent) are pitch class sets that are not subsets of the three triads discussed above, such as the major third between the soprano’s final F and the alto’s final
Return to text
18. As discussed above, the 5-second overlap between the bass’s C and the alto’s
Return to text
19. The pc set [012] is not possible as a simultaneity, but it comes tantalizingly close, as the tenor’s time bracket for D ends at 5’40”, just five seconds before the bass’s time bracket for C begins at 5’45”, and assuming that the alto is sustaining
Return to text
20. For example, see Sluchin and Malt 2012 for a computer-assisted interface for the performance and analysis of Two5, and Haskins 2004, 271 for a discussion of software proposed by Laura Kuhn that would automatically generate versions of Cage’s Number Pieces.
Return to text
21. Cage did occasionally call for performers to listen to one another. Haskins 2004 offers the example of Four4, in which performers listen to one another to avoid obscuring quiet sounds (271). I am not aware of any such instruction pertaining to Four2.
Return to text
22. See Lindau 2014 for a general discussion of “composer-sanctioned” recordings and performances of Cage’s works. For other specific instances, see Piekut 2011, ch. 1 on Cage, David Tudor, and the New York Philharmonic; Piekut 2011, ch. 4 on Cage and Charlotte Moorman; and Dohoney 2014 on Cage and Julius Eastman.
Return to text
Copyright Statement
Copyright © 2017 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
13446