Was Mesopotamian Tuning Diatonic? A Parsimonious Answer*
Jay Rahn
KEYWORDS: tuning, Mesopotamia, Greek Antiquity, psychoacoustics, plucked strings, diatonic scale
ABSTRACT: On the basis of assumptions and conclusions first advanced in 1968 concerning tuning instructions that were originally written down ca. 1800 BCE, Assyriologists have agreed that Mesopotamian tuning was diatonic. Nonetheless, Sam Mirelman (2013) has recently suggested that this consensus view is “uncomfortably familiar and Eurocentric.” As a follow-up to Mirelman’s misgiving, the present report begins by identifying flaws in the reasoning concerning Mesopotamian tuning that was disseminated more than half a century ago and have remained uncontested. The starting point of the present study is information directly recorded in Mesopotamian documents, as opposed to concepts dating from Greek Antiquity and beyond. This information includes the spatial ordering of strings and the relative fundamental frequencies of two pairs of strings on the sammû, a harp or lyre that is explicitly identified in cuneiform tablets, as well as the tuning instructions’ recursive and symmetrical patterning of prescriptions concerning the alterations of this instrument’s strings. At each step, this patterning involves loosening or tightening a string that is three or four strings away from the string that had just been tightened or loosened. Added to these observations are acoustical features of the harmonics produced by plucked strings, and the auditory roughness and smoothness produced by pairs of plucked strings that psychoacoustical studies have established as universally audible. On these bases, one can conclude that Mesopotamian tuning can be interpreted as diatonic in structure without assuming such notions as octave identity, scale degrees, and consonance, all concepts for which there is no known testimony until much later in the history of music theory.
DOI: 10.30535/mto.28.1.7
Copyright © 2022 Society for Music Theory
[1] As David Creese has reported, there is no direct evidence that the monochord existed prior to the Annals of Duris or the Sectio Canonis, both of which seem to have been written no earlier than ca. 300 BCE (2010, 97–103, 132–34). For an understanding of Mesopotamian tuning, which is documented ca. 1800 BCE, i.e., long before the Hellenic era, this absence of evidence poses potential difficulties. To be sure, Creese suggests that the small whole-number ratios of later monochord theory might have been realized somewhat earlier than 300 BCE by measurements applied to the manufacture of metal discs or panpipes (syringes) in Ancient Greece (2010, 93–97). However, as there is no evidence of such devices for tuning in Mesopotamia 1500 years earlier, the present study focuses on the possibility that Mesopotamian tuning was realized entirely by ear; specifically, by careful attention to the sounds of pairs of strings plucked simultaneously. In doing so, this account addresses an important misgiving recently raised by Sam Mirelman.
[2] Since a seminal study by David Wulstan (1968), the consensus view of Mesopotamian tuning has been that it was diatonic, comprising seven scale degrees, among which all but one of the 4ths and 5ths were perfect and the remaining 4th or 5th was, respectively, augmented or diminished. Indeed, this formulation has entered unchallenged into general accounts of music history for non-specialist readers (e.g., Taruskin 2010). However, as Mirelman has remarked, “We cannot be sure that such an interpretation is correct. Indeed, it seems uncomfortably familiar and Eurocentric” (2013, 54). In this regard, Wulstan approached original sources of Mesopotamian tuning from the vantage-point of Greek theory post-300 BCE.
The following account proceeds in several sections:
- A critical analysis of flaws in Wulstan’s original formulation that previous studies have not yet addressed;
- Formulation of a mathematical structure implicit in the only Mesopotamian sources that treat tuning in detail and that hinge on a single contrast between kinds of sounds produced by pairs of plucked strings;
- An acoustical and psychoacoustical interpretation of this contrast and its semantic counterparts in Mesopotamian writings and findings of more recent experimental and ethnological research;
- Constraints on the mathematical structure of section B that Mesopotamian sources directly imply concerning the fundamental frequencies produced in the course of tuning;
- Consequences of all the possible ways in which the interpretation of section C might be combined with the constraints of section D, leading to a single conclusion concerning Mesopotamian tuning; and
- A discussion summarizing the main bases of the reasoning in sections B to E and the possible relevance of the present study for understanding parallels between Mesopotamian tuning and tuning in Greek Antiquity.
A. Wulstan’s Interpretation of Mesopotamian Tuning
[3] At one point, Wulstan said, albeit somewhat noncommittally, “We may perhaps again make the assumption that there was a close correspondence between the Greek and Babylonian systems, at least as a working hypothesis” [emphases added] (1968, 218). Less vaguely, Wulstan also claimed, citing Plutarch’s [De Animae Procreatione] In Timeo, “It can also be assumed that the consonances of the fourth and fifth, together with the octave, were recognized in the Near East” [again, emphasis added] (1968, 217). Unfortunately for Wulstan’s assumption concerning Plutarch, the passage from In Timeo actually relates only that Pythagoras studied with “Zaratas,” i.e., Zoroaster (Goodwin 1874, 327–28). Understood narrowly, Plutarch’s comment is problematic both in general, as the period in which Zoroaster flourished has not yet been established (West 2013, 89–105), and in particular, as nothing is known directly of Zoroaster’s putative involvement with Pythagoras or with consonant fourths, fifths, and octaves.
[4] Understood more broadly as supporting a claim that Pythagoras brought to Greek civilization a formulation of consonant fourths, fifths, and octaves he had encountered in Persia or Mesopotamia, Wulstan’s citation of Plutarch is additionally problematic. No musical writings by Pythagoras or contemporary with Pythagoras are known, and Plutarch, a philosophical advocate of neo-Pythagoreanism and associated Orientalizing lore, lived more than five centuries after Pythagoras (Karamanolis 2020; Huffman 2019). Even more broadly, Zoroastrians, rather than Zoroaster, and Pythagoreans, rather than Pythagoras, might have come into close contact concerning tuning theory, e.g., as a result of Alexander the Great’s campaign against Persia (334–27 BCE) or as a consequence of the Greco-Persian Wars (fifth century BCE). However, such an historical relationship would require actual evidence in order for one to conclude that “the consonances of the fourth and fifth, together with the octave, were recognised in the Near East” without arguing proleptically backward from Ancient Greek tuning to a formulation of Mesopotamian tuning almost two millennia earlier (Wulstan 1968, 217).
[5] As a further basis for “at least a working hypothesis,” if not an assumption, that there was “a close correspondence between the Greek and Babylonian systems,” Wulstan referred to “trumpet-type and other instruments having notes of the ‘harmonic series’” (217–18) as evidence that the consonant third and sixth were recognized in the Near East. To be sure, the page Wulstan cited in Lavignac and de la Laurencie’s 1913 Encyclopédie (vol. 1, p. 41) reproduces part of a drawing published by Austen Henry Layard (1849–53, pl. 15; Rawlinson 1871, 538–39) that was based on an Assyrian relief from the seventh century BCE. However, the relevance of the trumpet-shaped detail depicted in the relief to tuning instructions for a stringed instrument written more than a thousand years earlier is far from obvious.
[6] In general, very little is known about trumpets in Mesopotamia. This very rare instance of a long trumpet from Mesopotamia was probably used in signalling for the workers shown in Layard’s image. There are also a couple of Early Dynastic (mid-third millennium BCE) instances of images that probably depict some form of trumpet or horn (see, e.g., the entry “Trompete” in Eberling et al. 2018, 144–46). In any event, the narrow straight shape of Layard’s drawing corresponds to the Egyptian trumpets found in Tut’ankhamūn’s tomb (ca. 1323 BCE) and the subject of a famous BBC radio broadcast in 1939 (James [1939] 2010 [1939] 2010). Although such instruments might have had Mesopotamian counterparts four centuries earlier, organological analysis of the single playable instrument from Ancient Egypt (Montagu 1978 and 2017) has concluded that it would be unlikely for one to produce more than three pitches. Furthermore, such instruments enter Wulstan’s account only in his argument concerning 3rds and 6ths, which was based “on the assumption that the Babylonian scale was similar to that of the Greater Perfect (Changeless) System of Ptolemy” [emphasis added] (Wulstan 1968, 218–20), whose Harmonics (2nd century CE) was based in turn on the monochord. In short, Wulstan concluded that such intervals would not realize a Pythagorean cycle of perfect 4ths and 5ths, which he regarded as implicit in the Mesopotamian tuning instructions.
[7] Wulstan closed his discussion of particular intervals with the claim that “as opposed to seconds and tritones, [the 3rds and 6ths and the perfect 4ths and perfect 5ths of later tuning] can be tuned accurately by ear” (1968, 218). In contrast to Wulstan’s claim concerning intervals that can be tuned accurately by ear, lyres and harps of Ganda court music in East Africa have been traditionally tuned aurally to a “pen-equidistant” scale in which each step is close to one-fifth of a perfect octave, i.e., approximately \(\frac{1200}{5} = 240\ \text{cents}\) (Wachsmann 1950; Gray 1993). In addition, Rytis Ambrazevičius has shown that a majority of scales in aurally transmitted tuning of traditional Lithuanian fiddle music are closer to equiheptatonic tuning, where the size of each step is approximately one-seventh of an octave (i.e., \(\frac{1200}{7} = \text{~}171\ \text{cents}\)), than to diatonic tuning (2017, 51). Ambrazevičius has reported similar results for traditional aurally transmitted polyphonic singing of Lithuania where there is “a distinct equitonic structure of scale steps” (2014, 41). Further, the present author (Rahn 2019) has shown that Burmese harp tunings, realized traditionally by ear, have comprised “small” and “Large” steps arranged systematically with variants that are, respectively, “tiny” and “medium,” and “Broad.” With regard to European-derived concert music, vocalists and performers of stringed instruments have accurately tuned 2nds and tritones by ear for centuries. Also, Wulstan’s notion of intervals “tuned accurately by ear” begs the question of how one would distinguish between accurate and inaccurate tuning. In this regard, perceptual experiments have long established that, at least for musicians trained in European-derived idioms, perception is “categorical,” insofar as identifying out-of-tune-ness is least probable for intervals whose fundamental-frequency ratios are close to “prototype” values. For instance, in terms of Alexander Ellis’s unit for measuring the magnitude of any interval (Helmholtz 1885, 446–51), the cent, i.e., one hundredth of a tempered semitone, the ideal value of a tempered major 3rd, i.e. four tempered semitones, is 400 cents. In contrast, out-of-tune-ness is most probable near “border” values, e.g., 350 and 450 cents (Aruffo et al. 2014, 187–88). In other words, probability and ranges of values are involved rather than crisp, either-or distinctions.
[8] Notwithstanding Wulstan’s anachronistic reasoning, organologically dubious claim, and vague generalization about interval perception, he touched on a less presumptuous basis for interpreting the Mesopotamian tuning instructions, stating that the 3rds, 6ths, and perfect 4ths and 5ths of subsequent European music “are the scientifically, and more important, aurally consonant intervals” (1968, 218). On one hand, recent research has shown that important determinants of “consonance” include “familiarity,” i.e., the extent to which certain intervals have been employed in a particular socio-cultural setting (Eerola and Lahdelma 2021); such information has been unavailable for Mesopotamian music. On the other hand, and especially because Wulstan did not follow through carefully on his idea of scientific and aural aspects of tuning, the present report includes an acoustical and psychoacoustical account of such pairs of tones with a view to determining what Mesopotamian tuning sounded like. Most importantly, to avoid relying on “uncomfortably familiar and Eurocentric” assumptions and arguments, this study shows that certain mathematical, acoustical, and psychoacoustical aspects of tone-pairs that are not culturally specific have counterparts in a distinction between pairs of tones that the Mesopotamian tuning instructions identified as zakû and la-zakû. As this distinction played a decisive role within the Mesopotamian tuning instructions’ mathematically coherent framework, the following discussion focuses on the structure of this framework before proceeding to the distinction between zakû and la-zakû.
B. The Modulo-7 Framework Implicit in the Tuning Instructions
Example 1. Numbers and names of strings
(click to enlarge)
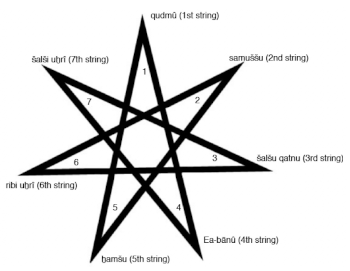
[9] Rather than pitches or abstract pitch classes, Mesopotamian tuning was formulated concretely in terms of strings. On being plucked, a string produces a harmonic spectrum, and among its partials the first, lowest harmonic, i.e., the spectrum’s fundamental frequency, is heard as the string’s pitch. Cuneiform tablets Nabnitu 32 (=U 3011=UET VII 126) and N. 4782, provide names and locations for nine strings from the front to the back of a lyre or harp. (Whereas Mirelman and Theo J. Krispijn [2009, 45] as well as Mirelman [2010, 49–51] have argued that the instrument, termed “sammû” in Akkadian, was a lyre, the following discussion is agnostic on this point and generally refers to the instrument merely as “the instrument.”) Example 1 gives numbers from 1 to 9 for these locations and names in the same order as the tablets’ nine lines.(1)
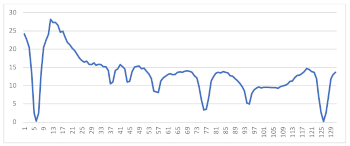
Example 2. Numbers and names of three- and four-string-step dichords
(click to enlarge)
[10] Example 2 shows another cuneiform tablet.(2) CBS 10996 provides names for 14 pairs of strings—termed “dichords” here, rather than “intervals” as in more recent music theory—and identifies the two strings of each dichord by means of the first seven string-numbers specified in the lists of Nabnitu 32 and N. 4782. Whereas each of the even-numbered dichords (i.e., the 2nd, 4th,
Example 3. La-zakû dichords in seven named tunings
(click to enlarge)
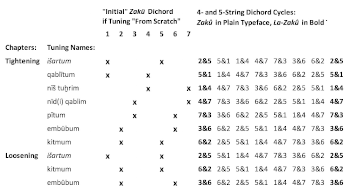
[11] Two cuneiform tablets, British Museum U. 7/80 = UET VII 74(3) and UET VI/3 899(4) convey prescriptions for turning any one of the seven tunings they identify by name into any of the other six named tunings by altering one of the first seven strings. (Note that the present account refers to “tunings” rather than to “scales” or “modes” of subsequent music theory.) In these tablets, there are two sets of prescriptions, termed “chapters” by Oliver Gurney (1968, 230–231). In the first chapter, strings are to be altered in the following order: 5, 1, 4, 7, 3, 6, and 2. In the second chapter, strings are to be altered in the opposite order as follows: 2, 6, 3, 7, 4, 1, and 5. Example 3 displays la-zakû dichords in seven named tunings. To be sure, not all of the prescriptions for these string alterations have survived, for UET VII 74 and UET VI/3 899, like many other Mesopotamian sources, are broken clay tablets. Nonetheless, what remains of the tuning prescriptions is patterned recursively and symmetrically. It is not merely a matter of altering the strings in the order just described. More precisely, a string is to be altered in the first chapter only if it is the higher-numbered string of a four-string dichord (e.g., string 6 of dichord 3&6) or the lower-numbered string of a five-string dichord (e.g., string 2 of dichord 6&2). A string is to be altered in the second chapter only if it is the higher-numbered string of a four-string dichord (e.g., string 6 of dichord 2&6) or the lower-numbered string of a 4-string dichord (e.g., string 2 of dichord 2&5). Of further significance, the photographs provided by Richard Dumbrill (2010, 110) and Mirelman (2013, 47) reveal there would originally have been room at the top of UET VII 74 (Dumbrill 2010, 110) for the instructions that Mirelman and Krispijn (2009, 44) have supplied in their reconstruction of the first chapter; similarly with regard to the second chapter, for which there would have been sufficient room at the bottom of both UET VII 74 and UET VI/3 899. A last critical detail to note is the order in which strings are altered in one chapter is the opposite in the other chapter. As a result, the ordering is recursive within the chapters and symmetrical between them: a mirror-like arrangement with reflection occurring at the alterations of strings 2 and 5.
Example 4. Acute, “great,” “star” heptagram
(click to enlarge)
[12] Successive strings in these orderings differ by three or four strings: e.g., \(5-1=4\); \(4-1=3\); \(7-4=3\); etc. In terms of a modulo-7 “clock,” as diagrammed by the acute, “great,” “star” heptagram or {7/3} polygon (Coxeter 1969, 36–38) inscribed on CBS 1766; the differences between the successive strings to be altered in the first chapter comprise three string-steps (see Example 4).(5) In a clockwise direction, there are three string-steps from 5 to 1: 5 6 7 1. From 1 to 4 there are three string-steps (1 2 3 4), and so forth. In the opposite, counter-clockwise direction, successively altered strings in the second chapter are also three string-steps apart: from 2 to 6 (2 1 7 6), from 6 to 3 (6 5 4 3), and so forth.
[13] In both the clockwise and counter-clockwise orderings, three string-steps comprise the shortest distance between the successively altered strings. Accordingly, one can regard the pairs of successively altered strings as Mesopotamian counterparts to what would be termed a congruence class in modular arithmetic, or an undirected pitch interval in modern music theory—e.g., Rahn 1980, 29, and Straus 2016, 9—or in this instance, an undirected difference of three string-steps. On one hand, the undirected difference between string 5 and string 1 is the same as the undirected differences between strings 1 and 5, 1 and 4, 4 and 1, 2 and 5, 5 and 2, etc. On the other hand, the directed difference from string 5 to string 1 is the same as the directed differences from 1 to 4, 2 to 5, etc., but not the same as the directed differences from 1 to 5, 4 to 1, 5 to 2, etc. In the initial chapter of UET VII 74,(6) the string to be altered is always the 4th of the four strings that are spanned in a clockwise three-string-step dichord that is identified as la-zakû: e.g., 5 of 2 3 4 5 in the 2&5 dichord, 1 of 5 6 7 1 in the 5&1 dichord, and so forth. In the second chapter, contents of which have survived in both UET VII 74 and UET VI/3 899, the string to be altered is always the 1st: e.g., 2 of 2 3 4 5 in the 2&5 dichord, 5 of 5 6 7 1 in the 5&1 dichord, and so forth.
[14] The pattern of alterations and the named tunings to which they are applied imply that alterations made in the first chapter are consistently undone in the second chapter. For example, the first chapter’s prescription for turning embūbum tuning into kitmum tuning involves changing string 6, and the second chapter’s prescription for turning kitmum tuning into embūbum tuning also involves string 6. Similarly, string 2 is altered to turn kitmum tuning into išartum tuning in the first chapter, and to turn išartum tuning into kitmum tuning in the second chapter, and so on for all the other tunings in the two chapters. Accordingly, one can consider the alterations in the first chapter to be the opposite of their counterparts in the second chapter. Insofar as only one of the first seven strings is altered in each instance, one can conclude that an alteration in one of the chapters would increase the string’s fundamental frequency, and the corresponding alteration in the other chapter would decrease the string’s fundamental frequency.
7-Fold Cycles of Three-String-Step Dichords
[15] UET VII 74 and UET VI/3 899 frame their prescriptions solely in terms of changing individual tunings among the seven named tunings into others of the seven. In this regard, an important feature of each of the seven tunings is that, as shown in Example 3, above, these cuneiform sources identify one, and only one, of its seven three-string-step dichords as la-zakû. As well, the cumulative, recursive effect of the order in which UET VII 74 and UET VI/3 899 list their prescriptions ensures that the remaining six three-string-step dichords in each tuning are zakû (Rahn 2011, 208–13). As Hans Martin Kümmel (1970, 260–61) observed, an additional consequence of the seven tunings’ structure is that each could be tuned “from scratch” by iterating six zakû three-string-step dichords. For example, one could realize the tuning named išartum by means of the following clockwise cycle of 6 zakû dichords:
$$ 5\text{&}1 \quad 1\text{&}4 \quad 4\text{&}7 \quad 7\text{&}3 \quad 3\text{&}6 \quad 6\text{&}2 $$Construed according to a clockwise ordering of strings, these three-string-step zakû dichords could be iterated in the following, string-by-string manner:
$$ 5\ 6\ 7\ 1 \quad 1\ 2\ 3\ 4 \quad 4\ 5\ 6\ 7 \quad 7\ 1\ 2\ 3 \quad 3\ 4\ 5\ 6 \quad 6\ 7\ 1\ 2 $$Alternatively, išartum could be realized as follows:
$$ 2\text{&}6 \quad 6\text{&}3 \quad 3\text{&}7 \quad 7\text{&}4 \quad 4\text{&}1 \quad 1\text{&}5 $$which corresponds to the following, counter-clockwise ordering, string-by-string:
$$ 2\ 1\ 7\ 6 \quad 6\ 5\ 4\ 3 \quad 3\ 2\ 1\ 7 \quad 7\ 6\ 5\ 4 \quad 4\ 3\ 2\ 1 \quad 1\ 7\ 6\ 5 $$Whereas both orderings of zakû three-string-step dichords result in the initial tuning of both chapters of UET VII 74 and UET VI/3 899, namely, išartum, išartum is not only the name of this tuning. išartum is also the name of the 2&6 dichord (Example 2, above), which is the first of the six zakû three-string-step dichords in the counter-clockwise generation of išartum as a named tuning. The same holds for the name of each tuning and the name of the first dichord in its counterclockwise generation.
7-Fold Cycles of Named Tunings
Example 5. Realizing seven tunings “from scratch”
(click to enlarge and see the rest)
[16] As illustrated in Example 5, the seven tunings could, in principle, cycle endlessly within the first chapter and endlessly within the second chapter.(7) Moreover, since the instrument is in išartum tuning at the end of the initial chapter and at the beginning of the subsequent chapter, all seven tunings could cycle endlessly through both chapters. A further consequence of the tuning instructions’ provision of opposite changes in the two chapters would be that no two tunings would have been farther apart than three re-tunings. For example, qablītum could be turned into embūbum via išartum and kitmum in the second chapter rather than via nīš tuhrim, nīd(i) qablim, and pītum in the first chapter. This aspect of the larger cycle that comprises both chapters could be of practical consequence, for re-tuning a smaller number of strings would reduce the effect of altering tension on the instrument’s individual strings. Especially in the case of a lyre, the resulting economy of string adjustments might well have minimized changes to the instrument’s stability (cf., e.g., concerning Ancient Greek lyres, Roberts 1981, 311 and Trosch 2015, 6–7).
C. Sounds Produced by Plucked Strings
[17] The modulo-7 framework discussed above is couched solely in terms of seven-named strings, natural numbers assigned to the seven strings on the basis of their location on the instrument, named pairs among these seven strings that span three counterclockwise string-steps, and two adjectives, zakû and la-zakû, that characterize these three-string-step pairs. In the latter regard, accounts of the tuning instructions have generally translated the Mesopotamian word “zakû” as “clear”or, in German, “rein” (Kümmel 1970, 255–62), which in English can correspond to “clear,” “pure” or “clean.” Each of these terms denotes a state of positive value, or “positive evaluation” in Charles Osgood’s cross-cultural findings concerning the “semantic differential” (1964, 172–184; Osgood et al. 1975). Further, each is matched in the translations by an opposite or complementary state of negative valence: for la-zakû, “unclear,” “impure,” or “unrein.”
[18] Of particular relevance here is Mesopotamian usage, for which Yitzhaq Feder (2014, 93) has reported the following contrasts between zakû and la-zakû in Akkadian writings: clear vs. cloudy or polluted as in water or beer, refined and uniform in composition vs. adulterated as in metals, and free vs. confined as of birds or persons. In each instance, the contrast between zakû and la-zakû correspond to positive vs. negative valence. Moreover, contexts for zakû involve a process, specifically one of clarification, refinement, or liberation, as opposed to a final result, as would clarity, purity, and freedom. Most important, such a process would involve a single change (e.g., uncleansed to cleansed) rather than several successive changes (e.g., uncleansed to cleansed to uncleansed to cleansed
[19] The tuning instructions employ the distinction between zakû and la-zakû in all (and only in) instances when they prescribe altering one string of a particular three- or four-string-step la-zakû dichord to change it into a zakû dichord and, as a consequence, one named tuning into another named tuning. This process is conveyed in one of the following ways, which are effectively equivalent:
If the instrument is in 3&7 tuning and the 6&3 dichord is la-zakû, you [alter] the 6th string and the 6&3 dichord will become zakû.
If the instrument is in 6&3 tuning and you play a la-zakû 2&6 dichord, you [alter] the 6th string and the instrument is in 3&7 tuning (see Mirelman and Krispijn 2009, 45).
Specific kinds of alteration are discussed below.
[20] Clearly, altering a string would raise or lower its fundamental frequency. Two aspects of a dichord would change if one of its strings’ fundamental frequencies was raised or lowered: the magnitude of the interval the dichord produces, which would correspond acoustically to its fundamental-frequency ratio, and its timbre or tone quality, which would correspond acoustically to its spectrum. As no device for measuring fundamental frequencies or fundamental-frequency ratios is known to have existed until more than a millennium later, it is quite plausible that timbre would provide an alternative basis for understanding what “zakû” and “la-zakû” referred to. Rather than a contrast between the magnitudes produced by a pair of strings, the difference between la-zakû and zakû could have been understood primarily as an audible contrast between timbres produced by a single pair of strings. More specifically, such a contrast could have depended on an acoustical contrast between the spectra produced when a pair of strings was plucked simultaneously more than once. Accordingly, the spectra that would be produced when a pair of strings was plucked could serve to illuminate the tuning instructions.
[21] Concerning the instrument employed to realize the tuning instructions, several aspects are unknown. These include the location on each string at which it was plucked, the direction and force of plucking, and the resonance of the instrument’s soundbox. Also unknown are the lengths of its strings as well as the mass of each string, its stiffness, and the amount of tension applied to it. In contrast, each of the latter features is effectively uniform for the subsequent monochord, because every tone was produced on a monochord by plucking a single string whose tones were resonated by a soundbox of uniform dimensions, and lengths along the string were determined by careful measurements.
Audio Example 1. 11 pairs of simultaneous tones whose waveforms are displayed in Example 6
Example 6. Waveforms of 11 pairs of simultaneous tones
(click to enlarge)
[22] Despite such limitations, one can be quite certain of some general features of the sound each string the Mesopotamian lyre or harp would produce. Acoustical research since Hermann von Helmholtz’s seminal treatise (1877; 1885) has confirmed that a plucked string produces several component waves, i.e., “partials” (Nave 2020), the frequencies of which are very close to whole-number multiples, i.e., “upper harmonics,” of its 1st partial’s frequency, i.e., its “fundamental frequency.” For example, a string whose fundamental frequency is 300 Hz, i.e., 300 cycles per second (near middle D4), produces, as its 2nd, 3rd, 4th, etc. harmonics, frequencies of approximately \(2 * 300=600\ \textit{Hz}\), \(3 * 300=900\ \textit{Hz}\), \(4 * 300=1200\ \textit{Hz}\), and so forth. Among these harmonics, the sound pressures or amplitudes of the first six tend to be greater than those that have higher frequencies.(8) In contrast, partials having higher frequencies mostly contribute to a tone’s “brightness” (CECM 2018). Accordingly, the tones employed in the audio demonstrations below comprise six partials of the same amplitude, as in Roel Plomp and Willem Levelt’s classic psychoacoustical study of pairs of simultaneous tones (1965, 556, Fig. 11). Audio Example 1, which consists of eleven pairs of simultaneous tones, is linked to Example 6, which comprises waveforms of the same eleven pairs of simultaneous tones, each of which contains six “harmonic” partials.(9)
[23] In Example 6, each pair of simultaneous tones caricatures how the sound of a pair of plucked strings changes, (i.e., its “envelope”), beginning with a sudden increase in perceived loudness that corresponds acoustically to a fairly rapid increase in sound pressure. During the remaining duration of each pair, perceived loudness decreases relatively slowly along with a decrease in total sound pressure. A comparison of Audio Example 1 and Example 6’s waveforms illustrates these changes in sound pressure. Listening to Example 1 while following along with Example 6 helps to understand these changes in perceived loudness for each of the eleven pairs. From the first pair to the eleventh pair, the lower tone remains the same in perceived pitch, which corresponds to it having a single fundamental frequency. In contrast, the other tones in the eleven pairs are successively higher in perceived pitch, corresponding to greater (i.e., faster) fundamental frequencies. Along with the increase in the upper tone’s fundamental frequency, there is an increase in the magnitude of the interval it forms with the lower tones. In this way, the tone-pairs of Example 6 illustrate sounds that might have been heard in Mesopotamia when tuning a pair of strings by plucking both simultaneously, gradually tightening one string to produce higher pitches while not changing the tension on the other. In this regard, a key aspect of the earliest known account of tuning in UET VII 74 and UET VI/3 899 is its repeated specification of altering one of the two strings of an individual dichord.
Roughness
[24] From the first to the eleventh pair of simultaneous tones illustrated in Example 6, there is not only a rise in the upper tones’ pitch and an increase in the magnitude of the intervals produced by the pairs of tones; there are also changes in the tone-pairs’ perceived tone quality or timbre. These changes correspond to a large-scale change from rougher to less rough timbre between the first and sixth tone-pairs and a similarly large-scale change from less rough to rougher timbre between the sixth and eleventh. For more than a century, the words “rough” and “roughness” have been the usual English translations of the technical terms “rauh” and “Rauhigkeit” that Helmholtz (1877, 192–93; 1885, 118–19) employed to describe this aspect of timbre. Perceiving such pairs of tones as more and less rough corresponds to, respectively, faster and slower acoustical interaction between one or more pairs of partials that comprise the sound waves of the two tones. Prominent within such roughness are relatively slow periodic fluctuations in loudness in the tone-pairs immediately before and after the 6th. These slow periodic fluctuations, which are discussed in the following section on “slow undulations”, are of considerable importance to understanding what someone playing a plucked-string instrument would have heard while tuning by ear in Mesopotamia, that is, without the guidance of such a device as the monochord.
[25] Modern measurements of the acoustical interactions that result in various amounts of perceived roughness have been based on several variables. These include 1) the absolute frequencies of the partials comprising the two simultaneously heard tones, 2), the differences between the frequencies of all the partials in the two tones within the limits of “critical bands” that have been traced to features of the cochlea (Fletcher 1940; Zwicker 1961), and 3) the amount of sound pressure in each of the tones’ partials (Plomp and Levelt 1965). Pantelis Vassilakis (2001, 26–45) has introduced a fourth variable for roughness measurement by calculating not just the absolute amounts of sound pressure in partials, but more precisely their relative amounts of sound pressure, observing that pairs of partials having the same amount of sound pressure result, ceteris paribus, in greater roughness than those having different amounts.
Example 7. Changes in roughness among 131 tone-pairs
(click to enlarge)
Audio Example 2. 131 pairs of simultaneous tones. The local minima occur at the following times: 15" (i.e., 15 seconds), 1'51"(i.e., 1 minute and 51 seconds), 2'12", 2'45", 3'45", 4'39", and 6'15"
[26] Example 7 and Audio Example 2 provide an overview of how roughness changes in tone-pairs the intervals of which range in magnitude from approximately a perfect prime (or unison) to approximately a perfect octave.(10) As in Example 6 and Audio Example 1, above, the fundamental frequency of one tone in each tone-pair is 300 Hz. Among the 131 tone-pairs, the other tone’s fundamental frequency ranges from ~291.46 Hz to ~617.58 Hz in increments of one-tenth of a tempered semitone, i.e., 10 cents. As graphed in Example 7, there are seven values at which the amount of roughness is at a local minimum. Measured in cents, the fundamental-frequency ratios of the local minima in Example 7 are as follow: 0, 320, 390, 500, 700, 880, and 1200. In turn, these values are close to the following fundamental-frequency ratios: 1/1, 6/5, 5/4, 4/3, 3/2, 5/3, and 2/1, whose logarithmic values, to the nearest cent, are, respectively, 0, 316, 386, 498, 702, 884, and 1200 cents. The latter fundamental-frequency ratios correspond to ideal magnitudes of the following intervals in much later European-derived music theory: respectively, perfect prime, minor 3rd, major 3rd, perfect 4th, perfect 5th, major 6th and perfect octave.
[27] In this regard, Richard Krantz and Jack Douthett (2011, 3–9), employing William Sethares’s (1993) parameterization of Plomp and Levelt’s roughness function, have shown how local roughness minima vary with the amplitudes of the lowest partials in a pair of tones. Whereas amplitudes tend to be smaller among higher harmonics, more local minima become salient as the amplitudes of all the harmonics approach a single value. If, for example, one tracks all of the first seven harmonics, one finds that local roughness minima in this cumulative process correspond to the following succession of fundamental-frequency ratios: 2/1, 3/2, 5/3, and 4/3. Only with considerable evening out of all the harmonics’ amplitudes are there local roughness minima that correspond to the fundamental-frequency ratios 5/4, 6/5, 7/4, and 7/6. Insofar as the first five harmonics are likely to play an important role in the roughness produced by pairs of plucked strings, the following discussion includes all five. In this regard, the 5th harmonic results in a local roughness minimum corresponding to the ratio 5/3, even if there is a relatively uneven distribution of amplitudes among the lowest harmonics. Accordingly, and with a view to avoiding confirmation bias, the 6th harmonic, which along with the 5th yields a local minimum corresponding to the ratio 6/5, is also included in the following discussion.
Slow Undulations
[28] The ratio of two tones’ fundamental frequencies corresponds to audible amounts of difference between them as whole, so that they are heard as a single pair of tones that has a particular magnitude or size, as in the distinction between a major 3rd and a minor 3rd. Yet at the same time, differences between the frequencies and sound pressures of two simultaneous tones’ constituent harmonic partials correspond to certain amounts of roughness. If the differences between two of the partials’ frequencies are relatively small and the sound pressures of these partials are both relatively large and similar in amount, the two tones are heard as a single pair of tones that has relatively slow undulations of loudness. These slow undulations occur at pairs of tones whose roughness is close to a local minimum and whose fundamental-frequency ratios are somewhat smaller or somewhat larger than such small whole-number ratios as 1/1, 6/5, 5/4, 4/3, 3/2, 5/3, and 2/1.
Example 8. Roughness and undulation near privileged ratios: 1/1, 2/1, 3/2, 5/3, 4/3, 5/4, and 6/5
(click to enlarge)
Audio Example 3. Seven privileged ratios: see Example 8
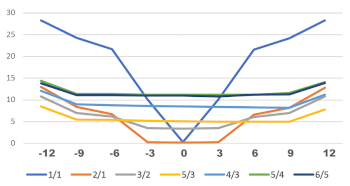
[29] Example 8 and Audio Example 3 focus more precisely than Example 7 on pairs of tones whose ratios coincide exactly with the privileged values 1/1, 6/5, 5/4, 4/3, 3/2, 5/3, and 2/1, and on pairs of tones whose ratios differ slightly from these. For each of the privileged ratios, Example 8 displays the amount of roughness produced by pairs of tones in which a particular harmonic partial of one tone has a frequency that differs by 12, 9, 6, 3, or 0 cycles per second from a particular harmonic partial of the other tone.(11) Such a difference results in an oscillation of sound pressure and a corresponding undulation of loudness at a rate of 12, 9, 6, 3, or 0 cycles per second. For instance, a tone whose fundamental frequency is precisely 450 Hz produces no undulation but still some residual roughness with a simultaneous tone whose fundamental frequency is precisely 300 Hz. If the fundamental frequency of the upper tone is \(450 \pm 1.5\ \textit{Hz}\), i.e., 448.5 or 451.5 Hz, its 2nd partial’s frequency is \(2 * 448.5=897\ \textit{Hz}\) or \(2 * 451.5=903\ \textit{Hz}\). It follows that this 2nd partial’s sound pressure produces with the sound pressure of the 300-Hz tone’s 3rd partial a loudness undulation of 3 cycles per second, since 897 Hz differs by 3 Hz from \(3 * 300=900\ \textit{Hz}\), and 903 Hz also differs from \(3 * 300=900\ \textit{Hz}\) by 3 Hz. Similarly, upper tones whose fundamental frequencies are 453 or 447, 454.5 or 445.5, and 456 or 444 Hz result in undulations of, respectively, 6, 9, and 12 cycles per second, as well as certain amounts of residual roughness. As Example 8 shows, tone-pairs whose fundamental frequencies coincide with the perfect-prime ratio (1/1) and the perfect-octave ratio (2/1) result in less residual roughness than those that coincide with the perfect-5th ratio (3/2). As well, those at the ratios for the major 6th (5/3), perfect 4th (4/3), major 3rd (5/4), and minor 3rd (6/5) result in successively greater roughness. Indeed, for the 6/5, 5/4, 4/3, and 5/3 ratios, roughness remains quite constant when there are 9 or fewer undulations per second.
[30] Concerning roughness in general, Helmholtz emphasized that “the whole sound is alternately reinforced and weakened”; that is, alternations of loudness in more or less rough sounds are a feature of two tones heard as a single whole, i.e., two tones heard jointly rather than severally (1877, 303; 1885, 181). Helmholtz considered the sound of slow undulations “by no means disagreeable,” noting as well that “slight de-tuning of modern organs and harmoniums imitates the trembling of the human voice and of violins” (1877, 279–80; 1885, 167–68). Such instances of slow pulsation of loudness or slow oscillation of pitch and even of spectrum at rates around six per second could be multiplied to include the tremulant and celeste stops on European pipe organs since the sixteenth century (Owen 2001 and Williams and Owen 2001) and the more recent vibrato and chorus effects of Hammond organs (Faragher 2011, 52), as well as the tremolo effects realized by vibraphones (Lotha 2018). To these could be added the periodic oscillation of fundamental-frequencies in vibratos and tremolos produced by expert vocalists and panpipe performers in European, African, and Andean traditions as well as the more precisely periodic undulations resulting from de-tuned fundamental frequencies within pairs of traditional Balinese metallophones whose sounds have been characterized as “shimmering” (Hood 1966; Rahn 1996, 17–23; and Tenzer 2000, 31–33).
[31] Helmholtz observed further in the same passage that:
3 beats in two seconds [i.e., undulation rates of 1.5 Hz], which cannot be observed without considerable attention,
. . . give no feeling of roughness [between tones whose fundamental-frequency ratios are very close to a unison].” In contrast, “the ear easily follows slow beats of not more than 4 to 6 in a second. The hearer has time to apprehend all their separate phases, and become conscious of each separately; he can even count them without difficulty. But when the interval between the two tones increases to about a Semitone, the number of beats becomes 20 or 30 in a second [e.g., relative to a fundamental frequency of 300 Hz, fundamental frequencies of 320 or 280 Hz, and 330 or 270 Hz, i.e., somewhat more than 100 cents], and the ear is consequently unable to follow them sufficiently well for counting (1877, 279–80; 1885, 167–68).
[32] Whereas certain idioms have consistently sought to produce slow periodic changes in some combination of loudness, pitch, and spectral timbre, musicians have also attempted to minimize them, if not to remove them entirely, as in Europe from the late fifteenth century onward (Lindley 1974). In any event, varying responses to periodic changes of loudness and pitch near privileged ratios during several centuries of European-derived music and in diverse, culturally independent settings indicate that slow undulation and faster beating are universally accessible to perception.
[33] From the preceding observations, one can conclude that roughness produced by pairs of plucked strings has at least two perceptible forms: relatively great amounts of roughness without slow undulation and relatively small amounts of roughness combined with slow undulation. One can also note that, in principle, roughness and undulation are acoustically absent only from a single sine tone. In any composite tone, and in any pair of simultaneous tones, there is always some roughness. Nonetheless, as Helmholtz observed, in a pair of tones that undulate extremely slowly (e.g., at a rate of ca. 1.5 Hz), undulation is not perceived. Further, in contrast to tones produced by bowed strings, tones produced by plucked strings are slightly inharmonic (Järveläinen et al. 1999), and as they constantly decrease in loudness, perception of roughness and undulation becomes attenuated. Moreover, nothing is known of the precision with which such Mesopotamian tuning mechanisms as sticks and wrappings (Kilmer 1998, 14, Fig. 1; and Schauensee 1998, 24, Fig. 5) would have been adjusted to alter the fundamental frequency of a plucked string (Kilmer 1998, 14, Fig. 1 and Schauensee 1998, 24, Fig. 5). Rather than realizing privileged ratios precisely, one can only claim that tuning a pair of plucked strings by ear might minimize roughness and reduce the rate of slow undulation within particular limits of perceptual acuity and instrument manufacture. Alternatively, slow undulation might have been realized, not only within particular limits of perceptual acuity but also within idiomatic norms. In either case, slow undulation would have provided a salient contrast with roughness and could very well have served as a guide to tuning a pair of strings by altering one of them.
[34] The terms that Helmholtz (1877, 302; 1885, 181) employed to describe acoustical and perceptual aspects of pairs of tones have been uniformly arranged along a single evaluative dimension. The sound of a pair of tones in which a harmonic partial of one tone differs little, or not at all, in frequency from the closest harmonic partial in the other tone is described as “most pleasant,” “undisturbed coexistence” in contrast to characterizations such as “restless fluctuation” and “disturbed coexistence” for a pair in which the closest harmonic partials differ greatly in frequency. Since Helmholtz, researchers have employed the same, evaluative dimension. (For example, Terhardt [2000], citing 14 studies, settles on “annoyance” and absence of annoyance.) Insofar as Helmholtz’s term “rough” and the Mesopotamian term “la-zakû” convey values on an evaluative semantic dimension, “rough” is a negative (bad) value whereas “zakû” is a positive (good) value. To coordinate both lexicons within a single semantic dimension, one might consider, at least for present purposes, the opposite or complement of “rough” to be “smooth.” Although Juan Roederer (2008, 38) has reserved the terms “smooth” and “smoothness” for pairs of sine tones whose frequencies differ by more than a critical band—e.g., 9.5% above and below for frequencies greater than ~500 Hz)—the adaptation of Helmholtz’s original formulation seems appropriate insofar as “smooth” would characterize not only the undulation-free sound of a pair of tones with a fundamental-frequency ratio corresponding precisely to one of the privileged values identified above for tones that have 6 harmonic partials, but also the slowly undulating sound of pairs whose fundamental-frequency ratios differ slightly from these values (e.g., by 6 Hz). Indeed, within such pairs that differ slightly, the periodic changes in loudness are much less steep than the sudden change at the pairs’ onsets: continual “rippling” in contrast with an abrupt “attack,” as conveyed by the pairs of tones in Example 6, above.
[35] Whereas roughness has been treated as a variable that can take continuous values within a single dimension, “zakû” and “la-zakû” might suggest a dimension having only two values. To be sure, the technical context of “zakû” and “la-zakû” in the tuning instructions comprises two states: a pair of strings exhibiting la-zakû sound and the same pair that becomes zakû. However, rather than implying a fixed pair of states, the tuning instructions imply a process, during which a tone-pair’s acoustical and perceptual counterpart would change in value monotonically, from greater to less roughness.
[36] At the tuning instructions’ successive starting-points, a pair of strings is la-zakû; thereupon, one of the strings is altered until the conclusion, at which point the pair of strings is zakû. Similarly, various contexts of zakû in Akkadian writings involve a process: e.g., clean garments, clean vegetables, and a clean slab. All of these refer to things that have been cleaned or cleansed; likewise, refined silver implies a process of purifying previously alloyed silver (Oppenheim 1961, 23–32). In each instance, there is an uninterrupted process of change from a lower to a higher value, from bad to good, or from worse to better. Accordingly, “clarified,” “purified,” or “cleansed” convey the tuning instructions’ use of “zakû” more precisely than “clear,” “pure,” or “clean,” and for “la-zakû” “unclarified,” “unpurified,” or “polluted” would be the counterparts (Rahn 2015, 2–4). By extension, the preceding acoustical and perceptual account of changing one string of a pair of strings would suggest not merely “smooth” and “rough” but “smoothed” and “unsmoothed,” or, to introduce another metaphor, “polished” and “unpolished.” Such metaphors could be multiplied, as they have been in European-derived studies of musical perception and as they were in general, non-musical usage in Akkadian. But without insisting on a Eurocentric outlook or its cousin, an outlook of extreme cultural relativism, such metaphors need not misrepresent the phenomenon if they convey a single evaluative dimension and they remain connected to cross-culturally accessible perception of differences that correspond to acoustical differences.(12)
[37] A remaining aspect of the process the tuning instructions specified involves its destination or completion. The much later Pythagorean tradition might have insisted that only a pair of strings that instantiates a particular ratio precisely is in fact “pure” or “clear” or “clean,” (or even “purified,” “clarified,” or “cleansed).” Such an abstract, ideal state, however, would be unverifiable and unfalsifiable with regard to human perception and production. Acoustically, as indicated above, the partials of plucked strings are at least slightly inharmonic, and the instrument’s tuning sticks and wrappings are of unknown precision. Moreover, perception of any sort is determined only within a particular range of uncertainty. Indeed, a series of perceptual experiments by Joos Vos (1982, 312) has shown that, whereas judgments of purity did not, on average, differ significantly from particular prototype ratios (e.g., 3/2 or 5/4), the distributions of purity judgments around such values were quite substantial. Specifically, 50% of the “pure” judgments were responses to pairs of tones with harmonic partials exhibiting fundamental-frequency values of more than 5 to 25 cents larger and smaller than the prototype ratios (Vos 1982, 310, Fig. 11). To be sure, one might resort to an extremely Platonic ontological position that such discrepant responses were merely evidence of a disjunction between appearance and reality.(13) Such a pose would, however, forfeit parsimony by presuming, beyond necessity, a transcendent reality that is, in principle, neither verifiable nor falsifiable.(14)
[38] Rather than insisting on a particular ratio as the conclusion of a tuning process, one can acknowledge that ratios within the immediate vicinity of a particular ratio would serve as such a destination. For ratios that differ slightly from prototype values, such as those that Helmholtz said “cannot be observed without considerable attention” and “give no feeling of roughness,” more prominent undulations in a monotonic process could have served as warnings, much as a yellow traffic light indicates that an intersection is very near and a required stop is imminent (1877, 279–80; 1885, 167–68). Accordingly, the ideal ratios of the following account should be understood as comprising a relatively small range of values rather than a single abstract value.
D. Factors Affecting Fundamental-Frequencies and Their Ratios
[39] Combining the modulo-7 framework outlined in part B and the auditory interpretation of dichord tuning developed in part C, one can ascertain how fundamental frequencies and their ratios would be realized in the seven tunings, specifically by observing that the instrument’s nine strings would have been successively larger, making their fundamental frequencies smaller. As Gurney observed (1994, 104), Mesopotamian harp depictions represented strings of different lengths with the shortest at the front, so that string 1 would be the shortest. Noting further that “strings on lyres are usually shown as approximately equal in length” he added, citing Subhi Anwar Rashid (1984, Abb. 45), that “it must be admitted that at least one representation, the stele from Telloh, clearly has the shortest strings in front.” To be sure, identifying which parts of a harp or lyre in a depiction would have corresponded to the front and back strings named in Nabnitu 32 and N. 4782 would depend on whether the musician, the listener, or the ornamental animal head that decorated certain instruments of the time was considered to be the front. Yet as Raoul Vitale (1982, 243–255) emphasized, the terms for the 3rd and 4th strings, “3rd thin” and “4th small,” clearly indicate that they were named in direct contrast with the terms for the 7th and 6th strings, which were, respectively, “3rd from behind” and “4th from behind” (see Example 1, above).
Example 9. Direction of fundamental frequencies from string 1 to string 7
(click to enlarge and see the rest)
[40] Although Vitale concluded that the names of strings 3 and 7 and strings 4 and 6 implied that fundamental frequencies of successive strings were uniformly smaller from string 1 to string 7, his observation would directly constrain the direction of only two dichords among \(C(7,2)=7 * \frac62 = 21\) dichords. To illustrate patterns of descending and ascending dichords that might have occurred among the first seven strings—assuming fundamental frequencies of strings 3 and 4 were greater than the fundamental frequencies of, respectively, strings 7 and 6—Example 9 shows the following cycle of zakû dichords in embūbum tuning as outlined in Example 5, above: 3&7, 7&4, 4&1, 1&5, 5&2, 2&6.
[41] In parts A and B of Example 9, the fundamental frequency of string 3 is set arbitrarily at 0, and in conformity with Vitale’s observations; string 7’s fundamental frequency is set at a general value that would be smaller than the fundamental frequency of string 3, namely, \(-x\), where \(x > 0\). If the undirected magnitude of the four-string-step dichords were the same as the undirected magnitude of the three-string-step dichords and the three-string-step dichords were positively directed, as in part A of Example 9, string 4’s fundamental frequency would be the same as string 6’s, namely, 0 (rather than greater). Moreover, there would be only three fundamental frequencies among the seven strings, namely, \(-x\), \(0\), and \(x\); as well, some fundamental frequencies would be the same from string to string (specifically, the unison dichords 1&2, 3&4, 4&5, and 5&6) and others would descend (2&3 and 6&7). In Part B of Example 9, the three-string-step dichords would be negatively directed and string 4’s fundamental frequency, \(-2x\), would be greater than string 6’s: \(-6x\), since \(-2x-(-6x)=4x\). Some fundamental frequencies in this case, notably, would descend from string to string (specifically, the one-string-step dichords 1&2, 3&4, 4&5, and 5&6) and some would ascend (2&3 and 6&7).
[42] In parts C, D, E, and F of Example 9, the three-string-step dichords differ in magnitude from the four-string-step dichords. In parts C and D, the four-string-step magnitudes, \(g\), are greater than the three-string-step magnitudes, \(s\): \(g>s\), where \(g>0\) and \(s>0\). In part C, the three-string-step dichords are positively directed and in part D they are negatively directed. In both, the 4th string’s fundamental frequency is greater than the 6th string’s, since, respectively, \(-g+s-(-3g+3s)=2g-2s>0\), and \(-g-s-(-3g-3s)=2g+2s>0\). Whereas some one-string-step dichords would descend in part D and others would ascend, in part C all would descend if \(-2g+3s>0\), i.e., \(s>2g/3s\).
[43] Finally, in parts E and F of Example 9, the three-string-step magnitudes, g, are greater than the four-string-step magnitudes, \(s\): \(g>s\), where \(g>0\) and \(s>0\). In part E, the three-string-step magnitudes are positively directed and the 4th string’s fundamental frequency is smaller than the 6th’s, since \(-s+g-(-3s+3g)=2s-2g < 0\). In part F, the three-string-step magnitudes are negatively directed and the 4th string’s fundamental frequency is greater than the 6th’s, since \(-s-g-(-3s-3g)=2s+2g>0\). In both, some one-string-step dichords would descend in part D and others would ascend. In short, four of the six ways in which relative magnitudes and directions of three- and four-string-step zakû dichords are combined result in the fundamental frequencies of strings 3 and 4 being greater than those of, respectively, strings 7 and 6. Only one of these combinations, C, also results in all six one-string-step dichords being uniformly negative in direction if, expressed as a logarithm, the smaller, three-string-step zakû ratio is greater than two-thirds the magnitude of the four-string-step zakû ratio.
Alterations of Fundamental Frequencies
[44] Also to be considered with regard to fundamental frequencies and their ratios are the kinds of alterations the tuning prescriptions specify when one tuning is changed into another. As conveyed in Example 3, above, and part B’s account of the seven tunings’ modulo-7 framework, one and only one, of the first seven strings was altered when changing one tuning into another, and this string was one of the strings of the tuning’s la-zakû dichord. Since the alterations in the first chapter mirror those in the second, one can consider them to have been opposites, so that an alteration in one of the chapters would increase a particular string’s fundamental frequency and an alteration in the other chapter would decrease it.
[45] The Akkadian term for “to loosen,” namely, nê’um (te-né-e-am-ma: “you loosen (for me),” occurs both intact and partially only in the second chapter, in the third line of the four-line paragraphs. Accordingly, one can infer that its opposite, an Akkadian term for tightening, originally occurred at the corresponding places in the first chapter (Krispijn 1990). At such places, Mirelman and Krispijn (2009, 43–45) have supplied the reconstructed Akkadian form ta-na-sà-aḫ/ḫa-ma (“you tighten (for me)”), an editorial decision justified by the appearance of the Akkadian word nu-su-[ḫu-um] (“tightening”) at the end of the first chapter. Nu-su-ḫu-um has the same root as ta-na-sà-aḫ/ḫa-ma (cf. the verb nasāḫum, to remove, subtract, deduct, in Oppenheim 1980, 1–15), and serves as the concluding rubric to the first chapter, albeit surviving there only partially. If Mirelman and Krispijn are correct, insofar as tightening would involve temporarily removing, subtracting, or deducting part of the length of a plucked string by rotating the string’s wrappings around the instrument’s crossbar, the first chapter would prescribe tightening particular strings, which would increase their fundamental frequencies, thereby changing the instrument’s first seven strings from one tuning to another. Conversely, the second chapter would prescribe loosening a particular string’s wrappings, which would decrease its fundamental frequency, again changing the instrument’s first seven strings from one tuning to another. In conformity with the preceding discussion of zakû as the end result of a process, tightening and loosening would involve a single uninterrupted change from rougher to smoother.
[46] Example 9 shows also that of the four combinations of relative magnitudes and directions of 3- and 4-string-step zakû dichords that would result in the fundamental frequencies of strings 3 and 4 being greater than the fundamental frequencies of, respectively, strings 7 and 6, only combination C would be consistent with the cycle of zakû dichords. According to the instructions, embūbum tuning would be changed into pītum tuning by turning embūbum’s three-string-step la-zakû dichord 3&6 into a zakû dichord by loosening string 3 and into kitmum tuning by tightening string 6. In Combinations B and F, loosening string 3 to produce a zakû dichord of, respectively, magnitude \(x\) and \(s\) would result in the same fundamental frequency as string 2 (see bold typeface in Example 9); tightening string 6 to produce a zakû dichord of, respectively, \(x\) and s would result in a fundamental frequency between \(0\) and, respectively, \(-2x\) and \(-s-g\), so that 6&3 would be a one-string-step dichord rather than a three-string-step dichord. Similar anomalies result in D, where loosening string 3 would produce a one-string-step dichord, as would tightening string 6. Only in C would loosening string 3 and tightening string 6 to change a la-zakû 6&3 dichord into a zakû dichord result in a fundamental frequency between string 2 and string 4 and between string 5 and string 6, respectively. In short, Vitale’s (1982) reasoning concerning strings 3, 4, 6, and 7 along with Mirelman and Krispijn’s (2009) account on loosening and tightening favor combination C of Example 9, where 1) the four-string-step dichords would be larger in their fundamental-frequency ratio than the three-string-step dichords, and 2) strings 1 to 7 would decline uniformly in their fundamental frequencies, albeit only if the three-string-step dichords were larger in their fundamental-frequency ratio than two-thirds the magnitude of the four-string-step dichords. Whereas the present account has not, so far, concluded that Mesopotamian tuning was diatonic, both Vitale (1982) and Gurney (1994), following Wulstan (1968), assumed as much. For Vitale, this assumption was a basis for concluding that the strings declined in fundamental frequency from 1 to 7 because of relationships between strings 3 and 7 and between strings 4 and 6; for Gurney (1994, n.5, 101) this assumption was a basis for concluding that the strings declined in fundamental frequency from 1 to 7 because of Vitale’s reasoning along with Krispijn’s (1990) reading of the Akkadian word nu-su-[ḫu-um] (“tightening”) at the end of the first chapter. Accordingly, and without adopting Wulstan’s flawed reasoning, one can note that uniform direction of fundamental frequencies would be consistent with harps and depictions of harps that have survived since the third millennium BCE. The stele from Telloh would be consistent with such a conclusion for lyres and would identify string 1 with the “front” of early Mesopotamian lyres and harps, including the decorative bull’s head on, e.g., the “Queen’s harp” and the “Peace” panel on the “’Standard’ of Ur” (Wooley 1934, vol. 2, 249-58; Kleiner and Mamiya 2005, 38–39).
[47] Most importantly, Example 9 shows that tightening string 6 or loosening string 3 would result in an additional constraint on the relative magnitudes of the three- and four-string-step zakûdichords: specifically, if string 3’s fundamental frequency is lower than 0, then \(4s-3g < 0\), i.e., \(s < 3g/4\); similarly, if \(-s\) is higher than \(-3g+3s\), then \((-s) - (-3g+3s)= 3g-4s > 0\), so that \(s < 3g/4\). Combined with the constraint that results from Vitale’s observation, the relative magnitudes of the 3- and 4-string-step zakû dichords, respectively, \(s\) and \(g\), are as follows:
$$ \frac{3g}{4} > s > \frac{2g}{3}\text{, where}\ s > 0,g > 0,\text{ and}\ s < g $$Octaves
[48] The latter constraint posited at the end of the previous paragraph on the magnitudes of the smaller, three-string-step dichords and larger, four-string-step dichords is of particular interest here, as it corresponds to the boundary values of the three-step generating interval for a special category of seven-degree well-formed scales, i.e., WF(7,2), in which the ratio 2/1 is the magnitude of the periodic, eight-step interval, i.e., the usual “octave,” and that mathematically comprises Easley Blackwood’s (1986) “recognizable diatonic tunings.” As formulated by Norman Carey (Carey 1998), well-formed structures are framed mathematically in terms of pitch classes rather than merely pitches. As a consequence, fundamental frequencies that instantiate a well-formed structure could range indefinitely lower or higher than the seven fundamental frequencies on which the preceding discussion of individual Mesopotamian tunings has focused. Further, as Carey has emphasized (1998, 159–63), the magnitude of a well-formed structure’s periodic interval need not correspond to the 2/1 ratio and is in principle arbitrary. Accordingly, the following discussion considers whether the tuning instructions specify, explicitly or implicitly, a periodic value. In this regard, how one interprets the tuning instructions’ reference to string 9 is of greatest consequence. When changing the tuning from išartum to kitmum, the tuning instructions prescribe loosening not only string 2 but also string 9. Because of the recursive and symmetrical structure of the first and second chapters, one can infer that changing kitmum into išartum would involve tightening not only the 2nd string but also the 9th. However, the tuning instructions do not indicate precisely the extent to which the 9th string is to be loosened or tightened. Although tightening string 2 in išartum would change 5&2 from la-zakû to zakû and the tuning from išartum to kitmum, the tuning instructions do not characterize the 2&9 dichord as zakû or la-zakû. Yet these are the only terms the instructions employ to describe dichords, and they employ them only for three- and four-step dichords among the first seven strings. Indeed, as Kilmer (1998, 15) has noted, there is no known Mesopotamian term for the octave, which here can be considered any dichord that would span eight strings, i.e., seven string-steps. The tuning instructions, furthermore, do not provide a name for the four-string-step dichord that comprises the 9th and 5th strings, nor do any known Mesopotamian tablets provide a term for dichords that comprise one of the first seven strings as well as the eighth or ninth string.
[49] In the absence of terms, or even circumlocutions, loosening or tightening the 9th string in a single continual change from roughness to smoothness for dichords comprising the 2nd and 9th and the 5th and 9th strings would be consistent with the present formulation. On one hand, the 9th string might have formed a unison, a fundamental-frequency ratio of 1/1, with the 2nd string. On the other hand, some other fundamental-frequency for the 9th string might have resulted in smooth ratios for 2&9 and 5&9. Both Rahn (2011, 205, 223–224, 228–229, 233–234) and Mirelman (2013, 46–47, 55) have suggested both of these possibilities. Of these two possibilities, a unison between the first and eighth strings is more doubtful.
[50] In YBC 11381 (Payne 2010, 292–93), the incipits of nine benedictions for various Assyrian gods are preceded by explicit designations of nine strings as listed in Mesopotamian tuning sources and numbered in YBC 11381 from 1 to 9: sa 1, sa 2,
[51] Of additional relevance to the possibility that strings 2 and 9 produced different fundamental frequencies would be the modulo-7 cycle of strings among all seven tunings. In such a modulo-7 framework, the 8th and 9th strings would be congruent with, respectively, the first and second strings. In each of the seven tunings, three- and four-string-step dichords are characterized as zakû or la-zakû. (In išartum and kitmum tunings, the three-string-step 5&2 dichord is, respectively, la-zakû and zakû.) As the second and ninth strings are congruent, and assuming that the fundamental-frequency ratios of zakû dichords that spanned four string-steps were perceptually the same (as would be those that spanned three string-steps), the four-string-step 5&9 dichord would be la-zakû in išartum and zakû in kitmum.
[52] A further consequence is that the ratio of the seven-string-step 2&9 dichord would be the product of these three- and four-string-step dichords’ ratios. Because of the tuning instructions’ recursive, symmetrical and cumulative structure, this relationship between particular three- and four-string-step dichords on one hand and a particular seven-string-step dichord on the other hand would obtain in each tuning. As such, this relationship would be of practical utility in loosening or tightening specific strings, for one could assess the change from roughness to smoothness when turning a three- or four-string-step la-zakû dichord into a zakû dichord by assessing the smoothness of, respectively, its four- or three-string-step counterpart and the seven-step dichord that spanned both dichords. In each of the seven tunings, tuning would be enhanced insofar as at least three of the following trichords would comprise smooth three-and four-string-step dichords: 1&4&8, 1&5&8, 2&5&9, and 2&6&9; in addition, in three of the tunings, all four trichords would be smooth. Taken together, these redundancies would provide a conjectural answer to a question Mirelman raised in the discussion period following his 2012 conference presentation on “Tuning Procedures in Ancient Iraq,” namely, “Why did the sammû have 9 strings?”
E. Pairs of Smooth Dichords as Potential Realizations of zakû String-Pairs
[53] The present section proceeds from the general constraint on the magnitudes of three- and four-string-step magnitudes to a consideration of the actual magnitudes that might have been realized consistent with the Mesopotamian tuning instructions. Section C of Example 9, discussed above, outlines a way in which a Mesopotamian musician could adjust a la-zakû pair of strings so that a single continual alteration of one string would turn it into a zakû dichord by smoothing or polishing its sound. Insofar as a plucked string’s spectrum would comprise six harmonic partials, there might be eleven ideal prototype ratios. Excluding the perfect prime’s 1/1 ratio (because it is assumed above that each of the first seven strings would produce a fundamental frequency different from each of the other six strings’ fundamental frequencies), these ratios would be 6/5, 5/4, 4/3, 3/2, 5/3, 2/1, 5/2, 3/1, 4/1, 5/1, and 6/1. Among these eleven ratios, there would be \(C(11,2)=\frac{11 * 10}{2}=55\) pairs.
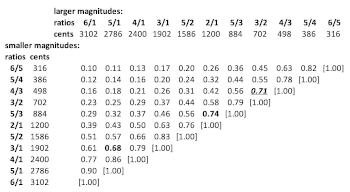
Example 10. Ratios of 55 pairs of ratios’ logarithms
(click to enlarge)
[54] Example 10 shows how these 55 pairs of ratios are related by calculating for each ratio its logarithm to the base \(2^{1/1200}\)— i.e., its value in cents—and for each pair the ratio of the smaller ratio’s value in cents divided by the larger’s in cents. As shown in Example 9, above, the smaller ratio of each pair would correspond to a three-string-step zakû dichord and the larger ratio would correspond to its four-string-step counterpart. Accordingly, the 55 pairs of zakû ratios would be as follow: 6/5 and 5/4, 6/5 and 4/3, 6/5 and 3/2,
At least one of the 55 pairs of ideal zakû ratios would have resulted in a tuning that was consistent with the factors discussed in part D, above.
[55] Among the 55 pairs of ideal zakû ratios, only three, which are highlighted by bold typeface in Example 10, would result in values of \(s\) and \(g\) such that \(\frac{3g}{4} > s \> \frac{2g}{3}\), where \(s>0\), \(g>0\), and \(s<g\). Of these, the ratio pair comprising 3/1 and 5/1 would be problematic, as they would result in three-and four-string-step la-zakû dichords whose magnitudes were, respectively \(3 * (g-s)=\text~2652\) cents and \(2 * (2s-g)=\text~2036\) cents. Tightening a string to change the ~2652-cent magnitude into its zakû version, namely, s=~1902 cents, would involve an interruption around the magnitude 4/1 = 2400 cents, which would produce a very high degree of smoothness; the same point applies to the change from ~2036 cents to g=~2652 cents. In contrast, the other two pairs of ratios would result in a change from roughness to smoothness that was not interrupted by intervening smoothness. Nonetheless, not only the ratios 3/1 and 5/1 but also the ratios 5/3 and 2/1, would result in quotients that would be very close to the boundary values for well-formedness that are implicit in the tuning instructions: if \(s=\log(\frac31)\) and \(g=\log(\frac51)\),then \(s=0.68g\) as compared with \(s=0.67\); if \(s=\log(\frac53)\) and \(g=\log(\frac21)\),then \(s=0.74g\) as compared with \(s=0.75g\). In contrast, if \(s=\log(\frac43)\)and \(g=log(\frac32)\),then \(s=0.71g\), which is approximately midway between the boundary values of \(0.67g\) and \(0.75g\). Accordingly, a practical advantage of the ideal, prototype ratios 4/3 and 3/2 would have been their capacity for resulting in the well-formed structure, which is implicit in the tuning instructions within relatively large ranges of values. In the history of European tuning theory, this capacity has been exploited when ideal tunings of the perfect 5th have been formulated mathematically as the ratios \(\frac32=\text~702\) cents, \(2^{7/12}=\text~700\) cents,and \(5^{1/4}=\text~696.6\) cents. In other musical traditions, where stringed instruments have been tuned entirely by ear, even greater ranges around prototype values have been produced: e.g., in court music of Burma/Myanmar and Uganda.
[56] An additional advantage of 4/3 and 3/2 as ideal, prototype ratios for Mesopotamian tuning would be that the seven-string-step dichords 2&9 and 1&8 could be tuned by changing their timbre from rough to smooth without requiring target spectra comprising relatively great amplitudes among harmonics higher than the 6th. On one hand, the ratios 5/3 and 2/1 would result in the ideal prototype ratio 10/3, which would involve comparing the 3rd harmonic produced by the upper tone with the 10th harmonic of the lower tone, and the ratios 3/1 and 5/1 would result in the ideal prototype ratio 15/1, which would involve comparing the 1st harmonic (i.e., the fundamental frequency) produced by the upper tone with the 15th harmonic of the lower tone. On the other hand, the ratios 4/3 and 3/2 would result in the ideal prototype ratio 2/1, which would involve comparing the 1st harmonic of the upper tone with the 2nd harmonic of the lower tone. In this regard, a corollary of Vassilakis’s (2001, 26–45) formulation of roughness is that roughness is more prominent, and hence the contrast between roughness and smoothness is more pronounced, if the amplitudes of the harmonics that result in roughness are similar. Of relevance to Vassilakis’s formulation, the modeling of Krantz and Douthett (2011) summarizes the extent to which the 2/1 ratio would tend to result in much more prominent contrast between roughness and smoothness than the ratios 10/3 and 15/1.
[57] The present study has attempted not to prejudice the possible candidates against harmonics lower than the 7th, especially as the amplitudes of harmonics plucked-string spectra vary to a certain extent among the first six. That said, it is undeniable that changes in the interaction of harmonics produced by plucked string-pairs with magnitudes far from and then close to the ideal fundamental-frequency ratios 2/1, 3/2, and 4/3 would tend to be relatively accessible to hearing. In particular, seven-string-step dichords with ideal fundamental-frequency ratios close to 2/1 would not only have provided a reliable basis for checking the tuning of zakû three- and four-string-step dichords; as well, they would have facilitated extensions of tuning beyond the sammû’s nine strings. Of relevance here, Bo Lawergren and Oliver Gurney (1987, 50–51) reported plucked string instruments having more than seven strings throughout much of Mesopotamian history, during an extended period that surrounded the time when terms employed in the tuning instructions continued to be inscribed on clay tablets. Specifically, they documented such instruments having as many as 15 strings in the third millennium, 12 in the second millennium, and 30 in the first millennium. Accordingly, if the 2&9 dichord, and hence the 1&8 dichord, was tuned from rough to smooth, it is plausible that all seven-string-step dichords were tuned in this way. As a consequence, music to which the tuning instructions were relevant might well have comprised counterparts to the compound intervals as well as the pitch classes and interval classes of later music theory. Indeed, the present formulation would extend directly to include smooth dichords spanning two registers, for the ideal fundamental-frequency ratio 4/1 could be tuned as readily as the zakû dichords’ ratios, 4/3 and 3/2.
F. Discussion
[58] The hypothesis introduced at the beginning of part E has been verified in a falsifiable manner. Indeed, one can argue even more narrowly that Mesopotamian tuning was perceptibly diatonic, with ideal zakû ratios of 4/3 and 3/2 and a smooth seven-string-step dichord ratio of 2/1 that would have facilitated musical practice for millennia. However, this conclusion is reached only by taking into account several factors, each of which is decisive. Relevant acoustical and psychoacoustical aspects of plucked strings include the following facts:
- Thinner and smaller plucked strings produce greater fundamental frequencies and higher perceived pitches than thicker and larger strings.
- Tightening and loosening a plucked string respectively increases and decreases its fundamental frequency and raise and lower its perceived pitch.
- Plucked simultaneously, pairs of strings produce audible roughness minima and smooth undulations that correspond to particular ideal fundamental-frequency ratios.
The contents of the tuning instructions and other Mesopotamian writings that are germane to reverse-engineering Mesopotamian tunings include the following information:
- the names of the strings on the instrument for tuning and their consequent spatial ordering; and
- the names of the seven dichords that spanned four and five of the instrument’s first seven named strings, and the consequent names of the seven tunings the tuning instructions identify.
Assumptions concerning the tuning instructions and other Mesopotamian writings, as well as acoustical and psychoacoustical aspects of plucked strings that are decisive to historically reconstructing Mesopotamian tuning are as follows:
- Each string produced a fundamental frequency different from the others.
- The fundamental-frequency ratios of zakû dichords that spanned four string-steps were perceptually the same, as were those that spanned three string-steps.
- The tuning instructions’ distinction between zakû and la-zakû corresponded to a “bottom-up” acoustical and psychoacoustical contrast, accessible universally, between, respectively, auditory smoothness and roughness, and, respectively, a contrast between positive and negative valence that was semantically consistent with the usage of “zakû” and “la-zakû” in other Mesopotamian writings and that has been found in subsequent cultural settings.
Example 11. Tuning “from scratch” with 4/3 and 3/2 and re-tuning by tightening
(click to enlarge and see the rest)
Example 12. Re-tuning by loosening
(click to enlarge and see the rest)
Audio Example 4. Tuning “from scratch” and re-tuning by tightening and loosening: see Examples 11 and 12
[59] Finally, a critical factor favoring the ideal fundamental-frequency ratios 4/3 and 3/2 as zakû magnitudes is their joint consistency with the ideal fundamental-frequency ratio 2/1, which could be tuned in exactly the same rough-to-smooth manner and serve as a seven-string-step means of verifying the magnitudes of its three- and four-string-step zakû segments. Consistent with this point, Example 11, Example 12 and Audio Example 4 illustrate how išartum tuning could have been realized “from scratch,” as discussed above (cf. Example 5), with the remaining tunings realized by successively tightening particular strings and then loosening particular strings in reverse order, returning “full circle” to išartum tuning. Examples 10 and 11 also indicate dichords in the re-tuning cycle that could have been checked by means of octaves that included strings 1 and 8 or strings 2 and 9.
[60] Having concluded that Mesopotamian tuning was diatonic and would favor the ratios 4/3 and 3/2 without assuming aspects of tuning known only for later cultural settings, one can assess the extent to which it was similar to tuning in Ancient Greece, rather than arguing backward in time from Ancient Greek tuning to Mesopotamian tuning. In this regard, the clearest parallels with Mesopotamian tuning are found in Aristoxenus’s approach. Like the Mesopotamian tuning instructions, and in contrast to other Greek writers, Aristoxenus advocated tuning by ear, rather than by means of “ratios of numbers” (Barker 1990, 149) that were later promoted by Ptolemy (Barker 1990, 275–391) and assumed by Wulstan and such earlier writers as Philolaus and Archytas (Barker 1990, 36–38 and 39–41). Just as tightening and loosening an individual string were central to Mesopotamian tuning, tensing and relaxing an individual string (or the human voice) were central to the process Aristoxenus advocated for tuning (Barker 1990, 128, 133–34, 142, 149, 157–58, 165–66). Moreover, similarly to the Mesopotamian tuning instructions, Aristoxenus assigned privileged status to certain pairs of tones tuned simultaneously: each sym-fōnia, literally, “together-sounding” pair (Barker 1990, 162, n. 77), had a magnitude he took as “given,” in contrast to each dia-fōnia, literally, “apart-sounding” pair, two tones tuned successively, i.e., “melodically.” As in the Mesopotamian tuning instructions, these privileged pairs of tones corresponded (judging from earlier and later Greek and Roman accounts) to values close to the ideal fundamental-frequency ratios 4/3 and 3/2. The ideal 2/1 ratio was treated as a combination (i.e., a “sum”) of these, rather than as an independent starting point for tuning (Barker 1990, 160) and constituted the basis for compound intervals spanning several registers (Barker 1990, 130, 139–40). Whereas the preceding account of Mesopotamian tuning acknowledges that the fundamental-frequency ratio of a zakû dichord would be audibly smooth rather than insisting on a single ideal value, Aristoxenus specified that a symfōnia pair could have “either no range of variation at all, being determined to a single magnitude, or else a range which is quite indiscernible” (Barker 1990, 168). This explanation anticipates Helmholtz’s account of slow undulations as “by no means disagreeable” and acknowledges the perceptual relevance of “qualitative identity” in contrast to the Pythagoreans’ specification of an ideal “numerical identity” (Forest 2020 ).
[61] Further, Mesopotamian tuning was effectively diatonic in the modern sense, realized by cycling perfect 4ths and 5ths among seven tones, and implicitly privileged as the only kind of tuning formulated in the instructions. For Aristoxenus, too, diatonic tuning, more precisely the tense (or “tenser” or “tensest”) diatonic tetrachord genus (Barker 1990, 166), was privileged—not only realized by cycling perfect 4ths and 5ths among 6 tones, but also dealt with first, so that other genera (soft diatonic as well as chromatic and enharmonic) could be understood as products of successively altering individual fundamental frequencies and, as a consequence, individual fundamental-frequency ratios (Barker 1990, 139; Franklin 2002, 447). Finally, it should be emphasized that the Mesopotamian tuning instructions provide no explicit basis for conflating the term “zakû” with later notions concerning “consonant” intervals. Instead, a dictionary entry for “zakû” might merely provide “audibly smooth, i.e., not rough” as its translation and specify three- and four-string-step dichords for tuning as its known literary context. Similarly, the “sammû” might be identified as a lyre or harp employed in tuning, that is, a “tuner,” an instrument for tuning.
Jay Rahn
York University (Canada)
Vanier College
4700 Keele Street
Ross Building, S900
Toronto, ON M3J 1P3
jayrahn@yorku.ca
Works Cited
Ambrazevičius, Rytis. 2014–16. “Dissonance/Roughness and Tonality Perception in Lithuanian Schwebungsdiaphonie.” Journal of Interdisciplinary Music Studies 8 (1-2): 39–53. http://musicstudies.org/wp-content/uploads/2017/03/Ambrazevicius_JIMS_16081202.pdf.
—————. 2017. “Scales in Lithuanian Traditional Fiddling: An Acoustical Study.” Proceedings of the 7th International Workshop on Folk Music Analysis: 50–55. http://fma2017.uma.es/docs/FMA2017_proceedings.pdf.
Aruffo, Christopher, Robert L. Goldstone, and David J. D. Earn. 2014. “Absolute Judgment of Musical Interval Width.” Music Perception 32 (2): 184–98. https://doi.org/10.1525/mp.2014.32.2.186.
Audacity Team. 2018. Audacity V.2.3.0. Free Software Foundation. https://www.audacityteam.org.
Barker, Andrew. 1990. Greek Musical Writings: II, Harmonic and Acoustic Theory. Cambridge University Press. https://doi.org/10.1017/CBO9780511585753.
Blackwood, Easley. 1986. The Structure of Recognizable Diatonic Tunings. Princeton University Press.
Burg, Jennifer, Jason Romney, and Eric Schwartz. 2016. Digital Sound & Music: Concepts, Applications, and Science. Franklin Beedle, Chapter Two. http://digitalsoundandmusic.com/chapters/ch2/.
Carey, Norman. 1998. Distribution Modulo 1 and Musical Scales. PhD diss., University of Rochester.
Center for Electronic and Computer Music (CECM). 2018. “What Is Timbre? Acoustics.” Introduction to Computer Music: Chapter One. Jacobs School of Music, Indiana University. https://cmtext.indiana.edu/acoustics/chapter1_timbre.php.
Coxeter, Harold Scott Macdonald. 1969. Introduction to Geometry. 2nd ed. Wiley.
Creese, David E. 2010. The Monochord in Ancient Greek Harmonic Science. Cambridge University Press.
Richard Crocker. 1978. “Remarks on the Tuning Text UET VII 74 (U. 7/80).” Orientalia 47 (1): 99–104.
—————. 1997. “Mesopotamian Tonal Systems.” Iraq 59: 189–202. https://doi.org/10.2307/4200443.
Crocker, Richard, and Anne Draffkorn Kilmer. 1984. “The Fragmentary Music Text from Nippur.” Iraq 46 (2): 81–85. https://doi.org/10.2307/4200217.
Duchesne-Guillemin, Marcelle. 1963. “Découverte d'une gamme babylonienne.” Revue de Musicologie 49 (126): 3–17. https://doi.org/10.2307/927207.
Dumbrill, Richard. 2005. The Archaeomusicology of the Ancient Near East. Trafford Publishing. https://www.academia.edu/875113/The_Musicology_and_Organology_of_the_Ancient_Near_East.
—————. 2010. “Evidence and Inference in Texts of Theory in the Ancient Near East.” Proceedings of the International Conference of Near Eastern Archaeomusicology (ICONEA 2008): 105–15. https://b-ok.cc/book/1073850/e4bfa1.
—————. 2017. “The Truth about Babylonian Music.” Near Eastern Musicology Online 4 (6): 91–121. http://nemo-online.org/wp-content/uploads/2017/08/INTERNET-6-02.-Article-NEMO-no.-4-6-2-Richard-Dumbrill-Truth-170822S.pdf.
—————. [n.d.]. “Is the Heptagram in CBS 1766 a Dial?” https://www.academia.edu/243925/Is_the_Heptagram_in_CBS_1766_a_Dial.
Eberling, Erich, Bruno Meissner, et al., eds. 2018. Reallexikon der Assyriologie und vorderasiatischen Archäologie. De Gruyter. http://publikationen.badw.de/de/rla.
Eerola, Tuomas, and Imre Lahdelma. 2021. “The Anatomy of Consonance/Dissonance: Evaluating Acoustic and Cultural Predictors across Multiple Datasets with Chords.” Music & Science 4. https://doi.org/10.1177/20592043211030471.
Faragher, Scott. 2011. The Hammond Organ: An Introduction to the Instrument and the Players Who Made It Famous. Hal Leonard.
Feder, Yitzhaq. 2014. “The Semantics of Purity in the Ancient Near East: Lexical Meaning as a Projection of Embodied Experience.” Journal of Ancient Near Eastern Religions 14 (1): 87–113. https://doi.org/10.1163/15692124-12341258.
Fletcher, Harvey. 1940. “Auditory Patterns.” Reviews of Modern Physics 12 (1): 47–65. https://doi.org/10.1103/RevModPhys.12.47.
Forest, Peter. 2020. “The Identity of Indiscernibles.” In The Stanford Encyclopedia of Philosophy, ed. Edward N. Zalta. https://plato.stanford.edu/archives/fall2008/entries/identity-indiscernible/.
Franklin, John Curtis. 2002. “Musical Syncretism in the Greek Orientalizing Period.” The Archaeology of Sound: Origin and Organisation. Studien zur Musikarchäologie III, Orient-Archäologie 10: 441–51.
Goodwin, William W. 1874. Plutarch: Plutarch’s Morals. Little, Brown, and Company. https://catalog.perseus.org/catalog/urn:cts:greekLit:tlg0007.tlg134.perseus-grc1
Gray, Catherine. 1993. “The Ugandan Lyre Endongo and Its Music.” British Journal of Ethnomusicology 2 (1): 117–42. https://doi.org/10.1080/09681229308567215.
Gurney, Oliver R. 1968. “An Old Babylonian Treatise on the Tuning of the Harp.” Iraq 30 (2): 229–33. https://doi.org/10.2307/4199853.
—————. 1994. “Babylonian Music Again.” Iraq 56: 101–6. https://doi.org/10.2307/4200387.
Helmholtz, Hermann von. 1877. Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik. 4th rev. ed. Friedrich Vieweg und Sohn. http://ks4.imslp.info/files/imglnks/usimg/d/d5/IMSLP90090-PMLP184676-Helmholtz,_Die_Lehre_von_den_Tonempfindungen,_4.Aufl._1877.pdf.
—————. 1885. On the Sensations of Tone as a Physiological Basis for the Theory of Music. Translated by Alexander Ellis. 2nd rev. ed. Longmans, Green, and Co.
Hood, Mantle. 1966. “Sléndro and Pélog Redefined.” Selected Reports 1 (1): 28–48.
Hopkins, Edward John, and Edward F. Rimbault. 1877. The Organ, Its History and Construction. 3rd ed. Robert Cocks.
Horowitz, Wayne. 2006. “A Late Babylonian Tablet with Concentric Circles from the University Museum (CBS 1766).” Journal of the Ancient Near Eastern Society 30 (1): 37–53.
Huffman, Carl. 2019. “Pythagoreanism: Neo-Pythagoreanism.” In The Stanford Encyclopedia of Philosophy, ed. Edward N. Zalta. https://plato.stanford.edu/entries/pythagoreanism/#4.
James, Thomas Garnet Henry. [1939] 2010. Tutankhamun’s Trumpets Played after 3000+ Years. https://www.youtube.com/watch?v=Qt9AyV3hnlc
_in_String_Instrument_Sounds_and_Implications_to_Digital_Sound_Synthesis.
Järveläinen, Hanna, Vesa Välimäki, and Matti Karjalainen. 1999. “Audibility of Inharmonicity in String Instrument Sounds, and Implications to Digital Sound Synthesis.” Proceedings of the International Computer Music Conference (ICMC’99): 359–62. https://www.researchgate.net/publication/228587669_Audibility_of_Inharmonicity
_in_String_Instrument_Sounds_and_Implications_to_Digital_Sound_Synthesis.
Karamanolis, George. 2020. “Plutarch.” In The Stanford Encyclopedia of Philosophy, ed. Edward N. Zalta. https://plato.stanford.edu/archives/sum2020/entries/plutarch/.
Kilmer, Anne Draffkorn. 1960. “Two New Lists of Key Numbers for Mathematical Operations.” Orientalia 29 (3): 273–308.
—————. 1965. “The Strings of Musical Instruments: Their Names, Numbers, and Significance.” In Studies in Honor of Benno Landsberger on his Seventy-Fifth Birthday, ed. Hans G. Güterbock and Thorkild Jacobsen, 261–8. Assyriological Studies 16. University of Chicago Press.
—————. 1971. “The Discovery of an Ancient Mesopotamian Theory of Music.” Proceedings of the American Philosophical Society 115 (2): 131–49. http://www.syriacstudies.com/2017/10/17/the-discovery-of-an-ancient-mesopotamian-theory-of-music-anne-draffkorn-kilmer/.
—————. 1998. “The Musical Instruments from Ur and Ancient Mesopotamian Music.” Expedition Magazine 40 (2): 12–19. https://www.penn.museum/sites/expedition/the-musical-instruments-from-ur-and-ancient-mesopotamian-music/.
—————. 2014. “Mesopotamian Music Theory since 1977.” Music in Antiquity: The Near East and the Mediterranean (Yuval 8): 92–101. https://jewish-music.huji.ac.il/sites/default/files/02%20%20Mesopotamian%20Music%20Theory%20Since%201977%20pp%2092-101%20Anne%20Draffkorn%20Kilmer%20incl%20title%20pages.pdf.
Kleiner, Fred S., and Christin J. Mamiya. 2005. Gardner's Art Through the Ages. 12th ed. Thomson/Wadsworth.
Krantz, Richard, and Jack Douthett. 2011. “The Role of Higher Harmonics in Interval Perception.” American Physical Society, Four Corners Section Meeting [Tucson, AZ, October 22]. https://www.researchgate.net/publication/235420603_The_Role_of_Higher_Harmonics_In_Musical_Interval_Perception.
Krispijn, Theo J. H. 1990. “Beiträge zur altorientalische Musikforschung 1: Šulgi und die Musik.” Akkadica 70: 1–27.
Kümmel, Hans Martin. 1970. “Zur Stimmung der babylonischen Harfe.” Orientalia 39 (2): 252–63.
Musée du Louvre. 1994. Musiques au Louvre. Éditions de la Réunion des Musées Nationaux.
Lavignac, Albert, and Lionel de la Laurencie. 1913. Encyclopédie de la Musique et Dictionnaire du Conservatoire. Librairie Delagrave. http://gallica.bnf.fr/ark:/12148/bpt6k123719d/f48.image.
Lawergren, Bo, and Oliver R. Gurney. 1987. “Sound Holes and Geometrical Figures: Clues to the Terminology of Ancient Mesopotamian Harps.” Iraq 49: 37–52. https://doi.org/10.2307/4200263.
Layard, Austen Henry. 1849–53. The Monuments of Nineveh: From Drawings Made on the Spot. John Murray. 2nd series. https://digi.ub.uni-heidelberg.de/diglit/layard1853/0084/image.
Lindley, Mark. 1974. “Early 16th-Century Keyboard Temperaments.” Musica Disciplina 28: 129–51.
Lotha, Gloria. 2018. “Vibraphone.” In Encyclopedia Britannica, ed. The Editors of Encyclopedia Britannica. https://www.britannica.com/art/vibraphone.
McDermott, Josh H., Schultz, A.F., Unduragga, E.A., Godoy, R.A. (2016). “Indifference to dissonance in native Amazonians reveals cultural variation in music perception”. Nature (535): 547–50. https://doi.org/10.1038/nature18635
Mirelman, Sam. 2008. “Tuḫru ‘Achilles’ Tendon?’.” Nouvelles assyriologiques brèves et utilitaires 2008/4: 89–90. http://sepoa.fr/wp/wp-content/uploads/2012/06/2008-4.pdf.
—————. 2010. “A New Fragment of Music Theory from Ancient Iraq.” Archiv für Musikwissenschaft 67: 45–51.
—————. 2012. “Tuning Procedures in Ancient Iraq.” Paper presented at the Second International Conference on Analytical Approaches to World Music, The University of British Columbia, May 11–13. http://aawmconference.com/wp-content/uploads/2018/12/mirelman_a.pdf.
—————. 2013. “Tuning Procedures in Ancient Iraq.” Analytical Approaches to World Music Journal 2 (2): 43–56. http://aawmjournal.com/articles/2013b/Mirelman_AAWM_Vol_2_2.html.
Mirelman, Sam, and Theo J. H. Krispijn. 2009. “The Old Babylonian Tuning Text UET VI/3 899.” Iraq 71: 43–52. https://doi.org/10.1017/S0021088900000735.
Montagu, Jeremy. 1978. “One of Tut'ankhamūn's Trumpets.” Galpin Society Journal 29 (May): 115–17. https://doi.org/10.2307/841867.
Montagu, Jeremy. 2017. “Tutankhamon's Trumpets and the Hatsos'rot.” Website of Jeremy Montagu. http://www.jeremymontagu.co.uk/tutankhamon.pdf.
Nakai, Mikio, and Kazuya Kawaguchi. 2006. “On the Inharmonicity of a String.” The Proceedings of the Dynamics and Design Conference. The Japan Society of Mechanical Engineers. https://doi.org/10.1299/jsmedmc.2006._109-1_.
Nave, Carl R. 2020. String Wave Solutions. Department of Physics and Astronomy, Georgia State University, Atlanta, GA. http://hyperphysics.phy-astr.gsu.edu/hbase/Waves/wavsol.html#c2.
Oppenheim, A. Leo, ed. 1961. The Assyrian Dictionary of the Oriental Institute of the University of Chicago (CAD). Vol. 21, Z. Oriental Institute. https://oi.uchicago.edu/sites/oi.uchicago.edu/files/uploads/shared/docs/cad_z.pdf.
—————, ed. 1980. The Assyrian Dictionary of the Oriental Institute of the University of Chicago (CAD). Vol. 11, N Part 2. Oriental Institute. https://oi.uchicago.edu/sites/oi.uchicago.edu/files/uploads/shared/docs/cad_n2.pdf.
Osgood, Charles Egerton 1964. “Semantic Differential Technique in the Comparative Study of Cultures.” American Anthropologist 66 (3): 171–200. https://doi.org/10.1525/aa.1964.66.3.02a00880.
Osgood, Charles Egerton, William H. May, and Murray Samuel Miron. 1975. Cross-Cultural Universals of Affective Meaning, Vol. 1. University of Illinois Press. https://openlibrary.org/works/OL1408923W/Cross-cultural_universals_of_affective_meaning?edition=crossculturaluni00osgo.
Owen, Barbara, 2001. “Tremulant.” In Grove Music Online. Oxford. https://doi.org/10.1093/gmo/9781561592630.article.49736
Payne, Elizabeth E. 2010. “A New Addition to the Musical Corpus.” In Opening the Tool Box, ed. Sarah C. Melville and Alice L. Sloysky, 291–300. Brill. https://doi.org/10.1163/9789004186569_019.
Penttinen, Henri, and Vesa Välimäki. 2004. “A Time-Domain Approach to Estimating the Plucking Point of Guitar Tones Obtained with an Under-Saddle Pickup.” Applied Acoustics 65 (12): 1207–20. https://doi.org/10.1016/j.apacoust.2004.04.008.
Plomp, Roel, and Willem Levelt. 1965. “Tonal Consonance and Critical Bandwidth.” Journal of the Acoustical Society of America 38 (4): 548-60. https://doi.org/10.1121/1.1909741.
Rahn, Jay. 1996. “Perceptual Aspects of Tuning in a Balinese Gamelan Angklung for North American Students.” Canadian University Music Review 16 (2): 1–43. https://doi.org/10.7202/1014424ar.
—————. 2011. “The Hurrian Pieces, ca. 1350 BCE: Part Two—From Numbered Strings to Tuned Strings.” Analytical Approaches to World Music Journal 1 (2): 204–69. http://www.aawmjournal.com/articles/2011b/Rahn_AAWM_Vol_1_2.htm.
—————. 2015. “Clarity, Impurity, and Discant Structure in Mesopotamian Music.” Paper presented at the Current Musicology 50th Anniversary Conference, Columbia University, March 28, 2015. https://www.academia.edu/25901702/Clarity_Impurity_and_Discant_Structure_in_Mesopotamian_Music.
—————. 2019. “Reformulating Burmese Harp Tunings.” Paper presented at the Analytical Approaches to World Music Special Topics Symposium: Computational Approaches to World Music Analysis, Royal Birmingham Conservatoire [Birmingham, UK, July 2]. https://conferences.iftawm.org/2019-birmingham/ Abstract at https://conferences.iftawm.org/wp-content/uploads/2019/06/FMA-AAWM-2019-Program-and-Abstracts.pdf, p. 18. Full text at https://yorkspace.library.yorku.ca/xmlui/handle/10315/36518.
Rahn, John. 1980. Basic Atonal Theory. Longman.
Rashid, Subhi Anwar. 1984. Musikgeschichte in Bildern, Bd. II, Musik des Altertums, Lfg. 2. VEB Deutscher Verlag für Musik.
Rawlinson, George. 1871. The Five Great Monarchies of the Ancient Eastern World, or, The History, Geography, and Antiquities of Chaldæa, Assyria, Babylon, Media, and Persia. 2nd ed. J. Murray. https://openlibrary.org/works/OL5160480W/The_five_great_monarchies_of_the_ancient_eastern_world.
Roberts, Helen. 1981. “Reconstructing the Greek Tortoise‐Shell Lyre.” World Archaeology 12 (3): 303–12. https://doi.org/10.1080/00438243.1981.9979805.
Roberts, William H. 2015. Physics and Psychophysics of Plucked-String Instruments. PhD diss., University of Cardiff. https://orca.cf.ac.uk/80117/1/2015robertswhphd.pdf.
Russell, Daniel A. 2004–11. “The Vibration of a Fixed-Fixed String.” Acoustics and Vibration Animations (webpage). https://www.acs.psu.edu/drussell/Demos/string/Fixed.html.
Roederer, Juan G. 2008. Physics and Psychophysics of Music, 4th edition, Springer-Verlag.
Schauensee, Maude de. 1998. “The ‘Boat-Shaped’ Lyre: Restudy of a Unique Musical Instrument from Ur.” Expedition Magazine 40 (2): 20–28. https://www.penn.museum/sites/expedition/the-boat-shaped-lyre/.
Sethares, William. 1993. “Local Consonance and the Relationship between Timbre and Scale.” Journal of the Acoustical Society of America 94 (3): 1218–28. https://doi.org/10.1121/1.408175.
Straus, Joseph N. 2016. Introduction to Post-Tonal Theory. 4th ed. W. W. Norton.
Sutherland, A. 2006. Mesopotamian Music Stele That Commemorates Gudea King of Lagash In Temple Foundation Ceremony. https://www.ancientpages.com/2016/12/12/mesopotamian-music-stele-that-commemorates-gudea-king-of-lagash-in-temple-foundation-ceremony/.
Taffou, Marine, Clara Suied, and Isabelle Viaud-Delmon. 2021. “Auditory Roughness Elicits Defense Reactions.” Scientific Reports 11 (956). https://pubmed.ncbi.nlm.nih.gov/33441758/.
Taruskin, Richard. 2010. “Beginnings, as Far as We Know Them.” In The Oxford History of Western Music Online: Music from the Earliest Notations to the Sixteenth Century. Oxford University Press.
Tenzer, Michael. 2000. Gamelan Gong Kebyar: The Art of Twentieth-Century Balinese Music. University of Chicago Press.
Terhardt, Ernst. 2000. Auditory Roughness. https://terhardt.userweb.mwn.de/ter/top/roughness.html.
Trosch, Joshua. 2015. “Reconstructing a Classical Kithara.” Undergraduate independent study paper. Office of Undergraduate Research, Washington University. https://www.academia.edu/12474248/Reconstructing_the_Classical_Kithara.
Välimäki, Vesa, Jyri Huopaniemi, Matti Karjalainen, and Zoltán Jánosy. 1996. “Physical Modeling of Plucked String Instruments with Application to Real-Time Sound Synthesis.” Journal of the Audio Engineering Society 44 (5): 331–53. https://www.aes.org/e-lib/browse.cfm?elib=7902.
Vassilakis, Panteleimon Nestor. 2001. Perceptual and Physical Properties of Amplitude Fluctuation and Their Musical Significance. PhD diss., University of California, Los Angeles. http://www.acousticslab.org/papers/VassilakisP2001Dissertation.pdf.
Vassilakis, Panteleimon Nestor, and Kelly Fitz. 2007. “SRA 2.0: Spectral and Roughness Analysis of Sound Signals 2.0” (web application). Musical Algorithms (website): http://www.acousticslab.org/roughness/index.html.
Vitale, Raoul. 1982. “La musique suméro-accadienne: gamme et notation musicale.” Ugarit-Forschungen 14: 241–63.
Vos, Joos. 1982. “The Perception of Pure and Mistuned Musical Fifths and Major Thirds: Thresholds for Discrimination, Beats, and Identification.” Attention, Perception and Psychophysics 32 (4): 297–313. https://doi.org/10.3758/BF03206236.
Wachsmann, Klaus. 1950. “An Equal Stepped Tuning in a Ganda Harp.” Nature 165: 40–41. https://doi.org/10.1038/165040a0.
Waerzeggers, Caroline, and Ronny Siebes. 2007 “An Alternative Interpretation of the Seven-Pointed Star on CBS 1766.” Nouvelles assyriologiques brèves et utilitaires (NABU) 2007 (2): 43–45. http://sepoa.fr/wp/wp-content/uploads/2012/06/2007-2.pdf.
West, Martin Litchfield. 1994. “The Babylonian Musical Notation and the Hurrian Melodic Texts.” Music & Letters 75 (2): 161–79. https://doi.org/10.1093/ml/75.2.161.
—————. 2013. Hellenica: Volume 3: Philosophy, Music and Metre, Literary Byways, Varia. Oxford University Press.
Widdess, Richard. 1993. “Sléndro and Pélog in India?” In Performance in Java and Bali: Studies in Narrative, Theatre, Music, and Dance, ed. Bernard Arps, 187-97. School of Oriental and African Studies, University of London.
Williams, Peter and Barbara Owen, 2001. “Organ Stop.” In Grove Music Online. Oxford. https://doi.org/10.1093/gmo/9781561592630.article.20446
Wooley, C. Leonard. 1934. Ur Excavations (2). Carnegie Corporation for the Joint Expedition of the British Museum and the Museum of the University of Pennsylvania to Mesopotamia. http://www.flutopedia.com/refs/Woolley_1934_UrExcavations_Vol02_excerpt_FP.pdf.
Wulstan, David. 1968. “The Tuning of the Babylonian Harp.” Iraq 30 (2): 215–28. https://doi.org/10.2307/4199852.
—————. 1971. “The Earliest Music Notation.’ Music and Letters LII (4): 365–82. https://doi.org/10.1093/ml/LII.4.365.
Zwicker, Eberhard. 1961. “Subdivision of the Audible Frequency into Critical Bands.” Journal of the Acoustical Society of America 33 (2): 248–49. https://doi.org/10.1121/1.1908630.
Footnotes
* I would like to thank Sam Mirelman and an anonymous reviewer for this journal for their helpful comments on an earlier version of this article.
Return to text
1. Based on:
- Nabnitu 32 (=U 3011=UET VII 126), i, lines 1 to 10: see, e.g., Kilmer 1960, 274–275; Duchesne-Guillemin 1963, 3–7; Kilmer 1965, 264–65; Wulstan 1968, 216–17; Kilmer 1971, 133; Wulstan 1971, 366–68; Crocker 1978, 100; Dumbrill 2005, 27; Mirelman 2013, 46; Kilmer 2014, 95.
- ii. N. 4782: see, e.g., Crocker and Kilmer 1984, 82; Dumbrill 2005, 27–29, 70–72; Mirelman 2013, 46; Kilmer 2014, 95.
Note that YBC 11381 identifies these strings by numbers, from 1 to 9 (Payne 2010, 292–293), whereas i and ii employ Sumerian and Akkadian designations.
Return to text
2. Based on CBS 10996: see, e.g., Kilmer 1960, 278–281, 298–300; Kilmer 1965, 265–67; Wulstan 1968, 216–18; Kilmer 1971, 134–135; Wulstan 1971, 366–68; Dumbrill 2005, 37; Mirelman 2008; Mirelman 2010, 49–50; Mirelman 2013, 52, Kilmer 2014, 95.
Return to text
3. Gurney 1968, Wulstan 1971, 368–70, Kilmer 1971, 140, Gurney 1994, 101–4; Dumbrill 2010, 110, Fig. 8.
Return to text
4. Mirelman and Krispijn 2009; Mirelman 2013, 47, Fig. 2.
Return to text
5. Inscribed on CBS 1766 (Dumbrill 2017, 27–28; Dumbrill n.d., 1–2), where the numbers from 1 to 7 (Horowitz 2006, 38) are aligned with Mesopotamian names of the first seven strings in Nabnitu 32 and N. 4782 (Waerzeggers and Siebes 2007, 43–44).
Return to text
6. Wulstan 1971, 220–23, Gurney 1968, 229–33, Kilmer 1971, 140–42, Gurney 1994, 101–4, Dumbrill 2005, 47.
Return to text
7. The order of the six zakû dichords in which the name of the first dichord is same as the name of the tuning is in plain typeface. The first of the six zakû dichords is highlighted by a pair of filled cells; the la-zakû dichord in each tuning is highlighted by bold typeface.
Return to text
8. Välimäki et al. 1996, 343, Fig. 21, Penttinen and Välimäki 2004, 1208, Figs. 1 and 2, Nakai and Kawaguchi 2006, 1, Fig.1, Roberts 2015, 19, Fig, 2.1, Burg et al. 2016, 19, Fig. 2.12, and Russell 2004–11.
Return to text
9. Each pair of tones lasts three seconds. The lower tone’s fundamental frequency remains the same whereas the upper tone’s fundamental frequency increases from the 1st to the 11th. The sounds of these tones are generated by means of Audacity Team (2018) software and can be heard at Audio Example 1.
Return to text
10. The tone-pairs’ magnitudes range from approximately a unison to approximately an octave. The roughness values (y-axis) were measured using the default, midpoint settings of the interactive online software of Vassilakis and Fitz (2007: see also Vassilakis 2001). The measured tones, comprising six harmonic partials of uniform amplitude, were generated by means of Audacity editing software 2.3.0 (Audacity Team 2018).
Return to text
11. From left to right, in the nine tone-pairs, the relevant harmonic of the upper tone differs from its counterpart in the lower tone by -12, -9, -6, -3, 0, +3, +6, +9, and +12 Hz, resulting in 12, 9, 6, 3, 0, 3, 6, 9, and 12 undulations per second. The tone-pairs were generated and their roughness was measured as specified for Example 7, above. The sounds of these tone-pairs can be heard at Audio Example 3.
Return to text
12. In this regard, Josh McDermott and colleagues (2016) found that among the Tsimane', an indigenous Amazonian group who had not encountered European-derived idioms or produced polyphonic music, sounds varying in roughness resulted in valence judgments that resembled those of Westerners and concluded that an aversion to roughness is apparently present cross-culturally. Moreover, a more recent study by neuroscientists Marine Taffou and colleagues (2021) has concluded that roughness produces aversive responses. To be sure, as the Amazonian study shows, the extent to which such responses and valence judgments are deployed in musical practice can differ from one setting to another, a feature of musical behavior McDermott et al. specify as “aesthetic.” Nonetheless, the present study insists only that such responses and judgements are accessible cross-culturally and hence could have been relevant to Mesopotamian tuning.
Return to text
13. The present point obtains for any analysis where the “real” values of interval magnitudes are considered, without qualification, to be rational numbers, as they have been since Plato’s Timaeus : cf. Plato’s Cave.
Return to text
14. The present study insists that a zakû dichord might comprise several values close to a certain ideal fundamental-frequency ratio rather than a single value. Whereas Aristoxenus would agree with this position, Pythagoreans would not.
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Fred Hosken, Editorial Assistant
Number of visits:
11022