“Your Soul is the Whole World”: The Spaces of Claude Vivier’s Siddhartha
Christopher Goddard
KEYWORDS: Musical space, orchestral texture, formula technique, group-based composition, Claude Vivier, Karlheinz Stockhausen, Hermann Hesse
ABSTRACT: At 28’ duration and scored for a massive orchestra of eighty-nine players, Siddhartha (1976) eclipses all other works in Claude Vivier’s catalogue in dramatic scope and sonic grandeur. The composition dates from soon after Vivier returned to Canada following his studies with Karlheinz Stockhausen in Cologne from 1972–74, which left a lasting impact on the young composer. Siddhartha showcases the extent of that influence in its diligent use of “formula technique” and its unconventional distribution of the orchestra into smaller groups on stage. In this article, I outline how the work’s principal melody transforms across contrasting spatial domains: in “acoustic space,” expressed in physical location on stage, and in “metaphorical space,” expressed in pitches-in-register. Using Hesse’s novel as a hermeneutic model, I then consider alternate poetic readings of the work vis-à-vis its interaction of spatial properties in the large-scale form. Ultimately, I argue that Siddhartha is a deeply personal piece that communicates, through the medium of musical structure, feelings of alienation and connection during an unsettled time in Vivier’s life.
DOI: 10.30535/mto.29.3.2
Copyright © 2023 Society for Music Theory
1. Introduction
[1] Siddhartha was composed from 1975–76, soon after Vivier returned to Canada following two formative years of study with Karlheinz Stockhausen in Cologne. A near thirty-minute sonic tour-de-force, the work bespeaks a restless creative spirit in search of his authentic voice. What strikes the listener on first hearing Siddhartha is its rich synthesis of seemingly contradictory styles. Much of the work is saturated in polychromatic sound, evincing the serial method favored by Vivier in his youth. It also features moments of stark melodic clarity that foreshadow the monodic approach of his artistic maturity. This basic opposition is mirrored in the temporal and geographic disparity between the work’s Hindu title and Western symphonic medium. As Bob Gilmore writes, Siddhartha “shows Vivier’s music at a time of momentous change” and represents “a considerable widening of the expressive nature of [his] musical language” (2014, 113–114).
[2] This essay examines how Claude Vivier employs different domains of musical space to articulate form in his orchestral work Siddhartha. I begin with an overview of Karlheinz Stockhausen’s conception of musical space, providing examples from his oeuvre that engage what I call “acoustic” and “metaphorical” space. I then show how Vivier confers structural status to both spatial domains in Siddhartha by employing them as evolving attributes of the principal melodic formula. As part of that discussion, I show how the interaction of these spaces gives rise to notable moments of instrumental timbre and propose a model for depicting their independent trajectories as a single unified contour. I conclude with a brief interpretive analysis of Vivier’s reception of the eponymous Hermann Hesse novel, in particular its “polarity motif” and the symbolic river which demarcates much of its narrative structure. I also explore how the composer may have been inspired to see points of overlap between the story and the circumstances of his own life.
2. Background: Stockhausen’s spatial thought
[3] In his 1959 lecture “Music in Space” (Musik im Raum), Stockhausen elevates spatiality, or “location,” to the level of pitch, duration, timbre, and dynamics as an essential “tone-characteristic” (1961, 73). In its pursuit of “equal participation of all tonal properties,” serialism ushered in a total dissolution of all polyphonic principles and thus “a permanent monody as the only possibility” (Stockhausen 1961, 70). Musical depth, Stockhausen argues, can therefore exclusively arise out of a “polyphony of spatial movements” achieved through an unconventional distribution of sound sources (Cott 1973, 46):(1)
It first became possible to articulate longer pointillist structures by giving them mobility in space, moving them from one place to another. This
. . . provided a solution to the problem of how to make simultaneous superimpositions of such pointillist structural strata comprehensible through a spatial distribution of the sound. (Stockhausen 1961, 70)
Though the above passage implies an equivalence between sonic motion and sonic layering as spatial effects, Stockhausen would later come to explore them as distinct compositional categories. Orchestral works such as Gruppen (1957) and Carré (1960) are characterized by the dynamic movement of sound masses around a centrally positioned audience, like the four-channel electronic media work Gesang der Jünglinge (1956) from the same period.(2) The idea of a “multilayered spatial composition” is introduced in Kontakte (1960), which plays with the listener’s sense of proximity and distance by layering strata of superimposed sound.(3) Using this technique, Stockhausen creates an illusion of spatial depth that is “analogous to the way we compose layers of melody and harmony in the two-dimensional plane of traditional music” (Stockhausen 1989, 106).
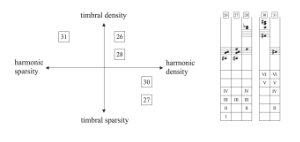
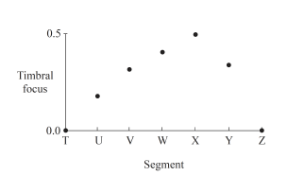
Example 1. Plotting harmonic and timbral density in five “moments” of Stockhausen’s Stop
(click to enlarge)
[4] Later works such as Mixtur (1964) and Stop (1965) exhibit more complex forays into musical space by dividing the orchestra into small clusters of instruments. Mixtur is comprised of five timbrally similar groups seated apart from each other either on stage or surrounding the audience, with seven loudspeaker groups placed among them providing ring modulations of the acoustic inputs. Whereas Kontakte (in its original version) simulates layers of depth through electroacoustic means, Mixtur achieves a more visceral result in its interplay of live instruments and real-time processing. In contrast to Mixtur, Stop divides its ensemble into six characteristic groups of mixed instruments, whose material is a succession of harmonic “moments” of predetermined duration, tempo, and rhythm. The number of pitches contained in these moments and the number of groups called upon for their iteration are determined separately, producing a kaleidoscope of timbral and harmonic densities. To visualize this, Example 1 situates moments 26, 27, 28, 30, and 31 of Stop on a two-dimensional Cartesian graph that plots harmonic density on its x axis (1–4 pitches) and timbral density on its y axis (1–4 groups). Stockhausen’s modular approach to pitch and orchestration in Stop would help lay the conceptual groundwork for the work that is the subject of this essay, composed some ten years later by his student Claude Vivier.
[5] In contrast to the open-form experimentations of the 1960s, Mantra (1970) for two pianos is a traditionally notated and staged composition that Jonathan Harvey describes as a “return to the ‘personal’ [and] an assertion of the individual mind” (1975, 126). The music of Mantra derives entirely from a melodic “formula” that is itself a concatenation of smaller linear fragments, or “limbs.” A series of contour-preserving expansions are applied to this formula, widening its ambitus and lengthening its duration. The sharp aesthetic pivot of Mantra can in fact be traced to ideas first laid out by the composer twelve years prior: by likening total parametric saturation to “a permanent monody” in Musik im Raum, Stockhausen hints at a lingering melodic dimension to his art.(4) Crossing that threshold on the conventional concert stage necessitated, however, a new means of projecting musical depth. As Robin Maconie writes, Stockhausen’s solution is to fully integrate the work’s micro- and macrocosmic structure:
The formula is more than a seed: it is an aural navigational aid superseding the cantus firmus, fugue or sonata subject, Wagnerian leitmotif, or Schoenbergian series, allowing the listener to follow the expansions and contractions of musical expression from the smallest detail to the largest structural component. (Maconie 2005, 222)
In the innovative “formula technique” of Mantra we encounter, in my view, the spatial polyphony of Stockhausen’s earlier works transmuted onto the written score—a procession from acoustic space to metaphorical space. By acoustic space I refer to the three-dimensional physical realm wherein sound events are experienced and processed by way of depth perception. By metaphorical space I refer to the gamut of pitches that proceed from an equal-tempered parsing of the frequency spectrum, which we commonly understand as spanning two-dimensionally from low to high (or vice-versa). I attribute this latter term in part to Lawrence Zbikowski’s work on musical metaphor and his notion of “cross-domain mapping,” which suggests that our understanding of abstract objects emerges out of real, embodied knowledge gained through sensory experience (2002).(5) By layering the formulaic statements of Mantra at contrasting pitch- and time-scales, Stockhausen links the physical with the imagined in a particularly vivid way. Just as the formula’s gradual widening of register implies an expansion of physical (or “acoustic”) space, its temporal dilation seems also to simulate the traveling of sound across ever-greater distances.
[6] Analogies between what I have called acoustic and metaphorical space have been central to our framing of theoretical concepts since Helmholtz.(6) The Austrian music psychologist Albert Wellek (1904–1972) was among the earliest scholars to address the topic of spatiality in sound, as distinct from an intrinsic “musical space.” Advancing an earlier model put forward by Ernst Kurth, Wellek proposes a distinction between what he calls “hearing space” (Gehörraum) and “tone space” (Tonraum) (Harley 1994, 62).(7) Gehörraum is the physical space in which sound is produced, and Tonraum is an ambiguous three-dimensional tonal space consisting of pitch, time, and “musical depth” (Wellek 1934). These spaces together form a complex four-dimensional Musikraum that amounts to our total perception of a musical work. While Kurth and Wellek viewed physical spatiality as a secondary musical property, later writers such as Edward Lippman argue for its importance as an object of study. In his 1952 doctoral dissertation Music and Space: A Study in the Philosophy of Music, Lippman attributes this prior bias to “the sound-ideal of Romanticism,” and calls for the elevated status of “the empirical world of sense-perception” in the twentieth century (Lippman 1952, 87).
Example 2. Stockhausen’s seating arrangement for Inori (© Stockhausen-Stiftung für Musik, Kürten, Germany)
(click to enlarge)
[7] Stockhausen came to embody Lippman’s consolidated vision of musical space in part because of his unique, cross-domain perception of the world.(8) For him, pitch and rhythm are merely points on a continuum of aural cognition; and as the Doppler effect demonstrates, pitch is itself a function of its speed moving through space (Cott 1973, 96–97). The appearance of Pole für 2 (1970), Ylem (1972) and Inori (1974) signaled new frontiers in Stockhausen’s ongoing spatial project. Pole is a site-specific piece written for the 50-loudspeaker array inside the German pavilion at the 1970 Osaka World’s Fair. In this work, the unique spherical properties of the pavilion inspired Stockhausen to construct an “aural architecture” that mediates between “tangible materials (that is, the physical, tactile boundaries of containment), and the intangible (the nature of sound as a kinetic and ephemeral phenomenon)” (Fowler 2010, 189). The imaginative Ylem intersects acoustic and metaphorical space in a purely instrumental setting, with the programmatic goal of depicting an expanding and contracting universe. Musicians in this nineteen-player work begin by sounding a tritone and then gradually widen their pitch material until the full range of their instruments is reached, while ten musicians carrying handheld instruments move slowly outward towards the left and right walls of the auditorium. In Inori, Stockhausen takes the bold step of redistributing an entire symphony orchestra according to instrumental location on the pitch continuum. While strings are placed in the front as in a conventional setup, the whole ensemble is divided by a registral “axis” running through the center of the stage, creating a stereophonic effect with low-sounding instruments seated stage-right and high-sounding instruments seated stage-left (see Example 2). Though this piece sees formula technique applied for the first time in an orchestral setting, the scalar dilations of Mantra are absent. Its register-defined stage configuration instead serves to elucidate a stratification of musical material along the frequency spectrum, brought to highest resolution in the fifth and final section of the work, Polyphony. It is clear that at the time of composing Inori, pitch and location were two aspects of a single, integrated vision of musical space in Stockhausen’s mind.(9)
3. The contrasting spaces of Siddhartha
[8] Claude Vivier’s studies with Stockhausen in Cologne began in autumn 1972 and concluded in the summer of 1974, just before the creation of Inori. The reverence held by the pupil for his mentor is well documented, and a necessary predicate for understanding his works from this period.(10) For Stockhausen’s part, pedagogy was always closely connected to his composition practice: Stop was conceived as a classroom study to demonstrate his creative process, and Mantra became the basis for a writing exercise administered to composers aspiring to enter his studio—including Claude Vivier. Arriving in Germany, the young Canadian had already undertaken modest experimentations in acoustic space, for example in Musik für das Ende (1971) for twenty voices divided into three groups. A work such as Liebesgedicht (1975), completed after Vivier’s time with Stockhausen, is unmistakably indebted to Mixtur in its segregation of the ensemble instruments into separate quartets of voices, winds, and brass.
Example 3. The Siddhartha formula
(click to enlarge)
Example 4. Six scalar dilations of the Siddhartha formula
(click to enlarge)
[9] Siddhartha was commissioned by the National Youth Orchestra of Canada for performance in their 1975–76 season.(11) At 28’ duration and scored for a vast orchestra of eighty-nine instruments, it is Vivier’s largest and most ambitious work. The structure of Siddhartha is founded on a recurring melody that reveals in its presentation and ensuing development the strong influence of Stockhausen’s formula technique. In his paper “Claude Vivier, Siddhartha, Karlheinz Stockhausen, la nouvelle simplicité et le râga” Jean Lesage outlines the accumulative processes that define this formula’s pitch and rhythm content (2008). Seven segments (or “limbs”) comprise the melody, which I label T through Z in Example 3. Following the initial
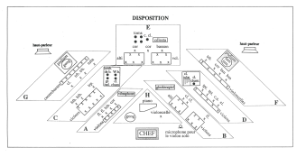
Example 5. Vivier’s suggested seating plan (© 1976 by Boosey & Hawkes, Inc. All Rights Reserved. Reprinted by Permission)
(click to enlarge)
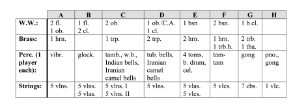
Example 6. Group composition by instrumental family
(click to enlarge)
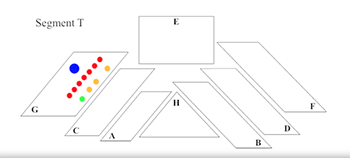
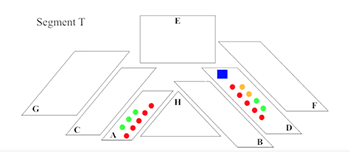
[10] The orchestra of Siddhartha is divided into eight groups labeled A through H in the score, all of which are seated contiguously within the confines of a conventional stage. As Example 5 shows, Vivier’s archetypal group configuration features one or two sets of string instruments in the front, a small collection of wind and brass instruments behind them, and a single percussionist placed to the rear or side. The trio of cello, piano and gong that comprises Group H defies this model somewhat, functioning instead as a sort of concertino solo group at the front of the stage.(14) Small exceptions can also be found in Group B, which lacks a brass instrument, and Group G, in which the placement of strings and winds is reversed (presumably to accommodate the size of the double basses). A summary of the individual group components can be viewed in Example 6. In effect, the redistributive pattern of Siddhartha produces eight orchestras-in-miniature that together amount to the dimensions of a full symphony orchestra—an integration of the microcosmic and the macrocosmic in the domain of musical texture.(15) The other organizing principle guiding Vivier’s group formation is proximity of range in metaphorical pitch space. Groups A, B and C feature high-sounding instruments, Groups D and E include instruments of a middle register, and Groups F and G contain exclusively low-sounding instruments. The registral profile of each group is also linked to their location in acoustic space on stage. In contrast to the stereophonic division of Stockhausen’s Inori, the orchestra of Siddhartha fans out radially from a central focal point occupied by the conductor. Groups A and B are positioned nearest to it, Groups C and D make up a middle tier, and Groups G, E, and F form an outer ring at the back of the stage. This orientation can be quickly summarized in the statement, spatial distance from the conductor is co-determinate with depth on the frequency spectrum.
[11] If one was to devise an ideal configuration for acoustically expressing the vast pitch range of an orchestra, a natural solution might be to stack instruments in a vertical line from the stage floor up to the rafters, with the largest at the bottom and the smallest at the top. This vertiginous arrangement would accord with our common low-to-high conception of pitch; it would not, however, have any real basis in the physics of sound (it may also raise some eyebrows among orchestra managers). When I played the piano part in a performance of Siddhartha at the Lucerne Festival in 2013, I vividly experienced its spatio-registral layout as a sonic reality. Musicians in Groups A through G would likely have perceived the island of pitch space they occupied, and sensed the larger design into which they fit. Seated immediately below the conductor as a member of Group H, I was able to hear the music from an acoustic “sweet spot” that Vivier might have imagined as the ideal listening position. As to the aural impression made upon the audience that evening, I can only speculate. Whether seated deep in the balcony or at the edge of the parterre, I suspect all listeners in the hall were able to grasp the parsing of sound into discrete registral depth planes, encoded by both the stage arrangement and the music itself.
Example 7. The continuum of orchestral configurations in Siddhartha
(click to enlarge)
[12] The heterodox orchestral layout for Siddhartha is overdetermined, in the sense that its implementation can be justified in multiple ways. From a pragmatic standpoint, having large, low-sounding instruments placed at the back of the stage introduces no new sightline issues for the other musicians. The configuration also invokes Stockhausen’s prized Doppler effect, which primes us to associate proximity with higher frequency and distance with lower frequency (in a standard concert hall most of the audience would be seated closer to the acoustic focal point than to the orchestra’s registral depths). Most importantly, it allows for two contrasting modes of sonic coherence to be manipulated independently, the one grounded in timbre/orchestration and the other grounded in register. In Vivier’s stage arrangement, localized sounds are registrally similar and timbrally heterogenous, while diffuse sounds feature registral variety and timbral homogeneity. Example 7 shows these contrasting configurations as opposite poles on a one-dimensional textural continuum. As we will see, Vivier toggles between both extremes, with important implications for the work’s large-scale form.
Video Example 1. Tracking the progression of the first formulaic statement (mm. 2–32) in acoustic space
(click to watch video)
Example 8. Comparing group entries on the first page of the score to the opening pitch contour of the formula
(click to enlarge and see the rest)
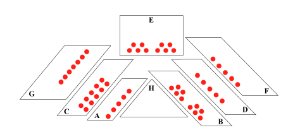
[13] Siddhartha begins with a dramatic opening presentation of the principal melody in m. 2. A tutti
Example 9. Segment U of the second formulaic statement (m. 43)
(click to enlarge)
Video Example 2. Tracking the progression of the second formulaic statement (mm. 42–70) in acoustic space
(click to watch video)
[14] The formula appears for a second time starting in m. 42. In this statement the perfect intra-group congruity of the opening measures is disturbed, however elements of that earlier texture persist. A characteristic instrumental configuration for this section can be seen in Example 9. In this excerpt, Segment U in m. 43 is voiced by all members of Group B in addition to the horn from Group F. Most segments in this statement follow a similar template, with one group playing tutti and another contributing one or two parts. These anterior instruments add subtle coloration to the prevailing group, often in a contrasting range as a sort of timbral “shadow.” Going on from m. 43, Group C plays Segments V and W (mm. 44–47) as an ensemble, receiving reinforcement from members of Group F and then Group A. The following Segments X (mm. 47–48) and Y (mm. 49–51) highlight Groups E and D in turn, with added support from Groups B and F respectively. Starting in m. 63, Segment Z features participation from three different areas of the stage for the first time, enlisting members of Groups A, H and F. Video Example 2 depicts the progression of instrumental distributions for this second formulaic statement in a flipbook-style video. No audio accompanies this example, to allow for easier viewing of the slowly unfolding texture. Juxtaposed with Video Example 1, this figure makes clear the incremental progression from intra-group to inter-group configurations that is underway.
Example 10. Measuring timbral focus in the second formulaic statement (mm. 42–70)
(click to enlarge)
Example 11. Plotting the evolution of timbral focus in the second formulaic statement (mm. 42–70)
(click to enlarge)
[15] At m. 42 the original formulaic scale (“Scale 1”) is repeated, likely as a means of drawing closer attention to the textural shift that has been initiated. Here Vivier also introduces variety in the intra-group distribution of metaphorical space. In contrast to the unisons of the first statement, this passage spins out melodic material across multiple register levels, belying the careful slotting of groups along the frequency spectrum. Returning to Example 9, we see that Segment U at m. 43 features six parts transposed at five register levels (taking into account the glockenspiel’s sounding two octaves above the notated pitches) for an overall span of four octaves. The flute and five violins of Group B, both beginning on
[16] In addition to its threefold group distribution, Segment Z at m. 63 also features harmonization—doubling at a non-octave interval—for the first time.(19) In Segments T through Y of the same formulaic statement, Vivier uses octaves to enrich the melody’s timbral profile; the harmonization that debuts in m. 63 merely broadens that embellishing function by further filling out pitch space. Our ability to hear harmonizing lines as timbral extensions of a melody results from a phenomenon that Steven McAdams calls “auditory grouping”:
Concurrent grouping determines how components of sounds are grouped together into musical events, a process referred to in psychology as auditory fusion. This grouping process precedes, and thus conditions, the extraction of the perceptual attributes of these events, such as timbre, pitch, loudness, duration, and spatial position. (McAdams 2019, 217)
Example 12. A reduction of Segment Z from the second formulaic statement (mm. 72–77)
(click to enlarge)
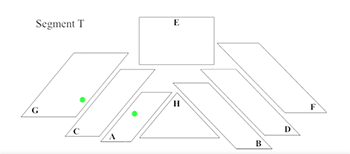
Segment Z at m. 63 is a fruitful case study in the degree to which the five attributes listed by McAdams contribute to perceptual fusion. Example 12 reduces the full segment into three staves representing Groups A, F, and H. In the upper two staves, Groups A and F articulate the formula verbatim at a distance of three octaves. We can identify several strong grouping cues in this doubling, including a consonant interval of transposition, rhythmic synchrony, and dynamic uniformity. Its timbral heterogeneity and spatial distance on stage are, by contrast, attributes that resist grouping, though not sufficiently to disturb the overall perception of fusion. The harmonizing cello line in the lower staff follows a similar contour to the formula, but wanders in its interval of transposition. To my ear, this divergence in pitch is more than adequately offset by the cello’s near rhythmic unison with the segment’s distinctive rhythmic profile.
[17] An interaction of metaphorical space and acoustic space also affects our hearing of this passage. Of the groups articulating the segment verbatim, it is the lower-sounding Group F that shares the registral bandwidth of the solo cello. In an ordinary performance setting these two lines would grate against each other discordantly, driving perceptual segregation. In the Siddhartha layout, this dissonance is somewhat alleviated by the gap separating Groups F and H on stage. Conversely, the proximity of Group A to Group H in acoustic space is balanced by the wide distance separating their respective lines in metaphorical space. In short, the solo cello line at m. 63 is reduced in its capacity to negatively impact perceptual grouping because of its distance from Groups A and F in the domains of metaphorical and acoustic space respectively. This facilitates our hearing the cello as a participant in the segment rather than as a contrapuntal line.
Example 13. Segments T and U from the fifth formulaic statement (mm. 204–205)
(click to enlarge)
[18] The first scalar expansion (“Scale 2”) takes place in the third statement of the formula at m. 70, widening its ambitus from 12 to 16 semitones. Further dilations occur in statements at m. 126 (“Scale 3”; 20 semitones) and m. 204 (“Scale 4”; 24 semitones). The melody’s durational expansion begins at m. 126. Starting with this fourth formulaic statement, each expansion augments the formula by 50% of its original rhythmic values until a multiplication coefficient of three is reached in the ninth and final statement at m. 381 (1.5x→2x→2.5x→3x). From statements three through five, inter-group textures overtake intra-group textures as the predominant instrumental configuration. To illustrate this, the score excerpt of Example 13 shows the first two segments of the fifth statement at m. 204. Rather than being locked into fixed horizontal planes, the melody dovetails between instruments in the manner of a Klangfarbenmelodie, or more precisely a Raum-Melodie (“space melody”).(20) In m. 204, the two formulaic pitches of Segment T are exchanged between Groups B and C, while Segment U at m. 205 contains an intricate inter-group hocket in 32nds. Fully formed chords harmonize this statement, adding depth and dimension to the melody as it claims ever-greater swathes of pitch space.
Example 14. Instrumentation for the complete seventh formulaic statement (mm. 251–302)
(click to enlarge)
Example 15. A reduction of Segments T, U, V, and W from the seventh formulaic statement (m. 251–260)
(click to enlarge and listen)
[19] The music of Example 13 appears at first glance to fulfill the large-scale textural transformation underlying Siddhartha: apart from Group H, the formula is now heard from every corner of the stage, having been fully dissolved into the orchestral mass. The instrumental sound, however, is heterogenous—a property it shares with preceding statements. As Example 7 showed, Vivier’s orchestral configuration contains both a textural and a timbral component. A complete inversion of the opening statement must therefore also be attended by homogeneity in the instrumental distribution of formulaic material. That inversion is indeed reached 48 measures later, at m. 251. In this seventh formulaic statement a string orchestra emerges ethereally out of the atomized orchestra, reprising the harmonization heard at m. 204.(21) The monochromatic Example 14 illustrates the instrumentation for all seven segments. “Traditional” voicings characterize this passage, as tightly packed chords in the middle register are undergirded by octaves and twelfths in the lower strings. In contrast to the formula presentation at m. 204, this statement is comprised of more defined instrumental lines, giving it the feel of a slow-moving chorale.(22) Example 15 provides a reduction of the first four segments and Audio Example 1 provides an accompanying sound file.
[20] Vivier’s choice to exclusively score this seventh statement for strings warrants a bit of unpacking. From my own perspective as a composer, I would consider it likely that he at one point weighed the option of passing the melody between instrumental families as it progresses between segments. Up until this moment Siddhartha has been highly variegated in its sonic character—a (serialism-infused) rebuttal of the traditional (tonality-infused) orchestral hierarchy. By suddenly pivoting to more conventional orchestrations, Vivier signals the structural salience of this passage to striking effect, an effect that is further accentuated by the preceding sixth statement, which reprises the original version of the formula in an arresting duo for piano and bass clarinet.(23) The composer’s preference for strings over woodwinds or brass can be understood in more practical terms, as the bloated rhythms of this statement (at two times the original formulaic values) might have presented considerable breathing issues for wind instruments. Using strings bypasses that issue and also creates, by virtue of their dynamic range, the opportunity to seamlessly steer the “chorale” into and out of the perceptual foreground as secondary material appears in other parts.
[21] In the 1988 recording of Siddhartha by Walter Boudreau and l’Orchestre Métropolitain de Montréal, the stirring passage just described occurs at 16’49” of its 27’ total duration. We can deduce from the Fibonacci series employed in the construction of the principal formula that Vivier occasionally relied upon mathematical proportions as part of his compositional method. The arrival of this moment at almost exactly the golden mean can therefore be taken as further evidence of its centrality to the overall form. From the audience’s perspective, the expressive impact made by the seventh statement is profound. Since the grand opening gesture, we have experienced a steady diffusion of consolidated sound objects, an entropic progression from unity to disunity. We are surprised to encounter at the endpoint of that disintegration not chaotic randomness, but another locus of organization based on the very property—instrumental homogeneity—that Vivier’s orchestral layout seeks to subdue. In one stroke, a fundamental tension of the work, that one form of sonic coherence must come at the expense of the other, is revealed.
Video Example 3. Tracking the progression of the eighth formulaic statement (mm. 304–270) through acoustic space
(click to watch video)
Example 16. A reduction of the climactic passage from mm. 371–380
(click to enlarge and listen)
[22] Had this seventh statement concluded Siddhartha, we might be inclined to construe the work’s poetic project as equilibrium; symmetry; yin-yang balance. This interpretation is thwarted, however, by the next formulaic appearance at m. 304. As Video Example 3 shows, the instrumentations for this eighth statement are a patchwork of distributions exhibiting no clear pattern. Traces of the preceding timbral homogeneity are visible in Segments V, X, and Y, while Segments T, U, and W each feature three or four different families. As this statement unfolds, it is unclear to the listener whether its configurations anticipate a return to intra-group textures or foreshadow some new organizational model. Its recapitulatory function is confirmed by the climactic passage that follows at m. 371, which can be seen in Example 16 and heard in Audio Example 2. Here intra-group textures are restored in the form of rapid sixteenth-note scales that sweep through registral space. A reverse Fibonacci series governs the time interval spanning each group entry, giving the passage a sense of controlled intensification. The scales themselves are distillations of each formulaic dilation (Scales 1–6 of Example 4), alternating transpositions at the fourth and at the octave. As a result, this passage recalls the dual
[23] Siddhartha closes with a recessive coda beginning at m. 381. In it, Vivier layers previously unheard versions of the formula in a dense sonic collage. One statement featuring Groups B, H, and D brings the ongoing process of formulaic expansion to its terminus, employing Scale 6 in 3x rhythmic augmentation. In a concurrent statement, Groups A and C articulate the formula in a brisk 0.5x rhythmic diminution with original pitches. Later in the coda we also encounter fragments of the formula in melodic inversion, at m. 389 (Groups A and E) and at m. 395 (Groups F and G). By superimposing different forms of the principal melody in this way, Vivier showcases its versatility while emulating the approach taken by Stockhausen in Mantra.(24) The polyphonic virtuosity of this section and its location in the overall form are reminiscent of stretto technique, the climactic device of fugue form in which subject entries overlap in anticipation of the final cadential arrival. Whereas Bach stretti are typically summarizing in function, the ambiguous coda of Siddhartha offers a glimpse of the formula’s limitless potential for reinvention beyond the boundaries of the work.
Example 17. An overview of the nine formulaic statements and their evolving spatial attributes
(click to enlarge)
[24] Example 17 provides a zoomed-out overview of the formula’s evolution in Siddhartha. The starting measures for nine total formulaic statements are enumerated at the top of the figure. Beneath this, six scalar dilations and four rhythmic augmentations are reduced in the upper two staves. The bulk of the example is dedicated to the formula’s textural morphology amongst the eight groups, which I notate using an original shorthand of empty and opaque noteheads. Through the first five statements, “tutti” configurations of four to five parts can be seen to gradually give way to more “soloistic” configurations of one to three parts. Statement 7 brings this process to its completion following the brief recapitulatory interlude of Statement 6. Statement 8 is transitional, portending the return of the opening configuration in m. 371, and Statement 9 concludes the work with a mixture of different textures. The bottom of the graphic tracks the large-scale shift from intra-group to inter-group configurations and its ensuing reversal in the second half of the piece.
[25] Comparing the upper and lower portions of Example 17, a clear divergence in the trajectories of the formulaic properties emerges. In the domain of pitch and rhythm, the formula undergoes an open, linear process of expansion. Its instrumental distribution on stage meanwhile follows a closed, cyclic process of return. I see this embedding of linear and cyclic structures as analogous to the overlapping of (linear) scale-step space and (cyclic) chromatic space that occurs in much of the tonal repertoire of the 19th century.(25) In a sense, the scalar expansions of the Siddhartha formula manifest a similar tension in their decoupling of pitch and pitch class. Each formulaic dilation is the product of select pitches being transposed up by octave(s) from the original semitonal scale—essentially a reordering of the chromatic gamut to fit a new ambitus. These dilations are measured by their raw distance in linear space while the background collection of pitch classes they draw from inhabit a cyclic space.
Example 18. A unified spatial model of the transforming formula in Siddhartha
(click to enlarge)
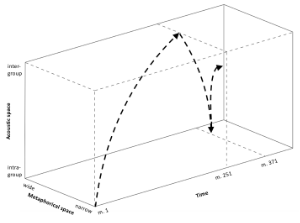
[26] The structures depicted in Example 17 can alternatively be consolidated in such a way that frames the evolving formulaic attributes as a single unfolding contour. Example 18 brings together the dimensions of time (x axis), metaphorical/pitch space (y axis), and acoustic space (z axis) into a unified geometric model.(26) The three-dimensional space depicted in this example could be understood as a representation of Albert Wellek’s concept of Musikraum, mentioned in the first part of this essay. In that context the vertical z axis would represent Gehörraum (the “auditory space of sound localization”) and the x and y axes together would represent the specifically musical Tonraum.(27) The developmental path of the formula begins at the origin and follows a broad arching movement as it traverses the x and y axes. The floor of the model is returned to at m. 371, after which the coda’s texture causes a brief ricocheting effect. Wellek’s “pure feeling space” offers an integrated, quasi-synesthetic perspective on Siddhartha by putting into graphic form Stockhausen’s original cross-domain paradigm (Di Stefano 2022, 177). The figure shown in Example 18 allows us to view the formula not as a collection of disparate attributes, but as a holistic structure with discrete directionality and shape.
4. Conclusion: Extra-musical considerations
[27] In his Hermann Hesse monograph, G. W. Field identifies within Siddhartha a “polarity motif” that underlies many of the novel’s major themes (1970, 76). The opposition being expressed pits the physical world against the ascetic world of “deadened sense perception,” manifesting in related dualisms such as materialism vs. spiritualism; sensuality vs. intellectuality; activism vs. passivity; affirmation vs. negation. Field sees this contrast as an allegory of Western and Eastern ontologies, as embodied in particular by Siddhartha and his friend, the monastic Govinda. Siddhartha’s “Faustian” striving gives rise to progress and metamorphosis, while Govinda represents the concept of metempsychosis, or eternal return (Field 1970, 80). These poles are transcended by a higher unity of “oneness” that becomes a motif in itself, symbolized by the river and the mystic syllable “om.”
[28] I see Vivier’s stratification of formulaic attributes as an attempt to weave Hesse’s polarity motif into the structural fabric of the piece. The programmatic basis for this strategy is best captured in an early episode of the novel, in which Siddhartha and Govinda muse on the direction their journey has taken:
“Now tell me, Govinda, are we really on the right path? Are we really approaching knowledge? Are we really approaching redemption? Or are we not perhaps going in a circle—we who thought we were escaping the cycle?”
Govinda said: “We have learned a lot, Siddhartha, we still have a lot to learn. We are not going in a circle, we are going upward. The circle is a spiral, we have already ascended several levels.” (Hesse 1999, 17)
Siddhartha’s query and Govinda’s statement each proffer a unique hermeneutic lens for analyzing the orchestral work. From the perspective of the protagonist, we might interpret the late recapitulation of the opening instrumental configuration as a negation of the ongoing formulaic expansion. Cyclic forces impede Siddhartha’s path to enlightenment, and his failure to escape them produces a tense inertia. Govinda, by contrast, invokes the shape of a spiral: a harmonious synthesis of both the linear and circular aspects of his “ascent.”(28) This perspective prompts us to hear the textural return in a more constructive light, renewed as it is by the ongoing transformations to the formula in pitch and duration. Though it does not resemble a spiral, Example 18 could be viewed as a portrayal of the latter perspective. Since the instrumental distributions evolve along a continuum of textures (refer back to Example 7), their cyclic progression can be represented in linear (one-dimensional)—as opposed to planar (two-dimensional)—space, which takes the form of a simple rising and falling curve along the figure’s z axis.
[29] The river, “always at all times the same and yet new in every moment,” is at the core of the novel’s unfolding action. According to Theodore Ziolkowski, it acts as a “natural border between the realms of spirit and sense” delimiting the three phases of the protagonist’s life, from his initial crossing to his subsequent return as a ferryman “attuned to the river’s song” (1965, 160). As a “projection of Siddhartha’s inner development into the realm of space,” the river is a clear antecedent for Vivier’s musical setting. Jean Lesage echoes Ziolkowski when he describes the formula’s “projection in time and space” in the context of analyzing its transformations in pitch and duration (2008, 111). By contrast, the larger story of Siddhartha seems to resemble the path taken by the formula through acoustic space. The inter-group configurations that frame the piece represent the forest where Siddhartha’s life begins and ends, while the interior intra-group configurations symbolize his venturing into the city beyond the river’s banks. The timbral homogeneity that emerges in the first two thirds of the work could also be an attempt to depict his closer attunement to sensual experience. It is somewhat paradoxical, however, that this family-centered instrumental recalibration aligns narratively with Siddhartha’s renunciation of his own Brahman tribe.
[30] Already a touchstone of hippie culture by the 1970s, Hesse’s novel would certainly have resonated with Vivier on a deeply personal level. His early years in a Catholic orphanage instilled in the composer a lifelong interest in mysticism, which like Siddhartha was inculcated through a childhood of quiet introspection. The move to Cologne was motivated by a desire to be among the disciples of Stockhausen, whose guru-like aura resembled Gotama, the exalted Buddha to whom Siddhartha makes his pilgrimage. Germany was also a place of sexual awakening for the young Canadian: like the novel’s protagonist, Vivier discovers the female body during his itinerant years, not as a celibate but as a free spirit exploring his latent bisexuality (Gilmore 2014, 83). Vivier wrote Siddhartha soon after settling back in Canada in 1974, where he faced an uncertain future as a working artist. In his biography of the composer, Bob Gilmore reveals the anxiety clouding this return to North America, which was more the result of economic necessity than an earnest wish to reintegrate into the Canadian music scene (2014, 96). I see the piece as an attempt by Vivier to give voice to the complex feelings he no doubt experienced during that time. Having had the world opened up to him abroad, in his return home he faced the difficult task of reconciling his past with a hard-won personal and creative freedom.
[31] The ambiguous coda of Siddhartha invites a variety of poetic interpretations. To my ears the densely layered polyphony of this section is a musical rendering of the river, which the text routinely refers to as a pluralistic entity (“softly sounded the river, singing in many voices”; “with a thousand eyes, the river looked at him”). As the site of the story’s apotheosis in the final chapters, the river fulfils its function as synthetic metaphor. The coda could in that sense be reckoned as external to the preceding music—a transcendence of its structure, evoking the achievement of a higher metaphysical level. With its mixture of intra- and inter-group blends, the coda also occupies a liminal place on the textural continuum, allowing it to potentially be viewed as a continuation of the ongoing orchestral redistribution. A third perspective may be gleaned from a remark Siddhartha makes to Gotama in the fourth chapter:
Yet now, according to that selfsame law, this unity and consistency of all things is nevertheless interrupted in once place: something strange, something new is pouring through a small gap into this world of unity, something that was not here before, something that cannot be shown and proved. (Hesse 1999, 31)
As I have previously noted, the coda’s sense of closure is diminished by the appearance of previously unheard formulaic transformations. These innovations could be understood as a disturbance to the equilibrium gained by the preceding textural recapitulation, producing fissure in the overall form. In this way the river can be seen as a symbol of renewal or even rebirth.
[32] The episodic nature of Hesse’s Siddhartha and its overarching theme of self-discovery places the story squarely within the Bildungsroman tradition. Opposing notions of “searching” and “finding” are reified in the contrasting orchestral configurations of Vivier’s score, both of which project a joint image of alienation and connection. By arranging the instruments around a central focal point in acoustic space, the composer implies an individual rather than collective experience of the piece, as embodied by the conductor and by extension Vivier himself. I take the view that the coda is essentially disruptive in function, and that its rupture reaches beyond the scope of Siddhartha to signify a broader affront to the “world of unity” and its avatar, Karlheinz Stockhausen. Vivier’s travels to Bali in the fall of 1976 would indeed see him crystallize “something strange, something new” in his musical language. The monodic aesthetic that materializes from this trip, catalyzed initially in Siddhartha, would become a hallmark of his mature style with profound implications for the next generation of Canadian composers.
Christopher Goddard
Gainesville, FL
ctdgoddard@gmail.com
Works Cited
Cohn, Richard. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199772698.001.0001.
Coenen, Alcedo. 1994. “Stockhausen’s Paradigm: A Survey of his Theories.” Perspectives of New Music 32 (2): 200–225. https://doi.org/10.2307/833609.
Cott, Jonathan. 1973. Stockhausen: Conversations with the Composer. Simon & Schuster.
Deutsch, Diana. 1974. “An Illusion with Musical Scales.” Journal of the Acoustical Society of America 56 (S1): s25. https://doi.org/10.1121/1.1914084.
Di Stefano, Nicole. 2022. “The Spatiality of Sounds: From Sound-Source Localization to Musical Spaces.” Aesthesis 15 (1): 173–85. https://doi.org/10.36253/Aisthesis-13617.
Field, George Wallace. 1970. Hermann Hesse. Twayne Publishers.
Fowler, Michael. 2010. “The Ephemeral Structure of Stockhausen’s Pole für 2.” Organised Sound 15 (3): 185–97. https://doi.org/10.1017/S1355771810000269.
Gilmore, Bob. 2014. Claude Vivier: A Composer’s Life. University of Rochester Press. https://doi.org/10.1017/9781580468411.
Griffiths, Paul. 2005. “Vivier.” In The Substance of Things Heard: Writings about Music, 184–98. University of Rochester Press.
Harley, Elizabeth. 1994. “Space and Spatialization in Contemporary Music: History and Analysis, Ideas and Implementation.” PhD diss., McGill University.
Harvey, Jonathan. 1975. The Music of Stockhausen. University of California Press.
Helmholtz, Hermann L. F. 1875. On the Sensations of Tone as a Psychological Basis for the Theory of Music. Translated by Alexander J. Ellis. Longmans, Green, and Co.
Hesse, Hermann. 1999. Siddhartha. Penguin Books.
Kurth, Ernst. [1969] 1931. Musikpsychologie. Reprint, Georg Olms Verlag.
Johnson, Mark. 1987. The Body in the Mind: The Bodily Basis of Meaning, Imagination, and Reason. University of Chicago Press. https://doi.org/10.7208/chicago/9780226177847.001.0001.
Lesage, Jean. 2008. “Claude Vivier, Siddhartha, Karlheinz Stockhausen, la nouvelle simplicité et le râga.” Circuit 18 (3): 107–20. https://doi.org/10.7202/019142ar.
Lippman, Edward A. 1952. “Music and Space: A Study in the Philosophy of Music.” PhD diss., Columbia University.
Maconie, Robin. 2005. Other Planets: The Music of Karlheinz Stockhausen. Scarecrow Press.
McAdams, Stephen. 2019. “Timbre as a Structuring Force in Music.” In Timbre, Acoustics, Perception, and Cognition, ed. Kai Seidenburg, Charalampos Saitis, Stephen McAdams, Arthur N. Popper, and Richard R. Fay, 211–43. Springer Handbook of Auditory Research. https://doi.org/10.1007/978-3-030-14832-4_8.
Mijnheer, Jaco. 1993. “Forward.” In Claude Vivier, Siddhartha (score). Boosey & Hawkes.
Miller, Paul. 2009. “Stockhausen and the Serial Shaping of Space.” PhD diss., University of Rochester.
Stockhausen, Karlheinz. 1961. “Music in Space”. Tr. Ruth Koenig, in die Reihe vol. 5 (“Reports—Analyses”), 67–82. Presser.
—————. 1965. Stop (score). Universal Edition.
—————. 1973–4. Inori (score). Universal Edition.
—————. 1989. Stockhausen on Music: Lectures and Interviews. Compiled by Robin Maconie. Marion Boyars Publishers.
Toop, Richard. 2005. Six Lectures from the Stockhausen Courses Kürten 2002. Stockhausen-Verlag.
Vivier, Claude. 1976. Siddhartha (score). Boosey & Hawkes.
Wellek A. 1934. “Der Raum in der Musik.” Arch Gesamm Psychol. 91: 396–422.
Wörner, Karl. 1973. Stockhausen: Life and Work. Translated by Bill Hopkins. University of California Press.
Zbikowski, L. M. 2002. Conceptualizing Music: Cognitive Structure, Theory, and Analysis. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195140231.001.0001.
Ziolkowski, Theodore. 1965. The Novels of Hermann Hesse: A Study in Theme and Structure. Princeton University Press.
Recordings
Recordings
Orchestre Métropolitain, Walter Boudreau, conductor. 1988. Over Time / Autour d’Ainola / Siddartha. Centrediscs. Compact disc.
Footnotes
1. Stockhausen claims to have taken an interest in heterodox instrumental placements “from the beginning,” and advocates for reimagined seating arrangements in the performance of classical scores (Cott 1973, 204). Taking the composer at his word, the radical orchestral distribution of a work such as Gruppen may be as much the solution to a structural impasse as it is a primary objective justified on technical grounds. The topic of spatiality in Stockhausen’s serial works is explored to great depth in Paul Miller’s doctoral dissertation “Stockhausen and the Serial Shaping of Space” (2009).
Return to text
2. Stockhausen originally recorded Gesang in five channels, even though a five-track playback machine did not yet exist. At the 1956 premiere, four speaker groups were positioned surrounding the audience and the fifth track was projected by a separate machine through a fifth loudspeaker placed on stage. The composer would later mix the fifth track onto the fourth track, which has since become the performance standard.
Return to text
3. Robin Maconie notes that Stockhausen’s exploration of depth layers was largely inspired by his work at the Cologne Radio electronic music studio. The time-stretching and frequency manipulations of Mantra also bear that technological influence (2005, 222).
Return to text
4. The orchestra piece Formel (1951), structured around an extended, quasi-formulaic tone-row divided into twelve segments, showcases Stockhausen’s penchant for melody from his earliest works.
Return to text
5. Zbikowski’s insights on musical metaphor are rooted in Mark Johnson’s notion of the image schema, a “recurring, dynamic pattern of our perceptual interactions and motor programs that gives coherence and structure to our experience” (1987, xiv).
Return to text
6. “Everything that is possible to happen in one part of space is equally possible in every other part of space and is perceived by us in precisely the same way. This is the case also with the musical scale
Return to text
7. According to Kurth our sense of musical space derives from inner, psychic processes and allows for the perception of “movement,” which for him is an essential feature of music. In Musikpsychologie (1931), Kurth considers the advantages and limitations of different representations of musical depth as a three-dimensional space.
Return to text
8. “I think in intervals of space, just as I think in intervals of pitch or durations” (Cott 1973, 92).
Return to text
9. It is noteworthy that during the same period Stockhausen composed Inori (1973–4), Diana Deutsch (1974) discovered and reported her famous “scale illusion” theory, which describes the illusory conjunction of pitch and location in a binaural environment.
Return to text
10. The composer Gilles Tremblay recounts an episode from this period in which Vivier calls Stockhausen “the greatest composer in the world” (Griffiths 2005, 186).
Return to text
11. The premiere was eventually cancelled due to the enormous technical and logistical demands posed by the work. Vivier never heard Siddhartha performed during his lifetime.
Return to text
12. Stockhausen’s Klavierstück IX (1955, rev. 1961) and Telemusik (1965), which incorporate the Fibonacci series into their durational sequence of musical events, would likely have influenced Vivier’s compositional strategy here.
Return to text
13. Drawing on the Indian origins of the title, Lesage analogizes this process to the concept of “raga,” which he defines as “a sort of continuum between scale and melody” (Lesage 2008, 114).
Return to text
14. The score itself reflects this anomaly, listing Group H between Groups C and D in the middle of the system.
Return to text
15. The effect of instruments sounding both individually and as part of a collective context recalls Karl Wörner’s assessment of Grüppen as a “synthesis of orchestral music, chamber music and solo music” (1973, 169).
Return to text
16. I am grateful to Centrediscs Records for allowing me to use this 1988 recording featuring conductor Walter Boudreau and the Orchestre Métropolitain.
Return to text
17. In the program notes to the Boosey & Hawkes publication of the score, Jaco Mijnheer describes the music of Siddhartha as “responding to a certain extent the Webernian dictum of maximum coherence within one work” (1993).
Return to text
18. I will note that although these properties both engage metaphorical space, I consider them more decorative in function than the structural expansions of the formula taking place concurrently over a longer time scale. This is a context-specific distinction that occurs at the intersection of pitch, timbre, and instrumental blend.
Return to text
19. The harmonizing lines in this work always occur below the formula in metaphorical space, presumably so as not to obscure its ongoing transformations. In later pieces such as the celebrated Lonely Child (1980), Vivier explores the inverse effect of stacking overtonal harmonies above the principal melody in a manner that resembles his contemporaries of the Spectralist school. Such subtle aggregation of instrumental timbres would be rather overshadowed by the massive proliferation of thematic material inside Siddhartha.
Return to text
20. Stockhausen makes common reference to the idea of “space melody” in his lectures. In Music in Space, the term is introduced in conjunction with an imaginary listening scenario in which 48 musicians are arranged in a straight line and each asked to play a note of the chromatic scale. In the later Four Criteria of Music, space melody indicates “movement up or down in space, or [describes] a particular configuration in a given space, at a certain speed” (1989, 103).
Return to text
21. Here Vivier once again keeps pitched material constant in order to draw attention to an important textural shift, mirroring a similar strategy used in the second formulaic statement at m. 42.
Return to text
22. I view the four-octave ambitus of this statement and its harmonization as a reprise of the four octave-levels explored by the initial formula (mm. 2–32) and the “dispersion” featured in the second statement (mm. 42–69).
Return to text
23. Though the musical content of this sixth statement is recapitulatory, its unusually threadbare instrumentation prompts me to hear it as anterior to (and thus nondisruptive of) the unfolding large-scale expansions of the formula. The function of this passage is to create a sense of anticipation for the pivotal seventh statement that follows, while perceptually bridging it to the original formula from which it is derived.
Return to text
24. For a detailed analysis of how Stockhausen layers formula presentations in Mantra, see Richard Toop, Six Lectures from the Stockhausen Courses Kürten 2002 (2005, 86).
Return to text
25. I credit Richard Cohn and his monograph Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature (2012) for this insight.
Return to text
26. Because the formula’s dilation in pitch aligns closely with its rhythmic expansion, it would have been possible for either value to be used as the y axis. I chose the former parameter because the temporal domain is already represented in the x axis.
Return to text
27. Technically, Wellek’s Tonraum is itself a three-dimensional space, however I omit from my model his ambiguous notion of “musical depth” so as not to introduce a (graphically unwieldy) fourth dimension.
Return to text
28. Spiral imagery recurs throughout the works of Stockhausen, not least Spiral (1968) for soloist and shortwave receiver. Govinda’s idea that the shape comprises two seemingly contradictory movements, circle and ascent, closely resembles how the German composer conceived of it. As Alcedo Coenen writes, the spiral represented to Stockhausen a combination of the circle and the arrow—an “integration of construction and adventure”—that “reflects the dialectical development towards spirituality” (1994, 208).
Return to text
Copyright Statement
Copyright © 2023 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Lauren Irschick, Editorial Assistant
Number of visits:
4589