Melodic Organization and Sequential Ordering of Galant Schemata: Implications for Eighteenth-Century European Musicianship*
Gilad Rabinovitch and Aaron Carter-Enyi
KEYWORDS: eighteenth-century music, schema theory, historical improvisation, pitch reduction, galant expositions, melodic fluency, Il filo, C. P. E. Bach
ABSTRACT: This article discusses the organization of galant schemata (Gjerdingen 2007) and its significance across the continuum of music-making from composition to improvisation (Nettl 1974). In Section 1, we argue that galant schemata should be defined more clearly as skeletal core tones, outlines for diminution, and surface formulas after Rabinovitch 2018, 2019a, and 2020a (see also Baragwanath 2020). We compare this organization briefly to additional musical systems discussed by Alaghband-Zadeh (2012), Stoia (2013), Mavromatis (2019), and Carter-Enyi (2021). In Section 2, we describe heuristics for moving from surface to individual soprano core tones, demonstrating how schematic melodic skeletons can be derived (bottom-up) through contrapuntal reduction. In Section 3, we address the sequential ordering of schemata within a first reprise or galant exposition (Burstein 2020) in the 1740s, based on a sample of 27 sections analyzed by hand according to the heuristics. We present a backbone of schemata featured in at least twelve of the pieces, which amounts to a tight script for schema successions. The emergent outline has implications for understanding schemata within form (Byros 2013, 2015; Caplin 2015; Neuwirth 2020; see also Burstein 2020), the linear constraints on skeletons, and schema successions in creative processes (Gjerdingen 2007; Sanguinetti 2012): we argue that it is possible to reconstruct broader linear and formal paths by tracking schema types recurring frequently in the sample. In Section 4, we discuss selected movements from the sixth collection of keyboard pieces for connoisseurs and amateurs by C. P. E. Bach, speculating on their mixture of compositional and improvisatory elements.
DOI: 10.30535/mto.30.1.7
Copyright © 2024 Society for Music Theory
Introduction
[0.1] This article discusses the organization of Gjerdingen’s (2007) galant schemata and its potential implications for understanding historical music-making across the continuum from composition to improvisation. In Section 1, we discuss schematic skeletons, outlines, and surface formulas associated with galant schemata, arguing that there is a need for greater precision in defining their melodic organization (after Rabinovitch 2018, 2019a, 2020a; cf. Baragwanath 2020). We reflect briefly on ways in which recent descriptions of additional musical systems (Alaghband-Zadeh 2012; Stoia 2013; Mavromatis 2019; Carter-Enyi 2021) can inspire our thinking about European galant music-making: galant schemata create a musical system in which skeletal melodic elements are embellished on the surface with more or less flexibility. Our brief comparative sketch suggests that there are benefits to focusing on schemata’s melodic organization.
[0.2] In Section 2, we survey a reductive analytical methodology based on Rabinovitch 2019a and 2020a that has allowed us to analyze 27 galant expositions (i.e., first reprises) of sonatas from the 1740s by hand and reduce them to soprano core tones. Though not fully formalized (Carter-Enyi and Rabinovitch 2021), our method nevertheless facilitated finding continuous soprano skeletons, whether or not an established schema type was present. Based on this prior work and on its present application, we argue that complete schemata can be reconstructed (bottom-up) through individual contrapuntal-reductive decisions. Moreover, the entire galant surface may be analyzed in this way even when it does not conform to a specific schema type established in scholarship.(1)
[0.3] Based on the continuous soprano skeletons within the 27 expositions, Section 3 demonstrates that recurring schemata within the sample create a statistical backbone for a formal trajectory. By selecting schema types recurring in at least 12 of the pieces, we derive a path of schemata, which amounts to a relatively tight script of slots (Byros 2015 after Schank and Abelson 1977) that may have served as signposts for rapid creativity. Focusing in on such recurring schemata makes it possible to reconstruct something akin to a Koch-style trajectory of resting points within a galant exposition (Burstein 2020’s term).(2) Note that our starting point is the identification of recurring schemata that are the content of various areas within an exposition, as opposed to focusing on motion towards resting points. Our entry point is also narrower than that of studies explicitly considering the interactions between schemata and Koch’s resting points (e.g., Byros 2015; Neuwirth 2020). Nevertheless, it is possible to reconstruct an approximation of the Kochian script through the schematic content in various stages of the galant journey. The constraints in the 1740s are particularly tight: this means that schemata—as linear-skeletal building blocks—create an archetypal soprano motion that bears superficial resemblance to the left branch of a Schenkerian interruption (Schenker 1979 [1935]). A priori, we do not posit an emergent linear trajectory or a Koch-style script of resting points. Though our methodology is open to parametric independence and to a matrix of local building blocks (see Brody 2016), the constraints on galant schemata in the 1740s are so tight that the resultant structures are schematic and generic through and through.(3)
[0.4] In Section 4, we analyze case studies from pieces by C. P. E. Bach that play upon the composition-improvisation continuum. In these sonata and fantasy movements from the sixth collection of piano pieces for connoisseurs and amateurs, the hybridity of improvisation and composition manifests itself both through improvisatory gestures and through play upon schema successions. Drawing in part on our prior discussions, we analyze the improvisatory rhetoric of two sonata expositions and the sonata-like properties of a fantasy excerpt. This final section is admittedly the most speculative; we include it, however, to stress that historical European notations should be analyzed not only as compositions but also as documentation of live music-making. The perspective of historical improvisation and the technical apparatus of this article allow us to speculate on improvisatory aspects of these pieces.
1. Galant Schemata as Skeletons, Outlines, and Formulas
[1.1] Robert Gjerdingen’s Music in the Galant Style (2007) offers a rich description of the formulas of eighteenth-century European music. In Gjerdingen’s view, a limited lexicon of patterns illuminates fluent galant musical speech in composition as well as improvisation. He argues that the training of European galant musicians was no different in principle than that of their eighteenth-century counterparts in Tehran, Delhi, Yogyakarta, or Seoul (Gjerdingen 2007, 370): musicians memorized patterns that could be spun out in a conventional order in composition or improvisation. According to Gjerdingen, galant musicians learned both local patterns as well as ways of stringing them together into a continuous thread. Reimagining historical improvisation based on the abilities of living improvisers, such as Arabic maqam-based performers or jazz musicians (cf. Jeffery 1992; Busse Berger 2005), makes sense, since the skills of past European musicians were presumably more comparable to those of performers in living traditions than to score-bound classical musicians. Improvisers in many traditions acquire a large mental storehouse of idiomatic patterns to be relied upon in live performance. It is equally clear that musical traditions differ in fundamental ways and that drawing analogies involves intellectual and ethical risks.(4) Nevertheless, we believe that this line of thinking has the potential to reposition historical European music-making as one tradition among many (Gjerdingen 2007, 370).(5) Our emphasis on melodic organization is pertinent, since it is shared by galant schemata and melodic formulas in additional traditions.
[1.2] There is, furthermore, considerable evidence that the relations between notation and sound were more flexible in eighteenth-century Europe than in today’s classical concert halls, even if musicians disagree on the degree to which we should stick to the score (Jerold 2008, 2012; Levin 2009). While we are sympathetic to the revival of classical improvisation, we would emphasize that our present study is theoretical, not practical.(6) Memorizing typical local patterns and successions with constrained forking paths facilitates rapid creativity in composition, improvisation, and everywhere in between. It follows that understanding the constrained behavior of schemata can illuminate historical improvisation. Surely, tight constraints facilitated creativity in improvisation as well as in rapid composition, with the latter activity documented in scholarship on partimenti and schemata (e.g., Gjerdingen 2007, 51 and 370–1; Sanguinetti 2012, 6).(7)
[1.3] Eighteenth-century music-making thus fits well into the continuum that Bruno Nettl (Nettl 1974) describes in a classic article: in musical traditions across the world, some practices remain relatively fixed between performances while others have more flexibility.(8) Eighteenth-century European music, with its diminutions, varied reprises, variations, and fantasies, certainly has practices that lie closer to the fixed side (e.g., diminutions and variations) and others that lie closer to the flexible side (e.g., fantasies and cadenzas).(9) Readers might be surprised that we list variations closer to the fixed side despite the fact that they were often improvised; in our view, the presence of a stable underlying template meant that this practice remained relatively close to a model even when improvised.(10) This stands in contrast to fantasies, in which materials are ordered more freely.
[1.4] Fixity and flexibility also manifest themselves in the building blocks of schemata themselves. On a near-surface level, skeletal schemata are embellished through surface diminutions with varying levels of fixity or flexibility, with some schemata having more freedom and others associated with more specific surface formulas. On the level of a phrase or section, complete galant schemata are concatenated within musical form in creative processes. The modular nature of schemata is widely recognized (e.g., Gjerdingen 2007; Sanguinetti 2012; Remeš 2020), but schemata’s trajectory within form still requires further description in typical galant repertoires, despite the availability of insightful studies (e.g., Byros 2013, 2015; Caplin 2015; Neuwirth 2020). The value of exploring schemata and form seems clear: as Vasili Byros observes, local schemata, phrase types, and broader formal scripts are all cognitive schemata that have top-down and bottom-up mutual dependencies (2015, 227). And as Markus Neuwirth (2020, 48) argues, musicians needed to learn not only how to form local voice-leading schemata but also where to embed them within form. Having charted galant expositions at length in his 2020 book, Poundie Burstein (2023) discusses long-range formal schemata as historically, pedagogically, and perceptually valid: these are qualities that are often associated in the schema-theoretic literature with local schemata, but less so with musical form. Since galant music is generic through and through, it is valuable to examine its conventions on all levels.
[1.5] Though Gjerdingen eschews the analysis of form, he already gives an account of schemata-within-form through his listing of transitional probabilities between individual schemata based on his complete-movement analyses in Music in the Galant Style (2007, 372). While we share his assumption that schema successions are statistically constrained, we believe that a clearer description of their trajectory is needed. There is a need to account not only for local transitional probabilities, but also for more global tendencies within a section. In addition, Gjerdingen’s analytical annotations imply a hierarchic organization that is not always clearly or sufficiently articulated in schema analysis. Where Gjerdingen distinguishes between regular and smaller-sized analytical circles, we describe schemata based on a threefold hierarchy (after Rabinovitch 2020a, 120–1; see also Rabinovitch 2018, 2019a; Baragwanath 2020):
- Galant core tones (Gjerdingen’s regular-sized scale-degree soprano circles)
- Hidden-polyphony outlines for diminution (e.g., High-, High- embellishing a Prinner), marked with smaller-sized circles
- Fixed formulas on the musical surface (e.g., Cudworth), or typical formulas for filling in diminution outlines, also marked by Gjerdingen with smaller-sized circles.
Articulating this organization more clearly can help us to understand the melodic aspect of schemata.(11) Surface formulas, skeletal notes, and outlines for melodic activity are distinct elements that are significant for music-making; however, they are not always presented clearly in analysis using schemata: Baragwanath’s (2020) particularly clear representation of skeletal notes and frameworks for diminution shows how these elements might be well differentiated.
[1.6] We have just described the near-surface organization of schemata. Taking a broader view, Gjerdingen and Bourne (2015, [2.2.1–6]) propose a non-uniform hierarchy for music, which they compare to a non-uniform view of language. (They contrast this approach with the recursive description of music in Schenkerian theory.) In language, the principles governing discourse coherence are different from those governing the syntax of a clause (or from morphological or phonological principles). By analogy, different musical levels require different descriptions: from the perspective of music-making, the act of embellishing and the act of combining schemata to form a musical section require separate accounts.(12) According to Gjerdingen and Bourne, schema-theoretic descriptions are sensitive to the various kinds of memory involved in producing linguistic or musical units of various sizes, including the constraints of working memory:
Tones combine into motives or brief melodies, which as emergent Gestalts cannot then be reduced to single tones. Individual voices join to make counterpoint and musical clauses like cadences, sequences, and thematic phrases. None of these can be reduced to single intervals or tones. Clause-like musical entities combine into a musical discourse, which again is different in kind from any of its components. At the level of discourse, one might say, for example, that “the opening theme returns.” Such an assertion depends on a recognition of similarity at the level of discourse, not on an imagined movement-wide web of counterpoint and/or harmony. (Gjerdingen and Bourne 2015, [2.2.4])
Even if this analogy is valid, the “discourse” that governs schema successions is closer to the constraints of a sonnet or a haiku than to free prose or ordinary speech.(13) The constraints on schemata are tight—both for immediate successions and for overall organization within a section—and general principles like “thematic return” are insufficient to describe them.
Example 1. A melodic family in Mode 1 Greek church chant, focusing on variants of the formulas D-init., G-med., and A-med
(click to enlarge)
[1.7] In a recent paper on improvisation and cognition, Panayotis Mavromatis (2019) proposes using hierarchical finite-state models to describe the cognitive processes associated with improvisation, expanding upon scholarship on the cognition of improvisation by Jeff Pressing (1988) and Philip Johnson-Laird (1991, 2002). In modeling Greek and Gregorian chant traditions, Mavromatis accounts for immediate transitions between notes as well as transitions between formulas to create a hierarchical model that is cognitively and computationally motivated. Although his examples come from chant, his model is applicable in principle to other musics. Like schema theorists, Mavromatis is concerned with the cognitive constraints imposed by working memory, which limits the chunks with which improvisers can work (see also Gjerdingen and Bourne 2015, [2.2.2]).(14) Mavromatis’s Figure 1, originally from Mavromatis (2005) and adapted in our Example 1, shows a melodic family in Greek chant. His Figure 2 (our Example 2) shows note-to-note transitional probabilities in a cadential formula. On a broader level, formulas are successively connected to one another, as shown in Mavromatis’s Figure 3 (our Example 3). The embedding of levels implies that, to facilitate live music-making, one may navigate performance simply by storing one state from each active graph in working memory.(15)
Example 2. Mavromatis’s (2019) figure 2, modeling note-to-note probabilities (click to enlarge) | Example 3. Mavromatis’s (2019) figure 3, modeling formula-to-formula probabilities (click to enlarge) |
[1.8] Mavromatis’s model also reflects analytical intuitions such as those captured in paradigmatic analysis (Ruwet 1987). Through the vertical alignment of melodic formulas that recur within a piece or a repertoire, we gain a sense of similarities and differences between performances. Moreover, we acquire an intuitive sense of the way in which formulas are connected, which can then be modeled probabilistically. Mavromatis shows how the results of his probabilistic model align with the intuitive goals of paradigmatic analysis. Though our article is less formal, we are likewise interested in both the internal organization of patterns and in their sequential ordering—as well as in bridging analytical intuitions and the normative paths in our sample. The forking paths of galant schemata seem less constrained than those of chant repertoires described by Mavromatis: we had to simplify both the surface and the successions to find intuitively meaningful representations.
[1.9] A brief look at descriptions of some additional musical systems can shed further light on the organization of melodic formulas. In her discussion of the North-Indian semi-classical ṭhumrī style, Chloe Alaghband-Zadeh (2012) proposes a continuum of “stock expressions”–“variable outlines”–“gestures”–“strategies” to describe the abilities of expert musicians in this tradition. Though expert musicians perceive this genre to be more flexible in comparison to its classical rāg-based counterparts (3–4), Alaghband-Zadeh’s analysis focuses on its formulaic nature (6). Part of her continuum is particularly relevant here: she distinguishes between “stock expressions,” plugged in almost verbatim on the surface, and more flexible “variable [melodic] outlines,” which can be fleshed out with greater freedom (20–31). Certain galant schemata can be thought of as “variable outlines,” while others are closer to “stock expressions.”
Example 4. Frankie and Johnnie schema paraphrased after Stoia (2013, 206, Example 8), comparison of the first four measures of several songs representing the schema
(click to enlarge)
[1.10] Nicholas Stoia’s analysis (2013) of schemata for early blues and country recordings show various degrees of freedom in harmonic and melodic organization. Some schemata, such as the “Frankie and Johnnie” type, which furnishes the melodic excerpts shown in Example 4, consist of “a harmonic progression that musicians associate primarily with a small number of specific discants, but which they also use to support original discants” (2013, 205). Stoia’s rich taxonomy—which we will not survey here&madsh;suggests that commonplace patterns range from relatively rigid melodic formulas to looser melodic (or harmonic) commonalities across a family of songs. These conventional outlines facilitate creativity, whatever the degree of spontaneity in any individual creative act.(16)
Example 5. Transcription of soloist’s melody sung over “Ngengele Gbaba Egwu” refrain (transcription by Jonathan Eldridge II)
(click to enlarge)
[1.11] An example of a tradition that uses improvisational outlines are ńfò (story songs) among the Igbo of eastern Nigeria. In a different study, we posit that melodic skeletons interact with the tone-language constraints of the Igbo language, combining thought by Ekwueme (1974, 1975) and Agawu (1995), both of whom theorized that reduction to underlying structures is a productive approach to analyzing West African music, Igbo and Ewe respectively. In “Ńgéngélé” (Example 5), (http://hdl.handle.net/20.500.12322/adept.ibo:0016, starting at timecode 4:10), the improvisatory framework of the lead voice complements the cycled refrain of the other voices while accommodating a varying text, including the pitch contour implied by the lexical tones of the text. Some words must have the correct linguistic tone level (H=high or L=low) to avoid mispronunciations that make them sound like other words (e.g., ákwá HH means “cry,” but ákwà HL means “cloth”). Because tone levels are similar to notes (discrete pitches), melismas are used sparingly. In the midst of considerable surface variation in the melodic shape, motivated by the tone language, we observe a highly consistent ()--- melodic skeleton, which sometimes extends to a longer outline of ()----(). The -- are more prominent in metric position, duration, or immediate repetition, but the prefix () and suffix () are slightly weaker but usually present. The shape of the outline suggests strong preference for contiguity (see Carter-Enyi and Rabinovitch 2021) and declination (Huron 2006) in the underlying melodic structure of this outline for vocal improvisation.
[1.12] In contrast to the surface variation motivated by the lexical tones of Igbo texts, an example of an outline from sub-Saharan Africa without the influence of lexical tone comes from a 2013 recording of KiKuria Praise-singing from the Kenya-Tanzania border (https://radar.auctr.edu/islandora/object/adept.kuj%3A0004.001 starting at timecode 00:25). In this example, the number of syllables sung on each pitch expands and contracts to accommodate the text but the contour does not need to change because of the absence of lexical tone, so long strings of words may be sung on a single pitch. A pentatonic scale is used, as is common in East Africa, seemingly the mode 4 pentatonic (----) with a strikingly absent . Similar to the Igbo example, the KiKuria singer seems to emphasize a downward skeleton of core tones within the collection ---. Do diatonic and pentatonic scales and their usage in sub-Saharan Africa arise from colonization and missionization?(17) While it is appropriate to observe similarity between the “Ńgéngélé” outline and a galant Prinner, it is highly doubtful this arises from strong familiarity with galant (or related) European musics: we believe it is more likely to reflect cross-cultural tendencies for contiguity and declination. Such tendencies are reflected in the “Ńgéngélé” outline, the KiKuria chant, and the galant Prinner (and style), which leaves room for exploration in future work.
[1.13] In our very brief comparative sketch, we have witnessed quite a variety of strategies and structures of music-making, which can inspire our thinking about European galant building blocks. Fixity and flexibility operate not only in music-making, but also within schemata. In galant music, some schemata are highly variable, while others are formulaic. (On a near-surface level, the greatest melodic flexibility seems to be in opening schemata such as the Meyer, and the most formulaic patterns are cadence patterns such as the Cudworth, a fixed surface formula.) Gjerdingen often labels an opening phrase or subphrase as a piece-specific Opening Gambit. This aligns with notions that pieces and phrases are most idiosyncratic in their beginnings. Whether we consider increased melodic predictability at phrase endings (Huron 2006, 154–58) or “characteristic” vs. “conventional” material (Caplin 1998), sections and phrases tend to be more unique at first and become more formulaic as they approach their ends. Even more strongly in the galant style, an Opening Gambit or head motive is commonly followed by a formulaic Prinner riposte. This is valid for either a piece-specific Opening Gambit or an interopus schema (e.g., Sol-Fa-Mi, Meyer). That Gjerdingen resorted to labeling divergent opening skeletons as Opening Gambit speaks to the difficulty in generalizing about openings.
Example 6. The Prinner, High-2, and “High-1” (cf. Gjerdingen’s 2007 “la-to-sol flourish”) as a variable outline for melodic diminutions
(click to enlarge)
Example 7. Composite representation of Prinner exemplars (from Symons 2017, 74)
(click to enlarge)
[1.14] Descriptions of additional traditions can contribute to repositioning European galant schemata: schemata are an example of generic melodic building blocks, which in this particular case are embedded in a contrapuntal and harmonic context. To borrow Alaghband-Zadeh’s useful terms, we can think of the Prinner as a variable outline for diminutions (Example 6). Gjerdingen (2007) associates this schema with the optional features “la-to-sol flourish” and High- drop. However, the “la-to-sol flourish” is a special case of a tendency to associate skeletal and —perhaps not only as part of a Prinner—with an outline confined by High-.(18) This variable outline may or may not contain the “la-to-sol” flourish. Surface melodic activity is often framed by the Prinner’s main core tones and these generic highpoints. Example 7, taken from Symons (2017, 74), is a composite image of several overlaid Prinners; notes recurring less frequently are gradually faded to white, such that the bottom line is a statistical “background.” Symons’s visualization demonstrates that core tones emerge as darkest (i.e., most common); hidden-polyphony outlines (High- and High-) are somewhat less common but still survive on the “background” level. As will be seen in upcoming sections, Symons’s statistical reduction has inspired our work on the sequential ordering of schemata.
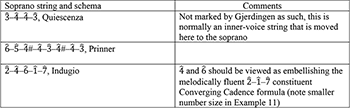
Example 10. The Converging Cadence / Indugio variable outline
(click to enlarge)
[1.15] The Cudworth Cadence presents a contrasting condition: it embellishes the skeletal Complete Cadence (Example 8) through a fixed surface formula (Example 9). As such, the Prinner and Cudworth gravitate respectively to the poles of flexibility and fixity in terms of their surface manifestations. The Indugio, or at least the part of it shown in Example 10, seems to occupy a middle position.(19) This schema’s stepwise string is associated with a typical framework for hidden polyphony with a High-.(20) The outline can be used verbatim on the surface or can be filled in with stepwise motion such as -----, --------. Our discussion of the Prinner, Cudworth, and Indugio sketches the possible relations between surface and skeletons (see also Rabinovitch 2018, 2019a, 2020a). Even in patterns that afford some freedom, typical outlines are framed by hidden-polyphony elements like the High-, facilitating rapid creativity.
Example 8. Gjerdingen’s Complete Cadence with a skeletal soprano (click to enlarge) | Example 9. The Cudworth Cadence (after Gjerdingen 2007), a fixed surface formula embellishing the Complete Cadence (click to enlarge) |
[1.16] As we have already explained, our method is grounded in a radically simplifying step: we focus on the soprano skeletons of schemata, as opposed to the multiple features of these prototypes. This has allowed us to engage in a brief comparative sketch of the relations between European galant skeletons and additional musical systems. It is true that reducing schemata to their soprano skeletons incurs a steep interpretive cost, losing the detailed descriptions that are typical in schema theory.(21) Doing so, however, allows us to investigate diminutions and sequential ordering in a generalized way. This focus, moreover, allows us to account for the complete musical surface. Even in the absence of specific schema types proposed so far, rethinking schema analysis as soprano reduction provides a more consistent description and complements schema theory’s micro-theoretical attention to individual patterns. (Note that in Gjerdingen’s analyses, in contrast, some portions of the piece are left unannotated.)(22) Our present understanding of Baragwanath’s (2020) reconstruction of the solfeggio tradition is that it supports such a view of diminutions mapped in the musician’s mind into individual skeletal solmization syllables, even in the absence of a specific schema. Baragwanath’s work reconstructs insider historical knowledge of a practical system in which melodic skeletons—and, to be fair, also bass lines—were conceptualized as solmization syllables. Thus, it turns out that our melodic-skeletal focus is not only useful in a comparative context but also resonates with a historical, tradition-specific conceptual and practical model that was deeply ingrained through solmization training.
2. From Surface to Skeleton
Between Surface Diminutions and Core Tones
[2.1] In the present section, we discuss diminutions and core tones from a reductive perspective, summarizing prior work and explaining how we applied it here to 27 galant expositions. In previous work reflecting an evolving understanding of schemata, we have shown that Gjerdingen’s analytical process can be approximated based on the following three heuristic principles:
- strong preference for outer-voice tritone resolutions (or local
V7 →I resolutions), in practice typically with local soprano → motion - preference for accented consonances and removal of accented dissonances; and
- preference for overall stepwise skeletal motion or melodic fluency (see Pastille 1990).
The second and third principles were implemented computationally in Carter-Enyi and Rabinovitch 2021 as a search for onset (#2) and contiguity (#3) in pattern finding; their ultimate weighting in computational implementations remains to be seen. It is hardly surprising that melodic reductions involve preference for metric stress, removal of dissonances, and a search for melodic fluency, as these represent basic intuitions operative in reductive analysis.(23) What may be surprising is the strong weighting of tritone resolution both in schema types (Rabinovitch 2018) and in the discovery of core tones (Rabinovitch 2019a), even though this crucial tonal building block harks back to François-Joseph Fétis’s (1844) appellative consonance. The preference for tritone resolutions suggests that skeleton finding also clarifies the key contexts on which schema scale-degree identities rely (Rabinovitch 2019a, 2019b). Though the principles themselves are not surprising, it seems significant that one can start at the surface and approximate the motion to a schematic skeleton based on them.(24)
Example 11. Analysis of excerpt from Simon Leduc, Op. 4, no. 1, mvt. 1, mm. 1–12 after Gjerdingen (2007, 290) and Rabinovitch (2019a, 9–10)
(click to enlarge)
Example 12. Emergent galant schemata in Example 11 with comments on discrepancies between Gjerdingen (2007) and our view
(click to enlarge)
[2.2] The first two principles, in fact, approximate Gjerdingen’s (2007) implicit reductive choices of individual core tones within a metric segment in approximately 85% of cases (Rabinovitch 2019a). Note, however, that reconstructing analyses on the basis of those principles relies on the metric segmentation implicit in Gjerdingen’s analyses (Rabinovitch 2019a). Example 11 paraphrases Gjerdingen’s analysis of a cantabile movement by Simon Leduc. His annotations imply a metric segmentation: for instance, soprano core tones are deployed one per measure in mm. 6–7, whereas m. 8 contains three true core tones,
[2.3] As mentioned earlier, the first two heuristics from Rabinovitch 2019a model Gjerdingen’s implicit reductive decisions at about 85%, yet this relies on his implicit segmentation. In order to discover core tones in pieces not already analyzed by an expert, we must add a melodic fluency heuristic (Pastille 1990; Rabinovitch 2020a): the emergent skeletons made of individual core tones contain both known schemata as well as other skeletal soprano patterns. Though the heuristics described here constitute a process of anti-embellishment or anti-diminution that resembles linear analysis, it is not difficult to see how this knowledge translated into creativity, since musicians knew how to relate scale degrees, points of metric stress, and intervallic or harmonic relations to the rest of the texture.
Analyzing A Sample of Galant Expositions from the 1740s
[2.4] For this project, 27 galant expositions from sonatas on imslp.org that carry dates in the 1740s were arbitrarily selected—with no composer represented more than once—under the assumption that continuo sonatas in the decade are highly generic and that the resulting sample would be reflective of musical practices at the time (see Appendix 1 for a complete listing of the composers and the titles of the sonatas). We use the term “galant expositions” after Burstein 2020; note that such sections have different conventions compared with the high-classical sonata. Expositions were selected without considering the form of the second reprises and how one might classify them in terms of thematic repetitions and tonal outline.(26) This repertoire is remarkably generic, despite the mix of regions and nationalities, as well as of relatively well-known figures (C. P. E. Bach, P. Locatelli, J. Stamitz) and more obscure ones (e.g., L. Patouart, N. Lavaux). Only major-mode expositions were included in hopes of creating a coherent view of schema successions. This was done in an environment in which the major mode was increasingly taking over musical usage.(27)
[2.5] All pieces were manually analyzed into soprano core tones and galant schemata; these results are collected in Appendix 2. While this was an informal, by-hand process, it was guided by the assumption that expert schema finding de facto represents implicit reductive heuristics. In other words, while the heuristics were taken as guiding principles for annotation, we should stress that the process at this stage was intuitive and not fully formalized. Core tones were selected whether or not resultant strings amounted to a known schema type proposed by Gjerdingen or others. Soprano skeletal strings not identified as a specific schema were encoded as “non-specific,” indicating their skeletal soprano string (again, see Appendix 2). All skeletons were transposed to C major for ease of comparison; the surface score and annotated skeletons are given in Appendix 3. As a side note, we observed the tendency to ascend through scale degrees ----- (respective to a local tonic) along with some variants emerging as a potential prototype in this repertoire (marked as “ascent” in our analyses). While proposing new schema types was emphatically not our goal, we make note of this one to point out that this discovery procedure may uncover new schema types.
Example 13. Francesco Geminiani, Sonata for Cello and Continuo, Op. 5 no. 3, mvt. 2,
(click to enlarge)
Example 14. Translating Geminiani’s exposition excerpt into a soprano-skeletal string. The indication “
(click to enlarge)
[2.6] Example 13 demonstrates how the principles for core-tone finding play out in a passage from one of the works analyzed, excerpted from exposition #10 in our sample by Francesco Geminiani (from his Sonata for Cello and Continuo, Op. 5 no. 3, mvt. 2). The color coding in Example 13 relates analytical choices of core tones to reductive principles of tritone-resolution (or local
[2.7] Core tones were represented monotonally respective to the global tonal center. This contrasts with Gjerdingen (2007) and others, who mark scale degrees respective to a local tonal center based on historical approaches that treated every local shift as a new frame of reference (Lester 1992, 82–87; Byros 2012). In describing schema successions, the tonal identity of a schema is crucial for its position within galant form (see also Prosser 2021, 103). Thus, a Prinner riposte’s soprano was annotated as (---) and a Modulating Prinner’s soprano as (---); a Comma in I (-) and a Comma in V (-) were likewise marked respective to the global tonal center. Since major-mode expositions in the decade move almost invariably from I to V, marking skeletal strings monotonally is extremely useful for understanding their embedding within a section.(28)
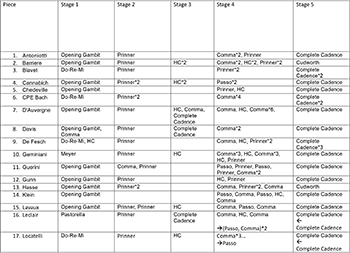
[2.8] Examples 15 and 16 present paradigmatic views of schema types and skeletal strings of schemata recurring frequently in our sample. Both are simplifying views; for a complete listing, please refer to Appendix 2.(29) Note first that out skeletal representation serves as a kind of scaffolding for the successive ordering of schemata within a section. Certain repetitions stem not from immediate repetitions in the original, but from the omission of intervening materials. The emergent view of schemata-within-form resonates with both Gjerdingen’s (2007) characterization and a Koch-style logic of resting points within an exposition (Byros 2015; Neuwirth 2020; Burstein 2020). Second, with regard to a threshold condition, we set it such that only schema types featured in twelve or more of the pieces were included. Our assumption was that schemata recurring in a higher number of pieces represented patterns that were regularly called upon in creative processes, while others represented less trodden byways.
Example 15. Synoptic view of schemata that passed the threshold (click to open PDF in new tab) | Example 16. Synoptic view of skeletal strings for schemata that passed the threshold (click to open PDF in new tab) |
[2.9] In order to select this threshold, we created a “foreground” to “background” series of representations, in which a threshold of 1 meant that all schemata in all pieces were included, whereas a threshold of 27 meant that only schemata featured in all 27 pieces were included (see Appendix 5). We then generated 27 versions of the schematic descriptions of the pieces. Post hoc, we selected the threshold of 12 since it occupied a good middleground between being too detailed and not detailed enough. Note that in the encoding without thresholding there are 322 schema instances, whereas in the encoding with a threshold of 12 (schemas that appear in fewer than 12 pieces are excluded) there are 248 instances.
[2.10] The effect of the thresholding can be seen by comparing the Geminiani excerpt in Examples 13–14 with its representation in Examples 15–16. The schemata that survive the thresholding in this part of the exposition are Meyer–Prinner–HC–Comma (repeated three times) in Example 15’s representational terms; in Example 16’s terms (n.b., with repetition excluded), they are the monotonal strings ---, ---, , -, -. The MATLAB script for the thresholding process, created by the second author, is available in
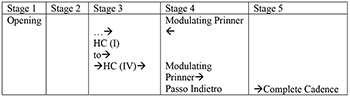
[2.11] Schema types that met the threshold were sorted intuitively into five stages of embedding within form: Stage 1, Opening Gambit; Stage 2, Prinner riposte; Stage 3, Post-Prinner cadence (often, but not always, a HC); Stage 4, Modulating Prinner, fragmented middle, pre-cadential cues (admittedly the messiest stage); and Stage 5, Final Cadence.(31) This intuitive encoding of stages can be seen in a separate column in Appendix 2, which serves as the basis for the simplified views of Examples 15–16. Not all stages are present in each exposition; nevertheless, this generic model represents a typical succession that bears resemblance to a Koch-style script of resting points, even though our entry point is that of schematic content (and not motion towards resting points). Stage 4 is the messiest in that it is sometimes occupied by a Modulating Prinner (---) or a Comma in the key of V (-) and sometimes by a larger number of schemata. In some cases, there is a clear pre-cadential cue of the Passo Indietro (
3. Schemata Embedded in Musical Form
[3.1] Having described our method in detail, it is time to zoom out and think about the significance of our results for understanding schemata and form as well as their global linear organization. In music-theoretical terms, stringing together patterns during improvisation is analogous to the problem of ordering schemata within form (Byros 2013, 2015; Caplin 2015; Neuwirth 2020), or creating a connective thread or Il filo (Gjerdingen 2007, chap. 27). Ostensibly, Gjerdingen eschews theories of form, declaring them objectionable and anachronistic.(32) Gjerdingen’s rhetoric aside, his descriptions often generalize about the position of schemata. For example, the Meyer and Sol–Fa–Mi often serve as openers for a piece or a section and the Fenaroli is associated with secondary-key area materials. Gjerdingen, moreover, does account for immediate transitional probabilities among schemata (2007, 372). As Neuwirth observes,
the fact that composers of the time did not adopt the theoretical apparatus of present-day Formenlehre does not imply that this apparatus is useless for describing the compositional behavior as manifest in written musical sources. Note also that Gjerdingen contradicts his own critique by occasionally falling back to terminology stemming from the Formenlehre tradition. Therefore, I do not see any reason why not to link concatenated voice-leading patterns with concepts from musical form. (2020, 53, fn. 18)
[3.2] The issue of schema successions leaves room for case studies such as the present one.(33) A useful starting point is to note Roger Schank and Robert Abelson’s (1977) distinction between scripts—rigid sequences of events—and looser plans, which are more abstract representations of how events might follow one another in the absence of a script (this distinction is adopted in Byros 2015; see also, Meyer 1989; Gjerdingen 1988).(34) The succession of individual schemata within a first reprise in the 1740s seems to us closer to a script than to a plan, despite exhibiting both rigid and more flexible areas in terms of content. The utility of such a tight script for improvisation (or rapid composition) is clear: by acquiring knowledge of building blocks (galant schemata), ways of embellishing them on the surface, and ways of stringing them together, musicians would have been able to create music rapidly.
[3.3] The constraints on schema successions in sonatas from the 1740s seem to have been stronger than in the high-classical style. Of course, the high-classical sonata exposition is the descendent of the earlier first reprise or galant exposition; galant composers were unaware that these formal prototypes would ultimately be viewed as footnotes in the evolution towards “sonata form” (Greenberg 2017, 2022). Though the interaction of schemata and resting points has been discussed productively by others (cited above), our study results—as preliminary as they might be—suggest that the Koch-style script can be reconstructed through the galant schematic content of different areas within the exposition.
[3.4] Thus, our Opening Gambit and Prinner riposte slots can be viewed as analogous to the process leading up to a Grundabsatz. The post-Prinner cadential slot is often equivalent to a Quintabsatz or a Satz-altering suffix that implies that the preceding process had actually been a Quintabsatz (see Burstein 2020, 44–45). The penultimate stage—despite appearing somewhat murky in our representations—suggests that a Quintabsatz in the key of V might occur at some point, while our final cadence column is equivalent to the end of a motion towards a conclusive Schlußsatz in V (see Burstein 2020, 73, ex. 4.5; Neuwirth 2020, 55, Table 1). Again, our view emerges not from considering motion towards resting points, but rather the skeletal content that occurs at various areas of a galant exposition. For instance, in looking for a Prinner riposte, our sole concern was that this was a skeletal pattern used in almost all of the works represented in our sample. Our larger argument is that—in addition to reconstructing local schemata as shown in Section 2—it is also possible to reconstruct a formal trajectory based on recurring schematic content.(35)
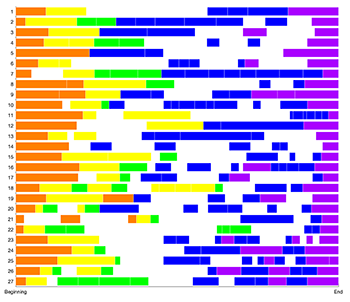
Example 17. An interopus comparison of the 27 pieces in the sample
(click to enlarge)
[3.5] The visualization in Example 17 was prepared in MATLAB by the second author through a novel script (included in Appendix 4). The implementation time-warps the duration data from schema encodings along the x-axis to align all 27 pieces in the sample. Analogous stages are indicated through color coding (Stage 1=orange; Stage 2=yellow; Stage 3=green; Stage 4=blue; Stage 5=purple). Past studies interested in comparing different renditions of the same melody have used time-warping, such as Will’s study of Australian Aboriginal music (2000). Here, rather than investigating slight variations introduced to a song’s surface by different performers, we apply the technique to a notated corpus to compare the underlying melodic structure of works within the same genre and decade. The visualization makes it clear that the schemata representing our stages—as opposed to “non-specific” strings or to those schemata that did not meet the threshold—do in fact constitute generic paths through major portions of the expositions.
Example 18. Quantz (Exposition #20), Skeleton of mm. 1–8
(click to enlarge)
[3.6] Whether from the point of view of schema concatenation or from the point of view of linear constraints and melodic fluency (cf. Pastille 1990, Metz 2017), the forking paths of galant schemata seem relatively constrained, which explains how they facilitated rapid creativity with rather narrow junctures of decision. To give one example for these similarities, note that certain pieces represented in Examples 15–16 that do not have the very common Prinner riposte still find their linear trajectory towards -, possibly proceeding to a HC or PAC in the home key; see, for instance, Quantz’s Sonata for flute/oboe/violin and continuo Op. 2, no. 1, mvt. 2 (#20 in our sample) (excerpted in Example 18). Whether we think about this in terms of traversing part of a linear trajectory or in terms of a motion towards a Quintabsatz, the “missing” Prinner riposte in Quantz’s piece does not affect the overall process.
Example 19. Skeleton of Exposition #17 by Locatelli
(click to enlarge)
[3.7] The skeleton of Locatelli’s exposition (#17 in our sample) from his Sonata for Violin and Continuo, Op. 8, no. 4, mvt. 2 is shown in Example 19: it is yet another example for the interaction between recurring schemata in our sample and the linear trajectory of the galant exposition. We should make note of a few technical details: the non-specific skeleton of m. 4 (marked with
[3.8] To cement our last point about galant schemata and their ordering as it relates to linear organization: we do not posit an overarching contrapuntal archetype. We remain open to parametric independence and a matrix-like view of schemata as they relate to linear and formal processes (cf. Brody 2016): one can easily imagine a stylistic stratum in which our method of analysis would reflect multiple linear routes through a section, perhaps with substantial zigzagging. Our reliance on melodic fluency brings our work closer to a Schenkerian logic, despite wide ideological and technical differences.(36) Of course, the precise relations among formal, cadential, and linear hierarchies (cf. Burstein 2020) cannot be solved in our matrix of schemata. For instance, the strong representation of the Prinner’s opening has to do with its recurrence in the sample, not with ways in which one might hierarchize it in Schenkerian theory.(37) Like the prominently represented Prinner riposte, the emergence of a concluding soprano cadential string, --, as a common strategy in the sample is not based on assumptions on how skeletal lines ought to behave—whether they “should” or “should not” descend based on some general principle.(38) Rather, that determination is made on the basis of the behavior of melodic skeletons viewed from our analytical angle, in which a final ascent is rare (see in particular Geminiani’s Sonata for Cello and Continuo, Op. 5, no. 3, mvt. 2 (#10 in our sample) in Appendix 3). Surely our approach would seem superficial to some and cogent to others: scholars will continue to have productive disagreements on contrapuntal schemata and their formal and linear ordering. Our goal is neither to brush aside points of friction nor to revel in polemics for their own sake. Rather, we would like to emphasize that the embedding of schemata within a formal section in the 1740s is a productive case study for interactions between schemata and global formal and linear organization.
4. Analytical Case Study: C. P. E. Bach’s Sonata/Fantasia Hybrids
[4.1] C. P. E. Bach’s compositions and treatise provide interesting case studies for the relations between schema successions and improvisation. Each of the two parts of his Versuch über die wahre Art das Clavier zu spielen (Essay on the True Manner of Playing Keyboard Instruments, Bach [1753/1762] 1949) ends with a description of an improvisation practice, varied reprises and free fantasy, respectively. Where varied reprises lie close to the fixity side of music-making (Nettl 1974), fantasies represent a more flexible practice. How might we draw on our prior discussions of schema successions in considering composition and improvisation in this composer’s work? C. P. E. Bach’s collections “for connoisseurs and amateurs” (für Kenner und Liebhaber) are intended for use in domestic music-making.(39) Bach clearly conceived of at least some fantasies in the collections as documentation for posterity of his live practice of improvising fantasies.(40) At the same time, the collections occupy a place on the continuum between compositional sonatas and improvisatory fantasies (along with eccentric rondos). Improvisatory rhetoric permeates some of the sonatas, whereas sonata-like organization influences some of the fantasies, which results in hybridity (cf. Head 2014, 261). Despite our focus here on examples from the sixth collection of 1787, these pieces can still be analyzed in reference to the older, galant script of schemata within an exposition. We note at the outset that these last pieces are more eccentric than those analyzed in previous sections. In response, the analyses in this section were carried out more in accordance with conventional schema analysis. Unlike in Section 3, the pieces are annotated with respect to local tonal centers; unlike in Section 2, the schemata are identified more liberally, not strictly based on heuristics. Even so, we will demonstrate how bottom-up core tone extraction interacts with the top-down schema finding in a particular formal location.(41)
Example 20. C. P. E. Bach, Sonata Wq. 61/2/iii, mm.1–25
(click to enlarge)
Example 21. C. P. E. Bach, Sonata Wq. 61/2/iii, outline of mm. 1–25
(click to enlarge)
[4.2] The expositions of the first and last movements of the sonata Wq. 61, no. 2 will illustrate. In the third movement (Examples 20 and 21), an Opening Gambit connects to a Passo Indietro in the “wrong” key of IV, to be followed by a Prinner with embedded Comma tonicizations. The asymmetrical and capricious arpeggiations, as well as the Passo Indietro respective to IV, make the beginning of this sonata unusual. However, the Prinner connecting to a HC suffix puts the sonata back on track. The following Modulating Prinner occupies its typical position and proceeds to a much Complete Cadence and a varied repetition of the unusual Opening Gambit as a closing gesture.
[4.3] Our schematic reading in Example 20, which might seem too free in light of prior discussions, nevertheless illustrates the interaction of bottom-up core-tone finding and top-down activation of schemata within form, especially as it applies to the Prinner→HC combination of mm. 8–12. According to the logic of Section 2, each soprano member of the Commas (or tritone resolutions) is taken as a core tone respective to a localized tonal center, in this case G major, E minor, and B minor. Our ultimate reading, ---- or Prinner→HC (respective to D major), prioritizes some of those core tones at the expense of others based on the expectation for this schema at this formal juncture. Thus, while tritone resolutions were important in the initial core-tone extraction, the ultimate reading depended on the formal embedding of schemata. Of course, the onset of the Prinner in m. 8 is unusual; one would ordinarily expect it to start on the downbeat. Moreover, core is shifted to a different octave in moving from m. 9 to m. 11. Only in m. 11 do surface tritone resolutions point unequivocally to a -- skeletal pattern ending with a HC suffix. In this capricious first reprise, we have to wait until m. 11 to encounter a more generic portion of the Prinner riposte skeleton.
Example 22. C. P. E. Bach, Sonata Wq. 61/2/i, mm. 1–24
(click to enlarge)
Example 23. C. P. E. Bach, Sonata Wq. 61/2/i, outline of mm. 1–24
(click to enlarge)
[4.4] We next consider the first part of the first movement of the same sonata (Examples 22–23). In this case, the opening combination of schemata is more unusual. Soon after, however, a Modulating Prinner—Passo Indietro—Complete Cadence succession completes the exposition in a conventional way, despite the capricious surface. The most notable surface irregularity is the rhythm of the modulating Prinner, whose core tones are spaced four, five, and four sixteenth notes apart, with the initial landing on the last sixteenth note of the measure; this sounds almost like an out-of-time performance of a hemiola. The title “sonata” suggests that these expositions lie on the composition side of the continuum. By looking at their capricious surface and schema successions, both typical and less typical, we can speculate on the creative process that gave rise to such unusual movements, perhaps a deliberate attempt to capture a fantasy-like take on a conventional formal outline.
Example 24. C. P. E. Bach, Fantasy Wq 61/3, mm. 1–36
(click to enlarge)
Example 25. C. P. E. Bach, Fantasy Wq. 61/3, outline of mm. 1–36
(click to enlarge)
Example 26. Summarizing formal milestones in Wq. 61/3, mm. 1–36
(click to enlarge)
[4.5] We now turn our attention to the fantasy Wq. 61, no. 3 (Examples 24–26). This work begins with a section that deviates from the conventional script for schema concatenation, while retaining key elements of it, including two (subverted) Modulating Prinners, as well as a Passo Indietro preceding a Complete Cadence. Through the Modulating Prinners, the fantasy makes two attempts to become a prototypical—and perhaps sonata-like and compositional—exposition; the second attempt succeeds and cadences in the key of V. The piece starts with improvisatory arpeggios and a bass outline of --
[4.6] Measures 13–14, remarkably, sound like a slow movement making its way to the conventional resting point of a HC in the fantasy’s key, B-flat major. This effect is, however, broken by an exploration of registral extremes in the Fonte of mm. 15–19. Measures 19–21 introduce a recitative-like improvisation in the minor mode, yet end on a bright, galant HC, which, again, might have seemed to serve as a landmark resting point, though in the key of IV rather than V. After the Fonte of mm. 22–25, the Modulating Prinner of mm. 26–27 serves to put the piece back on track in two senses: it is both in the correct tonality of F major (key of V), and supplies a potential building block to lead to a final cadence. This Modulating Prinner, too, is subverted after its first two events and leads to a rhetoric of preluding in mm. 28–29 and to the pause of m. 30. Measures 31–32 return to the slow movement style of mm. 13–14 and precede the pre-cadential Passo Indietro of mm. 34. The latter schema is unusual, since the - soprano in V is clear but the opening bass C♯ participates in a fantasy-like deception. Of course, the bass
[4.7] Example 26 provides a summary account of the milestones of this fantasy-exposition. After a fantasy-like opening, a Modulating Prinner (the expected Prinner in the key of V) surprisingly leads to backtracking in the script to the earlier milestone of a HC in the home key. Further confusion is caused by events leading to a HC in the key of IV, a wrong key. In a more successful attempt to become an orderly (and perhaps compositional) galant exposition, another Modulating Prinner (Prinner in V) leads to a Passo Indietro and Complete Cadence. All of these strategic manipulations involve both misplaced elements as well as play on improvisation-like and sonata-like gestures. In both the sonata excerpts and the fantasy excerpt analyzed here, surface rhetoric and the script of schemata within form display the hybridity of composition and improvisation. In the latter case, it sounds almost as if a free fantasy is trying to become a conventional composed sonata, perhaps foreshadowing the much-discussed opening to Beethoven’s “Tempest” sonata (Schmalfeldt 2011).
[4.8] The selected pieces for connoisseurs and amateurs by C. P. E. Bach not only highlight the hybridity of improvisatory and compositional elements, but also illustrate the role of conventional schemata and their succession in rapid music creation as captured in notated works. Any kind of historical reimagining—such as our reflections on improvisation and composition in these pieces—is speculative, but Bach provides us with clues through his notated works and treatise. Musical form can be reframed as a process of stringing together schemata in performance, with tight conventions facilitating automaticity. The technical issues discussed in this article—surface diminutions, conventional skeletons, and ways of stringing together schemata within form—all suggest paths for reimagining eighteenth-century European notations on a continuum from composition to improvisation.
Appendices
Appendix 1. List of pieces (PDF)
Appendix 2. Final GR_ACE_2024 data (Excel sheet)
Appendix 3. Skeletons and surface files (zip file)
Appendix 4. GR_ACE_2024 script (m file)
Appendix 5. GR_ACE_2024 thresholding results (zip file)
Gilad Rabinovitch
Aaron Copland School of Music
Queens College, CUNY
65-30 Kissena Boulevard
Flushing, NY 11367
gilad.rabinovitch@qc.cuny.edu
Aaron Carter-Enyi
Morehouse College
830 Westview Drive SW
Atlanta, GA 30314
aaron.carterenyi@morehouse.edu
Works Cited
Agawu, V. Kofi. 1995. African Rhythm: A Northern Ewe Perspective. Cambridge University Press.
Alaghband-Zadeh, Chloe. 2012. “Formulas and the Building Blocks of Ṭhumrī Style: A Study in ‘Improvised’ Music.” Analytical Approaches to World Music 2 (1). https://iftawm.org/journal/oldsite/articles/2012a/Zadeh_AAWM_Vol_2_1.htm.
Albrecht, Joshua, and David Huron. 2014. “A Statistical Approach to Tracing the Historical Development of Major and Minor Pitch Distributions, 1400–1750.” Music Perception 31 (3): 223–43. https://doi.org/10.1525/mp.2014.31.3.223.
—————. [1753/1762] 1949 Essay on the True Art of Playing Keyboard Instruments (Versuch über die wahre Art das Clavier zu spielen). Translated by William J. Mitchell. W. W. Norton.
Baragwanath, Nicholas. 2020. The Solfeggio Tradition: A Forgotten Art of Melody in the Long Eighteenth Century. Oxford University Press. https://doi.org/10.1093/oso/9780197514085.001.0001.
Blum, Stephen. 2023. Music Theory in Ethnomusicology. Oxford University Press. https://doi.org/10.1093/oso/9780199303526.001.0001.
Bourne, Janet. 2019. “From Decoration to Reinterpretation: Improvisation, Composition, and the Perception of Similarity in Variation Sets.” Paper presented at the 42nd annual meeting of the Society for Music Theory, Columbus, OH, November 7.
Brody, Christopher. 2016. “Parametric Interaction in Tonal Repertoires.” Journal of Music Theory 60 (2): 97–148. https://doi.org/10.1215/00222909-3651814.
Brown, Matthew. 1998. “Rothstein’s Paradox and Neumeyer’s Fallacies.” Intégral 12: 95–132.
Burstein, L. Poundie. 2020. Journeys through Galant Expositions. Oxford University Press. https://doi.org/10.1093/oso/9780190083991.001.0001.
—————. 2023. “Ponti di Formiche e ampi schemi tonali galanti” (“Ant Bridges and Long-Range Galant Schemata”). Keynote address at Gruppo di Analisi e Teoria Musicale conference, Conservatorio G. Martucci, Salerno, Italy, October 19–20.
Busse Berger, Anna Maria. 2005. Medieval Music and the Art of Memory. University of California Press. https://doi.org/10.1525/california/9780520240285.001.0001.
Byros, Vasili. 2012. “Meyer’s Anvil: Revisiting the Schema Concept.” Music Analysis 31 (3): 273–346. https://doi.org/10.1111/j.1468-2249.2012.00344.x.
—————. 2013. “Trazom’s Wit: Communicative Strategies in a ‘Popular’ yet ‘Difficult’ Sonata.” Eighteenth-Century Music 10 (2): 213–52. https://doi.org/10.1017/S1478570613000055.
Byros, Vasili. 2015. “’Hauptruhepuncte des Geistes’: Punctuation Schemas and the Late Eighteenth-Century Sonata.” In What is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire, ed. Pieter Bergé and Markus Neuwirth, 215–51. Leuven University Press. https://doi.org/10.2307/j.ctt14jxt45.10.
Caplin, William E. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford University Press. https://doi.org/10.1093/oso/9780195104806.001.0001.
—————. 2015. “Harmony and Cadence in Gjerdingen’s ‘Prinner.’” In What is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire, ed. Pieter Bergé and Markus Neuwirth, 17–57. Leuven University Press. https://doi.org/10.2307/j.ctt14jxt45.4.
Carter-Enyi, Aaron. 2021. “Tone Realization and Register Transformations in Nigerian Art Music: A Formal Analysis of Èkwúèmé and Olúrántí.” Perspectives of New Music 59 (2): 31–79. https://doi.org/10.30535/mto.27.4.2.
Carter-Enyi, Aaron, and Gilad Rabinovitch. 2021. “Onset and Contiguity: Melodic Feature Reduction and Pattern Discovery.” Music Theory Online 27 (4). https://doi.org/10.30535/mto.27.4.2.
Cowan, Nelson. 2001. “The Magical Number Four in Short-Term Memory: A Reconsideration of Mental Storage Capacity.” Followed by Open Peer Commentary and Author’s Response. Behavioral and Brain Sciences 24 (1): 87–185.
Ekwueme, Laz E. N. 1974. “Linguistic Determinants of Some Igbo Musical Properties.” Journal of African Studies 1 (3): 335–53.
—————. 1975. “Structural levels of rhythm and form in African music: With particular reference to the West Coast.” African Music: Journal of the International Library of African Music 5 (4): 27–35. https://www.jstor.org/stable/30249724.
Farraj, Johnny, and Sami Abu Shumays. 2019. Inside Arabic Music: Arabic Maqam Performance and Theory in the 20th Century. Oxford University Press.
Ferris, David. 2000. “C. P. E. Bach and the Art of Strange Modulation.” Music Theory Spectrum 22 (1): 60–88. https://doi.org/10.2307/745853.
Fétis, François-Joseph. 1844. Traité complet de la théorie et de la pratique de l’harmonie. Schlesinger.
Froebe, Folker. 2014. “Schema and Function.” Music Theory and Analysis 1 (1–2): 121–40. https://doi.org/10.11116/MTA.1.7.
—————. 2015. “On Synergies of Schema Theory and Theory of Levels: A Perspective from Riepel’s Fonte and Monte.” Zeitschrift der Gesellschaft für Musiktheorie 12 (1): 9–25. https://doi.org/10.31751/802.
Gjerdingen, Robert O. 1988. A Classic Turn of Phrase: Music and the Psychology of Convention. University of Pennsylvania Press.
—————. 2007. Music in the Galant Style. Oxford University Press. https://doi.org/10.1093/oso/9780195313710.001.0001.
Gjerdingen, Robert O., and Janet Bourne 2015. “Schema Theory as a Construction Grammar.” Music Theory Online 21 (2). https://doi.org/10.30535/mto.21.2.3.
Goldman, Andrew. 2022. “Returning to the Continuum: On the Value of Typological Distinctions in the Analysis of Improvisation.” Music Theory Online 28 (3). https://doi.org/10.30535/mto.28.3.4.
Gooley, Dana. 2018. Fantasies of Improvisation: Free Playing in Nineteenth-Century Music. Oxford University Press. https://doi.org/10.1093/oso/9780190633585.001.0001.
Greenberg, Yoel. 2017. “Of Beginnings and Ends: A Corpus-Based Inquiry into the Rise of the Recapitulation.” Journal of Music Theory 61 (2): 171–200. https://doi.org/10.1215/00222909-4149546.
—————. 2022. How Sonata Forms: A Bottom-Up Approach to Musical Form. Oxford University Press. https://doi.org/10.1093/oso/9780197526286.001.0001.
Head, Matthew. 2014. “Fantasia and Sensibility.” In The Oxford Handbook of Topic Theory, ed. Danuta Mirka, 259–78. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780199841578.013.001.
Hepokoski, James, and Warren Darcy. 2006. Elements of Sonata Theory: Norms, Types, and Deformations in the Late-Eighteenth-Century Sonata. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195146400.001.0001.
Horn, Katelyn, and David Huron. 2015. “On the Changing Use of the Major and Minor Modes, 1750–1900.” Music Theory Online 21 (1). https://doi.org/10.30535/mto.21.1.4.
Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. The MIT Press. https://doi.org/10.7551/mitpress/6575.001.0001.
Jeffery, Peter. 1992. Re-Envisioning Past Musical Cultures: Ethnomusicology in the Study of Gregorian Chant. The University of Chicago Press.
Jerold, Beverly. 2008. “How Composers Viewed Performers’ Additions.” Early Music 36 (1): 95–110. https://doi.org/10.1093/em/cam100.
—————. 2012. “The Varied Reprise in 18th-Century Instrumental Music: A Reappraisal.” Musical Times 153 (1921): 45–61. https://doi.org/10.2307/908488.
Johnson-Laird, Philip N. 1991. “Jazz Improvisation: A Theory at the Computational Level.” In Representing Musical Structure, ed. Peter Howell, Robert West, and Ian Cross, 291–325. Academic Press.
—————. 2002. “How Jazz Musicians Improvise.” Music Perception 19 (3): 415–42. https://doi.org/10.1525/mp.2002.19.3.415.
Koch, Heinrich Christoph. 1793. Versuch einer Anleitung zur Compoisition (Vol. 3). Adam Friedrich Böhme.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. The MIT Press.
Lester, Joel. 1992. Compositional Theory in the Eighteenth Century. Harvard University Press.
Levin, Robert. 2009. “Improvising Mozart.” In Musical Improvisation: Art, Education, and Society, ed. Gabriel Solis and Bruno Nettl, 143–49. University of Illinois Press.
London, Justin. 2022. “A Bevy of Biases: How Music Theory’s Methodological Problems Hinder Diversity, Equity, and Inclusion.“ Music Theory Online 28 (1). https://doi.org/10.30535/mto.28.1.4.
Mavromatis, Panayotis. 2005. “A Hidden Markov Model of Melody Production in Greek Church Chant.” Computing in Musicology 14: 93–112.
—————. 2019. “Hierarchical Structural Patterns in Improvised Music: Implications for Cognition.” Paper presented at the 42nd annual meeting of the Society for Music Theory, Columbus, OH, November 7.
Metz, Andreas. 2017. “Melodic Fluency in Keyboard Menuet Improvisation.” Paper presented at the 9th European Music Analysis Conference (EuroMAC), Strasbourg, France.
Meyer, Leonard B. 1967. Music, the Arts, and Ideas: Patterns and Predictions in Twentieth-Century Culture. The University of Chicago Press.
—————. 1989. Style and Music: Theory, History, and Ideology. University of Pennsylvania Press.
Miller, George A. 1956. “The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information.” Psychological Review 63 (2): 81–97. https://doi.org/10.1037/h0043158.
Mirka, Danuta. 2023. “Mozart’s ‘Operatic Cadence.’” Paper presented at the joint annual meeting of the American Musicological Society and the Society for Music Theory, Denver, CO, November 10.
Mitchell, Nathaniel. 2020. “The Volta: A Galant Gesture of Culmination.” Music Theory Spectrum 42 (2): 280“304. https://doi.org/10.1093/mts/mtaa006.
Mortensen, John. 2020. The Pianist’s Guide to Historic Improvisation. Oxford University Press.
Nettl, Bruno. 1974. “Thoughts on Improvisation: A Comparative Approach.” The Musical Quarterly 60 (1): 1–19. https://doi.org/10.1093/mq/LX.1.1.
Neumeyer, David. 1987. “The Ascending Urlinie.” Journal of Music Theory 31 (2): 275–303. https://doi.org/10.2307/843711.
Neuwirth, Markus. 2020. “Is there an Implicit Formenlehre in Fedele Fenaroli’s Solfeggi? Punctuation Schemes, Formal Functions, and Voice Leading Schemata.” In Neapolitan Musical Pedagogy of the Eighteenth Century: Theory, Sources and Reception (Pergolesi Studies), ed. Claudio Bacciagaluppi and Marilena Laterza, 47–77. Lang.
Neuwirth, Markus, Christopher Finkensiep, and Martin Rohrmeier. 2023. “Musical Schemata: Modelling Challenges and Pattern Finding (BachBeatles).” In Mixing Methods: Practical Insights from the Humanities in the Digital Age, ed. Birgit Schneider, Beate Löffler, Tino Mager, Carola Hein, 147–64. Transcript Verlag.
Norgaard, Martin. 2011. “Descriptions of Improvisational Thinking by Artist-Level Jazz Musicians.” Journal of Research in Music Education 59 (2): 109–27. https://doi.org/10.1177/0022429411405669.
Pastille, William. 1990. “The Development of the Ursatz in Schenker’s Published Works.” In Trends in Schenkerian Research, ed. Allen Cadwallader, 71–85. Schirmer.
Perlman, Marc. 2004. Unplayed Melodies: Javanese Gamelan and the Genesis of Music Theory. University of California Press. https://doi.org/10.1525/9780520930490.
Pressing, Jeff. 1988. “Improvisation: Methods and Models.” In Generative Processes in Music, Ed. John Sloboda, 129–78. Oxford University Press.
Prosser, Simon K. S. 2021. “A Schema-Theoretic Approach to Hierarchy in Eighteenth-Century Tonality.” PhD diss., The Graduate Center, City University of New York.
Rabinovitch, Gilad. 2018. “Gjerdingen’s Schemata Reexamined.” Journal of Music Theory 62 (1): 41–84. https://doi.org/10.1215/00222909-4450636.
—————. 2019a. “Implicit Counterpoint in Gjerdingen’s Schemata.” Music Theory & Analysis 6 (1): 1–49. https://doi.org/10.11116/MTA.6.1.1.
—————. 2019b. “Unplayed Galant Melodies, the Ubiquity of the Rarest Interval, and the Heyday of the Major Mode.” Empirical Musicology Review 14 (3–4): 90–134. https://doi.org/10.18061/emr.v14i3-4.6070.
—————. 2020a. “Hidden Polyphony, Linear Hierarchy, and Scale-Degree Associations in Galant Schemata.” Indiana Theory Review 36 (1–2): 114–66. https://doi.org/10.2979/inditheorevi.36.1-2.05.
—————. 2020b. “Concatenating and Embellishing Schemata in Historical Keyboard Improvisation.” In Das Universalinstrument: »Angewandtes Klavierspiel« aus historischer und zeitgenössischer Perspektive / The Universal Instrument: Historical and Contemporary Perspectives on “Applied Piano,” ed. Philipp Teriete and Derek Remeš, 85–122. Olms.
—————. 2020c. “Reimagining Historical Improvisation: An Analysis of Robert Levin’s Fantasy On Themes by W. A. Mozart, October 29, 2012.” Music Theory Online 26 (2). https://doi.org/10.30535/mto.26.2.11.
—————. 2022. “Haydn’s Schemata and Hexachords: Two Analytical Case Studies.” HAYDN: Online Journal of the Haydn Society of North America 12 (1).
—————. Forthcoming 2023. Review of The Solfeggio Tradition: A Forgotten Art of Melody in the Long Eighteenth Century, by Nicholas Baragwanath. Journal of Music Theory.
—————. Forthcoming 2024. “Navigating Schemata and Hexachords: Case Studies from Solfeggi by Giuseppe Aprile.” Music Theory & Analysis.
Remeš, Derek. 2020. “Some (Dis)Assembly Required: Modularity in the Keyboard Improvisation Pedagogy of Jacob Adlung and Johann Vallade.” Music Theory Online 26 (1). https://doi.org/10.30535/mto.26.1.5.
Ruwet, Nicolas. 1987. “Methods of Analysis in Musicology.” Translated by Mark Everist. Music Analysis 6 (1–2): 3–36. https://doi.org/10.2307/854214.
Rice, John. 2015. “The Morte: A Galant Voice-Leading Schema as Emblem of Lament and Compositional Building-Block.” Eighteenth-Century Music 12 (2): 157–81. https://doi.org/10.1017/S1478570615000287.
Sánchez-Kisielewska, Olga. 2016. “Interactions between Topics and Schemata: The Case of the Sacred Romanesca.” Theory and Practice 41: 47–80.
Sanguinetti, Giorgio. 2012. The Art of Partimento: History, Theory, and Practice. Oxford University Press.
Schank, Roger C., and Robert P. Abelson. 1977. Scripts, Plans, Goals, and Understanding: An Inquiry into Human Knowledge Structures. L. Erlbaum Associates.
Schmalfeldt, Janet. 2011. In the Process of Becoming: Analytic and Philosophical Perspectives on Form in Early Nineteenth-Century Music. Oxford University Press.
Schenker, Heinrich. 1979 [1935]. Free Composition (Der freie Satz): Volume III of New Musical Theories and Fantasies. Edited and translated by Ernst Oster. Longman.
Schwab-Felisch, Oliver. 2014. “The Butterfly and the Artillery: Models of Listening in Schenker and Gjerdingen.” Music Theory and Analysis 1 (1–2): 107–20. https://doi.org/10.11116/MTA.1.6.
Stoia, Nicholas. 2013. “The Common Stock of Schemes in Early Blues and Country Music.” Music Theory Spectrum 35 (2): 194–234. https://doi.org/10.1525/mts.2013.35.2.194.
—————. 2021. Sweet Thing: The History and Musical Structure of a Shared American Vernacular Form. Oxford University Press. https://doi.org/10.1093/oso/9780190881979.001.0001.
Symons, James. 2017. “A Cognitively Inspired Method for the Statistical Analysis of Eighteenth-Century Music, as Applied in Two Corpus Studies.” PhD Diss., Northwestern University.
Temperley, David. 2011. “Composition, Perception, and Schenkerian Theory.” Music Theory Spectrum 33 (2): 146–68. https://doi.org/10.1525/mts.2011.33.2.146.
Tilley, Leslie A. 2019. Making it Up Together: The Art of Collective Improvisation in Balinese Music and Beyond. The University of Chicago Press. https://doi.org/10.7208/chicago/9780226667744.001.0001.
Will, Udo. 2000. “Oral Memory in Australian Aboriginal Song Performance and the Parry-Kirk Debate: A Cognitive Ethnomusicological Perspective.” Proceedings of the International Study Group on Music Archaeology 10: 1–29.
Yu, Hainian. 2023. “Revisiting the Galant in Gjerdingenian Schemata.” Music Analysis 42 (3): 287–330. https://doi.org/10.1111/musa.12222.
Yust, Jason. 2018. Organized Time: Rhythm, Tonality, and Form. Oxford University Press. https://doi.org/10.1093/oso/9780190696481.001.0001.
Footnotes
* This article has benefitted greatly from the feedback of numerous colleagues at various stages: Janet Bourne, Andrew Goldman, and Panayotis Mavromatis, who were co-panelists at the SMT 2019 annual meeting in Columbus, OH, provided valuable insights at early stages. We are also grateful to attendees of the 2019 panel for their many helpful comments and suggestions. Olga Sánchez-Kisielewska, Jason Yust, and an anonymous reviewer provided perceptive commentaries on later versions of the manuscript. Finally, we thank Poundie Burstein for sharing with us a written version of a 2023 keynote lecture.
Return to text
1. See also Yu’s (2023) very recent addition to the schema-theoretic literature, which analyzes the complete surface of large-scale pieces by C. P. E. Bach and reflects on the stylistic purview of galant schemata.
Return to text
2. For a recent entry point into this formal trajectory, see Burstein (2020, 72–80) after Koch (1793).
Return to text
3. Yust 2018 shows that tonality, form, and rhythm can be treated as radically separate domains. Our reliance on schemata as building blocks implies generic ways of integrating tonality, rhythm, and form. We further note that our specific discovery procedure suggests that core tones are embedded in metric positions in conventional ways in pieces from the 1740s. In other words, we appear to be dealing with strong dependencies among musical parameters in this repertoire.
Return to text
4. In this sense, the case study in Rabinovitch 2020c (see [1.2.4]), which focuses on an improvisation in the style of Mozart by a living elite expert, Robert Levin, seems like a safer exercise.
Return to text
5. See also Carter-Enyi and Rabinovitch 2021 ([1.3]). Disagreements such as those described by Perlman (2004) among Javanese experts about the true underlying frame for gamelan music exemplify the divergence of expert intuitions and opinions within a single musical tradition that seems to revolve around a skeletal layer.
Return to text
6. For a useful recent didactical entry point, see Mortensen 2020.
Return to text
7. Of course, improvisation is often conceptualized as involving automaticity, which may be facilitated by tight constraints. Kofi Agawu (1995, 79) speaks of performers “sleep-walk[ing] their way from one harmony to the next,” while Martin Norgaard’s (2011, 122) interviewees “described feelings of automaticity during their improvisation.”
Return to text
8. We should keep in mind that improvisation is so typical in performance that it is often taken for granted (Blum 2023, 92); sharp distinctions between composition and improvisation and the markedness of classical improvisation tell us more about our own frames than about actual musical practices.
Return to text
9. Nettl’s continuum seems highly relevant to us for eighteenth-century galant music-making. For a recent reassessment of continuum models for improvisation from the perspective of embodied cognition, see Goldman 2022.
Return to text
10. The creativity that we associate with schemata in the 1740s has more to do with working within constraints than thinking outside the box. Yet as Leslie Tilley astutely observes, “The easy assumption is that more exploratory creativity is required as the model becomes less specific, or as the distance between the model and the realization increases. Yet
Return to text
11. Indeed, Baragwanath’s (2020) reconstruction of the solfeggio tradition supports this view of “skeletal” solmization syllables (roughly equivalent to core tones) vs. outlines for diminutions (cf. Rabinovitch 2020a). For preliminary reflections on hexachords and schemata beyond what was possible in the present article, see Rabinovitch 2022, 2023, 2024.
Return to text
12. For a classic discussion of the “fallacy of hierarchical uniformity,” see Meyer 1967 (96–97).
Return to text
13. Cf. also Prosser 2021 (100–101).
Return to text
14. See the discussion in Mavromatis 2019 of Miller 1956 and Cowan 2001.
Return to text
15. The spatial metaphors for improvisation that come up in highly divergent sources—e.g., finding a “circuitous” or “direct” route (Bach [1753/1762] 1949, 438) or navigating subway maps or a house with multiple rooms (Farraj and Shumays 2019, esp. 278–9)—inspire cautious optimism regarding connections between disparate traditions of music-making.
Return to text
16. Stoia (2021) tracks the origins of a stanza-level schema that facilitates the creation of new songs in a host of vernacular idioms.
Return to text
17. In our opinion, it is clear that equal temperament instruments were introduced by Europeans (and now manufactured and distributed to Africa by Japanese companies), but not so for the diatonic scale (or patterns within it)—and neither of these examples use any equal temperament instruments (in fact, the recorded performance of “Ńgéngélé” goes considerably sharp). KiKuria is a relatively small and less documented culture so there is only recent literature and documentation, but Igbo, a large ethnic group of over 30 million people, has had considerable documentation with audio recordings dating back to 1910. Nigerian-born music theorist Laz Ekwueme (b. 1936, a doctoral student of Allen Forte) grew up in a time when many Igbos were not aware or did not accept that they were part of a British colony. Many rural areas were not Christianized until after the Nigerian Civil War (1967–1970) and were missionized by fellow Igbos more so than westerners. Ekwueme felt that diatonic-like scales existed before colonialism or missionization (1974).
Return to text
18. See the discussions in Symons 2017 (74); Baragwanath 2020 (280); and Rabinovitch 2020a (131–37).
Return to text
19. Given our focus, we are interested here in the melodic outline for ending an Indugio more than in other features of the schema as Gjerdingen defines it. For instance, in Gjerdingen’s ex. 20.4 by Cimarosa (2007, 276), we are less interested in the bass oscillation between and with a passing ![]()
Return to text
20. Baragwanath’s (2020) reconstruction of hexachordal solmization suggests that both and in this case would have been solmized sol, which means that there was in fact a mental association between the stepwise cadential string and its typical embellishment through a hidden-polyphony outline for diminution (cf. Rabinovitch 2020a). See Baragwanath’s presentation of galant solmization deception or Inganno 2020, 121), and his mapping of the “high 2 drop” as a deceptive usage of solmization, in which High- is used instead of stepwise-connected based on their shared solmization syllable, sol (2020122, example 6.28a).
Return to text
21. Our focus deviates from the richness of micro-theoretical description in the schema-theoretic literature. Detailed descriptions of individual patterns (e.g., Byros 2012; Rice 2015; Sánchez-Kisielewska 2016; Mitchell 2020; Mirka 2023) have the added advantage of connecting musical patterns to cognitive, performative, and semiotic discourses.
Return to text
22. In discussing a movement by Galuppi, Gjerdingen recognizes that some passages may be “sui generis” rather than “off the shelf” schemata and states that his “goal is not to replace the tyrannies of modern musical analysis with a tyranny of galant schemata” (2007, 219). We do not view music theory’s pursuit of consistent and general explanations as tyrannical. See also the related yet complementary methodology of Yu (2023).
Return to text
23. See, e.g., Lerdahl and Jackendoff’s TSRPR 1 (Metrical Position) and TSRPR 2 (Local Harmony) (183, 160–62). Note also the comments in Temperley 2011 (153) about melodic fluency and accents.
Return to text
24. As Neuwirth, Finkensiep, and Rohrmeier (2023, 153) emphasize, in order to operationalize schemata one has to “reconsider and refine traditional descriptions and definitions,” as they exemplify by surveying divergent definitions of the Fonte. Surely our soprano-centric approach provides a narrower lens on schemata, which we hope would be helpful in finding paths towards them. Moreover, our present by-hand task of finding a soprano core tone respective to the bass in music from the 1740s is a narrower task than detecting complete schemata in complex polyphonic textures.
Return to text
25. As discussed in Rabinovitch 2020a (142), the High- and High- represent points of incongruence in the style, in which a peripheral element—or, if you will, outline for diminution—occupies a point of metric stress whereas the principal core tone, that is, or , respectively, is pushed to a weak metric position. Thus, the tendency of the Meyer or –
Return to text
26. As Greenberg’s (2017, 2022) work demonstrates, the evolution towards what we now think of as the high-classical sonata form can be tracked through crucial junctures in the second reprise. See also Burstein (2020, chapter 14).
Return to text
27. See the data in Albrecht and Huron 2014 and Horn and Huron 2015, which suggest that major-mode pieces became increasingly dominant in the production of eighteenth-century musicians, especially in the second half of the century. All of Gjerdingen’s (2007) full-movement analyses are of pieces in the major mode. See also the discussion of the major mode and rare diatonic intervals in Rabinovitch 2019b.
Return to text
28. Though Gjerdingen largely disregards the tonal identity of a schema respective to the global tonic, he differentiates in his probabilistic account (2007, 372) between Prinner and Modulating Prinner (i.e., Prinner in V). Otherwise, he does not distinguish between instances of schemata respective to different tonal centers. Compare this to Neuwirth’s observation that “the likelihood of an ‘Indugio’ schema preceding a cadence increases drastically if a secondary-theme section is about to approach its structural ending; by contrast, this likelihood is considerably reduced if we enter the primary-theme section” (2020, 53).
Return to text
29. A preliminary account of the sample is given in a pedagogical context in Rabinovitch 2020b, where we wonder whether linear constraints or schema successions are useful guiding principles in creating a galant exposition. While that essay contains a preliminary report, the present article goes into far greater detail.
Return to text
30. As mentioned, we were inspired by Symons’s composite graphic representation of the Prinner (reproduced above as Example 7): instead of core tones, hidden-polyphony outlines, and surface details, our statistical backbone consists of schema types recurring in a high-enough number of pieces in our sample.
Return to text
31. Almost needless to say, one might object that this is an artificial exercise in paradigmatic analysis and that it was impossible to unlearn galant formal norms while engaging in this sorting.
Return to text
32. For instance, Gjerdingen (2007, 415–16) writes that “many inherited approaches to eighteenth-century music are perhaps best understood as descendants of nineteenth- and early twentieth-century attempts to reinterpret the galant tradition—a tradition that, although in many ways antithetical to the bourgeois art of Romanticism, was nevertheless claimed by the Romantics as a crucial part of their patrimony. Galant music became the childhood of Romantic music, meaning that the galant was thought to be both childlike and suitable for children. An adult galant musician like Clementi, capable of great range and profundity, became known almost exclusively for tiny pieces used to teach beginning piano students in Victorian middle-class households. Galant musicians, thus viewed as genial children, were judged to lack an understanding of ‘higher’ form. At best, they seemed to stumble toward sonata form, with only Haydn and Mozart finally getting it right.”
Return to text
33. We should note that a theory of formal functions (Caplin 1998) and Sonata Theory (Hepokoski and Darcy 2006) are dedicated to later practices. Burstein (2020) describes the succession of resting points typical of galant expositions, but he is less interested in the schematic content of such sections and more in the overall script of motion towards resting points.
Return to text
34. In his recent critique of music theory and its biases, London (2022) likewise invokes the distinction between scripts and plans and discusses music theorists’ tendency to treat plans as if they are scripts. Yust (2018, chap. 11) discusses formal “recipes” such as Baldassare Galuppi’s usage of form in his keyboard sonatas. The generic conventions charted here through a different methodological lens can also be considered “recipes” for creating a section.
Return to text
35. Burstein (pers. comm.) observed that our selected decade somewhat predates the heyday of Koch’s script: we had chosen this decade primarily due to our impression that constraints on schemata—both on local diminutions and successions within form—are particularly tight.
Return to text
36. For additional views on schemata and linear analysis, see Froebe 2014, 2015 and Schwab-Felisch 2014. Of course, our reliance on pieces from the 1740s is one area of tension with the Schenkerian focus on the Germano-centric canon: the present article is an exploration of the psychology of convention (after Gjerdingen 1988) of musicians rather than of the narrow traditional analytical canon.
Return to text
37. The strikingly strong representation of a Prinner riposte in this sample has perhaps influenced our reading in a case like piece Lavaux’s Sonata for Flute and Continuo, Op. 2, no. 2, mvt. 2 (#15 in our sample), in which a ––– variant pattern was interpreted as a Prinner riposte, based in part on its formal position. See also the analytical engagement of an atypical and “impatient” Prinner in Haydn’s Symphony no. 14 in Burstein 2020, 242.
Return to text
38. See, e.g., Brown’s (1998) reactions to the views of Neumeyer (1987).
Return to text
39. Charting a later communicative context, Gooley (2018) connects the gradual decline in improvisation in the nineteenth century to the growing sizes of concert audiences in major European cities, who did not have the same musical abilities as eighteenth-century connoisseurs and amateurs. Working on a genre with improvisatory roots, Bourne (2019) tracks the difficulties in perceiving similarities between variations, including in challenging compositions like Beethoven’s sonata Op. 109.
Return to text
40. See the second quotation from a letter by Bach in Ferris 2000 (73, fn. 40).
Return to text
41. While the switch back to conventional schema analysis might be disappointing to some readers, we feel it is necessary here. If eccentric pieces from a later decade are more difficult to reduce to soprano core tones in comparison with sonatas from the 1740s, this tentatively supports the utility of our otherwise narrow chronological focus.
Return to text
Copyright Statement
Copyright © 2024 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Amy King, Editorial Assistant
Number of visits:
6342