A General Method for Composing a Canon Against a Cantus Firmus Using Sergei Taneev’s Double-Shifting Counterpoint

1. Introduction

[1.1] Over time, the technique of composing two voices in canonic imitation in accompaniment of a cantus firmus has become a lost art. During the late Renaissance, musicians developed their proficiency in this technique to the point that they could improvise this type of canon in real time, singing in discant polyphony “upon the book” (Cantare super librum) to a plainchant. Although this was a difficult and prestigious skill, it was apparently not uncommon. Philippe Canguilhem (2011, 55–59), for example, gives a compelling historical account of how the improvisation of canons upon the book was included among the tests of the candidates for an open position of choirmaster in Toledo in 1604. Counterpoint treatises began to address these kinds of improvised canons in the mid-sixteenth and early seventeenth centuries.⁽¹⁾ The basic method at the time, to be discussed in more detail later, was introduced into print by Vicente Lusitano (1553). It involved enumerating a list of consonant intervals that the leading voice of the canon is permitted to form in relation to the cantus firmus, given certain information about the type of canon and the melodic shape of the cantus firmus.

[1.2] In the late nineteenth and early twentieth centuries, a new cohort of authors returned to this topic, albeit with a significant difference in approach.⁽²⁾ With the practice of discant counterpoint having waned, these later authors drew upon the canonic chorale preludes and ground bass compositions of J. S. Bach as their primary compositional models. These later authors, seemingly unfamiliar with or uninterested in the systematic method proposed by the earlier authors, offered instead what amounts to a “trial-and-error” method.⁽³⁾ Considering the complexity of the contrapuntal problems involved, student composers working from these textbooks may have been disappointed by the lack of specific guidance, especially their hope of imitating the highly advanced canons of J. S. Bach offered up as models. Apart from the examples by Bach, canons composed to accompany a pre-composed melody became increasingly rare in written common-practice music, which partly accounts for the apparent neglect of this topic in counterpoint pedagogy.

[1.3] More recent scholarship has returned to the older systematic method of the late Renaissance and has advocated for it as a pedagogical tool (Collins 1992, 1993, 2008; Schubert 2007, 319–33). Although it is well-suited for courses on sixteenth-century counterpoint or historical improvisation, the Renaissance approach, as will be shown later, does not resolve the problem of how to compose such canons comprehensively. The practical challenges posed by improvisation may be overcome by acquiring specific competencies; as such, the Renaissance method focuses on addressing a particular subset of canonic solutions that are within the grasp of an extemporizing musician. The practical solution depended upon a large amount of rote memorization, the sheer difficulty of which has raised the eyebrows of later generations both in amazement and incredulity.⁽⁴⁾ That there are ways to construct this kind of canon beyond the methods given by the Renaissance authors is proven by the highly advanced canons written against a cantus firmus in the written literature, as will be discussed in sections 4 and 5.

[1.4] A comprehensive solution for the composition of canons against a cantus firmus can be achieved by applying Sergei Taneev’s (1856–1915) theories of movable counterpoint. It is true that Taneev himself does not directly address the problem of canons written against a cantus firmus in either of his published books (Taneiev [1909] 1962; Grove 1999); however, an approach based in his theory of double-shifting counterpoint does provide a general solution, even for canons written in contrary motion and other advanced imitative techniques.⁽⁵⁾ The explanation of this solution will require a detailed working-out that will take up the next two sections of this article. The working method that results, however, is surprisingly straightforward. This method can be used both to compose rule-based counterpoint exercises in the “strict” pedagogical tradition of Fux and Taneev⁽⁶⁾ and to analyze such canons in written repertoire. This article will treat the issue mainly from the perspective of written counterpoint exercises, before broadening the scope to consider improvisation and “singing upon the book” in the conclusion.

2. Key Concepts and Terminology

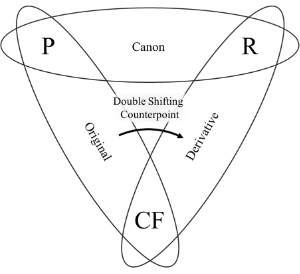
[2.1] Example 1, which shows the framework for a canon composed by Denis Collins (2008, 121) set against a cantus firmus, will illustrate some of the specialized vocabulary for this kind of canonic exercise. Collins selects the Dorian cantus firmus from Fux’s Gradus ad Parnassum and places it in the bass voice (abbreviated “CF” in the example). The soprano plays the role of the leading voice of the canon, or “proposta” (abbreviated “P”), following Taneev’s preferred terminology. Each note of the proposta is imitated by the “risposta” (abbreviated “R”) after being transposed to a new pitch level by a directed “interval of entrance”—in this case, downward by a fifth. The risposta also follows the proposta after a time delay of one whole note. In general, the duration of this delay between canonic voices will be referred to as the “distance of entrance” of the canon. The distance of entrance is not always one measure, and whenever a particular duration equal to the distance of entrance needs to be distinguished from another, the durations will be referred to as “time units.” In this example, whatever notes Collins chooses for the proposta in the first whole note of m. 1 will determine the notes for the risposta in the second whole note of that measure, so those two whole notes may be considered “corresponding” time units.

[2.2] Collins composed this canon using his own adaptation of the approach of the Renaissance, specifically the one outlined in the third edition of Zarlino’s Le istitutioni harmoniche (1573). This method allows Collins to identify and select workable whole-note consonances for each time unit. After having done this, he elaborates the canonic melody with faster note values and dissonances, also shown in Example 1. To specify how the proposta, risposta, and cantus firmus combine into a three-voice contrapuntal texture, it is useful to break this texture down into its three constituent two-voice combinations of P+CF, R+CF, and P+R, and to examine each individually. This is the approach taken by Russian composer and theorist Sergei Taneev, whose two books on counterpoint and canon provide significant insights into these relationships and their transformations (Taneiev [1909] 1962; Grove 1999).⁽⁷⁾ If all three two-voice combinations of an exercise are written in correct counterpoint, then the whole three-voice texture will also be correct and free of any voice-leading errors such as incorrectly treated dissonances, parallel octaves, etc.⁽⁸⁾ That being said, stylistically appropriate three-voice part writing often involves more than simply avoiding the most egregious kinds of two-voice errors, so three-voice harmony will be treated at length in section 3.

[2.3] Example 2 shows a two-voice “original” combination written by Taneev according to the rules of strict counterpoint (1962, 20). Taneev labels the voices of a combination using upper case Roman numerals: the top voice of the original combination is “I,” the lower voice is “II,” and the combination is “I+II.” Notice that the harmonic intervals in Example 2 are not labeled in the standard way. Instead of ordinal numerals (“third,” “fourth,” “fifth,” etc.), Taneev indicates the magnitude of an interval using cardinal numerals in which the unison = 0, the second = 1, the third = 2, etc. These cardinal numerals can be thought of as the number of diatonic steps separating I and II. Note that throughout this article, traditional interval names will be written with ordinal indicator suffixes (“2^nd” or “second,” etc.) to distinguish them from Taneev’s cardinal numerals. In cases where the voices of a combination move relative to one another, negative values represent the two voices of a combination moving closer together while positive values represent the voices moving apart. This system allows for basic addition and subtraction of generic intervals in diatonic music, comparable to the addition and subtraction of pitch intervals in post-tonal theory (Taneiev [1909] 1962, §26–30, 36–37).

[2.4] Continuing on, Taneev specifies three kinds of transformations that can be used to obtain new, “derivative” combinations from an original. Example 3 shows a derivative combination brought about by a “vertical shift,” in which one of the voices has been transposed to a new pitch level; in this case, the lower voice has been transposed upward by the interval of a tenth so that it now occurs above the upper one. This example corresponds to the topic of invertible counterpoint at the tenth, well known in traditional counterpoint instruction; in Taneev’s system, however, it is expressed as “II^v = −9,” indicating that the lower voice has been vertically shifted in the direction of the other voice by a tenth. Negative vertical shifts that result in an exchange of voices in the contrapuntal texture are referred to as “inverse” shifts. Instances of inverse shifts always involve negative harmonic intervals in the derivative combination, and this topic is synonymous with invertible or double counterpoint. Vertical shifts that do not result in an exchange in the texture are called “direct shifts”; for this reason, vertical-shifting counterpoint is a more inclusive concept than invertible counterpoint. Taneev refers to the sum of the vertical shifts in both voices of a given combination as the vertical-shift index (Jv), given by Equation (1):

(1) Jv = I^v + II^v

In the derivative of Example 3, Jv = −9 since voice I undergoes no vertical shift (0 + −9 = −9).

[2.5] The derivative in Example 4 shows another example of invertible counterpoint at the tenth, wherein voice I has been shifted down a third and voice II has been shifted up an octave (Jv = −2 + −7 = −9). The utility of Taneev’s arithmetic becomes apparent when one notices that the intervals of the original combination of Example 2 differ from those of the derivative combinations in Examples 3 and 4 by a fixed index value of −9. This insight informs one of Taneev’s fundamental equations:

(2) n = m + Jv

where n is an interval of the derivative combination and m is the corresponding interval of the original (Taneiev [1909] 1962, §§61–64, 44–47). Equation (2) can be algebraically rearranged to solve for the vertical-shift index:

(3) Jv = n - m

Note that this form of the equation is particularly useful in analysis.

[2.6] Example 5 shows a derivative combination brought about by a different kind of transformation: a “horizontal” shift, in which I occurs at the same pitch level but one half-note later than it did in the original combination. This derivative combination therefore has a different metrical alignment between I and II compared to the original, and the harmonic intervals of the derivative are newly formed and do not directly correspond with intervals from the original. The horizontal-shift index (“Jh”) in this case is one half measure—expressed in Taneev’s system as “Jh = $\frac{1}{2}$ (Taneiev [1909] 1962, §§348–59, 220–21). Example 6 shows a derivative combination brought about by what Taneev refers to as “double-shifting” counterpoint, which entails the simultaneous application of vertical and horizontal shifts. In this case, I has been horizontally shifted one measure to the right (Jh = 1) and vertically shifted upward by a sixth (Jv = 5).

[2.7] The central difficulty regarding how to compose a canon against a cantus firmus may be productively reframed using Taneev’s terminology. Example 7 shows a summary of the relationships between the two-voice combinations. If the P+CF combination is construed as an original two-voice combination, then R+CF can be seen as its derivative combination brought about by double-shifting counterpoint. This double shift involves applying to the proposta a vertical shift equal to the interval of entrance of the canon and a horizontal shift equal to the distance of entrance of the canon. The basic difficulty, then, of composing a canon against a cantus firmus lies in securing the correctness of this double shift, while at the same time composing the P+R combination as a canon in correct two-voice counterpoint.

[2.8] Taneev distinguishes between two kinds of consonant intervals subject to a vertical shift: “fixed consonances” and “variable intervals.” Example 8 shows an inversion table for invertible counterpoint at the twelfth (Jv = −11). The table is written twice to facilitate comparison with conventional counterpoint textbooks, first using Taneev’s cardinal numerals and then using the traditional ordinal numerals. In both cases, the top row lists the harmonic intervals formed in an original combination, counting upward from the unison to the nominal interval of inversion. The lower row lists the intervals of the derivative combination that correspond vertically with the original. Applied to Equation (2), the top row lists values for m in Equation (2), the lower row lists values for n, and the constant difference between the rows is Jv (Taneiev [1909] 1962 §33, 37). Fixed consonances are those that are consonant in both original and derivative forms, such as the unison, third, and fifth in Example 8. Variable intervals are those that change from consonance to dissonance or vice versa after the vertical shift, such as the sixth and seventh in Example 8.

[2.9] Example 9 shows a similar table constructed for invertible counterpoint at the fourth (Jv = −3). Invertible counterpoint at the fourth only properly occurs in the inverse portion of the table, where positive cardinal numerals in the original become negative or zero in the derivative. (Note that most of the original intervals in this small vertical-shift index do not invert.) Example 9 also shows a continuation of the table into direct-shifting intervals where both original and derivative are positive. A vertical bar indicates the boundary between inverse- and direct-shifting areas of the table. In a traditional table using ordinal numerals, there is no zero, nor are there negative numbers; due to this, the direct-shifting area of a table must instead be constructed by counting upward from the unison in the derivative row. This is the method that Nottebohm (1873, 148) shows in his discussion of Beethoven’s counterpoint studies with Albrechtsberger in the 1790s. This type of extended table is necessary for smaller vertical shifts, or any instance where the voices in a combination form a harmonic interval larger than the vertical-shift index.

[2.10] Although they would not have phrased their solution in these terms, the method adopted by the Renaissance contrapuntists cited above enumerates the original forms of the fixed consonances for the vertical shift that governs the relationship between P+CF of one time unit and R+CF of the next. Zarlino, like Lusitano before him, originally listed the permissible consonant intervals formed between proposta and cantus firmus in the prose of his text. Collins, in contrast, summarizes this information for a canon at the distance of one whole note with the cantus firmus in the lowest voice in the table shown as Example 10, and used the information in this table to compose the canonic exercise shown earlier in Example 1 (2008, 119).⁽⁹⁾ In selecting a proposta note for the first measure of Collins’s canon, the table shows that, for a canon with an interval of entrance at the lower fifth (the column labeled “↑4^th or ↓5^th”) and with the cantus firmus ascending by third into the next time unit (the row labeled “↑3^rd or ↓6^th”), the only permissible consonance is the perfect fifth; Collins therefore chooses the note A for the proposta on this first downbeat.⁽¹⁰⁾

[2.11] The diagonals of Example 10 form a regular pattern of fixed consonances that can be explained using Taneev’s arithmetic. Recall that the vertical-shift index can be given by Equation 3, Jv = n – m, where n is an interval from the derivative combination and m is the corresponding interval from the original. Example 11 shows some of the logic of this equation at work on the first downbeat of Collins’s canon from Example 1. The interval m for the original P+CF combination on this downbeat is 11, while the corresponding interval of the derivative R+CF combination in the next time unit is 5. Taneev’s formula tells us that the vertical-shift index is therefore −6, since 5 − 11 = −6. Notice that this formula requires known values for m and n, so a composer would only be able to use this formula to calculate the vertical-shift index after having composed the portion of the canon under investigation. This is therefore only a modest improvement on the trial-and-error method of the nineteenth century.

[2.12] Instead, I propose a different equation that would be more helpful.

(4) Jv = r + s

In Equation (4), r is the interval between notes of the cantus firmus in corresponding time units and s is the interval of entrance of the canon, as shown in Example 11. For canons where the distance of entrance is equal to the duration of each note of the cantus firmus, as in Collins’s exercise, r is simply a melodic interval of the cantus firmus. The value of r is positive if the cantus firmus moves away from the proposta and negative if it moves toward it (Taneiev [1909] 1962, §§66–67, 48–49). Likewise, the value of s is positive if the interval of entrance of the canon is directed away from the cantus firmus and negative if it is directed toward it. In this example, the cantus firmus ascends toward the proposta by a leap of a third (r = −2) and the interval of entrance is a perfect fifth in the direction of the cantus firmus (s = −4), so our new formula gives us the same solution: Jv = −2 + −4 = −6. Importantly, this new formula allows us to calculate the vertical-shift index using only information known prior to composing the proposta for a given time unit. Example 11 includes an inversion table for invertible counterpoint at the seventh. From this, we can see that the only fixed consonance in the direct-shifting area of the table is the fifth (or, rather, twelfth), which is the same fixed consonance that was indicated for this choice of note using Collins’s table in Example 10. The pattern of the diagonals in Example 10 arises from the fact that the rows and columns are ordered sequentially. The vertical-shift index of each cell is simply the sum of the value of its row, r, and the value of its column, s.

[2.13] Beyond his discussion of vertical shifting counterpoint, Taneev also gives practical advice on how to compose a counterpoint (which he abbreviated “CP”) against a cantus firmus in horizontal and double shifts (Taneiev [1909] 1962, 213). Example 12 shows the process for composing horizontal-shifting counterpoint (Taneiev [1909] 1962, 238–39). The cantus firmus is first placed in canonic imitation with itself at a distance of entrance equal in duration to the intended horizontal shift. The intended horizontal shift is two measures, thus the distance of entrance for the canonic voices is two measures. Taneev refers to the answering voice of this canon as the “imaginary” risposta (“IR”); throughout this article, the notes of an imaginary voice will be placed in parentheses. Importantly, this imaginary voice is placed without regard for whether the two-voice combination forms correct counterpoint. Taneev then composes a counterpoint that forms correct counterpoint with either version of the cantus firmus independently, without concern for the correctness of the three-voice combination; see Example 13. Taneev referred to this pseudo-three-voice complex as the “basic version.” Example 14 shows how the constituent two-voice combinations that involve the counterpoint can be extracted from the basic version to form original and derivative combinations that relate by a horizontal shift of Jh = −2.⁽¹¹⁾

[2.14] Composing double-shifting counterpoint is no more difficult. Whereas in Example 12 the cantus firmus was placed in canonic imitation with itself at the unison, Example 15 shows a basic version in which the IR follows the proposta one measure later and at an interval of entrance of a seventh above. The counterpoint in the middle voice threads between both versions of the cantus firmus, forming correct counterpoint with each independently. The two-voice original and derivative combinations that can be extracted from this basic version are related by a double shift. Voice I of the derivative combination in Example 15 has been vertically shifted a seventh lower compared to the original and horizontally shifted one measure earlier. Necessarily, the double shift that results from this method is the opposite of whatever interval and distance of entrance are chosen for the canonic proposta and imaginary risposta in the basic version. With Taneev’s concepts of vertical-, horizontal-, and double-shifting counterpoint in hand, we can now turn our attention to applying these tools to the composition of canonic exercises against a cantus firmus.

3. The Working Method

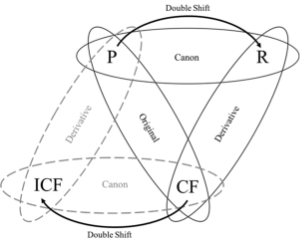
[3.1] Taneev’s theory of double-shifting counterpoint allows for a mastery of the problem of how to compose a canon against a cantus firmus well beyond the guess-and-check approach of the nineteenth century and the laborious cataloguing and memorization of fixed consonances of the sixteenth. The original working method proposed in this article involves applying an imaginary cantus firmus (abbreviated “ICF”) to a canonic exercise to clarify the type of contrapuntal writing required to ensure the correctness of the double shift that transforms the original P+CF combination into the derivative R+CF combination. The new canonic relationships are shown in Example 16. The imaginary cantus firmus will be placed in order to form a new canonic combination ICF+CF that shares the same canonic parameters as the P+R canon, but in which the imaginary cantus firmus leads and the actual cantus firmus follows.⁽¹²⁾ This means that the new P+ICF combination will form a transposed duplicate of the derivative R+CF combination. The proposta will therefore participate in one version of all three two-voice combinations—original, derivative, and canonic. Because of this, most of the composer’s attention can be placed on the proposta voice, ensuring that it forms correct two-voice combinations, P+CF and P+ICF, a task no more difficult than that of handling Taneev’s problem of double-shifting counterpoint (cf. Example 15, above). The only additional difficulty, compared to a normal problem of double-shifting counterpoint, is that the P+R combination must also work as a canon, which, fortunately, only requires those parts to be written in simple, non-shifting counterpoint (i.e., Jv = 0) with one another (Grove 1999, 45–67). The recommended working method consists of seven steps:

[3.2] 1. Decide upon the parameters of the canonic problem. This entails the determination of a cantus firmus, the distribution of the cantus firmus and canonic roles within the texture, and the interval and distance of entrance for the canon. Example 17 shows a sample setup for a canonic exercise. Fux’s Dorian cantus firmus occurs in the middle (alto) voice; the bass will play the role of the proposta, while the risposta will follow at the upper twelfth at a distance of one whole note in the soprano range. The intended first notes of the proposta and risposta are provisionally indicated in Example 17. At this early point, however, they are subject to change: only the interval and distance of entrance between the canonic voices needs to be selected. In a classroom setting, the parameters for the canonic problem could be set in advance by the instructor.

[3.3] 2. Find the placement of the imaginary cantus firmus and write it in, preferably on a separate staff as shown in Example 19. The imaginary cantus firmus is a transposition of the cantus firmus that is placed at a vertical shift that is the inverse of the interval of entrance and at a horizontal shift that is the inverse of the distance of entrance of the canon one intends to compose. In the case of the parameters for our example, this means that the cantus firmus is vertically shifted down a twelfth (rather than up) and horizontally shifted one whole note earlier (rather than later), as indicated by the dashed arrows in Example 18. This arrangement of cantus firmus and imaginary cantus firmus replicates in musical notation the logic of Equation (4): Jv = r + s. Taking m. 6 as an example, the cantus firmus leaps away from the proposta by a third (r = 2), and the interval of entrance is a twelfth upward from the proposta toward the cantus firmus (s = −11); therefore, Jv = 2 + −11 = −9. The harmonic interval formed between the cantus firmus and imaginary cantus firmus of each time unit (a tenth, or −9, in the case of m. 6) is therefore equal to the vertical-shift index that governs that time unit. This interval between cantus firmus and imaginary cantus firmus will be called the “guide interval.”

[3.4] 3. Use the information provided by the guide intervals to compose notes for the proposta. Example 19 shows each of the guide intervals of our exercise labeled above the imaginary cantus firmus, one for each time unit of the canon. In m. 1, for instance, the guide interval between the imaginary cantus firmus note B3 and the cantus firmus note D4 is a tenth, and so the proposta voice for this time unit should be composed according to the rules of invertible counterpoint at the tenth (Jv = −9). Example 19 also includes an inversion table for invertible counterpoint at the tenth; from this, one can verify that the octave of the original P+CF combination in m. 1 becomes a third in the derivative R+CF combination of m. 2 by the vertical shift indicated by the guide interval. Notes for the proposta may be chosen from outside the range of the guide interval in the direct-shifting area of an extended interval table; this will result in a voice crossing between risposta and cantus firmus in the derivative combination. These inversion tables include the same original forms of the fixed consonances as the Renaissance lists and Collins’s table from Example 10. Importantly, though, they provide additional context by pairing each original interval with its specific derivative interval and by including the complete range of fixed consonances, fixed dissonances, and variable intervals. One systematic way to compose the proposta voice is to construct and consult the interval table indicated by the guide interval for each time unit.

[3.5] Here, it should be noted that there is a second way of going about this step that is more economical, although perhaps less thorough. It involves viewing the mechanism in alternate terms as follows: the proposta note D3 of m. 1 forms a third above the imaginary cantus firmus, and this P+ICF combination is transposed to form the R+CF combination of the next time unit. From this perspective, one may forego the inversion table entirely and work directly with the musical notation. It is evident from scanning the possibilities of notes within the guide interval of m. 1 that only the notes D3, F3, and G3 form a consonant interval both above the imaginary cantus firmus and, independently, below it.⁽¹³⁾ This approach accords more closely with the manner of working recommended by Taneev in relation to Example 15, but the two ways of determining notes for the proposta are ultimately equivalent.

[3.6] 4. Write in the notes of the risposta voice of the subsequent time unit by transposing the proposta of the previous time unit by the interval and distance of entrance of the canon. As was shown with the arrow in Example 19, this means that our choice of D3 in the proposta in m. 1 determines the note A4 of the risposta in m 2. This is an entirely mechanical but important step.

[3.7] 5. Compose the proposta voice for the next time unit, which now contains risposta material. This step is nearly identical to Step 3, except that the choice of note for the proposta is now not only constrained by the cantus firmus and imaginary cantus firmus, but also by pre-composed notes in the risposta. The following advice for composing three voice textures is a summary of that given by Taneev (1962, §§70–94, 53–69; §§252–61, 163–69), which is itself a synthesis of many sources from the tradition of strict counterpoint. Broadly speaking, in all three-voice textures of this kind, two out of the three two-voice combinations will involve the bass, while one of them will involve only the upper parts. This is relevant, since in strict counterpoint there are two intervals that are treated differently depending on how they are distributed among the three combinations. One of these is the fourth, which is treated as a dissonance if it is formed with the bass but as an imperfect consonance if it occurs between upper parts, such as in $\genfrac{}{}{0px}{}{6}{3}$ and $\genfrac{}{}{0px}{}{8}{5}$ chords. The admission of the fourth as an imperfect consonance within upper-voice combinations adds somewhat to the depth of our lists of fixed consonances and variable intervals, and this can make it somewhat easier to compose suitable rispostas for time units with difficult vertical shifts. The other is the 9–8 suspension, which is forbidden between upper parts but permitted if it is formed between an upper part and the bass. In addition, there are new considerations for the composition of the entire three-voice combination, P+R+CF. When selecting a proposta note to form a three-note chord, we should prefer complete triads ($\genfrac{}{}{0px}{}{5}{3}$ and $\genfrac{}{}{0px}{}{6}{3}$) whenever possible. When a complete triad is not possible, incomplete triads that contain imperfect consonances (such as $\genfrac{}{}{0px}{}{8}{6}$ or $\genfrac{}{}{0px}{}{10}{8}$) are preferable to those that do not (such as $\genfrac{}{}{0px}{}{8}{5}$ or $\genfrac{}{}{0px}{}{8}{1}$). Most counterpoint treatises also place a preference on octave doublings of a pitch class over unison doublings, and doublings of the bass note are more common than doublings among the upper voices.

[3.8] Example 20 shows proposta notes chosen for mm. 2 and 3 of our sample exercise. In m. 2, the notes F and A had already been determined for the cantus firmus and risposta, so the choice of the note D in the bass to form a complete triad naturally suggests itself. This note appears to form a dissonance with the imaginary cantus firmus; however, we have the option of treating the fourth as a consonance, since the derivative R+CF combination takes place between the two upper parts of the texture. This fourth will only receive consonant support if the proposta is able to take either the note C in m. 3, forming a $\genfrac{}{}{0px}{}{6}{3}$ chord, or A, forming an $\genfrac{}{}{0px}{}{8}{5}$ chord. Our default attitude should be to try to make the note C work for the proposta in m. 3, since this option also forms a complete triad. This choice of the note C for the proposta in m. 3 would entail the note G for the risposta in m. 4, forming another fourth between upper parts.

[3.9] In m. 4 we encounter the first truly difficult moment of this exercise. The guide interval indicates that our proposta note must be composed according to the rules of invertible counterpoint at the ninth, whose only fixed consonance is the fifth (see inversion table in Example 21). A fifth in the proposta voice of m. 4 would be the note G, which happens to be one of the notes that will give consonant support to the fourth between upper parts. This will work, but it unfortunately forms an incomplete $\genfrac{}{}{0px}{}{8}{5}$ chord and, as shown in Example 21, it will result in a perfect fifth between risposta and cantus firmus in m. 5 that is approached in direct motion. These kinds of direct or “hidden” fifths are commonly disparaged by counterpoint authorities, but the examples of canonic exercises provided by Zarlino, Morley, and others demonstrate a particularly high tolerance for their use.

[3.10] Even though we have only one fixed consonance at our disposal for this measure, another possibility is available that avoids the direct fifth and the incomplete $\genfrac{}{}{0px}{}{8}{5}$ chord. Example 22 shows a solution for m. 4 that exploits variable intervals rather than fixed consonances. This involves delaying the proposta’s chord tone C in m. 3 with a dissonant 9–10 suspension with respect to the cantus firmus. This ninth, which behaves with a dissonant voice-leading function in the original combination, inverts into a consonant fifth on the downbeat of m. 4 in the derivative R+CF combination by invertible counterpoint at the thirteenth. Conversely, the consonant tenth of the P+CF combination on the third quarter note of m. 3 inverts into a dissonant fourth in the R+CF combination, which can now be justified as a stylistically permissible dissonance on beat three of the measure (in this case, as an accented passing tone). In general, variable intervals may be used whenever a consonant original interval corresponds with a correctly treated dissonant configuration in the derivative, and vice versa.

[3.11] 6. Repeat steps 3, 4, and 5 until all the time units of the canon have been filled up with a basic framework. Example 23 shows a continuation of the exercise that completes the canonic framework. This framework may consist entirely of whole-note consonances, as in Collins’s canon in Example 1 (and most of the examples given by the Renaissance authors), or it may contain those configurations necessary to justify the changes of function of variable intervals. Readers should keep in mind that the strict canonic imitation between proposta and risposta will likely need to be relaxed when approaching the cadence. Additionally, although some composers may wish to start at the beginning of the exercise and compose chronologically, it is often wise to compose proposta notes for time units out of chronological order to take care of difficult vertical shifts spotted in advance, such as the invertible counterpoint at the ninth of m. 4 in this sample exercise.

[3.12] 7. Elaborate the basic framework with faster note values, as shown in Example 24. These elaborations can be used to improve the basic framework in at least four ways. First, they can be used to correct errors in the whole-note framework: observe, for example, how the leap of a diminished fifth in the proposta voice between mm. 5 and 6 in Example 23 is ameliorated by stepwise motion in Example 24 (though it still outlines a dissonant interval). Second, they allow for injecting more dissonance into the voice leading, as with the suspensions in mm. 8–10 of Example 24. Third, these elaborations can serve to give the impression of a more filled-out harmony. For instance, in place of the incomplete $\genfrac{}{}{0px}{}{8}{5}$ chord in m. 6 of the framework in Example 23, we can achieve a complete triad on the third quarter note of that measure in Example 24 through the application of passing tones. Fourth and last, such elaboration can balance out the composite rhythm of the whole exercise and/or create a rhythmic arc. In Example 24, at least one sound event occurs on every half-note beat, as in the weak-beat entrances of the canonic voices in the first two measures. The completed exercise also features a rhythmic arc in terms of the composite rhythm: after beginning with a mainly half-note pulse, it quickens to quarter note motion in the middle before and slowing down again near the cadence.

[3.13] As has been mentioned, some vertical shifts are trickier to work with than others. Taneev shows that, because every vertical-shift index possesses at least one fixed consonance (Taneiev [1909] 1962, §97, 70), a successful double shift is always possible no matter what vertical shift the guide interval indicates for any particular time unit. At the same time, some vertical-shift indices only possess one fixed consonance; therefore there are certain sequences of consecutive guide intervals that can make solving the double shift for a given set of canonic parameters difficult or unworkable. Example 25 shows two such scenarios pointed out by Taneev (1962, 211). When, for instance, the cantus firmus and imaginary cantus firmus move together in parallel seconds, one of the canonic voices will be required to make parallel fifths on consecutive downbeats. (Guide intervals progressing in consecutive parallel sevenths also render a solution unworkable.) In general, we can assess whether the parameters of a given canonic exercise will afford a successful double shift only after we have discovered the guide intervals in Step 2 of the working method. The double shift is easiest if there is a preponderance of consonant guide intervals, such as octaves, tenths, and twelfths—which allow for the “textbook” kinds of invertible counterpoint—and especially unisons, which allow for simple counterpoint. The canonic parameters become more difficult as the number of dissonant guide intervals increases, especially parallel dissonances.

[3.14] This working method requires only minor changes for canonic exercises in which the cantus firmus is placed in one of the outer voices. Example 26 shows the beginning of an exercise in which the cantus firmus occurs in the bass, the alto takes the role of the proposta, and the soprano follows as risposta at the fifth above and one whole note later. The imaginary cantus firmus is therefore placed a fifth below and one whole note earlier than the cantus firmus. In this circumstance, we will no longer be selecting a note for the proposta from within the range of the guide interval, since the proposta now lies in a range above both the cantus firmus and the imaginary cantus firmus. In cases where Equation (4) gives a negative vertical-shift index, this selection from outside the guide interval only requires us to extend the associated interval table into direct shifting intervals, as was seen earlier in Example 11. Example 26 shows an example of a positive vertical shift index. In m. 7, the cantus firmus moves by step away from the proposta into m. 8 (r = 1) and the interval of entrance is a fifth upward, directed away from the cantus firmus (s = 4); here, Jv = 1 + 4 = 5. In cases such as these, we will need to modify Step 3 of the working method by employing interval tables based on direct shifts rather than invertible counterpoint. The table in Example 26 demonstrates a direct-shifting interval table using the Jv = 5 (a direct shift of a sixth) that governs the proposta in m. 7.

[3.15] Notice that the placement of the cantus firmus in an outer voice only changes the way we would select notes for the proposta in Step 3 if we chose to write out an interval table. For instance, we do not need to employ any mathematics to demonstrate the consonance of the note E for the proposta in m. 7 of Example 26 above both cantus firmus and imaginary cantus firmus; it is visually apparent in the musical notation. Similarly, exercises in which the cantus firmus occurs in the topmost voice may be composed with or without the aid of direct-shifting interval tables or the extension of inverse-shifting interval tables into direct-shifting intervals. Example 27 shows a completed exercise with the cantus firmus in the lowest voice, and Example 28 shows one composed with the cantus firmus in the topmost voice.

4. Advanced Canonic Techniques

[4.1] With some alterations, the novel working method of section 3 can also be used to compose more advanced types of canons against a cantus firmus. The trick, in every case, is to make the imaginary cantus firmus stand in the same canonic relationship to the cantus firmus as the proposta stands in relation to the risposta. The conceptual basis for these alterations is inspired in part by a copying device known as a pantograph, whose four arms resemble the relationships of the four two-voice combinations of our exercises; see Example 29 (1900, 114). The copyist’s hand traces an image with a stylus, while a second stylus fixed elsewhere on the device applies a copy of the image to a new surface. By adjusting the ratio of the lengths of the arms, the resulting copy can be enlarged or reduced in a fixed proportion compared to the original. Some pantographs allow the second stylus to face upwards so that the new copying surface is located above the original plane, which allows the copy to form a mirror image of the original. Advanced canonic techniques can be achieved by analogous transformations of the shape, proportion, and placement of the imaginary cantus firmus.

[4.2] One kind of advanced canon involves imitation in which the distance of entrance of the canon does not neatly align as a multiple of the duration of the measure. Example 30 shows the beginning of an exercise in which the risposta follows the proposta at the upper seventh and at a distance of three half notes. With this horizontal shift of one and a half measures, the downbeat notes of the proposta will occur and the second half-note beat of the riposta, and the second half-note beats of the proposta will occur on the downbeats of the riposta.⁽¹⁴⁾ In this case, the imaginary cantus firmus will appear syncopated with respect to the cantus firmus, and there will be two guide intervals per measure. This arrangement encourages changes of function and the use of variable intervals, since fixed dissonances may not be possible when the metrical configuration shifts between original and derivative combinations. For example, a dissonant passing tone on the third beat of the original cannot correspond with a dissonant passing tone on the downbeat of the derivative, but it may correspond with a consonance if a variable interval is employed.. Other than this, the working method is the same as that outlined in section 3. Example 31 shows a completed canon composed with these parameters. Example 32 shows a more complicated version of this same procedure, in which the horizontal shift moves the first and third half notes of each measure in the original combination onto the unaccented second and fourth half notes for the derivative. This interchange of strong and weak beats is sometimes referred to as imitation per arsin et thesin.

[4.3] Another possibility is to compose a canon in which the risposta imitates the proposta in contrary motion, effectively reversing the direction of each melodic interval.⁽¹⁵⁾ This requires a new method for identifying the placement of the imaginary cantus firmus and a new equation to solve for Jv. Example 33 shows the setup for a canon in contrary motion at the lower octave at a distance of one whole note in which the cantus firmus is placed in the middle voice. The ICF for a canon in contrary motion is not formed by a vertical shift of the cantus firmus, but rather by a vertical reflection of the cantus firmus through the same axis of inversion as the canonic voices. In the case of Example 33, we intend the initial note of the proposta, A4, to invert onto the note A3 of the risposta; this tells us that the vertical axis, modeled in diatonic space, is D4/E4. Each note of the proposta pairs with a conjugate note of the risposta by reflection through this axis, as shown in the rest of the example. Each note of the imaginary cantus firmus is a conjugate note of the cantus firmus, and the placement of each note is found by applying the opposite horizontal shift as the distance of entrance of the canon one intends to compose.⁽¹⁶⁾

[4.4] One further detail for a canon in contrary motion is that the Jv indicated by the guide intervals of this process does not obey Equation (2), where a derivative interval is defined as n = m + Jv. This is because however far a note of the proposta is above the imaginary cantus firmus (such as the sixth in m. 1 of Example 33), that is how far the corresponding note of the risposta will occur below the cantus firmus in the corresponding time unit (such as the sixth in m. 2). In other words, the magnitude of the intervals calculated using the guide intervals will be correct, but positive values for the derivative interval must be switched to negative and vice versa. A new equation can be used to specify this new relationship:

(5) n = -1 ⁢ ( m + Jv )

Example 34 shows a completed canon in contrary motion composed with the same parameters used in Example 33.

[4.5] One may compose proportional canons by applying the opposite stretching or compressing of the note values to the ICF as will obtain in the desired resultant canon. Example 35 shows a canon in augmentation in which we intend the risposta to move in note values twice that of the proposta; here, the note values of the imaginary cantus firmus have been halved compared to the cantus firmus. Conversely, Example 36 shows a canon in diminution in which we intend the risposta to move in note values half that of the proposta; in this case, the note values of the imaginary cantus firmus have been doubled. Since the note values of the imaginary cantus firmus are scaled proportionately, the distance of entrance of the canonic voices must also be scaled by the same proportion to find the correct placement of the first note of the imaginary cantus firmus. For example, since the distance of entrance for the canon in Example 35 is three whole notes, the first three whole notes of the cantus firmus correspond with three unseen half-notes (F, A, and G) in the imaginary cantus firmus prior to the beginning of the exercise. Likewise, the first five whole notes of the cantus firmus in Example 36 correspond with five unseen double whole notes (G, B, A, G, and C) prior to the beginning of the exercise. In addition to this proportional scaling of the imaginary cantus firmus and the distance of entrance, the imaginary cantus firmus should still be transposed by a vertical shift opposite to the interval of entrance of the canon; the other steps of the working method are identical.⁽¹⁷⁾

[4.6] Canons in retrograde motion composed against a cantus firmus, which involve the risposta voice imitating the proposta in a reverse ordering of notes from last to first, are the most difficult to compose. Example 37 shows an example of a canonic exercise in retrograde motion. Notice that the canonic voices cross paths in their reverse ordering of notes at a central midpoint between mm. 6 and 7. The arrows show the connection between corresponding time units symmetrical around this midpoint: the proposta note A3 in m. 6 corresponds with the risposta note A4 in m. 7 by the interval of entrance of an octave, the proposta’s C4 in m. 7 corresponds with the risposta’s C5 in m. 6, and so forth. The final measure has been doubled in duration in order to place the central midpoint between two measures, rather than within a measure. In the corresponding time units of mm. 5 and 8, we can see that the rhythm of the proposta in m. 5 has been retrograded in the risposta of m. 8, resulting in a metrical interchange of strong and weak beats within a measure; this is one of the factors that make this type of exercise difficult. The position of the imaginary cantus firmus is determined by a vertical shift of the cantus firmus opposite to the interval of entrance of the canonic voices and, instead of a horizontal shift, a horizontal reflection of the notes of the cantus firmus through the same central midpoint as the canonic voices.

[4.7] Recall from sections 2 and 3 that, in a standard canon, the corresponding time units used to calculate r in Equation (4) are directly adjacent to one another (in which case r is simply a melodic interval of the cantus firmus). In a retrograde canon, on the other hand, corresponding time units are positioned symmetrically around the midpoint of the canon and may be far apart from one another. In Example 37, the cantus firmus note in m. 4 is D, and the note in the corresponding m. 9 is F; therefore r = −2. The value is negative because, viewing the interval chronologically, the cantus firmus ascends between mm. 4 and 9 toward the proposta. The vertical-shift index for m. 4 is therefore a positive shift of a sixth (−2 + 7 = 5). The vertical-shift index will be different in the corresponding measure, however, since the cantus firmus descends, in a reverse-chronological sense, from m. 9 backwards to m. 4, and the sign for r in this case is positive (2 + 7 = 9).

[4.8] In the earlier exercises, the canonic P+R combination needed only to be composed in simple counterpoint. For a canon in retrograde motion, however, this combination must also be written under the constraints of some form of vertical-shifting counterpoint. This is because the notes chosen for the P+R combination must work in two different forms in corresponding time units—once before and once after the horizontal axis at the midpoint. The notes of the first half of the proposta will be vertically shifted in the direction of the risposta by the interval of imitation of the canon in order to become the notes of the risposta in the second half, and the same will be true of the notes of the risposta in the direction of the proposta. The vertical-shift index of the P+R combination for a canon in retrograde motion, which we can call “Jv(P+R),” can be given by the following equation:

(6) Jv ⁢ _{( P + R )} = -2 × | s |

where $\left|s\right|$ is the absolute value of the interval of entrance of the canon.⁽¹⁸⁾ In this case, the interval of entrance is an octave ($\left|s\right|$ = 7), and so the combination undergoes a negative vertical shift of two octaves upon reflection through the horizontal axis (−2 × 7 = −14). The same vertical shift will obtain for the P+R combination in all corresponding measures of an exercise. This additional constraint is what makes crab canons significantly more difficult to construct. It requires that the vertical shift within the P+R combination be planned out in the first step of the working method at the same time as the other canonic parameters of the exercise. The easiest interval of entrance for a retrograde canon is the unison, which allows for the P+R combination to be composed in simple counterpoint (−2 × 0 = 0). All other intervals of entrance will result in vertical shift indices that are negative even numbers.

[4.9] Perhaps surprisingly, it is easier to compose a canon in inverted retrograde motion against a cantus firmus than it is to compose one in simple retrograde motion. This may be related to the observation made by twelve-tone theorists that a pitch-class series more closely resembles its inverted retrograde form than either its inverted or retrograde forms, since the P and RI forms of a series share the same pitch-class intervals (Morris 1987, 56). The imaginary cantus firmus is determined by combining the methods used for canons in contrary motion and retrograde motion. The notes of the cantus firmus are vertically reflected through the same pitch axis and horizontally reflected through the same midpoint as the canon we intend to compose. Example 38 shows an inverted retrograde canon at the upper fifth written using this method. The vertical axis for this canon is F4, and the horizontal axis again occurs between mm. 6 and 7.

[4.10] Unlike a canon in retrograde motion, the harmonic intervals of the P+R combination for a canon in inverted retrograde motion are not subject to a vertical shift within corresponding measures. The third between F and A on the downbeat of m. 4, for instance, is reflected through the vertical axis of F4 to become the third between D and F and through the horizontal axis into the third beat of the corresponding m. 9. Similarly, the third brought about by voice crossing in m. 5 also results in a voice-crossed third in m. 8. This is because the reflection of notes through the vertical axis cancels out the harmonic inversion of the exchange of parts in the texture before and after the midpoint.⁽¹⁹⁾ The composer can thus be assured that the two-voice combination P+R is reflected through the horizontal and vertical axes in simple counterpoint—interval for interval—without acquiring any vertical shift along the way.

5. Analysis of Repertoire

[5.1] J. S. Bach, as is well known, wrote many canons against cantus firmi. As a result of the enduring popularity of works in this genre, such as the Goldberg Variations (BWV 988), and the Musical Offering (BWV 1079), most nineteenth- and twentieth-century counterpoint treatises that address canons composed against a CF concentrate on his work to the near exclusion of any other composer. An examination of some of these examples will show how the methods of the present study can be applied in analysis. The results of the analysis, moreover, will provide a perspective on the types of compositional decisions made by Bach, potentially providing new insights into his working method. It is important at the outset to keep in mind that the three-voice textures by Bach treated in this section are composed in the style of eighteenth-century keyboard counterpoint, as opposed to the ostensibly vocal (“strict”) counterpoint of the examples discussed above.⁽²⁰⁾

[5.2] Example 39 shows the first eight measures of the Canone all’Ottava from Variation 24 of the Goldberg Variations. The first thing that stands out about Bach’s canon is that the cantus firmus is not particularly firm, in that Bach elaborates the Goldberg bass line with additional notes. Some of these new notes are purely decorative while others impact the contrapuntal design. Example 40 shows the naïve placement of the imaginary cantus firmus that would have resulted for a canon at the upper octave at a distance of two measures, had Bach made no alterations to the ground bass. As such, the guide intervals of Example 40 summarize the basic problem Bach needed to solve for these canonic parameters in terms of vertical-shifting counterpoint. We can compare this to Example 41, which shows an analysis of the essential voice leading of the canon. This includes a reduction of the three-voice texture (somewhat in the manner of the “frameworks” of the earlier exercises) as well as the actual imaginary cantus firmus brought about by Bach’s alterations to the ground bass.

[5.3] Bach’s alterations substitute a guide interval of a ninth on the downbeat of m. 4 for the seventh that would have occurred naturally. Bach solves this relatively difficult vertical shift by exploiting a variable interval; the dissonant suspension of an eighteenth (compound fourth) of the P+CF combination becomes a tied consonance of a tenth in the R+CF combination in m. 6. Conversely, the descending stepwise resolution of the suspension to the note F♯ in m. 4 becomes a dissonant passing tone in m. 6. Bach’s alteration of the bass line so as to place the note E instead of C on the downbeat of m. 6 seems not to have been motivated by this change of function, since the G in the risposta of m. 6 could still have been treated as a tied consonance had the bass taken the expected note C. However, the proposta note B of m. 6 would not have formed a consonance with C. We can speculate that Bach chose to manipulate the bass line to achieve the note B in the proposta voice in this measure, so that the risposta in turn would arrive on a chord tone of the tonic triad for the perfect authentic cadence on the downbeat of m. 8. In the working method of section 3, the cadences were achieved by relaxing the strict imitation of the canonic voices nearing the end of each exercise. Bach, on the other hand, seemingly prefers to continue the imitation through the cadence, and instead relaxes the strictness of his cantus firmus.

[5.4] Example 42 shows the beginning of Variation 12 of the Goldberg Variations, and Example 43 shows an analysis of the essential voice leading and imaginary cantus firmus for this passage. For this canon in contrary motion, the ground bass is presented essentially unaltered. Notably, though, the framework of Bach’s proposta voice is nearly identical with that of the canon at the octave for the first four measures, as seen when comparing Examples 41 and 43. Even the descending octave leap in m. 3 merely adjusts the register of the melody; it does not fundamentally change the counterpoint between proposta and cantus firmus. Somehow, Bach discovered that the same P+CF original combination can produce an entirely different R+CF derivative combination by reflecting the proposta through the E4/F4 vertical axis and at a distance of one whole note instead of two. Not only does this give some indication of the depth of Bach’s pre-compositional planning, but it also suggests that Bach was willing to recycle canonic ideas from other variations and perhaps even sought out such opportunities. Denis Collins has pointed out similar pre-compositional planning of multi-voice contrapuntal designs in parallel sections of separate contrapuncti from the Art of Fugue (2018b, [54]).

[5.5] Example 44 shows the next canonic variation from the collection, also written in contrary motion. Example 45, as before, shows an analysis of the essential voice leading. Variation 15 contrasts audibly with Variation 12, as it is written in the minor mode and in a different tempo and meter. Yet the two canons share a remarkably similar contrapuntal framework (at least for the first few measures), which can be seen when comparing Examples 43 and 45. Variation 12 was a canon at the lower fourth, whereas Variation 15 takes an interval of entrance at the upper fifth. These two intervals are octave complements, but the proposta and risposta voices have also been inverted relative to one another in the texture. This means that the two variations have different verticals axes (B4 in the case of Variation 15 and E4/F4 in the case of Variation 12). However, these two axes map the same note names onto one another, which is what allows Bach to reuse the same basic shape for the first four measures of the canonic melody. The three canons of Variations 12, 15, and 24 could therefore be considered not only canonic variations on the same ground bass, but variations on the same three-voice canonic framework.

[5.6] As a final brief analysis, Example 46 shows the first eight measures of Variation 4 from the Canonic Variations on “Vom Himmel hoch da komm’ ich her,” BWV 769, and Example 47 shows an analysis of the essential voice leading. This variation is a rare example of an augmentation canon written against a cantus firmus. Accounting for the initial rests in both parts, we can understand the two canonic voices as beginning together on the downbeat of the first measure. The risposta in the bass of the second manual follows in note values twice that of the proposta in the first manual. Likewise, the seven half-note span of rest preceding the entrance of the first strophe of the chorale melody is compressed into seven quarter-notes worth of rest preceding the imaginary cantus firmus in Example 47. Notice that by allowing the canonic voices to begin as far as they do prior to the entrance of the cantus firmus (and no further), Bach ensures that the imaginary cantus firmus only overlaps with the cantus firmus on the third quarter note of m. 4, forming a solitary guide interval of an octave. Bach therefore significantly eases the difficulty of this kind of canon by ensuring that the proposta can be written almost entirely in simple counterpoint with respect to the cantus firmus, and that the only vertical shift that occurs is quite manageable. Similar gaps precede each of the subsequent strophes of the chorale melody.

[5.7] Many other, more complex examples of canons composed against a cantus firmus can be found in Bach’s output, notably in the Musical Offering. However, the brief examples given here are enough to invite preliminary speculation about Bach’s potential working methods. For instance, the fact that Bach was willing to alter the Goldberg ground bass in the approach to a cadence rather than the canonic imitation suggests that he viewed his task not so much like the written exercises explored in this article, but more like the realization of a trio-sonata texture in which the canonic upper parts take precedence over a composed or improvised accompanimental bass. In addition, Bach must have been familiar with a method that allowed him fine-tuned control over the double-shifting counterpoint of these canons. Whatever it was, it enabled the use of variable intervals and changes of function as well as some of the advanced techniques discussed in section 4, including, in one case from the Musical Offering, a canon written in both contrary motion and rhythmic augmentation.

6. Conclusion

[6.1] The method for composing canons against a cantus firmus outlined in this article consists of only two component techniques: vertical-shifting counterpoint and imaginary voices. The former has nearly ubiquitous coverage in counterpoint treatises going back many centuries in the form of invertible or double counterpoint. In contrast, the history of the latter, before Taneev, is much murkier. Taneev, for his part, speculated that the older writers knew more about horizontal-shifting counterpoint and imaginary voices than they were letting on in print, keeping the technique instead as something of a trade secret to be disclosed only to initiated apprentices.⁽²¹⁾ Nonetheless, at least one prefiguration of Taneev’s “basic version” can be found among the Renaissance contrapuntists. Example 48 shows a counterpoint composed by Thomas Morley that works against two cantus firmi independently (Morley 1597, 125),⁽²²⁾ and Peter Schubert has recently shown how such a device could have been used to improvise or compose sequential repetitions of melodic figures over plainchant (Schubert 2020). Although Morley does not demonstrate this explicitly, Example 49 shows how Morley’s counterpoint could be repeated verbatim to form a very long melodic sequence at the unison—a form of horizontal-shifting counterpoint predating Taneev by over three centuries. Taneev likely did not know of this example, since he discusses a few less clear-cut examples by Vincentino, Berardi, and Kirnberger, and he concludes that his theoretical investigation into horizontal- and double-shifting counterpoint was the first of its kind to be published.⁽²³⁾ In any case, it is difficult to discount Taneev’s suspicion that imaginary voices may have played a discreet role in Renaissance polyphonic practices.

[6.2] A musician improvising the leading voice of a canon against a cantus firmus would encounter at least two deficiencies when attempting to work from a memorized list of fixed consonances even when executed successfully. The first is that this method only provides solutions for the proposta note that involve fixed consonances, which only make up a subset of the available solutions. Variable intervals are a well-understood aspect of invertible counterpoint, but without connecting the canonic exercise to a particular kind of invertible counterpoint (or rather, vertical-shifting counterpoint), that knowledge cannot be leveraged by a composer or improviser. Opportunities for variable intervals are not uncommon, as was shown in the discussion of Example 22, and the many examples by Bach show that the effect can be quite elegant. Second, the interval lists specify the original forms of the fixed consonances, since those are the notes of the proposta that are of urgent concern to the improviser, but they do not indicate the specific quality of the corresponding derivative interval. Although the improviser could trust that the derivative interval would be a consonance with respect to the cantus firmus, they would have no way of knowing, on the basis of the list alone, whether the derivative consonance was perfect or imperfect; thus, errors involving perfect consonances would be unavoidable.

[6.3] An improviser imagining a transposed version of the cantus firmus would able be to see in their mind’s eye the interval formed between the proposta and imaginary cantus firmus, which is a simple transposition of the interval of the derivative R+CF combination. As was mentioned in paragraphs 3.5 and 3.14, this method does not require interval tables or memorization per se; an improviser would instead draw upon the same skills that allowed them to improvise a counterpoint in discant polyphony against one cantus firmus and apply those skills in weaving a counterpoint against two simultaneous cantus firmi in the manner described by Morley (1597) and Schubert (2020).⁽²⁴⁾ Additionally, this method would allow the improviser to discriminate between perfect and imperfect consonances in the derivative combination. An adept improviser might even notice opportunities to employ variable intervals. An imaginary cantus firmus could make the task of rapidly finding fluent solutions to a given canonic problem more manageable, although it would still be an impressive feat of concentration.

[6.4] The technique of an imaginary voice can also shed some new light on the distinction between a canon set to accompany a cantus firmus and the canonic imitation of the cantus firmus itself. Despite the apparent differences between these two techniques, especially from the listener’s perspective, their underlying compositional principles are deeply interrelated. This connection was hinted at by Johann Anton André in his discussion of canonic chorale preludes from his Lehrbuch der Tonsetzkunst (1838, 245). André advises his reader to select as cantus firmus a melody that moves primarily in stepwise motion and to check beforehand whether this cantus firmus can work in canon with itself. Example 50 shows André’s demonstration of how the first two strophes of the chorale melody “Freu dich sehr o meine Seele” work in canonic imitation at the lower octave at a distance of one whole note. Example 51 shows how André then composed canonic voices—also at the lower octave and at a distance of one whole note—with the chorale melody serving as cantus firmus.

[6.5] André is impressed that the canonic imitation of the cantus firmus with itself can be used as a testing survey (“prüfenden Übersicht”) to judge in advance the possibility of success for a canon composed to accompany it with the same parameters.⁽²⁵⁾ As we have seen in this article, the ICF+CF canonic combination does not need to form correct two-voice counterpoint to be used to determine the guide intervals for the proposta. However, if the parameters do generate a successful two-voice canon, then the resulting double shift will be quite easy to work with, since it is guaranteed to avoid the most difficult successions of guide intervals (as discussed earlier with respect to Example 25). In the case of André’s canon, the guide intervals of Example 50 indicate exclusively vertical-shifting counterpoint at the sixth, octave, tenth, and twelfth. Notice that André places his P+R combination at the same canonic parameters as his ICF+CF combination, rather than the opposite parameters as recommended in the working method of section 3. This results in his treating the R+CF combination as original and the P+CF combination as derivative, which means that if the vertical intervals of Example 50 were to be taken as guide intervals, they would govern the composition of the risposta voice rather than proposta. This is perhaps slightly less practical than the method proposed here, since we can assume that most composers would prefer to compose the proposta voice first. Nevertheless, the underlying mechanisms are identical.

[6.6] Along these lines, it is apparent from his several highly advanced examples that J. S. Bach understood the reciprocal relationship between the canonic treatment of a cantus firmus with itself and the opportunity it indicates for canonic accompaniment. We know from the many canonic chorale preludes from the Orgelbuchlein, BWV 599–644, for example, that Bach investigated the canonic potentials of his given melodies—likely testing them out at various canonic parameters early in the composition process, as André would later recommend. If a given melody happens to work in canon with itself at certain parameters, then this discovery could serve as a point of creative departure for the rest of the composition. As has been shown, though, even those canonic parameters that fail to produce a viable canon nevertheless provide crucial information about the potential for imitative counterpoint in the accompanying voices. The Musical Offering and the Canonic Variations on “Vom Himmel Hoch” both feature canonic treatment of the cantus firmus alongside canonic accompaniments. In the Goldberg Variations, in addition to the canonic variations in the set, Bach also composed fourteen canonic settings of the first eight notes of the ground bass against itself (BWV 1087) that place special attention on retrograde and contrary-motion techniques. This research into the canonic potential of the Goldberg bass line would have been useful in composing the canonic variations of the set, presuming Bach understood the connection between the guide intervals and the vertical-shifting counterpoint that they indicate.

[6.7] The almost perfect suitability of Taneev’s methods for disarming the complexities of this contrapuntal problem suggests that this may have been one of the topics he had intended to address had he not met with a premature death in 1915. A century after Taneev’s passing, Simon Desbruslais called for a renewal of interest in his theories within Western scholarship (2015, 16–17), and the number of publications on the topic within the last ten years gives confidence that this is underway. One way for Taneev’s ideas to become a topic of interest for others in addition to specialists in Russian music theory or mathematics and music theory would be to situate them in the standard counterpoint curriculum. For this purpose, canonic exercises written against a cantus firmus would be well suited for advanced students. Many of Taneev’s key concepts and vocabulary arise naturally when reasoning through this contrapuntal problem, which could allow counterpoint teachers an opportunity to introduce Taneev’s theories in a well-motivated musical context. Additionally, these exercises could provide an arena for interaction with other recent trends in music theory, including transformation theory and systematic investigations into improvised counterpoint (Schubert 2007; Desbruslais 2015; Collins 2015, 2018a). In all cases, Taneev’s methods are likely to provide essential insight.

Jacob Gran
Louisiana Tech University
School of Music
P.O. Box 3144
Ruston, LA 71272
jgran@latech.edu

Works Cited

André, Anton. 1838. Lehrbuch der Tonsetzkunst, zweiter Band, zweite Abtheilung, die Lehre der Nachahmung. Offenbach.

Azopardi, Francesco. 1786. Le Musicien Pratique. Vol. 1. Translated by N.E. Framery. Chez le Duc.

Bathe, William. c. 1596. A Briefe Introduction to the Skill of Song. Thomas Este.

Bellermann, Heinrich. [1862] 1904. Der Contrapunkt, 4th ed., J. Springer.

Bent, Margaret. 1983. “‘Resfacta’ and ‘Cantare Super Librum.’” Journal of the American Musicological Society 36 (3): 371–91. https://doi.org/10.1525/jams.1983.36.3.03a00020.

Berardi, Angelo. 1687. Documenti armonici. Vol. 2. Giacomo Monti.

Blackburn, Bonnie. 1987. “On Compositional Process in the Fifteenth Century.” Journal of the American Musicological Society 40 (2): 210–84. https://doi.org/10.2307/831517.

Broude, Ronald. 2020. “To Sing Upon the Book.” Textural Cultures 13 (1): 75–105. https://doi.org/10.14434/textual.v13i1.30071.

Brunelli, Antonio. 1610. Regole et dichiarationi di alcuni contrappunti doppi utili alli studiosi della musica & maggiormente a quelli che vogliono far contrappunto all’improviso. Cristofano Marescotti.

Bussler, Ludwig. 1877. Der strenge satz in der musikalischen kompositionslehre. C. Habel.

Calvisius, Seth. 1630. Melopoeia sive melodiae. 2nd ed. Johann Franck.

Canguilhem, Philippe. 2011. “Singing Upon the Book According to Vincente Lusitano.” Early Music History 30: 55–103. https://doi.org/10.1017/S0261127911000052.

—————, ed. 2013. Chanter sur le livre à la Renaissance: Les traités de contrepoint de Vicente Lusitano. Turnhout.

Cerone, Pietro. 1613. El Melopio y Maestro. Book IX. Giovanni Battista Gargano & Lucrecio Nucci.

Cerreto, Scipione. 1601. Della prattica musica vocale et strumentale. Giovanni Giacomo Carlino.

Collins, Denis. 1992. “Canon in Music Theory From c.1550 to c.1800.” PhD diss., Stanford University.

—————. 1993. “Zarlino and Berardi as Teachers of Canon.” Theoria 7: 103–23.

—————. 2008. “‘So You Want to Write a Canon?’ An Historically-Informed New Approach for the Modern Theory Class.” College Music Symposium 48: 108&ndash23.

—————. 2015. “Taneyev’s Theories of Moveable Counterpoint and the Music of J. S. Bach.” Bach 46 (2): 22–45. https://doi.org/10.1353/bach.2015.a808467.

—————. 2018a. “Approaching Renaissance Music Using Taneyev’s Theories of Movable Counterpoint.” Acta Musicologica 90 (2): 178–201.

—————. 2018b. “Horizontal-Shifting Counterpoint and Parallel-Section Constructions in Contrapuncti 8 and 11 from J. S. Bach’s Art of Fugue.” Music Theory Online 24 (4). https://doi.org/10.30535/mto.24.4.2.

Desbruslais, Simon. 2015. “The Western Reception of Sergei Taneyev.” Zhurnal Obshchestva teorii muzyki [Journal of the Society for Music Theory] 9.

Dubois, Théodore. 1901. Traité de contrepoint et de fugue. Heugel.

Ferand, Ernst. 1938. Die Improvisation in der Musik. Rhein-Verlag.

Ferand, Ernst. 1956. “Improvised Vocal Counterpoint in the Late Renaissance and Early Baroque.” Annales Musicologiques 4: 129–74.

Fétis, François-Joseph. 1846. Traité du contrepoint et de la Fugue: contenant l’exposé analytique des régles de la composition musicale depuis jusqu’à huit parties réelle. Vol. 2. Lafont.

Froebe, Folker. 2007. “Satzmodelle des Contrapunto alla mente und ihre Bedeutung für den Stilwandel um 1600.” Zeitschrift der Gesellschaft für Musiktheorie 4 (1–2): 13–55. https://doi.org/10.31751/244.

Goetschius, Percy. 1902. Counterpoint Applied in the Invention, Fugue, Canon and Other Polyphonic Forms. G. Schirmer.

Grove, Paul Richard. 1999. “Sergei Ivanovitch Taneev’s Doctrine of the Canon: A Translation and Commentary.” PhD diss., University of Arizona.

Habert, Johannes Evangelista. 1899. Beitrage zur Lehre von der Musikalischen Komposition, III Die Lehre von der Nachamung. Breitkopf & Härtel.

Hauff, Johann. 1872. Die Theorie der Tonsetzkunst. Vol. 4, Das Studium des Canons. Klimsch.

Honea, Ted, trans. 2020. Vincentio Lusitano: Introdutione Facilissima & novissima di Canto Fermo (1553); On Improvised Vocal Counterpoint. https://www.uco.edu/cfad/files/music/lusitano.pdf.

Ishizaka, Kimiko. 2014. “Goldberg Variations Complete (J. S. Bach BWV 988), with score, Kimiko Ishizaka piano.” OpenGoldberg, November 28, 2014. YouTube video, 1:22:22. https://youtu.be/15ezpwCHtJs.

Jeppesen, Knud. 1992. Counterpoint: The Polyphonic Vocal Style of the Sixteenth Century. Translated by Glen Haydon. Dover.

Lusitano, Vicente. 1553. Introduttione facilissima, et novissima, di canto fermo, figurato, contrapunto semplice, et in concerto. Antonio Blado.

Mann, Alfred. 1987. The Study of Fugue. Dover.

Marx, Adolf Bernhard. [1837] 1890. Die Lehre von der musikalischen Komposition, II Die freie Komposition. 2nd ed. Breitkopf & Härtel.

Michaelis, Alfred. 1886. Die Lehre von der freien und strengen Nachahmung: Studien in den höhern Formen des Tonsatzes. Carl Merseburger.

Morley, Thomas. 1597. A Plaine and Easie Introduction to Practicall Musicke. Peter Short.

Morris, Robert D. 1987. Composition with Pitch Classes: A Theory of Compositional Design. Yale University Press. https://doi.org/10.2307/j.ctt1xp3ss4.

—————. 1995. “The Structure of First-Species Canon in Modal, Tonal and Atonal Musics.” Intégral 9: 33–66.

Nanini, Giovanni Maria and Giovanni Bernardino. c. 1580. Regole di Contrappunto di Gio. M. Nanino e de suo fratello minore. Manuscript, Bologna, Civico Museo Bibliografico Musicale.

Norden, Hugo. 1970. The Technique of Canon. Branden Press.

Nottebohm, Gustav. 1873. Beethoven’s Studien, Erster Band. Beethoven’s Unterricht Bei J. Haydn, Albrechtsberger und Salieri. J. Rieter-Biedermann.

Picerli, Silverio. 1631. Specchio secondo di musica. Matteo Nucci.

Prey, Stefan. 2012. “Algorithmen zur Satztechnik und ihre Anwendung auf die Analyse.” Dissertation, Universität Osnabrück.

Priced Catalogue of Artists’ Materials. 1900. F. W. Devoe & C.T. Raynolds Co.

Prout, Ebenezer. [1891] 1893. Double Counterpoint and Canon. 2nd ed. Augener & Company.

Richter, Ernst Friedrich. 1888. A Treatise on Canon and Fugue: Including the Study of Imitation. Translated by Arthur W. Foote. Oliver Ditson Company.

Riemann, Hugo. 1888. Lehrbuch des einfachen, doppelten und imitierenden Kontrapunkts. Breitkopf & Härtel.

Rodio, Rocco. 1609. Regole di musica. Carlino & Vitale.

Schubert, Peter N. 2002. “Counterpoint Pedagogy in the Renaissance.” In The Cambridge History of Western Music Theory, ed. Thomas Christensen (Cambridge University Press): 503–33. https://doi.org/10.1017/CHOL9780521623711.018.

—————. 2007. “Hidden Forms in Palestrina’s First Book of Four-Voice Motets.” Journal of the American Musicological Society 60 (3): 483–556. https://doi.org/10.1525/jams.2007.60.3.483.

—————. 2007. Modal Counterpoint, Renaissance Style. 2nd ed. Oxford University Press.

Schubert, Peter. 2020. “Contrapunto Fugato: A First Step Towards Composing in the Mind.” Music Theory Spectrum 42 (2): 260–79. https://doi.org/10.1093/mts/mtaa009.

Scott, Ann Besser. 1971. “The Beginnings of Fauxbourdon: A New Interpretation.” Journal of the American Musicological Society 24 (3): 345–63. https://doi.org/10.2307/830274.

Segall, Christopher. 2014. “Sergei Taneev’s Vertical-Shifting Counterpoint: An Introduction.” Music Theory Online 20 (3). https://doi.org/10.30535/mto.20.3.9.

Smith, Carl. “5. Canon per augmentationem.” Audio. Recorded December 23, 1979, Delmar Baptist Church, St. Louis Missouri. Creative Commons Attribution-NonCommercial-NoDerivs 4.0. https://imslp.org/wiki/Vom_Himmel_hoch,_da_komm_ich_her,_BWV_769_(Bach,_Johann_Sebastian)#Recordings.

Taneiev, Sergei Ivanovitch. [1909] 1962. Convertible Counterpoint in the Strict Style. Translated by G. Ackley Brower. Bruce Humphries.

Tiersch, Otto. 1879. Kurzes praktische Lehrbuch für Contrapunkt und Nachahmung. Breitkopf & Härtel.

Tigrini, Orazio. 1588. Il compendio della musica. Ricciardo Amadino.

Zacconi, Lodovico. 1622. Prattica di Musica. Vol. 2, book 3. Alessandro Vincenti.

Zarlino, Gioseffo. [1558] 1573. Le istitutioni harmoniche. 3rd ed. F. Senese.

Footnotes

1. Authors of the late Renaissance and early baroque who wrote on this topic include Vicente Lusitano (1553, 22–24) Gioseffo Zarlino ([1558] 1573, 302–17) Giovanni Maria and Giovanni Bernardino Nanini (c. 1580), Orazio Tigrini (1588, 116–23), William Bathe (c. 1596), Thomas Morley (1597, 98–102), Scipione Ceretto (1601, 281–89), Rocco Rodio (1609, 1–34), Antonio Brunelli (1610), Pietro Cerone (1613, 592–93), Lodovico Zacconi (1622, 186–96; 200–206), Seth Calvisius (1630, fols. L2v–L8), Silverio Picerli (1631, 98–121), and Angelo Berardi (1687, 86–108). Many of the authors in this group simply restated the formulations of Lusitano and Zarlino or rendered the explanations using musical examples rather than in prose. As a sample of some of the secondary literature that situates these texts in relation to Renaissance improvised counterpoint, see Ferand 1938, 1956; Bent 1983; Blackburn 1987; Collins 1992, 338–72; Schubert 2002; Froebe 2007; Canguilhem 2013; Broude 2020; and Honea 2020.
Return to text

2. Later authors who address canons written against a cantus firmus include Francesco Azopardi (1786, 89–91; 111–13), Adolf Bernhard Marx ([1837] 1890, 464–65), Johann Anton André (1838, 245–49), Johann Hauff (1872, 59–71), Otto Tiersch (1879, 173–77), Alfred Michaelis (1886, 117–26), Ernst Friedrich Richter (1888, 44–46), Hugo Riemann (1888, 188–97), Ebenezer Prout ([1891] 1893, 191–20), Théodore Dubois (1901, 81–88), and Percy Goetschius (1902, 317–18). Those that deal with non-canonic imitation against a cantus firmus include François-Joseph Fétis (1846, 72–87), Ludwig Bussler (1877, 107–21), Heinrich Bellermann ([1862] 1904, 291–301), Johannes Evangelista Habert (1899, 93–112), and Knud Jeppesen (1992, 198, 216).
Return to text

3. “It will often happen that either the interval or the distance of time of the reply will be such that it will be quite impossible to continue the canon; in that case, a fresh attempt must be made at some other interval, or some other distance, until success rewards our efforts. . . [The student] must also be prepared for many disappointments; at first, indeed, he will probably have at least two or three failures to every success” (Prout [1891] 1893, 191, 193).
Return to text

4. The prose explanations in the primary sources of how this improvisation was accomplished are brief and frequently vague, leading to the following expressions of skepticism in the secondary literature: “One can only wonder how many errors escaped correction in this type of improvised canon. The conditions imposed on the performers appear to the modern reader as extraordinarily daunting” (Collins 1993, 114). “Perhaps the singer of the consequent voice could hear the notes sung by the guide and immediately imitate them, even when the time interval was as little as a minim. More likely, though, the guide was probably composed and rehearsed alone, memorized by the singer of the consequent, and finally performed as a canon” (Schubert 2002, 513). “[A canon against a CF] seems to me the hardest thing to improvise because it requires the most memorization” (Schubert 2007, 319).
Return to text

5. In the earlier Convertible Counterpoint in the Strict Style [1909], Taneev only defines the basic terminology of canonic imitation to explain the role that it plays in the construction of a basic version for horizontal- and double-shifting counterpoint (Taneiev [1909] 1962, §§315–16, 208), to be discussed in paragraph 2.13. The closest Taneev comes to describing the method of the present study is in §439, which deals with the composition of two non-imitative counterpoints within a four-voice basic version (Taneiev [1909] 1962, 267). He claims that the difficulties of writing such an exercise “increase to an excessive degree,” and recommends composing sectionally rather than with a pre-composed cantus firmus. Taneev had planned several sequels to this first book, none of which were completed before the time of his death in 1915. The Doctrine of the Canon [1929] was later compiled, edited, and published by Viktor Mikhaylovich Belyaev (Grove 1999, 24), but this text limits its focus to two-, three-, and four-voice canons and does not address canons composed in accompaniment of a cantus firmus.
Return to text

6. More specifically, we will adopt for this article the rules of strict counterpoint in the form summarized by Taneev ([1909] 1962, §§70–94, 53–69).
Return to text

7. The transliteration “Taneev” will be used throughout this article except in reference to Brower’s 1962 English translation of Convertible Counterpoint in the Strict Style and its page numbers, where Brower’s preferred “Taneiev” will be used. For two easily digestible synopses of Taneev’s main concepts, see Segall 2014 and Collins 2015.
Return to text

8. Taneev stresses the importance of this point more than once ([1909] 1962, 17; 169–70), and cites an explanation by Bellermann included in the fourth edition of Der Contrapunkt ([1862] 1904, 200–201). Taneev points out that the doubling of the dissonant note of a suspension is the only exception in which an incorrect three-voice combination may be constructed from two-voice combinations that are individually correct ([1909] 1962, §§264–68, 170–72). He also points out a case in which the inverse is true; in a three-voice texture two of the voices may form a dissonant suspension pattern and the third voice may double the “free note” of the suspension. Here, the three-voice combination is correct, but one of the two-voice combinations will appear to have an unprepared dissonance if viewed in isolation (Taneiev [1909] 1962, §269, 172–73)
Return to text

9. In his dissertation, Stefan Prey introduces a mathematical formula that can be used to rigorously identify the fixed consonances of a canon composed against a cantus firmus with given parameters (2012, 75–88). Prey then uses this formula to construct interval tables similar to the one used by Collins and similarly inspired by Zarlino and Berardi.
Return to text

10. In addition, improvisers working from these memorized lists would have had to rely on a separate class of rules to ensure consonant intervals in the canonic P+R combination, such as are given by Zarlino and others. This second class of rules forbids certain kinds of melodic motion for the proposta voice, and Collins gives a separate table summarizing these melodic rules (2008, 116). For a systematic, Taneev-compatible approach to this aspect of canon composition, see Morris 1995. An improvising musician would have needed to cross-check two memorized lists of intervals, one harmonic and the other melodic. If they could reach one of the permitted harmonic intervals in the relevant cell of Example 10 using one of the permitted melodic intervals for that kind of canon, then they could be assured that the resulting three-voice combination would consist exclusively of consonant intervals.
Return to text

11. Examples 12, 13, and 14 are a simplification based on Taneev’s Example 222 ([1909] 1962, 238–39). Taneev has his own self-consistent system for determining which of the combinations should be considered original and which derivative in relation to the basic version, but this is outside the scope of the present study.
Return to text

12. Taneev only uses the “+” sign to show that the joining of two voices forms a contrapuntally correct two-voice combination, preferring instead to show imaginary combinations that are not contrapuntally correct in the basic version. For the sake of easy comparison, this article will refer to imaginary combinations using the same notation.
Return to text

13. The diminished fifth between B and F can be treated as a consonance since it will be transposed to the perfect fifth between F and C in the derivative combination. Likewise, some apparent perfect fifths and fourths in the basic version may transpose into dissonant intervals in the derivative depending on the parameters of the canonic exercise. Taneev gives more than one option for dealing with this, but he mentions that the simplest is to employ musica ficta in the form of the occasional B♭ and F♯: “. . . writing in the original regardless as to whether or not an augmented fourth (or diminished fifth) will appear in the derivative, and when the problem is completed and the voices shifted, to make whatever correction is necessary for its removal” ([1909] 1962, §69, 50–52). In the Dorian canons of Examples 32 and 35, E♭s are used for similar reasons.
Return to text

14. Taneev ([1909] 1962, §§334–35, 214–15) discusses shifting voices from one part of the measure to another in greater detail.
Return to text

15. Taneev addresses the arrangement of the basic version that produces double-shifting counterpoint in contrary motion as well as augmentation ([1909] 1962, §§338–39, 216–18). See also Segall (2014, [17]–[23]) for more on how melodic inversion can be understood within the context of Taneev’s theory.
Return to text

16. Although rare, there are several examples of canons in contrary motion against a cantus firmus in the theoretical literature. Examples can be found by Zarlino ([1558] 1573, 327–28)—which is also present in the earlier 1558 edition—Morley (1597, 103), Calvisius (1630), Hauff (1872, 69–70), Riemann (1888, 190), and Prout (1893, 196).
Return to text

17. I do not recommend attempting to use Equation (4) to find the vertical-shift index for time units of a proportional canon. Directly calculating values for r is very difficult, since “corresponding” time units of a proportional canon are no longer separated by a constant duration (the distance of entrance of the canon). Rather, the fastest and surest method for finding the zones of imitative correspondence, and the Jv values associated with each, is simply to examine the guide intervals after determining the correct placement of the imaginary cantus firmus.
Return to text

18. For more on the specifics of the two-voice counterpoint between the P and R of a crab canon, see Hugo Norden (1970, 91–104) and Collins (1992, 259–65).
Return to text

19. Alfred Mann summarizes this well: “Harmonic as well as melodic inversion of two themes results in the exchange of intervals which is shown in the table of numbers quoted by Fux in his discussion of double counterpoint. When harmonic and melodic inversion are applied simultaneously, this exchange will therefore be canceled, and all intervals will remain the same. . .” (1987, 209n).
Return to text

20. In selecting Bach for analysis, we are in fact skipping over the earlier literature from the era of plainchant-based composition that Taneev himself might well have preferred to use as examples. In particular, the three-voice canonic versets from Jean Titelouze’s Hymnes de L’église could make excellent case studies in a classroom setting. Veni Creator 3, for example, is a canon at the upper octave at a distance of one half note composed against the same plainchant that Zarlino ([1558] 1573) gives as his primary example. Ave Maris Stella 3 and Conditor Alme Siderum 2 are also models of this canonic form.
Return to text

21. “No doubt this is an illustration of a fact often mentioned in music histories—that the old contrapuntists kept their knowledge secret, passing it on to the elect only verbally” (Taneiev [1909] 1962, 297).
Return to text

22. As the composer states, “both plaine songs must not bee sung at once: but I meane if there be two plaine songs given, to make a lesson which will agree with either of them, by themselves, but not with both at once” (Morley 1597, 125).
Return to text

23. “The writer [Berardi] could not have been unacquainted with the methods that yield such combinations” (Taneiev [1909] 1962, 296–97); “It may be asserted without exaggeration that the questions brought up in Part Two of this work have hitherto not only remained unsolved but have not even been stated, and that the study of them as here presented is the first of its kind” (Taneiev [1909] 1962, 298).
Return to text

24. Morley’s insights into imaginary voices may be related to the English tradition of “sighted” notes (i.e., transposed in the mind but not sung) and “voiced” notes in improvised faburden, a topic summarized by Ann Besser Scott (1971, 345–46).
Return to text

25. “Dieses Verfahren allein macht es aber freilich noch nicht aus, um jede ähnliche Melodie auch sogleich als einen Canon der einen oder der andern der oben genannien 2 Arten behandeln zu können; dass solches aber zur prüfenden Uebersicht einer hierauf zu gründenden canonischen Arbeit dienet, ist in die Augen springend” (André 1838, 246).
Return to text

Copyright Statement

Copyright © 2024 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.