A Voicing-Based Model for Additive Harmony
Damian J. Blättler
KEYWORDS: additive harmony, Parisian modernism, Ravel, Poulenc, Debussy, voicing
ABSTRACT: This article develops, for the Parisian modernist repertoire, a model of additive harmony in which voicing plays a foundational role. In comparison with the conventional extended-triad model of additive harmony, the voicing-based model better describes the range of novel verticalities used in tonal progressions in this repertoire, and the features that allow those verticalities to serve as stand-ins for common-practice chords. This study also enriches our understanding of the important developments in Western tonal language that took place in the late nineteenth and early twentieth centuries. Most research on these stylistic developments details how innovation within certain horizontal-domain pitch constraints allowed for the incorporation of new harmonic successions into tonal contexts; this paper demonstrates that a similar process can be read in the vertical domain, wherein adherence to certain vertical-domain pitch constraints allowed for the incorporation of new chords into tonal contexts.
Copyright © 2017 Society for Music Theory
Example 1. Reduction of the final cadence of Ravel, L’enfant et les sortilèges, R154–end
(click to enlarge)
[1] The music of composers working in Paris around the turn of the twentieth century is shot through with harmonic moments like that in Example 1, the final cadence of Ravel’s one-act opera L’enfant et les sortilèges (1925). These are moments where the Roman-numeral sense of a chord progression is clear, but the chords used in that progression are unconventional by common-practice standards. In the Ravel example, the first of the two bracketed chords is neither a triad nor a seventh chord (and in pitch-class terms is actually the scalar subset [B, C, D, E]; the pitches of the chorus evaporate upon the strings’ entrance), while the final G-major triad is accompanied by an
[2] This phenomenon is known as additive harmony, defined as the vertical enrichment of harmony with a clear Roman-numeral progression of triads and seventh chords.(1) Additive harmony is a common feature of this repertoire, borne in part from a turn-of-the-century desire to establish a compositional style, distinct from the dense counterpoint of German expressive maximalism, that involved renewed focus on the sensuous potential of chords, yet it is poorly accounted for by conventional harmonic theory.(2) Most discussions of the development of tonal language in the late nineteenth and early twentieth centuries focus on horizontal-domain procedures, considering how adherence to certain common-practice voice-leading principles (e.g. conjunct voice-leading, or a circumscribed set of background structures) allowed for the incorporation into tonal contexts of new harmonic successions.(3) In revealing underlying tonal logics, however, this kind of analysis often reduces away exactly those vertical-domain surface details that interest me in this study. (The reducing-away of vertical-domain details often relies on the extended-triad model of additive harmony, a model whose shortcomings will be discussed presently.) Studies that analyze the Parisian modernist repertoire in terms of systematizable properties of pitch collections often feature an analogous difference in priorities.(4) This work is valuable in that it develops alternate lenses through which to view this repertoire, but it does not always directly address tonal implications that lie on the musical surface and are essential to this repertoire’s aesthetic effect.(5)
Example 2. Comparison of the impact of chord inversion upon an additive chord and upon a triad
(click to enlarge)
[3] In common-practice harmony textbooks, discussion of additive harmony is generally limited to chapters toward the end. Most of these textbooks account for additive harmony with the extended-triad model of ninth, eleventh, and thirteenth chords; while the details vary, the basic logic of the model is that the seventh chord can accommodate further dissonances arranged in a stack of thirds upwards from the chordal seventh.(6) These ninth, eleventh, and thirteenth chords can expand the seventh chord, thereby incorporating new dissonances into tonal progressions. This model, however, does not adequately describe either the range of additive harmonies found in the Parisian modernist repertoire or the features of those harmonies that allow for their participation in tonal progression. Chief among the model’s flaws is that it inadequately addresses the crucial impact that voicing has on the identity of additive chords. While voicing is important in common-practice textures, it is particularly so in additive-harmonic textures because many additive chords include pitch classes from two or more categories of harmonic function.(7) The penultimate chord of L’enfant et les sortilèges contains G major’s dominant base (D) as well as its subdominant base (C) and the powerful functional agents from both the subdominant and tonic functions (E and B respectively).(8) Because of the presence of these competing elements, the character of a chord progression depends in part on the vertical ordering of these pitch classes, and chord inversion has a more disruptive effect in additive-harmonic contexts than in common-practice ones. In Example 2a, the pitch classes of the penultimate chord in Example 1 are inverted to create a root-position C major ninth chord; this changes the heard root of the pitch-class set <B, C, D, E> and therefore turns the original authentic progression into a plagal one. In Example 2b, the penultimate chord is replaced with a simple dominant triad, which is then inverted in Example 2c. Because the scale degrees in the new penultimate chord are all dominant-functional, Example 2c changes the level of finality of Example 2b, but not its perceived root or its basic functional character.
[4] Two insights can be drawn from these examples: first, pitch-class content alone is an inadequate determinant of the behavior of additive chords, and second, voicing is a particularly important one. The extended-triad model accommodates these insights only as awkward, after-the-fact supplements to its core machinery. The following passage from Ludmila Ulehla’s Contemporary Harmony (a text that contains one of the most thorough workings-out of the extended-triad model) illustrates this point:
Due to the upward climb of thirds, the thirteenth rightfully demands the highest position. Occasionally, it will permit the ninth to preside above, with the thirteenth directly beneath. The seventh of the chord must not be placed next to the thirteenth.
. . . With inversions, the root may be placed in the uppermost voice.. . . Nestled next to the seventh, [the thirteenth] becomes unclear and permits the upper tones to predominate. (Ulehla 1966, 100–101)
Example 3. Potential alternate readings of the penultimate chord of L’enfant et les sortilèges
(click to enlarge)
[5] Although insightful, such lists are ad-hoc and cumbersome; rather than offering any generalizable rules for the inversion of extended triads or the relative positioning of upper voices, Ulehla instead provides sets of rules for each type of extended triad and all of their chromatic alterations. Yet to forgo any discussion of voicing, as many common-practice harmony textbooks do, is to allow for an over-proliferation of labels that weakens the model’s mooted connection between chord structure and chord behavior.(9) All diatonic step classes are present in a full thirteenth chord, so if all inversions are possible and tones can be omitted (a common stipulation in presentations of the extended-triad model, so as to account for the fact that, in normative four- or five-voice textures, would-be eleventh and thirteenth chords will necessarily feature gaps), then any pitch combination can have any step class as a potential root. Example 3 shows how the L’enfant chord could naively be labeled a C ninth chord in fourth inversion with omitted fifth (chord a), an E thirteenth chord in third inversion with omitted third, ninth, and eleventh (chord b), or a B eleventh chord in first inversion with missing fifth and seventh (chord c). There is nothing inherent in the concept of extended triads that explains why these readings would be worse than that given in the initial discussion of Example 1. This disconnect between a chord’s behavior on the one hand and the relationship between its pitch-class set and abstract stacks-of-thirds on the other means that the extended-triad model is not a consistently applicable analytic tool for tonal passages in the Parisian modernist repertoire.
The Model
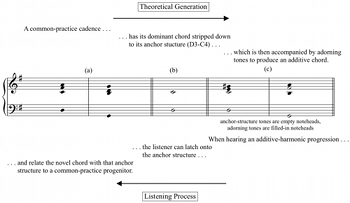
[6] The aim of this essay is to develop a model of additive harmony that, by making voicing its point of departure, better accounts for the incorporation of novel chords into this repertoire’s tonal passages. I conceive of additive harmonies in the Parisian modernist repertoire as the coincidence of anchor structures and adorning tones. An anchor structure is the vertical-domain component of a novel chord that allows for its participation in tonal progression—not a particular pitch-class subset of the chord, but rather a skeletal voicing involving the bass note.(10) Anchor structures produce “tonal plausibilities” for a chord: ways in which a novel chord can be heard as a version of a common-practice chord.(11) Anchor structures can then be decorated with a variety of adorning tones; adorning tones are pitches that color an additive harmony without undermining its potential tonal utility, constrained only by a general set of voicing restrictions that preserve a verticality’s qualia of chordness. This section of the article describes this model in two interconnected parts, first addressing the mechanism of anchor structures and tonal plausibilities before turning to adorning tones and voicing restrictions; the subsequent section discusses the benefits and applications of the model.
Anchor Structures & Tonal Plausibilities
Example 4. The relationship between a tonally plausible additive chord and a common-practice chord
(click to enlarge)
[7] This model posits that the novel chords in Parisian modernist tonal passages are filtered through listeners’ common-practice listening habits.(12) Common-practice chords have associated behaviors, and a tonal plausibility describes how additive chords might slot into those roles. The links between novel and familiar sonorities are created by anchor structures; these voicings strongly evoke common-practice chords and so allow additive chords to be heard as stand-ins for common-practice ones. Example 4 depicts the relationship between additive chords and common-practice chords as a two-stage process. When read from left to right, using the captions at the top of the figure, Example 4 presents a theoretical generation for additive chords. To generate an additive chord from the common-practice progression in (a), first strip down the common-practice chord until only its most basic, emblematic voicing remains; here, the V7 chord in G major is stripped down to its D3–C4 anchor structure (b). Next, decorate that anchor structure with adorning tones; in (c) these are E4 and
Example 5. Two-note anchor structures (t and e stand for ten and eleven)
(click to enlarge)
[8] Three two-note voicings can serve as anchor structures (i.e., can create a tonal plausibility for a novel verticality): the registrally ordered intervals (henceforth ro-intervals) of 7, 10, and 11 half steps above the bass note, or perfect fifth, minor seventh, and major seventh (Example 5).(14) They can do so because they have strongly defined roles in common-practice harmony. Ro-interval 7 strongly implies the root and fifth of a root-position consonant triad; in common-practice contexts it is not susceptible to enharmonic reinterpretation (doubly augmented fourths or doubly diminished sixths are extremely rare) and only rarely to reinterpretation as different chord members of an alternate chord.(15) Ro-interval 10 above the bass is almost always the root and seventh of a seventh chord (dominant, minor, or half-diminished). Ro-interval 10 can also comprise the pitches that form the augmented sixth in an augmented-sixth chord; even in these chords, however, the powerful latent suggestion of a seventh chord is what allows for the common enharmonic reinterpretation of augmented-sixth chords as dominant-seventh chords.(16) Ro-interval 11 is much more rare as a chord interval in common-practice contexts than ro-intervals 7 and 10, but it does still have clear connotations as a voicing above the bass: it is insusceptible to enharmonic reinterpretation and always represents the root and seventh of a major-seventh chord.
Example 6. Ravel, Ma mère l’Oye,“Laideronette, impératrice des pagodes,” mm. 16–24
(click to enlarge)
[9] In additive-harmonic textures, these ro intervals are lightning rods for common-practice tonal listening habits. For instance, the
[10] With two-note anchor structures, the bass note is also the root of the additive chord’s common-practice referent. In the cases of ro-intervals 7 and 10, this referential sense of root is buttressed by acoustic factors. Both are root-candidate-producing intervals, meaning that the upper pitch reinforces some of the overtones of the lower pitch (Parncutt 1988, 1997; Hofman-Engl 2006). Mark Yeary has pointed out that this feature is “taken as an ecological cue to objecthood” because most real-world sound sources (including the human voice) produce complex tones, meaning that verticalities featuring these ro-intervals are more likely to be perceived as integrated chords, rather than as tone clusters or as the coincidence of disassociated strata (2011, 23). Ro-interval 11 does not have its referential sense of root amplified by acoustic factors, but the implication that the bass note is the root is nevertheless secure as ro-interval 11 has the most unequivocal common-practice connotation.
Example 7. Three-note anchor structures
(click to enlarge)
Example 8. Examples of second-order anchor structures
8a. Ravel, Le tombeau de Couperin, “Rigaudon” mm. 1–8
(click to enlarge)
8b. Milhaud, Saudades Do Brasil, “Tijuca,” mm. 5–9
(click to enlarge)
Example 9. Inability of ro-interval 2 to support additive adornments
(click to enlarge)
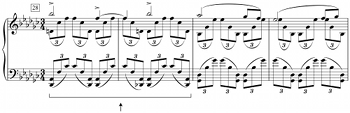
[11] Any other anchor structure will involve three notes. The set of minimal voicings that have a clear common-practice connotation and do not involve ro-intervals 7, 10, or 11 above the bass (which do not require an additional pitch to generate a tonal plausibility) are simply common-practice chords themselves: consonant triads in inversion, seventh chords in inversion with the omission of either the chordal third or fifth, and the diminished triad and its inversions. These are shown in Example 7; in all cases save for those marked with a single asterisk, the upper pitches of these voicings can appear in any order (e.g. a |38| anchor structure can be voiced as |83|). With three-note anchor structures, the bass note is not the root of the common-practice referent, and three-note anchor structures generally support fewer adorning tones than do two-note anchor structures. Two passages that make use of three-note anchor structures are shown in Example 8. In Example 8a, the opening phrase of the Rigaudon from Ravel’s Le tombeau de Couperin (1917), the |59| anchor structure in the last chord allows a root of G to be inferred; m. 8 can be heard as an additive dominant-to-tonic echo of the cadence in m. 7, even though the bass pitch is the same for both of m. 8’s chords. Example 8b, from “Tijuca” in Milhaud’s Saudades Do Brasil (1920), modulates from A major/minor to C major/minor using a |53|-anchored chord on the last beat of m. 8; that voicing creates the tonal plausibility that this eight-note chord is an applied dominant of C major/minor, with the pitches of the right hand interpreted as adorning tones.(18) Since the goal of the anchor-structure model is to highlight the minimal voicings that create tonal plausibilities for additive chords, when a full seventh chord is present, as in Example 8b, only those pitches necessary for the plausibility are considered part of the anchor structure (and consequently highlighted in the analytic notation); the B-natural3 could be omitted from Example 8b and the chord’s tonal potential would be the same.
[12] There are no other two-note anchor structures because the eight remaining ro-intervals by themselves lack the same connotative strength as ro-intervals 7, 10, and 11. The imperfect-consonance ro-intervals 3, 4, 8, and 9 are too interpretively flexible: for instance, in common-practice contexts ro-interval 9 above the bass could comprise the chordal third and root of a first-inversion minor triad, the seventh and fifth of a third-inversion dominant seventh chord, or the fifth and root of a second-inversion major triad. Ro-interval 6 is even more ambiguous than 3, 4, 8, or 9, as it could be the third and seventh of a first-inversion dominant seventh, the seventh and third of a third-inversion dominant seventh, the root and fifth/fifth and root of a diminished triad or half-diminished seventh chord, or any two pitches of a fully diminished seventh chord. Any of these five ro-intervals, then, if present above the bass of a novel verticality, would not by itself activate a clear sense of chord identity; other pitches would be required to clarify the verticality’s tonal plausibilities.
[13] The ro-intervals 1, 2, and 5 above the bass are the inversions of the ro-intervals of the two-note anchor structures. Ro-interval 5 has two broad roles as a chord interval in common-practice harmony—it can be the fifth and root of a second-inversion chord, or the seventh and third of either a half-diminished or minor-seventh chord in third inversion—and so it requires the presence of a third pitch to distinguish between these possibilities and produce a clear tonal plausibility.(19) (The distinction between a second-inversion triad and a third-inversion seventh chord is one that can be clarified vertically, whereas as the distinction between a German augmented-sixth chord and a dominant-seventh chord, or an Italian augmented-sixth chord and a dominant-seventh without a fifth—connotations grouped together by their ro-interval 10 anchor structures—can only be established in context.) As chord intervals in common-practice contexts, ro-intervals 1 and 2 are the seventh and root of third-inversion seventh chords (Example 9a). These ro-intervals do not readily serve as two-note anchor structures for additive harmonies, however, because any novel adornment of them undermines the initial tonal plausibility of a third-inversion seventh chord. By way of demonstration, Example 9b shows how combining ro-interval 2 with ro-intervals 5, 6, 8, or 9 simply produces common-practice chords, combining it with the anchor-structure ro-intervals 7, 10, or 11 produces competing tonal plausibilities that project the bass as a root, combining it with ro-interval 1 produces a tonally recalcitrant chromatic pitch-space cluster, and combining it with ro-intervals 3 or 4 (and voicing the resultant chords so as to follow the guidelines for voicing outlined in the next sub-section) also produces combinations that undermine the sense that the upper pitch of the ro-interval 2 is the chord’s root. Ro-intervals 1 and 2 are therefore not considered viable two-note anchor structures.
Example 10. Relative strength of anchor structures closer to the bass
(click to enlarge)
Example 11. Poulenc, Trois Pièces pour piano, “Pastorale,” mm. 3–6
(click to enlarge)
[14] An additive chord will generally have several potential anchor structures over its bass note, and therefore possess several tonal plausibilities.(20) Which plausibility is more prevalent depends of course on context (with interpretive utility being the ultimate arbiter in analytic decisions), but two general tendencies can be observed in this repertoire. The first is that, in a chord with multiple anchor structures, the anchor structure voiced closer to the bass is generally the more plausible usage and hearing, as Example 10 demonstrates. In (a), the |68| anchor structure (formed by E3,
Example 12. Interaction between two-note and three-note anchor structures in a similar register
(click to enlarge)
[15] The other tendency of competing anchor structures is that, when voiced in a similar register, anchor structures that project the bass note as a root (i.e. two-note anchor structures) generally supersede those that do not (i.e. three-note anchor structures). Example 12 demonstrates this point using the chord from “Laideronette, impératrice des pagodes” (Example 6). Chord (a) could serve as a |25| anchor structure for a verticality that evokes a minor-seventh chord in third inversion. Adding the rest of the pitches in (b), though, creates a |10| anchor structure that is more acoustically robust and functionally suggestive. The resultant tonal plausibility of
Adorning Tones and Voicing Restrictions
[16] The anchor-structure apparatus explains how certain skeletal voicings “anchor” novel chords into tonal contexts. These anchor structures are draped in various combinations of adorning tones, producing the diversity of chord color that is a distinguishing feature of the Parisian modernist repertoire. A few general constraints obtain as to which adornments are possible. Together, these preserve the Gestalt qualia of a chord: i.e., the perception of a verticality as integrated whole, and not merely as a collection of simultaneously sounding pitches that might be more readily understood as a tone cluster, the coincidence of disassociated pitch strata, or some other type of non-integrated sonority.(21) This qualia is vital in maintaining additive-harmonic passages’ connection to common-practice contexts. The primary restrictions on voicing in this repertoire are: (a) chords generally do not contain ro-interval 1, save for as minor ninths above the bass of two-note anchor structures; (b) chords generally do not contain consecutive whole-step adjacencies; and (c) chords rarely feature more than an octave between upper pitches (there may be more than an octave between the bass note and the second-lowest pitch).(21) I will now discuss these in turn.
Example 13. Ravel, Miroirs, “Alborada del gracioso,” mm. 126–40
(click to enlarge)
Example 14. Ravel, Ma mere l’Oye, “Pavane de la Belle au bois dormant,” mm. 5–8
(click to enlarge)
[17] Ro-interval 1 is treated with great care in the tonal passages of the Parisian modernist repertoire.(22) Ro-interval 1 is a flashpoint in any sonority and, rather than fostering perceived cohesion between tones, it introduces an acoustic roughness that counters against hearing a sonorous composite chord. Verticalities such as that in mm. 132–34 from Ravel’s “Alborada del gracioso” from Miroirs (1905; Example 13), with two adjacent instances of ro-interval 1 (
[18] This stylistic practice of generally avoiding ro-interval 1 when building chords has links to physiology and cognition. For one, the half step is always acoustically rough because the critical band (the frequency range within which two signals compete for the same receptor cells on the basilar membrane), although it varies in size depending on its position in the spectrum and from person to person, is never smaller than a major second (Mashinter 2006, 66). That acoustic roughness contributes to the half step consistently being ranked as the most dissonant equal-tempered interval in listener-opinion studies.(25) In an index produced by David Huron based on listeners rating the relative stability of intervals, the minor second ranks as three times more unstable than the next closest interval (1994, 290–93).(26) (The same study revealed that listeners do not give equivalent stability ratings to inversionally related intervals, a finding that buttresses this model’s focus upon ro-intervals rather than interval classes [293].) Arthur Samplaski’s dissertation, which used listener experiments to evaluate atonal models of chord similarity, also determined that the presence or absence of ro-interval 1 was the single most important element in listener judgments about chord similarity (1999, 217). This combination of acoustic roughness and perceptual salience means that ro-interval 1 can be a significant obstacle to chordal stability. In a 2006 study, Norman Cook and Takashi Fujisawa asked subjects to rate the stability of all possible trichords, with each trichord presented in a variety of voicings. The two elements found to be responsible for low stability ratings in the experimental results were (a) the presence of a half step and (b) two intervals of equal size; the presence of a half step, however, was the far more significant marker (112–13). Further studies by Keith Mashinter (2006) and Joos Vos (2006) corroborate Cook and Fujisawa’s findings. This line of research supports the present theory that the presence of ro-interval 1 in a verticality can undermine the Gestalt qualia of a chord in additive-harmonic textures.
Example 15. Marked use of ro-interval 1 in Auric, Prélude from L’Album des Six
15a. 1st theme, mm. 1–8
(click to enlarge)
15b. recapitulation, mm. 37–end
(click to enlarge and see the rest)
Example 16. Text and translation for Chabrier’s “Les Cigales”
(click to enlarge and see the rest)
Example 17. Chabrier’s “Les Cigales,” mm. 1–35
(click to enlarge)
Example 18. Scarcity of adornment options for three-note anchor structures
(click to enlarge and see the rest)
Example 19. Satie, Préludes Flasques, iv, mm. 1–8; three-note anchor structures
(click to enlarge)
[19] Also corroborating the importance of the ro-interval 1 voicing constraint in the Parisian modernist repertoire is that when ro-interval 1 does appear in additive-harmonic contexts, its use is often a marked event deployed to specific expressive ends. Two examples are discussed here. In Georges Auric’s Prélude from L’Album des Six (1919), the repeated use of ro-interval 1 adds a layer of narrative complexity to the Neoclassical piano miniature. The piece’s first theme is shown in Example 15a; it features jarring ro-interval 1 dissonances on the downbeats of mm. 1, 2, 7 and 8. The placement of these dissonances cuts against both the periodic structure of the melody and the expectation that the beginning and end of a non-modulating phrase will be that phrase’s most stable moments. A reading of this theme as “defective” in some sense, generated by the above observations and from the contrast between the ro-interval 1 dissonances and the blithely triadic melody in A major, finds further interpretive purchase at the recapitulation in the piece’s otherwise straightforward rounded binary form (Example 15b). The theme reappears only in a corroded state in mm. 39–46: the melody is now in A minor (and starts on a different scale degree, which preserves the initial melodic skip of a major third) and is placed over a
[20] Another piece that makes marked use of ro-interval 1 is Chabrier’s song “Les Cigales” (1890). Here, the presence or absence of ro-interval 1 is central to the song’s setting of its text (given in Example 16).(27) The poem’s verses describe the cicadas with minimal affection—their cries are described as “raucous” and the verses contain several bleak evocations of a parched midsummer landscape (e.g. “les tas de poussière gris,” “Tout et mort”). The setting of these verses features heavy use of ro-interval 1. In the first verse, shown in Example 17, this is between E5 and F5 in mm. 1–5 and m. 7, between
[21] The ro-interval 1 restriction, when considered in conjunction with the rules of thumb for anchor-structure interaction, helps explain why three-note anchor structures are relatively limited in use. Example 18 shows how a tightly voiced |35| anchor structure can only easily support one additive-harmonic adornment, an additional ro-interval 2. Of the other eight potential adorning pitches, three produce two-note anchor structures above the bass note that compete against the |35| anchor structure’s tonal plausibility, three more are off-limits because they would produce harsh ro-interval 1s, and the remaining two are uninteresting from an additive-harmonic standpoint because they complete common-practice chords. This exemplifies how there are limited ways of presenting novel inverted chords in additive-harmonic environments, and partially accounts for the prevalence of root-position chords in the Parisian modernist repertoire. The incorporation of novel sonorities into tonal contexts is easiest when the roots projected by voicings and those projected by bass lines work in concert, rather than at cross-purposes; the voicings reinforce the bass’s role as harmonic driver, and the bass’s motion actualizes the tonal plausibilities of the voicings.
[22] This does not mean, however, that the bass pitch alone necessarily defines an additive chord’s identity.(29) Counterexamples have already been discussed in Examples 8 and 11; Example 19, the opening of the last movement of Satie’s Préludes Flasques (1912), is a particularly rich example of an additive-harmonic passage where the root progression is not the same as the bass line. Here, three-note anchor structures allow for the combination of chromatic bass-line fragments and circle-of-fifth progressions with a simple melody that fixates on the tonic and dominant scale degrees. After mm. 1–2 move from (additive) tonic to (additive) subdominant, mm. 3–4 move through a D–G–C falling-fifth root progression over the chromatic bass line
[23] The second voicing constraint that obtains in this repertoire is that chords rarely feature consecutive whole-step adjacencies. This refers specifically to adjacent pitch-interval 2s in a voicing, not to multiple instances of ro-interval 2 in a chord (as in the first chord of m. 5 in Example 19) nor to a chord with multiple adjacent whole steps in pitch-class space (chords of this type, like the penultimate chord in Example 1, are generally voiced without consecutive adjacent whole tones). The restriction helps preserve the Gestalt qualia of a chord by maintaining a distinction between chord and scale. Joel Lester (1970), Joseph Straus (1987), and Olli Väisälä (1999) have all discussed how maintaining a distinction between stepwise motion and arpeggiation, and therefore between voice-leading and harmony, is necessary for prolongation because in its absence “it is virtually impossible to determine the voice-leading function of the melodic motions” (Straus 1987, 3); one can no longer distinguish between motion within a prevailing harmony and motion away from that harmony.
Example 20. Whole-step adjacencies in final tonic chords in the Parisian modernist repertoire
20a. reduction of Debussy, La mer, ii, R40–41
(click to enlarge)
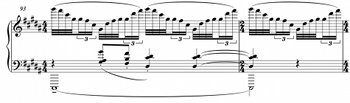
20b. Debussy, Estampes, “Pagodes,” mm. 93–98
(click to enlarge)
20c. Chabrier, “Les Cigales,” mm. 93–98
(click to enlarge)
Example 21. Debussy, “Les collines d’Anacapri,” mm. 1–8
(click to enlarge)
[24] In common-practice music, the line between harmonic intervals and voice-leading intervals is between three half steps and two half steps, meaning that the triad enjoys privileged status as “the maximal subset of the diatonic collection consisting entirely of non-adjacent elements” (Straus 1987, 3). Väisälä has suggested, however, that the definition of step and leap can be flexible and contextually defined; in an analysis of Schoenberg’s Kleines Klavierstück op. 19 no. 2, he posits that ro-interval 2 is a harmonic interval in the piece and that ro-interval 1 is the only voice-leading interval.(31) A shift is necessary for the Parisian modernist repertoire as well, because whole-tone adjacencies are commonplace and so must be viewed as valid chordal intervals (i.e. not just as the byproducts of octave replication or inversion). The telltale usage that supports this new status for pitch-interval 2 is the use of chords with such adjacencies as the final tonic of a piece, as in the second movement of Debussy’s La Mer (1905; Example 20a), in Debussy’s “Pagodes” from Estampes (1903; Example 20b), or in “Les Cigales” (Example 20c).(32) These chords are not in inversion—the heard tonic pitches here are the bass notes (an impression further reinforced in Example 20a by the falling-fifth approach in the bass). Nor are the major-second adjacencies understood as unresolved tensions; these chords are the contextually stable final tonics of their respective pieces.
[25] A distinction between chord and scale still persists in the Parisian modernist repertoire;(33) the point of division has simply been shifted to allow for the verticalization of single scale-step adjacencies. There is still one pitch interval reserved exclusively for step motions: pitch-interval 1; the ro-interval 1 constraint explains why pitch interval 1 rarely features in chord construction. And while the verticalization of one scale-step adjacency, pitch-interval 2, is now commonplace, the verticalization of consecutive scale steps is not;(34) adjacent whole tones are infrequent because verticalized scale steps produce a qualia that can be too cluster- or scale-like rather than chord-like. As with ro-interval 1, the rare appearance of consecutive adjacent whole tones is often a marked event. One such example is in the opening of Debussy’s “Les collines d’Anacapri” from the first book of the Préludes (1910; Example 21). The piece opens with the sonority B3–
[26] The last constraint that preserves the Gestalt qualia of a chord is that upper voices generally are voiced within an octave of one another. This condition also obtains in common-practice chordal writing, and has a partial basis in acoustics. Work by Reinier Plomp and Willem Levelt, later revisited and reworked by first Akio Kameoka and Mamora Kuriyagawa and then David Huron and Peter Sellmer, has shown that this principle of conventional four-part writing generally produces partials “whose distribution would be homogenous with regard to critical bands” (Huron and Sellner 1992, 130). There are also cognitive reasons why this constraint promotes the Gestalt qualia of a chord; Yeary has discussed how sonorities with tones separated by large distances in frequency may encourage the segregation of a single sonority into multiple steams or perceptual objects (2011, 103). This constraint, then, serves as another connection to the common-practice chord types that inform additive harmonies in this repertoire. This constraint is the most flexible of those listed here; as in common-practice writing, upper voices on occasion move further than an octave from each other before returning soon after.(36)
Benefits and Applications
[27] There are several benefits to conceiving of additive harmonies as a combination of anchor structures and adorning tones. For one, the model explains how chords of divergent pitch-class content can perform equivalent tonal functions; a two-note anchor structure can support a wide range of colorations without destabilizing its tonal plausibility. In Example 22, the three highlighted chords all serve as dominant chords in additive authentic cadences. The highlighted chord in Example 22a, found at the end of the two-measure fanfare motive from the final scene of Stravinsky’s Firebird (1910) and generated by the motion between versions of the step-class set [0135] in the upper parts, is diatonic and contains, along with the pitches of the
Example 22. The potential for chords to fulfill the same
tonal function despite divergent pitch-class and scale-degree content
22a. reduction of Stravinsky, Firebird, R206–208 (click to enlarge) 22c. reduction of Ravel, Introduction et allegro, R28 (click to enlarge) | 22b. reduction of Delius, Sea Drift, mm. 1–9 (click to enlarge) 22d. transposition of the highlighted chords from (a)–(c) into the same key, so as to compare anchor structures and pitch content (click to enlarge) |
Example 23. Different tonal plausibilities arising from distinct voicings of a single pitch-class/scale-degree collection
(click to enlarge)
Example 24. Ravel, Valses nobles et sentimentales, i; pitch-class set {G, A, B, D, E} voiced so as to have different tonal functions
(click to enlarge and see the rest)
[28] Conversely, the anchor-structure model also explains how a single pitch-class set or scale-degree collection can be voiced so as to have multiple tonal functions. Example 23 demonstrates this in the abstract; here chord (a) has an ro-interval |7| anchor structure, and so behaves most plausibly as an A-rooted chord adorned with
[29] Another benefit of the anchor-structure model is the omnivorous nature of its concept of adorning tones, which obviates the need for a proliferation of additive-harmonic chord categories. Many harmony texts maintain a conceptual distinction between extended triads (i.e. stacked-third chords) and added-note chords; other mooted chord types include chords with unresolved appoggiaturas or suspensions, intervallic structures, and polychords.(40) The chords in Example 22 could potentially be analyzed as belonging to distinct categories: the chord in the Stravinsky as a ninth chord with unresolved suspension (despite the absence of resolution for the suspended B), the chord in the Delius as an altered chord, and the chord in the Ravel as the polychord
Example 25. Dissonant passage tonally grounded by anchor structures
25a. Ravel, Le tombeau de Couperin, “Forlane,” mm. 1–9 (click to enlarge) | 25b. reduction of mm. 1–5 from (a); anchor structures shown in open noteheads (click to enlarge) |
Example 26. Piston’s guidelines for voicing a ninth chord
(click to enlarge)
Example 27. Flexibility of the third in two-note anchor-structure chords
27a. chromatically altered third in Satie’s Gymnopedie No. 1, mm. 36–39
(click to enlarge)
27b. omitted chordal third in Debussy’s “a fille aux cheveux de lin,” mm. 18–19
(click to enlarge)
Example 28. Comparison of Hull’s analysis and anchor-structure analysis of Butterworth, A Shropshire Lad, mm. 54–56
(click to enlarge)
[30] The anchor-structure model also highlights how additive harmony does not depend on tertian construction. The stacking of thirds is central to most other models of additive harmony, implicit in their focus on extended triads as ideal types and in their rules for voicing that preserve tertian construction at the musical surface. Example 26, from Piston’s Harmony, instantiates the latter tendency. Piston writes that chords [a] and [b] are to be avoided, [a] because the ninth is below the leading tone, and [b] because the absence of the third weakens “the characteristic sounds of the dominant ninth chord”; chord [c], which suggests a clean stack of thirds from G up through A, is Piston’s preferred version (1978, 339). A few texts are explicit about the centrality of stacked thirds in their conceptions of additive harmony; for instance, Leon Dallin writes that “Contemporary chords built in thirds have the closest relation to conventional harmonies since they continue the process by which triads and seventh chords are constructed, superimposition of thirds” (1957, 60).(42) In the current model, however, the most important component of an additive chord is its anchor-structure voicing and its attendant common-practice implications, not the presence or absence of tertian construction. In this view, chordal thirds are adorning tones, more akin to a ninth or a sixth above the bass than to the perfect fifth; in the Parisian modernist repertoire they are frequently either chromatically altered (as in the cadence in Example 27a, from Satie’s Gymnopédie No. 1 [1888]) or absent altogether (as in the cadence in Example 27b, from Debussy’s “La fille aux cheveux de lin” [1910], mm. 18-19; the dominant of
Methodological points
[31] Before concluding with a pair of analytic vignettes, I will briefly address two methodological points. One is the problem of “only seeing what you want to see” and shoehorning the complexities of the Parisian modernist repertoire’s additive-harmonic practice into common-practice categories. The anchor-structure model is not intended to be proscriptive; the goal is not to definitively say which chords “work” and which do not, but rather to discuss common formations, usages, and hearings. The wide range of verticalities produced by these composers’ fascination with color and sonority makes accounting for every single tonally participatory chord in the repertoire only an ideal towards which this project can strive, and not a fully attainable goal; Michael Russ has discussed how the success of models of early twentieth-century harmony can only ever be partial, because “every one of the 344 possible note-combinations [from Simon Harris’ exhaustive classification of chord types] has an awkward tendency to turn up somewhere” (1993, 325). Not all verticalities used in tonal contexts feature an anchor structure or conform to the voicing restrictions laid out here. These chords are not banished from the repertoire or labeled as aberrations; they are simply less common, and require more contextual incorporation. The model describes how certain pitch voicings provide opportunities for tonal listening; the aim is to remain sensitive to the novel characteristics of this music while still highlighting its dependence on and allusions to common-practice structures.
Example 29. Ravel, Valses nobles et sentimentales, mm. 56–61
(click to enlarge)
[32] The other, related issue is that of how ornamentation functions in additive-harmonic contexts. The increased dissonance levels and relative density of additive-harmonic contexts means that nonchord tones are more context-dependent in the Parisian modernist repertoire than in common-practice contexts.(44) In common-practice contexts, isolating nonstructural ornamentation is a relatively simple process: any tone that does not belong to a triad or a seventh chord is a nonchord tone. In additive-harmonic textures, though, many more notes can be part of a chord; indeed, one of the strengths of the anchor-structure model is that it allows for multiple adornments of a single tonal function. This does not mean, however, that nonchord ornamentation is no longer viable. Several factors contribute to the perception of nonchord ornamentation in this repertoire. For instance, vertical moments that do not conform to the general voicing restrictions discussed in paragraphs [17]–[27], since they resist integrated hearings as chords, can potentially be interpreted as the coincidence of a chord with nonchord elements (i.e., nonessential dissonance). Example 29, from the first of Ravel’s Valses nobles et sentimentales, is an example of a passage where such a hearing is likely. The highlighted verticalities do not conform to the general voicing restrictions in that they have an ro-interval 1 between the outer pitches of their right-hand notes. They are not, however, outside of conventional tonal chord syntax as a cluster or polychord might be—they participate in the passage’s chromatic descending-fifth sequence of |10|-anchored chords—and the consistent voice-leading of the upper part means that they are better interpreted as the coincidence of the descending-fifth sequence with the upper voice’s chromatic ascent from A4 to G5.
Example 30. Debussy, “La Puerta del Vino,” mm. 5–12
(click to enlarge)
Example 31. Reduction of Poulenc, Les biches, “Rag Mazurka,” R89
(click to enlarge)
[33] Another factor that can contribute to hearing nonchord tones in additive-harmonic contexts is gestural reference to common-practice ornamentation. Common-practice nonchord tones are defined by characteristic melodic motion; gestures emulating that motion in additive harmonic textures, even in the absence of a sharp dividing line between consonant chord intervals and dissonant ornamenting intervals, can constitute nonchord ornamentation of a chordal structure.(45) This phenomenon plays on contextual stability conditions that allow dissonant additive chords to serve as stable sites of resolution.(46) In Example 30, mm. 5–12 from Debussy’s prelude “La Puerta del Vino” (1913), all verticalities conform to the voicing restrictions discussed above (the ro-interval 1 created by D-natural4 over
[34] In Example 31, a reduction of the opening bars of the “Rag mazurka” from Poulenc’s ballet Les biches (1924), the combination of the factors discussed above serves to turn a major tenth into a dissonant suspension. The highlighted chord deviates from the model’s general voicing restrictions, as it features ro-interval 1 between B3 and both C4 and C5. The pitch C5, though, can be heard as a non-chord ornament, even though it is consonant against the bass
Analytic vignettes
Example 32. Epigraph to “Les entretiens de la Belle et de la Bête”
(click to enlarge)
[35] The various benefits of the anchor-structure approach can be brought to bear in the analysis of pieces such as “Les entretiens de la Belle et de la Bête,” the fourth movement of Ravel’s suite Ma mère l’Oye, which combines tonal structures with the expanded scalar palette of the Parisian modernist repertoire. The structure of “Les entretiens” is in the service of the piece’s epigraph, a three-part distillation of the tale of Beauty and the Beast (Example 32).(47) Ravel’s piece tracks the story in two broad parts—an initial section that presents the themes of Beauty (mm. 1–48) and the Beast (mm. 49–105) and a subsequent section that presents a troubled interaction between Beauty and the Beast (mm. 106–145) and then the Beast’s ultimate transformation (146–end).(48) The tonal realization of this narrative is dependent in part upon the tonal grounding produced by anchor structures and their interplay with symmetrical scales. The F major of Beauty’s opening material is quite delicate; not only is the material presented in F Lydian (the only consonant mode of the diatonic scale without a potential |10|-anchored dominant), but also, the opening melody avoids any two-note anchor structures over in the bass (Example 33a). |10|-anchored chords over are introduced finally in mm. 10 and 12, and precipitate a circle-of-fifths progression with |10|-anchored chords in mm. 13–23. The increase in tonal propulsion brings with it enticing and exotic whole-tone sonorities, namely the resolution-delaying tritone-substitute chords in mm. 18 and 20 and the echo thereof in m. 22.(49)
Example 33. Use of anchor structures to resolve the relationship between Beauty
and the Beast in Ravel, “Les entretiens de la Belle et de la Bête”
33a. Beauty’s theme; weakly anchored F-Lydian melody followed by |10|-anchored circle of fifths (click to enlarge) 33c. failed union of Beauty and the Beast; |10|-anchored chords indicated with arrows (click to enlarge) | 33b. Beast’s theme; use of symmetric scales and eschewal of tonal plausibilities (click to enlarge) 33d. anchor structures tonally resolve the Beast’s melody and symmetrical scales (click to enlarge) |
[36] These whole-tone sonorities foreshadow the use of symmetric scales in the Beast’s theme (Example 33b). While Example 20 demonstrated how tonally functional chords can derived from symmetrical scales, in this instance those potentials are not realized; the plausible |10|-anchored chords here do not progress in tonal fashion. This is also true when Beauty’s initial theme is superimposed over the Beast’s bass line in mm. 106–127 (Example 33c). Nearly every bar features ro-interval |10| above the bass and could plausibly participate in root motion down by fifth, but only the chord in m. 120 does so. In its sensitivity to these voicings, the anchor-structure model provides grounds for reading the passage’s effect not just as one of general ambiguity, but as one of frustrated desire. The passage can perhaps be understood as depicting the Beast’s failed proposal from the central line of the epigraph: the Beast’s musical material aspires to become tonally functional and so creates a host of tonally plausible chords, but those chords are ultimately unable to provide the tonal grounding that Beauty’s theme desires.
[37] Since the Beast is unable, in his original state, to satisfy Beauty’s latent desire and to provide her with tonal grounding, it falls instead to Beauty to transform the Beast with her profession of love. This is accomplished by using anchor structures to render the Beast’s material tonal. The Beast’s bass line is put in the upper voice at m. 147, and its
Example 34. Poulenc, Trois pièces pour piano, Pastorale, mm. 1–2
(click to enlarge)
[38] The anchor-structure model’s sensitivity to a range of tonal plausibilities, and to the subtle effect that shifts in voicing can have on those plausibilities, can also help construct a reading of the Pastorale from Poulenc’s Trois pièces pour piano. The piece opens with a mysterious sonority (Example 34) packed with conflicting potentials. The initial arpeggio C2–
Example 35. Exploration of the tonal potential of the opening chord in Poulenc, Trois pièces pour piano, Pastorale
35a. opening section casts C-rooted offspring of the chord as iiø7 in
(click to enlarge)
35b. middle section casts C-rooted chords as viiø7 in
(click to enlarge)
35c. final section emphasizes the ambiguous and unresolved nature of the chord
(click to enlarge)
[39] The appearances of this mysterious chord divide the piece into three sections: mm. 1–10, mm. 11–28, and mm. 29–35. Each of the sections makes a distinct attempt to tease out some of the potentials of the opening chord. The first section is shown as Example 35a. Measure 3 replaces the E and D of the whole-tone chord with
[40] The second section (Example 35b), which begins with a verbatim restatement of the opening bar, explores other tonal contexts for the C-rooted tonal plausibility of the mysterious chord. In m. 12 the chord is again transformed into a C half-diminished seventh chord, and m. 12 reprises the C–
[41] This way of utilizing a C-rooted chord is left behind in m. 15, which undermines the key of
[42] The third portion of the piece (Example 35c) embraces the ambiguity of the mysterious chord rather than attempting to tame it via transformation. The appearances of the chord in mm. 29–30 are altered to emphasize the chord’s whole-tone makeup:
[43] Voicing and additive harmony are topics on the margins of theories of harmony; conventional models of harmony privilege chord inversion, reduction, and deeper levels of tonal structure over surface details. This essay, though, has hopefully demonstrated not only how powerful a voicing-based model for additive harmony can be but also how the seemingly small, surface-detail topics of voicing and additive harmony relate to larger music-theoretical issues. For one, the anchor-structure model touches on how musical practices can relate to and be informed by our psychoacoustic apparatus. The strain of experimental research referenced in this article suggests that listeners are highly sensitive to voicing and other surface details. Many of the mechanisms of conventional theory, though, rely on concepts (such as interval class) that operate at a level of remove from the musical surface. The anchor-structure model bypasses much of that abstraction, and makes use of our fundamental cognitive processes—e.g. our ability to recognize acoustically salient intervals, or our sensitivity to the roughness of ro-interval 1—to describe how listeners interact with additive-harmonic surfaces. A good portion of the resultant pragmatic, figured-bass approach may be based on common sense, but it is common sense that is often either left unsaid or obscured by underdeveloped, back-of-the-book models of additive harmony. The anchor-structure model also engages with the methodological premise that one of the aims of music theory is to describe how musical structures relate to shared cultural assumptions between audiences and producers (Gjerdingen 2007, 16–19). Chord structure in the anchor-structure model is conceived of as a set of stylistic constraints that allowed novel chords to assimilate into the common-practice structures with which Parisian audiences of the time would have been familiar. To close, I will suggest that the anchor-structure model adds a new dimension to our understanding of the development of tonal language in the late nineteenth and early twentieth centuries. The most common narrative of that era is of how adherence to certain common-practice voice-leading principles allowed for the incorporation of new harmonic successions into tonal contexts. The anchor-structure model enables the development of additive harmony to be read in parallel fashion: it is adherence to certain vertical-domain common-practice principles—skeletal voicings derived from common-practice chords and generalized principles of pitch combination—that made the incorporation of new chords into tonal contexts possible.
Damian J. Blättler
Rice University
Shepherd School of Music
1408 Wichita St.
Houston, TX 77004
damian.blattler@rice.edu
Works Cited
Aldwell, Edward, and Carl Schachter. 2003. Harmony and Voice Leading, 3rd ed. Wadsworth.
Baker, James. 1990. “The Limits of Tonality in the Late Music of Franz Liszt.” Journal of Music Theory 34 (2): 145–73.
Bass, Richard. 1996. “From Gretchen to Tristan: The Changing Role of Harmonic Sequences in the Nineteenth Century.” 19th-Century Music 19 (1): 263–85.
—————. 2001. “Half-Diminished Functions and Transformations in Late Romantic Music.” Music Theory Spectrum 23 (1): 41–60.
Baur, Steven. 1999. “Ravel’s ‘Russian’ Period: Octatonicism in His Early Works, 1893–1908.” Journal of the American Musicological Society 52 (3): 531–92.
Benjamin, Thomas, Michael Horvit, and Robert Nelson. 2003. Techniques and Materials of Tonal Music: From the Common Practice Period to the Twentieth Century, 6th ed. Thomson-Wadsworth.
Bharucha, Jamshed J. 1996. “Melodic Anchoring.” Music Perception 13 (2): 383–400.
Brown, Matthew. 1993. “Tonality and Form in Debussy’s Prélude à ‘L’Après-midi d’un faune.’” Music Theory Spectrum 15 (2): 127–43.
Caron, Sylvain. 2002. “Tonal composition and New Perspectives on Fauré’s Harmony.” Canadian University Music Review 22 (2): 48-76.
Chailley, Jacques. 1986. Historical Treatise of Harmonic Analysis, trans. S. Kleinman. Alphonse Leduc.
Chapman, Alan. 1981. “Some Intervallic Aspects of Pitch-Class Set Relations.” Journal of Music Theory 25 (2): 275–90.
Chong, Eddy Kwong Mei. 2002. “Extending Schenker’s ‘Neue musikalische Theorien und Phantasien’: Towards a Schenkerian Model for the Analysis of Ravel’s Music.” PhD diss., Eastman School of Music.
Clough, John. 1979. “Aspects of Diatonic Sets.” Journal of Music Theory 23 (1): 45–61.
Cooke, Norman, and Takashi X. Fujisawa. 2006. “The Psychophysics of Harmony Perception: Harmony is a Three-Tone Phenomenon.” Empirical Musicology Review 1 (2): 106–26.
Cooper, Martin. 1951. French Music: From the Death of Berlioz to the Death of Fauré. Oxford University Press.
Dallin, Leon. 1957. Techniques of Twentieth Century Composition. Wm. C. Brown.
Day-O’Connell, Jeremy. 2007. Pentatonicism from the Eighteenth Century to Debussy. University of Rochester Press.
—————. 2009. “Debussy, Pentatonicism, and the Tonal Tradition.” Music Theory Spectrum 31 (2): 225–61.
Forte, Allen. 1979. Tonal Harmony in Concept and Practice, 3rd ed. Holt, Rinehart and Winston.
—————. 1991. “Debussy and the Octatonic.” Music Analysis 10 (1/2): 125–69.
Gauldin, Robert. 2004. Harmonic Practice in Tonal Music, 2nd ed. W.W. Norton.
Gjerdingen, Robert. 2007. Music in the Galant Style. Oxford University Press.
Green, Douglass M. 1992. “Review of The Music of Claude Debussy by Richard S. Parks.” Music Theory Spectrum 14 (2): 214–22.
Harris, Simon. 1990. A Proposed Classification of Chords in Early Twentieth-Century Music. Garland.
Harrison, Daniel. 1991. “Max Reger’s Motivic Technique: Harmonic Innovations at the Borders of Atonality.” Journal of Music Theory 35 (1/2): 61–92.
—————. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of its Precedents. University of Chicago Press.
—————. 2016. Pieces of Tradition: An Analysis of Contemporary Tonal Music. Oxford University Press.
Hasegawa, Robert. 2011. “An Acoustic Model for Chord Voicings in Post-Tonal Music.” Paper presented at the Biennial Meeting of the Society for Music Perception and Cognition, Rochester, NY.
Hatten, Robert S. 1994. Musical Meaning in Beethoven: Markedness, Correlation, and Interpretation. Indiana University Press.
Hindemith, Paul. 1942. The Craft of Musical Composition: Book 1 – Theoretical Part, trans. Arthur Mendel. Schott and Co.
Hofman-Engl, Ludger. 2006. “Virtual Pitch and Pitch Salience in Contemporary Composing.” Chameleon Group. http://www.chameleongroup.org.uk/research/virtual_pitch.pdf
Hull, A. Eaglefield. 1915. Modern Harmony: Its Explication and Application. Augener.
Huron, David, and Peter Sellner. 1992. “Critical Bands and the Spelling of Vertical Sonorities.” Music Perception 10 (2): 129–49.
—————. 1994. “Interval-Class Content in Equally-Tempered Pitch-Class Sets: Common Scales Exhibit Optimum Tonal Consonance.” Music Perception 11 (3): 289–305.
Hyde, Martha M. 1996. “Neoclassic and Anachronistic Impulses in Twentieth-Century Music.” Music Theory Spectrum 18 (2): 200–35.
Johnson, Graham, and Richard Stokes. 2000. A French Song Companion. Oxford University Press.
Kaminsky, Peter. 2003. “Composers’ Words, Theorists’ Analyses, Ravel’s Music: Sometimes the Twain Shall Meet.” College Music Symposium 43: 161–77.
—————. 2004. “Ravel’s Late Music and the Problem of ‘Polytonality.’” Music Theory Spectrum 26 (2): 237–64.
—————. 2008. “Ravel’s Programmatic Impulse.” Zeitschrift der Gesellschaft für Musiktheorie 5 (1): 31–50.
Katz, Adele. 1945. Challenge to Musical Tradition. Alfred A. Knopf.
Kielian-Gilbert, Marianne. 1990. “The Functional Differentiation of Harmonic and Transpositional Patterns in Liszt’s Consolation No. 4.” 19th-Century Music 14 (1): 48–59.
Kimball, Carol and Roger Waters, eds. 1995. The French Song Anthology – High Voice. Hal Leonard.
Kopp, David. 1997. “Pentatonic Organization in Two Piano Pieces by Debussy.” Journal of Music Theory 41 (2): 261–87.
Kostka, Stefan. 1989. Materials and Techniques of Twentieth Century Music. Prentice Hall College Division.
Kostka, Stefan, and Dorothy Payne. 2000. Tonal Harmony, with an Introduction to Twentieth-Century Music, 4th ed. McGraw-Hill.
Larson, Steve. 2002. “Musical Forces, Melodic Expectation, and Jazz Melody.” Music Perception 19 (3): 351–85.
Lenormand, René. 1915. A Study of Modern Harmony, trans. Herbert Antcliffe. Joseph Williams, Ltd.
Lester, Joel. 1970. “A Theory of Atonal Prolongation as Used in an Analysis for the Serenade, Op. 24 by Arnold Schoenberg.” PhD diss., Princeton University.
Lewin, David. 1987. “On the ‘Ninth-Chord in Fourth Inversion’ from Verklärte Nacht.” Journal of the Arnold Schönberg Institute 10 (1): 45–64.
—————. 1993. “A Transformational Basis for Form and Prolongation in Debussy’s ‘Feux d’artifice.’” In Musical Form and Transformation, 97–159. Yale University Press.
Levine, Mark. 1989. The Jazz Piano Book. Sher Music.
London, Justin. 2004. Hearing in Time: Psychological Aspects of Musical Meter. Oxford University Press.
Morgan, Robert. 1976. “Dissonant Prolongation: Theoretical and Compositional Precedents.” Journal of Music Theory 20 (1): 49–91.
Mashinter, Keith. 2006. “Calculating Sensory Dissonance: Some Discrepancies Arising from Models of Kameoka and Kuriyagawa, and Hutchinson and Knopoff.” Empirical Musicology Review 1 (2): 65–84.
McFarland, Mark. 2005. “Transpositional Combination and Aggregate Formation in Debussy.” Music Theory Spectrum 27 (2005): 187–220.
McGowan, John James. 2005. “Dynamic Consonance in Selected Piano Performances of Tonal Jazz.” PhD diss., Eastman School of Music.
—————. 2011. “Psychoacoustic Foundations of Contextual Harmonic Stability in Jazz Piano Voicings.” Journal of Jazz Studies 7 (2): 156–191.
Minturn, Neil. 1997. The Music of Sergei Prokofiev. Yale University Press.
Morris, Robert. 1995. “Equivalence and Similarity in Pitch and their Interaction with Pc-Set Theory. Jounal of Music Theory 39 (2): 207–43.
Navien, Charles Francis. 1982. “The Harmonic Language of L’horizon chimérique by Gabriel Fauré.” PhD diss., University of Connecticut.
Ottman, Robert W. 2000. Advanced Harmony: Theory and Practice, 5th ed. Prentice Hall.
Parks, Richard S. 1980. “Pitch Organization in Debussy: Unordered Sets in ‘Brouillards.’” Music Theory Spectrum 2: 119–34.
—————. 1985. “Tonal Analogues as Atonal Resources and Their Relation to Form in Debussy’s Chromatic Etude.” Journal of Music Theory 29 (1): 33–60.
—————. 1990. The Music of Claude Debussy. Yale University Press.
Parncutt, Richard. 1988. “Revision of Terhardt’s Psychoacoustical Model of the Root(s) of a Musical Chord.” Music Perception 6 (1): 65–94.
—————. 1997. “A Model of the Perceptual Root(s) of a Chord Accounting for Voicing and Prevailing Tonality.” In Music, Gestalt, and Computing: Studies in Cognitive and Systematic Musicology, ed. Marc Leman, 181–99. Springer-Verlag.
Persichetti, Vincent. 1961. Twentieth-Century Harmony. W.W. Norton.
Phillips, Edward R. 1993. “Smoke, Mirrors, and Prisms: Tonal Contradiction in Fauré.” Music Analysis 12 (1): 3–24.
Piston, Walter. 1978. Harmony, 4th ed., rev. Mark DeVoto. W.W. Norton and Company.
Pomeroy, Boyd. 2004. “Tales of Two Tonics: Directional Tonality in Debussy’s Orchestral Music.” Music Theory Spectrum 26 (1): 87–118
Ravel, Maurice. 1995. Mother Goose: 5 Children’s Pieces. Transcribed for solo piano by Lawrence Rosen. Hal Leonard.
Roig-Francolí, Miguel A. 2003. Harmony in Context. McGraw-Hill.
Russ, Michael. 1993. “Review of Skryabin and Stravinsky, 1908-1914: Studies in Theory and Analysis by Anthony Pople and A Proposed Classification of Chords in Early Twentieth-Century Music by Simon Harris.” Music and Letters 74 (2): 325.
Salzer, Felix. 1952. Structural Hearing: Tonal Coherence in Music. C. Boni.
Samplaski, Arthur G. 1999. “A Comparison of Perceived Chord Similarity and Predictions of Selected Twentieth-Century Chord-Classification Schemes, Using Multidimensional Scaling and Clustering Techniques.” PhD diss., Indiana University.
Samson, Jim. 1977. Music in Transition: A Study of Tonal Expansion and Atonality, 1900–1920. W.W. Norton.
Santa, Matthew. 2000. “Analyzing Post-Tonal Music: A Modulo-7 Perspective.” Music Analysis 19 (2): 167–201.
Silberman, Peter. 2007. “Analyzing Tonal Embellishment in Post-Tonal Music.” Paper presented at the annual meeting of the West Coast Conference of Music Theory and Analysis, Salt Lake City, UT.
Smith, Charles. 1986. “The Functional Extravagance of Chromatic Chords.” Music Theory Spectrum 8: 94–139.
Sobaskie, James. 2003. “The Emergence of Gabriel Fauré’s Late Musical Style and Technique.” Journal of Musicological Research 22 (3): 223–76.
Somer, Avo. 1995. “Chromatic Third-Relations and Tonal Structure in the Songs of Debussy.” Music Theory Spectrum 17 (2): 215–41.
—————. 2005. “Musical Syntax in the Sonatas of Debussy: Phrase Structure and Formal Function.” Music Theory Spectrum 27 (1): 67–96.
Spencer, Peter. 2003. The Practice of Harmony, 5th ed. Prentice Hall.
Steinke, Greg A. 1999. Bridge to Twentieth-Century Music: A Programed Course, rev. ed. Allyn and Bacon.
Straus, Joseph. 1987. “The Problem of Prolongation in Post-Tonal Music.” Journal of Music Theory 31 (1): 1–21.
Swinden, Kevin. 2005. “When Functions Collide: Aspects of Plural Function in Chromatic Music.” Music Theory Spectrum 27 (2): 249–82.
Taruskin, Richard. 2005. The Oxford History of Western Music. Oxford University Press.
Tymoczko, Dmitri. 1997. “The Consecutive-Semitone Constraint on Scalar Structure: A Link between Impressionism and Jazz.” Intégral 11: 135–79.
—————. 2002. “Stravinsky and the Octatonic: A Reconsideration.” Music Theory Spectrum 24 (1): 68–102.
—————. 2004. “Scale Networks and Debussy.” Journal of Music Theory 48 (2): 219–94.
—————. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. Oxford University Press.
Ulehla, Ludmila. 1966. Contemporary Harmony: Romanticism through the Twelve-Tone Row. The Free Press.
Väisälä, Olli. 1999. “Concepts of Harmony and Prolongation in Schoenberg’s Op. 19/2.” Music Theory Spectrum 21 (2): 207–83.
—————. 2002. “Prolongation of Harmonies Related to the Harmonic Series in Early Post-Tonal Music.” Journal of Music Theory 46 (1/2): 207–83.
Vos, Joos. 2006. “Commentary on ‘Calculating Sensory Dissonance: Some Discrepancies Arising from Models of Kameoka and Kuriyagawa, and Hutchinson and Knopoff’ by Keith Mashinter.” Empirical Musicology Review 1 (3): 180–81.
van der Bliek, Rob. 2007. “The Hendrix Chord: Blues, Flexible Pitch Relationships, and Self-Standing Harmony.” Popular Music 26 (2): 343–64.
Yeary, Mark Jerome. 2011. “Perception, Pitch, and Musical Chords.” PhD diss., University of Chicago.
Footnotes
1. The term “additive harmony” is adapted from Day-O’Connell 2007, 147. For a delineation of the different levels of specificity implied by the terms pitch-class root, functional harmony, and Roman-numeral harmony, see Harrison 2016, 102.
Return to text
2. For the purposes of this study, the 1889 Exposition Universelle, an event that capped the rehabilitation of French national pride after the humiliation of the Franco-Prussian War, can serve as a symbolic start date; it is around this time that Debussy and other composers of his generation started to differentiate their style from German music and the “Germanized” French music of Franck and his contemporaries. The additive-harmonic innovations of this generation were taken up by subsequent generations of French composers as well as foreign-born composers who wrote for Parisian audiences (e.g. Stravinsky, Martinů, and Prokofiev at various points in their careers). Additive-harmonic practice developed as a relatively cohesive practice up until the German occupation of France during World War II (1940), after which the European compositional mainstream turned more comprehensively toward atonal and serial composition. Since this repertoire’s focus on the sensuous potential of novel chords participates in French modernism’s general privileging of pleasure and beauty over passion and the sublime, and in order to avoid confusing that music written by French composers during 1889–1940 with the overlapping-but-not-coterminous set of music written for French audiences at the same time (with the majority of notable composers of the period working in Paris), I shall refer to this repertoire as the Parisian modernist repertoire. For a more detailed discussion see Cooper 1951, 18–21 and 34–77; Samson 1977, 34–35; and Taruskin 2005, 59–72.
Return to text
3. The majority of this work involves Schenkerian procedures and focuses on the chromatic German repertoire of the time period. This literature is too large to fully outline here; important studies include Baker 1990, Bass 1996 and 2001, Harrison 1991, Kielian-Gilbert 1990, Morgan 1976, and Smith 1986. Studies that have applied these techniques to the Parisian modernist repertoire that is my focus include Brown 1993, Caron 2002, Chong 2002, Katz 1945, Navien 1982, Phillips 1993, Pomeroy 2004, Salzer 1952, Samson 1977, Sobaskie 2003, Somer 1995, and Somer 2005.
Return to text
4. The vanguard scholarship in this area was done by Richard S. Parks (1980, 1985, 1990). Believing traditional tonal theory to be an inadequate tool for analyzing Debussy’s works, Parks instead makes use of an adapted form of Allen Forte’s pitch-class set theory; deep structure in Debussy’s music—the generator of its surface detail—is conceived of as recurring pitch collections and scales. Another study examining abstracted pitch-class collections in Debussy’s music is McFarland 2005. Many of the nexus set classes found by Parks (such as 5-35, 6-35, and 8-28) are also common scales, and it is this thread of Parks’ work that has been the most influential. Studies that deal with scales in Parisian modernist repertoire include Baur 1999, Day-O’Connell 2007 and 2009, Forte 1991, Kopp 1997, Lewin 1993, and Tymoczko 1997, 2002, and 2004.
Return to text
5. The case for retaining a focus on tonal structures in analysis of Debussy’s music in particular is made by Avo Somer and Douglass M. Green. Somer writes that “Despite pervasive and often radical chromaticism that may well demand a fresh evaluation of its tonal coherence, Debussy's musical language can be fully understood only in the light of its allegiance to tonal centricity and its transformations of classical harmonic practices” (1995, 215); Green more simply states that “How Debussy’s music is perceived is a knotty problem that is not helped by ignoring tonal associations in his works” (1992, 217).
Return to text
6. Textbooks that discuss additive harmony (however briefly) using the extended-triad model include Aldwell and Schachter 2003, Benjamin, Horvit, and Nelson 2003, Dallin 1957, Forte 1979, Gauldin 2004, Kostka 1989, Kostka and Payne 2000, Ottman 2000, Persichetti 1961, Piston 1978, Roig-Francolí 2003, Spencer 2003, Steinke 1999, and Ulehla 1966.
Return to text
7. Robert Hasegawa has also explored this phenomenon on acoustic grounds, stating that “[complex harmonies] are more ambiguous in their root implications, and thus more sensitive to changes in voicing” (2011, 5).
Return to text
8. The language of functional bases and agents is taken from Harrison 1994. Functional bases are scale degrees , , and as they relate to a tonal center as distilled expressions of tonic, subdominant, and dominant function, and functional agents those scale degrees that can express only a single function: for tonic, for subdominant, and for dominant (45–50). Swinden 2005 discusses functionally mixed chords in terms of local voice-leading motions, focusing generally on nineteenth-century Germanic repertoire.
Return to text
9. The case that the mechanical stacking of pitch-classes in thirds is insufficient for determining a chord’s root is also made in Tymoczko 2011, 169–70.
Return to text
10. The concept of anchor structures is an extrapolation of Ulehla’s discussion of how “Any combination of intervals can be mounted upon a low perfect fifth. It can be likened to an anchor grabbing the sands of tonality” (1966, 383). Ulehla’s discussion is limited to perfect fifths directly above low bass notes, with no pitches between the bass and the fifth; a similar discussion is found in Chailley 1986, 77. The term “anchor” is meant to refer to the nautical tool, not the psychological concept of anchoring, which describes how people have a cognitive bias in favor of initial pieces of information when making subsequent decisions; this latter concept is used in a music-theoretical context in Bharucha 1996.
Return to text
11. The term “tonal plausibility” is an adaptation of the term “syntactic plausibility” from Lewin 1987. Lewin’s article discusses the controversy surrounding the banning of a performance of Verklärte Nacht by a concert society because it contains a fourth-inversion Ab ninth chord. Schoenberg took great pains to justify the chord’s use, but Lewin argues that Schoenberg’s line of defense is misguided, and that the chord in question is more syntactically plausible either as a German 6th with added
Return to text
12. This is in line with Mark Jerome Yeary’s research indicating that “highly familiar sonorities are likely to form a kind of model or exemplar by which other, less familiar sonorities are judged” (2011, 54).
Return to text
13. This process is perhaps analogous to the process of entrainment in Justin London’s theory of meter. In London’s theory, when a listener confronts a set of heard durations, the listener’s mind entrains to them and filters them through a set of coherent metrical patterns (2004, 9–16). In the anchor-structure model of the listening process, the listener confronts new chords and filters them through a set of coherent common-practice chordal frameworks.
Return to text
14. The term registrally ordered interval is taken from Väisälä 1999 and 2002. Shortened to “ro-interval,” a registrally ordered interval is an equivalence class in which an interval and its inversion are not considered equivalent, but a simple interval and a compound version of that same interval are. Ro-intervals are measured in semitones, not scale steps. When used exclusively above the bass, ro-intervals are chromatic figured bass numbers (1995, 218–21).
Return to text
15. The most common exception to this last point is the supertonic seventh chord in first inversion. The point can be sustained, however, if this chord is considered instead to be a subdominant major triad with added sixth; this reading harks back to Rameau, with the tendency of to resolve to in the standard progression to V explained not as the essential dissonance of a seventh chord resolving downwards, but as a move necessary to avoid parallel fifths when the bass moves up to .
Return to text
16. One reason for the relative strength of ro-interval 10’s seventh-chord connotation (in comparison with its augmented-sixth-chord connotation) is the simple fact that seventh chords are more common than augmented-sixth chords. It further speaks to the relative strength of this connotation that, in the pairing of keys a half step apart via enharmonic reinterpretation, it is more common to first reinterpret an augmented-sixth chord as a dominant-seventh chord, moving to a key a half step above the initial one, than it is to first reinterpret a dominant-seventh chord as an augmented-sixth chord and therefore move to a key a half step below (in part because stepwise modulations upward are far more common than stepwise modulations downward); without prior warning, it is easier to reinterpret an augmented-sixth chord as a dominant-seventh chord than the other way around.
Return to text
17. Additive harmonies in this paper are labeled with the ro-intervals above the bass in ascending order, forming what Alan Chapman has termed an AB (above bass) set (1981, 276–77). Were these numbers arranged in order from smallest to largest, they would be one of Robert Morris’ FB (figured-bass) classes (1995, 218–21). While labeling the additive chords as AB sets rather than as FB classes is a slight hindrance when comparing two verticalities’ FB classes, it maintains ro-interval content within the upper voices of the chord, something that will be important in later discussions of voicing restrictions. Preserving the ordering of upper voices also brings the model in line with Arthur Samplaski’s finding that the ordering of adjacent pitches plays a large role in listener judgments of chord similarity (1999, 217).
Return to text
18. Despite Milhaud’s fondness for polytonal effects in general and in the Saudades do Brasil in particular, this chord is interpreted as an additive dominant of C rather than as
Return to text
19. Ro-interval 5’s usage as seventh and third of a minor-seventh chord in third inversion cannot be reconceptualized as a chord of the added sixth (as with ro-interval 7’s potential interpretation as third and seventh of the supertonic seventh chord in first inversion), since such chords are not used in second inversion.
Return to text
20. There is no conflict between anchor structures that reference the same common-practice progenitor, e.g. between ro-interval 7 and ro-intervals 10 or 11, since the fifth is generally a component of the common-practice seventh chords for which the 10- and 11-anchored chords are stand-ins. When both ro-interval 7 and either 10 or 11 are present, the analytic preference is to highlight the larger ro-interval as the anchor structure, as its presence generally makes ro-interval 7 omissible.
Return to text
21. Simon Harris has formulated a similar definition of chord, and notes its necessary malleability: “[a chord is] a collection of notes that seems to form a unit of simultaneous sounds—with all the difficulties and possible disagreements inherent in a such a subjective definition” (1990, 87).
Return to text
22. Proscriptions against minor ninths appear, often implicitly, in certain jazz theory texts (a tradition heavily concerned with the codification of additive harmony). For instance, the avoidance of half steps guides discussion of “upper structure chords” in Levine 1989. An upper-structure chord is formed by taking the tritone of a dominant seventh chord and then superimposing a triad atop it; the chords are labeled by the relationship of the upper triad to the absent root of the tritone’s dominant seventh. Levine lists nine possible upper-structure chords; although he never explicitly states it, the upper triads left off of that list (
Return to text
23. The composer whose body of work is an exception to this seems to be Prokofiev (who lived and worked in Paris from 1920 to 1936); Neil Minturn notes Prokofiev’s frequent tonal use of [0148] and [0347] pitch-class sets (1997, 61 and 209).
Return to text
24. An intriguing tabulation of all the possible ways of filling in a minor ninth with “chording intervals” (gaps of i[3], i[4], or i[5] between pitches), ranked from “hottest and spiciest to the most lightly flavored,” can be found in Harrison 2016, 60–61. The purview of Harrison’s book is the vast landscape of 20th- and 21st-century tonal practice (rather than the specific tonal passages of the Parisian modernist repertoire that are the focus of this study), and he does not discuss the individual chords’ potential tonal uses. The chords with minor 9ths that are most common in the Parisian modernist repertoire are all on the “spicier”/higher-tension side of the table, because Harrison’s ranking is predicated in part on the presence or absence of ic2 and ic6 dissonances; also, minor ninths might most easily serve as an extra layer of tension added to an already fraught chord, rather than as the lone jarringly sharp element in an otherwise stable chord.
Return to text
25. Acoustic roughness and listener judgments about dissonance and consonance are not always equivalent; Mashinter has shown that listeners rank the dyad C–B as more dissonant than the more frequently heard and “prettier” yet inherently acoustically rougher tetrad C–E–G–B (2006, 66).
Return to text
26. Huron’s study, and the others discussed in this paragraph, investigate the effects of the minor 2nd specifically, and not ro-interval 1 (an equivalence class comprising the minor second, the minor ninth, and further octave expansions). In the minor 9th, the acoustic roughness does not occur between the fundamentals of its two pitches as in the minor 2nd, but between the octave overtones of the lower pitch and the fundamental of the upper pitch; the acoustic roughness is weaker, but still pronounced.
Return to text
27. The translation is from Johnson and Stokes 2000, 71–72.
Return to text
28. Evidence that these chords were unusual for this repertoire is that Chabrier’s publisher requested the song’s dissonances be removed so as to make the song more palatable for (i.e., marketable to) amateur musicians (Kimball and Waters 1995, ix).
Return to text
29. A categorization of special cases in which the bass pitch alone does dictate a sense of chord root can be found in Harrison 2016, 111–12.
Return to text
30. The potential for the melody to skip from B4 to G4 on the last beat of the bar, rather than descend scalarly as it does, has been established in mm. 1 and 3.
Return to text
31. “The borderline between the small, ‘stepwise,’ and the larger intervals is, naturally, flexible and may vary according to the context” (Väisälä 1999, 236).
Return to text
32. Discussion of pentatonically generated additive harmony in La mer can be found in Day-O’Connell 2009, 241–45.
Return to text
33. In contrasting this repertoire to the saturated chromaticism of the Germanic school (Wagner, Strauss, and early Schoenberg), Dmitri Tymoczko writes that “composers like Rimsky-Korsakov, Debussy, and Ravel preserved a more conventional understanding of the relation between chord and scale, but with a significantly expanded musical vocabulary” (2004, 220).
Return to text
34. This constraint need only apply to consecutive whole steps, since consecutive semitones are not found in any of the common scales used in the Parisian modernist repertoire (Tymoczko 1997, 142), and the combination of a whole step and a half step or of two half steps is covered by the ro-interval 1 constraint.
Return to text
35. The first act of Debussy’s Pelléas et Mélisande (1902) and Charles Koechlin’s song “L’eau” (1899) also both end with chordally voiced pentatonic scales.
Return to text
36. For an alternative formulation of the vertical spacing requirements necessary for a chord, see Harrison 2016, 104–6.
Return to text
37. The analytic use of diatonic or mod7 set-classes is modeled on that in Santa 2000; the concept of the diatonic pitch-class set originates in Clough 1979.
Return to text
38. This chord resolves the piece’s tension between the keys of
Return to text
39. For a detailed discussion of the progression in mm. 1–2, see Kaminsky 2003, 163–64.
Return to text
40. A particularly wide range of chord types is presented in Steinke 1999: extended tertian chords, chords with added tones, chords with chromatic added tones (including chords with split members), polychords, clusters, pentatonic chords, whole-tone chords, and chords in fourths and fifths (197–232). An intriguing, idiosyncratic set of categories is found in Harrison 2016: discussing only tonic chords, Harrison distinguishes between articulated overtonal tonics (tonic chords with a clear division between triad and supplement; this category contains colored tonics, polychords, and chords with root representatives) and integrated overtonal tonics, in which it is hard to tease out the superfluous element (107–19).
Return to text
41. For a reduction that highlights the registral transfer of stepwise descending lines in this passage, see Hyde 1996, 209. The ability of two-note anchor structures to accommodate a range of adornments also allows for Ravel’s gambit of reharmonizing a fixed melody in a different tonal center; this happens in the first movement of the String Quartet, in the third of the Valses nobles et sentimentales, and for portions of a melody in Menuet sur le nom d’Haydn (1909), À la manière de . . . Borodine (1913) and the “Rigaudon” from Le tombeau de Couperin.
Return to text
42. See also Ottman 2000, 292. An acoustic basis for extended triads is occasionally argued for because beyond the (major) triad, the new pitches that appear in the overtone series arrive in a stack-of-thirds order: the 6th partial forms the (out-of-tune) interval of a compound minor 7th above the fundamental, the 8th partial forms a compound major 9th, the 10th partial forms a compound augmented 11th, and the 12th partial forms a compound major 13th. See Lenormand 1915, 7; Hull 1915, 94; and Ulehla 1966, 59; for discussion of the use of the overtone series in the jazz-theory tradition, see McGowan 2011, 169–73.
Return to text
43. Aldwell and Schachter interpret chords like the one in Example 27b as V\(\substack{7\\4}\) chords, i.e. V7 chords with an unresolved 4th: “[4ths and 6ths] will normally resolve to 3rds and 5ths . . . Sometimes, especially in nineteenth-century music, such dissonances are left unresolved, the resolutions being supplied mentally by the listener” (2003, 481). While the V\(\substack{7\\4}\) labeling works well in common-practice contexts, the case against relying on imagined resolutions for the explanation of twentieth-century harmonies is made by Paul Hindemith: “To explain the foregoing simple succession of three-tone chords, which is certainly not at all startling today, the academic theory of harmony has to employ the strangest devices. It may call them appoggiatura-chords or suspension-chords. But here it forgets that an essential part of the appoggiatura or suspension effect is resolution. As long as only the ‘dissonant’ chord is present, and not its resolution, the conditions of an appoggiatura are not fulfilled, and the chords must be looked upon as independent entities” (1942, 90–91).
Return to text
44. Similarly, the sharp dividing line between chord intervals and voice-leading intervals is also necessarily more context-dependent in additive-harmonic textures than in common-practice ones, as was highlighted in the discussion of the voicing restriction on adjacent whole tones in paragraphs [23]–[25].
Return to text
45. Leon Dallin goes so far as to claim that this melodic mimicry is the only way nonchord tones can be perceived in dissonant textures: “No clear distinction is possible when every conceivable dissonance is permissible within the harmony. Notes are perceived as being nonharmonic in modern music only when their resemblance to one of the familiar categories [of nonharmonic tones] is obvious” (1957, 146).
Return to text
46. The concept of contexual stability conditions is imported and adapted from Silberman 2007, which defines “tonal embellishment” as the stepwise resolution of a pitch or pitch-class from a less stable context into a more stable one (allowing for intervals larger than ic2 to be considered steps, should a passage feature consistent use of a gapped collection such as the pentatonic scale), and gives four conditions that project a chord as being contextually stable: chord A is more stable than chord B if chord A is (1) more consonant/less dissonant than chord B; (2) more frequently found at the beginning and/or end of formal units; (3) more salient in a domain other than consonance/dissonance and formal position (e.g. non-pitch characteristics, or through parallelism with other stable events); or (4) suggestive of a common-practice chord that would be stable in a common-practice context (the “tonal mimicry” condition).
Return to text
47. All musical examples from “Les entretiens” are from the version transcribed for solo piano by Lawrence Rosen (Milwaukee, WI, Hal Leonard, 1995).
Return to text
48. For a more involved discussion of the piece’s form and program, see Kaminsky 2008, 33–44.
Return to text
49. Kaminsky reads these chords as an expression of the Beauty’s subconscious desire for union with the Beast (2008, 39).
Return to text
50. The pitches in m. 28 also fit within the octatonic0,1 scale of the previous six beats; the whole-tone downbeat of m. 28 is one of the two whole-tone tetrads present in octatonic0,1.
Return to text
Copyright Statement
Copyright © 2017 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
22418