Pentatonic Xuangong 旋宮 Transformations in Chinese Music
Nathan L. Lam
KEYWORDS: Chinese modal theory, pentatonic scale, xuangong, transformational theory, Ren Guang, Joseph Koo Kar-Fai, Zhu Zaiyu, Tan Dun, Bright Sheng
ABSTRACT: The anhemitonic pentatonic scale is fundamental to Chinese music theory, and so is the concept of xuangong: transformations from one pentatonic scale to another. The vocabulary related to these transformations is as diverse as the musical contexts in which it appears; similar moves can be described using a multitude of perspectives, resulting in overlapping and, at times, confusing terminology. To describe xuangong transformations, I adopt the precise language of signature transformations to enrich, complement, and shed light on Chinese music theory. The four basic xuangong transformations are chromatic transposition (C, D, E, G, A → G, A, B, D, E), pentatonic transposition (C, D, E, G, A → G, A, C, D, E), bian-directed transformation (C, D, E, G, A → B, D, E, G, A), and qing-directed transformation (C, D, E, G, A → C, D, F, G, A). The last two are adapted from classical Chinese music theory, and they are analogous to key signature transformations in Western music. This paper discusses the structure of xuangong transformations, their application in Chinese music theory, and their analytical use in examples spanning Confucian court music, traditional instrumental music, Cantopop, and Chinese new music, both tonal and atonal.
DOI: 10.30535/mto.30.1.5
Copyright © 2024 Society for Music Theory
1. Introduction
[1.1] The anhemitonic pentatonic scale is fundamental to Chinese music theory, and so are the transformations from one pentatonic scale to another (Du 2019; Du and Qin 2007, 200–233). These transformations are known variously as xuangong 旋宮, modulation (zhuandiao/fandiao 轉調/犯調), or the theory of 60 modes (liushidiao 六十調).(1) The terms collectively describe modal relations involving the cycles of five pentatonic positions, of twelve chromatic pitch classes, and of their product (12 × 5 = 60). Yet, despite this structural simplicity, xuangong transformation is one of the knottiest areas of Chinese music theory. As Liu Yongfu 劉永福 describes,
對於 “旋宮轉調” 的理論表述, 歷來含混不清、令人費解。形形色色的概念 、術語, 如同層層迷霧, 遮擋著人們的 “視線”, 束縛著人們的思維, 阻礙著學科的建設, 致使 “普通人” 至今對此難以理解和認知。 (Liu 2005, 102) |
The theoretical expression of xuangong zhuandiao has always been ambiguous and puzzling. Like layers of fog, the different kinds of concepts and terms obscure “sight,” shackle thought, and hinder the field’s advancement; as a result, it is still difficult for “laypeople” to understand and comprehend. |
[1.2] Recent developments in mathematical music theory—particularly signature transformations (Hook 2008, 2023; Tymoczko 2005, 2020, 2023; Lam 2020)—have lent new theoretical and analytical perspectives to scalar collections. In the aesthetic framework of European classical music, the pentatonic scale has long been conceptualized as primitive and exotic (Lee 2020); mainstream textbooks today continue to perpetuate the view that the pentatonic scale is harmonically static and deficient in some way (Yu Wang 2020, para. 8). In this essay, I examine Chinese pentatonicism on its own terms, celebrating the richness and depth of Chinese music in its myriad forms. I explore how Western scale theory can shed light on foundational Chinese theory, how recent ideas in Western scale theory are implicit in centuries-old musical thought, and how a cross-cultural music theory operates in concept and practice.
Example 1.1. Transpositions between pentatonic structures in “Choiwan jeui yyut” 彩雲追月 (“Colorful Clouds Chasing the Moon”)
(click to enlarge and listen)
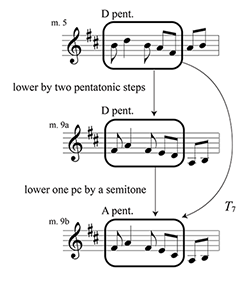
[1.3] Set to tango rhythms popular at the time, Ren Guang’s 任光 well-known tune “Choiwan jeui yyut”
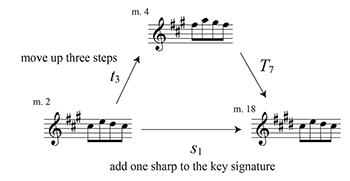
Example 1.2. “Choiwan jeui yyut,” motivic network with distinct versions of the syncopated motive (click to enlarge) | Example 1.3. Hook’s (2008, 139) analysis of Franz Schubert, “Valse sentimentale” D. 779, No. 13 (click to enlarge) |
[1.4] The three transformations in Example 1.2 belong to the group of xuangong transformations, and they are the pentatonic versions of Julian Hook’s (2008, 2023) diatonic signature transformations. For comparison, Example 1.3 shows a similar network of diatonic transformations in a waltz by Franz Schubert—moving up three steps, adding one sharp, and T7. In staff notation, diatonic transformations are more intuitive than pentatonic ones, since note names and key signatures naturally highlight diatonic relations. Tymoczko’s (2005, 2020, 2023) subsequent generalization of signature transformations to other scales promises wider application beyond the diatonic scale. Yet the way signature transformations manifest in music and music theory differs widely for each scale type. Xuangong theory is one such case. The following two sections will define xuangong transformations and how they intersect with Chinese music theory.
Part I. Theory
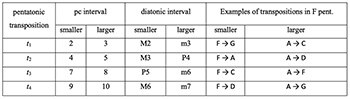
2. Chromatic and pentatonic transpositions
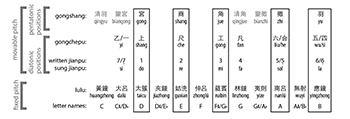
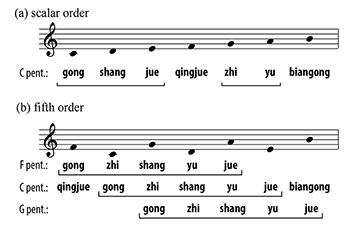
[2.1] Pentatonic xuangong transformations act on two elements recognized in ancient Chinese music theory (Example 2.1): twelve lülü 律呂, which are similar to pitch classes, and five pentatonic (scale-step) positions: gong 宮, shang 商, jue 角, zhi 徵, yu 羽 (Example 2.2a). By convention, position gong, the root or origin of fifth generation (Example 2.2b), represents the entire pentatonic set (yun 均) regardless of the mode (diao 調) or final (tou 頭). For example, the set DE
Example 2.1. Concordance of Chinese and Western note names in D pent., with C fixed to huangzhong by convention; common pianyin in grey (click to enlarge) | Example 2.2. D pent. in (a) scalar and (b) fifth orders (click to enlarge) |
[2.2] Formally, xuangong transformations act on a pentatonic pitch class, which is the ordered pair
(pcpent, posnote).
The first element, pcpent, is a mod-12 pc representing the pentatonic set by its gong.(4) For example, all notes in Example 2.2 belong to D pent., so all pcpent = 2 (assigning gong to D). The second element, posnote, is a pentatonic position.(5) Index numbers 0 to 4 (mod 5) represent positions gong to yu in step order. The two elements together describe the pentatonic context for each note, pcnote, which is not directly represented in the ordered pair. For example, (D, yu), or (2, 4), describes position yu in D pent., so the actual note is B. There are 60 different pentatonic pcs and as many xuangong transformations, discussed in detail below.
[2.3] Xuangong means “to rotate gong,” or for a lülü “to rotate as gong.” Liji 禮記 (Book of rites), supposedly compiled by Confucius (551–479 BCE), contains the earliest mention of xuangong (in its long form xuanxiang wei gong 還相為宮). In the Confucian cosmology of Liji, musical pitches exemplify nature’s cyclic and harmonious order:
Original |
Concise translation (mine) |
Expanded translation (Legge 1885, 382) |
|---|---|---|
五行、四時、十二月,還相為本也。 |
Five elements, four seasons, twelve months, rotate as the origin. |
The five elements in their movements alternately displace and exhaust one another. Each one of them, in the revolving course of the twelve months of the four seasons, comes to be in its turn the fundamental one for the time. |
五聲、六律、十二管,還相為宮也。 (Zheng 1980 [East Han], 1423) (6) |
Five notes, six lü, twelve pipes, rotate as position gong. |
The five notes of harmony, with their six upper musical accords, and the twelve pitch-tubes, come each, in their revolutions among themselves, to be the first note of the scale. |
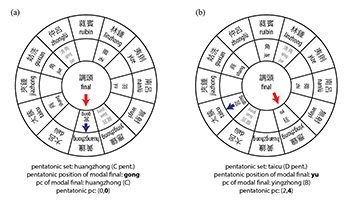
Example 2.3. Xuangong tone wheels at (0,0) and (2,4)
(click to enlarge)
[2.4] The cyclical idea was later realized as xuangong tone wheels in Yueshu yaolu 樂書要錄 (Yuan 2021 [ca. 680], 86) to describe modes in the abstract. My tone wheels in Example 2.3 have been substantially simplified. The two rings of the tone wheel correspond to the two elements of a pentatonic pitch class defined in [2.2]. The outer ring is the pitch-class clock face, the inner ring shows the five positions, and the gray labels show notes in one of the diatonic supersets (discussed in the next section). The arrows are my own addition. The blue arrow attached to gong affixes pentatonic positions in the inner ring to specific pcs/lülü in the outer ring. The red arrow in the middle locates the modal final within that pentatonic set. By default, tone wheels are set to huangzhong (C) and gong at 6 o’clock; see Example 2.3a. Example 2.3b shows position yu in D pent., (2, 4). The blue arrow points to taicu (D) and the red arrow points to yu, and the corresponding pc/lülü of yu is the modal final yingzhong (B). Below, I will examine transpositions that act on pcpent and posnote (each ring) individually and discuss examples in Chinese music where they perform structural roles. Then, I will discuss how the two transpositions interact.
[2.5] Xuangong transformations are structural to many genres. In guchuiyue 鼓吹樂—percussion-and-shawm music that accompanies funeral and temple rites (Li 1985; Jones 1995, 2007, 2010)—the chromatic transposition Tn takes on extraordinary significance.(7) Tn transposes pcpent by n semitones mod 12. The pentatonic position remains unchanged:
Tn(pcpent, posnote) = ((pcpent + n), posnote),
T12 = T0.
Example 2.4 and Audio Example 3. “Shuilong yin” 水龍吟 (“Water-dragon chant”) in bendiao 本調 (original key) and meihuadiao 梅花調 (plum blossom key)
(click to enlarge and listen)
Example 2.4 shows an excerpt of the qupai 曲牌 (fixed tune) called “Shuilong yin” 水龍吟 (“Water dragon chant”) played by the Hua 滑 family band from Yanggao, Shanxi province (Jones 2007, 91–99). The Hua family band plays the tune first in the home key, and then T10 transposes the home key into the plum blossom key.(8) (Poetic nomenclature like this is not uncommon.) A few things obscure the straightforward T10: improvised ornaments, non-pentatonic notes, and most importantly, octave shifts. The bell tone (lowest and loudest note) of the shawm is E, so at T10, players shift the resultant low D (and only that note) up an octave, creating large leaps and new melodic contours. Recognizing the qupai relies on one’s ability to identify invariant pentatonic positions under Tn.
[2.6] The pentatonic transposition tn transposes posnote by n steps modulo 5 without affecting pcpent:
tn(pcpent, posnote) = (pcpent, (posnote + n)),
t5 = t0.
In other words, tn describes transpositions inside the same pentatonic set.
Example 2.5 and Audio Example 4. “Guo jiang long” 過江龍 (“River-crossing dragon”), A and B section, incipits
(click to enlarge and listen)
[2.7] The pentatonic upper fifth, t3, is a structural transposition in several regional styles, including Cantonese opera, beiguan 北管, and Chaozhou zheng music. In Chaozhou zheng music, the qupai titled “Guo jiang long” 過江龍 (“River-crossing dragon”) alternates between zhengxian 正線 (home key) and fanxian 反線 (inverse key), which is t3 of the home key. The first note in Example 2.5 transposes like so:
t3(5, 3) = (5, (3 + 3)) = (5, 1).
Example 2.6. Correspondance of diatonic and pentatonic intervals in F pent.
(click to enlarge)
[2.8] In heptatonic notation, whether it is gongche notation 工尺譜, jianpu 簡譜 (localized Western solfège), or Western notation (see Example 2.1 above), pentatonic transformations are more challenging to identify than diatonic ones. Complexity arises from the fact that a given pentatonic interval can be one of two diatonic intervals; for example, one pentatonic step is 2 or 3 semitones, which could be a diatonic M2 or m3. In Example 2.5, all notes in the t3 of Guo jiang long move by a P5 except for A → F, which moves by a m6. The table in Example 2.6 lists all corresponding pentatonic and diatonic intervals in F pent.
Example 2.7. Duan Pingtai 段平泰, Course in Polyphonic Music (2013, 171), canon
(click to enlarge)
[2.9] In Chinese new music, tn can create rich contrapuntal relations. Duan Pingtai 段平泰 (2013, 171) teaches canons that imitate at pentatonic tn while adhering to diatonic harmony. In Example 2.7, Duan’s neo-Renaissance canon imitates at three pentatonic steps below (t–3 = t2), and it stays strictly within F pent. This canon is diatonically consonant every half note. But if the imitation were at T–7 instead of t–3, then the A in m. 4 would be
3. Bian- and qing-directed transformations
[3.1] The pentatonic scale shares properties with its complement, the diatonic scale (Clough et al. 1999,
Example 3.1. The central diatonic superset of a pentatonic scale in (a) scalar order and (b) fifth order
(click to enlarge)
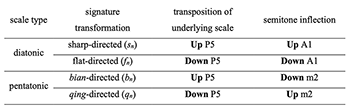
[3.2] Zhengyin 正音 refers to the proper pentatonic positions, and pianyin 偏音 refers to their semitone alterations. The pianyin prefix 變 bian (lit. change) lowers the position by one semitone; the opposite, 清qing (lit., clarity), raises the position by one semitone. Therefore, the C major diatonic set is gong, shang, jue, qingjue, zhi, yu, biangong (Example 3.1a), or, in letter names, C, D, E, E-qing, G, A, C-bian.(9) Biangong and qingjue are privileged pianyin, because they are adjacent to the zhengyin of C pent. in fifth order (Example 3.1b).
[3.3] Readers may encounter at least six definitions of bian in relation to xuangong.
Bian, in the most general sense: change or alteration (seen in Examples 3.3, 6.3, and 6.4).
Bianhuan lun 變換論 as the Chinese translation of Lewinian transformational theory.
Bianyin 變音 as an alternate to pianyin 偏音, encompassing semitone alterations of pentatonic positions in both directions.
Bian as a prefix to a pentatonic position (e.g., biangong), indicating its lowering by semitone.
bn as a generalized bian-directed transposition described below.
Hen 変 as a Japanese loanword from Chinese theory, the flat accidental in Western music.
Therefore, depending on the context, bian can mean alterations in general (definitions 1–3), or specifically a lowered semitone (definition 4). While the Chinese term for flat is simply “to lower” (jiang 降), in Japanese, the loanword hen (definition 6) also acts upon diatonic letter names.
Example 3.2. C pent. scale transformed by b1 and q1 via pivot notes biangong and qingjue
(click to enlarge)
[3.4] Example 3.2 illustrates bian- and qing-directed transformations adapted from Chinese theory. They operate on both elements of a pentatonic pitch class as defined in [2.2] above, that is, on (pcpent, posnote). The transformation labeled b1 refers to one specific bian: it lowers gong (posnote = 0) by a semitone to biangong and then reinterprets it as jue (posnote = 2) of the new scale. In Chinese, this move is shortened to “biangong as jue” 變宮為角.(10) Similarly, q1 is “qingjue as gong” 清角為宮, which raises qing (posnote = 2) to qingjue and then reinterprets it as gong (posnote = 0) of the new scale. The two transformations are inverses of each other:
biangong |
→ |
jue |
gong |
← |
qingjue |
Readers may appreciate a helpful memory aid here: “b” resembles a flat, and “q” is “b” upside-down.
As Example 3.2 shows, “biangong as jue” and “qingjue as gong” transpose both pcpent and posnote in a specific way. The note (C, gong), or (0, 0) is transformed like so:
b1(0, 0) = (7, 2),
q1(0, 0) = (5, 3).
[3.5] Generalizing this, the bian-directed transformation bn is the repeated application of “biangong as jue” n times.(11) The first element (pcpent + 7n) is calculated mod 12, and the second element (posnote + 2n) is calculated mod 5:
bn(pcpent, posnote) = ((pcpent + 7n) mod 12, (posnote + 2n) mod 5).
Likewise, the qing-directed transformation qn is the repeated application of “qingjue as gong” n times:
qn(pcpent, posnote) = ((pcpent + 5n) mod 12, (posnote + 3n) mod 5),
The inverse of bn is qn:
b1 = (q1)–1 = q–1,
q1 = (b1)–1 = b–1.
Sections below will explore a few important concepts in Chinese theory underpinned by q1.
Qupai variations
Example 3.3. “Lao liuban” 老六板 (“Old six beats”) and “Jinshe kuangwu” 金蛇狂舞 (“Wild dance of the golden snake”), arr. by Nie Er 聶耳, B sections
(click to enlarge and listen)
[3.6] “Baban” 八板 (“Eight beats”), an iconic qupai, has a bewildering assortment of titles and variations (Thrasher 1989, 73–82, 2016; Qian 1990, 9), and a notable subset of these variations are related by q±1.(12) Example 3.3 and Audio Example 5 compare two variants of “Baban”: “Lao liuban” 老六板 (“Old six beats”) and “Jinshe kuangwu” 金蛇狂舞 (“Wild dance of the golden snake”). The B section of “Jinshe” is largely q1 of “Lao liuban”. This variation technique is called gefan 隔凡 or bianfan 變凡 (skip or change fan), as q1 raises the gongche solfège from gong 工 to fan 凡 (the solfège equivalent of mi → fa).(13) Many pipa players are probably acquainted with this particular q1, since both versions are standard exam pieces (Central Conservatory of Music 2013). A similar q1 variation with rhythmic augmentation is known as “Fanwang gong” 梵王宮 (“Brahma’s palace” (Audio Example 6). The Buddhist title, meaning “Brahmā’s palace,” is a pun on “fan replaces gong” (fan wang gong凡忘工), or, in diatonic solfège, “fa replaces mi.”
Shawm fingering and qin tuning
Example 3.4. Terminology for shawm fingering (after Yang 1996; Li 2011)
(click to enlarge)
[3.7] In terminology for shawm fingering and qin tuning, bn and qn serve as pentatonic “key signatures” in the sense that they describe pentatonic sets as semitone alterations of an original set without specifying a tonic. In shawm termniology, jiezi 借字 (borrowed notes) describes the number and direction of semitone alterations from the shawm’s home key. The table in Example 3.4 shows terms adopted by musicians in Liaoning province (after Yang 1996; Lin 2011). Half-hole and fork fingerings limit the number of scales to seven, with three scales on either side.(14) On the qing-side, the term jie 借 counts the number of borrowed notes; on the bian-side, the term yashang 壓上 describes the successive lowering of the gongche position shang (the solfège equivalent of do).(15) For example, b2 of the home key (C pent.) is called “lower shang twice,” because the two alterations in D pent. are G →
Example 3.5. Common qin tunings
(click to enlarge)
[3.8] The standard tuning (zhengdiao 正調) of the qin’s seven strings are arranged in pentatonic steps (Example 3.5). A core subset of alternate tunings (waidiao 外調) are b±n of the standard tuning (Thompson n.d.a). In this context, man 慢 (loosen) and jin 緊 (tighten) are equivalents of bian and qing, respectively. While the naming schemes are not entirely consistent, each has its own logic. For example, manjuediao is b1 of the standard tuning. The name indicates that the new jue is a result of the loosened (man) gong, which is another way of saying “biangong as jue.” Each tuning is associated with tuning instructions that closely resemble a key signature, such as “loosen the third [string]” for manjuediao.
Piano etudes
[3.9] In Chinese new music, bian- and qing-directed transformations continue to be a vital compositional resource. In his children’s suite Yigong Variations (2000), for example, Li Yinghai
Example 3.6. Li Yinghai, Yigong Variations (2000), incipits (click to enlarge) | Example 3.7. (a) Li Yinghai, Wusheng yindiao gangqin zhifa lianxi 五聲音調鋼琴指法練習 (Pentatonic fingering exercises for piano) (click to enlarge) |
[3.10] In the exercise, the pianist arrives at T1 of the opening scale after five iterations of q1, therefore
q5 = T1 ; b5 = T11.
Similarly, after twelve iterations of q1, the pianist returns to C pent., one step higher (t1) than the original, consequently,
q12 = t1; b12 = t–1 = t4.
Li’s full exercise eventually iterates through all 60 modes, and it shows that b1 or q1 singularly generates all 60 transformations (including Tn and tn). The index numbers of qn and bn are calculated mod 60:
q60 = b60 = q0 = b0.
Example 3.8. Comparison of diatonic and pentatonic accidentals
(click to enlarge)
Example 3.9. Animated transposition of complementary diatonic and pentatonic sets
(click to view animation)
[3.11] While bian and qing are similar to changes in diatonic key signatures, I have avoided using Hook’s (2008) sharpwise (sn) and flatwise (fn) notation, since diatonic accidentals conflate the direction of fifth transposition and semitone inflection. For diatonic transformations, the key signature sharp is associated with congruent upward transposition: the underlying scale transposes up by P5 via an upward semitone inflection (Example 3.8). However, the pentatonic bn moves the underlying scale up a fifth by a downward semitone inflection, effectively disassociating directionality from accidentals. The contrast stems from the complementary relation of diatonic and pentatonic sets. Consider the complementary sets C dia. and
Example 3.10. “Choiwan jeui yyut,” motivic network, with annotations
(click to enlarge)
[3.12] I will conclude this section by revisiting “Choiwan jeui yyut”’s motivic network. The cumulative transformation in Example 3.10 can be written as t3b1 = T7. To verify this arithmetically, we can substitute each transformation with bn. Xuangong transformations commute; for example, t3b1 = b1t3. By formula [6] above, b1 = T7t2, so
b1t3 = T7t2t3 = T7.
By rearranging the equation above,
T7(b1)–1 = T7q1 = t3.
Readers may trace these pathways in Example 3.11, which shows all fifth transpositions of a C pent. scale. Example 3.12 expands the diagram to show all 60 forms of the C pent. scale.
Example 3.11. The fifth transpositions of a C pent. scale (click to enlarge) | Example 3.12. All 60 forms of the pentatonic scale (click to enlarge and see the rest) |
4. Historical terminology
[4.1] In the sections above, I have applied xuangong transformation to a wide range of musical structures, from melodic segments to entire pieces, and have extended conventional xuangong theory beyond its historical application to mode. As I explore below, contemporary scholars continue to work on foundational xuangong modal theory, and in this regard, my theory intersects with and sheds light on sustained debates on the labeling of modes, rotations, and modulations. To narrow the analytical object to modes only, rather than any kind of note, I will replace the symbols posnote and pcnote with posfinal and pcfinal, which denote the modal final as the analytical object in the subscript.
Labeling modes: weidiao/zhidiao 為調之調.
[4.2] Historically, pentatonic modes have been represented both as (pcpent, posfinal) or (pcfinal, posfinal).(18) Consider these two modes:
- for D, E, G, A, C, the pcpent is C, the pcfinal is D, and the posfinal is shang,
- for C, D, F, G,
B♭ , the pcpent isB♭ , the pcfinal is C, and the posfinal is shang.
In Song-era treatises, the mode label “C shang” could mean either of the two modes above, and the mixed use created a “confusion of modal terminology
- Wei 為, meaning “as,” disambiguates “C shang” as “C as shang” (huangzhong wei shang 黃鐘為商). This naming scheme corresponds to (pcfinal, posfinal) so that “C shang” refers to CDFG
B♭ . - Zhi 之, the possessive, disambiguates “C shang” as “shang of C pent” (huangzhong zhi shang 黃鐘之商). This naming scheme corresponds to (pcpent, posfinal) so that “C shang” refers to DEGAC.
[4.3] In the last century, Chinese scholars have standardized pentatonic mode labels with the weidiao system (pcfinal, posfinal), since these labels correspond to Western mode names like “C Dorian” (Chen 2002, 115). For instance, in “C shang,” C is the final. The present transformations, however, act upon zhidiao coordinates (pcpent, posfinal), since weidiao cannot directly account for pentatonic transformations (tn). The fact that one could label modes using weidiao coordinates and define transformations using zhidiao coordinates reflects the inherent richness of the system and the need for precise language.
Labeling rotations: zuo xuan/you xuan 左旋/右旋.
[4.4] One can describe a mode by tone-wheel rotations from its default (0, 0) state. Scholars have debated the precise meaning of historical terms related to rotation, such as “left,” “right,” “forward,” and “backward” (zuo xuan 左旋, you xuan 右旋, shun xuan 順旋, ni xuan 逆旋), respectively where ambiguity arises from different frames of references and the inherent flexibility of literary Chinese.(20) Much emphasis has been put on these terms as they define the very actions (xuan) of xuangong.(21)
[4.5] Following Huang (1993, 109–127), here is a basic interpretation. In Example 2.3, the outer ring of twelve lülü (or pc) is stationary, while the inner ring of pentatonic positions is movable. Huangzhong and gong are positioned at 6 o’clock by default. “Leftward” or “forward” rotation of the pentatonic ring corresponds to a zhidiao perspective. For the transformation C, D, E, G, A → B, D, E,
Labeling modulations: xuangong/fandiao 旋宮犯調.
[4.6] A debate erupted in the 2000s in an effort to clarify the meaning of two synonyms xuangong (rotating as gong) and fandiao (breaching the mode), both terms roughly meaning modulation (Chen 2002; Du 2003; Liu 2005; Qin 2006). In scholars’ efforts to unite overlapping terminology across millennia, the results are inevitably inconclusive. My own view aligns most closely with Qin Dexiang’s (2006) mathematically informed proposal:
- Tn is xuangong, since it changes pcpent, which is literally represented by gong;
- tn is fandiao, since it changes posfinal, which represents diao, the mode; bn (or qn) is xuangong fandiao, since it changes both pcpent and posnote.
The persisting ambiguity in labeling modes, rotations, and modulations illustrates the relational complexity at the heart of pentatonic transformations. While these issues may seem abstract, they concern foundational definitions of “xuan” and of modal relations.
Part II. Analysis
[5] Having set up the analytical tools, below, I examine five independent vignettes that demonstrate the breadth of music that engages with multiple pentatonic transformations on a structural level. I begin with transformations that complement form in a Cantopop song by Joseph Koo-Kar Fai and a character piece by Tan Dun. Then, I turn to the construction of mode cycles in Zhu Zaiyu’s treatise and in the oral tradition of Liaoning shawm bands. Lastly, I discuss Bright Sheng’s dissonant harmony generated by pentatonic transformations. Together, they paint a picture of transformations that unite music of vastly different types—historical and contemporary, regional and international, abstract and embodied, fantastical and practical, improvised and composed.
5. New Year Cantopop
Example 5.1 and Audio Example 7. Joseph Koo Kar-Fai 顧嘉煇 (music), James Wong Jim 黄霑 (lyrics), “Jukfuk nei” 祝福你 (“Bless you”) (1980)
(click to enlarge and listen)
[5.1] Xuangong transformations underpin one of the most famous Cantopop songs celebrating Lunar New Year, “Jukfuk nei” 祝福你 (“Bless you”), composed in 1980 by Joseph Koo Kar-Fai 顧嘉煇. Typical of Cantopop, the track combines the formal and harmonic structure of Western pop music with Cantonese instruments and melodic turns of phrase.
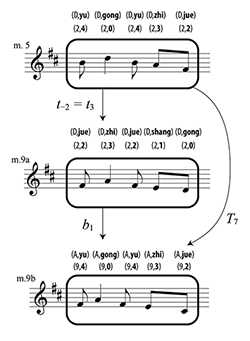
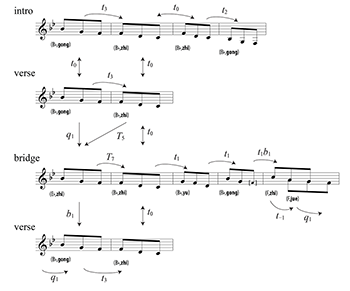
[5.2] “Jukfuk nei” is saturated with melodic xuangong transformations (Example 5.1 and Audio Example 7). The intro and verse are sentential parallel periods with the same harmonic structure: I–V in the antecedent and V–I in the consequent. The melodic variation between antecedents and consequents closely follows the harmony. The melody (mm. 1–3) in the antecedent transposes by t-2 from its tonic form
Example 5.2. Joseph Koo Kar-Fai, “Jukfuk nei,” motivic network
(click to enlarge)
[5.3] In comparison to the intro and verse, the bridge contains a larger variety of transformations that suggest a deeper motivic network. Example 5.2 connects the transformations in a single motivic network based on the opening “jukfuk nei“ hook (
[5.4] Pentatonic transformations go hand in hand with form and harmony in “Jukfuk nei”. Fifth-related t±2 underpins the intro and verse, while the tonally unstable bridge features q1, T±7, and a rapid succession of t1s. The enduring success of this song and the ubiquity of motivic transformations in it suggest it may be fruitful to explore the frequency and extent of these types of transformations in Cantopop.
6. A character piece
Example 6.1. Tan Dun 譚盾, “Eight Memories in Watercolor” (1978–79), Op. 1, “Staccato Beans,”
(click to enlarge)
[6.1] The examples so far have been melody-centric. In Tan Dun’s 譚盾 “Staccato Beans” from Eight Memories in Watercolor Op. 1 (1978–79), the most interesting xuangong transformations are in the harmony. The character piece for solo piano repeats a folk-like theme five times. Statements 1 and 3 of this theme have similar pentatonic Alberti-bass accompaniments, and phrases 2, 4, and 5 have a stepwise descending bass (Example 6.1). From phrase 1 to phrase 3, Tan transposes the melody and the final chord by a straightforward T5, moving from F pent. to
[6.2] In addition to T5, xuangong transformations provide other ways to move from F pent. to
DACA → (GDFD) →
[6.3] For phrase 2, Tan rearranges the Alberti bass in phrase 1 (D, A, C, A) into a half-note descent (D, C, A). In phrase 2, one can hear the full bass line as a t0 repetition of the D, C, A descent, or as note-by-note transpositions t–1, t–1, t2, t–1, t–1. The two are related; the cumulative t0 is equal to the first three note-by-note transpositions:
t0 = t–1t–1t2.
In phrase 4, this equation takes on more significance. Phrase 4 begins with the transposed and syncopated descent GFD (which is also doubled at t1 above), but it swaps the cumulative t0 for a T5, which momentarily brings the accompaniment into
T5 = t–1t–1t–1q1.
This sequence of events positions the last dyad at G
7. Confucian sequences
Xuangong pedagogy
[7.1] In his treatise Lülü jingyi 律呂精義 (Essence of tuning) (1596), Ming-dynasty prince Zhu Zaiyu 朱載堉 lavishly realizes xuangong theory through modal variations. While Zhu is known for the earliest calculation of twelve-tone equal temperament (xin fa mi lu 新法密率) (Rehding 2022, 260), his tuning theory was intertwined with modal theory through didactic qin etudes:
諸書雖載六十調八十四聲之說, 然有體無用,而初學難曉。今以琴發明則體用兼備,庶初學易曉也。 (1596, seq. 447) |
Although many texts describe the concept of 60 and 84 modes, they exist in theory only, not in practice, and they are difficult to understand for beginners. By contrast, the present use of the qin to expound modes combines theory and practice, so that modes may become easy to understand for beginners. |
[7.2] In the treatise, Zhu realizes pentatonic transformations primarily through “Nanfeng ge” 南風歌 (“Song of the southern wind”), which spans over a hundred pages in Lülü jingyi.(23)
Southern wind’s balm |
南風之薰兮 |
can soothe people’s anger. |
可以解吾民之慍兮 |
Southern wind’s timeliness |
南風之時兮 |
can enrich people’s wealth. |
可以阜吾民之財兮 |
|
According to legend, the song is composed by sage king Shun 舜 (ca. 2000 BCE). As Zhu points out:
舜彈五弦之琴,歌南風之詩,而天下治。 (Zhu 1596, seq. 546) |
Shun played the five-string qin, sang the poem of Southern Winds, and his realm was well governed. |
Example 7.1. Zhu Zaiyu 朱載堉, Lülü jingyi 律呂精義, Outer book 6 (1598, seq. 944), gongchepu short score of “Nanfeng ge” 南風歌)
(click to enlarge)
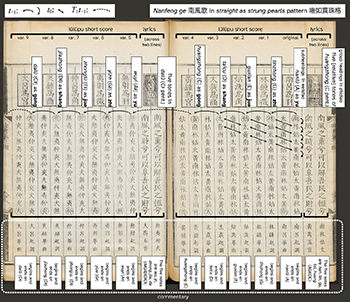
Weaving music theory and the Confucian ideal of moral governance, Zhu illustrates pentatonic transformations using the poem and the qin. Mimicking the style of Confucian state-ceremonial music (Lam 1998; Woo 2017), Zhu set “Nanfeng ge” to a looping pentatonic scale (Example 7.1).(25) In antiquarian court music played by a full orchestra and chorus, each syllabic note is extremely slow (5 bpm), equal in length, and elaborated by figurations. Songs also have explicit modal organization and melodic patterns associated with them (Lam 1998, 130–31).(26) A simple scale would not be out of place in this style. To illustrate aspects of qin tuning, Zhu only employs open strings.
Straight as strung pearls
[7.3] In the gongchepu version of “Nanfeng ge”, the diagonal invariants in Example 7.1 hint at internal symmetry. Six features characterize Zhu’s setting:
The entire song consists only of descending steps (t–1) in gongche notation:
A
工
gong (unrelated to gong 宮)
G
尺
che
E
一
yi
D
四
si
C
合
he
A
工
gong
⋮
⋮
⋮
Zhu labels this stepwise descent as the straight as strung pearls pattern (duan ru guanzhu ge 端如貫珠格), and he relates this to the Daoist idea of non-interference:
《樂記》曰:「大樂必易」,又曰「大樂與天地同和」,言其音調出於天生自然,不由人力編排,而累累乎端如貫珠,譬猶太羹玄酒,無味之中真味存焉。 (seq. 533) |
It is said in Book of music, ‘great music is simple,’ and ‘great music is in harmony with heaven and earth.’ They express how tones are self-so without human involvement, and so, when forming a sequence, tones in orderly succession are straight like strung pearls; like ceremonial sauce and wine, in no taste there exists true taste.(27) |
Example 7.2. Zhu Zaiyu. Lülü jingyi, Inner Book 6 (1598, seq. 534), first ten variations of “Nanfeng ge” in the straight as strung pearls pattern 端如貫珠格
(click to enlarge)
Each song begins and ends on the modal final.
Features 1 and 2 above constrain the poem’s length to 5n + 1 syllables. “Nanfeng ge” has (5⋅5) + 1 = 26 syllables.
The 5 + 8 = 13 poetic meter (dashed lines in Example 7.1) articulates a full t2 cycle (A, D, G, C, E, A), since (t–1)13 = t2. The cycle contains three P4s and one M3.
Each column transposes the song by t–1; five columns complete a modal cycle within the same set.
Features 1 and 5 explain the diagonal invariants. The score is a two-dimensional graph with the syllable-level t–1 on the y axis and the song-level t–1 on the x axis (Example 7.2). The diagonal invariants (t0) are the difference of the two axes.
As the six features show, Zhu enriches an otherwise ordinary t–1 with Daoist philosophy, melodic schemata, hierarchical sequences, modal cycles, and visual appeal.
Two ge 格
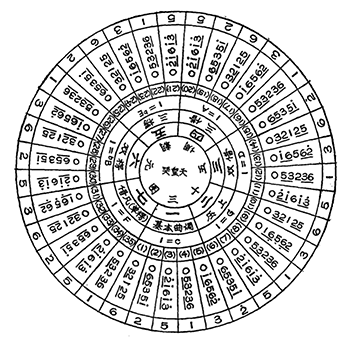
[7.4] In addition to the gongchepu in Example 7.1, Zhu iterates “Nanfeng ge” through all 60 modes in fully figurated qinpu (tablature) and lülüpu. The lülüpu score, based on the first character of each lülü, contains two different 60-mode cyclic patterns (ge 格) (Examples 7.2 and 7.3), and Zhu describes them like so:
右自南呂為羽,至於應鍾為宮,凡六十調,其名曰端如貫珠格。復自黃鍾之宮,至於林鍾之角,凡六十曲,其名曰循環無端格。此二格者,譬如先天八卦,橫圖縱圖,圓圖方圖,皆出於自然,非由人力也,學者宜詳味焉。中有難言之趣,當自得之耳。 (seq. 546) |
From nanlü as yu to yingzhong as gong, altogether 60 tones, they follow the pattern straight as strung pearls. From gong of huangzhong to jue of linzhong, altogether 60 tunes, they follow the pattern endless cycle. These two patterns—like the primordial eight trigrams, the horizontal and vertical diagrams, and the circular and square diagrams—are self-so without human involvement; scholars should investigate them in detail. Therein is indescribable delight; one must grasp it themselves. |
At the deepest hierarchical level, the two modulation patterns are metaphysical sequences connected to the Yi jing (I Ching) 易經. The modulating straight as strung pearls pattern doubly generates 60 modes by T1 and t–1. Example 7.2 shows the first spread of the mode cycle in lülüpu, of which the right side is identical to the gonchepu (Example 7.1), including the invariant diagonals. Each column transposes the song by t–1, and each page transposes the five columns by T1. The first page (right side of Example 7.2) shows “Nanfeng ge” in the five modes of huangzhong (C) pent., and the second page shows the five modes of dalu (
Example 7.3. Zhu Zaiyu. Lülü jingyi, Inner Book 6 (1598, seq. 540), first ten variations of “Nanfeng ge” in the endless cycle pattern
(click to enlarge)
[7.5] Elsewhere in Lülü jingyi, the endless cycle pattern (xunhuan wuduan ge 循環無端格) describes the equal-tempered lülü as a tone wheel, but as mode cycles, the term specifically describes the 60 modes singularly generated by q1. Example 7.3 shows the first two pages of the endless cycle pattern, and it highlights the changing note in each incipit. Each column transposes the song by q1, and each page transposes the five-cycle by q5 = T1.(28) The two cycles showcase the basic transformations tn, Tn, and qn. The straight as strung pearls pattern mirrors the pentatonic and chromatic rings of the xuangong tone wheel, and, like Hook’s signature transformations, the endless cycle pattern reveals the singular xuangong generator. Furthermore, Zhu fortifies pentatonic relations through rhetorical parallelism (dui-ou 對偶). He uses synonyms qu 曲 and diao 調 to refer to modal variants (“tune” and “tone” in my translation), and he pairs weidiao with the straight as strung pearls pattern (Example 7.2), and zhidiao with the endless cycle pattern (Example 7.3).
Qin tuning
Example 7.4. Qin tuning in Lülü jingyi reordered by b1 and T1 (Zhu’s original ordering in bold)
(click to enlarge)
[7.6] In “Nanfeng ge”, each change in pentatonic set necessitates retuning the qin.(29) In Lülü jingyi (seq. 450), Zhu expands common qin tunings (Example 3.5) to all 12 pentatonic sets (Example 7.4). In his diagrams, he orders qin tunings by T1 of the underlying pcpent, but they are actually generated by b±1 to maintain string tension, so each string varies by at most two semitones. Example 7.4 reorders Zhu’s tunings with b1 and T1 as the two axes.(30)
[7.7] As seen in the excerpts above, Zhu’s didactic ritual music is imbued with theoretical intent, and the degree to which Zhu luxuriates in transformations cannot be overstated. Confucian lyrics are set to music that recreates the legend of Shun’s harmonious rule. Sequences permeate all levels of “Nanfeng ge”, from syllable to poetic meter to mode cycles. In “combining theory and practice” (ti yong jianbei 體用兼備) (seq. 447), Zhu’s Confucian sequences affirm the complementary theories of xuangong transformation and equal temperament, allowing the qin to play in all 60 modes.
8. Funeral chaoyuan cycles
Example 8.1. “Ku huangtian” 哭皇天 (“Cry for heaven), from Li (1985, 93), original score in gongchepu by Zhang Hanchen 張漢臣 from Liaoyuan, Jilin province
(click to enlarge)
Example 8.2. Ku huangtian, five-key chaoyuan (each instance of the tune is abbreviated to its incipit and final)
(click to enlarge)
[8.1] Section 2 (Example 2.4) showcased a xuangong variation technique by Tn in guchuiyue. One can only imagine how difficult it is for a listener to follow a five-mode tn cycle (wu diao chaoyuan 五調朝元) or an expanded 35-mode cycle.(31) Countless instances of both cycles (chaoyuan) were meticulously transcribed in the volumes for Liaoning and Jilin province in the Anthology of Chinese Folk Instrumental Music 中國民族民間器樂曲集成 (Li et al. 1996, 2000). Often accelerating from extremely slow pulses—as slow as 3 bpm (Li et al. 1996, 61)—the cycles that were transcribed can easily last for over an hour (Yang 1996, 64–65). Transcriptions are plentiful, but unfortunately recordings remain rare, and the technique was thought to be extinct in the 2000s (Liu 2008, 28).
[8.2] Li Laizhang 李來璋 (1985; 1994) was one of the first to extensively theorize and transcribe these cycles. Example 8.1 shows “Ku huangtian” 哭皇天 (“Cry for heaven”) as it was played by Zhang Hanchen 張漢臣 from Liaoyuan, Jilin province (after Li 1985; 1994). Example 8.2 shows “Ku huangtian” repeated in a five-mode cycle, with each modal variant of “Ku huangtian” abbreviated to its incipit and final. The cycle here uses a pivot note technique, such that the last note of one modal variant becomes the first note of the new one (Li 1985). In other words, the chaoyuan tn is determined by the same tn between a tune’s first and last notes. Yet, as Li (1996, 63–65) and Lin (2011) demonstrate, the chaoyuan tn is cognized by shawm players as a minimally perturbed Tn , such that
- t1 = T2q2
- t2 = T5b1
- t3 = T7q1
- t4 = T10b2,
where, in general, t2n = q24n = T5nbn, and –2 ≤ n ≤ 2. For example, rather than thinking of t2 as transposing up two steps, musicians found it easier to imagine the T5 version and then apply b1 to it. According to this method, the first three notes of “Ku huangtian” at t2 would be cognized as E, D, C → (A, G, F) → A, G, E.
[8.3] Li (1994, 24) displays the thirty-five-mode cycle in a circular diagram (Example 8.3) using jianpu, which I have re-notated in staff notation (Example 8.4). To expand the five-mode chaoyuan to thirty-five modes, the last t2 is composed with a b1 to move to a new pentatonic set, forming the repeating block t2, t2, t2, t2, t2b1. Although this sequence would eventually exhaust all 60 forms of “Ku huangtian”, in practice, the diatonically tuned shawm can only fluently handle sets with up to three qing or three bian (see Example 3.4, line a above). After reaching the bian-most scale of A pent. in variation 20, players take a T6 shortcut to the qing-most scale of
Example 8.3. Ku huangtian, thirty-five-key chaoyuan cycle diagram by Li Laizhang 李來璋 (1985), notated in jianpu (incipit and final only) (click to enlarge) | Example 8.4. Ku huangtian, thirty-five-key chaoyuan cycle (incipit and final only) (click to enlarge) |
9. Xuangong × Viennese trichord
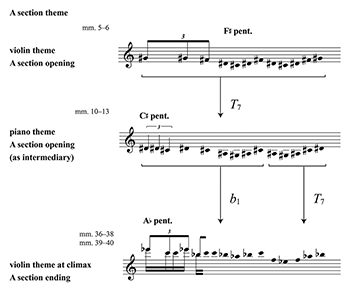
[9.1] Contemporary Chinese composers have seamlessly blended pentatonicism with modern dissonant idioms, such as serialism (Rao 2002), and have likewise integrated xuangong transformations to great effect. Chinese-American composer Bright Sheng is well known for his dissonant treatment of folk song influenced by Béla Bartók (Sheng 1998; Wong 2007). “Tibetan Air,” from Three Fantasies (2005) for violin and piano, features contrasting sets in the horizontal and vertical dimensions with the pentatonic set (02479) in the melody, and Viennese trichord (016) in the harmony. The violin and piano begin the movement with emphatic Viennese trichords and major sevenths (a subset of the trichord) in extreme registers. Then, with a dissonant accompaniment, the violin presents a long, spun-out pentatonic theme inspired by Tibetan folk song (Sheng n.d.).
[9.2] The entire movement is in ABA’ form, and my analysis will focus on transformations of the opening melody in the first two sections. Examples 9.1 to 9.2 briefly cover the A section, and Examples 9.2 to 9.5 describe the B section in greater detail. Sheng’s music has an irreducible complexity that pushes the current style of score annotation to its limit. From phrase to phrase, there are judicious additions and omissions of notes, lines with no clear segmentation, and seemingly familiar turns of phrase that are difficult to pinpoint. In the following examples, I have attempted to strike a balance between fidelity and clarity.
Example 9.1. Bright Sheng, Three Fantasies for violin and piano (2005), “Tibetan Air,” first and last presentations of the main theme in the A section with initial rhythm included for reference
(click to enlarge and listen)
[9.3] Transformations of the opening theme are dominated by simple fifth-based transpositions (Example 9.1). The violin starts with a melody in
Example 9.2. Bright Sheng, “Tibetan Air,” thematic link between A and B sections with initial rhythm included for reference
(click to enlarge)
[9.4] To link the A and B sections, the violin’s hushed B section reworks its A-section material by liberally omitting notes and by subtle b1 and b2 transpositions (Example 9.2). The violin plays the two versions back-to-back, so the linkage is relatively easy to hear.
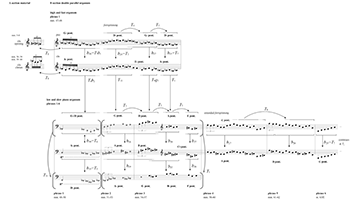
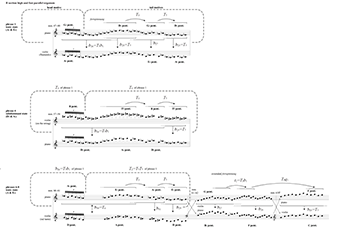
Example 9.3. Bright Sheng, “Tibetan Air,” B section double parallel organum: Phrase 1 of high/fast organum; phrases 1–6 of low/slow organum
(click to open PDF in new tab)
[9.5] The entire B section is a double parallel organum. The violin and piano play a high and fast two-voice organum (top of Example 9.3), and the piano also plays another low and slow three-voice organum (bottom of Example 9.3). (The lowest voice of the trio drops out mid-way.) The high and fast organum combines, in simultaneity, the violin parts that open and end the A section. Therefore, the opening parallel interval
[9.6] The high/fast organum continues into a fortspinnung (m. 48, top of Example 9.3)—to borrow a term from Baroque music—that develops the motive through various transformations. Horizontally, the melody transforms by T5, then T7. Vertically, the organum interval b26 teeters a bit, but it eventually settles on
[9.7] Phrase 2 of the low/slow organum (mm. 51–53, bottom of Example 9.3) varies the voicing of the (016) trichord. This time, the voicing (from top to bottom) sums to T1 rather than T11. Rather than voicing the chords with T6-then-T7 or T7-then-T6, Sheng’s composition yields b26-then-b29, transformations, which also sum to T1 (b26b29 = b55 = T1) and preserve the Viennese trichord. At the level of individual pcs, b26-then-b29 admits both T6-then-T7 and T7-then-T6 voicings. Compare, for example, the last two chords of phrase 2 (m. 53), which are, from top to bottom, G,
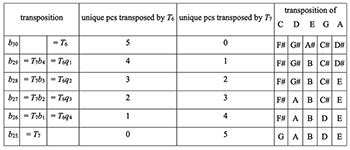
Example 9.4. The continuum from b30 to b25
(click to enlarge)
[9.8] From the observations above, a script for the organum interval emerges: it moves gradually from dissonance to consonance using the bn continuum from T6 = b30 to T7 = b25, which contain pc intervals that originate from (016). The table in Example 9.4 illustrates this process in greater detail. From b30 to b25, for each b–1 increment, one consonant T7 replaces one dissonant T6 until all intervals are consonant. In effect, xuangong transformations provide Sheng a finer gradation of transpositions between T6 and T7. The violin’s trajectory in the A section foreshadows this complex relation through the composition of fifth transpositions T7 and b1. While expressions such as b29, T7b4, and T6q1 may be mathematically equivalent, they suggest different experiential pathways. It is possible to hear the transformations all three ways, even as 29 successive bians. If the pianist playing Bright Sheng’s music had also studied Li Yinghai’s piano etudes (Example 3.7), they could be intimately familiar with the full cycle of 59 successive qings, and hear the 29 successive bians in that way.
Example 9.5. Bright Sheng, “Tibetan Air,” B section double parallel organum: Phrases 1, 4, and 6–8 of the high/fast organum Audio Example 9
(click to open PDF in new tab)
Audio Example 9. Bright Sheng, “Tibetan Air,” B section, Phrases 1, 4, and 6–8
[9.9] As the low/slow organum completes its dissonant-to-consonant trajectory spanning the entire B section, the high/fast organum completes this trajectory three times. The density of the organum forbids a complete representation here; Example 9.5 shows the tail end of the three trajectories (phrase 1, phrase 4, and phrases 6–8), where most of the action takes place. (Other phrases hover around b27 without resolving to b25 = T7.) The large dashed boxes in Example 9.5 show that the top voices of these phrases relate by some combination of fifth transposition. The top voice of phrase 4 is a verbatim T5 of phrase 1. And phrase 6 begins at b26 = T7b1 of phrase 1 (see Example 9.1 above), the same transformation governing the A-section violin trajectory and the opening organum interval.
[9.10] Each of the three trajectories in the high/fast organum have their own character (Example 9.5), but their Tn endings ensure both organum voices end with the jue-gong-shang tail motive. As discussed, Phrase 1 teeters around b26 before resolving to b25 = T7. Phrase 4 remains steadfast on b26, and it resolves to b25 = T7 only at the last minute. And, as a group, phrases 6–8 present the full, gradual shift from total dissonance to total consonance. Phrases 6–8 start at an easily audible b30 = T6, overshoots to b31, and gradually resolves to b25 = T7. The last stretch of this gradual shift (mm. 61–62) takes place over an extended fortspinnung that lengthens the tail motive by melodic transformations T5b±1 (bottom right of Example 9.5). The organum interval remains consonant until the A section returns as a stretto canon (m. 68, not shown).
[9.11] The networks above demonstrate the following:
Example 9.1: how the theme transposes by T7 and then b1 across the A section
Example 9.2: how the theme at T7b1 is reworked for the B section
Example 9.3: how the B section is structured as a double parallel organum, with the high/fast organum proceeding at a parallel T7b1 = b26 and the low/slow organum voiced as a Viennese trichord
Example 9.4: how the organum interval gradually shifts from the dissonant b30 = T6 to the consonant b25 = T7
The melodic dimension is defined by the pentatonic set, and the harmonic dimension is defined by the Viennese trichord, particularly its internal transpositions T6 and T7. The central transformation T7b1, containing both T7 and T6 of individual pcs, neatly captures the dynamic balance of dissonance and consonance.
10. Conclusion and my canons
[10.1] Xuangong transformation is subtly complex. For some, it guarantees “indescribable delight” (Zhu 1596, seq. 546), and for others, it creates unparalleled confusion (Pian 1967, 43; Liu 2005, 102). The goal of the present theory is to make the delights more describable and to clarify potential ambiguity, and it does so by providing precise language for pentatonic relations, and by connecting a rich variety of existing theories and analytical methods, old and new. The eclectic range of examples show the extent to which these transformations permeate Chinese culture, from New Year pop songs to rural funerals, from concert halls to court rituals, and from ancient cosmology to modern-day counterpoint. Similar 5-in-12 pentatonic structures exist in French impressionism, jazz improvisation (Ricker 1983), and guitar pedagogy (Kolb 2014), all of which are rich avenues for further study. I also write in the hope that xuangong may inspire new musical compositions.
Audio Example 10. Secret Symmetries, I
Audio Example 11. Secret Symmetries, II
Audio Example 12. Secret Symmetries, III
Audio Example 13. Secret Symmetries, IV
Audio Example 14. Secret Symmetries, V
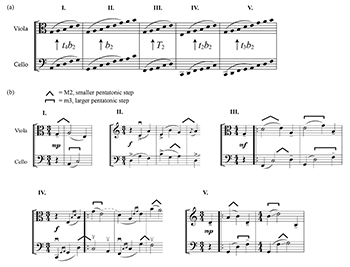
[10.2] My own musical offering, Secret Symmetries, movements I–V (2017) (Example 10.1), extend Duan Pingtai’s tn canon to a set of tnb2 canons at all five ns. My canons superimpose two pentatonic sets a M2 apart, whose union is the diatonic set (Example 10.2a). Movements II and III are privileged in that they consist of straightforward transformations t0b2 and t1b2 = T2, respectively. The central motive is a pentatonic step that varies in its intervallic size (m3/M2) and combinations of these sizes (Example 10.2b). For example, the t4b2 of mvt. I transforms the cello’s opening M2 into the violin’s m3. By comparison, in mvt. III, both parts begin with M2 and m3 in succession, and the T2 imitation ensures that the imitation never changes the specific interval size. The quarter-note delay further obscures the canon, encouraging repeated and engaged listening to fully hear the xuangong relations within.
Example 10.1. Nathan Lam, Secret Symmetries (2017) Audio Examples 10–14 (click to open PDF in new tab) | Example 10.2. Nathan Lam, Secret Symmetries (2017), (a) transposition scheme and (b) excerpts of pentatonic step motive (click to enlarge) |
Nathan L. Lam
林禮信
Eastman School of Music
26 Gibbs St.
Rochester NY 14604
nlam@esm.rochester.edu
Works Cited
Central Conservatory of Music 中央音樂學院. 2013. Zhongyang yinyue xueyuan hai neiwai kaoji qumu: pipa 中央音樂學院海內外考級曲目:琵琶 [Central Conservatory of Music domestic and international exam pieces: pipa]. Edited by Lin Shicheng 林石城. 中央音樂學院出版社 Central Conservatory of Music Press.
Chen Yingshi 陳應時. 2002. Yi zhong tixi liang ge xitong 一種體系 兩個系統 [One structure two systems]. 中國音樂學 Musicology in China 2002 (4): 109–16.
—————. 2004. Zhongguo yuelu xue tanwei 中國樂律學探微 [A study of Chinese musicology]. Shanghai Music Publishing House.
Clough, John, Nora Engebretsen, and John Kochavi. 1999. “Scales, Sets, and Interval Cycles: A Taxonomy.” Music Theory Spectrum 21 (1): 74–104. https://doi.org/10.2307/745921.
Ding Chengyun 丁承運. 1987. “Zhu zaiyu qin lu yanjiu 朱載堉琴律研究 [The study of Zhu Zaiyu’s qin tuning].” Yiyuan 藝苑 1987 (1).
Du Yaxiong 杜亞雄. 2003. “‘Xuangong,’ ‘fandiao’ zhi wo jian ‘旋宮, ‘犯調’ 之我見 [My view of ‘xuangong’ and ’fandiao’]. 中國音樂學 Musicology in China 2003 (3): 133–37.
—————. 2019. “Cujin chuantong yueli xiang zuoqu shijian de zhuanhua” 促進傳統樂理向作曲實踐的轉化 [Promoting the transformation of traditional music theory to compositional practice].” Yinyue wenhua yanjiu 音樂文化研究 2019 (2): 48–53.
Du Yaxiong 杜亞雄 and Qin Dexiang 秦德祥. 2007. Zhongguo yueli 中國樂理 [Chinese music theory]. 上海音樂學院出版社 Shanghai Conservatory of Music Press.
Duan Pingtai 段平泰. 2013. Fudiao yinyue jiaocheng 複調音樂教程 [Course in polyphonic music]. Vol. 2. 中央音樂學院出版社 Central Conservatory of Music Press.
Fan Zuyin 樊祖蔭. 2013. Zhongguo wushengxing diaoshi hesheng xiezuo jiaocheng 中國五聲性調式和聲寫作教程 [Composition course in Chinese pentatonic modal harmony]. 人民音乐出版社 People’s Music Publishing House.
Guo Shuqun 郭樹群. 1993. Lun Zhu zaiyu de xuangong sixiang 論朱載堉的旋宮思想 [On Zhu Zaiyu’s concept of xuangong]. Yinyue yanjiu 音樂研究 1993 (3): 46–55.
Hayashi Kenzō 林 謙三. 1936. Sui Tang yanyuediao yanjiu 隋唐燕樂調研究 [A study on yanyue tonality in the Sui and Tang dynasties]. 商務印書館 The Commercial Press.
Hook, Julian. 2008. “Signature Transformations.” In Music Theory and Mathematics: Chords, Collections, and Transformations, ed. Jack Douthett, Martha M. Hyde, and Charles J. Smith, 137–60. University of Rochester Press. https://doi.org/10.1017/9781580467476.008.
—————. 2023. Exploring Musical Spaces. Oxford University Press. https://doi.org/10.1093/oso/9780190246013.001.0001.
Huang Xiangpeng 黃翔鵬. 1993. Suliu tanyuan: Zhongguo chuantong yinyue yanjiu 溯流探源 :中國傳統音樂研究 [Tracing the stream to its source: studies of traditional Chinese music]. 人民音乐出版社 People’s Music Publishing House.
Jones, Stephen. 1995. Folk Music of China: Living Instrumental Traditions. Oxford University Press.
—————. 2007. Ritual and Music of North China: Shawm Bands in Shanxi. Routledge.
—————. 2010. “Living Early Composition: An Appreciation of Chinese Shawm Melody.” In Analysing East Asian Music: Patterns of Rhythm and Melody, ed. Simon Mills. Semar.
—————. 2017. “Walking Shrill: Shawm Bands in China.” Stephen Jones: A Blog, March 14, 2017. https://stephenjones.blog/2017/03/14/walking-shrill-shawm-bands-in-china/
Kolb, Tom. 2014. Connecting Pentatonic Patterns: The Essential Guide for All Guitarists. Hal Leonard.
Lam, Joseph Sui Ching. 1998. State Sacrifices and Music in Ming China: Orthodoxy, Creativity, and Expressiveness. State University of New York Press.
Lam, Nathan L. 2019. “Relative Diatonic Modality in Extended Common-Practice Music.” PhD diss., Indiana University. https://scholarworks.iu.edu/dspace/handle/2022/24636.
—————. 2020. “Modal Spelled Pitch Class, La-Minor Solfège, and Schubert’s Third Relations.” Journal of Music Theory 64 (2): 241–81. https://doi.org/10.1215/00222909-8550795.
Lee, Gavin. 2020. “Global Sonic Genealogy of the Pentatonic Scale.” Paper presented at the Annual Meeting of the Society for Music Theory, November. Virtual.
Legge, James, trans. 1885. The Lî Kî, I-X. The Sacred Books of China: The Texts of Confucianism, Part III. Clarendon. http://archive.org/details/sacredbooksofchi3conf.
Li Laizhang 李來璋. 1985. “Wudiaochaoyuan 五調朝元 [Five-mode cycle].” Yinyue Yanjiu 音樂研究 1985 (4): 93–101.
—————. 1994. “Dongbei guchuiyue yanjiu 東北鼓吹樂研究 [A study on Northeastern shawm and percussion music].” Jilin wenshi chuiban she 吉林文史出版社.
Li Ling 李凌, et al., ed. 1996. Zhongguo minzu minjian qiyue qu jicheng 中國民族民間器樂曲集成 [Anthology of Chinese folk instrumental music]. Liaoning Volume 遼寧卷. Zhongguo ISBN zhongxin 中國ISBN中心.
—————, ed. 2000. Zhongguo minzu minjian qiyue qu jicheng中國民族民間器樂曲集成 [Anthology of Chinese folk instrumental music]. Jilin Volume 吉林卷. Zhongguo ISBN zhongxin 中國ISBN中心.
Li Yinghai 黎英海. 2002 [1964]. Wusheng yindiao gangqin zhifa lianxi 五聲音調鋼琴指法練習 [Pentatonic fingering exercises for piano]. 人民音樂出版社 People’s Music Publishing House.
Lin Lin 林林. 2011. Wu diao chaoyuan, sanshiwu diao chaoyuan jiemei 五調朝元、三十五調朝元解昧 [Five-mode cycle, thirty-five-mode cycle explained]. Zhongguo Yinyuexue wang 中國音樂學網. Accessed February 2, 2022. https://musicology.cn/papers/papers_7129.html.
Liu Beini 劉貝妮. 2013. ‘Xuangong fangshi’ yanjiu zongshu ‘旋宮方式’ 研究綜述 [A critical survey of the ‘xuangong method’]. Xinghai yinyue xueyuan xuebao 星海音樂學院學報 Journal of Xinghai Conservatory of Music 133: 92–100.
Liu Yongfu 劉永福. 2005. Yi ge xitong liang ge cengci —個系統 兩個層次 [One system two layers]. 中央音樂學院學報 Journal of the Central Conservatory of Music 2005 (3): 102–6.
—————. 2008. “Jiezi tanze ‘借字’探賾’[Exploring ‘jiezi’].” Jiaoxiang 交響 27 (3): 28–30.
Pian, Rulan Chao 卞趙如蘭. 1967. Sonq Dynasty Musical Sources and Their Interpretation. Harvard University Press. https://doi.org/10.4159/harvard.9780674368675.
Qian Renkang 錢仁康. 1990. “’Lao baban’ yuanliu kao” «老八板» 源流攷 [A study on the origin of ‘Old Baban’]. Yinyue yishu 音樂藝術 1990 (2): 9–23.
Qin Dexiang 秦德祥. 2006. Zhongguo chuantong yinyue de ‘diaoxing secai bianhuan shoufa’ 中國傳統音樂的 ‘調性色彩變換手法’ [‘Modal color transformation techniques’ in Chinese traditional music].” 音樂藝術 The Art of Music 3 (2006): 58–67.
Rao, Nancy Yunwha. 2002. “Hearing Pentatonicism Through Serialism: Integrating Different Traditions in Chinese Contemporary Music.” Perspectives of New Music 40 (2): 190–231.
Rehding, Alexander. 2022. “Fine-Tuning a Global History of Music Theory: Divergences, Zhu Zaiyu, and Music-Theoretical Instruments.” Music Theory Spectrum 44 (2): 260–275. https://doi.org/10.1093/mts/mtac004
Ricker, Ramon. 1983. Pentatonic Scales for Jazz Improvisation. Van Nuys, Alfred Music.
Roeder, John. 2020. “Interactions of Folk Melody and Transformational (Dis)continuities in Chen Yi’s Ba Ban (1999).” Music Theory Online 26 (3). https://doi.org/10.30535/mto.26.3.12.
Sheng, Bright 盛宗亮. 1998. Batuoke yu xiandai zhongguo yinyue 巴托克與現代中國音樂 [Bartók and modern Chinese music]. 音乐艺术 The Art of Music 1998 (4): 55–56.
—————. n.d. “Three Fantasies.” Bright Sheng (website). Accessed February 2, 2022. http://www.brightsheng.com/programnotes/Three%20Fantasies.html.
Thompson, John 唐世璋. n.d.a. “Tuning a Qin.” John Thompson on the Guqin Silk String Zither. Accessed February 4, 2022. http://silkqin.com/08anal/tuning.htm.
—————. n.d.b. “Nan Feng Ge.” John Thompson on the Guqin Silk String Zither. Accessed February 4, 2022. http://www.silkqin.com/02qnpu/10tgyy/tg01nfg.htm.
Thrasher, Alan R. 1989. “Structural Continuity in Chinese Sizhu: The ‘Baban’ Model.” Asian Music 20 (2): 67–106. https://doi.org/10.2307/834021.
—————. 2016. “Baban, Instrumental Ideal and the Classic Repertoire.” In Qupai in Chinese Music: Melodic Models in Form and Practice. Routledge.
Tymoczko, Dmitri. 2005. “Voice Leadings as Generalized Key Signatures.” Music Theory Online 11 (4). https://www.mtosmt.org/issues/mto.05.11.4/mto.05.11.4.tymoczko.pdf.
—————. 2013. “Geometry and the Quest for Theoretical Generality.” Journal of Mathematics and Music 7 (2): 127–33. https://doi.org/10.1080/17459737.2013.818724.
—————. 2020. “Why Topology?” Journal of Mathematics and Music 14 (2): 114–69. https://doi.org/10.1080/17459737.2020.1799563.
—————. 2023. Tonality: An Owner’s Manual. Oxford University Press.
Wang Yueqing, Bao Qinggang, and Guan Guoxing. 2020. History of Chinese Philosophy Through Its Key Terms. Springer. https://doi.org/10.1007/978-981-15-2572-8.
Wong Hoi-Yan. 2007. “Bartók’s Influence on Chinese New Music in the Post-Cultural Revolution Era.” Studia Musicologica 48 (1–2): 237–43. https://doi.org/10.1556/smus.48.2007.1-2.16.
Woo Shingkwan 胡成筠. 2017. “The Ceremonial Music of Zhu Zaiyu 朱載堉的禮樂.” PhD diss., Rutgers University.
Yang Jiusheng 楊久盛. 1996. Guyue 鼓樂 [Shawm and percussion music]. In Zhongguo minzu minjian qiyue qu jicheng中國民族民間器樂曲集成 [Anthology of Chinese folk instrumental music], ed. Li Ling 李凌. Liaoning Volume 遼寧卷. Zhongguo ISBN zhongxin 中國ISBN中心.
Yu Wang, Anna. 2020. “Teaching the Cultural Commitments of Musical Structures and Their Theories.” Engaging Students: Essays in Music Pedagogy 8. https://doi.org/10.18061/es.v8i0.7736.
Yuan Wanqing 元萬頃. ca. 680. Yueshu yaolu 樂書要錄 [Key Points from the treatises of music]. https://archive.org/details/02074356.cn/page/n86/mode/2up.
Yuan Wanqing 元萬頃. 2021 [ca. 680]. “What Pentatonicism? – Key Points from the Treatises on Music (c. 680), Chapter 5:2 ‘The method for the mutual generation of the seven sheng’ and 5:3 ‘On how to understand the two bian notes.’” Translated by Hu Zhuqing S. 胡渚清. From the Reed Ashes Pavilion. 2021. https://chinesemusicsources.com/2021/05/20/what-pentatonicism-key-points-from-the-treatises-on-music-c-680-chapter-52-the-method-for-the-mutual-generation-of-the-seven-sheng-and-53-on-how-to-understand-the-two-bian-notes/.
Zheng Xuan 鄭玄, ed. 1980 [East Han]. Liji zhengyi 禮記正義 [Corrected interpretations of the Book of rites] Lower Volume. In Shisan jing zhushu 十十三經注疏 [Notes and commentaries to the thirteen Confucian classics] No. 22. 中華書局 Zhonghua Book Company.
Zhu Zaiyu 朱載堉. 1596. “Lülü jingyi 律呂精義 [Essence of tuning].” In Yuelu quanshu 樂律全書 [Comprehensive compendium on music]. https://nrs.harvard.edu/urn-3:FHCL:3744719 Accessed 19 January 2022.
Discography
Discography
Koo Kar-Fai, Joseph 顧嘉煇, and James Wong Jim 黃霑. 1993. Zhufu ni 祝福你. On Huana qunxing hesui jinqu xi shang jia xi 華納群星賀歲金曲 喜上加喜 [Warner Music Group all-star new year compilation: Double the happiness]. Warner Music Group 4509-91918-2.
Lam, Nathan. 2019. Secret Symmetries. Christa Cole and Richard Liu.
Ren Guang 任光. 2002. Caiyun zhui yue 彩雲追月 [Colorful clouds chasing the moon]. On Hu Meiyi yuediao mingqu 胡美儀粵調名曲 [Amy Wu: Famous Cantonese Tunes]. Fung hang 風行 2043. https://www.youtube.com/watch?v=pLoaeBBMkso.
Sheng, Bright 盛宗亮. 2009. Three Fantasies. On Bright Sheng: Spring Dreams. André-Michel Schub and Cho-Liang Lin. Naxos 8.570601.
Traditional. 1971. Guo jiang long 過江龍 [River-crossing dragon]. On Zhonguo guo yue daquan 中國國樂大全 [The complete Chinese classical music records]. Vol. 6 (LP). Four Seas Records 四海唱片.https://www.youtube.com/watch?v=g5X6Tm0Ihlk https://dl.lib.ntu.edu.tw/s/4seas/item/629300.
—————. 2003. Jinshe Kuangwu 金蛇狂舞 [Wild dance of the golden snake], Lao liu ban 老六板 [Old six beats]. On Pipa jingdian mingqu wushi shou 琵琶經典名曲五十首 [Fifty Pipa Classics] (VCD). Yang Jing 楊靖. Huanqiu yinxiang 環球音像.
—————. 2004. Shuilong yin [Chant of the water dragon]. On Walking Shrill: The Hua Family Shawm Band. PAN 2109.
—————. 2006. Fanwang gong 梵王宮 [Brahma’s temple]. On Yanyu, meng, Jiangnan 煙雨、夢、江南 [Misty rain, dreams, Jiangnan]. DVD and CD. Lu Chunling 陸春齡, Zhou Hui 周惠, Ma Shenglong 馬聖龍, Zhou Hao 周皓. Bai li changpian 百利唱片. https://www.youtube.com/watch?v=uCg_HQyLHXY.
Footnotes
1. All terms are romanized using Mandarin Hanyu Pinyin. The exceptions are Cantopop song titles, which are represented using Yale Romanization. Unless otherwise noted, all translations are my own.
Return to text
2. “Choiwan jeui yyut” is also known as “Jidu hua luo shi” 幾度花落時 (“When the flowers fall”) and “Hong chen” 紅塵 (“Fleeting world”) in popular music.
Return to text
3. In some styles, like yifan mode, fan is tuned sharper and yi lower.
Return to text
4. I have adapted the ordered-pair nomenclature I introduced for diatonic pitch classes in Lam 2020.
Return to text
5. Pentatonic positions here are analogous to diatonic positions in Lam (2019, 2020).
Return to text
6. The characters for xuan, 還 and 旋, are interchangeable in this context. “Six lü” refers to the whole-tone scale.
Return to text
7. I follow Jones (2017) in distinguishing the term shawm and suona for similar instruments. The former refers to the instrument rooted in oral traditions and traditional ceremonies, where it has different regional names such as weirwa, wazi, or laba. The latter is more commonly associated with conservatories and urbanized settings (Jones 2017).
Return to text
8. Shuilong yin is the only qupai that the Hua family band transpose regularly.
Return to text
9. Gong 工 in gongchepu (diatonic mi) and gong 宮 as a pentatonic position are unrelated.
Return to text
10. See Fan (2013, 117–27), for example.
Return to text
11. The bian- and qing-directed transformations can be heard as repeated voice-leading schemas (Tymoczko 2020, 119; 2005).
Return to text
12. Gong 工 in gongchepu (diatonic mi) and gong 宮 as a pentatonic position are unrelated. Readers of the present journal may be familiar with Chen Yi’s atonal variation of “Baban” (Roeder 2020).
Return to text
13. The homonyms fan 反 in fanxian and fan 凡 in bianfan are unrelated. Contrary to bian 變 in biangong 變宮, which is the lowering prefix (definition 4), bian 變 in bianfan 變凡 means “to change” (definition 1 in section 3.3), and it raises fan by semitone. See Du and Qin (2007, 200–233) for further discussion of terminology.
Return to text
14. Shawm playing varies from region to region, and so does its terminology (Jones 2007), so these terms are not universal.
Return to text
15. The gongche syllable shang is unrelated to the pentatonic position shang.
Return to text
16. Yigong 移宮 (moving gong) is another term for xuangong.
Return to text
17. “一、養成用鄰指彈奏小三度‘五聲式級進’的習慣,使隔指及鄰指都能應用。 二、熟悉鍵盤上各調及各調式的音階及一般音調” (Li 2002, i).
Return to text
18. Any two of the pentatonic elements pcfinal, pcpent, posfinal imply the remaining third.
Return to text
19. In Pian 1967, zhidiao weidiao appears as jy diaw wei diaw in the short-lived Gwoyeu Romatzyh romanization. Song appears as Sonq.
Return to text
20. Liu 2013 compares different perspectives on the history of terms relating to xuangong, including prominent interpretations by Huang (1993) and Chen (2004).
Return to text
21. For example, rotating the central arrow clockwise is the same as rotating the two rings counterclockwise, the directions “left” and “right” are ambiguous on the clockface, the relative direction might change if huangzhong and gong are placed on top or viewed upside-down.
Return to text
22. In a network similar to Examples 1.2 and 3.10, in Example 5.2, the arrows connecting the verse and the bridge show that t3T5 = q1.
Return to text
23. Note the perfect rhythm achieved through the exclamatory article xi 兮 that ends each line.
Return to text
24. Punctuation mine. Zhu is citing the “Book of music” in Records of the grand historian (史記-樂書) by Sima Qian 司馬遷 (ca. 100 BCE). Sections of it are nearly identical to the “Book of music” in Book of rites (禮記-樂記). The poem “Nanfeng ge” is purportedly authored by Shun, and it has inspired numerous musical works (Thompson n.d.b).
Return to text
25. See Woo 2017 (128) for the full score.
Return to text
26. Woo (2017, 154) estimates the tempo to be 5 bpm, or 12 seconds per beat, based on the prescribed choreography.
Return to text
27. Ziran 自然 here means “self-so” in the Daoist sense (Wang 2020, 233–41). Its meaning in modern Chinese, “natural,” is not exactly the same.
Return to text
28. Below each variation in Example 7.3, Zhu describes each semitone change as “bian,” from “one bian” up to “five bian”, that links one page to the next. Here, bian refers to the more general meaning, change, and each bian represents a q1 rather than b1.
Return to text
29. For a detailed discussion of Zhu’s qin tuning and related aspects of xuangong, see Guo (1993) and Ding (1987). Zhu’s huangzhong is tuned near E2 (Guo 1993).
Return to text
30. See Woo (2017, 261ff.) for additional commentary. Lülü jingyi Inner Book 7 continues with diatonic qin tuning.
Return to text
31. A seven-mode diatonic cycle also exists (Yang 1996, 65).
Return to text
32. Lin 2011, accessible online at https://musicology.cn/papers/papers_7129.html, provides transcribed examples for each tn.
Return to text
Copyright Statement
Copyright © 2024 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Andrew Eason, Senior Editorial Assistant
Number of visits:
15988